Coupled Multicomponent First Multiplicative Bogoyavlensky Lattice and Its Multisoliton Solutions

Abstract

This study addresses the complete integrability of a generalized multicomponent version of the first multiplicative Bogoyavlensky lattice with branched dispersion. The analysis is performed using the Hirota bilinear formalism and the periodic reduction technique. Initially, a two-dimensional mB1 lattice is considered, for which complete integrability is established by constructing its bilinear form and general multisoliton solutions via the Hirota bilinear formalism. A periodic reduction along the discrete independent variable is then applied to derive the coupled multicomponent mB1 lattice, along with its corresponding bilinear representation and multisoliton solutions. The resulting system serves as an integrable semi-discrete generalization of the classical Volterra-type equation. These findings contribute to the broader understanding of integrable lattice systems with branched dispersion relations and provide a constructive framework for obtaining explicit soliton solutions in multicomponent systems, which exhibit rich internal symmetry structures.

1. Introduction

Since the 1970s, Volterra-type systems, originally introduced by Hirota and Satsuma [1,2,3], have been intensively studied and continue to attract significant interest from various perspectives [4,5,6]. In the real world, the Volterra equations and their generalizations are of great importance, as the coupled Volterra equations are essential for modeling population dynamics. One notable direction involves their integrable extensions, commonly referred to in the literature as the Bogoyavlensky lattices [7,8,9]. These lattices constitute a class of integrable semi-discrete systems that generalize the classical Volterra lattice and emerge from discretizations of continuous integrable hierarchies such as the KdV [10,11]. These systems have been rigorously analyzed through Lax pair formulations [12,13,14] and Hamiltonian frameworks [15,16], including bi-Hamiltonian structures [17,18], master symmetries [19] and algebro-geometric solution perspective [20,21,22]. Subsequent efforts have extended these studies to multicomponent and multidimensional settings, including symmetry-based reductions from ${\mathbb{Z}}_N$-graded Lax pairs to Bogoyavlensky-type equations [23]. More recent research has pursued bilinear reformulations via Hirota’s method, periodic reductions, and the explicit construction of multisoliton solutions, highlighting the rich soliton dynamics and flexibility inherent in models with branched dispersion relations. Recently, four models of Bogoyavlensky lattices were analyzed in [24,25] using singularity analysis and Hirota’s bilinear method: the additive Bogoyavlensky lattice (aB), the first multiplicative Bogoyavlensky lattice (mB1), the second multiplicative Bogoyavlensky lattice (mB2) and the third multiplicative Bogoyavlensky lattice (B3).

In this paper, we build upon this work by focusing on the first multiplicative Bogoyavlensky lattice (mB1), extending it to a multicomponent system consisting of M coupled equations with branched dispersion relations. A similar approach was performed in [26] for the additive Bogoyavlensky lattice (aB), where a special case, which is also a particular case of coupled mB1 lattice, known as the coupled Lotka–Volterra system, was analyzed.

To establish the complete integrability of the coupled mB1 lattice, we use the well-known Hirota bilinear formalism [27] and the periodic reduction technique [28,29]. To verify the complete integrability of the system in Hirota’s framework, it is necessary to construct at least its three-soliton solution. We approach the problem via the Hirota method, as it is the most direct and optimized approach. Although very useful, the Lax pair method is rather complex, whereas the $g^{\prime }/g$ and $tanh$ methods mainly work for continuous systems.

To be more explicit, in the framework of Hirota’s direct method, the three-soliton condition (or three-soliton test) [30,31,32] serves as a fundamental criterion for determining the integrability of nonlinear evolution equations. The method is based on constructing exact multisoliton solutions through a bilinear representation of the analyzed equations.

After expressing the nonlinear equation in Hirota’s bilinear form, one seeks solutions in the form of exponential functions characterized by parameters corresponding to the soliton wave numbers and frequencies. The one-soliton and two-soliton solutions can generally be obtained for a broad class of nonlinear equations, whether integrable or not. However, the existence of a three-soliton solution is a much more restrictive property, as it reflects the ability to superpose three solitons while preserving their individual identities.

This three-soliton condition ensures that the nonlinear interactions among solitons are consistent with the principle of elastic scattering, a hallmark of integrable systems. Therefore, if a bilinear equation admits a consistent three-soliton solution (without imposing additional constraints on the parameters beyond those arising from the dispersion relation), the equation is considered integrable in the sense of Hirota.

Because it is obviously easier to construct the multisolitons for an equation than for a coupled system, the starting point of our analysis is a two-dimensional integrable mB1 lattice which can be extended into a coupled integrable form via the periodic reduction.

A fundamental aspect of these coupled systems is the phase structure of the individual components, which are characterized by the M-th roots of unity. Additionally, the presence of a branched dispersion relation enhances the flexibility of soliton interactions.

The paper has the following structure: after these introductory notes, Section 2 presents a generalization of the first multiplicative Bogoyavlensky model to a multicomponent (matrix) setting. More precisely, we discuss a coupled multicomponent semidiscrete first multiplicative Bogoyavlensky system and one particular case for which we build the Hirota bilinear form and the multisoliton solutions. Section 3 explores a two-dimensional first multiplicative Bogoyavlensky equation, defined on a lattice with two discrete independent variables. Using the Hirota bilinear formalism, the bilinear form is constructed and the multisolitons are derived, proving the complete integrability of the 2D-mB1. In Section 4 we demonstrate how the coupled mB1 lattice, together with the bilinear form and the multisolitons, can be directly derived from the 2D lattice and we plot the soliton solutions for some particular cases of the multicomponent mB1 lattice. Section 5 concludes with a summary of the main results.

2. The Coupled Multicomponent mB1 Lattice

Introduced by Bogoyavlensky in [33,34,35], the Bogoyavlensky lattices are nonlinear differential–difference systems that are continuous in time and discrete in space. Because of their rich mathematical structure and their integrable properties, these lattices have been approached from different points of view: Lax representation, Hamiltonian structure, conserved quantities, master symmetry, etc. But, to our knowledge, very little investigation has been made for coupled Bogoyavlensky lattices [22]. In the only article found on the subject, the authors develop the trigonal curve idea, analyzing asymptotic behaviors of the Baker–Akhierzer functions, and giving the algebro-geometric solutions for the coupled Bogoyavlensky lattices associated with a 3 × 3 matrix spectral problem.

We analyze the coupled multicomponent first multiplicative Bogoyavlensky lattice with branched dispersion from a different perspective and using different methods. The system under discussion has the compact form:

$${\displaystyle \frac{d}{dt}}Q(n,t)=Q(n,t)\left(\prod _{j=1}^N{E}_{{\sigma }_j}Q(n+j,t)E_{{\sigma }_{-j}}-\prod _{j=1}^N{E}_{{\sigma }_{-j}}Q(n-j,t)E_{{\sigma }_j}\right),$$

(1)

where $Q(n,t)$ is a diagonal matrix of complex functions $u_{\nu }(n,t)$, $\nu =\overline{1,M}$ (t denotes the continuous time variable, and n the discrete spatial variable with a step size equal to 1):

$$Q(n,t)=\left(\begin{array}{ccccc}{u}_1(n,t)& 0& 0& \dots & 0\\ 0& u_2(n,t)& 0& \dots & 0\\ 0& 0& u_3(n,t)& \dots & 0\\ \dots & \dots & \dots & \dots & \dots & \\ 0& 0& 0& \dots & u_M(n,t)\end{array}\right)$$

and $E_{{\sigma }_j}$ and $E_{{\sigma }_{-j}}$ are permutation matrices corresponding to the following permutations:

$${\sigma }_j=\left(\begin{array}{cccc}1& 2& \dots & M\\ 1+j& 2+j& \dots & M+j\end{array}\right),$$

$${\sigma }_{-j}=\left(\begin{array}{ccccc}1& 2& \dots & \dots & M\\ 1-j& 2-j& 3-j& \dots & M-j\end{array}\right),$$

where $\{n\pm j\mid n=1,2,\dots ,M\mid j=1,2,\dots ,N\}\subseteq \{1,2,\dots ,M\}$ because of the M- periodicity.

For example, in case of $M=2$, $N=2$, the permutations involved and the corresponding permutation matrices are:

$${\sigma }_1=\left(\begin{array}{cc}1& 2\\ 2& 1\end{array}\right)={\sigma }_{-1},{\sigma }_2=\left(\begin{array}{cc}1& 2\\ 1& 2\end{array}\right)={\sigma }_{-2},$$

$$E_{{\sigma }_1}=\left(\begin{array}{cc}0& 1\\ 1& 0\end{array}\right)=E_{{\sigma }_{-1}},E_{{\sigma }_2}=\left(\begin{array}{cc}1& 0\\ 0& 1\end{array}\right)=E_{{\sigma }_{-2}}.$$

For brevity, we must introduce the notations:

$$u_{\nu }(n+1,t)=\stackrel{\left(1\right)}{\overline{u_{\nu }}},u_{\nu }(n+2,t)=\stackrel{\left(2\right)}{\overline{u_{\nu }}},u_{\nu }(n+N,t)=\stackrel{\left(N\right)}{\overline{u_{\nu }}},\nu =\overline{1,M},$$

$$u_{\nu }(n-1,t)=\underset{\left(1\right)}{\underline{u_{\nu }}},u_{\nu }(n-2,t)=\underset{\left(2\right)}{\underline{u_{\nu }}},u_{\nu }(n-N,t)=\underset{\left(N\right)}{\underline{u_{\nu }}}.$$

Performing the products in this particular case and introducing the result in system (1) together with

$${\displaystyle \frac{d}{dt}}Q(n,t)=\left(\begin{array}{cc}\frac{d}{dt}{u}_1& 0\\ 0& \frac{d}{dt}{u}_2\end{array}\right),Q(n,t)=\left(\begin{array}{cc}{u}_1& 0\\ 0& u_2\end{array}\right),$$

we obtain

$$\left(\begin{array}{cc}\frac{d}{dt}{u}_1& 0\\ 0& \frac{d}{dt}{u}_2\end{array}\right)=\left(\begin{array}{cc}{u}_1& 0\\ 0& u_2\end{array}\right)\left(\begin{array}{cc}\stackrel{\left(1\right)}{\overline{u_2}}·\stackrel{\left(2\right)}{\overline{u_1}}-\underset{\left(1\right)}{\underline{u_2}}·\underset{\left(2\right)}{\underline{u_1}}& 0\\ 0& \stackrel{\left(1\right)}{\overline{u_1}}·\stackrel{\left(2\right)}{\overline{u_2}}-\underset{\left(1\right)}{\underline{u_1}}·\underset{\left(2\right)}{\underline{u_2}}\end{array}\right),$$

which can be written on components as

$$\begin{array}{ccc}\hfill {\displaystyle \frac{d}{dt}}{u}_1& =& u_1\left(\stackrel{\left(1\right)}{\overline{u_2}}·\stackrel{\left(2\right)}{\overline{u_1}}-\underset{\left(1\right)}{\underline{u_2}}·\underset{\left(2\right)}{\underline{u_1}}\right)\hfill \\ \hfill {\displaystyle \frac{d}{dt}}{u}_2& =& u_2\left(\stackrel{\left(1\right)}{\overline{u_1}}·\stackrel{\left(2\right)}{\overline{u_2}}-\underset{\left(1\right)}{\underline{u_1}}·\underset{\left(2\right)}{\underline{u_2}}\right).\hfill \end{array}$$

In the general case, so for any M and N, on components, system (1) admits the form

$$\begin{array}{ccc}\hfill {\displaystyle \frac{d}{dt}}{u}_1& =& u_1\left(\stackrel{\left(1\right)}{\overline{u_2}}·\stackrel{\left(2\right)}{\overline{u_3}}·\dots ·\stackrel{\left(N\right)}{\overline{u_{N+1}}}-\underset{\left(1\right)}{\underline{u_M}}·\underset{\left(2\right)}{\underline{u_{M-1}}}·\dots ·\underset{\left(N\right)}{\underline{u_{M-N+1}}}\right)\hfill \\ \hfill {\displaystyle \frac{d}{dt}}{u}_2& =& u_2\left(\stackrel{\left(1\right)}{\overline{u_3}}·\stackrel{\left(2\right)}{\overline{u_4}}·\dots ·\stackrel{\left(N\right)}{\overline{u_{N+2}}}-\underset{\left(1\right)}{\underline{u_1}}·\underset{\left(2\right)}{\underline{u_M}}·\dots ·\underset{\left(N\right)}{\underline{u_{M-N+2}}}\right)\hfill \\ \hfill \dots & =& \dots \dots \dots \dots \dots \hfill \\ \hfill {\displaystyle \frac{d}{dt}}{u}_{M-1}& =& u_{M-1}\left(\stackrel{\left(1\right)}{\overline{u_M}}·\stackrel{\left(2\right)}{\overline{u_1}}·\dots ·\stackrel{\left(N\right)}{\overline{u_{M+N-1}}}-\underset{\left(1\right)}{\underline{u_{M-2}}}·\underset{\left(2\right)}{\underline{u_{M-3}}}·\dots ·\underset{\left(N\right)}{\underline{u_{M-N-1}}}\right)\hfill \\ \hfill {\displaystyle \frac{d}{dt}}{u}_M& =& u_M\left(\stackrel{\left(1\right)}{\overline{u_1}}·\stackrel{\left(2\right)}{\overline{u_2}}·\dots ·\stackrel{\left(N\right)}{\overline{u_{M+N}}}-\underset{\left(1\right)}{\underline{u_{M-1}}}·\underset{\left(2\right)}{\underline{u_{M-2}}}·\dots ·\underset{\left(N\right)}{\underline{u_{M-N}}}\right).\hfill \end{array}$$

(2)

In a very compact manner, system (2) can be expressed as

$${\displaystyle \frac{d}{dt}}{u}_{\nu }=u_{\nu }\left(\prod _{j=1}^N\stackrel{\left(j\right)}{\overline{u_{\nu +j}}}-\prod _{j=1}^N\underset{\left(j\right)}{\underline{u_{\nu +M-j}}}\right),\nu =\overline{1,M}.$$

(3)

For clarity, we must mention that functions $u_{\nu }$, with $\nu =\overline{1,M}$, exhibit a M-periodicity, in the sense that $u_{M+1}=u_1,u_0=u_M,u_{-1}=u_{M-1}$. Considering the above compact form of coupled mB1 lattice in Equation (3), several well-known particular cases emerge straightforwardly.

For example, in case $M=1$, all $u_{\nu }$ in Equation (3) reduce to $u_1$, and (3) turns into the mB1 lattice solved via singularity analysis and Hirota bilinear formalism in [24]

$${\displaystyle \frac{d}{dt}}{u}_1=u_1\left(\prod _{j=1}^N\stackrel{\left(j\right)}{\overline{u_1}}-\prod _{j=1}^N\underset{\left(j\right)}{\underline{u_1}}\right).$$

(4)

Considering $N=1$, it is obviously from (4) that system (3) reduces to the well-known Lotka–Volterra [6]:

$${\displaystyle \frac{d}{dt}}{u}_1=u_1(\stackrel{\left(1\right)}{\overline{u_1}}-\underset{\left(1\right)}{\underline{u_1}}).$$

The well-known coupled semidiscrete Lotka–Volterra system [36] is a particular case of system (2) and can be obtained considering any M and $N=1$. On the components, the system has the following compact expression:

$${\displaystyle \frac{d}{dt}}{u}_{\nu }=u_1(\stackrel{\left(1\right)}{\overline{u_{\nu +1}}}-\underset{\left(1\right)}{\underline{u_{\nu +M-1}}}),\nu =\overline{1,M}$$

which was solved via the Hirota bilinear formalism in [26].

In order to prove complete integrability for the general case of coupled multicomponent mB1 lattice (2) for any M, there are a variety of established criteria and mathematical techniques that can be used. A standard proof of complete integrability for a partial discrete equation involves demonstrating the presence of an infinite number of independent integrals in involution, which can be obtained from the associated Lax pair [37]. Various other criteria and analytical methods have been widely employed in the literature to examine the integrability of nonlinear systems, such as complexity growth, singularity confinement, consistency around the cube, Lie symmetry approach [38], and auxiliary equation technique [39]. For constrained systems and gauge theories, the Becchi–Rouet–Stora–Tyutin (BRST) formalism [40] is also applicable. Instead of employing the traditional approaches for integrability, we adopt the Hirota bilinear formalism, which necessitates the existence of a general multisoliton solution. Specifically, the demonstration of complete integrability within the Hirota framework involves constructing solutions that represent multiple interactions among an arbitrary number of solitons, each characterized by arbitrary parameters and phases, and also taking into consideration all the branches that appear possible for the dispersion relations.

Particular Case of Coupled Multicomponent mB1 Lattice

We first discuss a particular case of coupled multicomponent mB1 lattice. Considering any M, but $N=2$, system (2) can be expressed on the components as

$$\begin{array}{ccc}\hfill {\displaystyle \frac{d}{dt}}{u}_1& =& u_1(\stackrel{\left(1\right)}{\overline{u_2}}·\stackrel{\left(2\right)}{\overline{u_3}}-\underset{\left(1\right)}{\underline{u_M}}·\underset{\left(2\right)}{\underline{u_{M-1}}})\hfill \\ \hfill {\displaystyle \frac{d}{dt}}{u}_2& =& u_2(\stackrel{\left(1\right)}{\overline{u_3}}·\stackrel{\left(2\right)}{\overline{u_4}}-\underset{\left(1\right)}{\underline{u_1}}·\underset{\left(M\right)}{\underline{u_{M-1}}})\hfill \\ & \dots & \hfill \\ \hfill {\displaystyle \frac{d}{dt}}{u}_{M-1}& =& u_{M-1}(\stackrel{\left(1\right)}{\overline{u_M}}·\stackrel{\left(2\right)}{\overline{u_1}}-\underset{\left(1\right)}{\underline{u_{M-2}}}·\underset{\left(2\right)}{\underline{u_{M-3}}})\hfill \\ \hfill {\displaystyle \frac{d}{dt}}{u}_M& =& u_M(\stackrel{\left(1\right)}{\overline{u_1}}·\stackrel{\left(2\right)}{\overline{u_2}}-\underset{\left(1\right)}{\underline{u_{M-1}}}·\underset{\left(2\right)}{\underline{u_{M-2}}}).\hfill \end{array}$$

(5)

The nonlinear substitution, involving the complex tau function $F_{\nu }(n,t)$ depending on two variables, one discrete (n) and one continuous (t),

$$u_{\nu }(n,t)={\displaystyle \frac{\stackrel{\left(2\right)}{\overline{F_{\nu }}}·\underset{\left(2\right)}{\underline{F_{\nu }}}}{\stackrel{\left(1\right)}{\overline{F_{\nu }}}·\underset{\left(1\right)}{\underline{F_{\nu }}}}},\nu =\overline{1,M},$$

where $F_{\nu }=F_{\nu }(n,t),\stackrel{\left(1\right)}{\overline{F_{\nu }}}=F_{\nu }(n+1,t),\stackrel{\left(2\right)}{\overline{F_{\nu }}}=F_{\nu }(n+2,t),\underset{\left(2\right)}{\underline{F_{\nu }}}=F_{\nu }(n-2,t),$ leads us the Hirota bilinear form of system (5):

$${\mathbf{D}}_{\mathbf{t}}\stackrel{\left(1\right)}{\overline{F_{\nu +1}}}•F_{\nu }+\stackrel{\left(1\right)}{\overline{F_{\nu +1}}}·F_{\nu }=\stackrel{\left(3\right)}{\overline{F_{\nu +3}}}·\underset{\left(2\right)}{\underline{F_{\nu -2}}},$$

(6)

where $D_t$ is the Hirota bilinear operator [27] defined as

$$D_t^{n}a\left(t\right)•b\left(t\right)={({\partial }_t-{\partial }_{t^{\prime }})}^{n}a\left(t\right)·b\left(t^{\prime }\right){|}_{t=t^{\prime }}.$$

In order to build the one-soliton solutions (1-ss) for coupled mB1 system (5), we consider the ansatz

$$F_{\nu }=1+{ϵ}_1^{\nu -1}{e}^{{\eta }_1},\nu =\overline{1,M},$$

where ${ϵ}_1$ is any of the M-th roots of unity, ${ϵ}_1\in \left\{e^{l\frac{2\pi i}{M}}\right\},l=\overline{1,M}$, and the phase has the form ${\eta }_1=k_{1}n+{\omega }_{1}t+{\eta }_1^{\left(0\right)}$ ($k_1$ is the wave number, ${\omega }_1$ is the angular frequency, and ${\eta }_1^{\left(0\right)}$ is an arbitrary phase).

Introducing the bilinear form (6) in a software like Wolfram Mathematica 10.1, and considering the above anzats for the one-soliton solution, we find the dispersion with M possible branches of dispersion for the soliton because it is parametrized by ${ϵ}_1$ which has M possible values:

$${\omega }_1=2{\displaystyle \frac{sinh(k_1+ln{ϵ}_1)sinh\frac{3(k_1+ln{ϵ}_1)}{2}}{sinh\frac{k_1+ln{ϵ}_1}{2}}}.$$

For the 2-ss we consider the following form for the tau function $F_{\nu }(n,t)$:

$$F_{\nu }=1+{ϵ}_1^{\nu -1}{e}^{{\eta }_1}+{ϵ}_2^{\nu -1}{e}^{{\eta }_2}+{ϵ}_1^{\nu -1}{ϵ}_2^{\nu -1}{e}^{{\eta }_1+{\eta }_2+A_{12}},\nu =\overline{1,M},$$

where ${\eta }_j=k_{j}n+{\omega }_{j}t+{\eta }_j^{\left(0\right)},j=\overline{1,2}$ and Mathematica 10.1 returns the interaction term ($i=1$, $j=2$):

$$e^{A_{ij}}={\displaystyle \frac{-cosh\frac{k_i-k_j+ln\frac{{ϵ}_i}{{ϵ}_j}}{2}+cosh\frac{7(k_i-k_j+ln\frac{{ϵ}_i}{{ϵ}_j})}{2}-({\omega }_i-{\omega }_j)sinh\frac{k_i-k_j+ln\frac{{ϵ}_i}{{ϵ}_j}}{2}}{cosh\frac{k_i+k_j+ln{ϵ}_i{ϵ}_j}{2}-cosh\frac{7(k_i+k_j+ln{ϵ}_i{ϵ}_j)}{2}+({\omega }_i+{\omega }_j)sinh\frac{k_i+k_j+ln{ϵ}_i{ϵ}_j}{2}}},$$

(7)

with M possible branches of dispersion for each of the two solitons:

$${\omega }_j=2{\displaystyle \frac{sinh(k_j+ln{ϵ}_j)sinh\frac{3(k_j+ln{ϵ}_j)}{2}}{sinh\frac{k_j+ln{ϵ}_j}{2}}},{ϵ}_j\in \left\{e^{l\frac{2\pi i}{M}}\right\},l=\overline{1,M},j=\overline{1,2}.$$

(8)

For the three-soliton solution, we use as an anzats

$$\begin{array}{c}\hfill F_{\nu }=1+{ϵ}_1^{\nu -1}{e}^{{\eta }_1}+{ϵ}_2^{\nu -1}{e}^{{\eta }_2}+{ϵ}_3^{\nu -1}{e}^{{\eta }_3}+{\left({ϵ}_1{ϵ}_2\right)}^{\nu -1}{e}^{{\eta }_1+{\eta }_2+A_{12}}+{\left({ϵ}_1{ϵ}_3\right)}^{\nu -1}{e}^{{\eta }_1+{\eta }_3+A_{13}}+\\ \hfill +{\left({ϵ}_2{ϵ}_3\right)}^{\nu -1}{e}^{{\eta }_2+{\eta }_3+A_{23}}+{\left({ϵ}_1{ϵ}_2{ϵ}_3\right)}^{\nu -1}{e}^{{\displaystyle \sum _{i=1}^3}{\eta }_i+{\displaystyle \sum _{1\le i<j}^3}{A}_{ij}},\end{array}$$

and the software returns the same forms for the phase factors and dispersion relations as before. The existence of the three-soliton solution, as mentioned in the Introduction section, is a strong integrability criterion. We can already state that the coupled mB1 system for $N=2$ is an integrable one because it satisfies the three-soliton condition [32].

Once we have the three-soliton solution, we can generalize it to an N-soliton solution via the induction method as in [4]. The $\mathcal{N}$-soliton solution for (5) has the general expressions for $F_{\nu }(n,t)$, $(\nu =\overline{1,M})$

$$F_{\nu }(n,t)=\sum _{{\mu }_1,..,{\mu }_{\mathcal{N}}=\{0,1\}}exp\left(\sum _{i=1}^{\mathcal{N}}{\mu }_i[{\eta }_i+(\nu -1)ln\left({ϵ}_i\right)]+\sum _{1\le i<j}^{\mathcal{N}}{\mu }_i{\mu }_j{A}_{ij}\right),$$

(9)

where ${\eta }_j=k_{j}n+{\omega }_{j}t+{\eta }_j^{\left(0\right)}$, $j=\overline{1,\mathcal{N}},$ and the interaction term has the same form as in (7), with the M branches of dispersion for each of the $\mathcal{N}$ solitons as in (8). The existence of the multisoliton solutions for system (5) proves its complete integrability in Hirota formalism.

3. The mB1 2D Lattice

To analyze and solve the coupled multicomponent mB1 lattice (1), where the function $Q(n,t)$, depends only on one discrete variable, the analysis can be initiated from the mB1 2D lattice, which is nothing but the mB1 lattice with an extra discrete variable, m, that will play an essential role in the periodic reduction. Assuming that $Q(n,m,t)$ is periodic only in the m direction and enforcing a periodic reduction along this coordinate in the 2D lattice,

$$\begin{array}{c}\hfill {\displaystyle \frac{d}{dt}}Q(n,m,t)=Q(n,m,t)\left(\prod _{j=1}^{N}Q(n+j,m+j,t)-\prod _{j=1}^{N}Q(n-j,m-j,t)\right),\end{array}$$

(10)

we derive coupled multicomponent systems associated with the mB1 lattice. The procedure is detailed in Section 4. But first we have to prove the complete integrability of the 2D lattice using the Hirota bilinear formalism.

3.1. The Hirota Bilinear Form for mB1 2D Lattice

For brevity, we must introduce the following notations for the up shifts and down shifts on n or m of the tau function $F(n,m,t)$ ($F_m$ for brevity):

$$F(n+\mu ,m+\mu ,t)=\stackrel{\left(\mu \right)}{\overline{F_{m+\mu }}},F(n-\mu ,m-\mu ,t)=\underset{\left(\mu \right)}{\underline{F_{m-\mu }}},F(n,m,t)=F_m.$$

Case N-odd, $N=2\mu +1$

By applying the bilinear substitution,

$$Q(n,m,t)={\displaystyle \frac{\stackrel{(\mu +2)}{\overline{F_{m+\mu +2}}}·\underset{(\mu +1)}{\underline{F_{m-\mu -1}}}}{\stackrel{(\mu +1)}{\overline{F_{m+\mu +1}}}·\underset{\left(\mu \right)}{\underline{F_{m-\mu }}}}},$$

(11)

it follows directly that

$$\prod _{j=1}^{N}Q(n+j,m+j,t)={\displaystyle \frac{\stackrel{(3\mu +3)}{\overline{F_{m+3\mu +3}}}·\underset{\left(\mu \right)}{\underline{F_{m-\mu }}}}{\stackrel{(\mu +1)}{\overline{F_{m+\mu +1}}}·\stackrel{(\mu +2)}{\overline{F_{m+\mu +2}}}}},\prod _{j=1}^{N}Q(n-j,m-j,t)={\displaystyle \frac{\stackrel{(\mu +1)}{\overline{F_{m+\mu +1}}}·\underset{(3\mu +2)}{\underline{F_{m-3\mu -2}}}}{\underset{(\mu +1)}{\underline{F_{m-\mu -1}}}·\underset{\left(\mu \right)}{\underline{F_{m-\mu }}}}}.$$

The right-hand side (RHS) and the left-hand side (LHS) of Equation (10) become

$$RHS={\displaystyle \frac{{\left(\underset{\left(\mu \right)}{\underline{F_{m-\mu }}}\right)}^2·\underset{(\mu +1)}{\underline{F_{m-\mu -1}}}·\stackrel{(3\mu +3)}{\overline{F_{m+3\mu +3}}}-\underset{(3\mu +2)}{\underline{F_{m-3\mu -2}}}·{\left(\stackrel{(\mu +1)}{\overline{F_{m+\mu +1}}}\right)}^2·\stackrel{(\mu +2)}{\overline{F_{m+\mu +2}}}}{{\left(\stackrel{(\mu +1)}{\overline{F_{m+\mu +1}}}\right)}^2·{\left(\underset{\left(\mu \right)}{\underline{F_{m-\mu }}}\right)}^2}},$$

$$LHS={\displaystyle \frac{-\underset{\left(\mu \right)}{\underline{F_{m-\mu }}}·\underset{(\mu +1)}{\underline{F_{m-\mu -1}}}\left({\mathbf{D}}_{\mathbf{t}}\stackrel{(\mu +2)}{\overline{F_{m+\mu +2}}}•\stackrel{(\mu +1)}{\overline{F_{m+\mu +1}}}\right)+\stackrel{(\mu +1)}{\overline{F_{m+\mu +1}}}·\stackrel{(\mu +2)}{\overline{F_{m+\mu +2}}}\left({\mathbf{D}}_{\mathbf{t}}\underset{(\mu +1)}{\underline{F_{m-\mu -1}}}•\underset{\left(\mu \right)}{\underline{F_{m-\mu }}}\right)}{{\left(\stackrel{(\mu +1)}{\overline{F_{m+\mu +1}}}\right)}^2·{\left(\underset{\left(\mu \right)}{\underline{F_{m-\mu }}}\right)}^2}}.$$

Introducing the results in Equation (10), we find a quadrilateral expression that we can decouple into the two following bilinear forms that must hold true simultaneously:

$$\underset{(\mu +1)}{\underline{F_{m-\mu -1}}}·\underset{\left(\mu \right)}{\underline{F_{m-\mu }}}=\stackrel{(\mu +1)}{\overline{F_{m+\mu +1}}}·\underset{(3\mu +2)}{\underline{F_{m-3\mu -2}}}+{\mathbf{D}}_{\mathbf{t}}\underset{(\mu +1)}{\underline{F_{m-\mu -1}}}•\underset{\left(\mu \right)}{\underline{F_{m-\mu }}},$$

(12)

$$\stackrel{(\mu +1)}{\overline{F_{m+\mu +1}}}·\stackrel{(\mu +2)}{\overline{F_{m+\mu +2}}}=\underset{\left(\mu \right)}{\underline{F_{m-\mu }}}·\stackrel{(3\mu +3)}{\overline{F_{m+3\mu +3}}}+{\mathbf{D}}_{\mathbf{t}}\stackrel{(\mu +1)}{\overline{F_{m+\mu +1}}}•\stackrel{(\mu +2)}{\overline{F_{m+\mu +2}}}.$$

(13)

We notice that Equation (13) is the up shift of Equation (12) with $(2\mu +2)$ steps, which means that the two bilinear forms, Equations (12) and (13) are one and the same.

For a more convenient bilinear form, we down shift Equation (13) with $(\mu +1)$ steps and obtain for the odd case

$${\mathbf{D}}_{\mathbf{t}}\stackrel{\left(1\right)}{\overline{F_{m+1}}}•F_m+\stackrel{\left(1\right)}{\overline{F_{m+1}}}·F_m=\stackrel{(2\mu +2)}{\overline{F_{m+2\mu +2}}}·\underset{(2\mu +1)}{\underline{F_{m-2\mu -1}}}.$$

(14)

Case N-even, $N=2\mu$

Considering the substitution

$$Q(n,m,t)={\displaystyle \frac{\stackrel{(\mu +1)}{\overline{F_{m+\mu +1}}}·\underset{(\mu +1)}{\underline{F_{m-\mu -1}}}}{\stackrel{\left(\mu \right)}{\overline{F_{m+\mu }}}·\underset{\left(\mu \right)}{\underline{F_{m-\mu }}}}},$$

(15)

we calculate the products

$$\prod _{j=1}^{N}Q(n+j,m+j,t)={\displaystyle \frac{\stackrel{(3\mu +1)}{\overline{F_{m+3\mu +1}}}·\underset{\left(\mu \right)}{\underline{F_{m-\mu }}}}{\stackrel{(\mu +1)}{\overline{F_{m+\mu +1}}}·\stackrel{\left(\mu \right)}{\overline{F_{m+\mu }}}}},\prod _{j=1}^{N}Q(n-j,m-j,t)={\displaystyle \frac{\stackrel{\left(\mu \right)}{\overline{F_{m+\mu }}}·\underset{(3\mu +1)}{\underline{F_{m-3\mu -1}}}}{\underset{(\mu +1)}{\underline{F_{m-\mu -1}}}·\underset{\left(\mu \right)}{\underline{F_{m-\mu }}}}}.$$

Following the same steps as in the odd case, we cast the mB1 2D lattice, (10), for the even case, into the following Hirota bilinear form:

$${\mathbf{D}}_{\mathbf{t}}\stackrel{\left(1\right)}{\overline{F_{m+1}}}•F_m+\stackrel{\left(1\right)}{\overline{F_{m+1}}}·F_m=\stackrel{(2\mu +1)}{\overline{F_{m+2\mu +1}}}·\underset{\left(2\mu \right)}{\underline{F_{m-2\mu }}}.$$

(16)

We notice that, because $N=2\mu +1$ in Equation (14) and $N=2\mu$ in Equation (16), the two equations are identical, which means that the Hirota bilinear form of mB1 2D lattice is

$${\mathbf{D}}_{\mathbf{t}}\stackrel{\left(1\right)}{\overline{F_{m+1}}}•F_m+\stackrel{\left(1\right)}{\overline{F_{m+1}}}·F_m=\stackrel{(N+1)}{\overline{F_{m+N+1}}}·\underset{\left(N\right)}{\underline{F_{m-N}}}.$$

(17)

But Equation (17) is also identical to the bilinear form of the additive Bogoyavlensky 2D lattice system, solved in [26]. This means that we already have the expressions for $F(n,m,t)$ and that we can easily construct the multisoliton solutions, considering the substitutions given in Equation (11), or Equation (15).

3.2. The Multisoliton Solutions for mB1 2D Lattice

The one-soliton solution for $N=2\mu$ is

$$Q(n,m,t)={\displaystyle \frac{\stackrel{(\mu +1)}{\overline{F_{m+\mu +1}}}·\underset{(\mu +1)}{\underline{F_{m-\mu -1}}}}{\stackrel{\left(\mu \right)}{\overline{F_{m+\mu }}}·\underset{\left(\mu \right)}{\underline{F_{m-\mu }}}}}=$$

$$={\displaystyle \frac{\left[1+e^{k_1(n+\mu +1)+p_1(m+\mu +1)+{\omega }_{1}t+{\eta }_1^{\left(0\right)}}\right]·\left[1+e^{k_1(n-\mu -1)+p_1(m-\mu -1)+{\omega }_{1}t+{\eta }_1^{\left(0\right)}}\right]}{\left[1+e^{k_1(n+\mu )+p_1(m+\mu )+{\omega }_{1}t+{\eta }_1^{\left(0\right)}}\right]·\left[1+e^{k_1(n-\mu )+p_1(m-\mu )+{\omega }_{1}t+{\eta }_1^{\left(0\right)}}\right]}},$$

where the anzats used in Mathematica 10.1 for $F_m$ in Equation (17) is

$$F(n,m,t)=1+e^{k_{1}n+p_{1}m+{\omega }_{1}t+{\eta }_1^{\left(0\right)}},(\forall )k_1\in \mathbb{R},p_1\in \mathbb{C}.$$

The dispersion relation that comes out has the form

$${\omega }_1=2{\displaystyle \frac{sinh\frac{(k_1+p_1)N}{2}sinh\frac{(k_1+p_1)(N+1)}{2}}{sinh\frac{k_1+p_1}{2}}}.$$

For the 2-soliton solution we consider

$$F(n,m,t)=1+e^{{\eta }_1}+e^{{\eta }_2}+e^{{\eta }_1+{\eta }_2+A_{12}},$$

where

$${\eta }_j=k_{j}n+p_{j}m+{\omega }_{j}t+{\eta }_j^{\left(0\right)},j=\overline{1,2}.$$

(18)

Mathematica returns the dispersion relation:

$${\omega }_j=2{\displaystyle \frac{sinh\frac{(k_j+p_j)N}{2}sinh\frac{(k_j+p_j)(N+1)}{2}}{sinh\frac{k_j+p_j}{2}}}$$

(19)

and the interaction phase

$$e^{A_{ij}}={\displaystyle \frac{-cosh\frac{k_i+p_i-k_j-p_j}{2}+cosh\frac{(k_i+p_i-k_j-p_j)(1+2N)}{2}-({\omega }_i-{\omega }_j)sinh\frac{k_i+p_i-k_j-p_j}{2}}{cosh\frac{k_i+p_i+k_j+p_j}{2}-cosh\frac{(k_i+p_i+k_j+p_j)(1+2N)}{2}+({\omega }_i+{\omega }_j)sinh\frac{k_i+p_i+k_j+p_j}{2}}}.$$

(20)

For the three-soliton solution, we use

$$F(n,m,t)=1+e^{{\eta }_1}+e^{{\eta }_2}+e^{{\eta }_3}+e^{{\eta }_1+{\eta }_2+A_{12}}+e^{{\eta }_1+{\eta }_3+A_{13}}+e^{{\eta }_2+{\eta }_3+A_{23}}+e^{{\displaystyle \sum _{i=1}^3}{\eta }_i+{\displaystyle \sum _{1\le i<j}^3}{A}_{ij}},$$

with the phase ${\eta }_j$ given in (18). The software returns the dispersion relations ${\omega }_j$ and the interaction phases $A_{ij}$ with the same forms as in (19) and (20) but for $j=\overline{1,3}$. With a software like Mathematica 10.1, one can easily check that the above soliton solutions satisfy the bilinear form (17). The three-soliton condition for complete integrability in the Hirota sense is satisfied. Using the induction method as in [4], the $\mathcal{N}$-soliton solutions can be expressed. ${\eta }_j$, ${\omega }_j$, $A_{ij}$ have the same forms as in (18)–(20) but for $j=\overline{1,\mathcal{N}}$, and $F(n,m,t)$ is

$$F(n,m,t)=\sum _{{\mu }_1,{\mu }_{\mathcal{N}}=\{0,1\}}exp\left(\sum _{i=1}^{\mathcal{N}}{\mu }_i{\eta }_i+\sum _{1\le i<j}^{\mathcal{N}}{\mu }_i{\mu }_j{A}_{ij}\right).$$

(21)

4. The Periodic Reduction

Starting from the completely integrable mB1 2D lattice (in two discrete dimensions) given in Equation (10), which we rewrite here for convenience,

$$\begin{array}{c}\hfill {\displaystyle \frac{d}{dt}}Q(n,m,t)=Q(n,m,t)\left(\prod _{j=1}^{N}Q(n+j,m+j,t)-\prod _{j=1}^{N}Q(n-j,m-j,t)\right),\end{array}$$

and using the periodic reduction technique, we can derive the coupled mB1 lattice (1), which is written on components as (2) and in a compact form as (3), considering that $Q(n,m,t)$ is a periodic function only with respect to the discrete variable m and with period M. In this stage, the main correspondence is given through

$$Q(n,m+\nu -1,t)\equiv u_{\nu }(n,t),\nu =\overline{1,M}.$$

Because of the M periodicity, we have to keep in mind the following relations:

$$Q(n,m+M,t)=Q(n,m,t)\equiv u_1,Q(n,m+M+1,t)=Q(n,m+1,t)\equiv u_2,$$

$$Q(n,m+M-1,t)=Q(n,m-1,t)\equiv u_M.$$

To exemplify the technique, let us first consider the two-periodic reduction on the m direction. We introduce below the notations that help us notice the correspondence between the mB1 2D lattice and the coupled mB1 lattice (2) for $M=2$:

$$Q(n,m,t)\equiv u_1(n,t),Q(n,m+1,t)\equiv u_2(n,t),Q(n,m+2,t)\equiv u_1(n,t),$$

$$Q(n,m-1,t)\equiv u_2(n,t),Q(n,m-2,t)\equiv u_1(n,t),Q(n,m+3,t)\equiv u_2(n,t).$$

Let us first consider the particular case $M=2,N=2$ and see the reduction:

$$\begin{gathered} {\displaystyle \frac{d}{dt}}Q(n,m,t)=Q(n,m,t)\left[Q(n+1,m+1,t)Q(n+2,m+2,t)-Q(n-1,m-1,t)Q(n-2,m-2,t)\right] \\ ⟶ \end{gathered}$$

$${\displaystyle \frac{d}{dt}}{u}_1(n,t)=u_1(n,t)\left(\stackrel{\left(1\right)}{\overline{u_2}}·\stackrel{\left(2\right)}{\overline{u_1}}-\underset{\left(1\right)}{\underline{u_2}}·\underset{\left(2\right)}{\underline{u_1}}\right).$$

(22)

We now need to perform one up shift on m-direction in the mB1 2D lattice and then perform the reduction

$$\begin{gathered} {\displaystyle \frac{d}{dt}}Q(n,m+1,t)=Q(n,m+1,t)\left[Q(n+1,m+2,t)Q(n+2,m+3,t)-Q(n-1,m,t)Q(n-2,m-1,t)\right] \\ ⟶ \end{gathered}$$

$${\displaystyle \frac{d}{dt}}{u}_2(n,t)=u_2(n,t)\left(\stackrel{\left(1\right)}{\overline{u_1}}·\stackrel{\left(2\right)}{\overline{u_2}}-\underset{\left(1\right)}{\underline{u_1}}·\underset{\left(2\right)}{\underline{u_2}}\right).$$

(23)

The two equations, (22) and (23), obtained using the 2-periodic reduction on the 2D lattice mB1 and its up shift on m, form the coupled mB1 corresponding system.

Applying the 2-periodic reduction in mB1 2D lattice and denoting for brevity

$$u_1(n+1,t)=\stackrel{\left(1\right)}{\overline{u_1}},u_1(n+2,t)=\stackrel{\left(2\right)}{\overline{u_1}},u_1(n+N,t)=\stackrel{\left(N\right)}{\overline{u_1}},$$

$$u_1(n-1,t)=\underset{\left(1\right)}{\underline{u_1}},u_1(n-2,t)=\underset{\left(2\right)}{\underline{u_2}},u_1(n-N,t)=\underset{\left(N\right)}{\underline{u_1}},$$

we get precisely (for even N)

$$\begin{array}{ccc}\hfill {\displaystyle \frac{d}{dt}}{u}_1& =& u_1\left(\stackrel{\left(1\right)}{\overline{u_2}}·\stackrel{\left(2\right)}{\overline{u_1}}·\dots ·\stackrel{(N-1)}{\overline{u_2}}·\stackrel{\left(N\right)}{\overline{u_1}}-\underset{\left(1\right)}{\underline{u_2}}·\underset{\left(2\right)}{\underline{u_1}}·\dots ·\underset{(N-1)}{\underline{u_2}}·\underset{\left(N\right)}{\underline{u_1}}\right)\hfill \\ \hfill {\displaystyle \frac{d}{dt}}{u}_2& =& u_2\left(\stackrel{\left(1\right)}{\overline{u_1}}·\stackrel{\left(2\right)}{\overline{u_2}}·\dots ·\stackrel{(N-1)}{\overline{u_1}}·\stackrel{\left(N\right)}{\overline{u_2}}-\underset{\left(1\right)}{\underline{u_1}}·\underset{\left(2\right)}{\underline{u_2}}·\dots ·\underset{(N-1)}{\underline{u_1}}·\underset{\left(2\right)}{\underline{u_2}}\right).\hfill \end{array}$$

For $N=1$, the above system turns into the well-known coupled Lotka–Volterra lattice:

$$\begin{array}{ccc}\hfill {\displaystyle \frac{d}{dt}}{u}_1& =& u_1\left(\stackrel{\left(1\right)}{\overline{u_2}}-\underset{\left(1\right)}{\underline{u_2}}\right)\hfill \\ \hfill {\displaystyle \frac{d}{dt}}{u}_2& =& u_2\left(\stackrel{\left(1\right)}{\overline{u_1}}-\underset{\left(1\right)}{\underline{u_1}}\right).\hfill \end{array}$$

Imposing the three-periodic reduction, the correspondence is made through

$$Q(n,m,t)\equiv u_1\left(n\right),Q(n,m+1,t)\equiv u_2\left(n\right),Q(n,m+2,t)\equiv u_3\left(n\right),$$

$$Q(n,m+3,t)\equiv u_1\left(n\right),Q(n,m-1,t)\equiv u_3\left(n\right),$$

and we get the coupled lattice with three equations (for N multiples of three)

$$\begin{array}{ccc}\hfill {\displaystyle \frac{d}{dt}}{u}_1& =& u_1\left(\stackrel{\left(1\right)}{\overline{u_2}}·\stackrel{\left(2\right)}{\overline{u_3}}·\stackrel{\left(3\right)}{\overline{u_1}}·\dots ·\stackrel{\left(N\right)}{\overline{u_1}}-\underset{\left(1\right)}{\underline{u_3}}·\underset{\left(2\right)}{\underline{u_2}}·\underset{\left(3\right)}{\underline{u_1}}·\dots ·\underset{\left(N\right)}{\underline{u_1}}\right)\hfill \\ \hfill {\displaystyle \frac{d}{dt}}{u}_2& =& u_2\left(\stackrel{\left(1\right)}{\overline{u_3}}·\stackrel{\left(2\right)}{\overline{u_1}}·\stackrel{\left(3\right)}{\overline{u_2}}·\dots ·\stackrel{\left(N\right)}{\overline{u_2}}-\underset{\left(1\right)}{\underline{u_1}}·\underset{\left(2\right)}{\underline{u_3}}·\underset{\left(3\right)}{\underline{u_2}}·\dots ·\underset{\left(N\right)}{\underline{u_2}}\right)\hfill \\ \hfill {\displaystyle \frac{d}{dt}}{u}_3& =& u_3\left(\stackrel{\left(1\right)}{\overline{u_1}}·\stackrel{\left(2\right)}{\overline{u_2}}·\stackrel{\left(3\right)}{\overline{u_3}}·\dots ·\stackrel{\left(N\right)}{\overline{u_3}}-\underset{\left(1\right)}{\underline{u_2}}·\underset{\left(2\right)}{\underline{u_1}}·\underset{\left(3\right)}{\underline{u_3}}·\dots ·\underset{\left(N\right)}{\underline{u_3}}\right).\hfill \end{array}$$

The coupled multicomponent mB1 lattice comes from the mB1 2D-lattice Equation (10) for any N, choosing a M-periodic reduction on m:

$$\begin{array}{ccc}\hfill {\displaystyle \frac{d}{dt}}{u}_1& =& u_1\left(\stackrel{\left(1\right)}{\overline{u_2}}·\stackrel{\left(2\right)}{\overline{u_3}}·\dots ·\stackrel{\left(N\right)}{\overline{u_{N+1}}}-\underset{\left(1\right)}{\underline{u_M}}·\underset{\left(2\right)}{\underline{u_{M-1}}}·\dots ·\underset{\left(N\right)}{\underline{u_{M-N+1}}}\right)\hfill \\ \hfill {\displaystyle \frac{d}{dt}}{u}_2& =& u_2\left(\stackrel{\left(1\right)}{\overline{u_3}}·\stackrel{\left(2\right)}{\overline{u_4}}·\dots ·\stackrel{\left(N\right)}{\overline{u_{N+2}}}-\underset{\left(1\right)}{\underline{u_1}}·\underset{\left(2\right)}{\underline{u_M}}·\dots ·\underset{\left(N\right)}{\underline{u_{M-N+2}}}\right)\hfill \\ \hfill \dots & =& \dots \dots \dots \dots \dots \hfill \\ \hfill {\displaystyle \frac{d}{dt}}{u}_{M-1}& =& u_{M-1}\left(\stackrel{\left(1\right)}{\overline{u_M}}·\stackrel{\left(2\right)}{\overline{u_1}}·\dots ·\stackrel{\left(N\right)}{\overline{u_{M+N-1}}}-\underset{\left(1\right)}{\underline{u_{M-2}}}·\underset{\left(2\right)}{\underline{u_{M-3}}}·\dots ·\underset{\left(N\right)}{\underline{u_{M-N-1}}}\right)\hfill \\ \hfill {\displaystyle \frac{d}{dt}}{u}_M& =& u_M\left(\stackrel{\left(1\right)}{\overline{u_1}}·\stackrel{\left(2\right)}{\overline{u_2}}·\dots ·\stackrel{\left(N\right)}{\overline{u_{M+N}}}-\underset{\left(1\right)}{\underline{u_{M-1}}}·\underset{\left(2\right)}{\underline{u_{M-2}}}·\dots ·\underset{\left(N\right)}{\underline{u_{M-N}}}\right).\hfill \end{array}$$

All N-soliton solutions of the coupled multicomponent mB1 lattice arise straightforwardly from the mB1 2D lattice (10). Examining the two bilinear forms, the connection between the corresponding lattices is clear:

• For mB1 (n,m,t) 2D lattice:

  $${\mathbf{D}}_{\mathbf{t}}\stackrel{\left(1\right)}{\overline{F_{m+1}}}•F_m+\stackrel{\left(1\right)}{\overline{F_{m+1}}}·F_m=\stackrel{(N+1)}{\overline{F_{m+1+N}}}·\underset{\left(N\right)}{\underline{F_{m-N}}},$$

  (24)
• For coupled multicomponent mB1 (n,t) lattice ($\nu =\overline{1,M}$):

  $${\mathbf{D}}_{\mathbf{t}}\stackrel{\left(1\right)}{\overline{F_{\nu +1}}}•F_{\nu }+\stackrel{\left(1\right)}{\overline{F_{\nu +1}}}·F_{\nu }=\stackrel{(N+1)}{\overline{F_{\nu +1+N}}}·\underset{\left(N\right)}{\underline{F_{\nu -N}}}.$$

  (25)

The two lattices, (10) and (1), are clearly connected, noting that the second index, m, of $Q(n,m,t)$ in the bilinear form (24) corresponds to $\nu =\overline{1,M}$ in the bilinear form (25), where $\nu$ serves as a parameter indexing the soliton solution $u_{\nu }(n,t)$ of the M-component mB1 lattice.

For example, if we consider $M=2$, when we apply the 2-periodic reduction and drop the m-dependence, parameter $p_j$ that appears in the definitions belongs to the set $\{-\pi \mathrm{i}$, $+\pi \mathrm{i}\}$, determining the dispersion relation to have any of the two branches.

In the case $M=3$, with the m-dependence dropped, we have $p_j\in \{-2\pi \mathrm{i}/3,+2\pi \mathrm{i}/3,2\pi \mathrm{i}\}$. Their exponentials are the cubic roots of unity, which generate the three branches of the dispersion relation.

In the general case, $\forall M$, when dropping the m-dependence, $p_j$ must belong to the set $\left\{\nu \frac{2\pi \mathrm{i}}{M}\right\}$, $\nu =\overline{1,M}$. Again, the exponentials of $p_j$ are the roots of unity, this time of order M. As a consequence, there are M possible branches of the dispersion relation for all solitons.

In light of the above analogy, the periodic reduction once again proves to be a highly effective method for deriving multisoliton solutions in multicomponent systems.

Solitonic Representations for Particular Cases of Multicomponent mB1 Lattice

We first summarize the results obtained for the coupled multicomponent first multiplicative Bogoyavlensky lattice with branched dispersion, Equation (1). In a compact manner, as we already stated, the multicomponent lattice can be written as

$${\dot{u}}_{\nu }=u_{\nu }\left(\prod _{j=1}^N\stackrel{\left(j\right)}{\overline{u_{\nu +j}}}-\prod _{j=1}^N\underset{\left(j\right)}{\underline{u_{\nu +M-j}}}\right),\nu =\overline{1,M}.$$

(26)

Consider the nonlinear substitutions:

• For N-odd ($N=2\mu +1$),

  $$u_{\nu }(n,t)={\displaystyle \frac{\stackrel{(\mu +2)}{\overline{F_{\nu }}}·\underset{(\mu +1)}{\underline{F_{\nu }}}}{\stackrel{(\mu +1)}{\overline{F_{\nu }}}·\underset{\left(\mu \right)}{\underline{F_{\nu }}}}},\nu =\overline{1,M}$$

  (27)
• For N-even ($N=2\mu$),

  $$u_{\nu }(n,t)={\displaystyle \frac{\stackrel{(\mu +1)}{\overline{F_{\nu }}}·\underset{(\mu +1)}{\underline{F_{\nu }}}}{\stackrel{\left(\mu \right)}{\overline{F_{\nu }}}·\underset{\left(\mu \right)}{\underline{F_{\nu }}}}},\nu =\overline{1,M},$$

  (28)

The lattice in (26) can be written in the Hirota bilinear form as

$${\mathbf{D}}_{\mathbf{t}}\stackrel{\left(1\right)}{\overline{F_{\nu +1}}}•F_{\nu }+\stackrel{\left(1\right)}{\overline{F_{\nu +1}}}·F_{\nu }=\stackrel{(N+1)}{\overline{F_{\nu +1+N}}}·\underset{\left(N\right)}{\underline{F_{\nu -N}}},$$

and admits multisoliton solution of the form (${\eta }_j=k_{j}n+{\omega }_{j}t+{\eta }_j^{\left(0\right)}$)

$$F_{\nu }(n,t)=\sum _{{\mu }_1,..,{\mu }_{\mathcal{N}}=\{0,1\}}exp\left(\sum _{i=1}^{\mathcal{N}}{\mu }_i[{\eta }_i+(\nu -1)ln\left({ϵ}_i\right)]+\sum _{1\le i<j}^{\mathcal{N}}{\mu }_i{\mu }_j{A}_{ij}\right),$$

with the interaction terms

$$e^{A_{ij}}={\displaystyle \frac{-cosh\frac{k_i-k_j+ln\frac{{ϵ}_i}{{ϵ}_j}}{2}+cosh\frac{(k_i-k_j+ln\frac{{ϵ}_i}{{ϵ}_j})(1+2N)}{2}-({\omega }_i-{\omega }_j)sinh\frac{k_i-k_j+ln\frac{{ϵ}_i}{{ϵ}_j}}{2}}{cosh\frac{k_i+k_j+ln{ϵ}_i{ϵ}_j}{2}-cosh\frac{(k_i+k_j+ln{ϵ}_i{ϵ}_j)(1+2N)}{2}+({\omega }_i+{\omega }_j)sinh\frac{k_i+k_j+ln{ϵ}_i{ϵ}_j}{2}}}$$

and the M possible branches of dispersion for each of the $\mathcal{N}$-solitons:

$${\omega }_j=2{\displaystyle \frac{sinh\frac{(k_j+ln{ϵ}_j)N}{2}sinh\frac{(k_j+ln{ϵ}_j)(N+1)}{2}}{sinh\frac{k_j+ln{ϵ}_j}{2}}},{ϵ}_j\in \left\{e^{l\frac{2\pi i}{M}}\right\},l=\overline{1,M},j=\overline{1,\mathcal{N}}.$$

Soliton solutions of these Volterra-type equations, when constructed using the Hirota bilinear method, exhibit several fundamental symmetries. One of the key symmetries is a discrete translational invariance, due to the lattice nature of the system—shifting the solution along the discrete spatial variable does not alter its form. Additionally, there is often a time-reversal symmetry in the underlying bilinear equations, reflecting the reversible dynamics of the integrable model.

Through the Hirota formalism, these systems also inherit parameter symmetries, where the soliton parameters (such as wave numbers) appear symmetrically in the solution, typically in exponential form. This leads to phase shift symmetry after soliton interactions—a hallmark of elastic scattering.

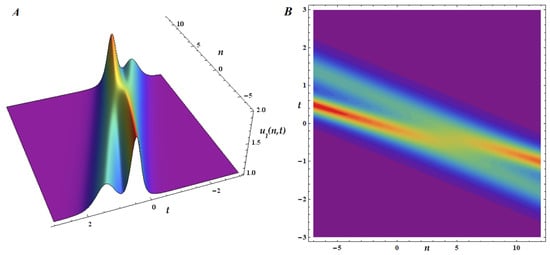
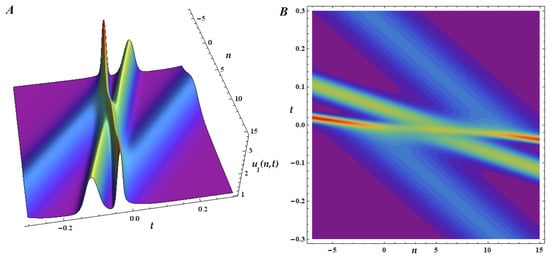
Using the software Mathematica 10.1, we plot in Figure 1, Figure 2 and Figure 3, both $3D$ surface and $2D$ contour plots, the 1-ss, 2-ss and 3-ss for (26) in the particular case $M=1$, in other words for the mB1 lattice, choosing different values of N and some suitable parameters and intervals.

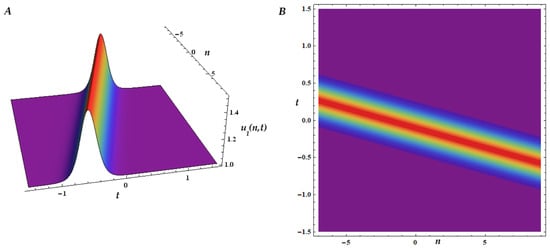
More precisely, Figure 1 describes the propagation in time, $-1.5<t<1.5$, for the one-soliton solution (1-ss) of mB1 lattice ($M=1$ in (26)), for $N=3$, given by (27), for $-7<n<9$, the chosen wave number $k_1=ln2$ and the arbitrary phase ${\eta }_1^{\left(0\right)}=1$. It is a bright soliton, a very localized wave packet that maintains its shape while traveling at a constant velocity. Its profile is bell-shaped and it is a stable structure that can propagate over long distances without changing shape due to the balance between dispersion and nonlinearity.

Figure 2 describes the two-soliton solution propagation of the mB1 lattice, for $N=2$, in the intervals $-3<t<3$ and $-7<n<12$, under the chosen wave numbers $k_1=ln2,k_2=ln3$ and the arbitrary phases ${\eta }_1^{\left(0\right)}=1,{\eta }_2^{\left(0\right)}=2$. The two-soliton interaction is also evident within the selected intervals. It is well-known that solitons undergo a phase shift during interactions, meaning that their position or phase changes after the interaction, this being a key feature of soliton behavior during interactions. Additionally, we observe a temporary change in amplitude, occurring only during the interaction.

The three-soliton solution of the mB1 lattice, for $N=4$, is plotted in Figure 3, for $-0.3<t<0.3$ and $-7<n<15$. We choose the wave numbers, $k_1=ln2,k_2=ln3,k_3=ln4$ and the arbitrary phases ${\eta }_1^{\left(0\right)}=1,{\eta }_2^{\left(0\right)}=2,{\eta }_3^{\left(0\right)}=3$. The interaction of the solitons, two by two, is visible both on the surface and contour plot, illustrating the elastic scattering. More precisely, the solitons retain their shape and amplitude after the collision, with only a phase shift as a result. All solitons are bright and illustrate a typical solitonic phenomenology with elastic interactions.

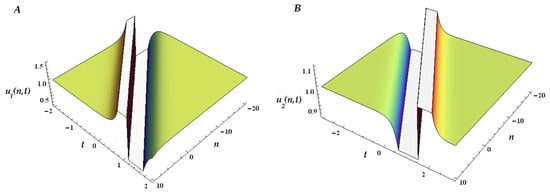
In Figure 4, Figure 5 and Figure 6 we plot the 1-ss, 2-ss, and 3-ss for the coupled mB1 lattice for $M=2$ and $N=3$. We represent below the 3D surfaces of the multisoliton solutions, $u_{\nu }(n,t)$ ($\nu =\overline{1,M}$), for the multicomponent mB1 lattice (26) with two coupled equations ($M=2$). As we only have two components, $u_1$ (plotted in (A)) and $u_2$ (plotted in (B)), each soliton can have any of the two possible branches of dispersion because ${ϵ}_j\in \{-1,+1\}.$

We have not displayed all the possibilities but some that involve the negative $ϵ$. We notice that parameter ${ϵ}_j=-1$ introduces some singularities in the soliton solution. These plots also illustrate a typical solitonic phenomenology with elastic interactions, visible in Figure 5 and Figure 6.

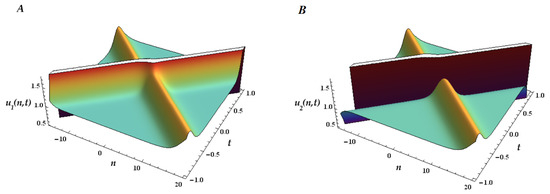
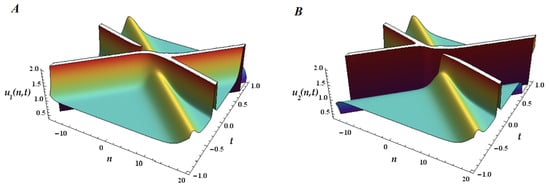
5. Conclusions

In this paper, we investigated the coupled multicomponent first multiplicative Bogoyavlensky lattice with branched dispersion relations, using the Hirota bilinear formalism and the periodic reduction. As a particular case, we first solved coupled M-component mB1 lattice for $N=3$, deducing its bilinear form and constructing its mulisoliton solutions. The soliton solutions of the Bogoyavlensky lattice are of particular importance, as the elastic interactions among localized solutions highlight the integrable and self-organizing character of the model.

The primary motivation of this study was to investigate the persistence of integrability in coupled lattices. The main conclusion that can be drawn from the results is that the new system (the coupled mB1 lattice) is a completely integrable system in the sense of Hirota. A distinguishing feature of such systems lies in the structure of their dispersion relations, which exhibit multiple branches. One of the physical and mathematical implications of having M dispersion branches consists in displaying all the possible speed directions for each component of the multisoliton solution. Additionally, the phase behavior of the components is characterized by the M-th roots of unity (M is the number of coupled equations), which exhibits multi-phase soliton interactions and branched symmetries in discrete media. The existence of multiple dispersion branches provides enhanced flexibility in the dynamics of soliton interactions.

Using the Hirota bilinear formalism, we demonstrated that the mB1 2D lattice is integrable, constructing the multisoliton solutions. Furthermore, we showed that applying a M-periodic reduction to the 2D-lattice equation, we generate the system of interest—the coupled multicomponent mB1 lattice—together with its bilinear form and the multisoliton solutions. This combination of techniques facilitated the construction of multisoliton solutions and proved that integrability survives in coupled lattices. The paper also presents graphical representations for the multisoliton solutions of mB1 lattice and 2-component mB1 lattice, illustrating the solitonic propagation in time and the elastic scattering that occurs.