1. Introduction
The profound symmetry between classical and fuzzy sets establishes a conceptual bridge, connecting the discrete binary world of sharp boundaries to a continuous realm characterized by gradual shades of membership. This duality fundamentally extends the absolute logic of “in or out” into a nuanced continuum, enabling the formal mathematical representation of vagueness and partial truth. With the development of fuzzy logic, scholars have proposed various logical algebras such as Residuated lattice [
1,
2], BL-algebra [
3] and MV-algebra [
4]. Among these logical algebras, MV-algebras originated with Chang’s work, serving as the algebraic semantics for the many-valued Łukasiewicz propositional logic, and have attracted extensive attention from scholars and been systematically studied from multiple perspectives such as topological properties [
5,
6], state theory [
7,
8], convex structure [
9], and ideal theory [
10,
11].
The concept of ideals has been systematically extended to the fuzzy setting, marking a significant advancement in the study of non-classical logical algebras. In 1994, Hoo [
12] initiated this line of research by applying fuzzy set theory to MV-algebras and introducing the notion of fuzzy ideals within this framework. Subsequently, in a further contribution [
13], Hoo deepened the investigation by examining various types of fuzzy ideals and demonstrating the fundamental equivalence between fuzzy implicative ideals and fuzzy Boolean ideals in MV-algebras. Building upon this foundation, Forouzesh [
14] formulated the concept of fuzzy p-ideals in MV-algebras and established its equivalence with both fuzzy Boolean ideals and fuzzy implication ideals, thereby reinforcing the interconnections among these generalized ideal types. For additional research developments concerning fuzzy ideals in MV-algebras, interested readers may consult references [
15,
16]. Concurrently with these algebraic developments, the evolution of fuzzy set theory has prompted a substantial generalization of truth-value structures, expanding from the conventional unit interval
to more abstract and broadly defined lattice-based frameworks, particularly including completely distributive lattices. This inspires us to wonder if there exists a more general case than
L-fuzzy ideals, which prompts us to extend the notion of
L-fuzzy ideals to a more general framework, so we study
L-fuzzy ideals in a degree of approach that can be used to characterize
L-fuzzy ideals from a new perspective.
Convexity [
17,
18] is a fundamental concept in modern mathematical research. It originated from the study of simple geometric problems in low-dimensional Euclidean spaces. Furthermore, convexity is also presented in numerous mathematical areas [
9,
19,
20,
21]. The extension of convex structures into fuzzy settings represents an important development in the fusion of algebraic and fuzzy mathematics. In 1994, Rosa [
22] pioneered this direction by generalizing classical convex structures to the fuzzy framework, thereby introducing the fundamental concept of fuzzy convex structures. This line of research was further advanced in 2009 when Maruyama [
23] expanded the theoretical foundation by adopting a completely distributive lattice as the lattice-value context, subsequently defining the more general
L-convex structures. A significant conceptual contribution came from Shi and Xiu [
24], who formulated the notion of
M-fuzzifying convex structures—an innovative framework that quantifies the degree to which a given subset satisfies the properties of a convex set. Building on this, they subsequently developed the comprehensive framework of
-fuzzy convex structures [
25]. When the lattices
L and
M coincide, an
-fuzzy convexity is conveniently abbreviated as an
L-fuzzy convex structure, a case that has since been extensively investigated from multiple perspectives [
26,
27,
28,
29]. It is well known that MV-algebras are closely related to topology. Convex structures, as structures similar to topological structures, also have a certain connection with MV-algebras. In our paper, we aim to construct
L-fuzzy convex structures and
L-convex structures in MV-algebras.
In a parallel development inspired by the quantitative approach of degree theory, Shi and Xin [
30] introduced the definition of
L-fuzzy subgroup degree, which provides a precise measure of how closely an arbitrary
L-fuzzy subset approximates the structure of an
L-fuzzy subgroup. The degree-based methodology has proven highly fruitful, serving as a foundation for subsequent extensions to various other algebraic structures [
31,
32,
33]. Motivated by these converging research streams, our paper aims to introduce the concept of
L-fuzzy ideal degree in MV-algebras; it can describe the degree to which an
L-fuzzy subset becomes an
L-fuzzy ideal. Thus the
L-fuzzy ideal degree can be regarded as a more general case of
L-fuzzy ideals. We aim to characterize
L-fuzzy ideals and study some properties of
L-fuzzy ideals from the view of
L-fuzzy ideal degree. In addition, we can construct an
L-fuzzy convex structure based on the
L-fuzzy ideal degree in an MV-algebra. Through the investigation of the
L-fuzzy ideal degree, it can establish its fundamental connections with
L-fuzzy ideals and
L-fuzzy convex structures. It is worth noting that the study of
L-fuzzy ideal degree can enrich the theory of
L-fuzzy ideals in MV-algebras and the theory of lattice-valued convex structures, thereby creating new bridges between fuzzy algebraic structures and fuzzy convex structures.
The organization of this paper is outlined below. In
Section 2, we collect some key notations and fundamental definitions with respect to MV-algebras and
L-fuzzy convex structures. In
Section 3, we propose the notion of
L-fuzzy ideal degree in MV-algebras based on the implication operator on a completely distributive lattice
L. Furthermore, we characterize the
L-fuzzy ideal degree by using four types of cut sets of
L-fuzzy subsets, which can establish the connection between
L-fuzzy ideal degree and
L-fuzzy ideal. In
Section 4, the
L-fuzzy convex structure is established from the
L-fuzzy ideal degree in an MV-algebra. We also focus on studying some properties of the
L-fuzzy convex structure, proving that the set of all
L-fuzzy ideals forms an
L-convex structure and giving its concrete
L-convex hull formula.
3. L-Fuzzy Ideal Degree in MV-Algebras
This section presents a new perspective to investigate L-fuzzy ideals in an MV-algebra, which is called L-fuzzy ideal degree. It can illustrate the extent to which an L-fuzzy subset qualifies as an L-fuzzy ideal.
The definition of
L-fuzzy ideal in residuated lattices was introduced by Kengne [
38]. Since MV-algebras are special cases of residuated lattices, we obtain the following definition of
L-fuzzy ideal in MV-algebras.
Definition 8
([
38])
. Let . Then we say ϕ is an L-fuzzy ideal provided that- (LI1)
for every , ⟹;
- (LI2)
for every , .
We next propose the concept of L-fuzzy ideal degree.
Definition 9. Define the mapping as follows: Then we say that is the L-fuzzy ideal degree in A. Remark 1. Let . In fact, can characterize the extent to which ϕ is an L-fuzzy ideal. Particularly, if , then for all with ,This impliesBy Definition 8, we get ϕ is an L-fuzzy ideal. Conversely, assuming ϕ is an L-fuzzy ideal, we can easily get that . Hence, ϕ is an L-fuzzy ideal if and only if . We next present examples for the L-fuzzy ideal degree.
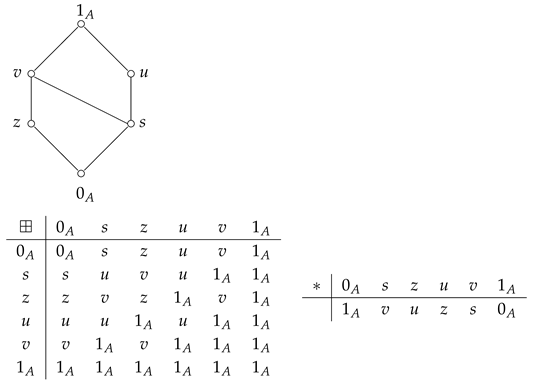
Example 1. Consider an MV-algebra . The Hasse diagram and Cayley tables associated with A are shown below.![Symmetry 17 01906 i001 Symmetry 17 01906 i001]() Let be a completely distributive lattice with Hasse diagram as follows.
Let be a completely distributive lattice with Hasse diagram as follows. ![Symmetry 17 01906 i002 Symmetry 17 01906 i002]() It is not difficult to see that the implication operation on L is induced as follows:
It is not difficult to see that the implication operation on L is induced as follows: (1)
Define byBy Definition 9, it can be proved that . Since , we obtainThus ϕ is not an L-fuzzy ideal.(2)
Define as follows:By Definition 9, we get . Thus ϕ is an L-fuzzy ideal. Example 2.
Consider the MV-algebra defined in Example 1 and .
(1)
Define as follows:It can be proved that . Since , we obtainThus ϕ is not an L-fuzzy ideal.(2)
Define as follows:It can be proved that . By Remark 1, we get ϕ is an L-fuzzy ideal. To give some characterizations for the L-fuzzy ideal degree, we first give the lemma as follows.
Lemma 2.
Let . Then for any , if and only if for all with , Proof. Take
such that
. Then
⟺ for any
with
,
⟺ for any
with
,
⟺ for any
with
,
as desired. □
We next study the characterization for the L-fuzzy ideal degree.
Proof. Let
fulfill
By Lemma 2, we know that for all
with
,
This results that
Thus we obtain
Let
fulfill
Then there exists
satisfying for all
with
,
such that
. Then it follows that for all
with
,
Hence
The arbitrariness of
t implies
as desired. □
In [
30,
33], some characterizations for
L-fuzzy filter degree and
L-fuzzy subgroup degree are given via cut sets of
L-fuzzy sets. We follow the proof idea in [
30,
33] and treat the empty set as an ideal; we explore some characterizations for the
L-fuzzy ideal degree in MV-algebras in the following.
Theorem 2.
Let . Then
- (1)
;
- (2)
Proof. (1) Suppose for each
,
is an ideal of
A. Take
with
. Let
. Then we obtain
and
, so
. By the assumption,
is an ideal. Since
and
, we obtain
which means
Let
and
. Then we obtain
and
. By the assumption,
is an ideal and
. Thus
, so
This gives that
Conversely, suppose for all
with
,
and
. For any
, we prove
is an ideal of
A. If
and
, then
. This suggests that
So we obtain
. If
, then
This gives that
Hence, by Definition 2,
is an ideal. Thus we get the result
as desired.
(2) By (1), one can see that that
Conversely, we state that
Let
. Then for any
,
is an ideal. For any
, since
, we obtain
It follows from
and
that
is an ideal for any
. Thus
is an ideal, implying that
is an ideal. Hence
This gives that
as desired. □
Theorem 3.
Let . Then
- (1)
;
- (2)
.
Proof. (1) Suppose that for any with , take with and . Let . We prove that is an ideal.
If
and
, then
. From
, we have
From
, we get
Thus
. If
, then
Since
we obtain
Thus
This gives that
. So
is an ideal. It results that
Conversely, let
such that
. Suppose that
is an ideal. Then for all
with
, we next show that
If
, then it follows from
that
So we obtain
. This gives
is an ideal of
A, which implies
. Thus
Since
e is arbitrary, we obtain
Hence
Similarly, for any
, we can get
This results that
(2) Since
we obtain
By (1) we first obtain
Conversely, suppose
and
is an ideal for all
satisfying
. In the following, we prove
and
for all
satisfying
. Let
and
. Then
Thus
and
, which implies
. Since
is an ideal, we obtain
, i.e.,
. So
; this gives
. Thus
We can similarly prove
. This shows
Hence
as desired. □
Proof. Let
fulfill
and
for any
with
. Suppose that
such that
. We next show that
is an ideal of
A. Let
and
. If
, then
. It follows from
that
By the fact that
and
, i.e.,
, we get
, a contradiction. Thus we can get
Similarly, for all
, we obtain
This results that
Conversely, let
and
fulfill
. Suppose that
is an ideal of
A. Next, we show that for all
with
, it holds
For any
with
, let
such that
. Then we obtain
It results that
. By the assumption,
is an ideal. This gives that
, i.e.,
Since
e is arbitrary, we obtain
Similarly, for any
, we can get
It results that
as desired. □
Theorem 5.
Let . If for all . Then Proof. Suppose that such that and for all with . For any , we next prove that is an ideal of A.
If
and
, then
So we obtain
. If
, then
Thus
This gives that
Conversely, let
. Suppose for every
satisfying
,
is an ideal
A, we next show
Let
. Since
we obtain
This gives
. So we can get that
is an ideal of
A. It follows from
that
. So we obtain
From the arbitrariness of
e, it holds that
Hence
.
Let
. By
we get
This gives that
By the assumption, we can get
is an ideal of
A. Thus
implying that
. From the arbitrariness of
e, it holds that
This gives
Hence,
as desired. □
By the fact is an L-fuzzy ideal if and only if , we provide some characterizations for L-fuzzy ideals by using their cut sets.
Proposition 1.
Let . Then the statements listed below are equivalent:
- (1)
ϕ is an L-fuzzy ideal;
- (2)
Each , is an ideal;
- (3)
Each , is an ideal;
- (4)
Each , is an ideal;
- (5)
Each , is an ideal;
- (6)
Each , is an ideal.
Proof. (1) ⇒ (2) Suppose
is an
L-fuzzy ideal. Let
,
such that
and
. Since
is an
L-fuzzy ideal, we obtain
Thus
Let
. Then
. Since
is an
L-fuzzy ideal, by (LI2), we obtain
i.e.,
. Hence
is an ideal.
(2) ⇒ (3) is obvious.
(3) ⇒ (1) By Theorem 2 (2), we get
By the fact that for any
,
is an ideal, we obtain
It follows from Remark 1 that
is an
L-fuzzy ideal.
(1) ⇒ (4) Suppose that
is an
L-fuzzy ideal. For every
, let
, i.e.,
. Since
is an
L-fuzzy ideal, we get
Hence
Let
and
. Then
and
. It implies
Since
is an
mapping, we obtain
From (I2), we get
i.e.,
. Therefore
is an ideal.
(4) ⇒ (5) is obvious.
(5) ⇒ (1) Theorem 3 (2) implies that
Since
is an ideal of
A for all
, it holds that
Again by Remark 1, we can get that
is an
L-fuzzy ideal.
(1) ⇒ (6) Let be an L-fuzzy ideal. For every , let , i.e., . We thus obtain This implies , i.e., .
Let
and
, i.e.,
, then
Since
is an
L-fuzzy ideal, it holds that
This implies
, i.e.,
. Therefore
is an ideal.
By Theorem 4, we know that
Since
is an ideal for every
, it holds that
Again by Remark 1, we can get that
is an
L-fuzzy ideal. □
Proposition 2.
Let . If for all , then we obtain the following equivalent statements:
- (1)
ϕ is an L-fuzzy ideal of A;
- (2)
is an ideal for any ;
- (3)
is an ideal for any .
Proof. The proof is analogous to that of Theorem 1, and we omit it. □
4. L-Fuzzy Convex Structure in MV-Algebras
This section establishes that the degree measure of L-fuzzy ideals within an MV-algebra precisely corresponds to an L-fuzzy convex structure, and systematically examines its fundamental properties. Furthermore, we demonstrate that the family of all L-fuzzy ideals in an MV-algebra constitutes a well-defined L-convex structure, and derive its explicit L-convex hull formulation.
Next, we prove that is an L-fuzzy convex structure in an MV-algebra A.
Theorem 6.
Let be the L-fuzzy ideal degree in A. Then is an L-fuzzy convex structure on A.
Proof. It is easily seen that .
Take any subfamily
. Then
For any directed subfamily
, we next show
Take
with
. Then
for all
. By Lemma 2, we know for any
with
,
Next we show for all
with
.
Take any
. So there exists an
and
such that
Since
is directed, there exists
satisfying
and
. This gives that
which implies that for all
,
Hence, we obtain for any
,
Similarly, we get for any
with
,
By Lemma 2, we get
From the arbitrariness of
d, we obtain
.
Hence, by Definition 5, we obtain that is an L-fuzzy convex structure on A. □
It is known that
L-fuzzy convexity-preserving mappings and
L-fuzzy convex-to-convex mappings are the links connecting two
L-fuzzy convex structures. In [
33], the authors discussed the connection between morphisms in effect algebras and
L-fuzzy convex-to-convex mapping. Following their proof method, we relax the condition of morphisms and require a mapping between two MV-algebras to be an ⊞-morphism; we next explore the relationship between the ⊞-morphisms and
L-fuzzy convexity-preserving mappings,
L-fuzzy convex-to-convex mapping.
Theorem 7.
Let be an order-preserving ⊞-morphism between two MV-algebras. If , are the L-fuzzy ideal degrees on and , respectively, then is L-fuzzy convexity-preserving.
Proof. Take
. Then
The equation (★) holds from the following fact: since
g is an ⊞-morphism, we obtain
.
Therefore, by Definition 7 (1), g is L-fuzzy convexity-preserving. □
Theorem 8.
Let be a monotonic ⊞-morphism between two MV-algebras. If , are the L-fuzzy ideal degrees on and , respectively, then is an L-fuzzy convex-to-convex mapping.
Proof. Take
. Then
The inequality (★) holds from the following fact: we claim that
Take
. Since
we have
and
. Then there exist
and
with
and
such that
and
, thus
Hence
Therefore, by Lemma 1 (5) we get
The inequality (△) holds from the following fact: since g is a monotonic ⊞-morphism, , by Definition 3, we obtain implies . Furthermore, since g is an ⊞-morphism, we have . Since , we get . By the fact that in △, thus the inequality (△) holds.
Therefore, by Definition 7 (2), g is L-fuzzy convex-to-convex. □
From the perspective of L-fuzzy ideal degree, some properties of L-fuzzy ideals are investigated as follows.
Proposition 3.
Let be an order-preserving ⊞-morphism between two MV-algebras. If η is an L-fuzzy ideal of , then is an L-fuzzy ideal of .
Proof. Assume
and
are the
L-fuzzy ideal degrees of
and
, respectively. Since
is an
L-fuzzy ideal of
, we have
. From Theorem 7, we get
g is
L-fuzzy convexity-preserving, implying that
Hence
Thus
. Therefore,
is an
L-fuzzy ideal of
. □
Proposition 4.
Let be a monotonic ⊞-morphism between two MV-algebras. If ϕ is an L-fuzzy ideal of , then is an L-fuzzy ideal of .
Proof. Assume and are the L-fuzzy ideal degrees of and , respectively. By Theorem 8, we get g is L-fuzzy convex-to-convex, implying that . Since is an L-fuzzy ideal of , we have Hence . Therefore is an L-fuzzy ideal of . □
Example 3.
Let . Consider the MV-algebra defined in Example 1 and the MV-algebra whose Hasse diagram and Cayley tables are defined as follows:
Define the mapping byIt can be checked that g is an order-preserving ⊞-morphism. Define byIt can be checked that η is an L-fuzzy ideal of the MV-algebra B. By Theorem 3, we get is an L-fuzzy ideal of the MV-algebra A, whereIn fact, is precisely the L-fuzzy ideal ϕ defined in Example 2, thus is an L-fuzzy ideal of A. Corollary 1.
Let be a collection of MV-algebras and be the direct product of , where . If is the projection, then : is an L-fuzzy convexity-preserving mapping for every .
Proof. Obviously is an order-preserving ⊞-morphism between two MV-algebras, so by Theorem 7, we get is an L-fuzzy convexity preserving mapping for all . □
Proposition 5.
Let be a collection of MV-algebras and be the direct product of , where . Then .
Proof. Let
be the projection. It is clear that
. Since
is an
L-fuzzy ideal degree, we obtain
Since
is
L-fuzzy convexity preserving by Corollary 1, the last inequality holds. □
From [
25], we get
is an
L-convex structure for any
. The
L-convex hull of the
L-convex structure
is defined as follows: for
,
We denote all
L-fuzzy ideals in an MV-algebra by
. By Remark 1 we know,
. Thus
is precisely the least
L-fuzzy ideal containing
. In the following, we will give the concrete
L-convex hull formula.
Theorem 9.
Let and . DefineThen is the L-convex hull of the L-convex structure . Proof. We first show that
Firstly, we prove that
, that is,
is an
L-fuzzy ideal of
A.
Let
. For any
such that
, it must hold that
. Thus
Let
. Take
such that
. Then we obtain
and
. It follows that there exist
with
such that
and there exist
with
such that
Hence we obtain
and
This gives that
Thus
Therefore,
.
Next, we show that for any
with
, it holds that
. Since for any
,
we obtain
.
Hence Therefore, is the L-convex hull of the L-convex structure . □
 Let be a completely distributive lattice with Hasse diagram as follows.
Let be a completely distributive lattice with Hasse diagram as follows. 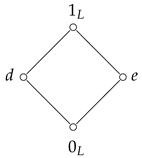 It is not difficult to see that the implication operation on L is induced as follows:
It is not difficult to see that the implication operation on L is induced as follows:




