Hyperparameter-Optimized RNN, LSTM, and GRU Models for Airline Stock Price Prediction: A Comparative Study on THYAO and PGSUS
Abstract
1. Introduction
2. Related Works
3. Materials and Methods
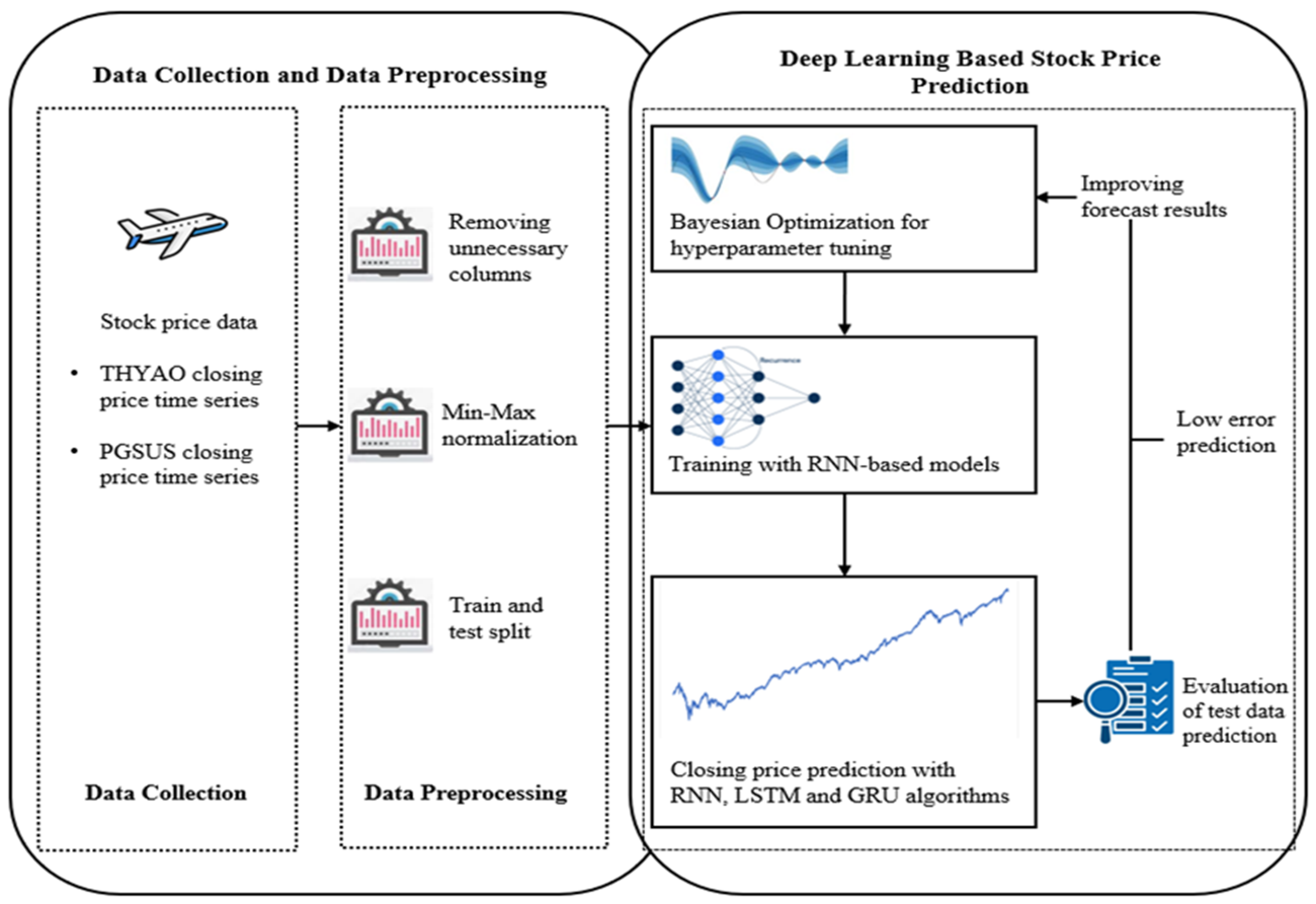
3.1. Deep Learning-Based Stock Price Prediction Model
3.2. RNN
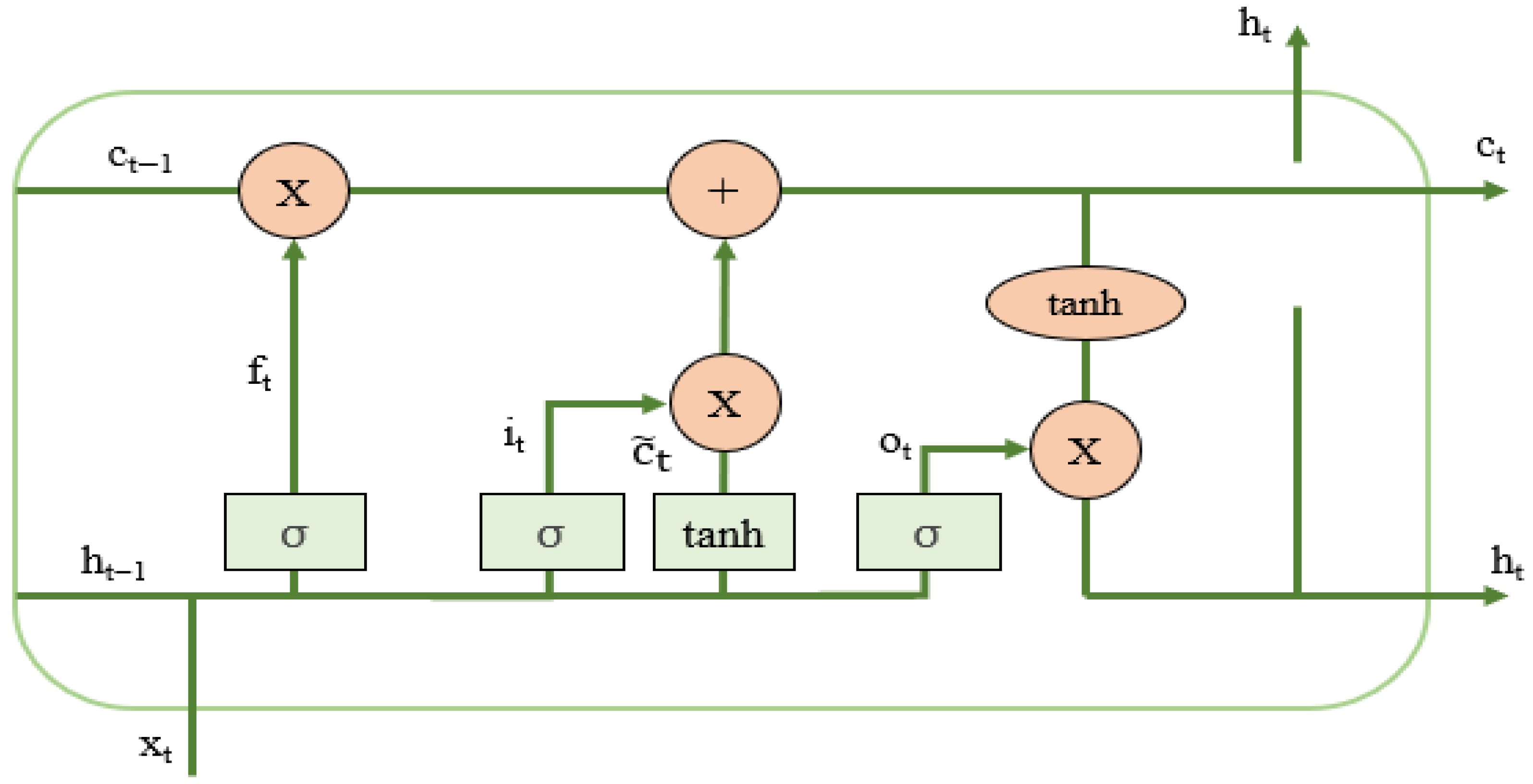
3.3. LSTM
- Candidate Cell State:
- 2.
- Input Gate: Controls how much of the candidate cell state is added:
- 3.
- Forget Gate: Regulates how much of the previous cell state is retained:
- 4.
- Cell State Update:
- 5.
- Output Gate: Determines the hidden state output:
- 6.
- Hidden State Calculation:
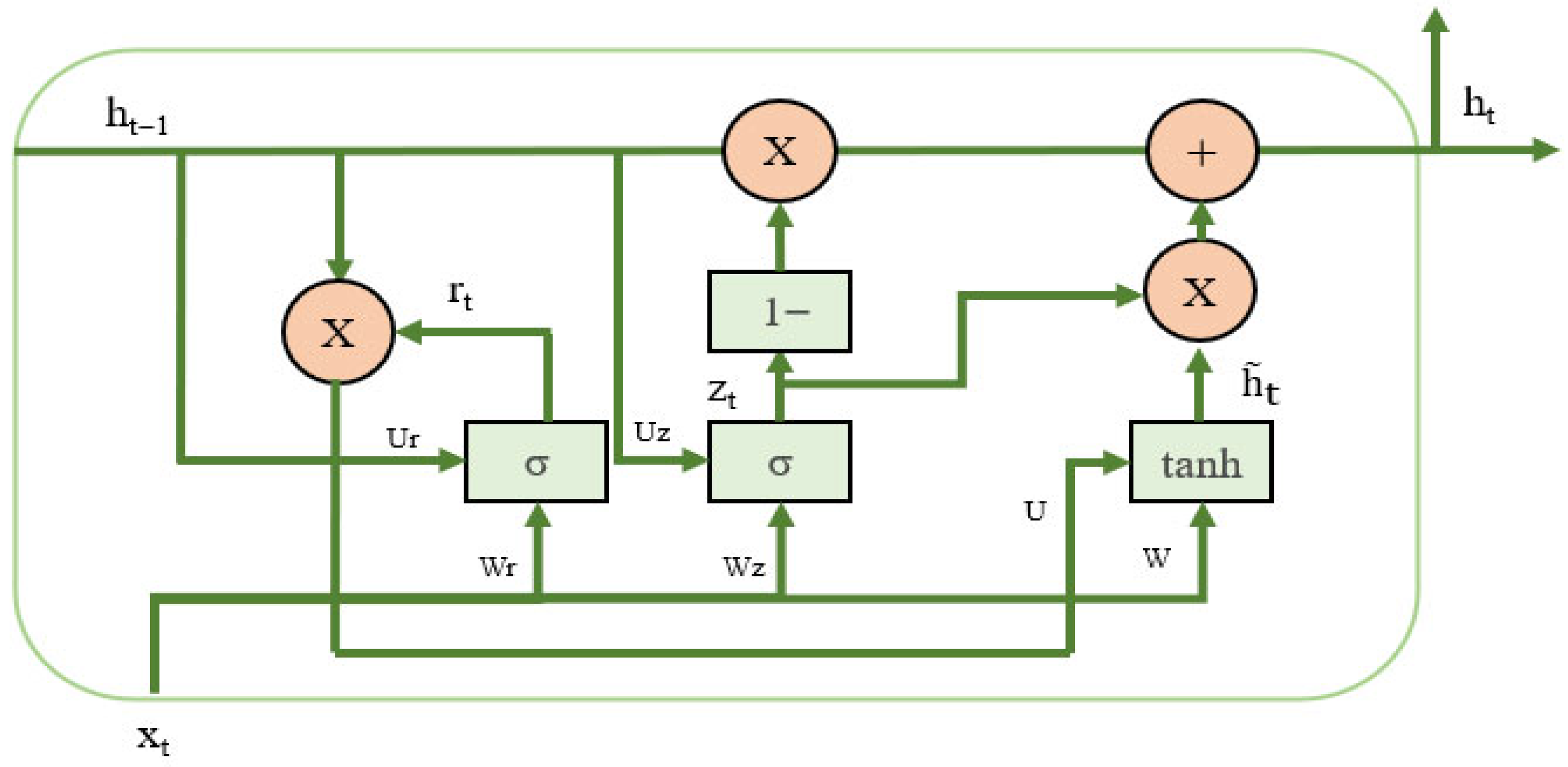
3.4. GRU
3.5. Hyperparameter Optimization
| Algorithm 1: Bayesian Optimization |
| for t = 1,2,3… Determine xt by optimizing the acquisition function u on function f: yt = f(xt) Augment the data D1:t = {D1:t−1, (xt,yt)} and update the posterior of function f End for |
3.6. Evaluation Metrics
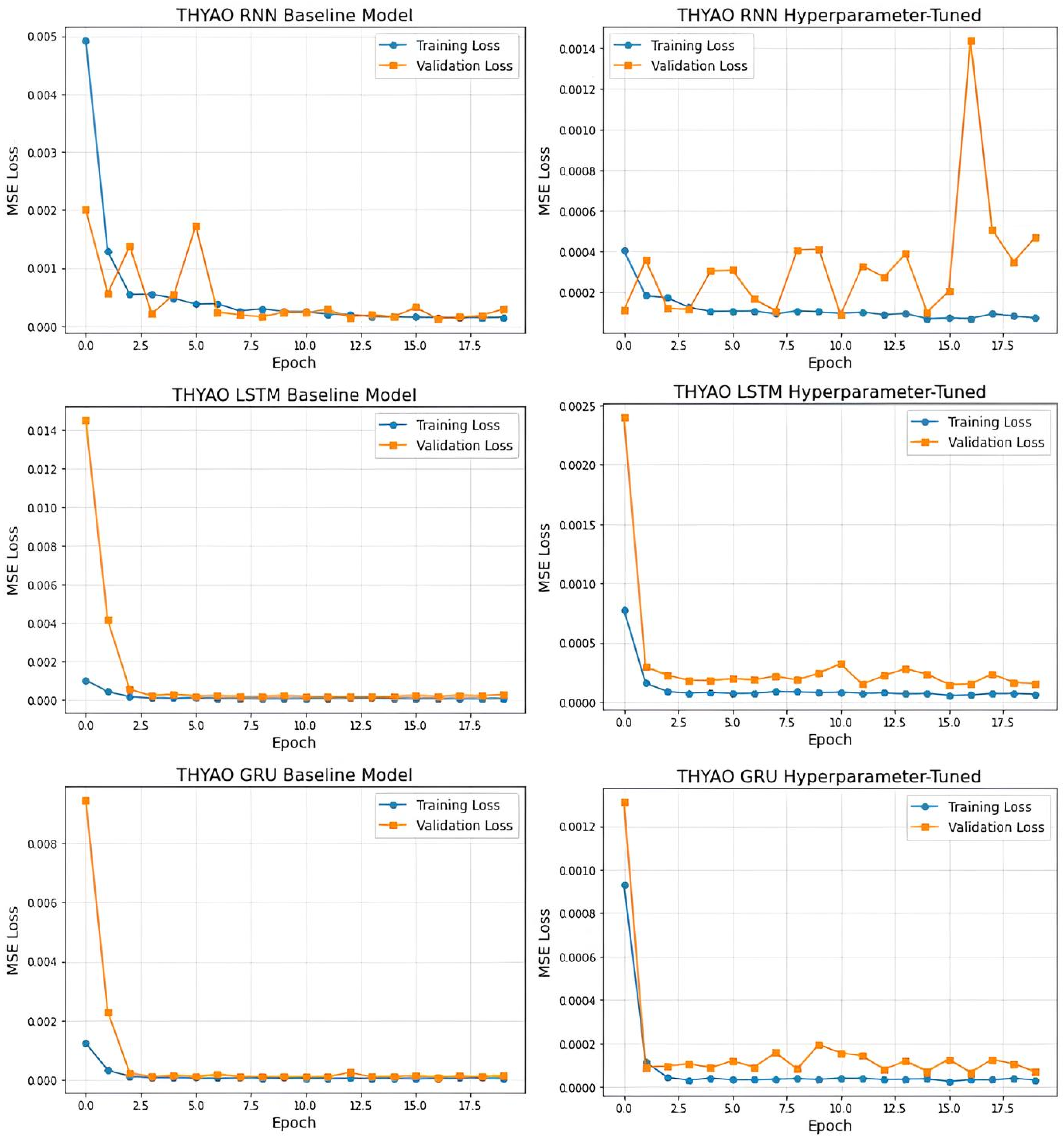
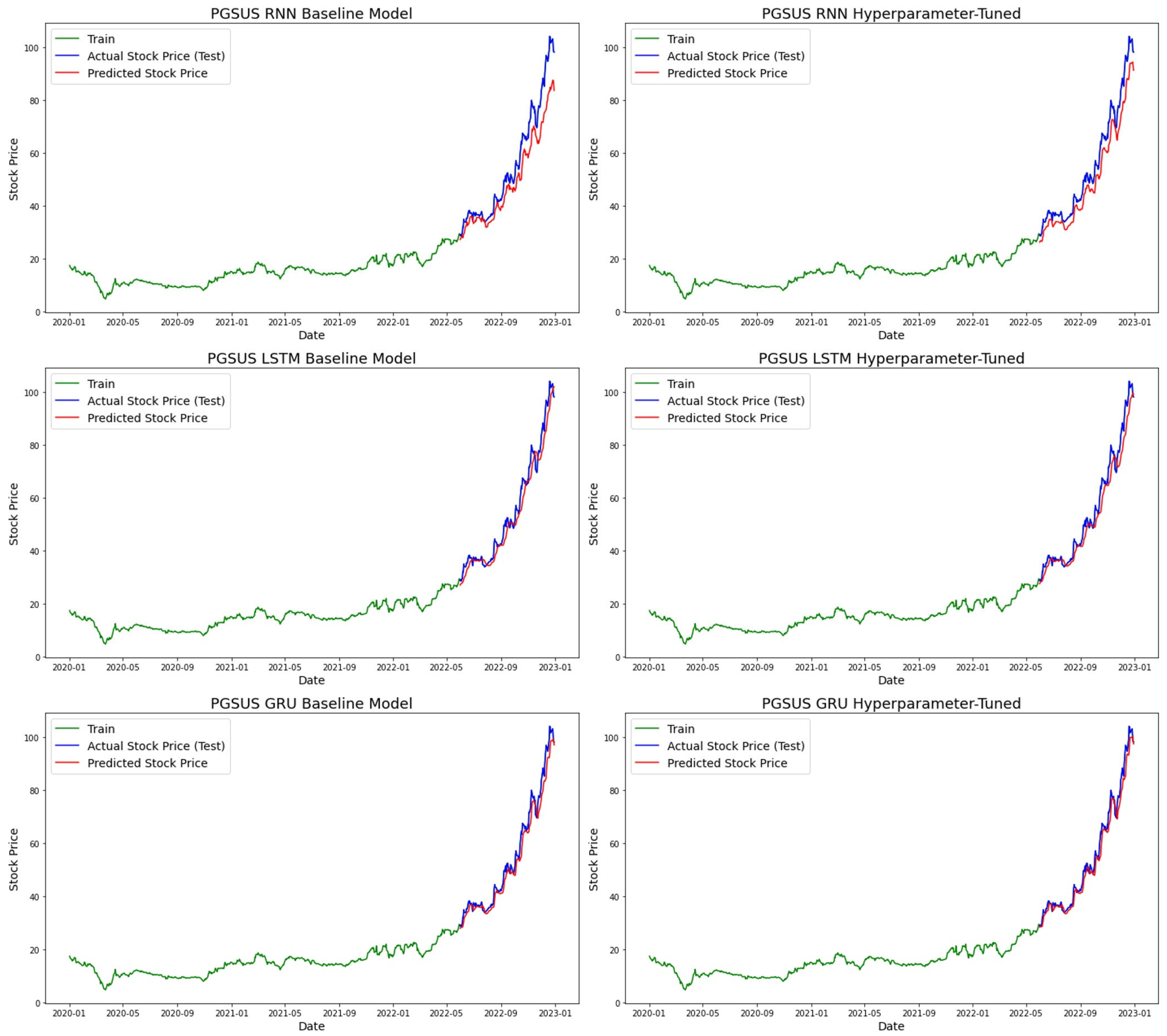
4. Results and Analysis
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Erden, C. Derin Öğrenme ve ARIMA Yöntemlerinin Tahmin Performanslarının Kıyaslanması: Bir Borsa İstanbul Hissesi Örneği. Yönetim Ekon. Derg. 2023, 30, 419–438. [Google Scholar] [CrossRef]
- Shahi, T.B.; Shrestha, A.; Neupane, A.; Guo, W. Stock price forecasting with deep learning: A comparative study. Mathematics 2020, 8, 1441. [Google Scholar] [CrossRef]
- Md, A.Q.; Kapoor, S.; AV, C.J.; Sivaraman, A.K.; Tee, K.F. Novel optimization approach for stock price forecasting using multi-layered sequential LSTM. Appl. Soft Comput. 2023, 134, 109830. [Google Scholar] [CrossRef]
- Ren, S.; Wang, X.; Zhou, X.; Zhou, Y. A novel hybrid model for stock price forecasting integrating Encoder Forest and Informer. Expert Syst. Appl. 2023, 234, 121080. [Google Scholar] [CrossRef]
- Horobet, A.; Zlatea, M.L.E.; Belascu, L.; Dumitrescu, D.G. Oil price volatility and airlines’ stock returns: Evidence from the global aviation industry. J. Bus. Econ. Manag. 2022, 23, 284–304. [Google Scholar] [CrossRef]
- Akusta, A. Time Series Analysis of Long-Term Stock Performance of Airlines: The case of Turkish Airlines. Polit. Ekon. Kuram 2024, 8, 160–173. [Google Scholar] [CrossRef]
- Xiao, D.; Su, J. Research on stock price time series prediction based on deep learning and autoregressive integrated moving average. Sci. Program. 2022, 2022, 4758698. [Google Scholar] [CrossRef]
- Ji, X.; Wang, J.; Yan, Z. A stock price prediction method based on deep learning technology. Int. J. Crowd Sci. 2021, 5, 55–72. [Google Scholar] [CrossRef]
- Mukherjee, S.; Sadhukhan, B.; Sarkar, N.; Roy, D.; De, S. Stock market prediction using deep learning algorithms. CAAI Trans. Intell. Technol. 2021, 8, 82–94. [Google Scholar] [CrossRef]
- Hoque, K.E.; Aljamaan, H. Impact of hyperparameter tuning on machine learning models in stock price forecasting. IEEE Access 2021, 9, 163815–163830. [Google Scholar] [CrossRef]
- Xu, X.; McGrory, C.A.; Wang, Y.; Wu, J. Influential factors on Chinese airlines’ profitability and forecasting methods. J. Air Transp. Manag. 2020, 91, 101969. [Google Scholar] [CrossRef]
- Chang, V.; Xu, Q.A.; Chidozie, A.; Wang, H. Predicting Economic Trends and Stock Market Prices with Deep Learning and Advanced Machine Learning Techniques. Electronics 2024, 13, 3396. [Google Scholar] [CrossRef]
- Kumar, R.; Kumar, P.; Kumar, Y. Multi-step time series analysis and forecasting strategy using ARIMA and evolutionary algorithms. Int. J. Inf. Technol. 2021, 14, 359–373. [Google Scholar] [CrossRef]
- Ji, G.; Yu, J.; Hu, K.; Xie, J.; Ji, X. An adaptive feature selection schema using improved technical indicators for predicting stock price movements. Expert Syst. Appl. 2022, 200, 116941. [Google Scholar] [CrossRef]
- Chen, Y.; Huang, W. Constructing a stock-price forecast CNN model with gold and crude oil indicators. Appl. Soft Comput. 2021, 112, 107760. [Google Scholar] [CrossRef]
- Mashadihasanli, T. Stock Market Price Forecasting Using the Arima Model: An Application to Istanbul, Turkiye. J. Econ. Policy Res./İktisat Polit. Araştırmaları Derg. 2022, 9, 439–454. [Google Scholar] [CrossRef]
- Ferdinand, F.V.; Santoso, T.H.; Saputra, K.V.I. Performance comparison between Facebook Prophet and SARIMA on Indonesian stock. In Proceedings of the 2023 IEEE International Conference on Industrial Engineering and Engineering Management (IEEM), Singapore, 18–21 December; pp. 1–5.
- Henrique, B.M.; Sobreiro, V.A.; Kimura, H. Stock price prediction using support vector regression on daily and up to the minute prices. J. Financ. Data Sci. 2018, 4, 183–201. [Google Scholar] [CrossRef]
- Gorde, P.S.; Borkar, S.N. Comparative analysis of linear regression, random forest regressor and LSTM for stock price prediction. In Proceedings of the 2024 8th International Conference on Computing, Communication, Control and Automation (ICCUBEA), Pune, India, 23–24 August 2024; pp. 1–5. [Google Scholar]
- Raudys, A.; Goldstein, E. Forecasting detrended volatility risk and financial price series using LSTM neural networks and XGBOOST Regressor. J. Risk Financ. Manag. 2022, 15, 602. [Google Scholar] [CrossRef]
- Ecer, F.; Ardabili, S.; Band, S.S.; Mosavi, A. Training Multilayer Perceptron with Genetic Algorithms and Particle Swarm Optimization for Modeling Stock Price Index Prediction. Entropy 2020, 22, 1239. [Google Scholar] [CrossRef]
- Khuat, T.T.; Le, M.H. An application of artificial neural networks and fuzzy logic on the stock price prediction problem. JOIV Int. J. Inform. Vis. 2017, 1, 40–49. [Google Scholar]
- Sunny, M.a.I.; Maswood, M.M.S.; Alharbi, A.G. Deep Learning-Based Stock Price Prediction using LSTM and Bi-Directional LSTM model. In Proceedings of the 2020 2nd Novel Intelligent and Leading Emerging Sciences Conference (NILES), Giza, Egypt, 24–26 October 2020; pp. 87–92. [Google Scholar]
- Bhavani, A.; Ramana, A.V.; Chakravarthy, A.S.N. Comparative Analysis between LSTM and GRU in Stock Price Prediction. In Proceedings of the 2022 International Conference on Edge Computing and Applications (ICECAA), Tamilnadu, India, 13–15 October 2022; pp. 532–537. [Google Scholar]
- Lu, W.; Li, J.; Li, Y.; Sun, A.; Wang, J. A CNN-LSTM-Based model to forecast stock prices. Complexity 2020, 2020, 6622927. [Google Scholar] [CrossRef]
- Chen, Y.; Fang, R.; Liang, T.; Sha, Z.; Li, S.; Yi, Y.; Zhou, W.; Song, H. Stock price forecast based on CNN-BILSTM-ECA model. Sci. Program. 2021, 2021, 2446543. [Google Scholar] [CrossRef]
- Xu, C.; Li, J.; Feng, B.; Lu, B. A financial time-series prediction model based on multiplex attention and linear transformer structure. Appl. Sci. 2023, 13, 5175. [Google Scholar] [CrossRef]
- Li, X.; Chen, S.; Qiao, X.; Zhang, M.; Zhang, C.; Zhao, F. Multi-perspective Learning Based on Transformer for Stock Price Trend. Int. J. Comput. Intell. Syst. 2025, 18, 1–18. [Google Scholar] [CrossRef]
- Bhandari, H.N.; Rimal, B.; Pokhrel, N.R.; Rimal, R.; Dahal, K.R.; Khatri, R.K. Predicting stock market index using LSTM. Mach. Learn. Appl. 2022, 9, 100320. [Google Scholar] [CrossRef]
- Chong, E.; Han, C.; Park, F.C. Deep learning networks for stock market analysis and prediction: Methodology, data representations, and case studies. Expert Syst. Appl. 2017, 83, 187–205. [Google Scholar] [CrossRef]
- Gupta, U.; Bhattacharjee, V.; Bishnu, P.S. StockNet—GRU based stock index prediction. Expert Syst. Appl. 2022, 207, 117986. [Google Scholar] [CrossRef]
- Chandra, R.; Chand, S. Evaluation of co-evolutionary neural network architectures for time series prediction with mobile application in finance. Appl. Soft Comput. 2016, 49, 462–473. [Google Scholar] [CrossRef]
- Naik, N.; Mohan, B.R. Novel Stock Crisis Prediction Technique—A Study on Indian Stock Market. IEEE Access 2021, 9, 86230–86242. [Google Scholar] [CrossRef]
- Aker, Y. Analysis of price volatility in BIST 100 index with time series: Comparison of Fbprophet and LSTM model. Avrupa Bilim Ve Teknol. Derg. 2022, 35, 89–93. [Google Scholar] [CrossRef]
- Liu, B.; Yu, Z.; Wang, Q.; Du, P.; Zhang, X. Prediction of SSE Shanghai Enterprises index based on bidirectional LSTM model of air pollutants. Expert Syst. Appl. 2022, 204, 117600. [Google Scholar] [CrossRef]
- Zhou, C. Long Short-term Memory Applied on Amazon’s Stock Prediction. Highlights Sci. Eng. Technol. 2023, 34, 71–76. [Google Scholar] [CrossRef]
- Saini, A.; Singh, N.; Singh, R.K.; Sachan, M.K. Financial Time Series Prediction on Apple stocks using machine and deep learning models. In Proceedings of the 2024 International Conference on Electrical, Computer and Energy Technologies (ICECET), Sydney, Australia, 25–27 July 2024; pp. 1–6. [Google Scholar]
- Gülmez, B. Stock price prediction with optimized deep LSTM network with artificial rabbits optimization algorithm. Expert Syst. Appl. 2023, 227, 120346. [Google Scholar] [CrossRef]
- Zhang, J.; Ye, L.; Lai, Y. Stock price prediction using CNN-BILSTM-Attention model. Mathematics 2023, 11, 1985. [Google Scholar] [CrossRef]
- Ali, M.; Khan, D.M.; Alshanbari, H.M.; El-Bagoury, A.A.-A.H. Prediction of complex stock market data using an improved hybrid EMD-LSTM model. Appl. Sci. 2023, 13, 1429. [Google Scholar] [CrossRef]
- Jaiswal, R.; Singh, B. A hybrid convolutional recurrent (CNN-GRU) model for stock price prediction. In Proceedings of the 2022 IEEE 11th International Conference on Communication Systems and Network Technologies (CSNT), Indore, India, 23–24 April 2022; pp. 299–304. [Google Scholar]
- Song, H.; Choi, H. Forecasting stock market indices using the recurrent neural network based hybrid models: CNN-LSTM, GRU-CNN, and ensemble models. Appl. Sci. 2023, 13, 4644. [Google Scholar] [CrossRef]
- Singh, U.; Tamrakar, S.; Saurabh, K.; Vyas, R.; Vyas, O. Optimizing hyperparameters of deep learning models for stock price prediction. In Proceedings of the 2024 15th International Conference on Computing Communication and Networking Technologies (ICCCNT), Kamand, India, 24–28 June 2024; pp. 1–7. [Google Scholar]
- Chauhan, A.; Shivaprakash, S.J.; Sabireen, H.; Md, A.Q.; Venkataraman, N. Stock price forecasting using PSO hypertuned neural nets and ensembling. Appl. Soft Comput. 2023, 147, 110835. [Google Scholar] [CrossRef]
- Chung, H.; Shin, K. Genetic Algorithm-Optimized Long Short-Term Memory Network for stock market prediction. Sustainability 2018, 10, 3765. [Google Scholar] [CrossRef]
- Chen, X.; Yang, F.; Sun, Q.; Yi, W. Research on stock prediction based on CED-PSO-StockNet time series model. Sci. Rep. 2024, 14, 27462. [Google Scholar] [CrossRef]
- Yan, J.; Huang, Y. MambaLLM: Integrating Macro-Index and Micro-Stock Data for Enhanced Stock Price Prediction. Mathematics 2025, 13, 1599. [Google Scholar] [CrossRef]
- Torres, J.F.; Hadjout, D.; Sebaa, A.; Martínez-Álvarez, F.; Troncoso, A. Deep learning for Time Series Forecasting: A survey. Big Data 2020, 9, 3–21. [Google Scholar] [CrossRef] [PubMed]
- Lu, M.; Xu, X. TRNN: An efficient time-series recurrent neural network for stock price prediction. Inf. Sci. 2023, 657, 119951. [Google Scholar] [CrossRef]
- Sagheer, A.; Kotb, M. Time series forecasting of petroleum production using deep LSTM recurrent networks. Neurocomputing 2018, 323, 203–213. [Google Scholar] [CrossRef]
- Hochreiter, S.; Schmidhuber, J. Long Short-Term memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef]
- Cao, J.; Li, Z.; Li, J. Financial time series forecasting model based on CEEMDAN and LSTM. Phys. A Stat. Mech. Its Appl. 2018, 519, 127–139. [Google Scholar] [CrossRef]
- Mahjoub, S.; Chrifi-Alaoui, L.; Marhic, B.; Delahoche, L. Predicting energy consumption using LSTM, Multi-Layer GRU and Drop-GRU neural networks. Sensors 2022, 22, 4062. [Google Scholar] [CrossRef]
- Pirani, M.; Thakkar, P.; Jivrani, P.; Bohara, M.H.; Garg, D. A comparative analysis of ARIMA, GRU, LSTM and BILSTM on financial Time Series forecasting. In Proceedings of the 2022 IEEE International Conference on Distributed Computing and Electrical Circuits and Electronics (ICDCECE), Ballari, India, 23–24 April 2022; pp. 1–6. [Google Scholar]
- Önder, G.T. Comparative Time series analysis of SARIMA, LSTM, and GRU models for global SF6 emission Management System. J. Atmos. Sol. -Terr. Phys. 2024, 265, 106393. [Google Scholar] [CrossRef]
- Jiang, X.; Xu, C. Deep Learning and Machine Learning with Grid Search to Predict Later Occurrence of Breast Cancer Metastasis Using Clinical Data. J. Clin. Med. 2022, 11, 5772. [Google Scholar] [CrossRef]
- Bergstra, J.; Bengio, Y. Random search for hyper-parameter optimization. J. Mach. Learn. Res. 2012, 13, 281–305. [Google Scholar]
- Snoek, J.; Larochelle, H.; Adams, R.P. Practical bayesian optimization of machine learning algorithms. In Proceedings of the Neural Information Processing Systems, Red Hook, NY, USA, 3–6 December 2012; Volume 2. [Google Scholar]
- Lee, S.; Kim, J.; Kang, H.; Kang, D.; Park, J. Genetic algorithm based deep learning neural network structure and hyperparameter optimization. Appl. Sci. 2021, 11, 744. [Google Scholar] [CrossRef]
- Teixeira, D.M.; Barbosa, R.S. Stock Price Prediction in the Financial Market Using Machine Learning Models. Computation 2024, 13, 3. [Google Scholar] [CrossRef]
- Chen, P.; Boukouvalas, Z.; Corizzo, R. A deep fusion model for stock market prediction with news headlines and time series data. Neural Comput. Appl. 2024, 36, 21229–21271. [Google Scholar] [CrossRef]
- Yang, L.; Shami, A. On hyperparameter optimization of machine learning algorithms: Theory and practice. Neurocomputing 2020, 415, 295–316. [Google Scholar] [CrossRef]
- Wu, J.; Chen, X.Y.; Zhang, H.; Xiong, L.D.; Lei, H.; Deng, S.H. Hyperparameter optimization for machine learning models based on Bayesian optimization. J. Electron. Sci. Technol. 2019, 17, 26–40. [Google Scholar]



| Reference | Data | Forecasting Target | Time Interval | Proposed Model |
|---|---|---|---|---|
| [29] | S&P 500 index | Closing price | 2006–2020 | LSTM |
| [30] | KOSPI market | Stock returns | 2010–2014 | DNN |
| [31] | CNX-Nift | Opening price | 1996–2020 | GRU |
| [32] | NASDAQ | Closing price | 2006–2010 | RNN |
| [23] | Google stock market | Stock price | 2004–2019 | LSTM, BiLSTM |
| [33] | NIFTY 50 | Stock crisis event | 2007–2021 | DNN |
| [34] | BIST-100 index | Closing price | 2021–2021 | LSTM |
| [35] | SSE Shanghai Enterprises index | Closing price | 2014–2020 | GRU, LSTM, BiLSTM |
| [36] | Amazon’s stock | Opening price | 1997–2021 | LSTM |
| [37] | Apple Stocks | Closing price | 2018–2023 | LSTM, CNN |
| [38] | DJIA index | Stock price | 2018–2023 | Rabbits Optimization algorithm (ARO)-LSTM |
| [39] | CSI300 index | Closing price | 2011–2021 | CNN-BiLSTM |
| [40] | KSE-100 index | Closing price | 2015–2022 | Empirical Mode Decomposition (EMD)-LSTM |
| [41] | Tesla Stock Price | Closing price | 2010–2017 | CNN-RNN, CNN-LSTM, CNN-GRU |
| [42] | DOW | Closing price | 2000–2019 | CNN-LSTM, GRU-CNN |
| Layer | Hyperparameter | Search Range |
|---|---|---|
| Layer 1 | Hidden unit (per layer) | 32, 50, 64, 96 or 128 |
| Activation functions | ReLU, tanh or sigmoid | |
| Dropout rate (ratio) | 0.2, 0.3, 0.4 or 0.5 | |
| Layer 2 | Hidden unit (per layer) | 32, 50, 64, 96 or 128 |
| Activation functions | ReLU, tanh or sigmoid | |
| Dropout rate (ratio) | 0.2, 0.3, 0.4 or 0.5 | |
| Global | Optimization solver | Adam or Rmsprop |
| Model | Variant | MSE | RMSE | MAE | MedAE | MAPE (%) |
|---|---|---|---|---|---|---|
| RNN | Baseline | 120.036 | 10.956 | 8.653 | 6.031 | 9.390 |
| RNN | Hyperparameter-Tuned | 75.904 | 8.712 | 7.614 | 6.552 | 9.060 |
| LSTM | Baseline | 21.436 | 4.630 | 3.396 | 2.363 | 4.200 |
| LSTM | Hyperparameter-Tuned | 15.466 | 3.933 | 2.973 | 2.297 | 3.650 |
| GRU | Baseline | 14.181 | 3.766 | 2.655 | 1.664 | 3.220 |
| GRU | Hyperparameter-Tuned | 10.206 | 3.195 | 2.432 | 1.878 | 3.050 |
| Model | Variant | MSE | RMSE | MAE | MedAE | MAPE (%) |
|---|---|---|---|---|---|---|
| RNN | Baseline | 65.980 | 8.123 | 6.283 | 4.641 | 9.790 |
| RNN | Hyperparameter-Tuned | 36.882 | 6.073 | 5.273 | 4.294 | 9.270 |
| LSTM | Baseline | 17.098 | 4.135 | 3.185 | 2.231 | 5.560 |
| LSTM | Hyperparameter-Tuned | 19.186 | 4.380 | 3.263 | 2.318 | 5.460 |
| GRU | Baseline | 13.598 | 3.688 | 2.730 | 1.743 | 4.630 |
| GRU | Hyperparameter-Tuned | 10.443 | 3.232 | 2.326 | 1.391 | 3.970 |
| Compared Model | Metric | GRU Tuned Mean | Other_Mean | Better Model | Wilcoxon Statistic | p_Value |
|---|---|---|---|---|---|---|
| RNN (Tuned) | MAPE (%) | 2.991 | 9.080 | GRU (Tuned) | 3 | 0.0098 |
| RNN (Tuned) | RMSE | 3.263 | 9.110 | GRU (Tuned) | 3 | 0.0098 |
| LSTM (Tuned) | MAPE (%) | 2.991 | 4.617 | GRU (Tuned) | 0 | 0.0020 |
| LSTM (Tuned) | RMSE | 3.263 | 4.876 | GRU (Tuned) | 1 | 0.0039 |
| GRU (Baseline) | MAPE (%) | 2.991 | 3.397 | GRU (Tuned) | 12 | 0.1309 |
| GRU (Baseline) | RMSE | 3.263 | 3.673 | GRU (Tuned) | 14 | 0.1934 |
| Compared Model | Metric | GRU Tuned Mean | Other_Mean | Better Model | Wilcoxon Statistic | p_Value |
|---|---|---|---|---|---|---|
| RNN (Tuned) | MAPE (%) | 3.882 | 14.075 | GRU (Tuned) | 0 | 0.0020 |
| RNN (Tuned) | RMSE | 3.088 | 9.902 | GRU (Tuned) | 1 | 0.0039 |
| LSTM (Tuned) | MAPE (%) | 3.882 | 7.089 | GRU (Tuned) | 0 | 0.0020 |
| LSTM (Tuned) | RMSE | 3.088 | 5.238 | GRU (Tuned) | 0 | 0.0020 |
| GRU (Baseline) | MAPE (%) | 3.882 | 4.559 | GRU (Tuned) | 17 | 0.3223 |
| GRU (Baseline) | RMSE | 3.088 | 3.621 | GRU (Tuned) | 12 | 0.1309 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sezgin, F.H.; Algorabi, Ö.; Sart, G.; Güler, M. Hyperparameter-Optimized RNN, LSTM, and GRU Models for Airline Stock Price Prediction: A Comparative Study on THYAO and PGSUS. Symmetry 2025, 17, 1905. https://doi.org/10.3390/sym17111905
Sezgin FH, Algorabi Ö, Sart G, Güler M. Hyperparameter-Optimized RNN, LSTM, and GRU Models for Airline Stock Price Prediction: A Comparative Study on THYAO and PGSUS. Symmetry. 2025; 17(11):1905. https://doi.org/10.3390/sym17111905
Chicago/Turabian StyleSezgin, Funda H., Ömer Algorabi, Gamze Sart, and Mustafa Güler. 2025. "Hyperparameter-Optimized RNN, LSTM, and GRU Models for Airline Stock Price Prediction: A Comparative Study on THYAO and PGSUS" Symmetry 17, no. 11: 1905. https://doi.org/10.3390/sym17111905
APA StyleSezgin, F. H., Algorabi, Ö., Sart, G., & Güler, M. (2025). Hyperparameter-Optimized RNN, LSTM, and GRU Models for Airline Stock Price Prediction: A Comparative Study on THYAO and PGSUS. Symmetry, 17(11), 1905. https://doi.org/10.3390/sym17111905






