Experimental and Numerical Investigation of Projectile Penetration into Thin Concrete Targets at an Angle of Attack
Abstract
1. Introduction
- Studies on the Influence of Incidence and Attack Angles: He Xiang et al. [1] developed a theoretical model to analyze the oblique penetration of projectiles into layered geomaterials such as soil and concrete, which showed good agreement with experimental data. Duan et al. investigated the evolution of projectile attitude during the penetration of concrete targets at non-zero incidence angles, identifying several characteristic stages and correlating them with target responses [2]. Dong et al. [3,4] and Chen et al. [5] conducted both experimental and numerical studies on oblique penetration, highlighting the effects of projectile geometry and incidence angle on attitude deviation and penetration depth. Dong et al. [6] further investigated penetration characteristics of pyramidal projectiles into concrete targets, expanding the understanding of shape influence on penetration mechanisms. Moreover, Li et al. [7,8] proposed models addressing projectile blunting and asymmetric flow fields, emphasizing their impact on trajectory stability.
- Research on Concrete Material Properties: to enhance penetration resistance, attention has shifted toward ultra-high-performance concrete (UHPC) and steel–concrete composite structures. Sun et al. [9] found that fiber-reinforced UHPC effectively suppresses asymmetric crater formation. Ning et al. [10] compared the penetration resistance of UHPC and granite, demonstrating UHPC’s superior performance. Sun et al. [11] highlighted that interfacial bonding strength governs the efficiency of oblique penetration. The studies by Wang et al. [12] and Jurecs et al. [13] further analyzed the evolution of attack angle and residual mass in extremely high-strength concrete.
- Numerical Modeling and Experimental Investigations: Li et al. [14] compared four widely used concrete strength models and found that the RHT and TCK models better capture concrete damage, while the HJC and KCC models provide more accurate predictions of residual projectile velocity. Teng et al. [15] analyzed the response of reinforced concrete under oblique impact using finite element methods, providing early insights into concrete damage mechanisms under inclined loading. Yang et al. [16] conducted combined attack angle and obliquity penetration tests using a 152 mm hydrogen-driven gun, verifying the applicability of the ACE and Forrestal formulas under oblique impact conditions. Chen et al. [17] proposed an approximate method for predicting the penetration depth of rigid projectiles into concrete targets covered with yaw-inducing layers, considering the effects of tilt and attack angles and validating the model through experiments. Li et al. [7] established a two-dimensional oblique penetration trajectory model, emphasizing the role of asymmetric ejecta in deflecting trajectories. In terms of experimental observation, Jiang et al. [18] investigated the mechanism of multilayer interfacial structures and demonstrated how the presence of water layers further intensified the evolution of projectile attitude.
2. Experimental Investigation
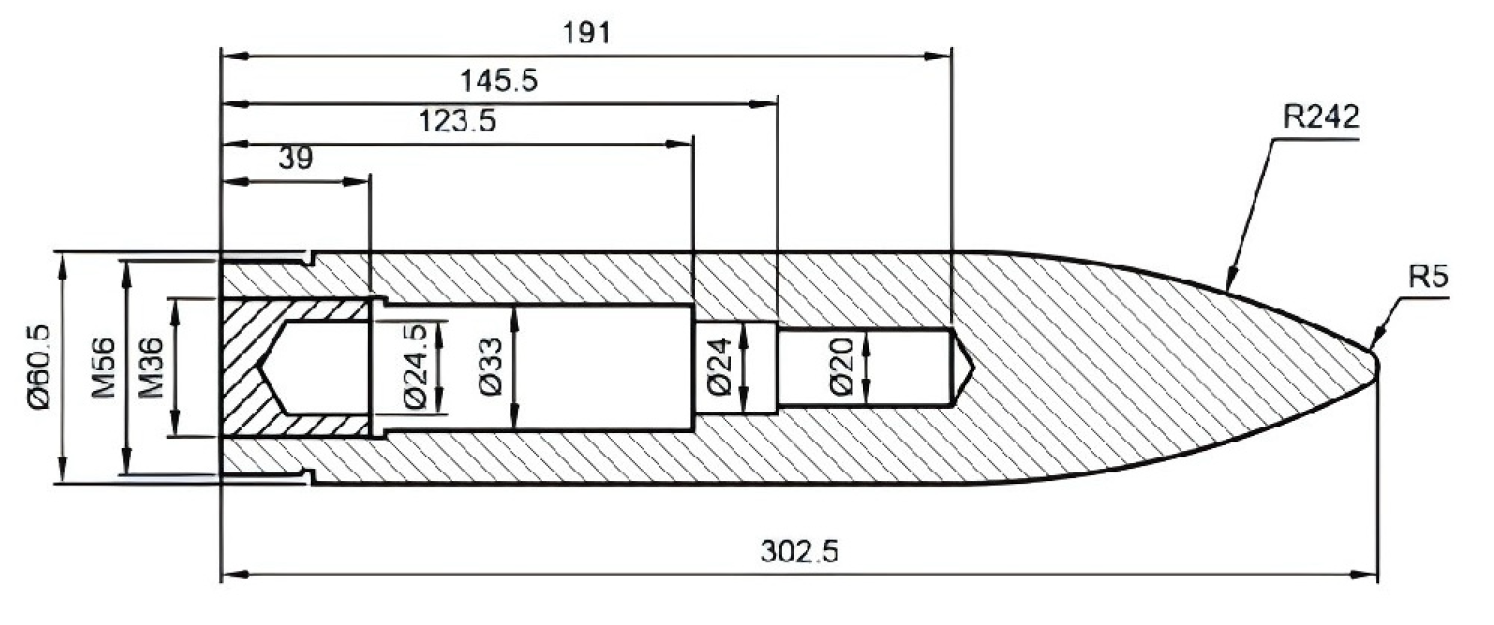
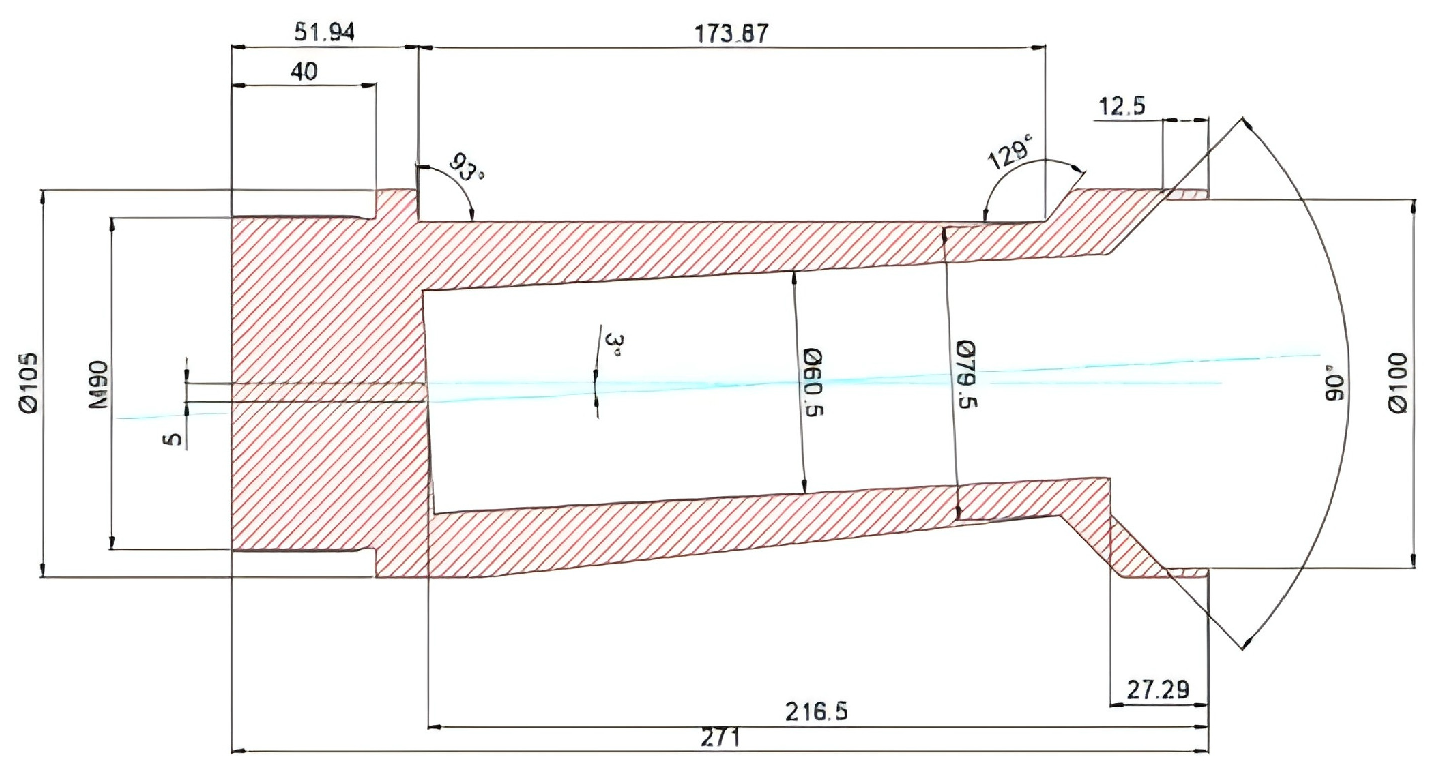
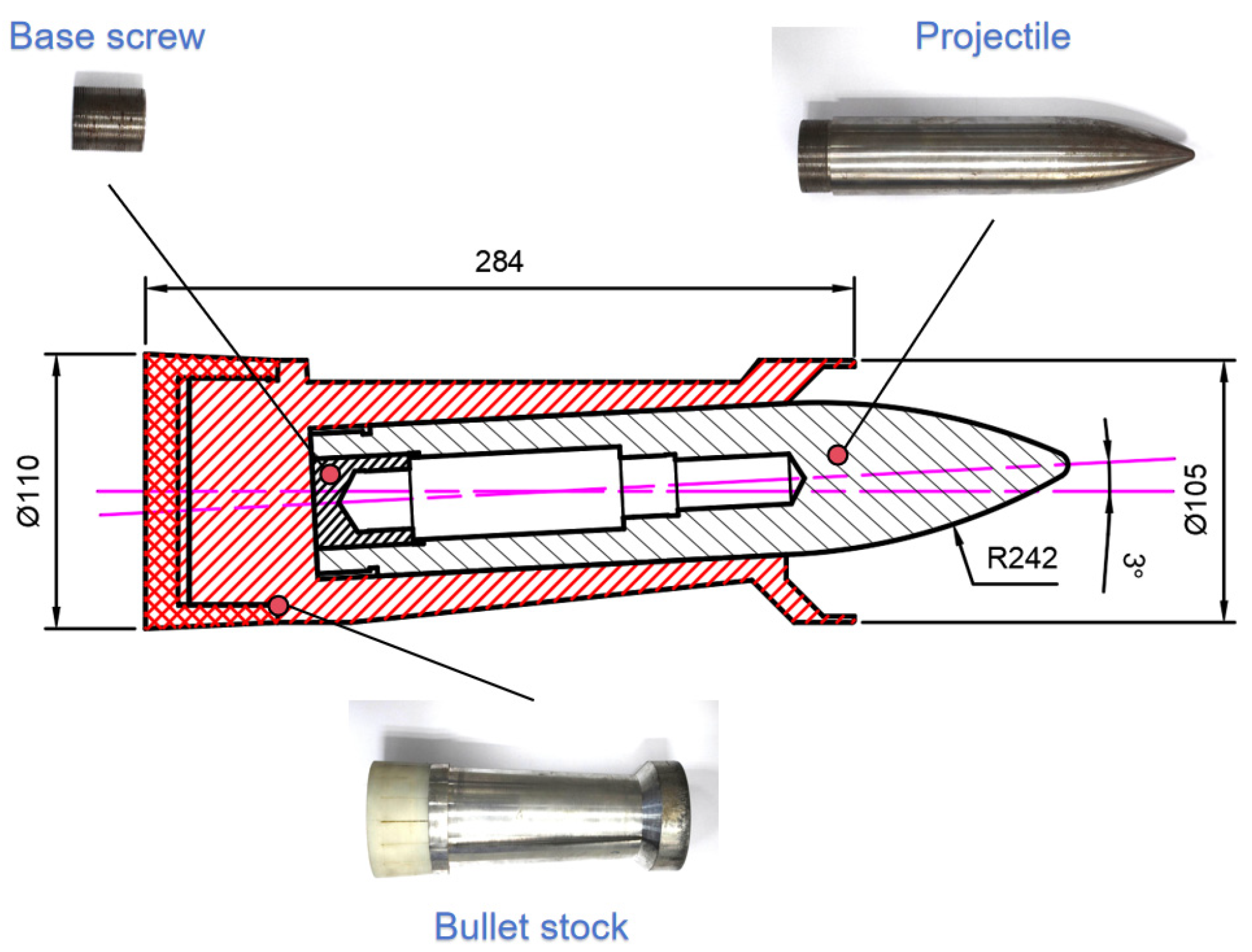
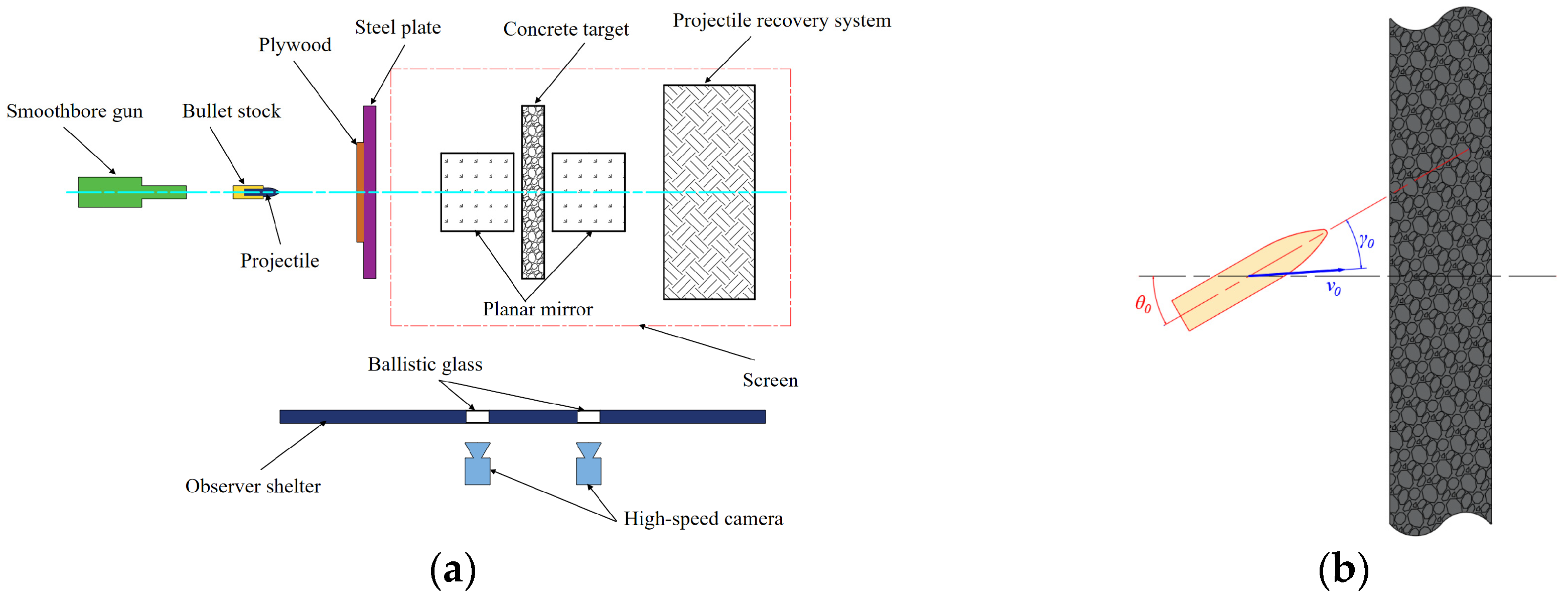
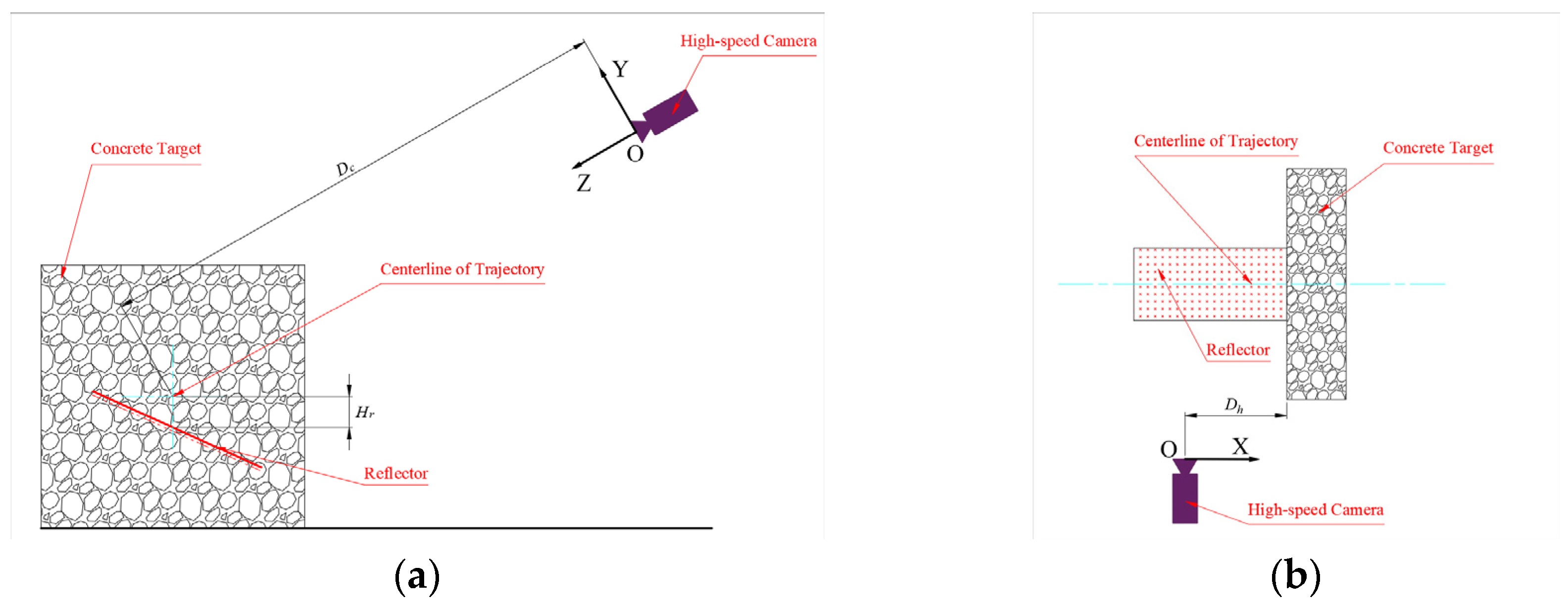
2.1. Experimental Design
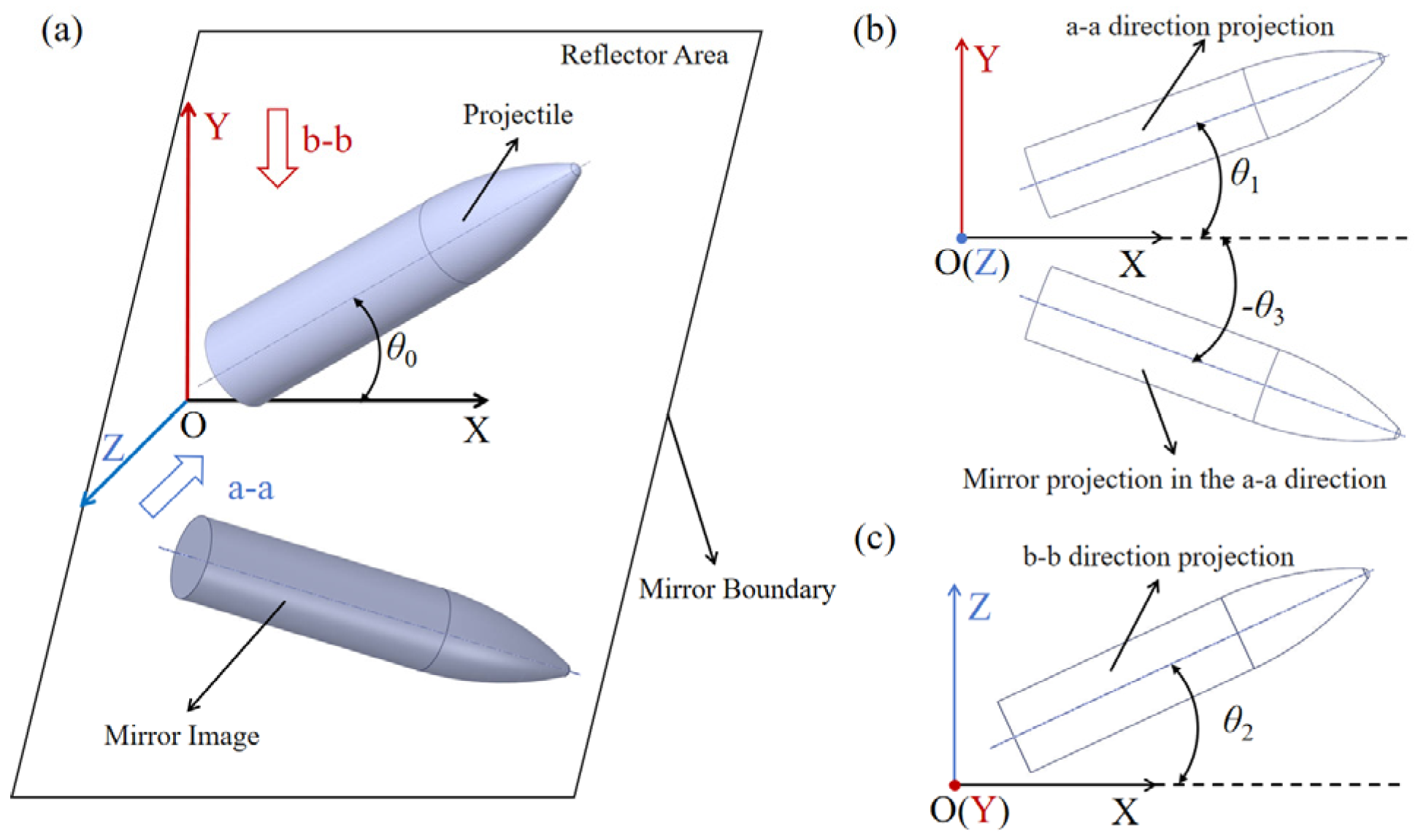
2.2. Measurement System
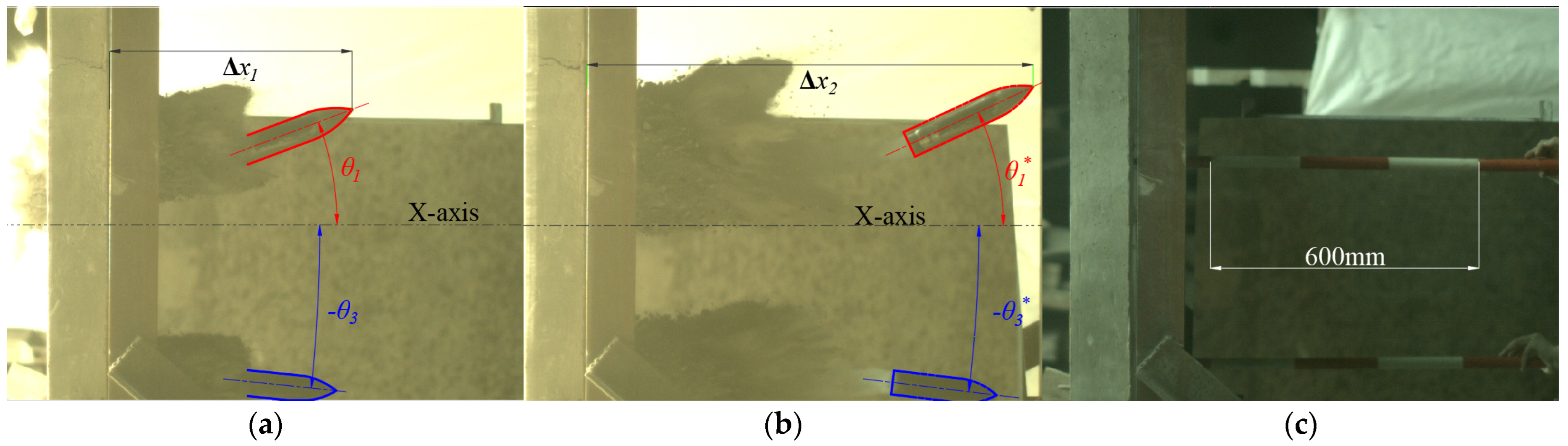
2.3. Experimental Results and Analysis
2.4. Analysis of Experimental Errors
3. Numerical Investigation
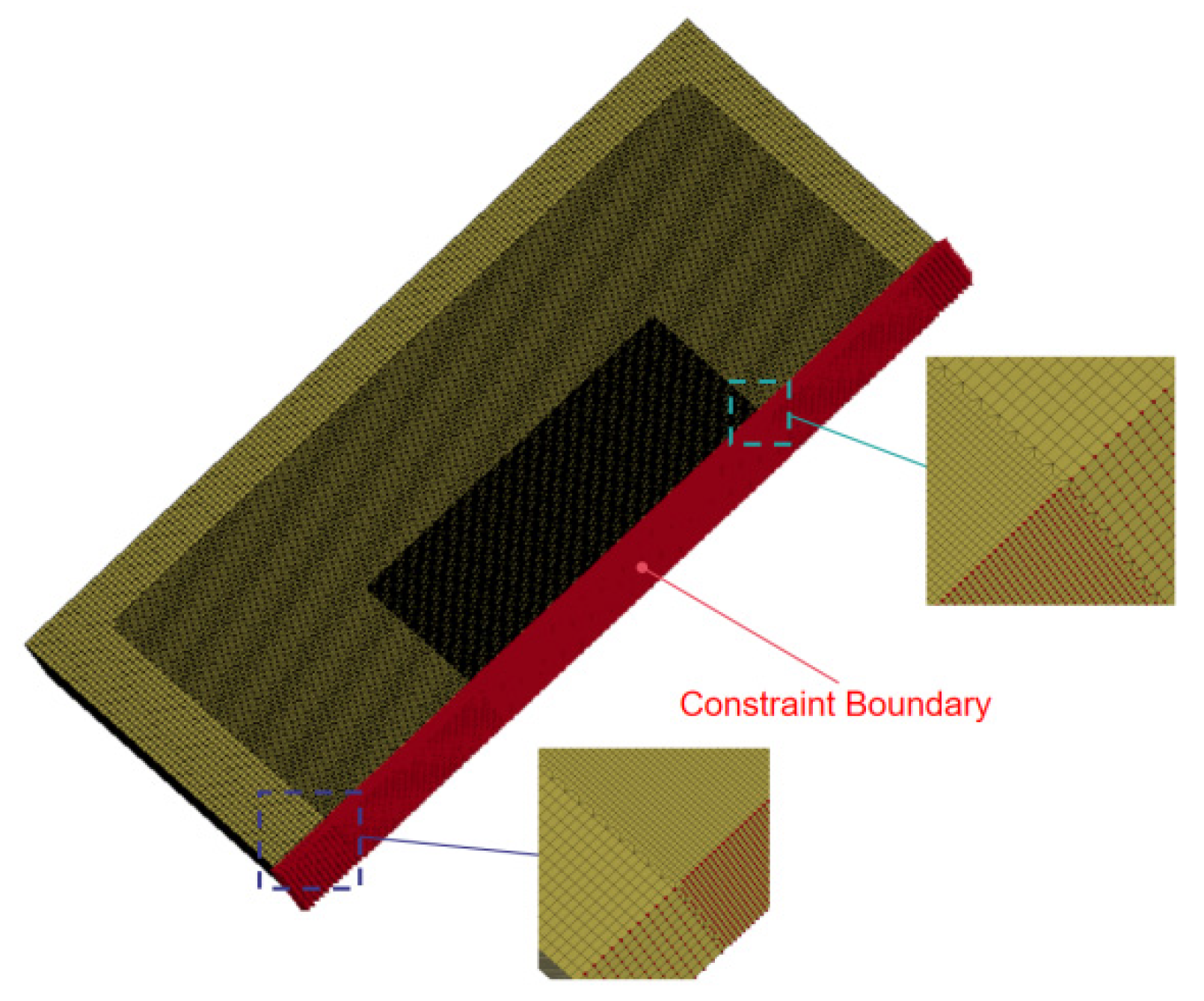
3.1. Introduction of Numerical Model
3.2. Mesh Convergence Analysis
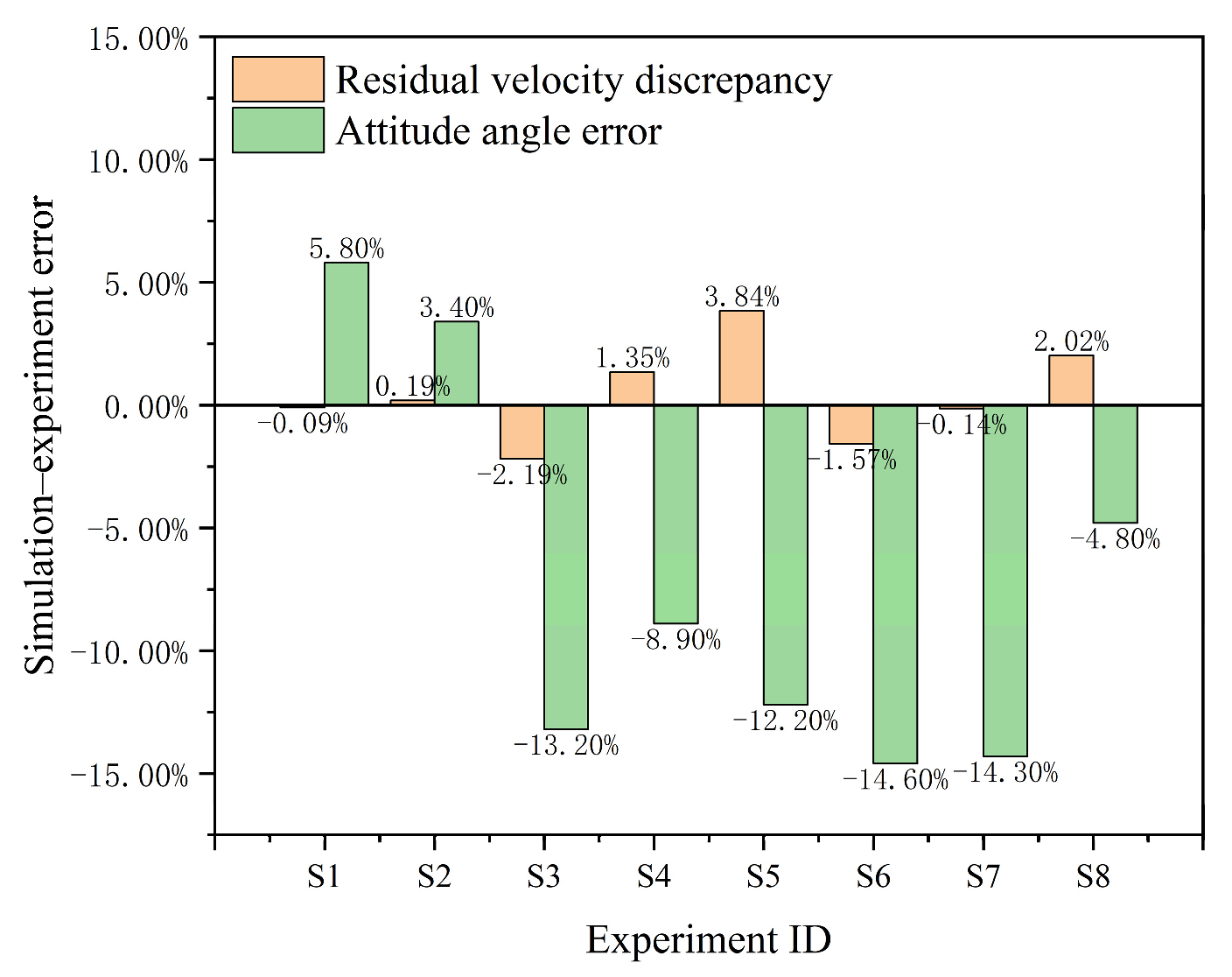
3.3. Validation of Numerical Model
3.4. Numerical Analyses
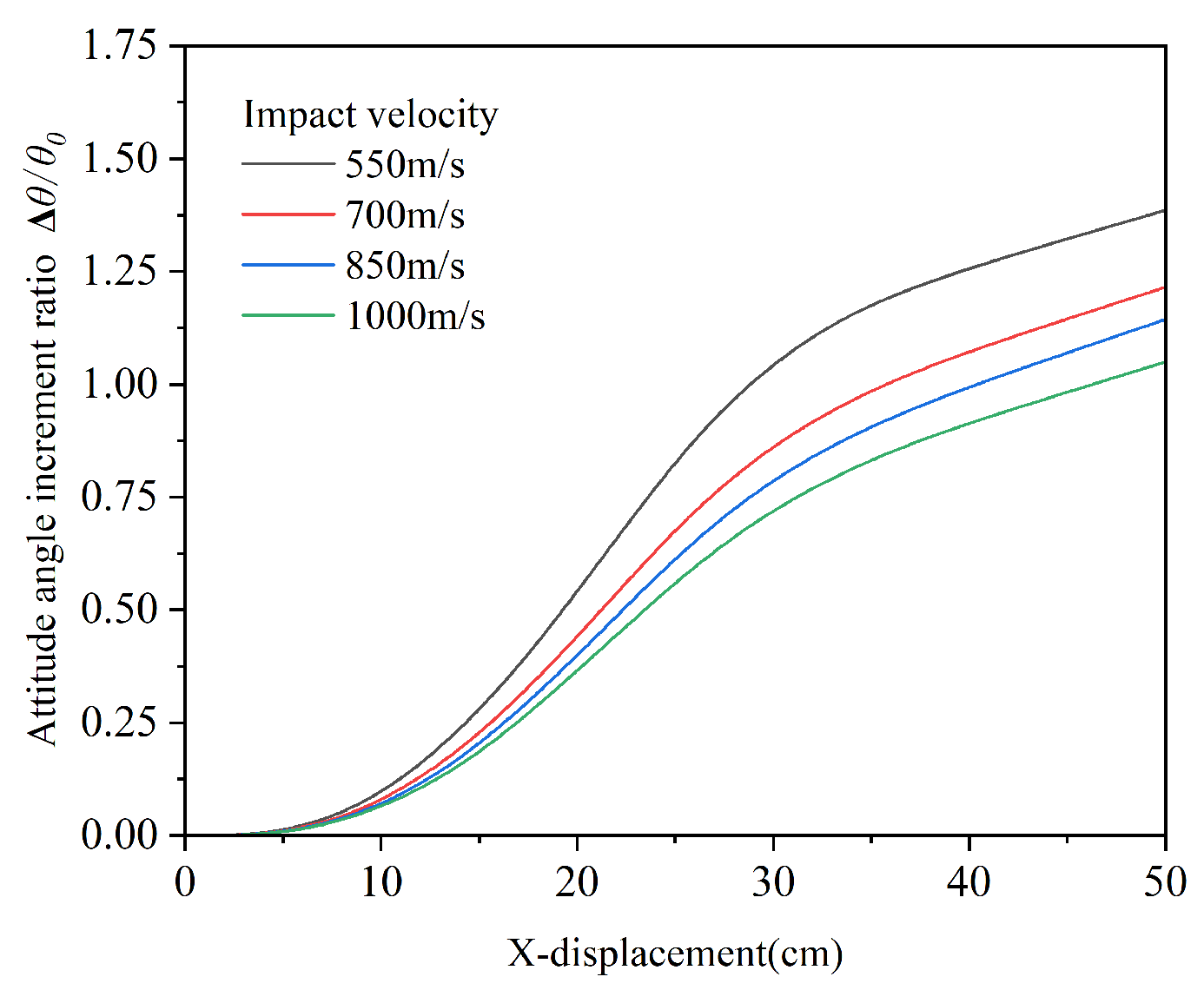
3.4.1. Influence of Impact Velocity
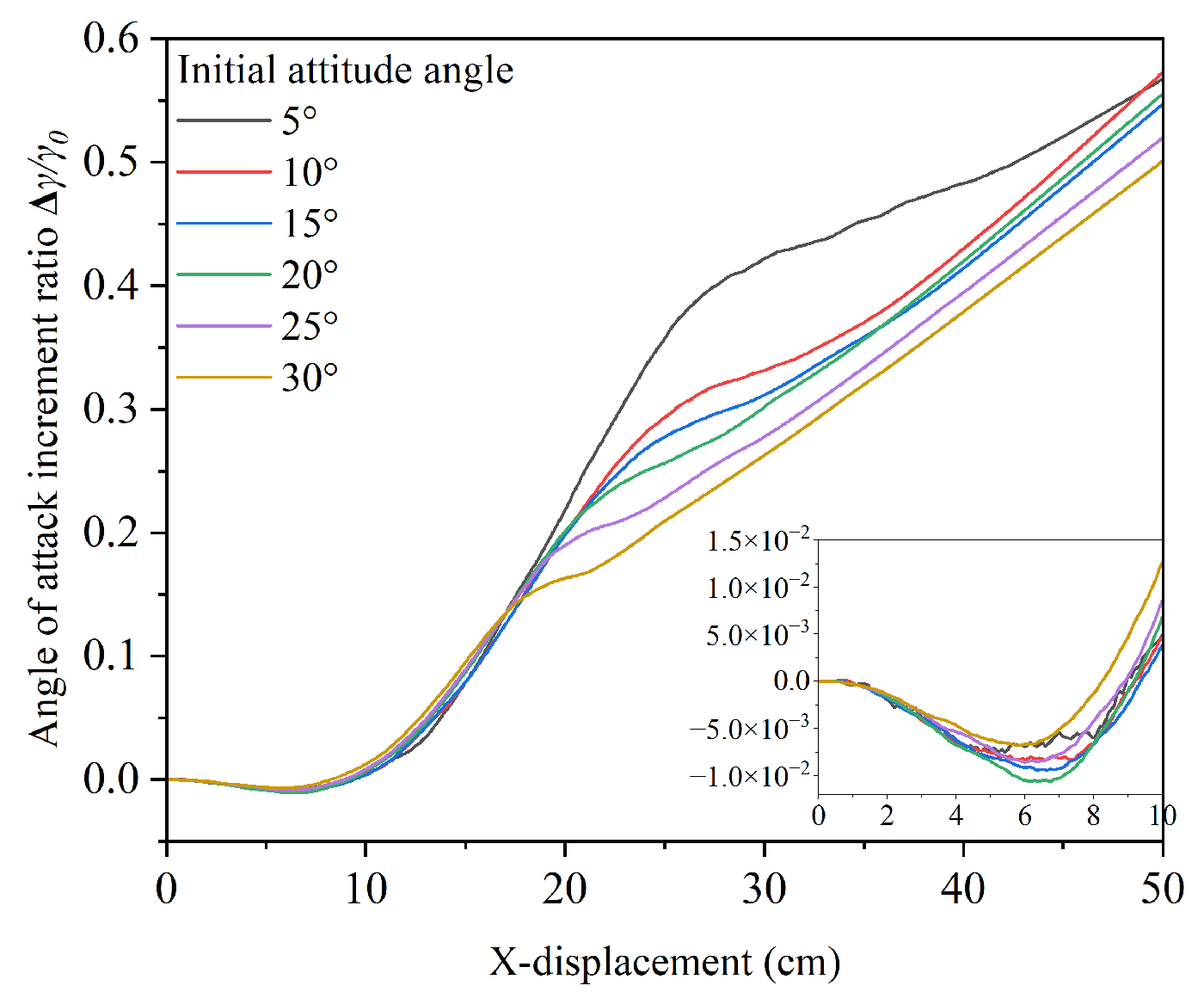
3.4.2. Influence of Initial Attitude Angle
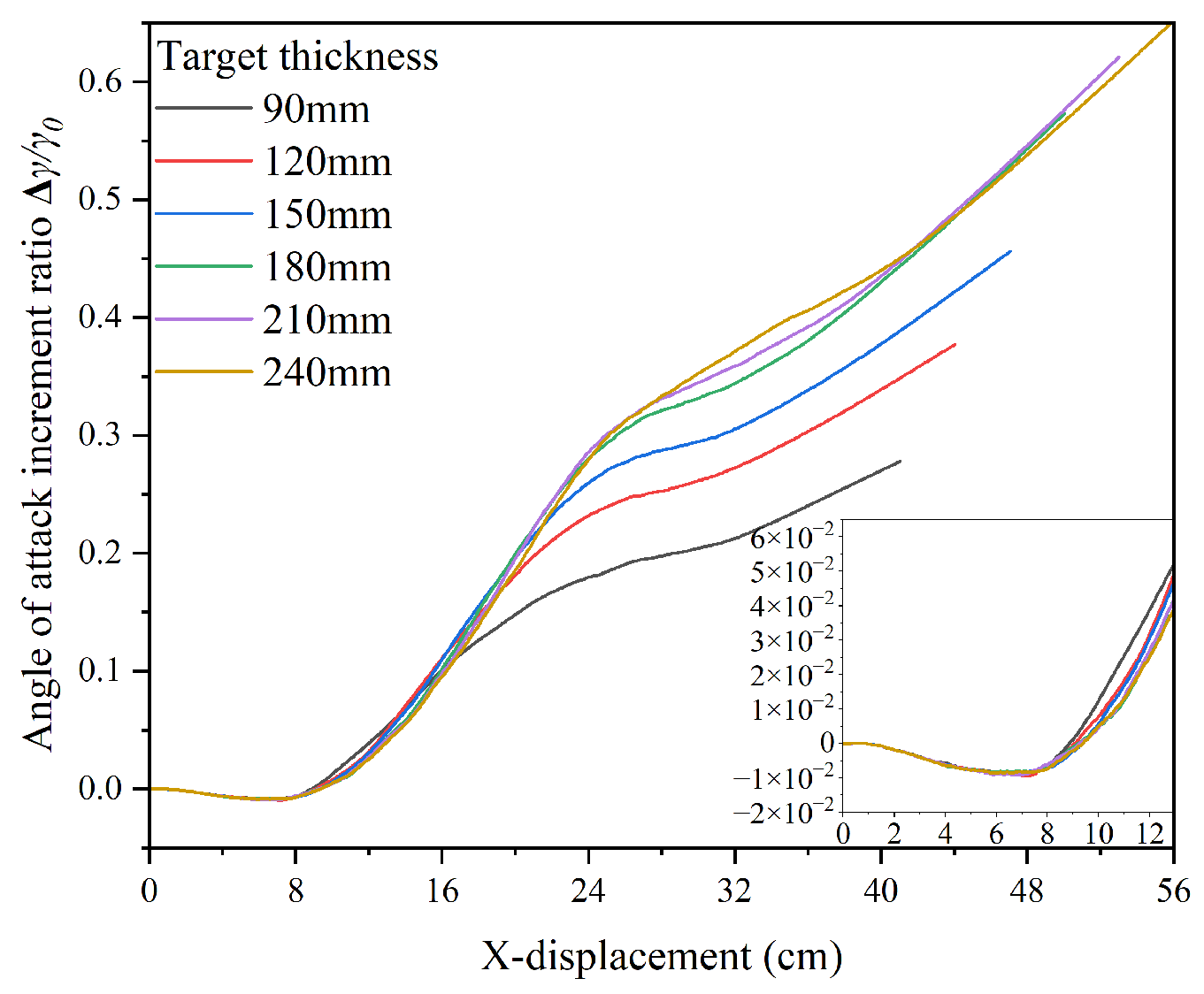
3.4.3. Influence of Target Plate Thickness
4. Conclusions
- The use of a three-petal bullet stock with offset geometry, as designed in this study, in combination with a smoothbore gun, effectively establishes a controllable angle of attack penetration condition. When integrated with the projectile flight attitude measurement system, this setup enables accurate measurement and recording of key parameters during angle of attack penetration tests into concrete targets. Due to the resolution limitations of the high-speed imaging system, the projectile contour becomes partially obscured by dust after perforating the target, which reduces the measurable profile and increases the error in the calculated three-dimensional attitude angle. Despite this limitation, the measurement error remains within 5°. This setup, while tailored to short-range impact conditions, establishes a methodological basis for extended applications with projectile trajectory considerations.
- By employing the RHT strength model along with a suitably refined mesh, the numerical simulation successfully captures the oblique penetration behavior of projectiles penetrating concrete targets. The simulated horizontal velocity deviates from experimental measurements by less than 5%, and the attitude angle error remains within 4°, demonstrating good agreement and model fidelity.
- During angle of attack penetration into thin concrete targets, the post-penetration attitude angle of the projectile is negatively correlated with its velocity and positively correlated with the target plate thickness.
- The evolution of the projectile’s angle of attack throughout the penetration process can be divided into four distinct stages:
- -
- In the crater formation stage, the angle of attack gradually decreases.
- -
- In the penetration plugging stage, it increases rapidly.
- -
- During the breakthrough plugging stage, the growth slows down.
- -
- After exiting the target, the angle of attack increases at a constant angular velocity.
- Under varying initial attitude angles, the post-penetration attitude angle increases with the initial attitude angle. However, both the attitude angle rate and angle of attack rate reach their maximum values when the initial attitude angle is around 15° and then gradually decrease as the initial attitude angle continues to increase. An increase in the initial attitude angle leads to stronger non-axial forces acting on the projectile, which in turn amplify the deflecting moment. This causes a portion of the translational kinetic energy to be converted into rotational kinetic energy about the transverse axis, thereby inducing greater fluctuations in the horizontal velocity. These findings are in agreement with the results reported by Dong and Chen et al.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
AI Statement
References
- He, X.; Sun, G.; Xu, X.; Yang, J. Theoretical analysis of oblique penetration of projectiles with a certain angle of attack into concrete and rock media. In Proceedings of the National Conference on Structural Safety and Protection Engineering, Luoyang, China, 16–21 August 2007. (In Chinese). [Google Scholar]
- Duan, Z.; Li, S.; Ma, Z.; Ou, Z.; Huang, F. Attitude deflection of oblique perforation of concrete targets by a rigid projectile. Def. Technol. 2019, 15, 700–707. [Google Scholar] [CrossRef]
- Dong, H.; Liu, Z.; Wu, H.; Gao, X.; Pi, A.; Huang, F. Study on penetration characteristics of high-speed elliptical cross-sectional projectiles into concrete. Int. J. Impact Eng. 2019, 132, 103311. [Google Scholar] [CrossRef]
- Dong, H.; Wu, H.; Ren, G.; Lv, Y.; Quan, X.; Li, M.; Huang, F. Complexity of space trajectory and macro-micro failure mechanism of elliptical projectile penetrating concrete at high velocity. Int. J. Impact Eng. 2025, 169, 105386. [Google Scholar] [CrossRef]
- Chen, X.; Lu, F.; Zhang, D. Penetration trajectory of concrete targets by ogived steel projectiles—experiments and simulations. Int. J. Impact Eng. 2018, 122, 202–213. [Google Scholar] [CrossRef]
- Dong, H.; Wu, H.; Liu, Z.; Gao, X.; Pi, A.; Li, J.; Huang, F. Penetration characteristics of pyramidal projectile into concrete target. Int. J. Impact Eng. 2020, 143, 103583. [Google Scholar] [CrossRef]
- Li, X.; Liu, Y.; Yan, J.; Shi, Z.; Wang, H.; Xu, Y.; Huang, F. High-speed penetration of ogive-nose projectiles into thick concrete targets. Def. Technol. 2024, 20, 11–23. [Google Scholar] [CrossRef]
- Li, P.; Zhang, X.; Liu, C.; Deng, Y.; Sheng, Q.; Wang, J. Trajectory characteristics of oblique penetration of projectile into concrete targets considering cratering effect. Int. J. Impact Eng. 2024, 185, 104864. [Google Scholar] [CrossRef]
- Sun, W.; Zhang, W.; Yan, J.; Gao, X.; Wu, Y.; Ni, W.; Feng, J. Multi-scale study on penetration performance of steel fiber reinforced ultra-high performance concrete. Constr. Build. Mater. 2022, 330, 127263. [Google Scholar] [CrossRef]
- Ning, H.; Ren, H.; Wang, W.; Nie, X. Impact resistance of ultra-high-performance concrete composite structures. Materials 2023, 16, 7456. [Google Scholar] [CrossRef] [PubMed]
- Sun, S.; He, X.; Liu, F.; Chen, J.; Gou, S. Experimental and numerical investigation on anti-penetration mechanism of steel-concrete composite structures. Structures 2025, 71, 108083. [Google Scholar] [CrossRef]
- Wang, W.; Song, X.; Yang, J.; Liu, F.; Gao, W. Experimental and numerical research on the effect of ogive-nose projectile penetrating UR50 ultra-early-strength concrete. Cemen. Concr. Compo. 2023, 136, 104902. [Google Scholar] [CrossRef]
- Jurecs, S.P.; Tabei, A. Simulation of the Effects of Angle of Attack and Projectile Contour in Damage Development in Reinforced Concrete. Designs 2021, 5, 49. [Google Scholar] [CrossRef]
- Li, J.; Liu, Y.; Li, P.; Wang, H.; Chen, P. Study on the suitability of concrete constitutive models for perforation simulation. Materials 2024, 17, 5562. [Google Scholar] [CrossRef] [PubMed]
- Teng, T.; Chu, Y.; Chang, F.; Chin, H. Numerical analysis of oblique impact on reinforced concrete. Cemen. Concr. Compo. 2005, 27, 481–492. [Google Scholar] [CrossRef]
- Yang, Z.; Lv, Z.; Wu, B. Comparative analysis of depth prediction formulas for oblique penetration of projectiles with angle of attack into concrete. J. Ordnance Equip. Eng. 2014, 35, 37–40. (In Chinese) [Google Scholar]
- Chen, W.; Zhang, Y.; Guo, Z.; Zou, H. Penetration of rigid projectile into concrete target with effect of attack angle: Theory and experiment. Int. J. Struct. Stab. Dyn. 2017, 17, 1750080. [Google Scholar] [CrossRef]
- Jiang, A. Study of attitude deflection and trajectory yawing mechanism of concrete wedge-water layer combination structures for long rod ogive-nosed projectiles. Int. J. Impact Eng. 2025, 204, 105392. [Google Scholar] [CrossRef]
- Warren, T.L.; Poormon, K.L. Penetration of 6061-t6511 aluminum targets by ogive-nosed var 4340 steel projectiles at oblique angles: Experiments and simulations. Int. J. Impact Eng. 2001, 25, 993–1022. [Google Scholar] [CrossRef]
- Zhang, H.; Xiang, X.; Huang, B.; Wu, Z.; Chen, H. Static homotopy response analysis of structure with random variables of arbitrary distributions by minimizing stochastic residual error. Comput. Struct. 2023, 288, 107153. [Google Scholar] [CrossRef]
- Wu, C. Research on Anti-Penetration Performance of Concrete Target at Mesoscale. Ph.D. Thesis, Nanjing University of Science & Technology, Nanjing, China, 2019, unpublished. [Google Scholar]
- Jia, T.; Wu, H.; Dong, H.; Cheng, L.; Zheng, Z. Numerical Simulation Study on the Mechanical Properties of Concrete Under Rapid Stress Cycling. In Proceedings of the International Conference on Computational & Experimental Engineering and Sciences, Changsha, China, 25–29 May 2025; Springer: Cham, Switzerland, 2025. [Google Scholar]







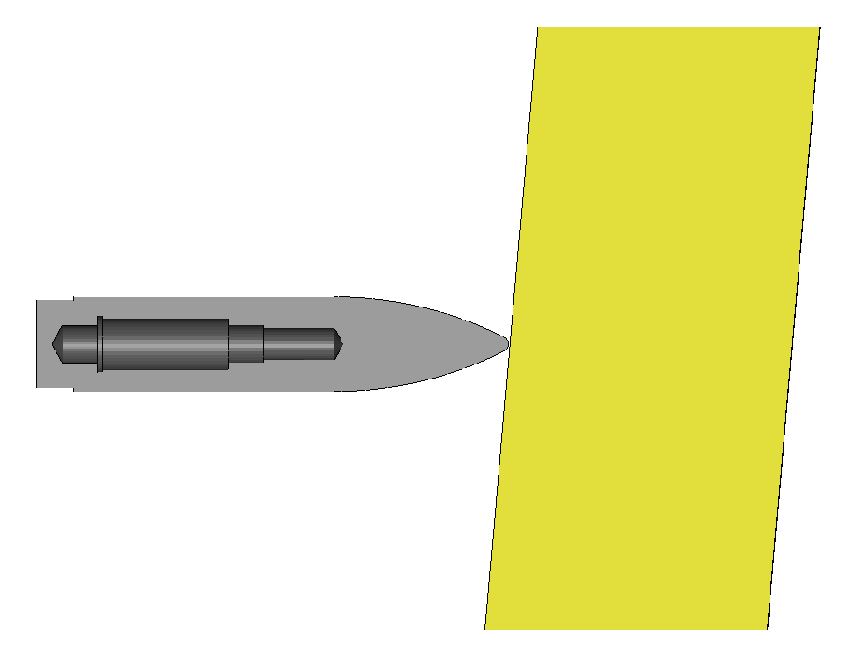
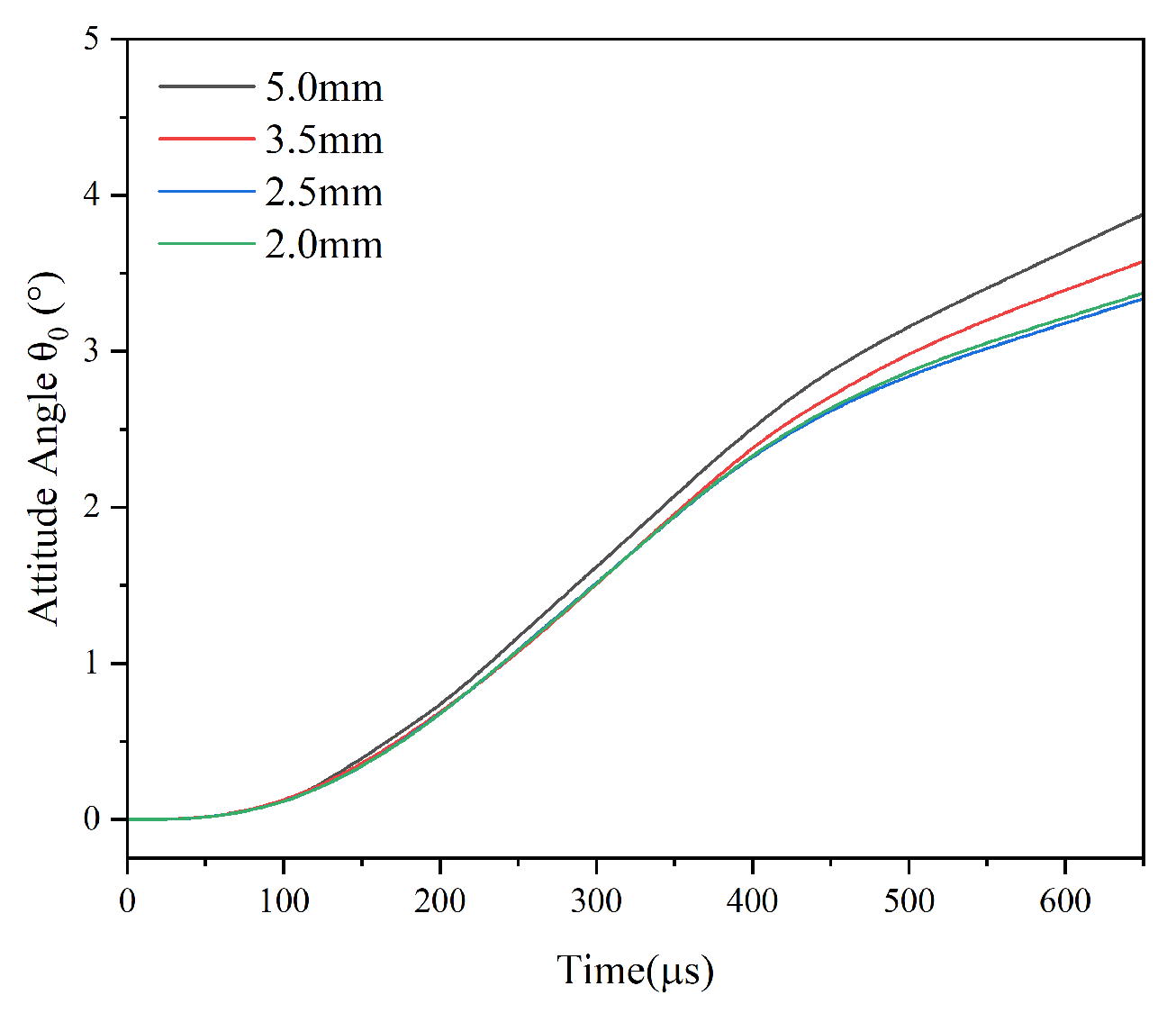
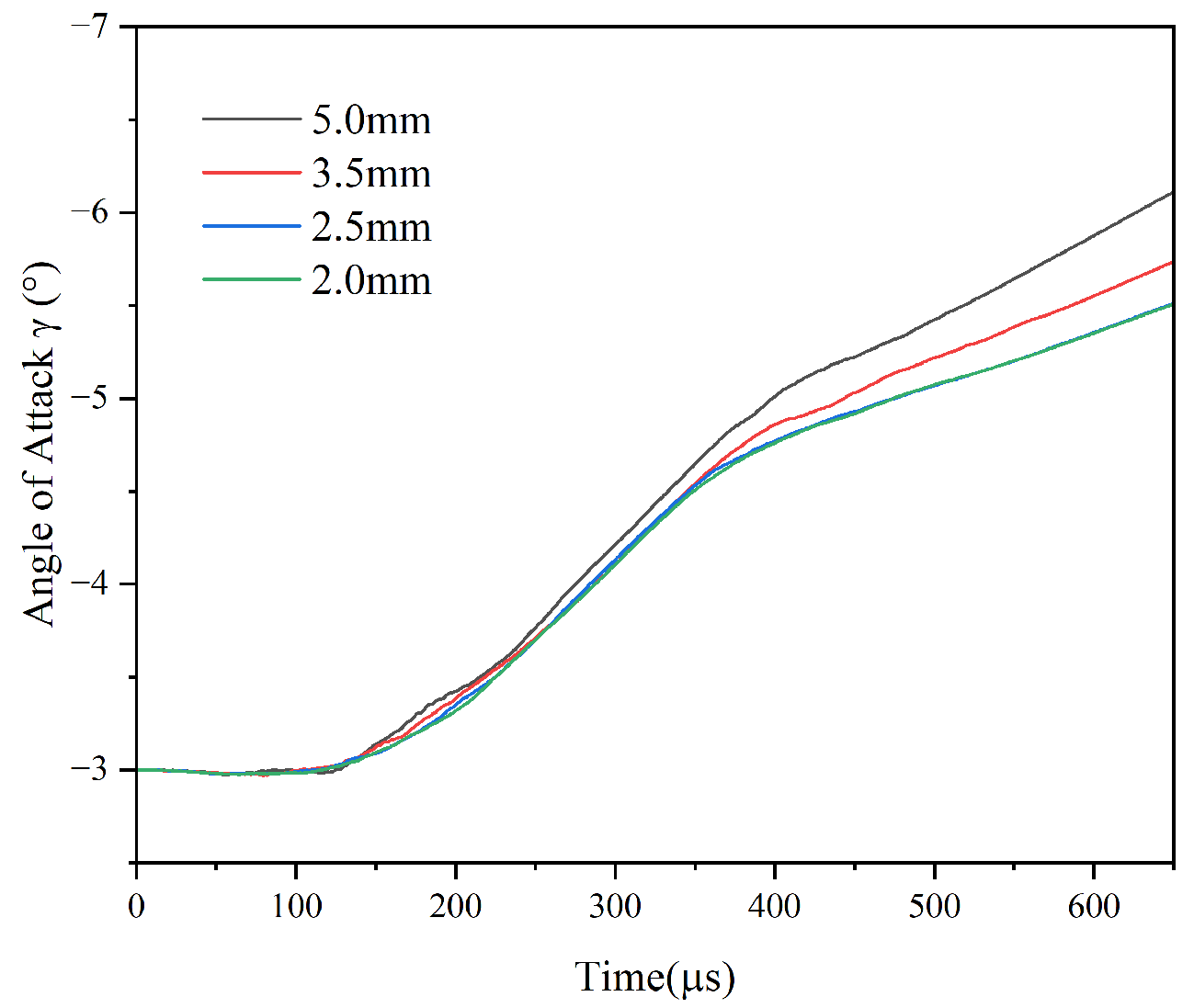



| Mass Ratio | Strength Grade | |||
|---|---|---|---|---|
| Cement | Water | Fine Aggregate | Coarse Aggregate | |
| 1 | 0.4 | 1.45 | 2.49 | C35 |
| No. | Impact Velocity (m/s) | Angle of Attack (°) | Target Thickness (mm) |
|---|---|---|---|
| 1# | 500 | 3 | 120 |
| 2# | 750 | 3 | 100 |
| 3# | 500 | 3 | 90 |
| 4# | 500 | 3 | 125 |
| 5# | 500 | 5 | 123 |
| 6# | 600 | 5 | 150 |
| 7# | 600 | 2 | 90 |
| 8# | 600 | 2 | 120 |
| No. | Pre-Impact Horizontal Velocity, Vf (m/s) | Pre-Impact Attitude Angle, θ0f (°) | Post-Impact Horizontal Velocity, Vb (m/s) | Post-Impact Attitude Angle, θ0b (°) | Target Plate Thickness, Th (mm) | Nose–Rear Surface Distance, Dt (mm) |
|---|---|---|---|---|---|---|
| S1 | 484.0 | 2.9 | 456.9 | 10.3 | 123 | 971.6 |
| S2 | 743.0 | 2.3 | 718.6 | 5.9 | 104 | 894.9 |
| S3 | 489.2 | 4.2 | 480.4 | 12.9 | 93 | 876.2 |
| S4 | 481.3 | 4.2 | 445.5 | 12.3 | 125 | 654.6 |
| S5 | 505.2 | 8.1 | 450.0 | 21.3 | 123 | 672.8 |
| S6 | 568.8 | 8.9 | 522.8 | 25.3 | 151 | 668.6 |
| S7 | 576.5 | 2.3 | 558.6 | 5.6 | 94 | 556.2 |
| S8 | 603.5 | 2.3 | 564.9 | 6.3 | 122 | 597.6 |
| Experiment ID | S1 | S2 | S3 | S4 | S5 | S6 | S7 | S8 |
|---|---|---|---|---|---|---|---|---|
| Pixel size in physical units (mm) | 1.4 | 1.4 | 1.6 | 1.5 | 1.5 | 1.4 | 1.2 | 1.8 |
| Experiment ID | Pre-Penetration | Post-Penetration | ||||||
|---|---|---|---|---|---|---|---|---|
| θ0min | θ0max | θ0min − θ0t | θ0max − θ0t | θ0min | θ0max | θ0min − θ0t | θ0max − θ0t | |
| S1 | 2.0 | 4.0 | −0.9 | 1.1 | 9.1 | 11.7 | −1.2 | 1.4 |
| S2 | 1.3 | 3.4 | −1.0 | 1.1 | 4.6 | 7.2 | −1.3 | 1.3 |
| S3 | 2.8 | 5.7 | −1.4 | 1.5 | 10.6 | 13.7 | −2.3 | 0.8 |
| S4 | 2.9 | 5.6 | −1.3 | 1.4 | 9.6 | 15.1 | −2.7 | 2.8 |
| S5 | 6.8 | 9.4 | −1.3 | 1.3 | 18.8 | 23.9 | −2.5 | 2.6 |
| S6 | 7.7 | 10.5 | −1.2 | 1.6 | 23.6 | 26.8 | −1.7 | 1.5 |
| S7 | 1.5 | 3.2 | −0.8 | 0.9 | 3.5 | 7.9 | −2.1 | 2.3 |
| S8 | 1.0 | 3.9 | −1.3 | 1.6 | 3.7 | 9.5 | −2.6 | 3.2 |
| RO | SHEAR | ONEMPA | EPSF | B0 | B1 | T1 | A |
| 2.27 | 0.1611 | −6 | 2.0 | 1.22 | 1.22 | 0.3527 | 1.6 |
| N | FC | FS* | FT* | Q0 | B | T2 | E0C |
| 0.61 | 2.34 × 10−4 | 0.18 | 0.1 | 0.6805 | 0.0105 | 0 | 3 × 10−11 |
| E0T | EC | ET | BETAC | BETAT | PTF | GC* | GT* |
| 3 × 10−12 | 3 × 1022 | 3 × 1022 | 0.04435 | 0.046083 | 1 × 10−4 | 0.53 | 0.7 |
| XI | D1 | D2 | EPM | AF | NF | GAMMA | A1 |
| 0.5 | 0.04 | 1 | 0.01 | 1.6 | 0.61 | 0 | 0.3527 |
| A2 | A3 | PEL | PCO | NP | ALPHA | ||
| 0.3958 | 0.0904 | 1.5567 × 10−4 | 0.06 | 3 | 1.21145 | ||
| No. | Experimental Result | Numerical Result | Error | ||||
|---|---|---|---|---|---|---|---|
| Post-Impact Horizontal Velocity, Ve (m/s) | Post-Impact Attitude Angle, θ0e (°) | Post-Impact Horizontal Velocity, Vs (m/s) | Post-Impact Attitude Angle, θ0s (°) | ΔV/Ve | Δθ0 | Δθ0/θ0e | |
| S1 | 456.9 | 10.3 | 456.5 | 10.9 | −0.09% | 0.6 | 5.8% |
| S2 | 718.6 | 5.9 | 720 | 6.1 | 0.19% | 0.2 | 3.4% |
| S3 | 480.4 | 12.9 | 469.9 | 11.2 | −2.19% | −1.7 | −13.2% |
| S4 | 445.5 | 12.3 | 451.5 | 11.2 | 1.35% | −1.1 | −8.9% |
| S5 | 450.0 | 21.3 | 467.3 | 18.7 | 3.84% | −2.6 | −12.2% |
| S6 | 522.8 | 25.3 | 514.6 | 21.6 | −1.57% | −3.7 | −14.6% |
| S7 | 558.6 | 5.6 | 557.8 | 4.8 | −0.14% | −0.6 | −14.3% |
| S8 | 564.9 | 6.3 | 576.3 | 6.0 | 2.02% | −0.3 | −4.8% |
| No. | Impact Velocity (m/s) | Residual Horizontal Velocity (m/s) | Attitude Angle After Penetration (°) | Angle of Attack After Penetration (°) |
|---|---|---|---|---|
| Vel1 | 550 | 475.4 | 23.9 | 15.2 |
| Vel2 | 700 | 624.2 | 22.2 | 15.4 |
| Vel3 | 850 | 772.5 | 21.4 | 15.7 |
| Vel4 | 1000 | 917.8 | 20.5 | 15.5 |
| No. | Initial Attitude Angles (°) | Residual Horizontal Velocity (m/s) | Attitude Angle After Penetration (°) | Angle of Attack After Penetration (°) |
|---|---|---|---|---|
| Ang1 | 5 | 793.0 | 9.9 | 7.8 |
| Ang2 | 10 | 772.5 | 21.4 | 15.7 |
| Ang3 | 15 | 737.5 | 32.4 | 23.2 |
| Ang4 | 20 | 696.0 | 43.3 | 31.1 |
| Ang5 | 25 | 650.6 | 52.8 | 38.0 |
| Ang6 | 30 | 605.7 | 61.7 | 45.0 |
| No. | Target Thicknesses (mm) | Residual Horizontal Velocity (m/s) | Attitude Angle After Penetration (°) | Angle of Attack After Penetration (°) |
|---|---|---|---|---|
| Thi1 | 90 | 819.1 | 14.8 | 12.8 |
| Thi2 | 120 | 804.7 | 16.9 | 13.8 |
| Thi3 | 150 | 789.3 | 18.8 | 14.6 |
| Thi4 | 180 | 772.5 | 21.4 | 15.7 |
| Thi5 | 210 | 751.3 | 23.4 | 16.2 |
| Thi6 | 240 | 728.7 | 25.6 | 16.5 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tao, Z.; Li, W.; Zhu, W.; Xu, J.; Ma, R. Experimental and Numerical Investigation of Projectile Penetration into Thin Concrete Targets at an Angle of Attack. Symmetry 2025, 17, 1904. https://doi.org/10.3390/sym17111904
Tao Z, Li W, Zhu W, Xu J, Ma R. Experimental and Numerical Investigation of Projectile Penetration into Thin Concrete Targets at an Angle of Attack. Symmetry. 2025; 17(11):1904. https://doi.org/10.3390/sym17111904
Chicago/Turabian StyleTao, Zheng, Wenbin Li, Wei Zhu, Junjie Xu, and Rui Ma. 2025. "Experimental and Numerical Investigation of Projectile Penetration into Thin Concrete Targets at an Angle of Attack" Symmetry 17, no. 11: 1904. https://doi.org/10.3390/sym17111904
APA StyleTao, Z., Li, W., Zhu, W., Xu, J., & Ma, R. (2025). Experimental and Numerical Investigation of Projectile Penetration into Thin Concrete Targets at an Angle of Attack. Symmetry, 17(11), 1904. https://doi.org/10.3390/sym17111904






