Hesitant Fuzzy Multi-Granulation Rough Set Model Based on Similarity Assessment
Abstract
1. Introduction
1.1. Literature Review
1.2. Research Gap and Motivation
1.3. Contribution and Paper Organization
2. Mathematical Foundation
3. The MAGDM Based on a Diversified Multiple-Attribute Hesitant Fuzzy Information System
3.1. Diversified Multiple Attribute Hesitant Fuzzy Information System
3.2. The Ranking of MAGDM in Hesitant Fuzzy Environments
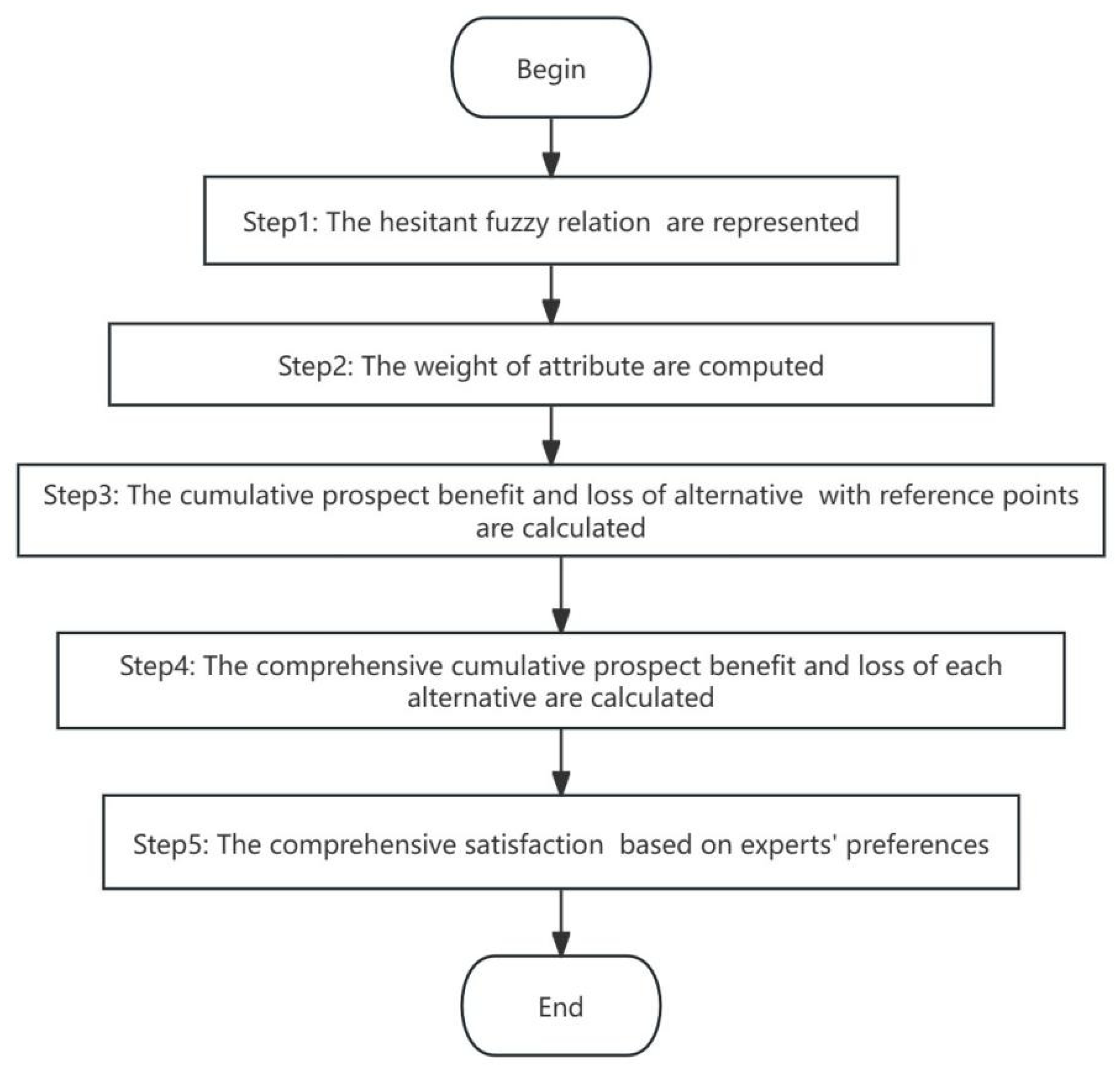
4. Key Steps for the Solution of the Diversified MAGDM Problem
5. An Illustrative Example
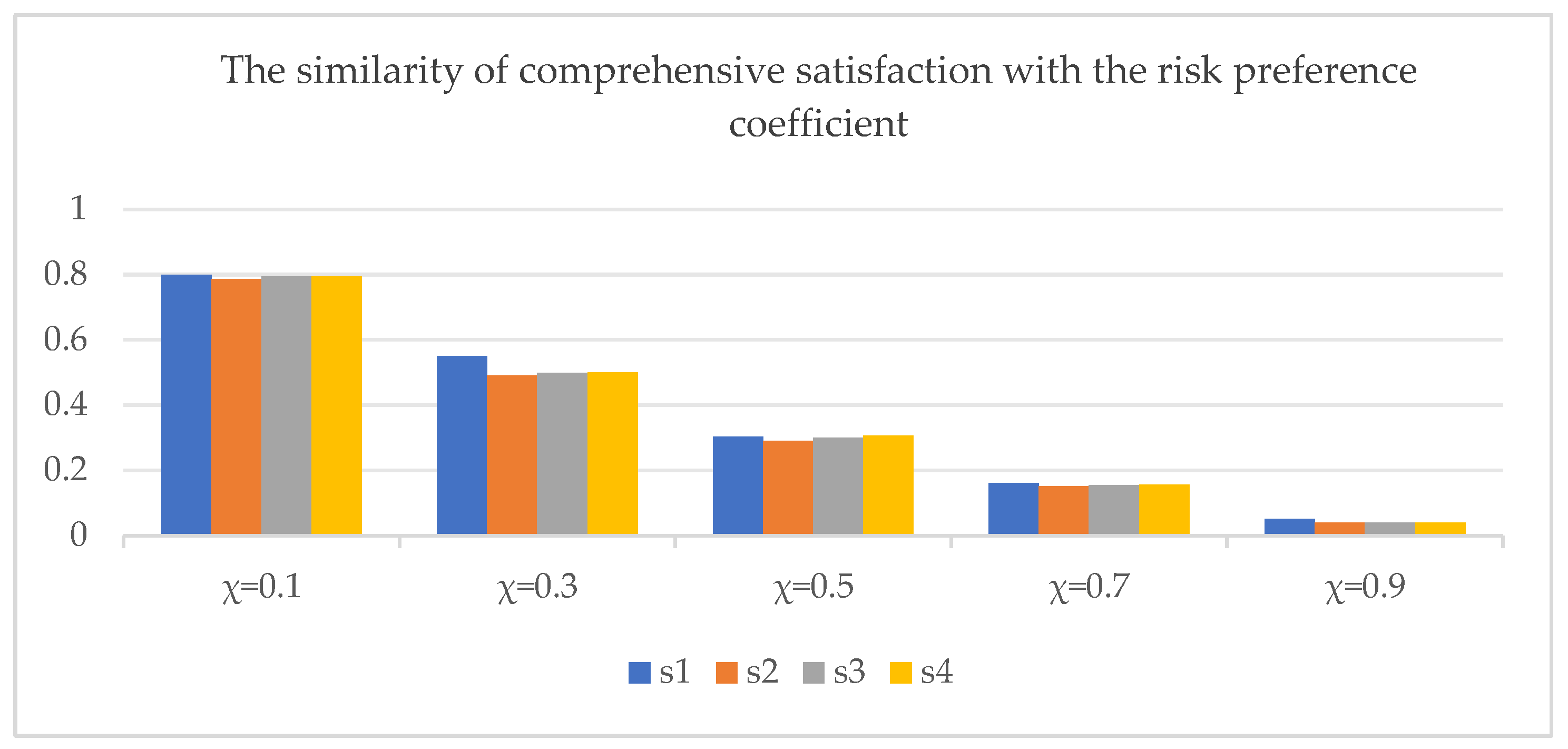
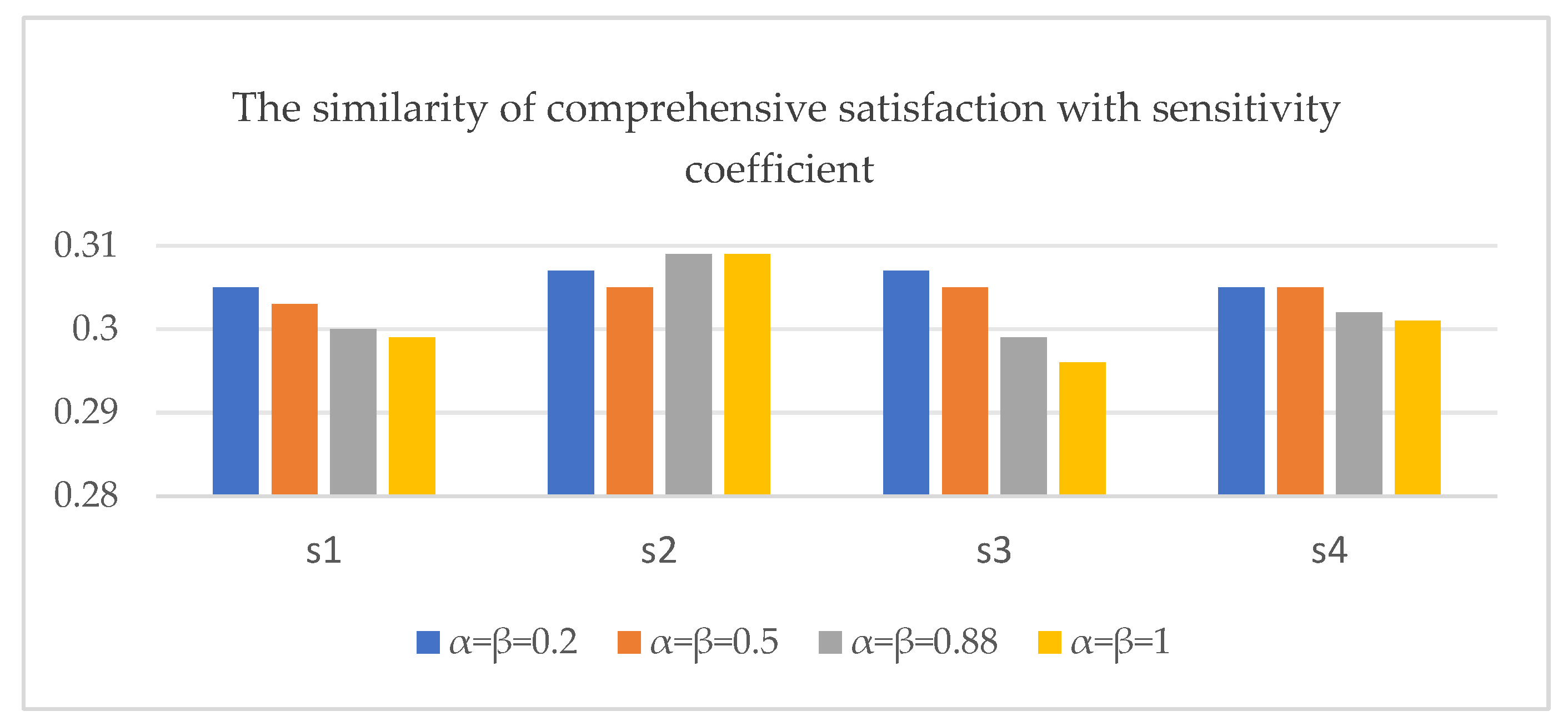
6. Discussion and Recommendations
6.1. Comparison with Other Methods
6.2. The Fairness of Evaluation
- There should be no significant difference in expert evaluation for each applicant.
- There should be no significant difference in the evaluation of the same applicant by various experts.
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Feng, F.; Zheng, Y.; Sun, B.; Akram, M. Novel score functions of generalized orthopair fuzzy membership grades with application to multiple attribute decision making. Granul. Comput. 2021, 7, 95–111. [Google Scholar] [CrossRef]
- Zhang, B.; Dong, Y.; Feng, X.; Pedrycz, W. Maximum Fuzzy Consensus Feedback Mechanism With Minimum Cost and Private Interest in Group Decision-Making. IEEE Trans. Fuzzy Syst. 2021, 29, 2689–2700. [Google Scholar] [CrossRef]
- Li, J.; Shao, Y.; Qi, X. On variable-precision-based rough set approach to incomplete interval-valued fuzzy information systems and its applications. J. Intell. Fuzzy Syst. 2021, 40, 463–475. [Google Scholar] [CrossRef]
- Chen, K.; Tan, J.; Zhu, C.; Liu, G.; Gastaldo, P. Some Information Measures for Interval-Valued Hesitant Fuzzy Sets in Multiple Criteria Decision-Making. Int. J. Intell. Syst. 2024, 2024, 6186183. [Google Scholar] [CrossRef]
- Ali, W.; Shaheen, T.; Haq, I.U.; Toor, H.G.; Akram, F.; Jafari, S.; Uddin, Z.; Hassan, M.M. Multiple-Attribute Decision Making Based on Intuitionistic Hesitant Fuzzy Connection Set Environment. Symmetry 2023, 15, 778. [Google Scholar] [CrossRef]
- Dai, X.; Sun, B.; Bai, J.; Ye, J.; Chu, X. Double-quantitative multi-granularity kernel fuzzy rough sets model and its application in rheumatoid arthritis risk assessment. Int. J. Mach. Learn. Cybern. 2024, 16, 1–23. [Google Scholar] [CrossRef]
- Krishankumar, R.; Garg, H.; Arun, K.; Saha, A.; Ravichandran, K.S.; Kar, S. An integrated decision-making COPRAS approach to probabilistic hesitant fuzzy set information. Complex Intell. Syst. 2021, 7, 2281–2298. [Google Scholar] [CrossRef]
- Zhao, P.; Yue, Q.; Deng, Z. Two-sided matching decision making for probabilistic hesitant fuzzy numbers. J. Intell. Fuzzy Syst. 2023, 44, 5699–5709. [Google Scholar] [CrossRef]
- Castillo, O.; Muhuri, P.K.; Melin, P.; Pulkkinen, P. Emerging Issues and Applications of Type-2 Fuzzy Sets and Systems. Eng. Appl. Artif. Intell. 2020, 90, 103596. [Google Scholar] [CrossRef]
- Ning, B.; Wei, G.; Lin, R.; Guo, Y. A novel MADM technique based on extended power generalized Maclaurin symmetric mean operators under probabilistic dual hesitant fuzzy setting and its application to sustainable suppliers selection. Expert Syst. Appl. 2022, 204, 117419. [Google Scholar] [CrossRef]
- Mao, W.; Zhang, K.; Liu, X.; Tang, J. An optimization-based three-way decision for multi-criteria ranking strategy considering intuitionistic fuzzy concept. Inf. Sci. 2024, 654, 119850. [Google Scholar] [CrossRef]
- Wang, Z.-C.; Ran, Y.; Chen, Y.; Yang, X.; Zhang, G. Group risk assessment in failure mode and effects analysis using a hybrid probabilistic hesitant fuzzy linguistic MCDM method. Expert Syst. Appl. 2022, 188, 116013. [Google Scholar] [CrossRef]
- Sun, B.; Qi, C.; Ma, W.; Wang, T.; Zhang, L.; Jiang, C. Variable precision diversified attribute multigranulation fuzzy rough set-based multi-attribute group decision making problems. Comput. Ind. Eng. 2020, 142, 106331. [Google Scholar] [CrossRef]
- Chu, X.; Sun, B.; Chu, X.; Wu, J.; Han, K.; Zhang, Y.; Huang, Q. Multi-granularity dominance rough concept attribute reduction over hybrid information systems and its application in clinical decision-making. Inf. Sci. 2022, 597, 274–299. [Google Scholar] [CrossRef]
- Zhang, H.; Zhan, J.; He, Y. Multi-granulation hesitant fuzzy rough sets and corresponding applications. Soft Comput. 2019, 23, 13085–13103. [Google Scholar] [CrossRef]
- Wu, J.; Chang, J.; Cao, Q.; Liang, C. A trust propagation and collaborative filtering based method for incomplete information in social network group decision making with type-2 linguistic trust. Comput. Ind. Eng. 2019, 127, 853–864. [Google Scholar] [CrossRef]
- Ye, J.; Sun, B.; Chu, X.; Zhan, J.; Bao, Q.; Cai, J. A Novel Diversified Attribute Group Decision-Making Method Over Multisource Heterogeneous Fuzzy Decision Systems With Its Application to Gout Diagnosis. IEEE Trans. Fuzzy Syst. 2023, 31, 1780–1794. [Google Scholar] [CrossRef]
- Ye, J.; Zhan, J.; Sun, B. A three-way decision method based on fuzzy rough set models under incomplete environments. Inf. Sci. 2021, 577, 22–48. [Google Scholar] [CrossRef]
- Yang, B.; Hu, B.Q. Fuzzy neighborhood operators and derived fuzzy coverings. Fuzzy Sets Syst. 2019, 370, 1–33. [Google Scholar] [CrossRef]
- Zhang, S.; Xu, Z.; Wu, H. Fusions and preference relations based on probabilistic interval-valued hesitant fuzzy information in group decision making. Soft Comput. 2019, 23, 8291–8306. [Google Scholar] [CrossRef]
- Li, Z.; Zhang, P.; Xie, N.; Zhang, G.; Wen, C.-F. A novel three-way decision method in a hybrid information system with images and its application in medical diagnosis. Eng. Appl. Artif. Intell. 2020, 92, 103651. [Google Scholar] [CrossRef]
- Akram, M.; Ali, G.; Alcantud, J.C.R. A new method of multi-attribute group decision making based on hesitant fuzzy soft expert information. Expert Syst. 2023, 40, e13357. [Google Scholar] [CrossRef]
- Ali, G.; Afzal, A.; Sheikh, U.; Nabeel, M. Multi-criteria group decision-making based on the combination of dual hesitant fuzzy sets with soft expert sets for the prediction of a local election scenario. Granul. Comput. 2023, 8, 2039–2066. [Google Scholar] [CrossRef]
- Chu, X.; Sun, B.; Li, X.; Han, K.; Wu, J.; Zhang, Y.; Huang, Q. Neighborhood rough set-based three-way clustering considering attribute correlations: An approach to classification of potential gout groups. Inf. Sci. 2020, 535, 28–41. [Google Scholar] [CrossRef]
- Hu, Q.; Qin, K.; Yang, L. A constructing approach to multi-granularity object-induced three-way concept lattices. Int. J. Approx. Reason. 2022, 150, 229–241. [Google Scholar] [CrossRef]
- Cheng, D.; Zhou, Z.; Cheng, F.; Wang, J. Deriving heterogeneous experts weights from incomplete linguistic preference relations based on uninorm consistency. Knowl. Based Syst. 2018, 150, 150–165. [Google Scholar] [CrossRef]
- Sun, B.; Zhou, X.; Lin, N. Diversified binary relation-based fuzzy multigranulation rough set over two universes and application to multiple attribute group decision making. Inf. Fusion 2020, 55, 91–104. [Google Scholar] [CrossRef]
- Sun, B.; Zhang, M.; Wang, T.; Zhang, X. Diversified multiple attribute group decision-making based on multigranulation soft fuzzy rough set and TODIM method. Comput. Appl. Math. 2020, 39, 186. [Google Scholar] [CrossRef]
- Gupta, S.; Joshi, D.K.; Awasthi, N.; Pant, M.; Joshi, B.P.; Chaube, S. Distance and similarity measures of Hesitant bi-fuzzy set and its applications in renewable energy systems. Math. Comput. Simul. 2024, 219, 321–336. [Google Scholar] [CrossRef]
- Liang, X.; Guo, J.; Liu, P. A consensus model considers managing manipulative and overconfident behaviours in large-scale group decision-making. Inf. Sci. 2024, 654, 119848. [Google Scholar] [CrossRef]
- Zhang, C.; Li, D.; Liang, J.; Wang, B. MAGDM-oriented dual hesitant fuzzy multigranulation probabilistic models based on MULTIMOORA. Int. J. Mach. Learn. Cybern. 2020, 12, 1219–1241. [Google Scholar] [CrossRef]
- Farhadinia, B.; Xu, Z. Developing the comparison techniques of probabilistic hesitant fuzzy elements in multiple criteria decision making. Soft Comput. 2020, 25, 331–342. [Google Scholar] [CrossRef]
- Alcantud, J.C.R.; Campión, M.J.; Induráin, E.; Munárriz, A. Scores of hesitant fuzzy elements revisited: “Was sind und was sollen”. Inf. Sci. 2023, 648, 119500. [Google Scholar] [CrossRef]
- Liao, H.; Qin, R.; Gao, C.; Wu, X.; Hafezalkotob, A.; Herrera, F. Score-HeDLiSF: A score function of hesitant fuzzy linguistic term set based on hesitant degrees and linguistic scale functions: An application to unbalanced hesitant fuzzy linguistic MULTIMOORA. Inf. Fusion 2019, 48, 39–54. [Google Scholar] [CrossRef]
- Jiang, H.; Hu, B.Q. A decision-theoretic fuzzy rough set in hesitant fuzzy information systems and its application in multi-attribute decision-making. Inf. Sci. 2021, 579, 103–127. [Google Scholar] [CrossRef]
- Zeng, W.; Song, G.; Yin, Q.; Guo, P. Some new distance measures of hesitant fuzzy sets and its application in group decision making. In Proceedings of the 2019 15th International Conference on Computational Intelligence and Security (CIS) 2019, Macao, China, 13–16 December 2019; pp. 118–122. [Google Scholar]
- Ma, W.; Lei, W.; Sun, B. Three-way group decisions based on multigranulation hesitant fuzzy decision-theoretic rough set over two universes. J. Intell. Fuzzy Syst. 2020, 38, 2165–2179. [Google Scholar] [CrossRef]
- Ma, W.; Lei, W.; Sun, B. Three-way group decisions under hesitant fuzzy linguistic environment for green supplier selection. Kybernetes 2020, 49, 2919–2945. [Google Scholar] [CrossRef]
| Parameters | Definitions |
|---|---|
| Non-empty finite universes | |
| A condition attribute set | |
| A decision attribute set | |
| Decision-making object | |
| The serial number of the decision-maker | |
| The weight of attributes | |
| Distance measure | |
| The binary hesitant fuzzy relation between and | |
| Sensitivity coefficient, | |
| Loss aversion coefficient, | |
| Risk preference coefficient, | |
| Priority order of alternative | |
| The weight of the experts | |
| Consensus threshold, | |
| The threshold for assessment, |
| (0.2, 0.3) | (0.1, 0.2) | (0.6, 0.8) | (0.4, 0.5) | ||||
| (0.1, 0.3) | (0.1, 0.2) | (0.4, 0.5) | (0.6, 0.8) | ||||
| (0.3, 0.6) | (0.3, 0.5) | (0.6, 0.8) | (0.5, 0.7) |
| {0.6, 0.8} | {0.2, 0.25} | {0.2, 0.3} | {0.4, 0.5} | |
| {0.5, 0.8} | {0.2, 0.4} | {0.2, 0.4} | {0.2, 0.8} | |
| {0.4, 0.6} | {0.2, 0.5} | {0.2, 0.5} | {0.3, 0.5} | |
| {0.6, 0.9} | {0.2, 0.4} | {0.5, 0.6} | {0.2, 0.6} |
| {0.5} | {0.6, 0.8} | {0.1, 0.3} | {0.3, 0.5} | |
| {0.2, 0.5} | {0.7, 0.9} | {0.3, 0.5} | {0.4, 0.5} | |
| {0.2, 0.6} | {0.8} | {0.1, 0.5} | {0.1, 0.5} | |
| {0.5} | {0.2, 0.5} | {0.4, 0.5} | {0.5, 0.6} |
| {0.5, 0.6} | {0.4, 0.5} | {0.5} | {0.4, 0.5} | |
| {0.4, 0.5} | {0.4, 0.6} | {0.2, 0.5} | {0.4, 0.6} | |
| {0.3, 0.5} | {0.5} | {0.5, 0.6} | {0.2, 0.3} | |
| {0.5} | {0.4, 0.5} | {0.4, 0.6} | {0.2, 0.5} |
| 1.114 | 1.317 | 1.238 | 1.307 | |
| 2.936 | 3.038 | 3.026 | 2.815 |
| 1.083 | 1.298 | 1.166 | 1.038 | |
| 2.421 | 2.682 | 2.421 | 2.466 |
| 1.057 | 1.237 | 1.072 | 1.037 | |
| 2.376 | 3.391 | 2.682 | 2.572 |
| 0.300 | 0.310 | 0.295 | 0.304 |
| Methods | The Rankings |
|---|---|
| Method in Reference [17] | |
| Method in Reference [27] | |
| The proposed method |
| 0.026 | 0.014 | 0.030 | |
| 0.015 | 0.030 | 0.003 | |
| 0.032 | 0.014 | 0.025 | |
| 0.057 | 0.003 | 0.003 |
| k = 1 | k = 2 | k = 3 | |
|---|---|---|---|
| 0.041 | 0.146 | 0.111 | |
| 0.132 | 0.091 | 0.112 | |
| 0.143 | 0.130 | 0.116 | |
| 0.098 | 0.089 | 0.087 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ren, J.; Cao, B. Hesitant Fuzzy Multi-Granulation Rough Set Model Based on Similarity Assessment. Symmetry 2025, 17, 1903. https://doi.org/10.3390/sym17111903
Ren J, Cao B. Hesitant Fuzzy Multi-Granulation Rough Set Model Based on Similarity Assessment. Symmetry. 2025; 17(11):1903. https://doi.org/10.3390/sym17111903
Chicago/Turabian StyleRen, Junxiao, and Bo Cao. 2025. "Hesitant Fuzzy Multi-Granulation Rough Set Model Based on Similarity Assessment" Symmetry 17, no. 11: 1903. https://doi.org/10.3390/sym17111903
APA StyleRen, J., & Cao, B. (2025). Hesitant Fuzzy Multi-Granulation Rough Set Model Based on Similarity Assessment. Symmetry, 17(11), 1903. https://doi.org/10.3390/sym17111903





