Squeezing-Induced Entanglement and Sub-Poissonian Statistics in an Extended Jaynes–Cummings Model with Pair Coherent Fields
Abstract
1. Introduction
2. Model and Dynamics
3. Quantumness Measures and Results
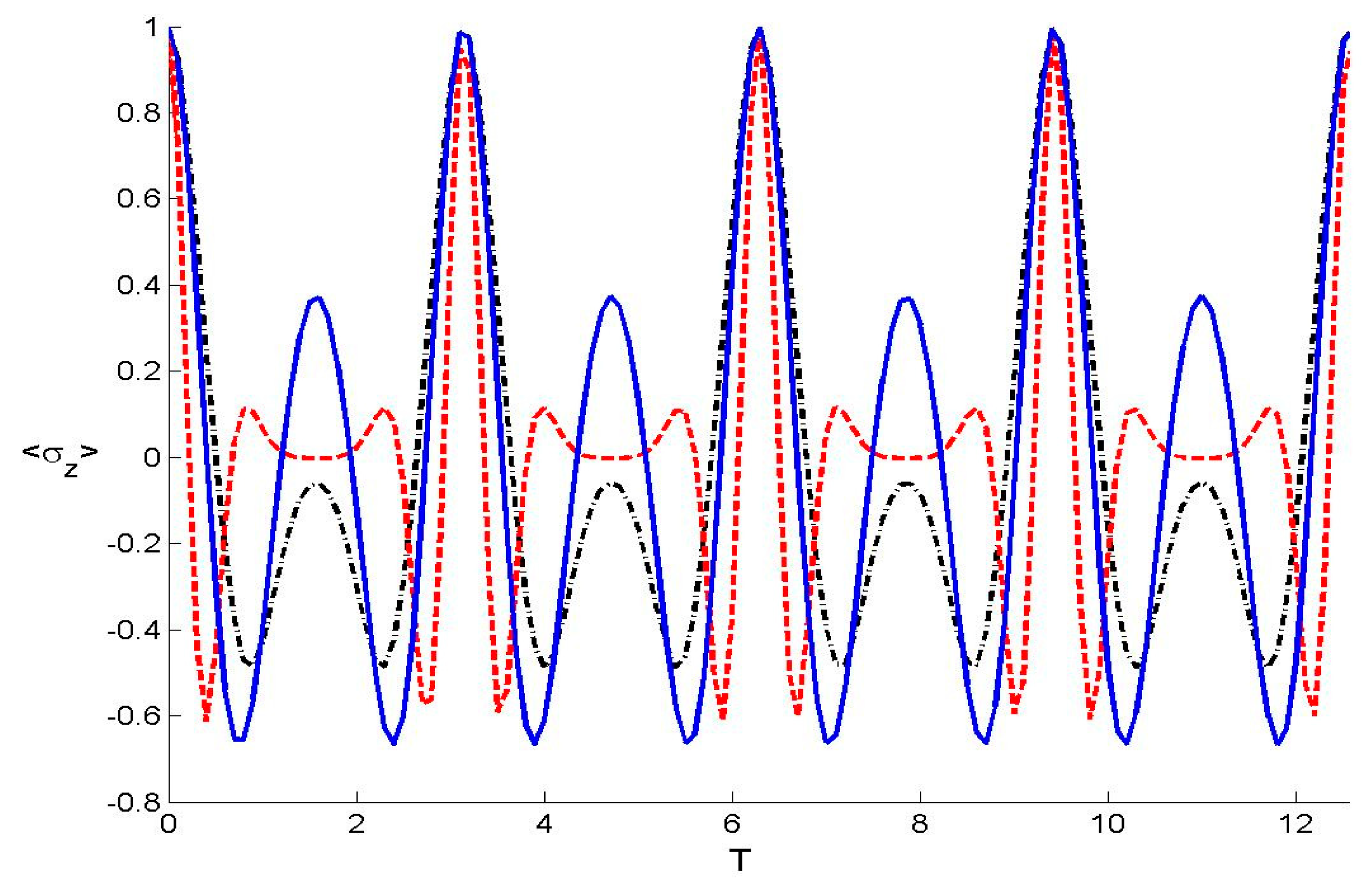
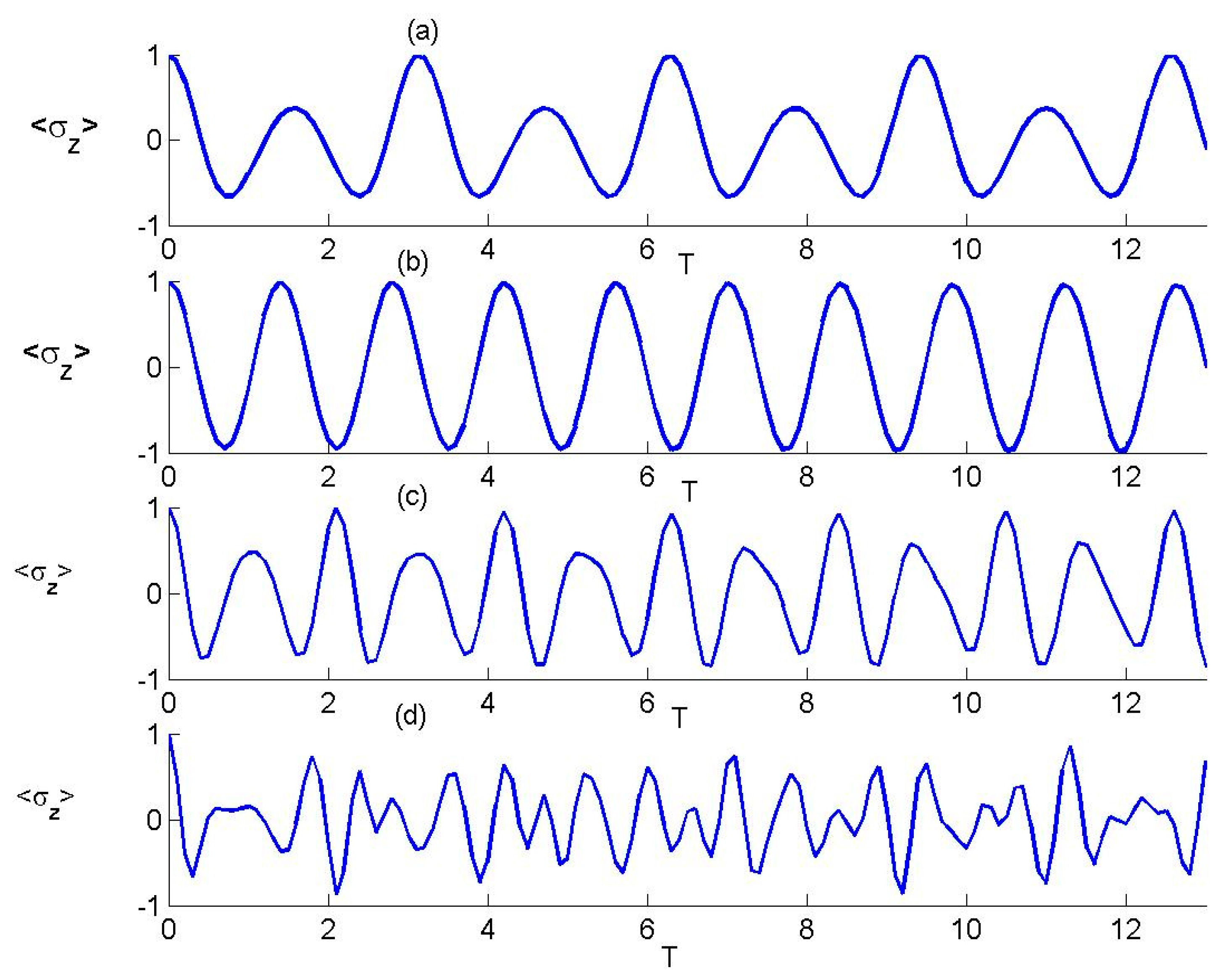
3.1. Atomic Dynamics
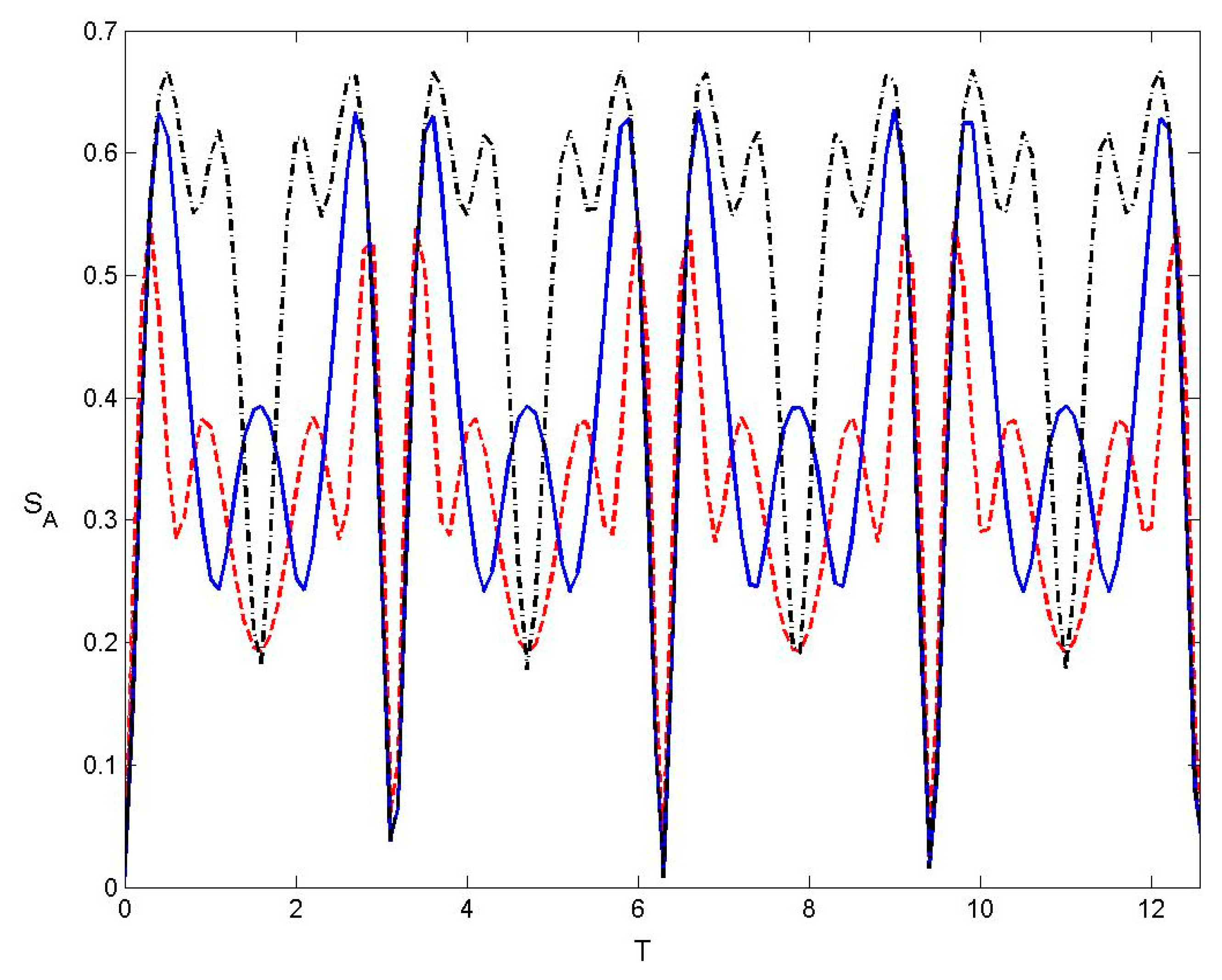
3.2. Entropy of Subsystems and Entanglement

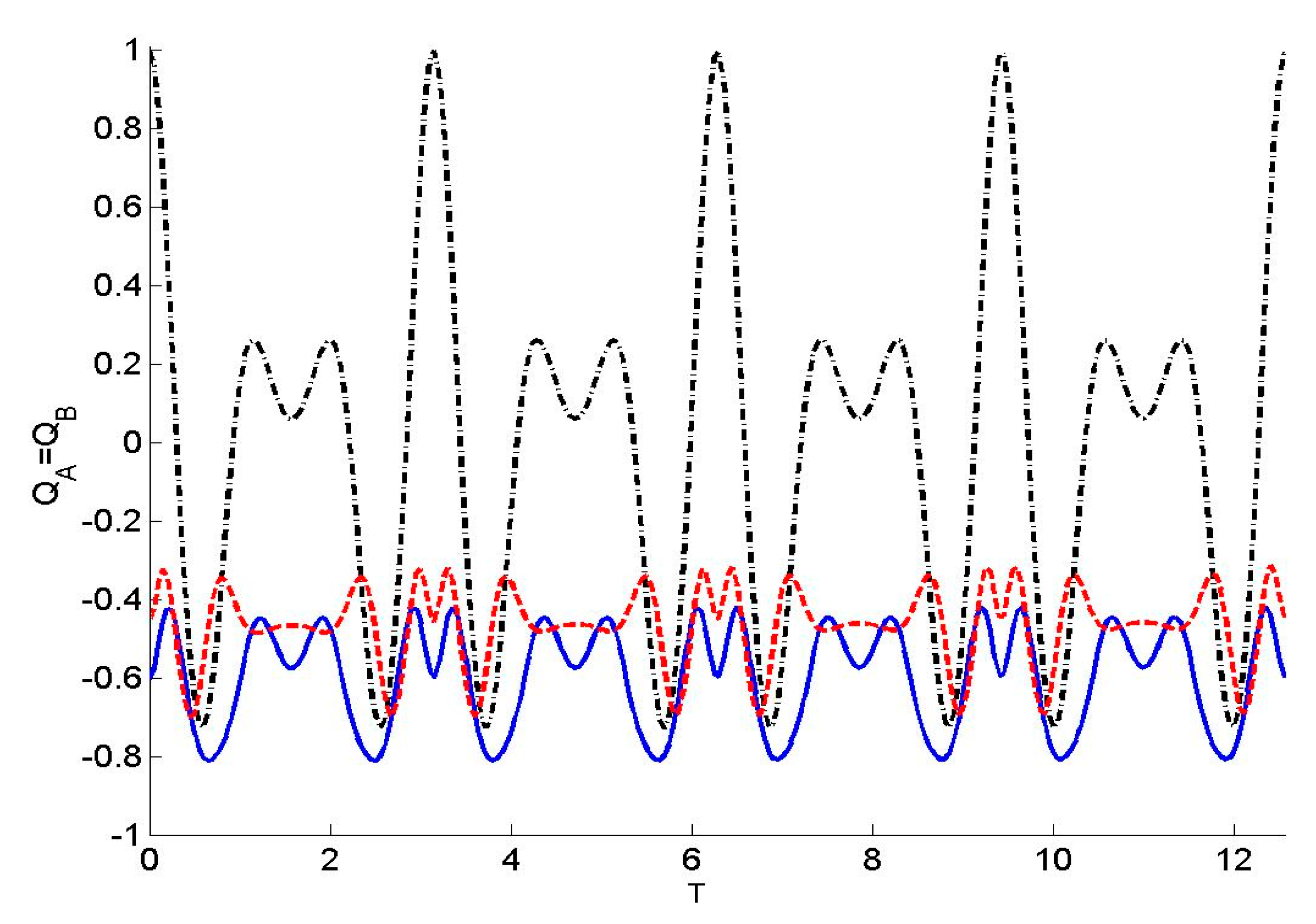
3.3. Statistical Properties of Two-Mode Squeezed Field
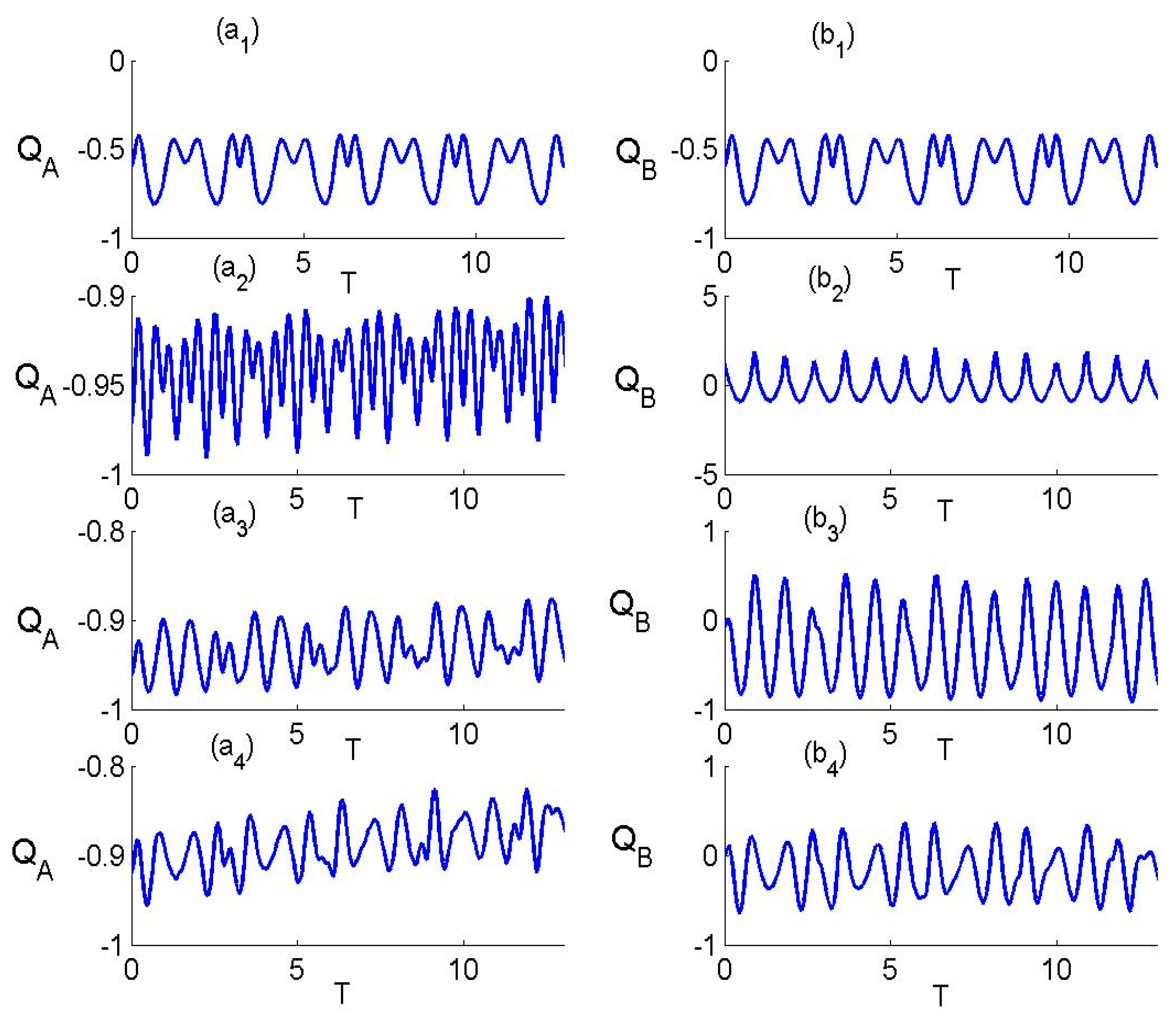


4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A. Derivations of Key Quantities
Appendix A.1. Atomic Population Inversion
Appendix A.2. Atom–Field Entanglement
Appendix A.3. Mandel’s Parameter
Appendix A.4. Cauchy–Schwarz Inequality (CSI) Violation
References
- Jaynes, E.T.; Cummings, F.W. Comparison of Quantum and Semiclassical Radiation Theory with Application to the Beam Maser. Proc. IEEE 1963, 51, 89–99. [Google Scholar] [CrossRef]
- Joshi, A.; Puri, R.R. Effects of the Binomial Field Distribution on Collapse and Revival Phenomena in the Jaynes–Cummings Model. J. Mod. Opt. 1987, 34, 1421–1432. [Google Scholar] [CrossRef]
- Puri, R.R.; Agarwal, G.S. Finite-Q Cavity Electrodynamics: Dynamical and Statistical Aspects. Phys. Rev. A 1987, 35, 3433–3449. [Google Scholar] [CrossRef]
- Yeazell, J.A.; Mallalieu, M.; Stroud, C.R., Jr. Observation of the Collapse and Revival of a Rydberg Electronic Wave Packet. Phys. Rev. Lett. 1990, 64, 2007–2010. [Google Scholar] [CrossRef] [PubMed]
- Raimond, J.M.; Goy, P.; Gross, M.; Fabre, C.; Haroche, S. Collective Absorption of Blackbody Radiation by Rydberg Atoms in a Cavity: An Experiment on Bose Statistics and Brownian Motion. Phys. Rev. Lett. 1982, 49, 117–120. [Google Scholar] [CrossRef]
- Eberly, J.H.; Narozhny, N.B.; Sanchez-Mondragon, J.J. Periodic Spontaneous Collapse and Revival in a Simple Quantum Model. Phys. Rev. Lett. 1980, 44, 1323–1326. [Google Scholar] [CrossRef]
- Almalki, S.; Berrada, K.; Abdel-Khalek, S.; Eleuch, H. Interaction of a Four-Level Atom with a Quantized Field in the Presence of a Nonlinear Kerr Medium. Sci. Rep. 2024, 14, 1141. [Google Scholar] [CrossRef]
- Berrada, K.; Sabik, A.; Khalil, E.M.; Abdel-Khalek, S. Geometric Phase and Wehrl Phase Entropy for Two Superconducting Qubits in a Coherent Field System under the Effect of Nonlinear Medium. Chaos Solitons Fractals 2024, 178, 114371. [Google Scholar] [CrossRef]
- Rempe, G.; Walther, H.; Klein, N. Observation of Quantum Collapse and Revival in a One-Atom Maser. Phys. Rev. Lett. 1987, 58, 353–356. [Google Scholar] [CrossRef]
- Short, R.; Mandel, L. Observation of Sub-Poissonian Photon Statistics. Phys. Rev. Lett. 1983, 51, 384–387. [Google Scholar] [CrossRef]
- Li, P.; Ning, X.-J.; Zhang, Q.; You, J.Q. Dressed-State Coherent Population Trapping in a V-Type Atom. J. Phys. B At. Mol. Opt. Phys. 2008, 41, 235401. [Google Scholar] [CrossRef]
- Joshi, A. Nonlinear Dynamical Evolution of the Driven Two-Photon Jaynes–Cummings Model. Phys. Rev. A 2000, 62, 043812. [Google Scholar] [CrossRef]
- Budini, A.A.; de Matos Filho, R.L.; Zagury, N. Dissipation and Decoherence in the Generalized Jaynes–Cummings Model. Phys. Rev. A 2003, 67, 033815. [Google Scholar] [CrossRef]
- Cordero, S.; Lopez-Pena, R.; Castaños, O.; Nahmad-Achar, E. Quantum Phase Transitions of Three-Level Atoms Interacting with a One-Mode Electromagnetic Field. Phys. Rev. A 2013, 87, 023805. [Google Scholar] [CrossRef]
- Cordero, S.; Castaños, O.; López-Peña, R.; Nahmad-Achar, E. Reduced Bases for a Three-Level Atom Interacting with a Two-Mode Radiation Field. Phys. Rev. A 2019, 99, 033811. [Google Scholar] [CrossRef]
- Cordero, S.; Nahmad-Achar, E.; Lopez-Pena, R.; Castaños, O. Polychromatic Phase Diagram for n-Level Atoms Interacting with ℓ Modes of an Electromagnetic Field. Phys. Rev. A 2015, 92, 053843. [Google Scholar] [CrossRef]
- Tavis, M.; Cummings, F.W. Exact Solution for an N-Molecule—Radiation-Field Hamiltonian. Phys. Rev. 1968, 170, 379–384. [Google Scholar] [CrossRef]
- Bennett, C.H.; Wiesner, S.J. Communication via One- and Two-Particle Operators on Einstein-Podolsky-Rosen States. Phys. Rev. Lett. 1992, 69, 2881–2884. [Google Scholar] [CrossRef]
- Ekert, A.K. Quantum Cryptography Based on Bell’s Theorem. Phys. Rev. Lett. 1991, 67, 661–663. [Google Scholar] [CrossRef] [PubMed]
- Bennett, C.H.; Brassard, G.; Crépeau, C.; Jozsa, R.; Peres, A.; Wootters, W.K. Teleporting an Unknown Quantum State via Dual Classical and Einstein-Podolsky-Rosen Channels. Phys. Rev. Lett. 1993, 70, 1895–1899. [Google Scholar] [CrossRef]
- Berrada, K. Photon-Added Deformed Peremolov Coherent States and Quantum Entanglement. Axioms 2024, 13, 289. [Google Scholar] [CrossRef]
- Berrada, K.; Fanchini, F.F.; Abdel-Khalek, S. Quantum Correlations between Each Qubit in a Two-Atom System and the Environment in Terms of Interatomic Distance. Phys. Rev. A 2012, 85, 052315. [Google Scholar] [CrossRef]
- Josse, V.; Dantan, A.; Bramati, A.; Pinard, M.; Giacobino, E. Continuous Variable Entanglement Using Cold Atoms. Phys. Rev. Lett. 2004, 92, 123601. [Google Scholar] [CrossRef]
- Wasilewski, W.; Jensen, K.; Krauter, H.; Renema, J.J.; Balabas, M.V.; Polzik, E.S. Generation of Two-Mode Squeezed and Entangled Light in a Single Temporal and Spatial Mode. Opt. Express 2009, 17, 14444–14457. [Google Scholar] [CrossRef]
- Josse, V.; Dantan, A.; Bramati, A.; Giacobino, E. Entanglement and Squeezing in a Two-Mode System: Theory and Experiment. J. Phys. B At. Mol. Opt. Phys. 2004, 37, S532–S542. [Google Scholar] [CrossRef]
- Gerry, C.C. Two-Mode Squeezed Pair Coherent States. J. Mod. Opt. 1995, 42, 585–594. [Google Scholar] [CrossRef]
- Gerry, C.C. Correlated Two-Mode SU(1,1) Coherent States: Nonclassical Properties. J. Opt. Soc. Am. B 1991, 8, 685–690. [Google Scholar] [CrossRef]
- Agarwal, G.S. Nonclassical Statistics of Fields in Pair Coherent States. J. Opt. Soc. Am. B 1988, 5, 1940–1947. [Google Scholar] [CrossRef]
- Ekert, A.K.; Palma, G.M.; Barnett, S.M.; Knight, P.L. Establishment of Correlated Pure States through Decay in a Squeezed Reservoir. Phys. Rev. A 1989, 39, 6026–6029. [Google Scholar] [CrossRef] [PubMed]
- Ekert, A.K.; Knight, P.L. Correlations and Squeezing of Two-Mode Oscillations. Am. J. Phys. 1989, 57, 692–697. [Google Scholar] [CrossRef]
- Huang, J.; Kumar, P. Photon-Counting Statistics of Multimode Squeezed Light. Phys. Rev. A 1989, 40, 1670–1674. [Google Scholar] [CrossRef]
- Nielsen, M.A.; Chuang, I.L. Quantum Computation and Quantum Information; Cambridge University Press: Cambridge, UK, 2010. [Google Scholar]
- Horodecki, R.; Horodecki, P.; Horodecki, M.; Horodecki, K. Quantum entanglement. Rev. Mod. Phys. 2009, 81, 865. [Google Scholar] [CrossRef]
- Li, Y.; Nemilentsau, A.; Argyropoulos, C. Resonance Energy Transfer and Quantum Entanglement Mediated by Epsilon-Near-Zero and Other Plasmonic Waveguide Systems. Nanoscale 2019, 11, 14635–14647. [Google Scholar] [CrossRef] [PubMed]
- Ma, J.; Cao, J. Förster Resonance Energy Transfer, Absorption and Emission Spectra in Multichromophoric Systems. I. Full Cumulant Expansions and System-Bath Entanglement. J. Chem. Phys. 2015, 142, 094106. [Google Scholar] [CrossRef] [PubMed]
- Qiu, H.; Ye, S.; Bao, W.; Cao, J.; Argyropoulos, C. Efficient Entanglement between Two Long-Distance Quantum Emitters Mediated by Dark-Gap-Plasmon Waveguides. Phys. Rev. B 2024, 110, 075432. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Algarni, M.; Berrada, K.; Abdel-Khalek, S. Squeezing-Induced Entanglement and Sub-Poissonian Statistics in an Extended Jaynes–Cummings Model with Pair Coherent Fields. Symmetry 2025, 17, 1893. https://doi.org/10.3390/sym17111893
Algarni M, Berrada K, Abdel-Khalek S. Squeezing-Induced Entanglement and Sub-Poissonian Statistics in an Extended Jaynes–Cummings Model with Pair Coherent Fields. Symmetry. 2025; 17(11):1893. https://doi.org/10.3390/sym17111893
Chicago/Turabian StyleAlgarni, Mariam, Kamal Berrada, and Sayed Abdel-Khalek. 2025. "Squeezing-Induced Entanglement and Sub-Poissonian Statistics in an Extended Jaynes–Cummings Model with Pair Coherent Fields" Symmetry 17, no. 11: 1893. https://doi.org/10.3390/sym17111893
APA StyleAlgarni, M., Berrada, K., & Abdel-Khalek, S. (2025). Squeezing-Induced Entanglement and Sub-Poissonian Statistics in an Extended Jaynes–Cummings Model with Pair Coherent Fields. Symmetry, 17(11), 1893. https://doi.org/10.3390/sym17111893






