Abstract
The presence of phase diffusion noise may lead to the loss of quantum measurement advantages, resulting in measurement results that cannot beat the standard quantum limit (SQL). Squeezing is considered an effective method for reducing the detrimental effect of phase diffusion on a measurement. Reasonable use of squeezing can make a measurement exceed the SQL. The Mach–Zehnder (MZ) interferometer has been exploited as a generic tool for precise phase measurement. Describing the reduction in quantum advantage caused by phase diffusion in an MZ interferometer that can be mitigated by squeezing is not easy to handle analytically because the input state changes from a pure state to a mixed state after experiencing the diffusion noise in the MZ interferometer. We introduce a truncated MZ interferometer, a symmetrical structure that can achieve the same potential phase sensitivity as the conventional MZ interferometer. This scheme can theoretically explain how phase diffusion reduces phase estimation and why squeezing counteracts the presence of phase diffusion. Using the Gaussian property of the input state and the characteristic of Gaussian operation in the squeezing, the two orthogonal field quantities of the quantum state are squeezed and anti-squeezed to different degrees, and the analytic results are obtained. This result can beat the SQL and provide reliable theoretical guidance for the experiment. The truncated MZ interferometer is more straightforward to build and operate than the conventional MZ interferometer. Moreover, it mitigates the phase diffusion noise via the squeezing operation, thus making it useful for applications in quantum metrology.
1. Introduction
Quantum metrology is fundamental in physics and invaluable for a wide range of applications, attracting the attention of many researchers [1,2,3]. Sometimes, the parameters cannot be measured directly in the quantum light field, so the phase of the light field is often chosen as an ideal parameter for measurement [4,5,6], and the scheme of phase estimation is theoretically proposed [7,8,9], comprising mainly optical interferometry and homodyne measurements [10,11]. Interferometers can provide the most precise measurements. Recently, physicists with the advanced Laser Interferometer Gravitational-Wave Observatory (LIGO) observed the gravitational waves [12]. The Mach–Zehnder (MZ) interferometer and its variants have been used as a generic model to realize precise measurement of a phase [13]. However, the light field will inevitably interact with the environment in the dynamic process and be disturbed by noise, such as photon loss and the most damaging phase diffusion noise, which have been studied by many researchers [14,15,16,17,18,19,20,21,22,23,24,25,26]. How to improve the phase sensitivity in the presence of photon loss and phase diffusion noise or how to mitigate the disadvantageous effect is crucial for the practical application of the MZ interferometer and its variants.
For interferometers, the photon loss is a typical decoherence process that should be taken into account. The general frame for estimating the ultimate precision limit in the presence of photon loss has been analyzed [14,15,16,17], where this decoherence process can be described by a set of Kraus operators, and the corresponding lower bounds in quantum metrology are given by the quantum Cramér-Rao bound (QCRB) usage of quantum Fisher information (QFI) [27]. It establishes the best precision that can be attained with a given quantum probe [28,29,30,31,32,33,34,35,36,37,38,39]. Phase diffusion represents stochastic fluctuations of the estimated phase shift. Such an effect may be caused by any process that stochastically varies the effective optical lengths traveled by the photons, such as thermal deformations or the micro-motions of the optical elements. The role of phase-diffusive noise in phase estimation has been investigated for qubit [22,40,41], condensate systems [42,43], continuous-variable systems [24], and quantum communication systems [44]. The study of the the behavior of the QFI within the phase diffusion model was, for the first time, carried out by the Paris group [24], where they considered indefinite-photon-number Gaussian input states and studied numerically the achievable precision and the structure of optimal input states. This noise is considered the most detrimental because it destroys the off-diagonal elements of the density matrix. If this input quantum state is not affected by phase diffusion, its phase shift will not change, but this quantum state is utterly useless for phase estimation [24]. Yet, the fundamental analytical bounds on precision have not been verified. Escher et al. [45] presented a variational approach to show an analytical bound based on purification techniques, which explicitly depends on the mathematical description of the noise. The weak measurements and joint estimation were used to deal with the phase and phase diffusion simultaneously for quantum metrology [46,47]. For fixed-particle number probe states, the analytical bounds associated with the simultaneous local estimation of phase and phase diffusion were derived [48]. Using the minimization over the purifications method of Ref. [15], Hu et al. showed an analytical bound of the SU(1,1) interferometer in the presence of phase diffusion and photon losses for an arbitrary input pure state [49]. The collective measurements offered an avenue to multi-parameter quantum-enhanced sensing even in the presence of large amounts of decoherence [50].
The optimizations of phase estimation with photon losses have been discussed [51]. According to the QCRB, the first beam splitter should be unbalanced to improve the precision when photon losses are unbalanced, regardless of the detection method. Unbalanced losses are unavoidable for multipass interferometry, such as, in the laser interferometer space antenna (LISA) proposal [52,53], where the signal interference arm suffering significant propagation loss is designed to return and interfere with the lossless local reference arm. The optimization of the splitting ratio is helpful for applications with significant unbalanced loss, which is realized in experiments [54,55]. On the other hand, how to counteract the adverse effects caused by phase diffusion was also studied. In recent years, the scheme of using an optical parametric oscillator (OPO) to counteract phase diffusion has attracted attention and has been implemented experimentally [56,57]. Inspired by this, injecting squeezing directly after encoding is also considered an ideal solution. Squeezing has been theoretically explained as an effective means of reducing phase diffusion, consistent with existing experimental phenomena [58], thus providing a basis for subsequent loss research and new ideas. However, due to the emergence of phase noise, we will not be able to obtain the upper bound of the QFI that can be analyzed [59], which makes the result not look so clear. Therefore, it is worth studying whether the disadvantageous effect of phase diffusion can be mitigated in the MZ interferometer and whether its working principle can be explained analytically.
In this paper, we introduce a truncated MZ interferometer, similar to the truncated SU(1,1) interferometer (called the SU(1,1) interferometer because it is described by the SU(1,1) group [60]) [61], which not only achieves the same potential phase sensitivity as the traditional MZ interferometer but also simplifies the theoretical treatment of phase diffusion noise. In this truncated MZ interferometer, combined with the relevant characteristics of the Gaussian state [62], the Gaussian state is injected, and then a model is theoretically constructed to counteract the phase noise. The phase uncertainty is selected as an appropriate parameter for the measurement results. Mixed states caused by phase noise are challenging to theoretically handle in conventional interferometers. However, a truncated MZ interferometer can solve this problem.
2. Truncated MZ Interferometer
2.1. Model
In the traditional MZ interferometer, the light field is divided into two beams after passing through the first beam splitter and entering the interferometer’s two arms. After experiencing different physical processes, the light field is combined in the second beam splitter. Then, it is output to the detector to measure the quantity we want to measure. However, the feasibility of the above scheme has certain limitations. When there is phase diffusion noise in one or both arms of the interferometer, the light field will become a mixed state before combining, making it difficult to obtain a suitable and convenient expression method that is used to describe the output state of the light field after passing through the interferometer. According to Ref. [61], we introduced a truncated MZ interferometer as an ideal measurement tool, in which the upper arm is the detection arm and the lower arm is the conjugate arm, as shown in Figure 1. After the first beam splitter splits the light field, it then suffers a phase shift. It finally enters the detectors behind the two arms of the interferometer, respectively, avoiding the process of combining beams.
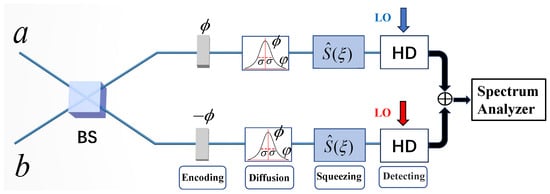
Figure 1.
Schematic of the truncated Mach–Zehnder interferometer. a and b denote two light modes in the interferometer. The phase diffusion corresponds to the application of a random, Gaussian-distributed phase shift with variance , and the mean is equal to the estimated parameter . The squeezing operation is introduced after the phase noise. BS: beam splitter; : phase shift; HD: homodyne detection; and LO: local oscillator.
Since the upper and lower arms of the interferometer are symmetrical, they can be described by the same theoretical equations but with different subscripts. For homodyne detection, we define the quadrature operators of the probe and conjugate the arms, which are given by
where and are the local oscillator phases at the homodyne detectors. The joint quadrature operator is
We estimate the phase by two measurements performed on the state after phase encoding. In particular, we measure the two results of in Equation (3) by changing and to be orthogonal. We call the two results and . Then, the phase to be estimated is [56,57]
Then, according to the law of variance propagation, we can obtain
where , . The phase uncertainty is a significant physical quantity. The smaller it is, the more accurate our measurement is.
2.2. Phase Estimation
In the truncated MZ interferometer, we input the coherent state into one arm (arm a) and the vacuum state into the other arm (arm b). After passing through the beam splitter, there is a coherent state and Since the truncated interferometer has symmetrical properties, we choose to encode symmetric and in both arms to facilitate our measurement of the phase uncertainty, as shown in Figure 2.
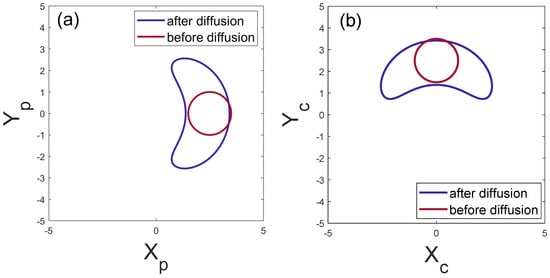
Figure 2.
Phase–space representation of a coherent state (red) and its phase–diffused counterpart (blue). (a) Probe arm and (b) Conjugate arm. Parameters: , . The effect of phase noise on the uncertainty of the and quadratures is clear.
In order to obtain a set of suitable orthogonal field quantities, we symmetrically choose , for the , and , for the . Now, let us look at the results of the measurement. When and , we obtain
and
then
Similarly, when and , we have
and
then
Using Equation (5), we can therefore obtain the phase uncertainty in the lossless case
This is the SQL of the truncated MZ interferometer for the coherent state input. If the injected coherent state is , the SQL is , which is exactly the same as the conclusion in Ref. [56].
2.3. Phase Estimation with Phase Diffusion
Decoherence is the result of the interaction between the quantum system and the environment during its evolution. Three typical decoherence modes are phase diffusion, photon loss, and detection loss. The photon losses in the interferometer are modeled by adding fictitious beam splitters, which have been studied [15].
Here, this scheme mainly studies phase diffusion, which represents the phase noise of collective dephasing. Assume that the phase diffusion corresponds to applying a random, Gaussian-distributed phase shift with variance and the mean is equal to the estimated parameter . The evolution of the initial state is expressed as
where , and the symbol represents the amplitude of phase diffusion. Considering the initial input state , then the evolved state may be written as
where . The density matrix of the output mixed state is obtained when the phase noise is Gaussian noise. From the form of the above matrix, we can see that when phase diffusion exists, the matrix elements on the diagonal of the matrix are not affected by noise, indicating energy conservation, but the off-diagonal items of the matrix are suppressed exponentially, indicating that the phase information carried by the state is destroyed.
We assume that the amplitude of phase diffusion in the probe arm and conjugate arm are and , respectively. When noise appears, the light field in the two arms will change from a pure state to a mixed state. When and , we obtain
and
Similarly, when and , we obtain
and
In the presence of phase diffusion in the truncated MZ interferometer, we obtain the phase uncertainty
Define a physical quantity (, 1, 2) related to the loss of the two arms. Then, the above Equation (23) can be simplified to
From the above calculation results, we can see that when phase diffusion noise appears, the orthogonal field quantities of the quantum states in the two arms will be expanded to varying degrees, thus making the phase uncertainty even greater. Moreover, due to the beam-splitting effect of the MZ interferometer, there is an initial phase difference between the two arms, so the quantum states in the detection arm and the conjugate arm will change in different directions in the phase space, as shown in Figure 2. At the optimal point , the phase uncertainty is given by
When , the above Equation (24) becomes
Comparing Equation (16) with Equation (26), we can see that when there is no loss in the interferometer, the square of the phase uncertainty is inversely proportional to the average number of photons, reaching the SQL . In the presence of phase diffusion, the phase uncertainty will increase by a factor and an additional noise term. Next, we use a method that injects squeezing in opposite directions into each arm to counteract this detrimental effect.
3. Phase Noise Optimization
In order to reduce the impact of this noise as much as possible, as shown in Figure 1, after the phase diffusion noise, a squeezed operation is applied, which is given by
where is the squeezed parameter, r is the squeezed amplitude, and is the squeezed angle. When we take , it means that we adopt the anti-squeezed scheme, and the above equation is .
In any arm of the truncated interferometer, when losses are not present, we can obtain the measurement results for any detection reference phase
Especially, when or , we have
or
The coherent state is a Gaussian state commonly used in measurement schemes. After defining a set of orthogonal field operators and , we will be able to obtain two crucial physical quantities of the Gaussian state: the one-dimensional moment vector R
and the covariance matrix ()
The squeezed operation is also a Gaussian operation, affecting the evolution of the one-dimensional moment vector R and of the Gaussian state in the dynamic process. Since the phase noise model we established here is a Gaussian noise model, the effect of squeezing on the evolution of Gaussian states in the phase space will not be destroyed by noise.
The phase diagrams of the two arms are different due to the existence of an initial phase difference. We add a symmetrically squeezed operation in the opposite direction in the two arms. The probe arm injects reverse squeezing, and the conjugate arm injects positive squeezing. Therefore, in the presence of phase diffusion, by adding the squeezed operation, we can obtain
and
Substituting the above results into Equation (5), the optimized phase uncertainty is given by
At the optimal point , the above Equation (35) becomes
When the squeezed intensity , the squeezing operation can always slow down the impact of noise on the measurement results. In particular, when the loss coefficient , Equation (36) becomes
The result shows that squeezing can be used as a powerful tool in quantum measurements to reduce the negative effects of phase diffusion. The numerical results are shown in Figure 3 and Figure 4. Because of the symmetry expression in both arms, we can use the optimization of one arm to represent our optimization effect. In Figure 3, we can see how a phase-diffused coherent state is modified by the evolution through the squeezing operation, and the phase diffusion noise is reduced as the squeezed degree r increases.
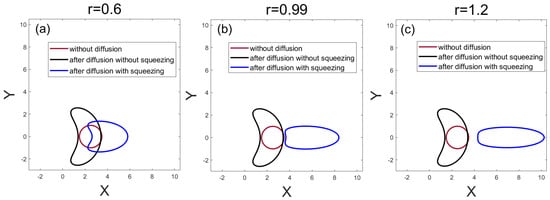
Figure 3.
Phase–space representation of a coherent state (red), its phase–diffused counterpart with squeeze counteraction (blue) and without squeeze counteraction (black) for and . Fluctuations of the Y quadrature are reduced after the squeezing operation.
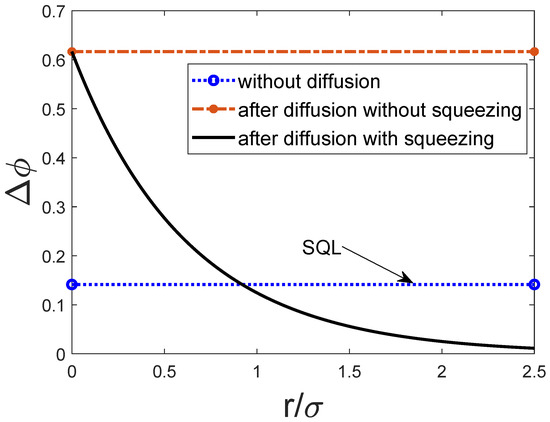
Figure 4.
The phase uncertainty (solid line) versus the normalized squeezed degree r/, where and . The dotted line denotes the SQL and the dot–dashed line denotes the phase uncertainty affected by the phase diffusion.
From the results in Figure 4, we can see that the effect of squeezing to counteract phase diffusion noise seems perfect and can even reach the shot noise limit in the presence of noise. However, there are still several issues that need further elaboration. Firstly, we have established a Gaussian noise model to describe the phase noise during the measurement process to know the effect of this noise on the measurement accurately. However, in actual measurements, the physical model of phase diffusion noise does not evolve precisely as we wanted, leading to a decrease in the ability of squeezing optimization. Secondly, during the experimental operation, to add the squeezing operation, some unavoidable adverse effects may be brought, which will also decrease the optimization effect. However, it is undeniable that even if the above practical operation problems exist, the squeezing operation can still reduce diffusion noise.
4. Conclusions
In the presence of phase diffusion, the accuracy of the measurement will be worse than the SQL. To counteract the adverse effects, we introduced a truncated MZ interferometer model and studied its phase uncertainty in the presence of phase diffusion. In this truncated MZ interferometer, combined with the relevant characteristics of the Gaussian state, we find that the squeezing operation can counteract this effect of phase diffusion and a theoretical explanation is given. Using this result, we can obtain the exact squeezing strength to optimize the loss (in the case of Figure 4, when , the squeezing just offsets the adverse effects of the loss). Although the structure of the interferometer is symmetrical, the beam splitter in the truncated MZ interferometer brings a phase difference to the two arms, causing the phase of the two arms to rotate 90 degrees. To optimize the phase diffusion noise, we anti-symmetrically add squeezing and anti-squeezing in the two symmetrical arms. This strategy is beneficial to quantum precision measurement in lossy environments and will bring reliable theoretical guidance to the experimental application.
In schemes that use interferometers for phase measurements, the phase diffusion noise will reduce measurement accuracy. Using squeezing operation can combat phase diffusion and improve measurement accuracy. We study phase diffusion countermeasures for truncated MZ interferometers and give corresponding analytical expressions. The same noise environment exists in the nonlinear interferometers [13,61]. Although the nonlinear interferometers can maximize the advantages of quantum measurement, for measurement methods that use the phase information carried by light as the measurement medium, the impact of phase diffusion noise on measurement is also fatal. The measurement strategy used here is expected to be used in lossy nonlinear interferometers to bring out the measurement advantages of nonlinear interferometers. The current phase diffusion noise is Gaussian distribution. For non-Gaussian noise, further theoretical research is needed. Finally, considering the loss and optimizing the beam splitting ratio of the beam splitter [55] are also aspects that require further detailed research in the future.
Author Contributions
Conceptualization, Q.L. and C.-H.Y.; methodology, Q.L.; software, C.-H.Y. and Q.L.; validation, Q.L. and C.-H.Y.; formal analysis, Q.L.; investigation, Q.L. and H.M.; resources, L.C. and C.-H.Y.; data curation, Q.L.; writing—original draft preparation, Q.L.; writing—review and editing, Q.L., W.Z. and C.-H.Y. All authors have read and agreed to the published version of the manuscript.
Funding
This work is supported by the Innovation Program for Quantum Science and Technology 2021ZD0303200; The National Natural Science Foundation of China Grants No. U23A2075, No. 12274132, No. 11974111, No. 12234014, No. 11654005; Shanghai Municipal Science and Technology Major Project under Grant No. 2019SH ZDZX01; Innovation Program of Shanghai Municipal Education Commission No. 202101070008E00099; the National Key Research and Development Program of China under Grant No. 2016YFA0302001; and Fundamental Research Funds for the Central Universities. W. Z. acknowledges additional support from the Shanghai Talent Program.
Data Availability Statement
The original contributions presented in the study are included in the article.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| SQL | Standard quantum limit |
| MZ | Mach–Zehnder |
| LISA | Laser interferometer space antenna |
| BS | Beam splitter |
| HD | Homodyne detection |
| LO | Local oscillator |
| OPO | Optical parametric oscillator |
| LIGO | Laser interferometer gravitational-wave observatory |
| QCRB | Quantum Cramér-Rao bound |
| QFI | Quantum Fisher information |
| CM | Covariance matrix |
References
- Braunstein, S.L.; Caves, C.M. Statistical distance and the geometry of quantum states. Phys. Rev. Lett. 1994, 72, 3439–3443. [Google Scholar] [CrossRef]
- Giovannetti, V.; Lloyd, S.; Maccone, L. Quantum-enhanced measurements: Beating the standard quantum limit. Science 2004, 306, 1330–1336. [Google Scholar] [CrossRef]
- Giovannetti, V.; Lloyd, S.; Maccone, L. Advances in quantum metrology. Nat. Photon. 2011, 5, 222–229. [Google Scholar] [CrossRef]
- Carruthers, P.; Nieto, M.M. Phase and Angle Variables in Quantum Mechanics. Rev. Mod. Phys. 1968, 40, 411–440. [Google Scholar] [CrossRef]
- Lynch, R. The quantum phase problem: A critical review. Phys. Rep. 1995, 256, 367–436. [Google Scholar] [CrossRef]
- Susskind, L.; Glogower, J. Quantum mechanical phase and time operator. Phys. Phys. Fiz. 1964, 1, 49–61. [Google Scholar] [CrossRef]
- Armen, M.A.; Au, J.K.; Stockton, J.K.; Doherty, A.C.; Mabuchi, H. Adaptive homodyne measurement of optical phase. Phys. Rev. Lett. 2002, 89, 133602. [Google Scholar] [CrossRef]
- Higgins, B.L.; Berry, D.W.; Bartlett, S.D.; Mitchell, M.W.; Wiseman, H.M.; Pryde, G.J. Demonstrating Heisenberg-limited unambiguous phase estimation without adaptive measurements. New. J. Phys. 2009, 11, 073023. [Google Scholar] [CrossRef]
- Nagata, T.; Okamoto, R.; O’Brien, J.L.; Sasaki, K.; Takeuchi, S. Beating the standard quantum limit with four-entangled photons. Science 2007, 316, 726–729. [Google Scholar] [CrossRef]
- Hradil, Z. Estimation of counted quantum phase. Phys. Rev. A 1995, 51, 1870–1873. [Google Scholar] [CrossRef] [PubMed]
- Pezzé, L.; Smerzi, A.; Khoury, G.; Hodelin, J.F.; Bouwmeester, D. Phase detection at the quantum limit with multiphoton Mach-Zehnder interferometry. Phys. Rev. Lett. 2007, 99, 223602. [Google Scholar] [CrossRef]
- Abbott, B.P.; Abbott, R.; Abbott, T.; Abernathy, M.R.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; et al. Observation of Gravitational Waves from a Binary Black Hole Merger. Phys. Rev. Lett. 2016, 116, 061102. [Google Scholar] [CrossRef]
- Liang, X.; Yu, Z.; Yuan, C.-H.; Zhang, W.; Chen, L. Phase Sensitivity Improvement in Correlation-Enhanced Nonlinear Interferometers. Symmetry 2022, 14, 2684. [Google Scholar] [CrossRef]
- Demkowicz-Dobrzanski, R.; Dorner, U.; Smith, B.J.; Lundeen, J.S.; Wasilewski, W.; Banaszek, K.; Walmsley, I.A. Quantum phase estimation with lossy interferometers. Phys. Rev. A 2009, 80, 013825. [Google Scholar] [CrossRef]
- Escher, B.M.; de Matos Filho, R.L.; Davidovich, L. General framework for estimating the ultimate precision limit in noisy quantum-enhanced metrology. Nat. Phys. 2011, 7, 406–411. [Google Scholar] [CrossRef]
- Demkowicz-Dobrzanski, R.; Kolodynski, J.; Guta, M. The elusive Heisenberg limit in quantum-enhanced metrology. Nat. Commun. 2012, 3, 1063. [Google Scholar] [CrossRef]
- Yue, J.D.; Zhang, Y.R.; Fan, H. Quantum-enhanced metrology for multiple phase estimation with noise. Sci. Rep. 2014, 4, 5933. [Google Scholar] [CrossRef]
- Berry, D.W.; Michael, J.W.; Wiseman, H.M. Stochastic Heisenberg Limit: Optimal Estimation of a Fluctuating Phase. Phys. Rev. Lett. 2013, 111, 113601. [Google Scholar] [CrossRef] [PubMed]
- Chaves, R.; Brask, J.B.; Markiewicz, M.; Kołodynski, J.; Acin, A. Noisy Metrology beyond the Standard Quantum Limit. Phys. Rev. Lett. 2013, 111, 120401. [Google Scholar] [CrossRef] [PubMed]
- Dur, W.; Skotiniotis, M.; Frowis, F.; Kraus, B. Improved Quantum Metrology Using Quantum Error Correction. Phys. Rev. Lett. 2014, 112, 080801. [Google Scholar] [CrossRef]
- Kessler, E.M.; Lovchinsky, I.; Sushkov, A.O.; Lukin, M.D. Quantum Error Correction for Metrology. Phys. Rev. Lett. 2014, 112, 150802. [Google Scholar] [CrossRef] [PubMed]
- Brivio, D.; Cialdi, S.; Vezzoli, S.; Gebrehiwot, B.T.; Genoni, M.G.; Olivares, S.; Paris, M.G.A. Experimental estimation of one-parameter qubit gates in the presence of phase diffusion. Phys. Rev. A 2010, 81, 012305. [Google Scholar] [CrossRef]
- Alipour, S.; Mehboudi, M.; Rezakhani, A.T. Quantum Metrology in Open Systems: Dissipative Cramer-Rao Bound. Phys. Rev. Lett. 2014, 112, 120405. [Google Scholar] [CrossRef] [PubMed]
- Genoni, M.G.; Olivares, S.; Paris, M.G.A. Optical Phase Estimation in the Presence of Phase Diffusion. Phys. Rev. Lett. 2011, 106, 153603. [Google Scholar] [CrossRef]
- Genoni, M.G.; Olivares, S.; Brivio, D.; Cialdi, S.; Cipriani, D.; Santamato, A.; Vezzoli, S.; Paris, M.G.A. Opical interferometry in the presence of large phase diffusin. Phys. Rev. A 2012, 85, 043817. [Google Scholar] [CrossRef]
- Feng, X.M.; Jin, G.R.; Yang, W. Quantum interferometry with binary-outcome measurements in the presence of phase diffusion. Phys. Rev. A 2014, 90, 013807. [Google Scholar] [CrossRef]
- Braunstein, S.L.; Caves, C.M.; Milburn, G.J. Generalized uncertainty relations: Theory, examples, and Lorentz invariance. Ann. Phys. 1996, 247, 135–173. [Google Scholar] [CrossRef]
- Toth, G.; Apellaniz, I. Quantum metrology from a quantum information science perspective. J. Phys. A 2014, 47, 424006. [Google Scholar] [CrossRef]
- Pezzè, L.; Smerzi, A. Quantum theory of phase estimation. In Atom Interferometry; Tino, G.M., Kasevich, M.A., Eds.; Proceedings of the International School of Physics “Enrico Fermi” Series; IOS Press: Varenna, Italy, 2014; Volume 188, pp. 691–741. [Google Scholar]
- Demkowicz-Dobrzanski, R.; Jarzyna, M.; Kolodynski, J. Quantum limits in optical interferometry. Prog. Opt. 2015, 60, 345–435. [Google Scholar]
- Wang, X.B.; Hiroshima, T.; Tomita, A.; Hayashi, M. Quantum information with Gaussian states. Phys. Rep. 2007, 448, 1–111. [Google Scholar] [CrossRef]
- Monras, A. Phase space formalism for quantum estimation of Gaussian states. arXiv 2013, arXiv:1303.3682. [Google Scholar]
- Pinel, O.; Jian, P.; Treps, N.; Fabre, C.; Braun, D. Quantum parameter estimation using general single-mode Gaussian states. Phys. Rev. A 2013, 88, 040102(R). [Google Scholar] [CrossRef]
- Liu, J.; Jing, X.; Wang, X. Phase-matching condition for enhancement of phase sensitivity in quantum metrology. Phys. Rev. A 2013, 88, 042316. [Google Scholar] [CrossRef]
- Gao, Y.; Lee, H. Bounds on quantum multiple-parameter estimation with Gaussian state. Eur. Phys. J. D 2014, 68, 347. [Google Scholar] [CrossRef]
- Jiang, Z. Quantum Fisher information for states in exponential form. Phys. Rev. A 2014, 89, 032128. [Google Scholar] [CrossRef]
- Safranek, D.; Lee, A.R.; Fuentes, I. Quantum parameter estimation using multi-mode Gaussian states. New J. Phys. 2015, 17, 073016. [Google Scholar] [CrossRef]
- Jiao, G.F.; Wang, Q.; Yu, Z.; Chen, L.Q.; Zhang, W.; Yuan, C.H. Effects of losses on the sensitivity of an actively correlated Mach-Zehnder interferometer. Phys. Rev. A 2021, 104, 013725. [Google Scholar] [CrossRef]
- Chang, S.; Ye, W.; Rao, X.; Wen, J.; Zhang, H.; Gong, Q.; Huang, L.; Luo, M.; Chen, Y.; Hu, L.; et al. Intramode-correlation–enhanced simultaneous multiparameter-estimation precision. Phys. Rev. A 2022, 106, 062409. [Google Scholar] [CrossRef]
- Teklu, B.; Genoni, M.G.; Olivares, S.; Paris, M.G.A. Phase estimation in the presence of phase diffusion: The qubit case. Phys. Scr. 2010, 2010, 014062. [Google Scholar] [CrossRef]
- Trapani, J.; Teklu, B.; Olivares, S.; Paris, M.G.A. Quantum phase communication channels in the presence of static and dynamical phase diffusion. Phys. Rev. A 2015, 92, 012317. [Google Scholar] [CrossRef]
- Liu, Y.C.; Jin, G.R.; You, L. Quantum-limited metrology in the presence of collisional dephasing. Phys. Rev. A 2010, 82, 045601. [Google Scholar] [CrossRef]
- Tikhonenkov, I.; Moore, M.G.; Vardi, A. Optimal Gaussian squeezed states for atom interferometry in the presence of phase diffusion. Phys. Rev. A 2010, 82, 043624. [Google Scholar] [CrossRef]
- DiMario, M.T.; Kunz, L.; Banaszek, K.; Becerra, F.E. Optimized communication strategies with binary coherent states over phase noise channels. Npj Quantum Inf. 2019, 5, 65. [Google Scholar] [CrossRef]
- Escher, B.M.; Davidovich, L.; Zagury, N.; de Matos Filho, R.L. Quantum Metrological limits via a variational approach. Phys. Rev. Lett. 2012, 109, 190404. [Google Scholar] [CrossRef]
- Vidrighin, M.D.; Donati, G.; Genoni, M.G.; Jin, X.M.; Kolthammer, W.S.; Kim, M.S.; Datta, A.; Barbieri, M.; Walmsley, I.A. Joint estimation of phase and phase diffusion for quantum metrology. Nat. Commun. 2014, 5, 3532. [Google Scholar] [CrossRef] [PubMed]
- Altorio, M.; Genoni, M.G.; Vidrighin, M.D.; Somma, F.; Barbieri, M. Weak measurements and the joint estimation of phase and phase diffusion. Phys. Rev. A 2015, 92, 032114. [Google Scholar] [CrossRef]
- Szczykulska, M.; Baumgratz, T.; Datta, A. Reaching for the quantum limits in the simultaneous estimation of phase and phase diffusion. Quantum Sci. Technol. 2017, 2, 044004. [Google Scholar] [CrossRef]
- Hu, X.-L.; Li, D.; Chen, L.Q.; Zhang, K.; Zhang, W.; Yuan, C.-H. Phase estimation for an SU(1,1) interferometer in the presence of phase diffusion and photon losses. Phys. Rev. A 2018, 98, 023803. [Google Scholar]
- Conlon, L.O.; Vogl, T.; Marciniak, C.D. Approaching optimal entangling collective measurements on quantum computing platforms. Nat. Phys. 2023, 19, 351–357. [Google Scholar] [CrossRef] [PubMed]
- Cooper, J.J.; Dunningham, J.A. Towards improved interferometric sensitivities in the presence of loss. New. J. Phys. 2011, 13, 115003. [Google Scholar] [CrossRef]
- Vinzenz, W.; Johanna, B.; Claus, B.; Karsten, D.; Antonio, G.; Felipe, G.; Gerhard, H.; Jim, H.; Oliver, J.; Christian, K. Noise sources in the ltp heterodyne interferometer. Clas. Quantum Grav. 2006, 23, S159. [Google Scholar]
- Markus, O.; Gerhard, H.; Karsten, D. Tdi and clock noise removal for the split interferometry configuration of lisa. Clas. Quantum Grav. 2012, 29, 205003. [Google Scholar]
- Huang, W.; Liang, X.; Zhu, B.; Yan, Y.; Yuan, C.H.; Zhang, W.; Chen, L.Q. Protection of noise squeezing in a quantum interferometer with optimal resource allocation. Phys. Rev. Lett. 2023, 130, 073601. [Google Scholar] [CrossRef]
- Huang, W.; Liang, X.; Yuan, C.H.; Zhang, W.; Chen, L.Q. Optimal phase measurements in a lossy Mach-Zehnder interferometer with coherent input light. Res. Phys. 2023, 50, 106574. [Google Scholar] [CrossRef]
- Cialdi, S.; Suerra, E.; Olivares, S.; Capra, S.; Paris, M.G.A. Squeezing Phase Diffusion. Rev. Lett. 2020, 124, 163601. [Google Scholar] [CrossRef]
- Notarnicola, M.N.; Genoni, M.G.; Cialdi, S.; Paris, M.G.A.; Olivares, S. Phase noise mitigation by a realistic optical parametric oscillator. J. Opt. Soc. Am. B 2022, 39, 1059–1067. [Google Scholar] [CrossRef]
- Frascella, G.; Agne, S.; Khalili, F.Y.; Chekhova, M.V. Overcoming detection loss and noise in squeezing-based optical sensing. npj Quantum Inf. 2021, 7, 72. [Google Scholar] [CrossRef]
- Carrara, G.; Genoni, M.G.; Cialdi, S.; Paris, M.G.A.; Olivares, S. Squeezing as a resource to counteract phase diffusion in optical phase estimation. Phys. Rev. A 2020, 102, 062610. [Google Scholar] [CrossRef]
- Yurke, B.; McCall, S.L.; Klauder, J.R. SU(2) and SU(1 1) interferometers. Phys. Rev. A 1986, 33, 4033. [Google Scholar] [CrossRef] [PubMed]
- Anderson, B.E.; Gupta, P.; Schmittberger, B.L.; Horrom, T.; Hermann-Avigliano, C.; Jones, K.M.; Lett, P.D. Phase sensing beyond the standard quantum limit with a variation on the SU(1,1) interferometer. Optica 2017, 4, 752–756. [Google Scholar] [CrossRef]
- Olivares, S. Quantum optics in the phase space A tutorial on Gaussian states. Eur. Phys. J. Top. 2012, 203, 3–24. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).