Modeling Computer Virus Spread Using ABC Fractional Derivatives with Mittag-Leffler Kernels: Symmetry, Invariance, and Memory Effects in a Four-Compartment Network Model

Abstract

The spread of computer viruses poses a critical threat to networked systems and requires accurate modeling tools. Classical integer-order approaches had failed to capture memory effects inherent in real digital environments. To address this, we developed a four-compartment fractional-order model using the Atangana–Baleanu–Caputo (ABC) derivative with Mittag-Leffler kernels. We established fundamental properties such as positivity, boundedness, existence, uniqueness, and Hyers–Ulam stability. Analytical solutions were derived via Laplace transform and homotopy series, while the Variation-of-Parameters Method and a dedicated numerical scheme provided approximations. Simulation results showed that the fractional order strongly influenced infection dynamics: smaller orders delayed peaks, prolonged latency, and slowed recovery. Compared to classical models, the ABC framework captured realistic memory-dependent behavior, offering valuable insights for designing timely and effective cybersecurity interventions. The model exhibits structural symmetries: the infection flux depends on the symmetric combination $L+I$ and the feasible region (probability simplex) is invariant under the flow. Under the parameter constraint $\delta =\theta$ (and equal linear loss terms), the system is equivariant under the involution $(L,I)\mapsto (I,L)$, which is reflected in identical Hyers–Ulam stability bounds for the latent and infectious components.

1. Introduction

Malware and computer viruses continue to threaten networked systems, causing data breaches, financial losses, and systemic vulnerabilities. Mathematical modeling, especially frameworks inspired by epidemic dynamics, offers a principled way to capture propagation, assess defenses, and predict resilience. Classical (integer-order) epidemic models adapted from biological contexts [1,2,3,4] provide valuable insights, but neglect memory and hereditary effects that are ubiquitous in digital settings: latent infections, delayed antivirus responses, and long-terme persistence motivates a move beyond standard ODEs toward memory-aware formulations.

Fractional calculus extends differentiation to non-integer orders and is well suited for systems with heredity and fading memory [5,6,7,8]. Of particular relevance is the Atangana–Baleanu–Caputo (ABC) operator with a non-singular Mittag-Leffler kernel [9,10,11], which preserves non-locality without kernel singularities and has been successfully applied across biology, epidemiology, viscoelasticity, and control [12,13,14,15,16,17,18]. For the stability theory in Caputo fractional differential systems, see [19]. Related applications span computer-virus modeling [20,21], pneumonia [22,23,24], thermo/poroelastic and nanofluid problems [25,26,27,28,29], diabetes [30,31,32,33,34,35,36], and zoonoses [37,38,39,40,41]. We note also the “$\alpha$–Fractional Integral and Derivative” of [42], whose kernel and memory structure differ from the ABC operator; in contrast, our work adopts the ABC formulation to better capture hereditary effects without singular behavior at $t=0$.

In this paper, we formulate a new four-compartment model for computer-virus transmission using the ABC derivative in the Caputo sense. The model captures the evolution of susceptible, latent, infectious, and antivirus-protected devices, and extends existing formulations by incorporating non-local memory via the Mittag-Leffler kernel. We rigorously establish non-negativity, boundedness, existence-uniqueness, and Hyers–Ulam stability with explicit constants [43,44,45]. Analytical representations are derived using the Laplace transform and homotopy series, while the Variation-of-Parameters Method (VPM) and a tailored numerical scheme [46,47] yield practical approximations. Simulations demonstrate that the fractional order $\epsilon$ strongly shapes infection dynamics—smaller values delay peaks, prolong latency, and slow antivirus activation—confirming that fractional-order modeling captures realistic memory-dependent behavior in digital ecosystems.

This research contributes to digital epidemiology and computational cybersecurity by providing a comprehensive, memory-aware framework that can underpin optimal control, feedback design, and learning-based countermeasures [48,49,50,51]. In contrast to classical integer-order virus models (e.g., [21]), which overlook non-local memory and often presume exponential recovery, our ABC-based formulation furnishes (i) a fractional mechanism that more faithfully represents hereditary effects; (ii) a rigorous analysis ensuring well-posedness and Hyers–Ulam stability; (iii) analytical and numerical tools adapted to ABC operators; (iv) quantitative evidence that memory modulates peak timing, latency duration, and protection dynamics; and (v) new structural insights into infection–recovery balance under fractional dynamics. Taken together, these elements articulate the objectives and methodology of the study and bridge epidemic-inspired modeling with the realities of cyber-infection processes.

Our ABC fractional malware model exhibits several symmetry properties that highlight its relevance to Symmetry: (i) Permutation symmetry in the infection term: the susceptible flux depends only on the symmetric combination $L+I$, so exchanging L and I leaves the S-equation unchanged. (ii) Equivariance under $(L,I)$-swap: when $\delta =\theta$ and the linear loss rates of L and I are equal, the full vector field is invariant under the involution $\sigma (L,I)=(I,L)$. (iii) Invariant sets and simplex symmetry: the nonnegative orthant and the normalized simplex $\mathrm{\Delta }=\left\{\right(S,L,I,A)\ge 0:S+L+I+A=1\}$ remain forward invariant, providing a geometric symmetry of the phase space through coordinate-wise reflections at the boundary. (iv) Symmetry in stability bounds: on the parameter submanifold $\delta =\theta$, the Hyers–Ulam stability constants for L and I coincide, reflecting the $(L,I)$-equivariance.

These symmetry features provide a unifying perspective for our theoretical analysis and guide the interpretation of the numerical experiments that follow.

• Summary of structural symmetries: Infection pressure: symmetric sum $L+I$. Equivariance: $(L,I)\mapsto (I,L)$ for $\delta =\theta$. Invariant geometry: forward invariance of the cone and simplex. Stability symmetry: identical Hyers–Ulam bounds for L and I.

The remainder of the paper is organized as follows: Section 2 provides the preliminary concepts and definitions. Section 3 presents the mathematical model of the fractional order for malware propagation. Section 4 is devoted to the solution of the proposed model, including Section 4.1 on positivity and boundedness, Section 4.2 on existence and uniqueness, Section 4.3 on Hyers–Ulam stability, Section 4.4 on the analytic solution, and Section 4.5 on the Iterative Variation-of-Parameters Technique. Section 5 develops the numerical approximation scheme. Section 6 discusses the results, and Section 7 concludes the study.

2. Background

The two-parameter Mittag-Leffler function was first introduced as a generalization of the classical Mittag-Leffler function by Wiman [52], and later formalized in modern treatments by Gorenflo and collaborators [53]. It is defined, for $\epsilon >0$ and $\rho >0$, as

$$E_{\epsilon ,\rho }\left(\zeta \right)=\sum _{m=0}^{\infty }{\displaystyle \frac{{\zeta }^m}{\mathrm{\Gamma }(\epsilon m+\rho )}}.$$

When the second parameter is unity $(\rho =1)$, this is reduced to the classic one-parameter Mittag-Leffler function introduced by Mittag-Leffler [54]:

$$E_{\epsilon }\left(\zeta \right)=\sum _{m=0}^{\infty }{\displaystyle \frac{{\zeta }^m}{\mathrm{\Gamma }(\epsilon m+1)}}.$$

The Caputo–Atangana–Baleanu (CAB) fractional derivative is distinguished by its non-local and nonsingular kernel properties, characterized via convolution with a Mittag-Leffler kernel. For a sufficiently smooth function $h\left(\mathrm{t}\right)\in C^1(0,T)$ and order $0<\epsilon <1$, the CAB derivative is given by

$${}^{\mathrm{CAB}}\mathcal{D}_{0,t}^{\epsilon }h\left(\mathrm{t}\right)={\displaystyle \frac{C\left(\epsilon \right)}{1-\epsilon }}{\int }_0^t{\displaystyle \frac{dh\left(\xi \right)}{d\xi }}{\mathcal{M}}_{\epsilon }\left(-{\displaystyle \frac{\epsilon }{1-\epsilon }}{(t-\xi )}^{\epsilon }\right)d\xi ,$$

where $C\left(\epsilon \right)$ is a normalization constant, typically expressed as $C\left(\epsilon \right)=1-\epsilon +\omega /\mathrm{\Gamma }\left(\epsilon \right)$, and ${\mathcal{M}}_{\epsilon }(·)$ denotes the one-parameter Mittag-Leffler function.

Theorem 1

([9,18]). Consider the fractional differential equation involving the CAB operator:

$${}^{\mathrm{CAB}}\mathcal{D}_t^{\epsilon }h\left(\mathrm{t}\right)=\psi \left(\mathrm{t}\right).$$

Then, the unique solution can be explicitly represented as

$$h\left(\mathrm{t}\right)={\displaystyle \frac{1-\epsilon }{C\left(\epsilon \right)}}\psi \left(\mathrm{t}\right)+{\displaystyle \frac{\epsilon }{C\left(\epsilon \right)\mathrm{\Gamma }\left(\epsilon \right)}}{\int }_0^t\psi \left(\xi \right){(t-\xi )}^{\epsilon -1}d\xi .$$

In a similar context, the associated fractional integral operator related to the CAB derivative takes the form:

$${}^{\mathrm{CAB}}\mathcal{I}_t^{\epsilon }\left[\phi \left(\mathrm{t}\right)\right]={\displaystyle \frac{1-\epsilon }{C\left(\epsilon \right)}}\phi \left(\mathrm{t}\right)+{\displaystyle \frac{\epsilon }{C\left(\epsilon \right)\mathrm{\Gamma }\left(\epsilon \right)}}{\int }_0^t\phi \left(\xi \right){(t-\xi )}^{\epsilon -1}d\xi .$$

An alternative formulation of the CAB fractional derivative, specifically in the Caputo sense with Mittag-Leffler kernel, is given by

$${}^{\mathrm{CAB}}\mathcal{D}_t^{\epsilon }\mathrm{\Phi }\left(\mathrm{t}\right)={\displaystyle \frac{C\left(\epsilon \right)}{1-\epsilon }}{\int }_0^t{\mathrm{\Phi }}^{\prime }\left(\mathrm{t}\right){\mathcal{M}}_{\epsilon }\left(-{\displaystyle \frac{\epsilon }{1-\epsilon }}{(t-\mathrm{t})}^{\epsilon }\right)d\mathrm{t},$$

where $\epsilon \in (0,1)$, and $C\left(\epsilon \right)$ is a normalization function ensuring the derivative behaves consistently as $\epsilon \to 0$ or 1.

The Laplace transform of the CAB fractional derivative for a function $f\left(\mathrm{t}\right)$ is expressed as

$$\mathcal{L}\left\{{}^{\mathrm{CAB}}\mathcal{D}_t^{\epsilon }f\left(\mathrm{t}\right)\right\}\left(s\right)={\displaystyle \frac{C\left(\epsilon \right)}{1-\epsilon }}·{\displaystyle \frac{s^{\epsilon }\tilde{f}\left(s\right)-s^{\epsilon -1}f\left(0\right)}{s^{\epsilon }+\frac{\epsilon }{1-\epsilon }}},$$

where $\tilde{f}\left(s\right)=\mathcal{L}\left\{f\left(\mathrm{t}\right)\right\}\left(s\right)$ denotes the Laplace transform of $f\left(\mathrm{t}\right)$.

The CAB derivative enjoys the following important properties:

1.

Linearity: For any $\alpha ,\beta \in \mathbb{R}$ and functions ${\psi }_1,{\psi }_2$ in the domain of ${}^{\mathrm{CAB}}D_t^{\epsilon }$,

$${}^{\mathrm{CAB}}D_t^{\epsilon }\left(\alpha {\psi }_1\left(t\right)+\beta {\psi }_2\left(t\right)\right)=\alpha {}^{\mathrm{CAB}}D_t^{\epsilon }{\psi }_1\left(t\right)+\beta {}^{\mathrm{CAB}}D_t^{\epsilon }{\psi }_2\left(t\right).$$

2.

Non-singular kernel: Unlike classical Riemann–Liouville or Caputo operators, the CAB derivative employs the Mittag-Leffler kernel, which is non-singular and non-local, thus avoiding divergence at $t=0$ and capturing long-memory effects.

3.

Consistency with integer order: If $\epsilon \to 1$, then

$$\underset{\epsilon \to 1}{lim}{}^{\mathrm{CAB}}D_t^{\epsilon }\psi \left(t\right)={\psi }^{\prime }\left(t\right),$$

and if $\epsilon \to 0$, the derivative is reduced to $\psi \left(t\right)-\psi \left(a\right)$, thereby bridging fractional and integer-order calculus.

4.

Positivity of the kernel: The kernel $E_{\epsilon }(-\frac{\epsilon }{1-\epsilon }{(t-\tau )}^{\epsilon })$ is positive and decreasing in t, which ensures that the CAB operator preserves non-negativity in dynamical systems.

5.

Memory effect: The non-local structure implies that ${}^{\mathrm{CAB}}D_t^{\epsilon }\psi \left(t\right)$ depends on the entire history of $\psi \left(\tau \right)$ for $\tau \in [a,t]$, capturing hereditary and fading memory effects crucial in modeling biological and digital epidemics.

These properties make the CAB derivative particularly suitable for applications in malware propagation modeling, where memory, latency, and delay phenomena play a central role.

3. Mathematical Model of Fractional-Order for Malware Propagation

We propose a fractional-order mathematical model that captures the transmission dynamics of computer malware within a networked environment. Distinct from classical integer-order approaches, this model incorporates memory-dependent effects via the Caputo–Atangana–Baleanu (CAB) fractional differential operator, characterized by a non-local kernel constructed from the Mittag-Leffler function. The computing network is categorized into four mutually exclusive states: vulnerable devices denoted by $\mathtt{S}\left(t\right)$, covertly infected devices denoted by $\mathtt{L}\left(t\right)$, actively contagious devices denoted by $\mathtt{I}\left(t\right)$, and protected devices equipped with antivirus software denoted by $\mathtt{A}\left(t\right)$. The classical integer-order model governing the time evolution is given by

$$\left\{\begin{array}{c}{\displaystyle \frac{d\mathtt{S}\left(t\right)}{dt}}=\mathrm{\Lambda }-\kappa \mathtt{S}\left(t\right)\left(\mathtt{L}\left(t\right)+\mathtt{I}\left(t\right)\right)-\mathrm{\Lambda }\mathtt{S}\left(t\right),\hfill \\ {\displaystyle \frac{d\mathtt{L}\left(t\right)}{dt}}=\kappa \mathtt{S}\left(t\right)\left(\mathtt{L}\left(t\right)+\mathtt{I}\left(t\right)\right)-(\delta +\mathrm{\Lambda })\mathtt{L}\left(t\right),\hfill \\ {\displaystyle \frac{d\mathtt{I}\left(t\right)}{dt}}=\delta \mathtt{L}\left(t\right)-(\theta +\mathrm{\Lambda })\mathtt{I}\left(t\right),\hfill \\ {\displaystyle \frac{d\mathtt{A}\left(t\right)}{dt}}=\theta \mathtt{I}\left(t\right)-(\iota +\mathrm{\Lambda })\mathtt{A}\left(t\right),\hfill \end{array}\right.$$

where each term represents infection, latency, contagion, or protection dynamics.

To incorporate hereditary and fading memory characteristics observed in real-world malware spread and antivirus activation delays, we extend the system by replacing classical derivatives with the CAB fractional derivative of order $\epsilon \in (0,1)$. The fractional-order variant is

$$\left\{\begin{array}{c}{}^{\mathrm{CAB}}D_t^{\epsilon }\mathtt{S}\left(t\right)=\mathrm{\Lambda }-\kappa \mathtt{S}\left(t\right)\left(\mathtt{L}\left(t\right)+\mathtt{I}\left(t\right)\right)-\mathrm{\Lambda }\mathtt{S}\left(t\right),\hfill \\ {}^{\mathrm{CAB}}D_t^{\epsilon }\mathtt{L}\left(t\right)=\kappa \mathtt{S}\left(t\right)\left(\mathtt{L}\left(t\right)+\mathtt{I}\left(t\right)\right)-(\delta +\mathrm{\Lambda })\mathtt{L}\left(t\right),\hfill \\ {}^{\mathrm{CAB}}D_t^{\epsilon }\mathtt{I}\left(t\right)=\delta \mathtt{L}\left(t\right)-(\theta +\mathrm{\Lambda })\mathtt{I}\left(t\right),\hfill \\ {}^{\mathrm{CAB}}D_t^{\epsilon }\mathtt{A}\left(t\right)=\theta \mathtt{I}\left(t\right)-(\iota +\mathrm{\Lambda })\mathtt{A}\left(t\right).\hfill \end{array}\right.$$

(1)

Model variables and parameters:

• $\mathtt{S}\left(t\right)$: Number of vulnerable devices at time t.
• $\mathtt{L}\left(t\right)$: Number of devices carrying latent (dormant) infections.
• $\mathtt{I}\left(t\right)$: Number of actively infected devices spreading malware.
• $\mathtt{A}\left(t\right)$: Number of antivirus-protected devices.
• $\mathrm{\Lambda }$: Rate of device addition and removal.
• $\kappa$: Malware transmission rate.
• $\delta$: Transition rate from latent to active infection.
• $\theta$: Transition rate from infection to antivirus-protected state.
• $\iota$: Neutralization rate of antivirus-protected devices.

The state variables of the fractional-order system in Equation (1) are defined on the nonnegative real line,

$$t\in [0,\infty ),(\mathtt{S}\left(t\right),\mathtt{L}\left(t\right),\mathtt{I}\left(t\right),\mathtt{A}\left(t\right))\in {\mathbb{R}}_{\ge 0}^4.$$

Thus, the model describes the evolution of the four compartments for all future times starting from the initial instant $t=0$.

To ensure well-posedness of the initial value problem, we prescribe

$$S\left(0\right)=S_0\ge 0,L\left(0\right)=L_0\ge 0,I\left(0\right)=I_0\ge 0,A\left(0\right)=A_0\ge 0,$$

where $(S_0,L_0,I_0,A_0)$ are the given initial populations of susceptible, latent, infected, and antivirus-protected devices, respectively. These conditions guarantee that the solution trajectory of the system remains in ${\mathbb{R}}_{\ge 0}^4$ for all $t\ge 0$, consistent with the non-negativity property proved in Section 3. This fractional-order formulation accounts for lag effects and memory retention, enabling more realistic modeling of malware spread, delayed antivirus responses, and persistent dormant infections.

Two equilibria are of particular interest:

• Malware-Free Equilibrium (MFE): Malware is eradicated due to effective defenses.
• Endemic Malware Equilibrium (EME): Malware persists due to inadequate protection or rapid spread.

Representative parameter values associated with these regimes are listed in Table 2. Fractional calculus enriches the dynamics by capturing delayed peaks, slower recovery rates, and smoother transitions, which are essential for modeling realistic cyberattack scenarios and mitigation strategies.

The mathematical formulation of our malware model is directly inspired by epidemiological models traditionally used in biology. In classical SIR-type epidemic models, the population is divided into compartments such as Susceptible, xposed/Latent, Infectious, and Recovered. Each compartment describes the health status of individuals, and transitions between compartments represent infection, progression of disease, or recovery.

To adapt this framework to computer viruses, we established the following analogies:

• Susceptible humans → Vulnerable devices: In epidemiology, susceptible individuals can contract a disease; in networks, vulnerable computers without antivirus protection can be infected by malware.
• Latent (exposed) humans → Covertly infected devices: In biology, exposed individuals carry the pathogen but do not yet show symptoms; similarly, a device may host hidden malware that is not yet spreading but is capable of becoming active later.
• Infectious humans → Actively contagious devices: An infectious person can spread disease; likewise, an actively infected computer spreads malware through connections, downloads, or shared files.
• Recovered humans → Antivirus-protected devices: Just as recovery with immunity prevents reinfection, installation of antivirus software protects devices from further infection or neutralizes active threats.

The transition terms were adapted accordingly: the infection rate $\kappa S(L+I)$ models malware transmission through contact between vulnerable and infected devices; the latency-to-active transition $\delta L$ corresponds to dormant malware becoming contagious; the transition $\theta I$ represents activation of antivirus protection; and removal rates $(\mathrm{\Lambda },\iota )$ reflect device turnover and security updates.

This systematic mapping preserves the structure of biological compartmental models while reinterpreting the compartments and parameters in the context of digital epidemiology. It enables us to exploit the rich analytical and numerical tools of epidemic modeling while tailoring the interpretation to computer virus propagation.

Proposition 1

(Equivariance and invariant sets). Consider the ABC fractional system for $(S,L,I,A)$.

1.

(Symmetric infection pressure) The S-equation depends on L and I only through the symmetric combination $L+I$.

2.

(Invariant cone/simplex) The nonnegative orthant ${\mathbb{R}}_{\ge 0}^4$ is forward invariant. If the variables are normalized by $N\left(t\right)=S+L+I+A$ to lie in $\mathrm{\Delta }=\{x\ge 0:\sum x=1\}$, then Δ is forward invariant.

3.

(Equivariance under $(L,I)$-swap) If $\delta =\theta$ and the linear loss terms of L and I are equal, then the vector field is equivariant under the ${\mathbb{Z}}_2$ action $\sigma (L,I)=(I,L)$; i.e., $F\circ \sigma =\sigma \circ F$.

Proof sketch.

(1) follows since S only sees $\kappa S(L+I)$. (2) follows from the quasi-positivity of the vector field and boundedness of the total population, implying forward invariance of ${\mathbb{R}}_{\ge 0}^4$ and, after normalization, of $\mathrm{\Delta }$. (3) Under $\delta =\theta$ and equal linear losses, the L- and I-equations become identical upon swapping L and I, and the remaining equations are unchanged under $\sigma$, which yields equivariance. □

4. The Solution of the Proposed Mathematical Model

In this section, we establish the existence and uniqueness of solutions to the fractional-order system (1) in the sense of mild solutions, that is, solutions expressed in the equivalent integral form of the Caputo–Atangana–Baleanu derivative. Specifically, we seek functions

$$(\mathtt{S}\left(t\right),\mathtt{L}\left(t\right),\mathtt{I}\left(t\right),\mathtt{A}\left(t\right))\in C([0,T],{\mathbb{R}}_{\ge 0}^4)$$

satisfying the system of integral equations associated with (1). The proof is carried out using fixed-point theory under Lipschitz and boundedness conditions on the nonlinear operators.

4.1. Positivity and Uniform Boundedness of Solutions

We analyze key qualitative attributes of the CAB fractional-order virus propagation model, notably the positivity and boundedness of the system’s state variables. The Atangana–Baleanu–Caputo (CAB) fractional derivative of a function $h\left(\mathrm{t}\right)\in C^1\left([0,T]\right)$ is defined by

$${}^{\mathrm{CAB}}\mathcal{D}_{\mathrm{t}}^{\epsilon }h\left(\mathrm{t}\right)={\displaystyle \frac{C\left(\epsilon \right)}{1-\epsilon }}{\int }_0^{\mathrm{t}}{h}^{\prime }\left(u\right){\mathcal{M}}_{\epsilon }\left(-{\displaystyle \frac{\epsilon }{1-\epsilon }}{(\mathrm{t}-u)}^{\epsilon }\right)du,$$

where $0<\epsilon <1$, $C\left(\epsilon \right)$ is a normalization function normalized so that $C\left(0\right)=C\left(1\right)=1$, and ${\mathcal{M}}_{\epsilon }(·)$ denotes the Mittag-Leffler function of order $\epsilon$.

Theorem 2

(Positivity/Nonnegativity). Assume $\mathtt{S}\left(0\right),\mathtt{L}\left(0\right),\mathtt{I}\left(0\right),\mathtt{A}\left(0\right)\in {\mathbb{R}}_{\ge 0}$. Then every solution $(\mathtt{S},\mathtt{L},\mathtt{I},\mathtt{A})$ of the CAB fractional system (1) satisfies

$$\mathtt{S}\left(t\right),\mathtt{L}\left(t\right),\mathtt{I}\left(t\right),\mathtt{A}\left(t\right)\ge 0\mathit{for}\mathit{all}t\ge 0.$$

Proof. 

Step 1 (Integral form and positivity of the kernel). For $0<\epsilon <1$, the CAB derivative admits the equivalent Volterra form

$$\mathcal{X}\left(t\right)=\mathcal{X}\left(0\right)+{\displaystyle \frac{1-\epsilon }{\mathcal{N}\left(\epsilon \right)}}{F}_{\mathcal{X}}(t,\mathbf{X}\left(t\right))+{\displaystyle \frac{\epsilon }{\mathcal{N}\left(\epsilon \right)\mathrm{\Gamma }\left(\epsilon \right)}}{\int }_0^t{(t-\tau )}^{\epsilon -1}{F}_{\mathcal{X}}(\tau ,\mathbf{X}\left(\tau \right))d\tau ,$$

for each component $\mathcal{X}\in \{\mathtt{S},\mathtt{L},\mathtt{I},\mathtt{A}\}$, where $\mathbf{X}={(\mathtt{S},\mathtt{L},\mathtt{I},\mathtt{A})}^{\top }$ and $F={(F_{\mathtt{S}},F_{\mathtt{L}},F_{\mathtt{I}},F_{\mathtt{A}})}^{\top }$ is the right-hand side of (1). Since $\mathcal{N}\left(\epsilon \right)>0$, $\mathrm{\Gamma }\left(\epsilon \right)>0$, and ${(t-\tau )}^{\epsilon -1}\ge 0$ for $0\le \tau \le t$, the integral kernel is nonnegative and the affine weight $(1-\epsilon )/\mathcal{N}\left(\epsilon \right)$ is also nonnegative.

• Step 2 (Quasi-positivity of the vector field). Let ${\mathbb{R}}_{\ge 0}^4=\{(x_1,\dots ,x_4):x_i\ge 0\}$. A vector field F is quasi–positive on ${\mathbb{R}}_{\ge 0}^4$ if

  $$F_i(t,\mathbf{x})\ge 0\mathrm{whenever}\mathbf{x}\in {\mathbb{R}}_{\ge 0}^4\mathrm{and}{x}_i=0.$$
• For (1), writing explicitly

  $$\begin{array}{cc}\hfill F_{\mathtt{S}}& =\mathrm{\Lambda }-\kappa \mathtt{S}(\mathtt{L}+\mathtt{I})-\mathrm{\Lambda }\mathtt{S},\hfill \\ \hfill F_{\mathtt{L}}& =\kappa \mathtt{S}(\mathtt{L}+\mathtt{I})-(\delta +\mathrm{\Lambda })\mathtt{L},\hfill \\ \hfill F_{\mathtt{I}}& =\delta \mathtt{L}-(\theta +\mathrm{\Lambda })\mathtt{I},\hfill \\ \hfill F_{\mathtt{A}}& =\theta \mathtt{I}-(\iota +\mathrm{\Lambda })\mathtt{A},\hfill \end{array}$$

  we have, for any $(\mathtt{S},\mathtt{L},\mathtt{I},\mathtt{A})\in {\mathbb{R}}_{\ge 0}^4$,

  $$\begin{array}{cc}\hfill {F_{\mathtt{S}}|}_{\mathtt{S}=0}& =\mathrm{\Lambda }\ge 0,\hfill \\ \hfill F_{\mathtt{L}}{|}_{\mathtt{L}=0}& =\kappa \mathtt{S}(\mathtt{L}+\mathtt{I})\ge 0,\hfill \\ \hfill F_{\mathtt{I}}{|}_{\mathtt{I}=0}& =\delta \mathtt{L}\ge 0,\hfill \\ \hfill F_{\mathtt{A}}{|}_{\mathtt{A}=0}& =\theta \mathtt{I}\ge 0.\hfill \end{array}$$
• Hence F is quasi–positive on ${\mathbb{R}}_{\ge 0}^4$.
• Step 3 (First-exit contradiction). Let $K={\mathbb{R}}_{\ge 0}^4$. Assume, for contradiction, that the solution exits K. Define the first exit time

  $$t^{\mathrm{\star }}:=inf\{t>0:\mathbf{X}\left(t\right)\notin K\}.$$

  By continuity, $\mathbf{X}\left(t\right)\in K$ for $t\in [0,t^{\mathrm{\star }}]$ and $\mathbf{X}\left(t^{\mathrm{\star }}\right)\in \partial K$. Thus, for some component, say $\mathcal{X}\in \{\mathtt{S},\mathtt{L},\mathtt{I},\mathtt{A}\}$, we have $\mathcal{X}\left(t^{\mathrm{\star }}\right)=0$ and $\mathcal{X}\left(t\right)\ge 0$ on $[0,t^{\mathrm{\star }}]$.

Using the integral form at $t^{\mathrm{\star }}$ and the nonnegativity of the kernel weights,

$$\mathcal{X}\left(t^{\mathrm{\star }}\right)=\mathcal{X}\left(0\right)+{\displaystyle \frac{1-\epsilon }{\mathcal{N}\left(\epsilon \right)}}{F}_{\mathcal{X}}(t^{\mathrm{\star }},\mathbf{X}\left(t^{\mathrm{\star }}\right))+{\displaystyle \frac{\epsilon }{\mathcal{N}\left(\epsilon \right)\mathrm{\Gamma }\left(\epsilon \right)}}{\int }_0^{t^{\mathrm{\star }}}{(t^{\mathrm{\star }}-\tau )}^{\epsilon -1}{F}_{\mathcal{X}}(\tau ,\mathbf{X}\left(\tau \right))d\tau .$$

On $[0,t^{\mathrm{\star }}]$, all components are nonnegative; in particular, at the boundary point $\mathbf{X}\left(t^{\mathrm{\star }}\right)\in \partial K$ we have $F_{\mathcal{X}}(t^{\mathrm{\star }},\mathbf{X}\left(t^{\mathrm{\star }}\right))\ge 0$ by quasi-positivity (Step 2). Moreover, by continuity of F and $\mathbf{X}$ and the fact that $\mathbf{X}\left(\tau \right)\in K$ for $\tau \in [0,t^{\mathrm{\star }}]$, we also have $F_{\mathcal{X}}(\tau ,\mathbf{X}\left(\tau \right))\ge -C\mathcal{X}\left(\tau \right)$ for some $C\ge 0$ (locally, F is Lipschitz and $F_{\mathcal{X}}(·,·)$ is at worst linear in $\mathcal{X}$ with a nonnegative inhomogeneous part at $\mathcal{X}=0$). In particular, the integral term is bounded below by a nonnegative quantity whenever $\mathcal{X}\left(\tau \right)=0$, and cannot generate a negative jump.

Hence

$$\mathcal{X}\left(t^{\mathrm{\star }}\right)\ge \underset{\ge 0}{\underbrace{\mathcal{X}\left(0\right)}}+\underset{\ge 0}{\underbrace{{\displaystyle \frac{1-\epsilon }{\mathcal{N}\left(\epsilon \right)}}{F}_{\mathcal{X}}(t^{\mathrm{\star }},\mathbf{X}\left(t^{\mathrm{\star }}\right))}}+\underset{\ge 0}{\underbrace{{\displaystyle \frac{\epsilon }{\mathcal{N}\left(\epsilon \right)\mathrm{\Gamma }\left(\epsilon \right)}}{\int }_0^{t^{\mathrm{\star }}}{(t^{\mathrm{\star }}-\tau )}^{\epsilon -1}{F}_{\mathcal{X}}(\tau ,\mathbf{X}\left(\tau \right))d\tau }}\ge 0.$$

Therefore, $\mathcal{X}\left(t^{\mathrm{\star }}\right)\ge 0$, contradicting the assumption that $t^{\mathrm{\star }}$ is a first exit time to negative values. Thus, no exit occurs and $\mathbf{X}\left(t\right)\in K$ for all $t\ge 0$.

• Step 4 (Component-wise boundary checks, explicit). For completeness, evaluating at the faces of K:

  $$\left\{\begin{array}{c}\begin{array}{cc}\hfill {}^{\mathrm{CAB}}\mathcal{D}_t^{\epsilon }\mathtt{S}{|}_{\mathtt{S}=0}& =\mathrm{\Lambda }\ge 0,\hfill \\ \hfill {}^{\mathrm{CAB}}\mathcal{D}_t^{\epsilon }\mathtt{L}{|}_{\mathtt{L}=0}& =\kappa \mathtt{S}(\mathtt{L}+\mathtt{I})\ge 0,\hfill \\ \hfill {}^{\mathrm{CAB}}\mathcal{D}_t^{\epsilon }\mathtt{I}{|}_{\mathtt{I}=0}& =\delta \mathtt{L}\ge 0,\hfill \\ \hfill {}^{\mathrm{CAB}}\mathcal{D}_t^{\epsilon }\mathtt{A}{|}_{\mathtt{A}=0}& =\theta \mathtt{I}\ge 0,\hfill \end{array}\hfill \end{array}\right.\mathrm{for}(\mathtt{S},\mathtt{L},\mathtt{I},\mathtt{A})\in K.$$

  which is exactly the quasi-positivity used above.

Combining Steps 1–4 yields forward invariance of ${\mathbb{R}}_{\ge 0}^4$ under the CAB flow, i.e., $\mathtt{S}\left(t\right),\mathtt{L}\left(t\right),\mathtt{I}\left(t\right),\mathtt{A}\left(t\right)\ge 0$ for all $t\ge 0$. □

Theorem 3.

Define the total state sum $\mathrm{\Omega }\left(\mathrm{t}\right)=\mathtt{S}\left(\mathrm{t}\right)+\mathtt{L}\left(\mathrm{t}\right)+\mathtt{I}\left(\mathrm{t}\right)+\mathtt{A}\left(\mathrm{t}\right)$. Then $\mathrm{\Omega }\left(\mathrm{t}\right)$ is uniformly bounded on $[0,T]$.

Proof. 

Summing the fractional differential equations yields

$$\begin{array}{cc}\hfill {}^{\mathrm{CAB}}\mathcal{D}_{\mathrm{t}}^{\epsilon }\mathrm{\Omega }\left(\mathrm{t}\right)& =\mathrm{\Lambda }-\kappa \mathtt{S}(\mathtt{L}+\mathtt{I})-\mathrm{\Lambda }\mathtt{S}\hfill \\ & +\kappa \mathtt{S}(\mathtt{L}+\mathtt{I})-(\delta +\mathrm{\Lambda })\mathtt{L}\hfill \\ & +\delta \mathtt{L}-(\theta +\mathrm{\Lambda })\mathtt{I}\hfill \\ & +\theta \mathtt{I}-(\iota +\mathrm{\Lambda })\mathtt{A}.\hfill \end{array}$$

Simplifying the expression by canceling terms

$$\begin{array}{cc}\hfill {}^{\mathrm{CAB}}\mathcal{D}_{\mathrm{t}}^{\epsilon }\mathrm{\Omega }\left(\mathrm{t}\right)& =\mathrm{\Lambda }-\mathrm{\Lambda }\mathtt{S}-\mathrm{\Lambda }\mathtt{L}-\mathrm{\Lambda }\mathtt{I}-\mathrm{\Lambda }\mathtt{A}-\iota \mathtt{A}\hfill \\ & =\mathrm{\Lambda }-\mathrm{\Lambda }\mathrm{\Omega }\left(\mathrm{t}\right)-\iota \mathtt{A}\left(\mathrm{t}\right)\hfill \\ & \le \mathrm{\Lambda }-\mathrm{\Lambda }\mathrm{\Omega }\left(\mathrm{t}\right).\hfill \end{array}$$

Setting $\xi \left(\mathrm{t}\right):=\mathrm{\Omega }\left(\mathrm{t}\right)$, we have the inequality

$${}^{\mathrm{CAB}}\mathcal{D}_{\mathrm{t}}^{\epsilon }\xi \left(\mathrm{t}\right)\le \mathrm{\Lambda }-\mathrm{\Lambda }\xi \left(\mathrm{t}\right).$$

Applying the standard comparison principle for CAB fractional inequalities, solving the associated equality

$${}^{\mathrm{CAB}}\mathcal{D}_{\mathrm{t}}^{\epsilon }\xi \left(\mathrm{t}\right)=\mathrm{\Lambda }-\mathrm{\Lambda }\xi \left(\mathrm{t}\right),$$

and using the properties of the Mittag-Leffler function, the solution is bounded by

$$\xi \left(\mathrm{t}\right)\le \xi \left(0\right)E_{\epsilon }(-\mathrm{\Lambda }{\mathrm{t}}^{\epsilon })+\mathrm{\Lambda }{\mathrm{t}}^{\epsilon }{E}_{\epsilon ,\epsilon +1}(-\mathrm{\Lambda }{\mathrm{t}}^{\epsilon }),$$

where $E_{\alpha ,\beta }\left(z\right)$ is the two-parameter Mittag-Leffler function. Since the Mittag-Leffler function with a negative argument is bounded and completely monotonic for $0<\epsilon <1$, there exists a constant M so that

$$\mathrm{\Omega }\left(\mathrm{t}\right)\le max\left(\mathrm{\Omega }\left(0\right),1\right)=M,\forall \mathrm{t}\in [0,\infty ).$$

Hence, the total population remains uniformly bounded. □

4.2. Existence and Uniqueness of Solutions

In order to prove the existence and uniqueness of solutions for the fractional-order malware propagation model involving the Caputo–Atangana–Baleanu (CAB) derivative, we rewrite the system into an equivalent integral formulation through the CAB fractional integral operator. This reformulation enables the application of fixed-point theorems in an appropriate function space.

Consider the CAB-fractional system describing malware dynamics:

$$\left\{\begin{array}{c}{}^{\mathrm{CAB}}\mathcal{D}_t^{\epsilon }\mathtt{S}\left(\mathrm{t}\right)=\mathrm{\Lambda }-\kappa \mathtt{S}\left(\mathrm{t}\right)\left(\mathtt{L}\left(\mathrm{t}\right)+\mathtt{I}\left(\mathrm{t}\right)\right)-\mathrm{\Lambda }\mathtt{S}\left(\mathrm{t}\right),\hfill \\ {}^{\mathrm{CAB}}\mathcal{D}_t^{\epsilon }\mathtt{L}\left(\mathrm{t}\right)=\kappa \mathtt{S}\left(\mathrm{t}\right)\left(\mathtt{L}\left(\mathrm{t}\right)+\mathtt{I}\left(\mathrm{t}\right)\right)-(\delta +\mathrm{\Lambda })\mathtt{L}\left(\mathrm{t}\right),\hfill \\ {}^{\mathrm{CAB}}\mathcal{D}_t^{\epsilon }\mathtt{I}\left(\mathrm{t}\right)=\delta \mathtt{L}\left(\mathrm{t}\right)-(\theta +\mathrm{\Lambda })\mathtt{I}\left(\mathrm{t}\right),\hfill \\ {}^{\mathrm{CAB}}\mathcal{D}_t^{\epsilon }\mathtt{A}\left(\mathrm{t}\right)=\theta \mathtt{I}\left(\mathrm{t}\right)-(\iota +\mathrm{\Lambda })\mathtt{A}\left(\mathrm{t}\right),\hfill \end{array}\right.$$

where all variables and parameters are defined appropriately.

Using the integral representation for the CAB derivative, the system is equivalently expressed as

$$\left\{\begin{array}{c}{\displaystyle \mathtt{S}\left(\mathrm{t}\right)={\mathtt{S}}_0+\frac{1-\epsilon }{C\left(\epsilon \right)}{\mathrm{\Psi }}_1\left(\mathrm{t}\right)+\frac{\epsilon }{C\left(\epsilon \right)\mathrm{\Gamma }\left(\epsilon \right)}{\int }_0^t{\mathrm{\Psi }}_1\left(\mathrm{t}\right)d\mathrm{t},}\hfill \\ {\displaystyle \mathtt{L}\left(\mathrm{t}\right)={\mathtt{L}}_0+\frac{1-\epsilon }{C\left(\epsilon \right)}{\mathrm{\Psi }}_2\left(\mathrm{t}\right)+\frac{\epsilon }{C\left(\epsilon \right)\mathrm{\Gamma }\left(\epsilon \right)}{\int }_0^t{\mathrm{\Psi }}_2\left(\mathrm{t}\right)d\mathrm{t},}\hfill \\ {\displaystyle \mathtt{I}\left(\mathrm{t}\right)={\mathtt{I}}_0+\frac{1-\epsilon }{C\left(\epsilon \right)}{\mathrm{\Psi }}_3\left(\mathrm{t}\right)+\frac{\epsilon }{C\left(\epsilon \right)\mathrm{\Gamma }\left(\epsilon \right)}{\int }_0^t{\mathrm{\Psi }}_3\left(\mathrm{t}\right)d\mathrm{t},}\hfill \\ {\displaystyle \mathtt{A}\left(\mathrm{t}\right)={\mathtt{A}}_0+\frac{1-\epsilon }{C\left(\epsilon \right)}{\mathrm{\Psi }}_4\left(\mathrm{t}\right)+\frac{\epsilon }{C\left(\epsilon \right)\mathrm{\Gamma }\left(\epsilon \right)}{\int }_0^t{\mathrm{\Psi }}_4\left(\mathrm{t}\right)d\mathrm{t},}\hfill \end{array}\right.$$

where the nonlinear terms ${\mathrm{\Psi }}_i$ are defined as

$$\begin{array}{cc}\hfill {\mathrm{\Psi }}_1(t,\mathtt{S},\mathtt{L},\mathtt{I},\mathtt{A})& =\mathrm{\Lambda }-\kappa \mathtt{S}\left(\mathrm{t}\right)\left(\mathtt{L}\left(\mathrm{t}\right)+\mathtt{I}\left(\mathrm{t}\right)\right)-\mathrm{\Lambda }\mathtt{S}\left(\mathrm{t}\right),\hfill \\ \hfill {\mathrm{\Psi }}_2(t,\mathtt{S},\mathtt{L},\mathtt{I},\mathtt{A})& =\kappa \mathtt{S}\left(\mathrm{t}\right)\left(\mathtt{L}\left(\mathrm{t}\right)+\mathtt{I}\left(\mathrm{t}\right)\right)-(\delta +\mathrm{\Lambda })\mathtt{L}\left(\mathrm{t}\right),\hfill \\ \hfill {\mathrm{\Psi }}_3(t,\mathtt{S},\mathtt{L},\mathtt{I},\mathtt{A})& =delta\mathtt{L}\left(\mathrm{t}\right)-(\theta +\mathrm{\Lambda })\mathtt{I}\left(\mathrm{t}\right),\hfill \\ \hfill {\mathrm{\Psi }}_4(t,\mathtt{S},\mathtt{L},\mathtt{I},\mathtt{A})& =\theta \mathtt{I}\left(\mathrm{t}\right)-(\iota +\mathrm{\Lambda })\mathtt{A}\left(\mathrm{t}\right).\hfill \end{array}$$

Theorem 4.

Suppose the initial data $({\mathtt{S}}_0,{\mathtt{L}}_0,{\mathtt{I}}_0,{\mathtt{A}}_0)\in {\mathbb{R}}_{+}^4$ and the state functions are bounded, i.e., there exist constants $M_1,M_2,M_3,M_4>0$ so that

$$\parallel \mathtt{S}\parallel \le M_1,\parallel \mathtt{L}\parallel \le M_2,\parallel \mathtt{I}\parallel \le M_3,\parallel \mathtt{A}\parallel \le M_4.$$

Then each nonlinear operator ${\mathrm{\Psi }}_i$ satisfies a Lipschitz condition on the Banach space $C([0,T],{\mathbb{R}}^4)$.

Proof. 

We verify the Lipschitz continuity of each ${\mathrm{\Psi }}_i$.

For ${\mathrm{\Psi }}_1$,

$$\parallel {\mathrm{\Psi }}_1({\mathtt{S}}_1,\mathtt{S},\mathtt{L},\mathtt{I},\mathtt{A})-{\mathrm{\Psi }}_1({\mathtt{S}}_2,\mathtt{S},\mathtt{L},\mathtt{I},\mathtt{A})\parallel \le \left(\kappa (2M_2+M_3)+\mathrm{\Lambda }\right)\parallel {\mathtt{S}}_1-{\mathtt{S}}_2\parallel =:L_1\parallel {\mathtt{S}}_1-{\mathtt{S}}_2\parallel .$$

For ${\mathrm{\Psi }}_2$,

$$\parallel {\mathrm{\Psi }}_2(\mathtt{S},{\mathtt{L}}_1,\mathtt{I},\mathtt{A})-{\mathrm{\Psi }}_2(\mathtt{S},{\mathtt{L}}_2,\mathtt{I},\mathtt{A})\parallel \le \left(\kappa M_1+\delta +\mathrm{\Lambda }\right)\parallel {\mathtt{L}}_1-{\mathtt{L}}_2\parallel =:L_2\parallel {\mathtt{L}}_1-{\mathtt{L}}_2\parallel .$$

For ${\mathrm{\Psi }}_3$,

$$\parallel {\mathrm{\Psi }}_3(\mathtt{S},\mathtt{L},{\mathtt{I}}_1,\mathtt{A})-{\mathrm{\Psi }}_3(\mathtt{S},\mathtt{L},{\mathtt{I}}_2,\mathtt{A})\parallel =(\theta +\mathrm{\Lambda })\parallel {\mathtt{I}}_1-{\mathtt{I}}_2\parallel =:L_3\parallel {\mathtt{I}}_1-{\mathtt{I}}_2\parallel .$$

For ${\mathrm{\Psi }}_4$,

$$\parallel {\mathrm{\Psi }}_4(\mathtt{S},\mathtt{L},\mathtt{I},{\mathtt{A}}_1)-{\mathrm{\Psi }}_4(\mathtt{S},\mathtt{L},\mathtt{I},{\mathtt{A}}_2)\parallel =(\iota +\mathrm{\Lambda })\parallel {\mathtt{A}}_1-{\mathtt{A}}_2\parallel =:L_4\parallel {\mathtt{A}}_1-{\mathtt{A}}_2\parallel .$$

Hence, each ${\mathrm{\Psi }}_i$ is Lipschitz continuous with constants

$$L_1=\kappa (2M_2+M_3)+\mathrm{\Lambda },L_2=\kappa M_1+\delta +\mathrm{\Lambda },L_3=\theta +\mathrm{\Lambda },L_4=\iota +\mathrm{\Lambda }.$$

□

Theorem 5

(Existence and Uniqueness). Let $L_i$, $i=1,\dots ,4$, be the Lipschitz constants as defined above. If there exists a time $T>0$ so that

$$\underset{1\le i\le 4}{max}\left\{{\displaystyle \frac{1-\epsilon }{C\left(\epsilon \right)}}{L}_i+{\displaystyle \frac{\epsilon }{C\left(\epsilon \right)\mathrm{\Gamma }\left(\epsilon \right)}}{L}_{i}T\right\}<1,$$

then the CAB fractional system admits a unique solution $(\mathtt{S},\mathtt{L},\mathtt{I},\mathtt{A},W)\in C([0,T],{\mathbb{R}}_{+}^4)$.

Proof. 

Define the operator $\mathcal{M}=({\mathcal{M}}_1,{\mathcal{M}}_2,{\mathcal{M}}_3,{\mathcal{M}}_4)$ on $C([0,T],{\mathbb{R}}^4)$ by

$${\mathcal{M}}_1[\mathtt{S},\mathtt{L},\mathtt{I},\mathtt{A}]\left(\mathrm{t}\right)={\mathtt{S}}_0+{\displaystyle \frac{1-\epsilon }{C\left(\epsilon \right)}}{\mathrm{\Psi }}_1\left(\mathrm{t}\right)+{\displaystyle \frac{\epsilon }{C\left(\epsilon \right)\mathrm{\Gamma }\left(\epsilon \right)}}{\int }_0^t{\mathrm{\Psi }}_1\left(\mathrm{t}\right)d\mathrm{t},$$

and similarly for ${\mathcal{M}}_2,{\mathcal{M}}_3,{\mathcal{M}}_4$. Given the Lipschitz bounds and condition above, $\mathcal{M}$ is a contraction mapping.

By the Banach Fixed Point Theorem, $\mathcal{M}$ has a unique fixed point in $C([0,T],{\mathbb{R}}_{+}^4)$, which corresponds to the unique solution of the fractional system. □

4.3. Hyers–Ulam Stability

Definition 1

([43]). Consider the fractional system defined with the Caputo–Atangana–Baleanu (CAB) derivative:

$$\left\{\begin{array}{c}{}^{\mathrm{CAB}}\mathcal{D}_t^{\epsilon }\mathtt{S}\left(\mathrm{t}\right)={\mathrm{\Phi }}_1(t,\mathtt{S},\mathtt{L},\mathtt{I},\mathtt{A}),\hfill \\ {}^{\mathrm{CAB}}\mathcal{D}_t^{\epsilon }\mathtt{L}\left(\mathrm{t}\right)={\mathrm{\Phi }}_2(t,\mathtt{S},\mathtt{L},\mathtt{I},\mathtt{A}),\hfill \\ {}^{\mathrm{CAB}}\mathcal{D}_t^{\epsilon }\mathtt{I}\left(\mathrm{t}\right)={\mathrm{\Phi }}_3(t,\mathtt{S},\mathtt{L},\mathtt{I},\mathtt{A}),\hfill \\ {}^{\mathrm{CAB}}\mathcal{D}_t^{\epsilon }\mathtt{A}\left(\mathrm{t}\right)={\mathrm{\Phi }}_4(t,\mathtt{S},\mathtt{L},\mathtt{I},\mathtt{A}),\hfill \end{array}\right.$$

where $t\in [0,T]$. This system is said to be Hyers–Ulam stable if there exist constants ${\epsilon }_i>0$, $i=1,2,3,4$, so that for all t,

$$\left\{\begin{array}{c}\left|\mathtt{S}\left(\mathrm{t}\right)-{}_0\mathcal{J}_t^{\epsilon }{\mathrm{\Phi }}_1(\mathtt{S},\mathtt{L},\mathtt{I},\mathtt{A}\right|\le {\epsilon }_1,\hfill \\ \left|\mathtt{L}\left(\mathrm{t}\right)-{}_0\mathcal{J}_t^{\epsilon }{\mathrm{\Phi }}_2(\mathtt{S},\mathtt{L},\mathtt{I},\mathtt{A}\right|\le {\epsilon }_2,\hfill \\ \left|\mathtt{I}\left(\mathrm{t}\right)-{}_0\mathcal{J}_t^{\epsilon }{\mathrm{\Phi }}_3(\mathtt{S},\mathtt{L},\mathtt{I},\mathtt{A}\right|\le {\epsilon }_3,\hfill \\ \left|\mathtt{A}\left(\mathrm{t}\right)-{}_0\mathcal{J}_t^{\epsilon }{\mathrm{\Phi }}_4(\mathtt{S},\mathtt{L},\mathtt{I},\mathtt{A}\right|\le {\epsilon }_4,\hfill \end{array}\right.$$

where ${}_0\mathcal{J}_t^{\epsilon }$ denotes the CAB fractional integral operator.

Let $\left({\mathtt{S}}^{*},{\mathtt{L}}^{*},{\mathtt{I}}^{*},W^{*}\right)$ be an approximate solution satisfying

$$\left\{\begin{array}{c}|\mathtt{S}\left(\mathrm{t}\right)-{\mathtt{S}}^{*}\left(\mathrm{t}\right)|\le {\rho }_1{\delta }_1,|\mathtt{L}\left(\mathrm{t}\right)-{\mathtt{L}}^{*}\left(\mathrm{t}\right)|\le {\rho }_2{\delta }_2,\hfill \\ |\mathtt{I}\left(\mathrm{t}\right)-{\mathtt{I}}^{*}\left(\mathrm{t}\right)|\le {\rho }_3{\delta }_3,|\mathtt{A}\left(\mathrm{t}\right)-W^{*}\left(\mathrm{t}\right)|\le {\rho }_4{\delta }_4,\hfill \end{array}\right.$$

for constants ${\rho }_i,{\delta }_i>0$. Then, the system is Hyers–Ulam stable.

Theorem 6

([43,44,45]). If the bounds from the previous definition hold, the CAB fractional system is Hyers–Ulam stable.

Proof. 

Consider the first component $\mathtt{S}\left(t\right)$ and its approximation $S^{*}\left(t\right)$. We have

$$\begin{array}{cc}\hfill |\mathtt{S}\left(t\right)-S^{*}\left(t\right)|& =|{}_0\mathcal{J}_t^{\epsilon }{\mathrm{\Phi }}_1(S,L,I,A)-{}_0\mathcal{J}_t^{\epsilon }{\mathrm{\Phi }}_1(S^{*},L^{*},I^{*},A^{*})|\hfill \\ & \le \left({\displaystyle \frac{1-\epsilon }{C\left(\epsilon \right)}}+{\displaystyle \frac{\epsilon }{C\left(\epsilon \right)\mathrm{\Gamma }\left(\epsilon \right)}}\right)\left(\kappa (2M_2+M_3)+\mathrm{\Lambda }\right)\parallel S-S^{*}\parallel \hfill \\ & =:{\rho }_1{\delta }_1,\hfill \end{array}$$

where $C\left(\epsilon \right)$ is the CAB normalization constant and $\mathrm{\Gamma }\left(\epsilon \right)$ is the Euler gamma function. Thus,

$${\rho }_1=\left({\displaystyle \frac{1-\epsilon }{C\left(\epsilon \right)}}+{\displaystyle \frac{\epsilon }{C\left(\epsilon \right)\mathrm{\Gamma }\left(\epsilon \right)}}\right)\left(\kappa (2M_2+M_3)+\mathrm{\Lambda }\right).$$

Analogously, for the remaining components we obtain

$$\left\{\begin{array}{c}|\mathtt{L}\left(t\right)-L^{*}\left(t\right)|\le \left({\displaystyle \frac{1-\epsilon }{C\left(\epsilon \right)}}+{\displaystyle \frac{\epsilon }{C\left(\epsilon \right)\mathrm{\Gamma }\left(\epsilon \right)}}\right)(\kappa M_1+\delta +\mathrm{\Lambda }){\delta }_2=:{\rho }_2{\delta }_2,\hfill \\ |\mathtt{I}\left(t\right)-I^{*}\left(t\right)|\le \left({\displaystyle \frac{1-\epsilon }{C\left(\epsilon \right)}}+{\displaystyle \frac{\epsilon }{C\left(\epsilon \right)\mathrm{\Gamma }\left(\epsilon \right)}}\right)(\theta +\mathrm{\Lambda }){\delta }_3=:{\rho }_3{\delta }_3,\hfill \\ |\mathtt{A}\left(t\right)-A^{*}\left(t\right)|\le \left({\displaystyle \frac{1-\epsilon }{C\left(\epsilon \right)}}+{\displaystyle \frac{\epsilon }{C\left(\epsilon \right)\mathrm{\Gamma }\left(\epsilon \right)}}\right)(\iota +\mathrm{\Lambda }){\delta }_4=:{\rho }_4{\delta }_4.\hfill \end{array}\right.$$

Therefore, the system is Hyers–Ulam stable with explicit constants

$$\begin{array}{cc}\hfill {\rho }_1& =\left({\displaystyle \frac{1-\epsilon }{C\left(\epsilon \right)}}+{\displaystyle \frac{\epsilon }{C\left(\epsilon \right)\mathrm{\Gamma }\left(\epsilon \right)}}\right)\left(\kappa (2M_2+M_3)+\mathrm{\Lambda }\right),\hfill \\ \hfill {\rho }_2& =\left({\displaystyle \frac{1-\epsilon }{C\left(\epsilon \right)}}+{\displaystyle \frac{\epsilon }{C\left(\epsilon \right)\mathrm{\Gamma }\left(\epsilon \right)}}\right)(\kappa M_1+\delta +\mathrm{\Lambda }),\hfill \\ \hfill {\rho }_3& =\left({\displaystyle \frac{1-\epsilon }{C\left(\epsilon \right)}}+{\displaystyle \frac{\epsilon }{C\left(\epsilon \right)\mathrm{\Gamma }\left(\epsilon \right)}}\right)(\theta +\mathrm{\Lambda }),\hfill \\ \hfill {\rho }_4& =\left({\displaystyle \frac{1-\epsilon }{C\left(\epsilon \right)}}+{\displaystyle \frac{\epsilon }{C\left(\epsilon \right)\mathrm{\Gamma }\left(\epsilon \right)}}\right)(\iota +\mathrm{\Lambda }).\hfill \end{array}$$

These expressions clearly demonstrate that the stability of each compartment is affected by both the memory effect ($\epsilon$) and the transition rates governing infection and recovery. In particular, as $\epsilon \to 1$, the constants reduce to their classical integer-order counterparts, while for $\epsilon <1$, the memory effect scales the stability bounds, showing slower but more persistent convergence under perturbations. □

Remark 1

(Symmetry in stability constants). When $\delta =\theta$ and the linear loss rates of L and I coincide, the Lipschitz moduli entering the Hyers–Ulam bounds for L and I match. Consequently, the stability constants ${\rho }_2$ and ${\rho }_3$ are equal, reflecting the $(L,I)$-equivariance in Proposition 1(3). This explains the near-identical transient envelopes of $L\left(t\right)$ and $I\left(t\right)$ in the symmetric parameter regime.

4.4. Analytic Solution of the CAB Fractional Computer Virus Model

Applying the Laplace transform to system (1) and using the identity

$$\mathcal{L}\left\{{}^{\mathrm{CAB}}\mathcal{D}_t^{\epsilon }u\left(t\right)\right\}\left(s\right)={\displaystyle \frac{C\left(\epsilon \right)}{1-\epsilon }}·{\displaystyle \frac{s^{\epsilon }\tilde{u}\left(s\right)-s^{\epsilon -1}u\left(0\right)}{s^{\epsilon }+\frac{\epsilon }{1-\epsilon }}},$$

we obtain, for the first equation,

$${\displaystyle \frac{C\left(\epsilon \right)}{1-\epsilon }}·{\displaystyle \frac{s^{\epsilon }\tilde{\mathtt{S}}\left(s\right)-s^{\epsilon -1}\mathtt{S}\left(0\right)}{s^{\epsilon }+\frac{\epsilon }{1-\epsilon }}}={\displaystyle \frac{\mathrm{\Lambda }}{s}}-\mathcal{L}\left\{\kappa \mathtt{S}\left(t\right)\left(\mathtt{L}\left(t\right)+\mathtt{I}\left(t\right)\right)+\mathrm{\Lambda }\mathtt{S}\left(t\right)\right\}.$$

Solving for $\tilde{\mathtt{S}}\left(s\right)$ yields

$$\tilde{\mathtt{S}}\left(s\right)={\displaystyle \frac{\mathtt{S}\left(0\right)}{s}}+{\displaystyle \frac{\mathrm{\Lambda }\left((1-\epsilon )s^{\epsilon }+\epsilon \right)}{C\left(\epsilon \right)s^{\epsilon +1}}}-{\displaystyle \frac{(1-\epsilon )s^{\epsilon }+\epsilon }{C\left(\epsilon \right)s^{\epsilon }}}·\mathcal{L}\left\{\kappa \mathtt{S}(\mathtt{L}+\mathtt{I})+\mathrm{\Lambda }\mathtt{S}\right\}.$$

Taking the inverse Laplace transform, we obtain the analytic representation

$$\mathtt{S}\left(t\right)=\mathtt{S}\left(0\right)+{\displaystyle \frac{\mathrm{\Lambda }}{C\left(\epsilon \right)}}\left[(1-\epsilon )+{\displaystyle \frac{\epsilon t^{\epsilon }}{\mathrm{\Gamma }(\epsilon +1)}}\right]-{\mathcal{L}}^{-1}\left\{{\displaystyle \frac{(1-\epsilon )s^{\epsilon }+\epsilon }{C\left(\epsilon \right)s^{\epsilon }}}·\mathcal{L}\left\{\kappa \mathtt{S}(\mathtt{L}+\mathtt{I})+\mathrm{\Lambda }\mathtt{S}\right\}\right\}.$$

Similarly, for the remaining components, we have

$$\begin{array}{cc}\hfill \mathtt{L}\left(t\right)& =\mathtt{L}\left(0\right)+{\mathcal{L}}^{-1}\left\{{\displaystyle \frac{(1-\epsilon )s^{\epsilon }+\epsilon }{C\left(\epsilon \right)s^{\epsilon }}}·\mathcal{L}\left\{\kappa \mathtt{S}(\mathtt{L}+\mathtt{I})-(\delta +\mathrm{\Lambda })\mathtt{L}\right\}\right\},\hfill \\ \hfill \mathtt{I}\left(t\right)& =\mathtt{I}\left(0\right)+{\mathcal{L}}^{-1}\left\{{\displaystyle \frac{(1-\epsilon )s^{\epsilon }+\epsilon }{C\left(\epsilon \right)s^{\epsilon }}}·\mathcal{L}\left\{\delta \mathtt{L}-(\theta +\mathrm{\Lambda })\mathtt{I}\right\}\right\},\hfill \\ \hfill \mathtt{A}\left(t\right)& =\mathtt{A}\left(0\right)+{\mathcal{L}}^{-1}\left\{{\displaystyle \frac{(1-\epsilon )s^{\epsilon }+\epsilon }{C\left(\epsilon \right)s^{\epsilon }}}·\mathcal{L}\left\{\theta \mathtt{I}-(\iota +\mathrm{\Lambda })\mathtt{A}\right\}\right\}.\hfill \end{array}$$

We now define the linear operator

$$\mathfrak{F}\left[u\right(t\left)\right]=\mathcal{L}\left[u\right(t\left)\right],\mathrm{with}\mathrm{property}\mathfrak{F}\left(c\right)=0\forall c\in \mathbb{R}.$$

The nonlinear operator corresponding to $\mathtt{S}\left(t\right)$ is

$$N\left[{\varphi }_{\mathtt{S}}(t;q)\right]=\mathcal{L}\left[{\varphi }_{\mathtt{S}}(t;q)\right]-\mathtt{S}\left(0\right)-{\displaystyle \frac{\mathrm{\Lambda }}{C\left(\epsilon \right)}}\left[(1-\epsilon )+{\displaystyle \frac{\epsilon t^{\epsilon }}{\mathrm{\Gamma }(\epsilon +1)}}\right]+{\displaystyle \frac{(1-\epsilon )s^{\epsilon }+\epsilon }{C\left(\epsilon \right)s^{\epsilon }}}·\mathcal{L}\left\{\kappa {\varphi }_{\mathtt{S}}({\varphi }_{\mathtt{L}}+{\varphi }_{\mathtt{I}})+\mathrm{\Lambda }{\varphi }_{\mathtt{S}}\right\}.$$

The zeroth-order deformation equation is then constructed as

$$(1-q)\mathfrak{F}\left[{\varphi }_j(t;q)-u_{j,0}\left(t\right)\right]=q\hslash N\left[{\varphi }_j(t;q)\right],j\in \{\mathtt{S},\mathtt{L},\mathtt{I},\mathtt{A}\},$$

where $q\in [0,1]$ is the embedding parameter and ℏ is the convergence-control parameter.

The m-th order deformation equation is written as

$$\mathcal{L}\left[u_{j,m}\left(t\right)-{\chi }_m{u}_{j,m-1}\left(t\right)\right]=\hslash R_m(u_{j,m-1},t),$$

which, upon inversion, gives

$$u_{j,m}\left(t\right)={\chi }_m{u}_{j,m-1}\left(t\right)+\hslash R_m(u_{j,m-1},t).$$

For each compartment, the final series solutions are as follows:

$$\begin{array}{cccc}\hfill \mathtt{S}\left(t\right)& =\sum _{m=0}^{\infty }{\mathtt{S}}_m\left(t\right),\hfill & \hfill \mathtt{L}\left(t\right)& =\sum _{m=0}^{\infty }{\mathtt{L}}_m\left(t\right),\hfill \\ \hfill \mathtt{I}\left(t\right)& =\sum _{m=0}^{\infty }{\mathtt{I}}_m\left(t\right),\hfill & \hfill \mathtt{A}\left(t\right)& =\sum _{m=0}^{\infty }{\mathtt{A}}_m\left(t\right).\hfill \end{array}$$

4.5. Iterative Variation-of-Parameters Technique

The Iterative Variation-of-Parameters Technique (IVPT) is a robust and effective method for obtaining approximate solutions to nonlinear fractional differential systems. Especially suitable for fractional models involving Caputo–Atangana–Baleanu (CAB) derivatives, it incorporates memory effects and manages nonsingular kernels naturally. Consider the CAB-fractional system given by

$$\left\{\begin{array}{c}{}^{\mathrm{CAB}}\mathcal{D}_{\mathrm{t}}^{\epsilon }\mathtt{S}\left(\mathrm{t}\right)=\mathrm{\Lambda }-\kappa \mathtt{S}\left(\mathrm{t}\right)\left(\mathtt{L}\left(\mathrm{t}\right)+\mathtt{I}\left(\mathrm{t}\right)\right)-\mathrm{\Lambda }\mathtt{S}\left(\mathrm{t}\right),\hfill \\ {}^{\mathrm{CAB}}\mathcal{D}_{\mathrm{t}}^{\epsilon }\mathtt{L}\left(\mathrm{t}\right)=\kappa \mathtt{S}\left(\mathrm{t}\right)\left(\mathtt{L}\left(\mathrm{t}\right)+\mathtt{I}\left(\mathrm{t}\right)\right)-(\delta +\mathrm{\Lambda })\mathtt{L}\left(\mathrm{t}\right),\hfill \\ {}^{\mathrm{CAB}}\mathcal{D}_{\mathrm{t}}^{\epsilon }\mathtt{I}\left(\mathrm{t}\right)=\delta \mathtt{L}\left(\mathrm{t}\right)-(\theta +\mathrm{\Lambda })\mathtt{I}\left(\mathrm{t}\right),\hfill \\ {}^{\mathrm{CAB}}\mathcal{D}_{\mathrm{t}}^{\epsilon }\mathtt{A}\left(\mathrm{t}\right)=\theta \mathtt{I}\left(\mathrm{t}\right)-(\iota +\mathrm{\Lambda })\mathtt{A}\left(\mathrm{t}\right),\hfill \end{array}\right.$$

subject to the initial conditions

$$\mathtt{S}\left(0\right)={\mathtt{S}}_0,\mathtt{L}\left(0\right)={\mathtt{L}}_0,\mathtt{I}\left(0\right)={\mathtt{I}}_0,\mathtt{A}\left(0\right)={\mathtt{A}}_0.$$

CAB fractional integral operator:

$${\mathcal{J}}^{\epsilon }f\left(\mathrm{t}\right):={\displaystyle \frac{1}{\mathrm{\Gamma }\left(\epsilon \right)}}{\int }_0^{\mathrm{t}}{(\mathrm{t}-s)}^{\epsilon -1}f\left(s\right)ds,0<\epsilon <1.$$

Let ${\{{\mathtt{S}}_n\left(\mathrm{t}\right),{\mathtt{L}}_n\left(\mathrm{t}\right),{\mathtt{I}}_n\left(\mathrm{t}\right),{\mathtt{A}}_n\left(\mathrm{t}\right)\}}_{n=0}^{\infty }$ be the sequence of successive approximations generated by the IVPT. The iterative scheme is given by

$$\left\{\begin{array}{c}{\mathtt{S}}_{n+1}\left(\mathrm{t}\right)={\mathtt{S}}_0+{\mathcal{J}}^{\epsilon }\left[\mathrm{\Lambda }-\kappa {\mathtt{S}}_n\left(\mathrm{t}\right)\left({\mathtt{L}}_n\left(\mathrm{t}\right)+{\mathtt{I}}_n\left(\mathrm{t}\right)\right)-\mathrm{\Lambda }{\mathtt{S}}_n\left(\mathrm{t}\right)\right],\hfill \\ {\mathtt{L}}_{n+1}\left(\mathrm{t}\right)={\mathtt{L}}_0+{\mathcal{J}}^{\epsilon }\left[\kappa {\mathtt{S}}_n\left(\mathrm{t}\right)\left({\mathtt{L}}_n\left(\mathrm{t}\right)+{\mathtt{I}}_n\left(\mathrm{t}\right)\right)-(\delta +\mathrm{\Lambda }){\mathtt{L}}_n\left(\mathrm{t}\right)\right],\hfill \\ {\mathtt{I}}_{n+1}\left(\mathrm{t}\right)={\mathtt{I}}_0+{\mathcal{J}}^{\epsilon }\left[\delta {\mathtt{L}}_n\left(\mathrm{t}\right)-(\theta +\mathrm{\Lambda }){\mathtt{I}}_n\left(\mathrm{t}\right)\right],\hfill \\ {\mathtt{A}}_{n+1}\left(\mathrm{t}\right)={\mathtt{A}}_0+{\mathcal{J}}^{\epsilon }\left[\theta {\mathtt{I}}_n\left(\mathrm{t}\right)-(\iota +\mathrm{\Lambda }){\mathtt{A}}_n\left(\mathrm{t}\right)\right].\hfill \end{array}\right.$$

The initial approximations are chosen as constants from the initial data:

$${\mathtt{S}}_0\left(\mathrm{t}\right)={\mathtt{S}}_0,{\mathtt{L}}_0\left(\mathrm{t}\right)={\mathtt{L}}_0,{\mathtt{I}}_0\left(\mathrm{t}\right)={\mathtt{I}}_0,{\mathtt{A}}_0\left(\mathrm{t}\right)={\mathtt{A}}_0.$$

With each iteration, the approximations are refined and higher-order approximations are obtained. This process leads to fractional power series expansions

$$\begin{array}{cc}\hfill \mathtt{S}\left(\mathrm{t}\right)& \approx {\mathtt{S}}_0+{\displaystyle \frac{{\mathrm{t}}^{\epsilon }}{\mathrm{\Gamma }(\epsilon +1)}}+{\displaystyle \frac{{\mathrm{t}}^{2\epsilon }}{\mathrm{\Gamma }(2\epsilon +1)}}+{\displaystyle \frac{{\mathrm{t}}^{3\epsilon }}{\mathrm{\Gamma }(3\epsilon +1)}}+{\displaystyle \frac{{\mathrm{t}}^{4\epsilon }}{\mathrm{\Gamma }(4\epsilon +1)}}+\dots ,\hfill \\ \hfill \mathtt{L}\left(\mathrm{t}\right)& \approx {\mathtt{L}}_0+{\displaystyle \frac{{\mathrm{t}}^{\epsilon }}{\mathrm{\Gamma }(\epsilon +1)}}+{\displaystyle \frac{{\mathrm{t}}^{2\epsilon }}{\mathrm{\Gamma }(2\epsilon +1)}}+{\displaystyle \frac{{\mathrm{t}}^{3\epsilon }}{\mathrm{\Gamma }(3\epsilon +1)}}+{\displaystyle \frac{{\mathrm{t}}^{4\epsilon }}{\mathrm{\Gamma }(4\epsilon +1)}}+\dots ,\hfill \\ \hfill \mathtt{I}\left(\mathrm{t}\right)& \approx {\mathtt{I}}_0+{\displaystyle \frac{{\mathrm{t}}^{\epsilon }}{\mathrm{\Gamma }(\epsilon +1)}}+{\displaystyle \frac{{\mathrm{t}}^{2\epsilon }}{\mathrm{\Gamma }(2\epsilon +1)}}+{\displaystyle \frac{{\mathrm{t}}^{3\epsilon }}{\mathrm{\Gamma }(3\epsilon +1)}}+{\displaystyle \frac{{\mathrm{t}}^{4\epsilon }}{\mathrm{\Gamma }(4\epsilon +1)}}+\dots ,\hfill \\ \hfill \mathtt{A}\left(\mathrm{t}\right)& \approx {\mathtt{A}}_0+{\displaystyle \frac{{\mathrm{t}}^{\epsilon }}{\mathrm{\Gamma }(\epsilon +1)}}+{\displaystyle \frac{{\mathrm{t}}^{2\epsilon }}{\mathrm{\Gamma }(2\epsilon +1)}}+{\displaystyle \frac{{\mathrm{t}}^{3\epsilon }}{\mathrm{\Gamma }(3\epsilon +1)}}+{\displaystyle \frac{{\mathrm{t}}^{4\epsilon }}{\mathrm{\Gamma }(4\epsilon +1)}}+\dots .\hfill \end{array}$$

A memory-sensitive approximation framework captures the hereditary and dynamic features of computer malware spread using this iterative method. Under mild regularity conditions, the iterations converge rapidly and can be effectively implemented with computational software such as MATLAB or Python.

5. Numerical Approximation Scheme

To numerically approximate fractional differential equations defined via the Caputo–Atangana–Baleanu (CAB) derivative, we recast the general integral form into one involving Mittag-Leffler kernels combined with discrete interpolation. Building on recent methodologies [10,18], consider the fractional problem

$${}^{\mathrm{CAB}}\mathcal{D}_t^{\epsilon }\psi \left(t\right)=\mathrm{\Xi }(t,\psi \left(t\right)),0<\epsilon <1,$$

which admits the following integral equivalent:

$$\psi \left(t\right)={\psi }_0+{\displaystyle \frac{1-\epsilon }{\mathcal{N}\left(\epsilon \right)}}\mathrm{\Xi }(t,\psi \left(t\right))+{\displaystyle \frac{\epsilon }{\mathrm{\Gamma }\left(\epsilon \right)\mathcal{N}\left(\epsilon \right)}}{\int }_0^t\mathrm{\Xi }(\tau ,\psi \left(\tau \right)){(t-\tau )}^{\epsilon -1}d\tau ,$$

where $\mathcal{N}\left(\epsilon \right)$ is the normalization constant related to the CAB operator, and $\mathrm{\Gamma }(·)$ is the classical Gamma function.

At the discrete temporal nodes $t_{m+1}=(m+1)h$, the approximation scheme reads

$$\psi \left(t_{m+1}\right)\approx {\psi }_0+{\varpi }_0\mathrm{\Xi }(t_m,\psi \left(t_m\right))+{\varpi }_1\sum _{\ell =0}^m{\int }_{t_{\ell }}^{t_{\ell +1}}\mathrm{\Xi }(\tau ,\psi \left(\tau \right)){(t_{m+1}-\tau )}^{\epsilon -1}d\tau ,$$

with weights defined as

$${\varpi }_0={\displaystyle \frac{\mathrm{\Gamma }\left(\epsilon \right)(1-\epsilon )}{\mathrm{\Gamma }\left(\epsilon \right)(1-\epsilon )+\epsilon }},{\varpi }_1={\displaystyle \frac{\epsilon }{\mathrm{\Gamma }\left(\epsilon \right)+\epsilon (1-\mathrm{\Gamma }(\epsilon \left)\right)}}.$$

Approximating $\mathrm{\Xi }(\tau ,\psi (\tau \left)\right)$ in $[t_{\ell },t_{\ell +1}]$ using linear interpolation, we obtain the iterative scheme

$${\psi }_{m+1}={\psi }_0+{\varpi }_0\mathrm{\Xi }(t_m,{\psi }_m)+{\displaystyle \frac{1}{(\epsilon +1)\mathcal{N}\left(\epsilon \right)}}\sum _{\ell =0}^m\left[h^{\epsilon }\mathrm{\Xi }(t_{\ell },{\psi }_{\ell }){\mathcal{A}}_{\epsilon ,\ell ,1}-h^{\epsilon }\mathrm{\Xi }(t_{\ell -1},{\psi }_{\ell -1}){\mathcal{A}}_{\epsilon ,\ell ,2}\right],$$

where $\mathrm{\Xi }(t_{-1},{\psi }_{-1})\equiv 0$, and

$$\begin{array}{cc}\hfill {\mathcal{A}}_{\epsilon ,\ell ,1}& =h^{\epsilon +1}{\displaystyle \frac{{(m+1-\ell )}^{\epsilon }(m-\ell +2+\epsilon )-{(m-\ell )}^{\epsilon }(m-\ell +2+2\epsilon )}{\epsilon (\epsilon +1)}},\hfill \\ \hfill {\mathcal{A}}_{\epsilon ,\ell ,2}& =h^{\epsilon +1}{\displaystyle \frac{{(m+1-\ell )}^{\epsilon +1}-{(m-\ell )}^{\epsilon }(m-\ell +1+\epsilon )}{\epsilon (\epsilon +1)}}.\hfill \end{array}$$

For the vector-valued system

$${}^{\mathrm{CAB}}\mathcal{D}_t^{\epsilon }\mathbf{Y}\left(t\right)=\mathrm{\Psi }(t,\mathbf{Y}),\mathbf{Y}=\left(\begin{array}{c}\mathtt{S}\left(t\right)\\ \mathtt{L}\left(t\right)\\ \mathtt{I}\left(t\right)\\ \mathtt{A}\left(t\right)\end{array}\right),$$

the scheme applies component-wise, yielding for example

$$\begin{array}{cc}\hfill S_{m+1}& =S_0+{\varpi }_0\left[\mathrm{\Lambda }-\kappa S_m(L_m+I_m)-\mathrm{\Lambda }{S}_m\right]+{\displaystyle \frac{1}{(\epsilon +1)\mathcal{N}\left(\epsilon \right)}}\sum _{\ell =0}^m\{h^{\epsilon }\left[\mathrm{\Lambda }-\kappa S_{\ell }(L_{\ell }+I_{\ell })-\mathrm{\Lambda }{S}_{\ell }\right]{\mathcal{A}}_{\epsilon ,\ell ,1}\hfill \\ & -h^{\epsilon }\left[\mathrm{\Lambda }-\kappa S_{\ell -1}(L_{\ell -1}+I_{\ell -1})-\mathrm{\Lambda }{S}_{\ell -1}\right]{\mathcal{A}}_{\epsilon ,\ell ,2}\},\hfill \end{array}$$

and similarly for $L_{m+1},I_{m+1},A_{m+1}$.

Remark 2.

In the original draft, the fractional order was denoted inconsistently as θ or ϑ in this section. These have now been corrected to ε, ensuring uniform notation across all analysis, proofs, and numerical schemes.

5.1. Numerical Experiments with Varying Initial Conditions

To complement the order-sweep experiments, we investigate how the system responds to different initial conditions while keeping parameters fixed. Unless otherwise stated, we use $\epsilon \in \{0.7,0.9\}$, step size $h={10}^{-2}$, and time horizon $T=100$. The CAB scheme described earlier is used for all runs.

For each scenario in

Table 1. Initial conditions used in the experiments. Total population is $N_0=S_0+L_0+I_0+A_0$.

Scenario	${\mathit{S}}_0$	${\mathit{L}}_0$	${\mathit{I}}_0$	${\mathit{A}}_0$
Low-seed (LS)	$0.99$	$0.00$	${10}^{-4}$	$0.01$
Moderate (MOD)	$0.90$	$0.05$	$0.05$	$0.00$
High-seed (HS)	$0.70$	$0.10$	$0.20$	$0.00$

, we simulate the system (1) with the same parameter vector $(\mathrm{\Lambda },\kappa ,\delta ,\theta ,\iota )$ as in the baseline experiment. We summarize qualitative observations below; quantitative peak measures can be tabulated alongside the figures.

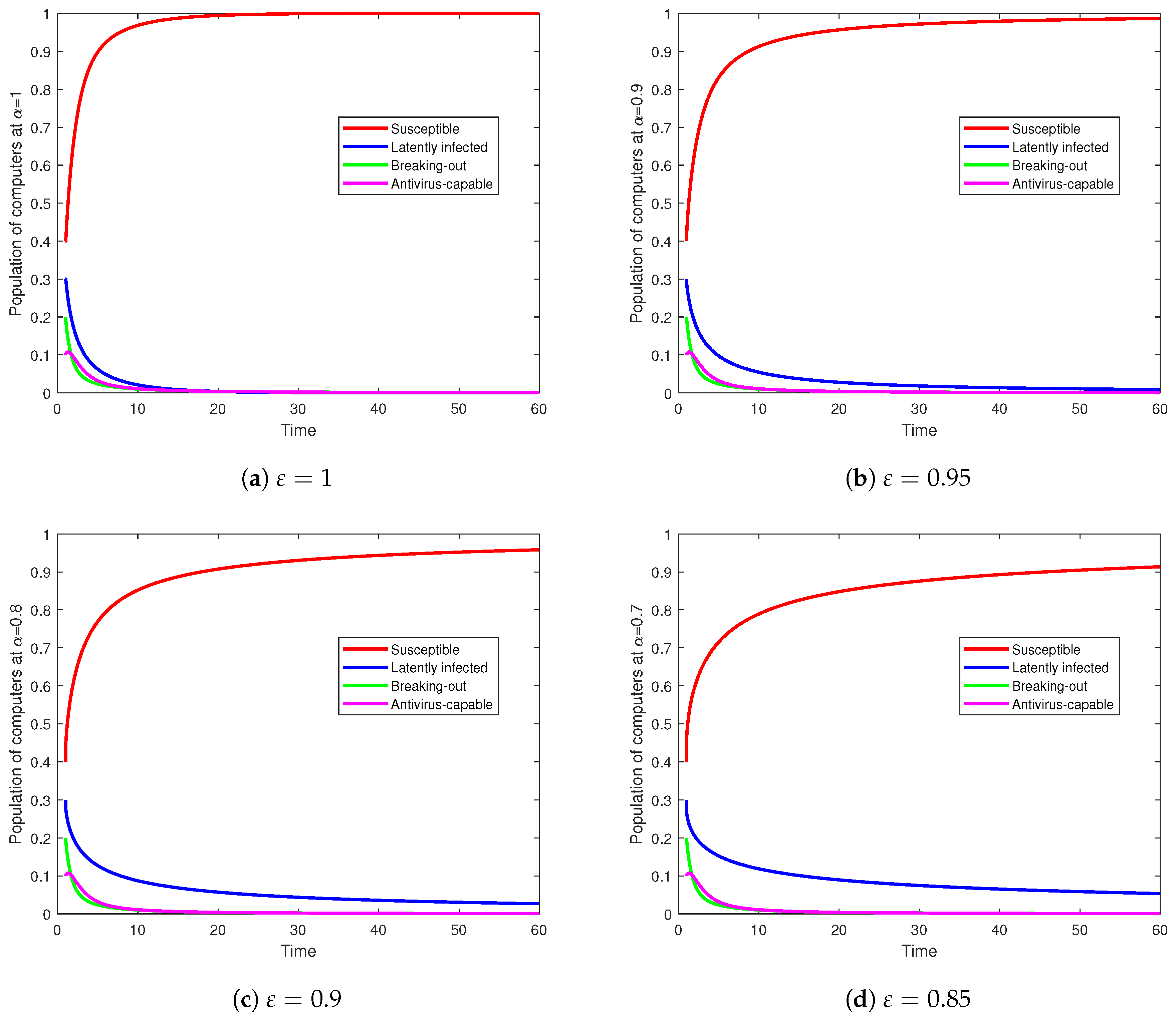
• Qualitative findings (consistent across parameters used).

• Peak size and timing (in $\mathtt{I}\left(t\right)$). Increasing $I_0$ (LS → MOD → HS) monotonically increases the early growth rate and advances the time-to-peak. For the same parameters, the HS scenario reaches a larger peak earlier than LS.
• Latency reservoir ($\mathtt{L}\left(t\right)$). Larger $I_0$ seeds a larger latent pool via $\kappa S(L+I)$, producing a broader $\mathtt{L}\left(t\right)$ shoulder before decay. This effect is more pronounced for smaller $\epsilon$ due to stronger memory.
• Protected devices ($\mathtt{A}\left(t\right)$). Since A grows through $\theta I$, scenarios with larger $I_0$ accumulate protection more rapidly and saturate earlier; small $\epsilon$ slows the relaxation, yielding longer tails in $\mathtt{A}\left(t\right)$.
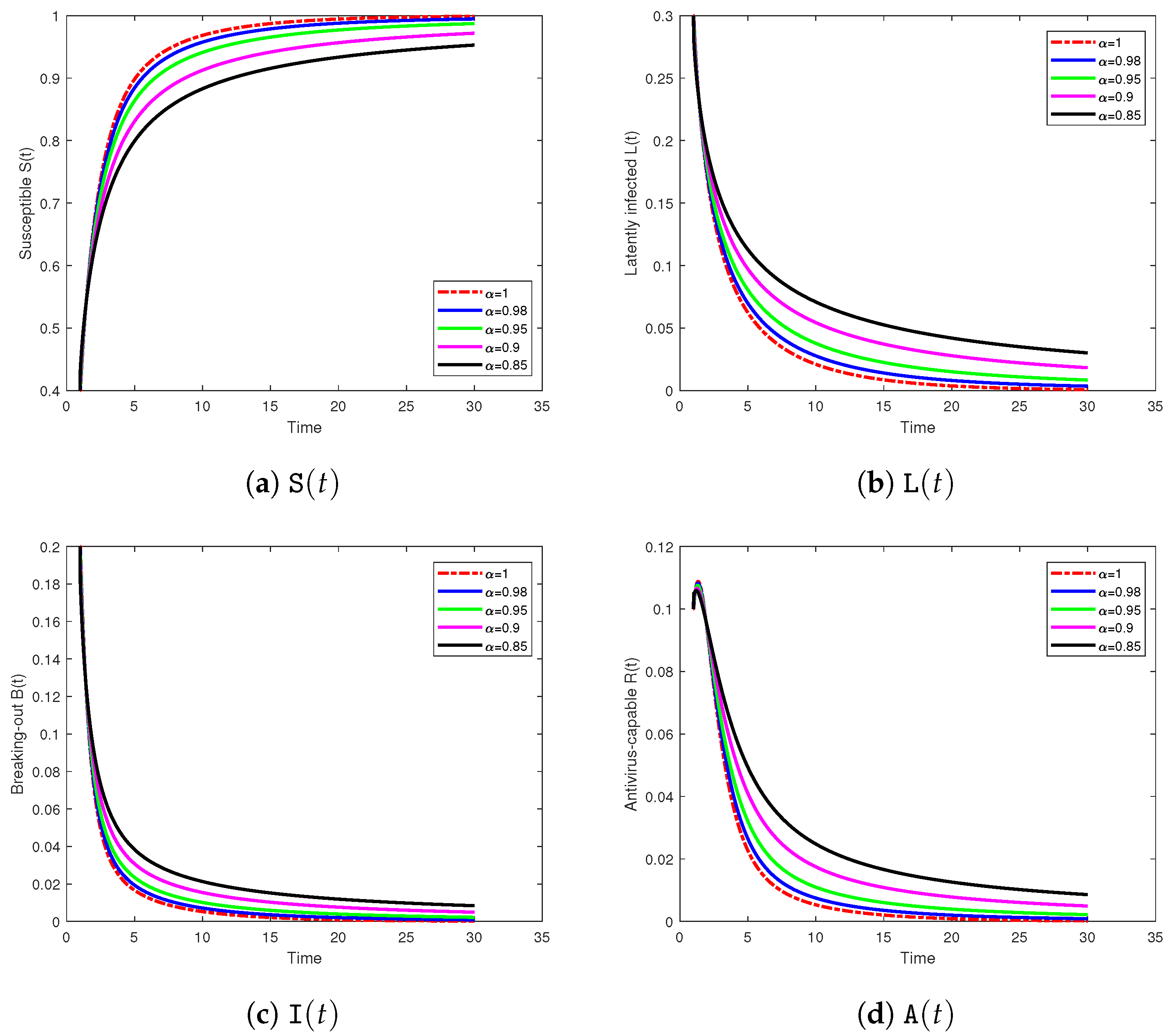
• Effect of fractional order. For fixed initial data, smaller $\epsilon$ delays peaks and lengthens transients (consistent with the order-sweep results), but the ordering across initial-condition scenarios (HS > MOD > LS in early growth and peak size) is preserved.

5.2. Strategy for Choosing Parameters

The choice of parameter values in

Table 2. Parameter settings for the computer virus propagation model [20].

Parameter	Description	Value
$\mathrm{\Lambda }$	Rate of network device addition/removal	$0.5$
$\kappa$	Malware transmission rate	$0.5$ (safe), $0.8$ (infectious)
$\delta$	Transition from latent to active infection	$0.001$
$\theta$	Transition from infection to antivirus-protected state	$0.2$
$\iota$	Removal/neutralization rate of protected devices	$0.4$

was guided by two main considerations: biological analogy to epidemic models and realistic representation of digital networks. The strategy can be summarized as follows:

• Turnover rate $\mathrm{\Lambda }$. This was fixed at $0.5$ to represent moderate addition and removal of devices within the network. The value was chosen to balance the inflow of susceptible devices with the natural loss of old or offline systems, ensuring that the system does not trivially collapse to zero population.
• Transmission rate $\kappa$. We considered two scenarios: $\kappa =0.5$ for a baseline “safe state’’ with limited malware spread, and $\kappa =0.8$ for a more aggressive “infectious state.’’ These values were selected to span the range of moderate-to-high transmission observed in analogous epidemic models, and to test how the system transitions between malware-free and endemic states.
• Latency-to-activation rate $\delta$. The small value $\delta =0.001$ was chosen to capture the realistic property of modern malware, which often remains dormant for extended periods before becoming active. This reflects the hidden threat of stealth infections.
• Antivirus activation rate $\theta$. We set $\theta =0.2$ to model an intermediate level of antivirus responsiveness: not instantaneous but not negligible. This allows us to test the influence of delayed security deployment on system stability.
• Protected-device removal rate $\iota$. The value $\iota =0.4$ was selected to represent moderate loss of antivirus protection, such as through outdated signatures or unpatched software. A higher value would lead to rapid reinfection, while a lower value would imply unrealistically permanent immunity.

This selection strategy ensures that the parameters lie in a range where both malware-free and endemic behaviors can be observed. By combining slow latency activation, moderate antivirus response, and different infection rates, the examples demonstrate the effect of fractional-order memory on delaying infection peaks, prolonging latency, and slowing recovery.

Table 2 lists the parameters explicitly defined and used in system (1). The chosen values represent typical rates for device turnover, malware transmission, infection progression, and antivirus protection.

The initial conditions are given by

$$\mathtt{S}\left(0\right)=0.4,\mathtt{L}\left(0\right)=0.3,\mathtt{I}\left(0\right)=0.2,\mathtt{A}\left(0\right)=0.1,$$

representing a network where $40\%$ of devices are initially susceptible, $30\%$ latent carriers, $20\%$ actively infected, and $10\%$ already antivirus-protected.

5.3. Numerical Study

To investigate the effect of the fractional order $\epsilon$, we perform simulations of the system for several values of $\epsilon \in \{1,0.98,0.95,0.9\}$. The numerical scheme described in Section 6 is employed with a step size $h=0.01$ over a simulation horizon $T=100$.

Figure 1 shows the individual trajectories of $\mathtt{S}\left(t\right)$, $\mathtt{L}\left(t\right)$, $\mathtt{I}\left(t\right)$, and $\mathtt{A}\left(t\right)$. As $\epsilon$ decreases, the infection spreads more slowly: susceptible devices decline at a slower rate, latency persists longer, and both infection and recovery are delayed. Figure 2 presents the full system for $\epsilon =1.0,0.95,0.9,0.85$. With stronger memory (smaller $\epsilon$), the system evolves more gradually, confirming the key role of fractional order in shaping malware dynamics. These results demonstrate that the CAB fractional derivative successfully captures realistic non-local memory effects, which are absent in classical integer-order models.

6. Discussion

We summarize the outcomes of the proposed CAB fractional-order computer virus model using the parameters in Table 2 and initial conditions $(S_0,L_0,I_0,A_0)=(0.4,0.3,0.2,0.1)$.

Figure 1 and Figure 2 display the dynamics for $\epsilon \in \{1,0.98,0.95,0.9,0.85\}$. As $\epsilon$ decreases, non-local memory strengthens and slows transitions: $\mathtt{S}\left(t\right)$ declines more gradually, $\mathtt{L}\left(t\right)$ persists longer, $\mathtt{I}\left(t\right)$ peaks later with smaller magnitude, and $\mathtt{A}\left(t\right)$ accumulates more slowly. At $\epsilon =1$, the model recovers the classical (faster) integer-order behavior. This shows that the CAB operator captures latency, delayed contagion, and delayed protection in digital environments.

• Low seed ($I_0={10}^{-4}$). The outbreak onset is slow and antivirus activation is delayed.
• Moderate seed ($I_0=0.05$). The peak occurs earlier and is higher, and protection ramps up sooner.
• High seed ($I_0=0.2$). A rapid early peak is followed by faster growth of $\mathtt{A}\left(t\right)$; memory still prolongs recovery relative to $\epsilon =1$.

For each run we report the peak infection level $I_{max}$ and its timing $t_{\mathrm{peak}}$, as well as the final protection $\mathtt{A}\left(t\right)$ at the horizon $T=100$.

Figure 1 (component-wise). Smaller $\epsilon$ delays susceptibility loss, enlarges the latent reservoir, reduces and postpones the infection peak, and slows protection buildup.

Figure 2 (system-level). Decreasing $\epsilon$ acts as a control knob that stretches transients and prolongs virus persistence before stabilization.

• Device turnover $\mathrm{\Lambda }$. This term injects and removes devices, sustaining susceptibility when large.
• Transmission $\kappa$. It governs infection pressure; higher values push the system toward endemicity.
• Latency activation $\delta$. Small $\delta$ yields long dormant phases before devices become infectious.
• Antivirus activation $\theta$. Larger $\theta$ shortens infectious periods and accelerates protection.
• Protection loss $\iota$. Larger $\iota$ erodes immunity and raises reinfection risk.

The CAB framework reproduces integer-order dynamics at $\epsilon =1$, introduces tunable memory that delays peaks and lengthens transients for $\epsilon <1$, and aligns with the cybersecurity realities of latent malware, delayed detection, and gradual deployment of defenses. These properties make $\epsilon$ a meaningful policy/design parameter for timing updates and countermeasures, while highlighting the sensitivity to $\kappa$, $\theta$, and $\iota$.

7. Conclusions

In this study, we developed and analyzed a novel fractional-order model for computer virus spread using the Atangana–Baleanu–Caputo (ABC) derivative. The model incorporates the Mittag-Leffler kernel, enabling the memory effects and non-local dynamics often present in digital environments. Key mathematical properties such as non-negativity, boundedness, existence, uniqueness, and Hyers–Ulam stability were established. Laplace transform, the homotopy series method, and the Variation-of-Parameters Method (VPM) were used to derive analytical and approximate solutions. A numerical scheme tailored to the ABC derivative was also constructed to visualize system dynamics.

The simulation results confirmed the critical impact of fractional order $ϵ$ on infection dynamics. Lower values of $ϵ$ correspond to stronger memory effects, leading to slower infection and recovery processes. This highlights the importance of fractional-order calculus in modeling and simulating real-world cybersecurity problems. Overall, the proposed model provides a powerful framework for understanding, predicting, and ultimately mitigating computer virus spread in complex networked systems. Future work may include optimal control strategies and machine learning integration for enhanced predictive and protective capabilities.

The model’s symmetric infection pressure, invariant feasible region, and $(L,I)$-equivariance on a natural parameter submanifold provide a symmetry-based lens on existence, Hyers–Ulam stability, and the qualitative ordering of transients under fractional memory.