An Enhanced MOPSO Algorithm for Multi-Objective UAV Path Planning in Mountainous Environments

Abstract

Path planning for unmanned aerial vehicles (UAVs) in mountainous environments requires satisfying terrain clearance and obstacle avoidance constraints while optimizing path length, flight time, and energy consumption. To address these challenges, this paper proposes EC-MOPSO (Epsilon-dominance and Crowding-distance-based Multi-Objective Particle Swarm Optimization). Inspired by the principle of symmetry, the algorithm integrates an adaptive parameter adjustment mechanism with a $\epsilon -$ dominance–crowding archiving strategy to balance global exploration and local exploitation through spatially symmetric archive management. A safety-repairable B-spline trajectory model ensures smooth and feasible flight paths under complex terrain conditions. Simulation results show that EC-MOPSO reduces path length by 10–40%, improves normalized hypervolume by over 25%, and decreases performance variance by 20–25%, confirming faster convergence and higher robustness compared with representative multi-objective optimization approaches. Ablation studies further verify that both the adaptive parameter mechanism and the $\epsilon -$ dominance–crowding strategy significantly enhance convergence stability and overall optimization performance. Overall, EC-MOPSO provides an adaptive and reliable optimization framework for generating efficient, safe, and energy-aware UAV trajectories in real-world mountainous rescue missions.

1. Introduction

Unmanned aerial vehicles (UAVs) are increasingly deployed in diverse applications such as agriculture, battlefield reconnaissance, firefighting, and emergency communications in mountainous areas, demonstrating significant practical potential. Most existing research, however, has concentrated on agricultural and reconnaissance missions, while comparatively little attention has been given to emergency communication scenarios in complex mountainous environments. These environments, characterized by steep peaks, dense forests, and sudden disturbances such as flocks of birds, impose not only the conventional objectives of minimizing path length, flight time, and energy consumption but also strict safety requirements related to terrain clearance and obstacle avoidance [1,2,3,4]. Consequently, intelligent optimization algorithms have become indispensable tools for UAV path planning under such conditions.

Traditional multi-objective optimization algorithms, including NSGA-II [5], MOPSO [6], and SPEA2 [7], have been widely applied to solve problems with conflicting objectives by approximating the Pareto front. Although these approaches can balance trade-offs among multiple criteria, they are prone to premature convergence and loss of diversity when confronted with complex constraints [8]. To improve their robustness, researchers have proposed hybrid and adaptive strategies tailored to UAV path planning. For instance, Pehlivanoglu et al. [9] combined ant colony optimization (ACO), Voronoi diagrams, and clustering techniques to accelerate convergence and enhance path feasibility. Xiao et al. [10] introduced an adaptive area weight adjustment (AAWA) strategy into MOEA/D, effectively balancing path length against terrain threat. Lu [11] integrated rapidly exploring random trees (RRTs) with dynamic potential field adjustments, improving obstacle avoidance and trajectory smoothness. Other representative works include discrete particle swarm optimization (DPSO) for large-scale efficiency [12], octree-based NSGA-II for safety-aware trajectories [13], improved gray wolf optimization (GWO) with chaotic initialization and adaptive mutation for 3D path planning [14], and enhanced SPEA2 with adaptive crossover for bi-objective UAV delivery [15]. Collectively, these studies demonstrate continuous progress in convergence, feasibility, and diversity for UAV trajectory optimization.

Beyond these algorithm-specific developments, researchers have introduced new dominance relations, decomposition strategies, and learning-enhanced frameworks. Xu et al. [16] proposed a Minkowski distance–based evolutionary algorithm, and later the same group [17] developed a hierarchical decomposition framework to improve solution quality and distribution. Mai et al. [18] designed a dual adaptive ACO with dynamic pheromone rules, while Tan et al. [19] combined Q-learning with PSO for multi-UAV coordination. Huang et al. [20] incorporated differential evolution into ACVDEPSO for adaptive convergence, and Zhang et al. [21] improved constraint handling for archive stability. These advancements reflect a clear trend toward hybrid, adaptive, and cooperative frameworks that balance convergence and diversity in complex UAV applications.

Previous studies have shown that UAV path-planning optimization algorithms have evolved from static optimization toward adaptive and cooperative paradigms. However, under dynamic and irregular mountainous environments, existing methods still struggle to maintain convergence stability, population diversity, and trajectory feasibility. Most approaches optimize one objective at the expense of others, leading to premature convergence, loss of feasible solutions, or unstable performance. The main objective of this study is to develop a framework capable of adaptively coordinating these competing goals under complex terrain constraints, achieving balance among convergence, diversity, and feasibility. The proposed unified optimization framework needs to integrate adaptivity and feasibility awareness while maintaining computational efficiency and reliable performance for UAV mountain missions.

Therefore, this study proposes a multi-objective particle swarm optimization (EC-MOPSO) algorithm based on $\epsilon -$ dominance and crowding distance to address these challenges. This algorithm integrates $\epsilon -$ dominance and crowding distance mechanisms to maintain a balanced and well-distributed Pareto profile. Inspired by the principle of symmetry, which emphasizes balance and consistency within the optimization process, it employs adaptive parameter adjustment to balance exploration and exploitation. Furthermore, it introduces a safe and repairable B-spline function representation to ensure smooth and feasible UAV trajectories. Through these mechanisms, the EC-MOPSO algorithm achieves stable convergence, enhanced diversity, and reliable path generation for UAV operations in complex mountainous environments.

The major contributions of this paper are summarized as follows:

• Epsilon-dominance archive with crowding-distance pruning: By combining $\epsilon -$ dominance with crowding distance, the archive maintains a diverse and convergent approximation of the Pareto front, reducing the risk of premature convergence.
• Adaptive parameter adjustment: Inertia weight and learning factors are updated dynamically during the optimization process, enabling the swarm to shift smoothly from global exploration to local refinement.
• Safety-repairable B-spline trajectory generation: Waypoints are interpolated by B-splines and adjusted through a repair mechanism that enforces clearance margins, altitude limits, and curvature smoothness, producing feasible and dynamically consistent UAV paths.
• Computational complexity analysis: A theoretical evaluation using Big-O notation is conducted to assess the asymptotic efficiency of the proposed EC-MOPSO. The analysis shows that it maintains the same computational order as standard MOPSO while achieving higher practical efficiency through $\epsilon -$ dominance pruning and structured archive management.

The remainder of this paper is organized as follows: Section 2 reviews related work and presents the problem statement; Section 3 provides a detailed description of the proposed EC-MOPSO algorithm; Section 4 presents the experimental parameter setups; Section 5 reports the experimental analysis; and finally, Section 6 concludes the paper and outlines future research directions.

2. Related Work and Problem Formulation

To provide a comprehensive foundation for the proposed EC-MOPSO algorithm, this section reviews existing research on UAV path planning and formulates the corresponding optimization problem. Section 2.1 presents an overview of representative multi-objective optimization algorithms, highlighting their evolution from classical dominance-based methods to adaptive and learning-driven frameworks, and analyzing their respective strengths and limitations in complex terrains. Subsequently, Section 2.2 defines the UAV path-planning problem as a constrained multi-objective optimization model, detailing the environment modeling, objective functions, and safety-related constraints that collectively determine feasible and efficient flight trajectories. These analyses establish the theoretical groundwork for the EC-MOPSO framework and its subsequent experimental validation.

2.1. Overview of Related Work

Research on UAV path planning has focused on balancing flight distance, time, and energy consumption while ensuring path feasibility and adaptability in complex terrains. Classical multi-objective algorithms such as NSGA-II, SPEA2, and MOEA/D approximate the Pareto front effectively but suffer from high computational cost, slow convergence, and limited adaptability to dynamic terrain constraints. Their fixed parameters and post-processing feasibility checks often lead to infeasible or discontinuous paths, reducing reliability. To enhance feasibility, hybrid approaches such as ACO–Voronoi and RRT–Potential Field combine metaheuristic search with geometric repair. Although they improve obstacle avoidance, these methods handle constraints after optimization and lack real-time adaptability. Adaptive and learning-based algorithms, including ACVDEPSO and Q-learning PSO, introduce dynamic parameter control to balance exploration and exploitation but increase algorithmic complexity and are difficult to tune for real-time missions. Recent studies have explored new dominance relations and density-based archiving mechanisms, such as Minkowski-based evolutionary algorithms and hierarchical decomposition, to stabilize Pareto diversity. However, these methods remain sensitive to terrain-induced constraints and parameter scaling.

Among various metaheuristic frameworks, MOPSO provides a simple yet powerful basis for multi-objective optimization, offering faster convergence, fewer control parameters, and greater flexibility in integrating adaptive strategies. Its particle-swarm dynamics make it particularly suitable for continuous optimization tasks such as UAV trajectory planning.

Table 1 summarizes the advantages and disadvantages of some of the above algorithms. As shown in Table 1, most existing algorithms emphasize only one aspect—convergence, adaptability, or feasibility—while few achieve all simultaneously. These limitations highlight the need for a unified framework that maintains convergence stability, preserves diversity, and embeds feasibility constraints directly within the optimization loop. Cross-domain advances in IoT systems [22,23] further demonstrate that adaptive coordination and lightweight decision mechanisms can enhance robustness and efficiency. However, these IoT-oriented approaches operate under relatively stable network conditions and are not directly applicable to dynamic, high-dimensional UAV environments. Inspired by these findings, this study extends such principles to UAV path planning through the proposed EC-MOPSO, which integrates $\epsilon -$ dominance and crowding-distance archiving, adaptive parameter control, and a safety-repairable B-spline trajectory framework for feasible and efficient flight in mountainous environments.

Table 1. Comparison of representative algorithms related to UAV path planning.

Algorithm	Core Mechanism	Strengths	Limitations
NSGA-II	Non-dominated sorting; parent–offspring elitism	Efficient and maintains population diversity	Slower convergence under complex constraints
SPEA2	Strength-based fitness; external archive with k-nearest truncation	Stable Pareto distribution; strong archive management	Higher computational cost; parameter sensitivity
Standard MOPSO	Velocity–position update; fixed inertia and learning factors	Simple structure and fast convergence	Premature convergence; poor diversity preservation
MOEA/D-AAWA	Weight-vector decomposition; adaptive area weighting	Clear trade-off between path length and terrain threat; scalable	Weight dependence; scaling sensitivity
MOBCA	Besiege-and-conquer mechanism; grid-based diversity maintenance with archive-prioritized replacement	Strong boundary exploration; competitive convergence and diversity	Parameter sensitivity; grid overhead in high-dimensional spaces
Q-learning PSO	Reinforcement-learning-based adaptive control	Strong adaptability and dynamic exploration–exploitation balance	Algorithmic complexity; difficult real-time tuning
EC-MOPSO	$\epsilon -$ dominance and crowding-distance archive; adaptive parameter tuning; safety-repairable trajectory operator	Stable convergence; uniform diversity; embedded feasibility	Requires threshold calibration for adaptive triggers

2.2. Problem Formulation

UAV path planning in complex mountainous environments requires a systematic problem formulation that integrates environment modeling, objective design, and safety constraints. In this work, the problem is modeled as a constrained multi-objective optimization framework that minimizes path length, flight time, and energy consumption while satisfying critical safety requirements such as altitude limits, terrain clearance, and minimum turning radius. These objectives and constraints together ensure efficient and feasible flight trajectories in challenging terrains [24,25].

2.2.1. Environment Modeling

Environment modeling plays a crucial role in UAV path planning, as terrain accuracy directly affects trajectory feasibility and safety [26]. Existing methods can be broadly classified into two categories: real-data-based models and mathematical simulation models. The former employs digital elevation models (DEMs) [27], LiDAR point clouds [28], or remote sensing data to reconstruct realistic terrain profiles for rescue and surveillance tasks. The latter generates synthetic landscapes using mathematical functions, offering greater flexibility and control over terrain complexity [29].

In this study, the mountainous environment is generated through the superposition of multiple Gaussian peaks and refined with Perlin noise to capture local irregularities, followed by Gaussian filtering for smoothness. The height at each grid point $\left(i,j\right)$ is defined as:

$$Z\left(i,j\right)={\displaystyle \sum _{k=1}^N{h}_k·\exp \left\{-{\left(\frac{i-i_k}{x_{s,k}}\right)}^2-{\left(\frac{j-j_k}{y_{s,k}}\right)}^2\right\}}+\alpha \cdot Perlin\left(i,j\right)$$

(1)

where $N$ is the number of peaks, $h_k$ is the height of the $k-th$ peak, and $\left(i_k,j_k\right)$ are its center coordinates. The parameters $\left(x_{s,k},y_{s,k}\right)$ control the spread of each Gaussian peak. The Perlin noise term introduces stochastic variations with scaling factor $\alpha$, while Gaussian filtering ensures smooth but realistic elevation transitions. This approach preserves both large-scale terrain features and fine-grained irregularities, providing a controllable yet realistic testing environment for UAV path planning algorithms.

2.2.2. UAV Path Optimization Model

UAV path planning in mountainous environments can be expressed as a constrained multi-objective optimization problem. The objective is to simultaneously minimize flight distance, flight time, and energy consumption while maintaining feasible trajectories under altitude, clearance, and dynamic turning constraints [30]. In this paper, the optimization model is expressed as:

$$\begin{array}{l}\underset{x\in \Omega }{\min }F\left(x\right)={\left(f_1(x),f_2(x),f_3(x)\right)}^T\\ s.t.\left\{\begin{array}{l}{z}_i\ge z_{\mathrm{terrain}}\left(xi,yi\right)+\mathrm{margin},i=1,\dots N\\ z_{\min }\le z_i\le z_{\max },i=1,\dots N\\ R_i={\displaystyle \frac{{{\displaystyle v}}^2}{g\tan \theta }}\ge R_{\min },i=1,\dots N-1\\ d_{obs,i}\ge D_{safe,i},i=2,\dots ,N\end{array}\right.\end{array}$$

(2)

here, $x=\left(P_1,P_2,\dots ,P_N\right)$ is the decision vector, where each waypoint is represented as $P_i=\left(x_i,y_i,z_i\right)$. The feasible set $\Omega$ is determined by:

• Altitude limits [31]: UAV altitude must remain within $\left[z_{\min },z_{\max }\right]$
• Terrain clearance [32]: UAV must fly above the terrain elevation plus a fixed safety margin
• Safe clearance [33]: UAV must satisfy a dynamic clearance requirement:

  $$\begin{array}{l}{d}_{obs,i}=z_i-z_{\mathrm{terrain}}(x_i,y_i)\\ D_{safe,i}=r_{\min }+k_{1}v+k_2\left|z_i-z_{i-1}\right|\end{array}$$

  (3)

  where $d_{obs,i}$ is the actual clearance and $D_{safe,i}$ is the required clearance depending on speed and climb rate.
• Turning radius constraint [34]: The local turning radius must exceed the minimum value $R_{\min }={\displaystyle \raisebox{1ex}{$v^2$}\!\left/ \!\raisebox{-1ex}{$g\tan \theta $}\right.}$.

These constraints ensure that the UAV maintains sufficient clearance, stable turning behavior, and feasible flight dynamics under varying topographic conditions.

2.2.3. Objective Function Modeling

To evaluate UAV trajectories in mountainous environments, three objectives are optimized simultaneously: total path length, flight time, and energy consumption with penalties.

• Total path length ($f_1(x)$):

  $$f_1(x)={\displaystyle \sum _{i=1}^{N-1}‖P_{i+1}-P_i‖}$$

  (4)

  here, $P_i=\left(x_i,y_i,z_i\right)$ denotes the $i-th$ waypoint, and $N$ is the total number of waypoints. The function $f_1(x)$ represents the total Euclidean length of the flight path. Minimizing this objective ensures that the UAV follows a shorter and more efficient route.
• Flight time under constant velocity ($f_2(x)$):

  $$f_2(x)={\displaystyle \sum _{i=1}^{N-1}\frac{‖p_{i+1}-p_i‖}{v}}$$

  (5)

  in this definition, $v$ is the UAV’s constant cruise velocity. The function $f_2(x)$ reflects the total flight time of the trajectory, which is critical for rapid response in emergency missions.
• Energy consumption with penalties ($f_3(x)$):

  $$f_3(x)=\alpha {\displaystyle \sum _{i=1}^{N-1}{d}_{xy}(i)+\beta {\displaystyle \sum _{i=1}^{N-1}{d}_z(i)}}+P\mathrm{enalty}$$

  (6)

  where $d_{xy}(i)=\sqrt{{(x_{i+1}-x_i)}^2+({\mathrm{y}}_{\mathrm{i}+1}{-\mathrm{y}}_{\mathrm{i}}{)}^2}$ denotes horizontal displacement, $d_z(i)=\left|z_{i+1}-z_i\right|$ represents vertical displacement, $\alpha ,\beta$ are weighting coefficients for horizontal and vertical energy costs, Penalty is an additional term aggregating violations of flight constraints, such as altitude limits, terrain clearance, safe clearance and turning radius. This objective ensures that both energy efficiency and flight safety are simultaneously considered.

2.2.4. Constraint Modeling

To guarantee flight safety and feasibility in mountainous environments, the UAV trajectory must satisfy a set of constraints. These constraints ensure that the path avoids collisions, respects physical flight limits, and maintains proper forward progress:

• Altitude constraint:

  $$z_{\min }\le z_i\le z_{\max },i=1,\dots N$$

  (7)

  where $z_{\min }$ and $z_{\max }$ are the lower and upper altitude limits. This constraint guarantees that the UAV operates within the permissible flight envelope.
• Terrain clearance constraint:

  $$z_i\ge z_{\mathrm{terrain}}\left(x_i,y_i\right)+\mathrm{margin},i=1,\dots ,N$$

  (8)

  here, $z_{\mathrm{terrain}}(x,y)$ denotes the terrain elevation at horizontal position $(x,y)$, and margin is a fixed safety buffer. This constraint ensures that the UAV always maintains a vertical clearance above the terrain surface.
• Safe clearance constraint (dynamic margin):

  $$\begin{array}{l}{d}_{obs,i}=z_i-z_{\mathrm{terrain}}(x_i,y_i)\\ D_{\mathrm{safe},i}=r_{\min }+k_{1}v+k_2\left|z_i-z_{i-1}\right|\\ d_{obs,i}\ge D_{\mathrm{safe},i},i=2,\dots N\end{array}$$

  (9)

  where $d_{obs.i}$ is the actual clearance, $D_{\mathrm{safe},i}$ is the required dynamic clearance. $r_{\min }$ is the minimum safe distance, $k_1$ and $k_2$ are safety coefficients, and $v$ is the UAV speed. This constraint adapts the required clearance to flight dynamics.
• Turning radius constraint:

  $$R_i={\displaystyle \frac{v^2}{g\tan \theta }},R_i\ge R_{\min },i=2,\dots ,N$$

  (10)

  here, ${\theta }_i$ is the turning angle at waypoint $P_i$, $g$ is gravitational acceleration, and $R_{\min }={\displaystyle \raisebox{1ex}{$v^2$}\!\left/ \!\raisebox{-1ex}{$g\tan {\theta }_{\max }$}\right.}$ is the minimum turning radius derived from the maximum bank angle ${\theta }_{\max }$. This constraint ensures that the UAV can physically execute the planned turns.

In summary, this section establishes the mathematical foundation for UAV path optimization under complex terrain constraints. The defined objectives and constraints collectively ensure feasible, safe, and energy-efficient flight trajectories, forming the basis for the adaptive optimization framework proposed in Section 3.

3. Proposed Algorithm of EC-MOPSO

Traditional MOPSO often fails to achieve stable convergence and feasible trajectories in complex mountainous environments due to three inherent limitations. (I) The fixed learning factors and inertia weight cause premature convergence, as swarm diversity rapidly declines under highly non-convex fitness landscapes. (II) The standard Pareto dominance mechanism lacks density regulation, leading to archive overcrowding and uneven solution distribution, which compromises convergence control. (III) The absence of embedded feasibility mechanisms results in infeasible or discontinuous UAV paths that violate altitude, clearance, or turning constraints [35,36].

To overcome these challenges, this study proposes EC-MOPSO (Epsilon-dominance and Crowding-distance-based Multi-Objective Particle Swarm Optimization), which integrates a unified $\epsilon -$ dominance and crowding-distance archiving strategy, an adaptive parameter adjustment mechanism, and a trajectory repair operator. Following the symmetry principle, the algorithm preserves balance between exploration and exploitation during swarm evolution. These mechanisms collectively regulate convergence, diversity, and feasibility throughout the optimization process. Specifically, the $\epsilon -$ dominance and crowding-distance mechanisms maintain a well-distributed Pareto front and prevent archive redundancy; the adaptive parameter control dynamically balances global exploration and local exploitation; and the trajectory repair operator ensures real-time compliance with terrain and safety constraints. Through the integration of these components, EC-MOPSO achieves stable convergence, enhanced population diversity, and reliable UAV trajectories under complex mountainous conditions.

This section introduces the core mechanisms of the proposed EC-MOPSO algorithm. Specifically, Section 3.1 presents the overall framework, including its pseudocode and flowchart. The subsequent subsections detail the four key mechanisms designed in this study and provide their corresponding pseudocode implementations. In addition, Section 3.5 conducts a computational complexity analysis using Big-O notation to evaluate the algorithm’s time and space efficiency. To better understand the meaning of some of the symbols used in this paper, Table 2 lists the main mathematical symbols and parameters.

Table 2. List of Symbols used in EC-MOPSO Algorithm.

Symbol	Definition/Description	Type/Unit
$N$	Population size (number of particles)	Integer
$D$	Dimensionality of the search space	Integer
$P_i=(x_i,y_i,z_i)$	$i-th$ waypoint representing UAV position	Vector
$W=\left(w_1,\dots ,w_n\right)$	Set of UAV waypoints forming a trajectory	Set
$Z\left(x,y\right)$	Terrain elevation function	Function (m)
$z_{\min },z_{max}$	Minimum and maximum flight altitude	Scalar (m)
$x_{\min },x_{\max },y_{\min },y_{\max }$	Horizontal and vertical terrain boundaries	Scalar (m)
m	Safety margin above terrain surface	Scalar (m)
v	Particle velocity vector	Vector
${\varpi }_{\max },{\varpi }_{\min }$	Maximum and minimum values of inertia weight	Scalar
$C_{1,\max },C_{1,\min },C_{2,\max },C_{2,\min }$	Upper/lower bounds for factors	Scalar
t, T	Current and maximum iteration index	Integer
$R_{\min }$	Minimum turning radius constraint	Scalar (m)
g	Gravitational acceleration (9.8 m/s2)	Constant
$\theta$	Local turning angle	Scalar (rad)
$\epsilon =({\epsilon }_1,{\epsilon }_2,{\epsilon }_3)$	Tolerance vector in $\epsilon -$ dominance rule	Vector
$\delta$	Position deduplication threshold	Scalar
$D_{safe,i}$	Required dynamic clearance	Scalar (m)
$d_{obs.i}$	actual clearance	Scalar (m)
$\alpha ,\beta$	Weighting coefficients for horizontal/vertical energy	Scalar
$k_1,k_2$	Safety coefficients in clearance constraint	Scalar

3.1. General Framework of EC-MOPSO

This section describes the overall procedure of the proposed EC-MOPSO algorithm. The inputs include the population size $N$, the feature dimension $D$, the start and end position $P_1,P_2$, the terrain elevation map $Z\left(x,y\right)$, altitude limits $z_{\min },z_{\max }$ and the safety margin. The output is the optimized non-dominated path set $Pop$. The general framework is summarized in Algorithm 1.

Algorithm 1: General Framework of EC-MOPSO

Input: $N$, $D$, $P_1$, $P_2$, $Z$, $z_{\min }$, $z_{\max }$, margin;

Output: Archive, Best;

1: $\mathrm{Pop}\leftarrow \mathrm{InitializePopulation}$($N$, $D$, $P_1$, $P_2$);            //Initialize the population

2: $\mathrm{Pop}\leftarrow \mathrm{PreRepair}$($Pop$, $Z$, margin, $z_{\min }$, $z_{\max }$);    //Pre-repair: Clip XY to boundaries

3: $\mathrm{Archive}\leftarrow \varnothing$;

4: while not Terminate do

5:        $\mathrm{Fitness}\leftarrow \mathrm{EvaluateFitness}\_\mathrm{Bspline}\left(\mathrm{Pop}\right)$;             //Evaluate $f_1,f_2,f_3$

6:        $\mathrm{Archive}\leftarrow \mathrm{UpdateArchive}\left(\mathrm{Pop}\cup \mathrm{Archive}\right)$;        //$\epsilon -$ dominance

7:        $\mathrm{Archive}\leftarrow \mathrm{PruneByCrowding}\left(\mathrm{Archive}\right)$;         //Crowding distance pruning

8:        ($\varpi$,$C_1$,$C_2$)$\leftarrow \mathrm{AdaptiveSchedule}(iter)$;             //Adaptive parameter adjustment

9:            for each $p\in \mathrm{Pop}$ do;

10:               $\mathrm{Leader}\leftarrow \mathrm{SelectLeader}\left(\mathrm{Archive}\right)$;

11:               $v\leftarrow \varpi \cdot v+c_1\cdot rand\cdot \left(pbest-pos\right)+c_2\cdot rand\cdot \left(Leader-pos\right)$;

12:               $pos\leftarrow \mathrm{Clamp}\left(Pos+v\right)$;

13:               $pos\leftarrow \mathrm{RepairTrajectory}$($pos$, $Z$, margin, $z_{\min }$, $z_{\max }$);   //Track repair

14:               $pos\leftarrow \mathrm{UpdatePbest}(p)$;

15:         end for;

16: end while;

17: $\mathrm{Best}\leftarrow \mathrm{SelectFinal}\left(\mathrm{Archive}\right)$;

18: return Archive, Best;

The algorithm begins by initializing the particle population within the feasible solution space. Each particle encodes a UAV trajectory as a sequence of three-dimensional waypoints. During initialization, each particle represents a candidate path defined by B-spline control points, where the first and last waypoints are fixed at the start and end positions, and five intermediate waypoints are randomly generated within the terrain boundaries. At each generation, all particles are re-evaluated according to three objectives—path length, flight time, and energy consumption—with additional penalty terms for violations of altitude, terrain clearance, or turning constraints. A trajectory repair operator is applied during initialization to ensure that waypoints satisfy terrain clearance and altitude limits. After initialization, the algorithm enters the iterative optimization stage. The $\epsilon -$ dominance and crowding-distance mechanisms jointly update the Pareto archive to eliminate redundant solutions and maintain population diversity. The adaptive parameter module dynamically adjusts the inertia weight and learning coefficients to preserve symmetry between global exploration and local exploitation. After velocity and position updates, each waypoint is clamped within the feasible spatial bounds, and the trajectory repair operator corrects infeasible points to ensure real-time path feasibility. The iterative process continues until the maximum number of generations (200) is reached, as beyond this point the normalized hypervolume values of all algorithms exhibit negligible improvement, indicating convergence. Finally, the algorithm outputs the non-dominated path set. Figure 1 illustrates the complete workflow of EC-MOPSO, which consists of initialization, iterative update, trajectory repair, and archive maintenance.

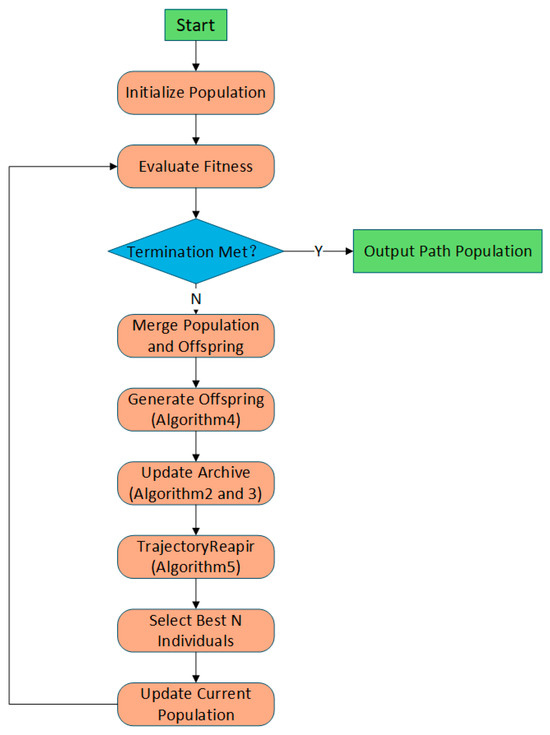
Figure 1. Flowchart for the general framework of EC-MOPSO.

3.2. $\epsilon -$ Dominance Archive and Crowding Distance Pruning

In EC-MOPSO, two complementary mechanisms are integrated to jointly maintain population diversity and ensure convergence: the $\epsilon -$ dominance archive and crowding distance pruning. The $\epsilon -$ dominance strategy primarily controls convergence by eliminating weakly dominated or redundant solutions, while the subsequent crowding distance pruning refines the archive to preserve diversity and prevent clustering of similar solutions. This sequential combination ensures that neither convergence pressure nor diversity maintenance overwhelms the optimization process. By balancing these two mechanisms, the algorithm effectively avoids premature convergence, maintains a well-distributed Pareto front, and guarantees feasible UAV trajectories under complex constraints. The overall procedure is summarized in Algorithms 2 and 3.

3.2.1. $\epsilon -$ Dominance Archive Update

In standard MOPSO, Pareto dominance may lead to excessive archive size because small numerical differences in objective values cause nearly identical solutions to be preserved. To address this, EC-MOPSO employs an $\epsilon -$ dominance criterion that introduces a tolerance vector:

$$\epsilon =({\epsilon }_1,{\epsilon }_2,{\epsilon }_3)=\left(1,0,{10}^4\right)$$

(11)

Given two solutions $f(p)$ and $f(a)$, $f(p)$ $\epsilon -$ dominates $f(a)$ if:

$$f(p){\underset{\_}{\prec }}_{\epsilon }f(a)\iff f_i(p)\le f_i(a)+{\epsilon }_i,\forall i\in \left\{1,\dots ,M\right\},\exists j:f_j(p)<f_j(a)-{\epsilon }_j$$

(12)

This definition ensures that only solutions exhibiting a significant improvement in at least one objective are retained, preventing the archive from being flooded with nearly identical points. The archive update begins by merging the current particle population P with the existing archive A and the previous global Pareto set.

Each candidate in the combined set is compared under the $\epsilon -$ dominance rule. If a candidate $\epsilon -$ dominates an archived solution, the dominated one is removed; if it is not $\epsilon -$ dominated by any existing solution, it is inserted into the archive. To further remove redundancy and maintain spatial symmetry, solutions whose position vectors are closer than a fixed distance threshold $\delta ={10}^{-6}$ are treated as duplicates and discarded. Unlike dynamic parameters, $\delta$ is fixed throughout all iterations for computational consistency. The detailed procedure is summarized in Algorithm 2.

Algorithm 2: $\epsilon -$ Dominance Archive Update

Input: Population $P$, Archive $A$, tolerance vector $\epsilon$, distance threshold $\delta$, maximum archive size K;

Output: Updated Archive $A$, global Pareto set G;

1: $S\leftarrow P\cup A$;     //merge population and archive

2: $\mathrm{initialize} A\leftarrow \varnothing$;

3: for each $p\in S$ do;     //Sequentially evaluate each candidate

4:            if $\cancel{\exists } a\in A$ such that $f(a){\underset{\_}{\prec }}_{\epsilon }f(p)$;

5:                    Remove all $a\in A$ with $f(p){\underset{\_}{\prec }}_{\epsilon }f(a)$;

6:                    insert $p$ to $A$;

7:            end if;

8: end for;

9: Remove duplicates in A with Euclidean distance < $\delta$;

10: Set $G\leftarrow A$; //Global set equals the updated archive (used for leader selection).

11: if $\left|A\right|>K$ then; //Check archive overflow.

12:            $A\leftarrow \mathrm{PruneArchiveByCrowding}\left(A,K\right)$;  //Invoke crowding-distance pruning

13:            $G\leftarrow A$;   //Synchronize the global set with pruned archive.

14: end if;

15: return A, G;

3.2.2. Crowding Distance Pruning and Leader Selection

To maintain population diversity and prevent premature convergence, the archive $A$ is further processed using crowding distance pruning and leader selection. After the $\epsilon -$ dominance update, the archive may still contain more individuals than the predefined maximum size. In such cases, the crowding distance is calculated for each individual to measure how densely it is surrounded by neighbors in the objective space. Formally, for each objective $m\in \left\{1,2,3\right\}$, solutions in $A$ are sorted by their objective values $f_m$ and the boundary solutions are assigned an infinite crowding distance to ensure their preservation. For intermediate solutions, the crowding distance is calculated as:

$$d_i={\displaystyle \sum _{m=1}^M\frac{{{\displaystyle f}}_{i+1}^m-{{\displaystyle f}}_{i-1}^m}{{{\displaystyle f}}_{\max }^m-{{\displaystyle f}}_{\min }^m}}$$

(13)

where ${{\displaystyle f}}_{i+1}^m$ and ${{\displaystyle f}}_{i-1}^m$ are the neighboring solutions $i$ in objective $m$, A larger $di$ indicates that the solution lies in a less crowded region, thus contributing more to population diversity. When the archive size exceeds the limit, individuals with the smallest crowding distance are iteratively pruned until $‖A‖$ reaches the threshold. This ensures that only representative solutions widely spread across the Pareto front remain. Moreover, leader selection is conducted by probabilistically choosing individuals from $A$ according to their crowding distances: solutions with higher d_i have a greater chance to guide the swarm, thus balancing convergence pressure and exploration capability. The detailed procedure is summarized in Algorithm 3.

Algorithm 3: Crowding Distance Pruning and Leader Selection

Input: Archive $A$, maximum archive size K;

Output: Pruned archive $A$, selected leader $l$;

1: if $\left|A\right|>K$ then;

2:   for each objective $m=1,\dots ,M$;

3:      sort $A$ by $f_m$; assign boundary solution $d=\infty$;

4:        for each solution $i\in A$;

5:           $d_i\leftarrow d_i+{\displaystyle \frac{{{\displaystyle f}}_{i+1}^m-{{\displaystyle f}}_{i-1}^m}{{{\displaystyle f}}_{\max }^m-{{\displaystyle f}}_{\min }^m}}$;      //Sum the normalized interval differences.

6: end for;

7: Sort A by descending $d_l$; retain top K solutions

8: end if; 9: Randomly select $l\in A$ as leader;

11: return A, $l$;

3.3. Adaptive Parameter Adjustment

In standard MOPSO, the search process often suffers from an imbalance between global exploration and local exploitation, which may cause premature convergence or oscillation around suboptimal solutions [37,38,39]. This drawback becomes particularly critical in UAV path planning for emergency rescue in mountainous environments, where both rapid convergence and feasible trajectory generation are essential. To address this issue, EC-MOPSO introduces an adaptive parameter adjustment mechanism, aiming to dynamically tune algorithmic coefficients according to the evolutionary stage. In this mechanism, the inertia weight ($\varpi$) and learning factors ($C_1$,$C_2$) are adaptively updated across iterations to maintain symmetry between exploration and exploitation. During early generations, a larger inertia weight encourages broader exploration of the search space, while in later stages it decreases to refine promising regions. Similarly, the cognitive learning factor $C_1$ gradually declines to reduce excessive self-learning, whereas the social learning factor $C_2$ increases to strengthen cooperation within the swarm, thereby maintaining diversity and improving convergence stability. The inertia weight $\varpi$ is updated according to

$$\varpi ={\varpi }_{\max }-({\varpi }_{\max }-{\varpi }_{\min })\cdot {\displaystyle \frac{t}{T}}$$

(14)

where t is the current iteration number and T is the maximum number of iterations. The coefficients are adjusted as follows:

$$\begin{array}{l}{C}_1=C_{1,\max }-(C_{1,\max }-C_{1,\min })\cdot {\displaystyle \frac{t}{T}}\\ C_2=C_{2,\max }+(C_{2,\max }-C_{2,\min })\cdot {\displaystyle \frac{t}{T}}\end{array}$$

(15)

In this paper, the parameter bounds are selected as: ${\varpi }_{\max }=0.9$, ${\varpi }_{\min }=0.3$, $C_{1,\min }=1.5$, $C_{1,\max }=2.5$, $C_{2,\min }=1.0$, $C_{2,\max }=1.0$. These ranges follow the classical PSO stability region proposed by Shi and Eberhart [40] and Clerc and Kennedy [41], ensuring a smooth transition from global to local search. At early stages, higher $\varpi$ and $C_1$ emphasize individual exploration, while at later stages, reduced $\varpi$ and increased $C_2$ promote cooperative refinement near the Pareto front. A small grid verification (±0.2 around each bound) on mountainous benchmarks confirmed the robustness of these settings with low sensitivity and consistent hypervolume improvement. The detailed procedure is summarized in Algorithm 4.

Algorithm 4: Adaptive Parameter Adjustment

Input: $t$, $T$, ${\varpi }_{\max }$, ${\varpi }_{\min }$, $C_{1,\max }$, $C_{1,\min }$, $C_{2,\max }$, $C_{2,\min }$;

Output: updated parameters $\varpi$, $C_1$, $C_2$;

1: $\varpi \leftarrow {\varpi }_{\max }-({\varpi }_{\max }-{\varpi }_{\min })\cdot (t/T)$;              //Linearly decreases inertia weight

2: $C_1\leftarrow C_{1,\max }-(C_{1,\max }-C_{1,\min })\cdot (t/T)$;      //Gradually decreases cognitive factor

3: $C_2\leftarrow C_{2,\max }+(C_{2,\max }-C_{2,\min })\cdot (t/T)$;    //Gradually increases social factor

4: return $\varpi$, $C_1$, $C_2$;

3.4. Trajectory Repair Operator

In complex mountainous environments, UAV trajectories frequently become infeasible due to collisions with terrain, violation of altitude limits, or deviation beyond the map boundary [42,43]. Such infeasible solutions not only reduce optimization efficiency but also pose serious risks in real-world emergency rescue scenarios, where safe and reliable flight paths are critical. To address these challenges, EC-MOPSO introduces a trajectory repair operator that adaptively modifies infeasible intermediate waypoints to restore path feasibility while maintaining the diversity and spatial symmetry of the trajectory. Although the repair operator is applied after each position update, it acts locally and only adjusts infeasible waypoints that violate topographic or safety constraints. Feasible segments of the trajectory remain unchanged, ensuring that the search space is not overly restricted. This soft correction mechanism prevents the population from entering invalid regions while preserving overall diversity and exploration capability.

The repair mechanism addresses three main aspects:

• Boundary constraint: for any waypoint $(x,y,z)$, the horizontal coordinates must satisfy.

  $$x\in \left[x_{\min },x_{\max }\right],y\in \left[y_{\min },y_{\max }\right]$$

  (16)
• Altitude constraint: the vertical coordinate is adjusted to:

  $$z^{\prime }=\min \left(\max \left(z,z_{\min },Z(x,y)+m\right),z_{\max }\right)$$

  (17)

  where $Z(x,y)$ is the terrain height at $(x,y)$, m is the safety margin, $z_{\min }$ and $z_{\max }$ are the minimum and maximum altitude bounds.
• Feasibility adjustment: when the terrain elevation plus safety margin exceeds the maximum altitude, the waypoint is shifted horizontally along the negative gradient direction of terrain elevation to locate a feasible region. This repair strategy guarantees that each UAV path remains above the terrain with sufficient clearance, avoids penetration into infeasible regions, and ensures compliance with altitude limits. The detailed procedure is summarized in Algorithm 5.

Algorithm 5: Trajectory Repair Operator

Input: waypoint set $W=\left\{w_1,\dots ,w_n\right\}$, terrain $Z(x,y)$, bounds $\left[x_{\min }.x_{\max }\right],\left[x_{\min }.x_{\max }\right],\left[x_{\min }.x_{\max }\right]$, safety margin m;

Output: repaired waypoint set $W^{\prime }$;

1: for each intermediate waypoint $w_i=\left(x_i,y_i,z_i\right),i=2,\dots ,n-1$ do;

2: $x_i\leftarrow \mathrm{clip}\left(x_i,x_{\min },x_{\max }\right)$;            //confine x within horizontal map boundary

3: $y_i\leftarrow \mathrm{clip}\left(y_i,y_{\min },y_{\max }\right)$;         //confine y within vertical map boundary

4: $z_{\mathrm{terrain}}\leftarrow Z\left(x_i,y_i\right)$;           //obtain terrain height at current (x, y)

5: $z_i\leftarrow \min (\max (z_i,z_{\min },z_{\mathrm{terrain}}+m),z_{\max })$;    //enforce altitude and safety margin limits

6:      while $z_{\mathrm{terrain}}+m>z_{\max }$ and $\mathrm{shift}\_\mathrm{attempts}<\mathrm{maxTry}$ do;

7:      $\nabla z(x_i,y_i)=\left(\partial z/\partial x,\partial z/\partial y\right)$;         //compute terrain gradient at current point

8:      shift $\left(x_i,y_i\right)$ along $-\nabla Z$ direction; //move horizontally downhill to reduce altitude

9:      update $z_{\mathrm{terrain}}=Z(x_i,y_i)$;         //recompute terrain height after shifting

10:      $z_i\leftarrow \min \left(\max \left(z_i,z_{\min },z_{\mathrm{terrain}}+m\right).z_{\max }\right)$; //readjust altitude after each shift

11:      end while;

12: end for;

13: return $W^{\prime }$;

3.5. Computational Complexity Analysis

To further evaluate the computational efficiency of the proposed EC-MOPSO algorithm, this section analyzes its time and space complexity using Big-O notation. The total computational cost mainly includes three components: fitness evaluation, archive update, and adaptive parameter adjustment with trajectory repair.

During each generation, the fitness of all particles is calculated according to three objectives (path length, flight time, and energy consumption) along with penalty terms for constraint violations such as terrain collision or excessive turning curvature. Each particle performs B-spline interpolation and trajectory sampling, leading to a fitness-evaluation complexity of $O(N\times M)$, where $N$ denotes the population size and $M$ is the number of sampled points per path (approximately 400).

The $\epsilon -$ dominance and crowding-distance mechanisms are then used to update the Pareto archive. This process involves pairwise comparisons and sorting among particles and archived solutions, resulting in a computational complexity of $O(N^2)$, Adaptive parameter adjustment and waypoint-repair operations are executed once per particle, contributing an additional linear complexity of $O(N)$. Therefore, the overall time complexity per generation can be expressed as $O(N^2+N\times M)$. Since $M$ is a fixed constant determined by the path sampling resolution, the term $N\times M$ grows linearly and is dominated by the quadratic term, which allows the complexity to be approximated as $O(N^2)$. For the entire optimization process over $T$ generations, the total time complexity is $O(T{N}^2)$.

The space complexity of EC-MOPSO is $O(N+A)$ where $A$ denotes the maximum size of the non-dominated archive. This includes storage for all particle positions, velocities, and archived solutions. Compared with standard MOPSO, which also has $O(T{N}^2)$ complexity, EC-MOPSO achieves higher computational efficiency through $\epsilon -$ dominance pruning that eliminates redundant dominance checks. In contrast, decomposition-based algorithms such as MOEA/D and grid-based frameworks such as MOBCA require additional grid partitioning and density estimation, resulting in approximately $O(T{N}^3)$ complexity.

Therefore, EC-MOPSO maintains the same asymptotic complexity as standard MOPSO while achieving better practical efficiency through structured archive management and adaptive parameter control.

4. Experimental Setups

To verify the effectiveness of the proposed EC-MOPSO algorithm for UAV path planning in mountainous environments, a series of experiments were conducted under a unified framework. This section presents the parameter design and evaluation metrics, laying the foundation for the comparative analysis in Section 5. Specifically, Section 4.1 introduces four comparison algorithms, while Section 4.2 describes the construction of test cases based on Equation (1). To further validate the appropriateness of the selected parameters, a Taguchi orthogonal experiment is conducted in Section 4.3. Finally, Section 4.4 outlines the evaluation metrics employed in this study.

4.1. Comparative Algorithms

To ensure fairness and representativeness in the experimental results, three widely recognized multi-objective optimization algorithms were selected as comparative algorithms for comparison with the proposed EC-MOPSO. The details are as follows:

• Standard MOPSO: The classical Multi-Objective Particle Swarm Optimization (MOPSO) algorithm is based on swarm intelligence, where each particle represents a candidate solution and updates its position by learning from both personal best and global best experiences, gradually approaching the Pareto front [44]. As one of the earliest swarm-based approaches applied to multi-objective problems, standard MOPSO shows certain advantages in convergence speed and computational efficiency. However, it often suffers from premature convergence and uneven distribution of solutions when handling complex constraints or high-dimensional objectives. In this study, it is selected as a baseline to verify the improvements of EC-MOPSO in convergence accuracy and solution diversity.
• NSGA-II: The Non-dominated Sorting Genetic Algorithm II (NSGA-II) is one of the most classical and widely adopted evolutionary algorithms in the field of multi-objective optimization [45]. It maintains solution diversity and balance through fast non-dominated sorting and crowding distance mechanisms, and has been extensively applied in UAV path planning as well as other engineering optimization problems. Its advantages lie in robustness and maturity, while in constrained complex environments it may incur higher computational costs and risk of insufficient local convergence. Here, NSGA-II serves as a benchmark to evaluate the relative performance of EC-MOPSO against evolutionary algorithms.
• SPEA2: The Strength Pareto Evolutionary Algorithm 2 (SPEA2) is an archive-based multi-objective optimization algorithm, which enhances convergence and diversity through fitness assignment and archive truncation strategies [46]. SPEA2 has clear strengths in archive management and maintaining solution quality, but its search capability strongly depends on archive maintenance and may exhibit limitations in highly constrained scenarios. It is chosen here to assess the advantages of EC-MOPSO in improving archive management strategies.
• MOBCA: The Multi-Objective Besiege and Conquer Algorithm (MOBCA) is a recently developed swarm-based optimizer inspired by collective behavior and adaptive coordination mechanisms [47]. It divides the population into multiple armies that cooperate and compete through besieging and conquering strategies to balance exploration and exploitation. MOBCA has shown strong performance in maintaining population diversity and avoiding premature convergence, particularly in multimodal or complex landscapes. However, its event-driven grid division and soldier allocation strategies increase computational complexity. It is therefore included to benchmark EC-MOPSO against a modern, high-diversity swarm optimizer that emphasizes adaptive coordination.

In summary, these four algorithms represent swarm intelligence, evolutionary optimization and archive-based elitism, which are the four mainstream approaches in multi-objective optimization. A systematic comparison with them provides a comprehensive evaluation of the performance advantages and improvements introduced by EC-MOPSO in UAV path planning tasks.

4.2. Test Cases

To evaluate the performance of the algorithms in realistic scenarios, a set of test cases was designed based on a three-dimensional mountainous environment. The environment was defined as a cubic space of (100, 100, 120), generated using Equation (1) with a fixed random seed $rng(666)$ to ensure consistency across all experiments. The terrain was constructed by superimposing multiple Gaussian peaks, adding Perlin noise perturbations, and applying Gaussian smoothing, which produces irregular fluctuations and better simulates the complexity of real mountainous landscapes. All experiments were executed on a desktop workstation equipped with an Intel Core i5-12400F CPU (2.50 GHz), 16 GB RAM, and an NVIDIA RTX 4060 GPU. The algorithms were implemented in MATLAB R2023a and run under Windows 10 (64-bit). Figure 2 illustrates several terrain instances generated with different random seeds, highlighting the diversity and complexity of the test environments. Within this setting, the UAV path planning problem was modeled as a trajectory consisting of seven waypoints, with the start point fixed at (1, 1, 40) and the end point at (95, 95, 50), while the five intermediate waypoints were optimized by the algorithms. The optimization objectives considered were Path Length, Flight Time, and Energy consumption, reflecting the balance between efficiency, timeliness, and energy usage. To ensure feasibility and safety, several constraints were imposed, including a minimum flight altitude of 15 m, a maximum altitude of 120 m, a minimum terrain clearance of 10 m, kinematic restrictions on the turning radius to ensure maneuverability. This design of test cases provides an environment that is both controlled and consistent, while sufficiently complex to capture the challenges of mountainous rescue missions, thereby offering a reliable foundation for algorithm comparison.

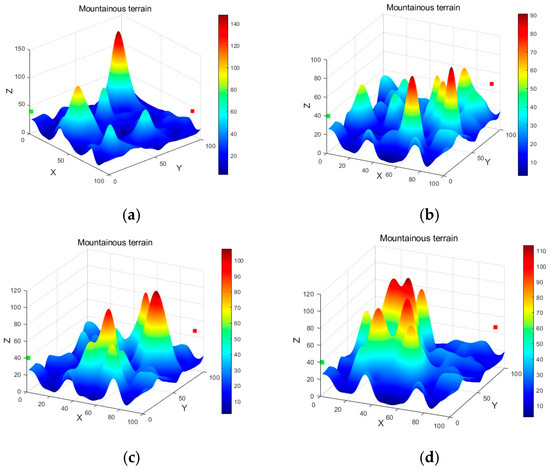
Figure 2. Different terrains generated with different random seeds. (a) $rng(888)$. (b) $rng(100)$. (c) $rng(666)$. (d) $rng(1234)$.

4.3. Parameter Settings and Taguchi Orthogonal Design

In multi-objective particle swarm optimization (MOPSO), the algorithm’s performance is highly sensitive to parameter configurations. Conventional parameter tuning methods, such as empirical selection or single-factor sensitivity analysis, often fail to capture the joint effects of multiple parameters. A full factorial experiment with five factors and three levels would require $3^5=243$ runs, which is computationally expensive. To overcome this limitation, we adopt the Taguchi orthogonal design (TOD), which selects a representative subset of parameter combinations to significantly reduce the number of experiments while still capturing the main effects of each factor.

Based on existing studies and the characteristics of the algorithm, five key control factors were selected for this experiment: population size ($N$), maximum number of generations ($T$), inertia weight range ($\varpi$), cognitive factor ($C_1$) and social factor ($C_2$). Each factor was assigned three levels, as summarized in Table 3.

Table 3. Experimental factors and levels.

Factor	Level l	Level 2	Level 3
population size ($N$)	50	100	200
maximum number of generations ($T$)	100	150	200
inertia weight range $\varpi$	(0.2, 0.8)	(0, 3, 0.9)	(0.4, 1.0)
cognitive factor ($C_1$)	(1.0, 2.0)	(1.5, 2.5)	(2.0, 3.0)
social factor ($C_2$)	(1.0, 2.0)	(1.5, 2.5)	(2.0, 3.0)

Since the experiment involves five factors with three levels each, a full factorial design would require 243 runs. To achieve efficiency, we adopt the L27 orthogonal array, which requires only 27 runs. Compared with smaller arrays such as L9 or L18, the L27 design ensures a balanced and comprehensive coverage of all factor-level combinations, making it the most suitable choice for this study.

To comprehensively evaluate the performance of different parameter settings, the Orthogonal Design Score (ODS) is employed. The ODS integrates multiple objectives into a single performance index by normalizing each objective and aggregating them through a weighted geometric mean. The formula is defined as follows:

$$ODS=\underset{x\in P}{\max }{{\displaystyle \prod _{k=1}^m\left(\frac{f_k^{\max }-f_k(x)}{f_k^{\max }-f_k^{\min }}\right)}}^{w_k}$$

(18)

where $P$ denotes the set of Pareto solutions obtained by the algorithm, $x\in P$ represents an individual solution within the Pareto set; $m$ is the total number of objectives, $f_k(x)$ is the value of the $k-th$ objective for solution $x$, $f_k^{\max }$ and $f_k^{\min }$ are the maximum and minimum values of the objective, and ${\varpi }_k$ is the weight.

The normalized ODS value ranges from 0 to 1. For each solution $x\in P$, the formula evaluates its relative performance across all objectives by normalization. The geometric aggregation ensures that a solution must perform consistently well across all objectives to achieve a high score. Finally, the maximum score across the Pareto set is selected as the ODS value of that parameter configuration. Based on this metric, we further apply ODS to parameter sensitivity analysis, which quantifies the overall performance under different experimental configurations and thus supports the subsequent orthogonal experiments.

A total of 27 parameter combinations were tested according to the L27 design. Each run was repeated three times, and the average ODS value was recorded to mitigate stochastic variation. The results are summarized in Table 4. In this table, numbers 1, 2, and 3 denote the groupings of Level 1, Level 2, and Level 3.

Table 4. L27 orthogonal experimental results (ODS values).

Run	N	T	$\mathit{\varpi }$	C1	C2	OSD Value (Mean ± Std.)
1	1	1	1	1	1	0.858302 ± 0.000634
2	1	1	2	1	2	0.857019 ± 0.005132
3	1	1	3	1	3	0.856679 ± 0.001131
4	1	2	1	2	1	0.860406 ± 0.000454
5	1	2	2	2	2	0.860029 ± 0.000265
6	1	2	3	2	3	0.858493 ± 0.000373
7	1	3	1	3	1	0.859906 ± 0.000160
8	1	3	2	3	2	0.857414 ± 0.004822
9	1	3	3	3	3	0.858782 ± 0.001270
10	2	1	1	2	2	0.85833 ± 0.009451
11	2	1	2	2	3	0.859629 ± 0.000696
12	2	1	3	2	1	0.86007 ± 0.000514
13	2	2	1	3	2	0.860322 ± 0.000371
14	2	2	2	3	3	0.860431 ± 0.000228
15	2	2	3	3	1	0.860619 ± 0.000121
16	2	3	1	1	2	0.861996 ± 0.000154
17	2	3	2	1	3	0.862627 ± 0.000193
18	2	3	3	1	1	0.862969 ± 0.000153
19	3	1	1	3	3	0.859103 ± 0.000283
20	3	1	2	3	1	0.860434 ± 0.000264
21	3	1	3	3	2	0.858072 ± 0.000170
22	3	2	1	1	3	0.850132 ± 0.000291
23	3	2	2	1	1	0.86013 ± 0.000252
24	3	2	3	1	2	0.858112 ± 0.000084
25	3	3	1	2	3	0.860563 ± 0.000205
26	3	3	2	2	1	0.860588 ± 0.000111
27	3	3	3	2	2	0.860518 ± 0.000056

Each parameter configuration in the L27 orthogonal design was executed three independent times under different random seeds to assess result consistency. The mean and standard deviation of the ODS values obtained from these repetitions are reported in Table 4. The inclusion of standard deviations provides a clearer view of experimental stability, showing that most deviations are below 0.002, which confirms the robustness and reproducibility of the proposed EC-MOPSO algorithm under varying parameter settings. Based on these averages, the main effects plot was drawn, as shown in Figure 3. In Figure 3, the horizontal axis represents each factor and its levels, while the vertical axis represents the corresponding average ODS values. The shape of the curves reflects the sensitivity of ODS to different factor levels: larger fluctuations indicate stronger influence of the factor on the results.

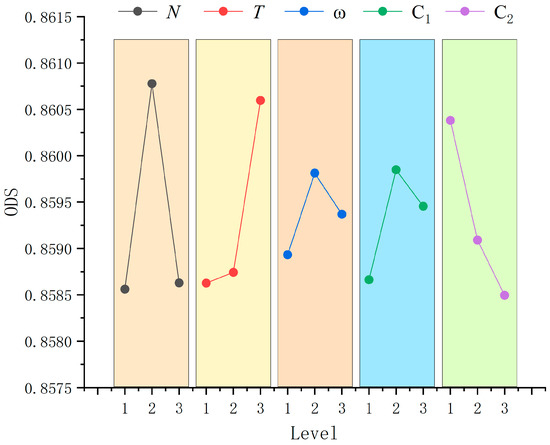
Figure 3. Main effects plots of the factors.

As shown in Figure 3, the population size ($N$) increases sharply from Level 1 (50) to Level 2 (100) and then decreases at Level 3 (200), indicating that $N$ is the most influential factor, with the best level being Level 2 (N = 100). The maximum generations ($T$) show a steady upward trend, with ODS continuously increasing from Level 1 (100) to Level 3 (200), suggesting that larger iteration counts improve optimization performance; thus, the best level is Level 3 (T = 200). The inertia weight range ($\varpi$) exhibits a moderate effect, reaching its peak ODS value at Level 2 (0.3, 0.9), which achieves a good balance between exploration and exploitation; therefore, Level 2 is optimal. The cognitive factor ($C_1$) performs best at Level 2 (1.5, 2.5), indicating that both too small and too large values weaken performance. In contrast, the social factor ($C_2$) decreases consistently, with ODS dropping from Level 1 (1.0, 2.0) to Level 3 (2.0, 3.0); this suggests that excessive social learning leads to premature convergence, making Level 1 the optimal choice.

In summary, the optimal parameter configuration is determined as: N = 100 (Level 2), T = 200 (Level 3), $\varpi$ = (0.3, 0.9) (Level 2), $C_1$ = (1.5, 2.5) (Level 2), and $C_2$ = (1.0, 2.0) (Level 1).

The experimental parameter settings are summarized in Table 5. In addition to the five parameters mentioned above, the experiment also provides the number of waypoints, starting point, end point, terrain margin, minimum and maximum flight altitude.

Table 5. Parameter Settings.

Parameter	Parameter Value	Parameter	Parameter Value
Population size	100	Minimum altitude	15 m
Max generations	200	Maximum altitude	120 m
Waypoints	7	Inertia weight	${\varpi }_{\max }=0.9,{\varpi }_{\min }=0.3$
Terrain margin	10	Cognitive factor	$C_{1\max }=2.5,C_{1\min }=1.5$
Number of mountain peaks	10	Social factor	$C_{2\max }=2.0,C_{2\min }=1.0$
Start point coordinates	(1 m, 1 m, 40 m)	End point coordinates	(95 m, 95 m, 50 m)

4.4. Performance Metrics

For performance evaluation, the normalized hypervolume (HV) was adopted as the core metric to quantitatively measure the quality of the obtained solution sets in the objective space. The HV indicator simultaneously captures two essential aspects of multi-objective optimization: convergence and diversity. On the one hand, a larger HV value indicates that the solution set is closer to the true Pareto front, reflecting superior convergence accuracy. On the other hand, HV also measures the extent of coverage and the uniformity of distribution across the objective space, thus preventing biased evaluation based solely on a single objective. To ensure reliability of the results, each algorithm was independently executed 30 times under identical conditions, and both the mean and standard deviation of the HV values were recorded to comprehensively assess algorithmic stability and robustness. Furthermore, the Wilcoxon rank-sum test was applied with a significance level of 5% to verify whether the performance differences among algorithms were statistically significant. This non-parametric test is particularly suitable for comparing outcomes of repeated experiments without assuming specific data distributions. Through the integration of these evaluation procedures, the experimental study provides a thorough and unbiased assessment of the algorithms in terms of convergence, distribution quality, stability, and statistical significance.

5. Experimental Comparison and Analysis

In this section, a comparative analysis is conducted under the parameter framework established in Section 4 to verify the superiority of the proposed EC-MOPSO algorithm. In Section 5.1, the proposed algorithm is compared with the comparison algorithms in terms of path performance, Pareto set distribution, and hypervolume (HV). Furthermore, to validate the effectiveness of the proposed improvement mechanisms, Section 5.2 presents ablation experiments to assess the individual contributions of each mechanism.

5.1. Comparative Analysis with Representative Algorithms

To demonstrate the superiority of the proposed EC-MOPSO algorithm over the compared methods, this section provides a comprehensive analysis from three perspectives: the final path, the Pareto solution set, and the HV indicator.

5.1.1. Analysis of Final Paths

In mountainous emergency rescue scenarios, path planning must not only ensure feasibility and safety but also take into account time efficiency and energy consumption [48]. Figure 4a,b illustrate the flight trajectories generated by the four algorithms under the same environment, where distinct differences can be observed.

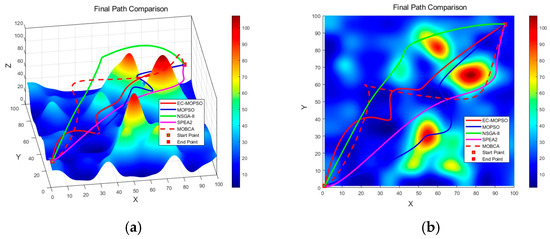
Figure 4. Final paths generated by different algorithms. (a) front view; and (b) top view.

The path generated by NSGA-II exhibits a pronounced detour, as shown in Figure 4a, where the algorithm tends to select high-altitude routes. Although this approach ensures flight safety, it considerably increases both path length and flight time, making it unsuitable for time-critical emergency rescue missions. The trajectory obtained by MOPSO shows unnecessary detours and fluctuations, with high randomness in certain local areas. Compared with EC-MOPSO, MOPSO produces longer routes that pass closer to mountain peaks, thereby increasing the risk of collisions. The path produced by SPEA2 lies between those of MOPSO and NSGA-II, exhibiting moderate smoothness but still containing redundant turns and backtracking. This suggests that SPEA2 fails to fully leverage its convergence advantages in complex terrains and struggles to balance high-dimensional constraints with multiple optimization objectives. In contrast, the MOBCA achieves smoother and more stable trajectories through its grid-based archiving mechanism and adaptive besiege–conquer strategy. As shown in Figure 4a, MOBCA effectively avoids major mountain peaks and maintains moderate terrain clearance. Its generated paths are shorter and safer than those of SPEA2 and NSGA-II, yet remain slightly longer than those produced by EC-MOPSO. However, due to its discrete grid update process, MOBCA exhibits minor local oscillations in some regions, indicating slightly lower convergence precision than EC-MOPSO under the same number of iterations. Overall, the proposed EC-MOPSO algorithm delivers the most balanced and reliable trajectories among all compared methods. It effectively bypasses mountainous regions while maintaining short path lengths and stable flight altitudes. As illustrated in Figure 4b, EC-MOPSO produces paths that are closest to the optimal route, minimizing unnecessary deviations while ensuring sufficient terrain clearance. These results confirm that the proposed improvements significantly enhance convergence stability and achieve a superior trade-off among the competing objectives of safety, efficiency, and energy consumption.

In summary, the paths generated by EC-MOPSO achieve a better trade-off between path length and safety, particularly in avoiding complex mountainous regions. The resulting trajectories are shorter and smoother, enabling the algorithm to satisfy safety constraints while better fulfilling the core requirements of emergency rescue missions in mountainous environments, namely speed, safety, and energy efficiency.

5.1.2. Analysis of Pareto Solution Sets

In multi-objective optimization problems, the Pareto set reflects the trade-offs among different objectives, where each non-dominated solution represents a feasible path that balances path length, flight time, and energy consumption. Ideally, an algorithm should be able to approximate the Pareto front as broadly as possible, achieving both strong convergence and good distribution [49]. To demonstrate the superiority of the proposed EC-MOPSO algorithm over the compared methods, we analyze the Pareto solution sets obtained by five algorithms. The results are shown in Figure 5.

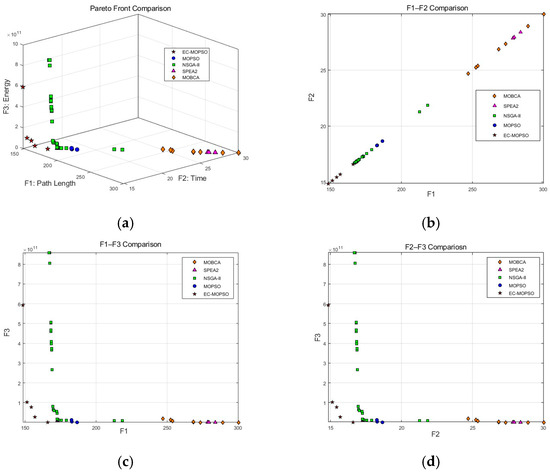
Figure 5. Comparison of Pareto solution sets obtained by different algorithms. (a) Comparison in three-dimensional objective space. (b) Comparison in the F1–F2 dimension. (c) Comparison in the F1–F3 dimension. (d) Comparison in the F2–F3 dimension.

As illustrated in Figure 5a–d, Figure 5a depicts the distribution of solutions in the three-dimensional objective space. Each scatter point represents a feasible UAV trajectory generated by the corresponding algorithm, where the three coordinates denote path length (F1), flight time (F2), and energy consumption (F3), respectively. Since each algorithm produces multiple non-dominated feasible trajectories with varying performance at the end of evolution, the average value of each objective within the obtained solution set is adopted to objectively evaluate the overall optimization capability of the algorithms.

Clear performance differences can be observed among the five algorithms. The EC-MOPSO algorithm produces a compact set of solutions located closer to the ideal corner and achieves superior average performance across all three objectives. In terms of average path length (F1) and flight time (F2), EC-MOPSO achieves reductions of 39.9%, 15.6%, 10.9%, and 42.3% compared with NSGA-II, MOPSO, SPEA2, and MOBCA, respectively, demonstrating excellent convergence speed and time efficiency. The obtained Pareto front is smooth and continuous, reflecting both better convergence and a more balanced distribution that covers a wider region of the objective space. In contrast, NSGA-II, due to its non-dominated sorting mechanism, generates a relatively larger number of solutions distributed across multiple fronts, especially near the boundaries. Although this improves coverage, the quality and concentration of the solutions are insufficient. MOBCA shows the lowest convergence rate and the widest dispersion of solutions, with overall path length and flight time approximately 40% higher than those of EC-MOPSO, indicating weaker convergence and stability. From the perspective of average energy consumption (F3), NSGA-II achieves slightly lower mean values than EC-MOPSO, while SPEA2 yields the highest energy consumption. Overall, EC-MOPSO reduces average energy consumption by approximately 37.9% compared with SPEA2, though its mean energy remains slightly higher than that of MOPSO and NSGA-II, suggesting room for further improvement in energy optimization. MOBCA exhibits the highest overall energy level among the five algorithms, with an average energy consumption nearly two orders of magnitude greater than that the others, indicating poor coordination between energy and flight time objectives.

To further illustrate these differences, Figure 5b–d present the pairwise projections of the objective functions. In Figure 5b, EC-MOPSO approaches the ideal boundary while maintaining shorter average paths and flight times, achieving an overall performance improvement of approximately 25–40% compared with the four baseline algorithms. NSGA-II generates a larger number of solutions but with a scattered distribution, many of which are far from optimal. MOPSO shows a similar trend to NSGA-II but produces fewer solutions, whereas SPEA2 mainly clusters in the upper-right region, showing inferior performance overall. MOBCA occupies the uppermost area of the F1–F2 plane, where both the path length and flight time are about 40% higher than those of EC-MOPSO, reflecting slow convergence and limited search efficiency. In Figure 5c, EC-MOPSO maintains a clear advantage in balancing average path length and energy consumption, with its solutions densely distributed near the optimal front. Although its average energy consumption is slightly higher than that of MOPSO and NSGA-II, it remains significantly lower than that of SPEA2 (by approximately 38%), demonstrating stable control capability under complex constraints. NSGA-II contains several high-energy solutions, indicating insufficient constraint handling and cost control. SPEA2 and MOPSO maintain relatively low energy consumption but at the expense of longer paths and reduced diversity. MOBCA’s solutions are distributed at the far end of the F1–F3 plane, with overall energy levels roughly 40% higher than those of EC-MOPSO, revealing poor convergence between distance and energy objectives. In Figure 5d, EC-MOPSO consistently dominates the lower-left region, achieving shorter average flight times and more stable performance. Its average flight time is approximately 40% shorter than that of NSGA-II and 16% and 11% shorter than those of MOPSO and SPEA2, respectively. NSGA-II exhibits a scattered distribution with higher energy consumption, while SPEA2 performs the worst in terms of flight time—an unfavorable result for emergency rescue scenarios. Although MOPSO achieves relatively low energy consumption, its average flight time remains longer than that of both NSGA-II and EC-MOPSO. MOBCA occupies the upper boundary of the F2–F3 plane, where both flight time and energy consumption are about 40–45% higher than those of EC-MOPSO, confirming its limited capacity for multi-objective coordination.

In summary, EC-MOPSO demonstrates clear superiority over the four baseline algorithms in terms of average performance on both the three-dimensional Pareto front and the two-dimensional projections. Although NSGA-II produces the largest number of solutions, their distribution is more scattered and inconsistent in quality. SPEA2 and MOPSO perform worse than NSGA-II in both solution quantity and quality. MOBCA exhibits the weakest convergence and the highest overall cost, with all three objectives approximately 40% higher on average than those of EC-MOPSO, indicating limited balance and convergence stability. Overall, EC-MOPSO achieves better convergence and stability, producing a more compact and higher-quality Pareto set. It achieves about 10–40% improvement in average path length and flight time while maintaining stable energy performance, providing a more practical and reliable optimization framework for UAV path planning in emergency rescue missions.

5.1.3. Analysis of HV and Statistical Significance

To systematically evaluate the convergence behavior and solution quality of the algorithms, normalized hypervolume, HV, was adopted as the primary performance indicator. Figure 6 presents the HV convergence trajectories over 200 generations. The results show that EC-MOPSO achieved a rapid increase within the first 40 generations, with HV quickly exceeding 0.65, followed by a slight improvement around the 140th generation, and finally stabilized at approximately 0.73. This demonstrates superior capability in both rapid convergence and sustained optimization. In contrast, NSGA-II converged to about 0.63 at around the 100th generation and then stagnated. SPEA2 exhibited a similar trend, stabilizing near 0.60, SPEA2 exhibited a similar trend, stabilizing around 0.60, while MOPSO performed poorly, with HV remaining around 0.56, showing no significant improvement. MOBCA showed the slowest convergence and lowest HV growth, stabilizing around 0.43 after 150 generations, indicating weak search capability and poor convergence stability. These results indicate that EC-MOPSO not only converges faster but also produces higher-quality solution sets. In emergency rescue scenarios, such early rapid convergence combined with later steady improvement enables the planning module to generate high-quality solutions more quickly, thereby reducing mission preparation time.

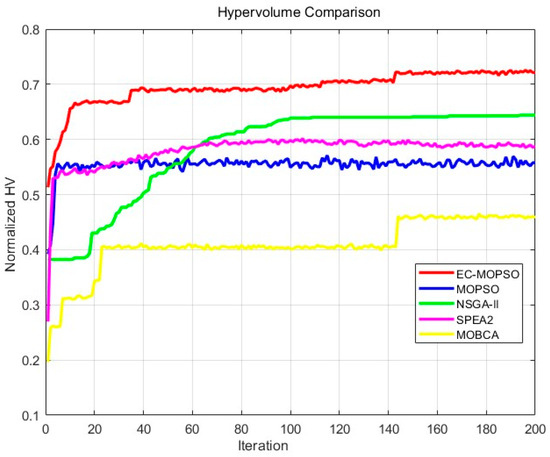
Figure 6. HV variation curves of different algorithms.

To eliminate the influence of randomness, each algorithm was independently executed 30 times under identical environmental conditions, and the hypervolume values were recorded. Table 6 summarizes the mean, extreme, and standard deviation results. EC-MOPSO achieved the highest mean HV value of 0.7270, which was about 30.3%, 17.2%, 22.9%, and 69.0% higher than those of MOPSO, NSGA-II, SPEA2, and MOBCA, respectively. It also obtained the smallest standard deviation of 0.0084, indicating superior performance and strong stability. NSGA-II ranked second with a mean HV of 0.6200, but its larger deviation of 0.0195 suggested weaker robustness and less consistent convergence. SPEA2 reached a mean HV of 0.5913, slightly lower than NSGA-II. MOBCA showed the lowest mean HV (0.4302) and a relatively large standard deviation (0.0229), indicating the weakest convergence efficiency and stability among all tested methods.

Table 6. Normalized HV values.

Algorithm	Maximum Value	Minimum Value	Mean Value	Std.
EC-MOPSO	0.7444	0.7103	0.7270	0.0084
MOPSO	0.5872	0.5224	0.5580	0.0165
NSGA-II	0.6444	0.5589	0.6200	0.0195
SPEA2	0.6316	0.5327	0.5913	0.0282
MOBCA	0.4826	0.3948	0.4302	0.0229

To further compare the robustness and convergence stability of the algorithms, Figure 7 illustrate the HV distributions obtained from 30 independent runs. These two figures reflect the stability and consistency of each algorithm from different perspectives. From the heatmap, EC-MOPSO shows a concentrated bright yellow region (around 0.72), indicating that it consistently achieves high performance across multiple runs. NSGA-II exhibits a slightly wider distribution with moderate fluctuations, while SPEA2 presents a more dispersed blue-green pattern with a generally lower performance level. MOPSO appears in darker blue, reflecting lower average performance. MOBCA occupies the dark-blue area at the bottom of the heatmap, where HV values remain consistently low and vary significantly, indicating the weakest convergence stability and consistency among all algorithms. The boxplot provides a statistical perspective on the HV distribution. In each boxplot, the red line represents the median value, the box corresponds to the interquartile range, the whiskers indicate the typical variability range, and the red “+” symbols mark outliers. As shown in Figure 8, EC-MOPSO has the narrowest box, the highest median, and almost no outliers, suggesting minimal fluctuation and the strongest robustness. NSGA-II and SPEA2 have wider boxes with moderate variability, while MOPSO shows even greater dispersion and lower stability. MOBCA’s box is positioned at the lowest level with long whiskers, reflecting large fluctuations and the weakest robustness. Overall, the heatmap and boxplot jointly demonstrate—both visually and statistically—that EC-MOPSO exhibits significantly better stability and consistency across multiple runs compared with the other algorithms, whereas MOBCA shows the most dispersed performance distribution, indicating poor convergence behavior and low robustness.

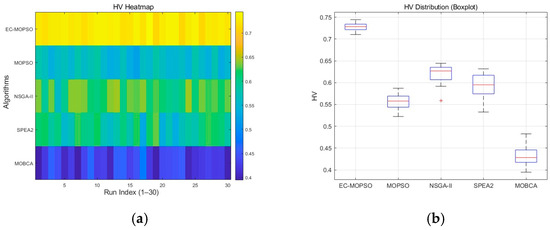
Figure 7. HV distribution diagram of different algorithms. (a) Heatmap. (b) Boxplots.

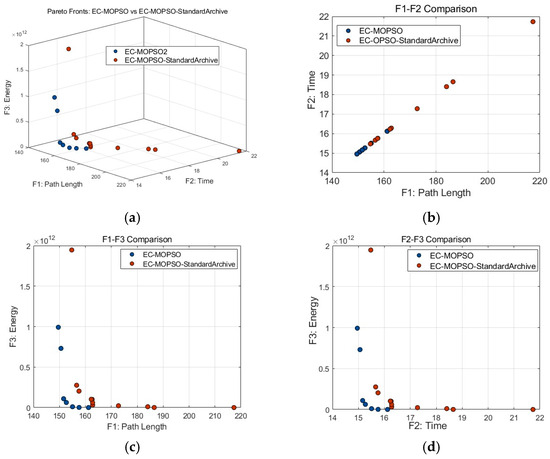
Figure 8. Comparison of Pareto solution sets between EC-MOPSO and EC-MOPSO-Standard Archive. (a) Comparison in three-dimensional objective space. (b) Comparison in the F1–F2 dimension. (c) Comparison in the F1–F3 dimension. (d) Comparison in the F2–F3 dimension.

To verify the statistical significance of these differences, the Wilcoxon rank-sum test was employed. Since multiple pairwise comparisons were involved, Holm’s step-down correction was applied to control the accumulation of Type I errors. This procedure maintains statistical power while effectively suppressing false significance caused by multiple testing. The results are summarized in Table 7, where a check mark denotes a statistically significant difference between two algorithms at the 5% confidence level. The table provides a clear pairwise comparison among EC-MOPSO, MOPSO, NSGA-II, SPEA2, and MOBCA, enabling the identification of which algorithms differ significantly in terms of overall performance. The main benefit of this analysis lies in verifying that the improvements achieved by EC-MOPSO are not random but statistically robust. As shown in Table 7, EC-MOPSO exhibits significant advantages over all four baselines, with Holm-adjusted p-values on the order of ${10}^{-10}$. This confirms that EC-MOPSO’s superiority in convergence, stability, and diversity is statistically validated. Moreover, the significance matrix helps to quantify the reliability of comparisons between algorithms, providing objective evidence that EC-MOPSO delivers consistent and reproducible optimization performance across multiple experimental runs.

Table 7. Significance analysis among different algorithms.

Algorithm	EC-MOPSO	MOPSO	NSGA-II	SPEA2	MOBCA
EC-MOPSO	—	✓	✓	✓	✓
MOPSO	✓	—	✓	✓	✓
NSGA-II	✓	✓	—	✓	✓
SPEA2	✓	✓	✓	—	✓
MOBCA	✓	✓	✓	✓	—

“✓“ indicates a significant difference.

In summary, EC-MOPSO demonstrates overwhelming advantages in the three-dimensional UAV path planning problem. It not only converges rapidly within limited generations but also consistently achieves high-quality solution sets across multiple runs, significantly outperforming the four comparison algorithms. This characteristic is particularly valuable in emergency rescue scenarios, where the ability to quickly generate reliable flight paths can effectively reduce response time and improve mission success rates.

5.2. Ablation Study

To further validate the effectiveness of the proposed EC-MOPSO algorithm, a series of ablation studies were conducted. The purpose of these experiments is to systematically remove or simplify key mechanisms of the algorithm in order to evaluate their individual contributions to overall performance, thereby clarifying their roles and necessity in UAV path planning under complex mountainous environments. Three ablation studies were carried out in this section, focusing, respectively, on the archive management strategy, the adaptive parameter control mechanism, and the path-repair operator. All experiments were conducted under the unified experimental environment and evaluation framework described in Section 4. The normalized hypervolume (HV) was used as the performance indicator, with each configuration independently executed 30 times. Statistical testing at the 5% significance level was performed to ensure the reliability and validity of the results.

5.2.1. Ablation on Archive Management Strategy

As shown in Figure 8, Figure 9 and Figure 10, Figure 8a presents the Pareto fronts of EC-MOPSO and the baseline version using the standard archive strategy. The comparison reveals clear differences across all three objectives. In terms of path length (F1) and flight time (F2), EC-MOPSO achieves average reductions of about 9.9% for both metrics, generating shorter and more efficient trajectories with faster convergence. Regarding energy consumption (F3), although the mean value slightly increases due to a few high-penalty cases, the best energy solution obtained by EC-MOPSO is 22.1% lower than that of the standard-archive version, demonstrating more stable control of energy-intensive maneuvers. Overall, EC-MOPSO forms a smoother and more continuous Pareto front with lower overall dispersion, while the baseline algorithm produces scattered points and several high-energy outliers, indicating weaker convergence and insufficient diversity preservation. In Figure 8b (F1–F2), both algorithms exhibit a similar linear trade-off, but EC-MOPSO dominates the lower-left region, achieving simultaneous reductions in path length and flight time. In Figure 8c (F1–F3), EC-MOPSO maintains shorter paths without causing a nonlinear increase in energy consumption, reflecting higher optimization efficiency and better cost balance. In Figure 8d (F2–F3), EC-MOPSO’s solutions are more compact and concentrated near the ideal corner, whereas the standard-archive version remains widely dispersed with several abnormal points. These results verify that the proposed dominance-archive and crowding-distance pruning mechanisms effectively enhance convergence stability and maintain a well-distributed Pareto front in complex rescue scenarios.

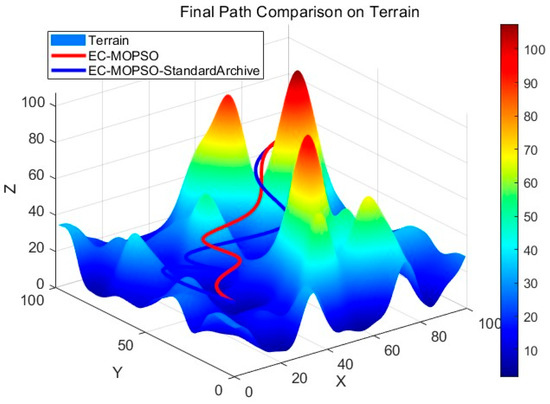
Figure 9. Final path comparison.

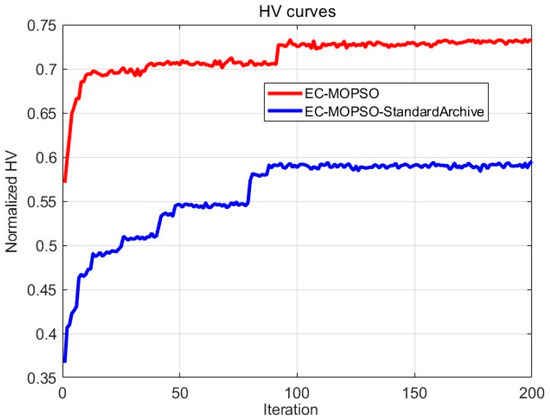
Figure 10. Comparison of HV values.

Figure 9 shows the final paths generated on the mountainous terrain. The trajectory planned by EC-MOPSO is smoother and maintains stable altitude changes when crossing ridges, avoiding sharp peak edges and maintaining safe clearance. Conversely, the baseline method produces paths closer to the ridges, which may introduce potential clearance risks and unnecessary detours, leading to additional time and energy costs. This difference is particularly significant for emergency rescue operations, where unstable or inefficient paths could directly delay mission completion.

Figure 10 compares the normalized HV values across iterations. EC-MOPSO shows a clear quantitative advantage throughout the evolution process. Its normalized HV curve rises rapidly within the first 50 iterations and achieves a distinct step-like increase around iteration 80, reaching near-stable convergence after approximately 120 generations. In contrast, the baseline Standard Archive algorithm exhibits a much slower improvement rate and stabilizes at a significantly lower HV level, reflecting limited exploration capability and weaker convergence efficiency. According to Table 8, EC-MOPSO achieves a mean HV value of 0.7270, which is about 23.2% higher than the baseline’s 0.5902, confirming its superior overall optimization ability and wider coverage of the Pareto front. Moreover, EC-MOPSO maintains a lower standard deviation (0.0084) compared to the baseline (0.0109), representing an improvement of approximately 22.9% in stability. Its HV range (0.7103–0.7444) remains consistently above that of the baseline (0.5730–0.6100), demonstrating both stronger convergence and reduced sensitivity to stochastic variations. These results quantitatively verify that the dominance archive and crowding-distance pruning mechanisms not only accelerate convergence but also enhance robustness and reliability across multiple independent runs.

Table 8. Normalized HV values (EC-MOPSO and EC-MOPSO- Standard Archive).

Algorithm	Maximum Value	Minimum Value	Mean Value	Std.
EC-MOPSO	0.7444	0.7103	0.7270	0.0084
Standard Archive	0.6100	0.5730	0.5902	0.0109

In summary, the ablation study demonstrates that the integration of $\epsilon -$ dominance and crowding distance pruning significantly improves both the quality and stability of the obtained solutions. These mechanisms ensure more comprehensive exploration of the objective space and prevent premature convergence, ultimately providing UAV rescue missions in mountainous environments with faster, safer, and more energy-efficient flight paths.

5.2.2. Ablation on Adaptive Parameter Control Mechanism

To verify the effectiveness of the adaptive parameter adjustment mechanism, we designed a comparative ablation experiment between EC-MOPSO and its ablation version, EC-MOPSO-Fixed Params, in the same mountainous emergency rescue environment. The only difference between the two algorithms lies in whether the inertia weight and learning factors are adaptively adjusted, while all other settings remain identical. The comparison results are shown in Figure 11, Figure 12 and Figure 13. From the overall Pareto front distribution, it is evident that EC-MOPSO achieves superior performance across all three objectives. Specifically, in terms of path length (F1) and flight time (F2), EC-MOPSO achieves reductions of approximately 23.6% compared with the fixed-parameter version, indicating faster convergence and better trajectory coordination. In contrast, in terms of average energy consumption (F3), EC-MOPSO’s mean value increases due to a few penalty-induced trajectories, but its best feasible energy solution is about 25.6% lower, showing that the adaptive mechanism still provides improved control of energy-intensive maneuvers. Overall, its solution set exhibits a more compact and uniform distribution with a clearly lower F3 dimension, forming a complete Pareto front. This indicates that the adaptive mechanism effectively balances the three objectives and avoids high-energy-consumption inferior solutions.

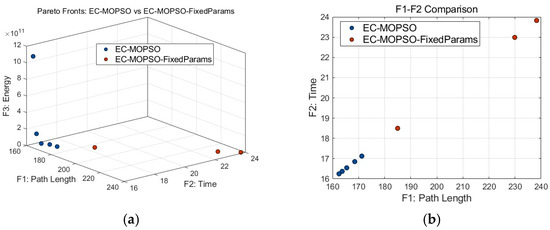
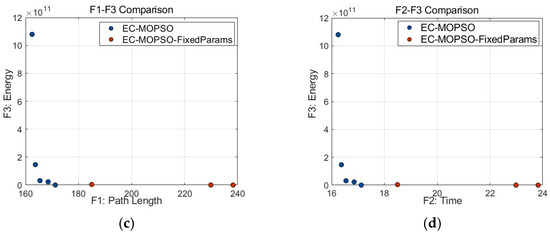
Figure 11. Comparison of Pareto solution sets between EC-MOPSO and EC-MOPSO-Fixed Params. (a) Comparison in three-dimensional objective space. (b) Comparison in the F1–F2 dimension. (c) Comparison in the F1–F3 dimension. (d) Comparison in the F2–F3 dimension.

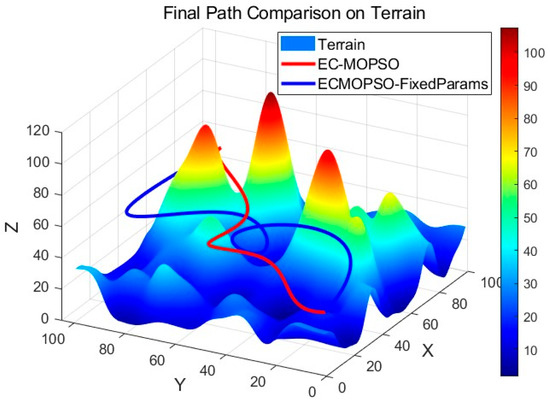
Figure 12. Final path comparison.

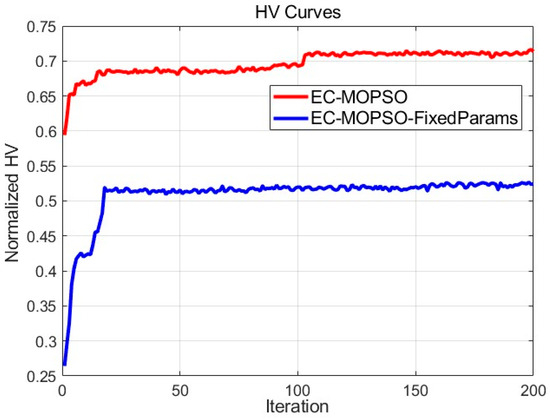
Figure 13. Comparison of HV values.

In contrast, EC-MOPSO-Fixed Params produces scattered solutions with several abnormally high values, reflecting insufficient exploration and weaker convergence. To further analyze the quality of the obtained solutions, we examine the Pareto fronts from multiple dimensions. In Figure 11b (F1–F2), the solutions of EC-MOPSO are concentrated closer to the lower-left corner, demonstrating its ability to simultaneously shorten path length and reduce flight time, thereby achieving stronger objective coordination. The comparison algorithm, however, shows more dispersed solutions, with some points exhibiting excessively long flight times, indicating a lack of global balance under speed constraints and turning penalties. Figure 11c (F1–F3) highlights the superiority of EC-MOPSO in energy optimization. Although its mean energy consumption is slightly higher, the increase in path length does not result in a nonlinear rise in energy cost, suggesting more efficient energy utilization and smoother path planning. Conversely, the Fixed Params version shows large fluctuations in path length, with some shorter paths incurring abnormally high energy costs, reflecting unreasonable climbing or sharp turning maneuvers. In Figure 11d (F2–F3), the solutions of EC-MOPSO are more tightly clustered and biased toward the lower-left corner, indicating that both flight time and energy consumption are effectively controlled. The comparison algorithm again shows scattered solutions, where some are energy-efficient but suffer from excessively long flight times, highlighting an imbalance among objectives. Such imbalance could delay rescue missions or cause energy shortages, thereby reducing mission success rates.

Figure 12 presents the final flight paths generated on the 3D terrain. The trajectories planned by EC-MOPSO are smoother, reasonably bypassing mountains and obstacles while maintaining safe clearance. Particularly in long-distance segments, the proposed algorithm generates fewer turns, reducing energy consumption and improving flight stability. In contrast, the Fixed Params version shows unnecessary detours, which not only increase flight time but also cause additional energy costs, posing risks in real rescue operations.

As shown in Figure 13, EC-MOPSO demonstrates a rapid improvement in HV during the early iterations, followed by a secondary expansion around the 90th generation, and finally stabilizes at approximately 0.72. In contrast, EC-MOPSO-Fixed Params increases slowly and plateaus around 0.52, resulting in an absolute difference of about 0.20, corresponding to a relative improvement of approximately 38%. This clearly indicates that the adaptive parameter adjustment mechanism significantly enhances the convergence speed and overall optimization capability. Meanwhile, EC-MOPSO exhibits a smoother and more stable convergence process with smaller fluctuations. To further eliminate randomness, thirty independent runs were conducted under identical conditions, and the results are summarized in Table 9. EC-MOPSO achieved an average HV of 0.7270, representing an improvement of about 27% compared with the Fixed Params version (0.5713). Regarding extreme values, EC-MOPSO’s HV values range narrowly from 0.7103 to 0.7444, while the Fixed Params version shows a wider range from 0.5301 to 0.6024, indicating both lower mean performance and poorer stability. In terms of standard deviation, EC-MOPSO achieved 0.0084, roughly twice as stable as Fixed Params (0.0160). These results confirm that the adaptive mechanism not only improves optimization performance but also significantly enhances stability and robustness across multiple independent runs.

Table 9. Normalized HV values (EC-MOPSO and EC-MOPSO- Fixed Params).

Algorithm	Maximum Value	Minimum Value	Mean Value	Std.
EC-MOPSO	0.7444	0.7103	0.7270	0.0084
Fixed Params	0.6024	0.5301	0.5713	0.0160

In summary, the ablation experiments clearly demonstrate that adaptive parameter adjustment enables dynamic control of particle search strategies throughout the evolutionary process, improving the balance between exploration and exploitation. In UAV mountainous emergency rescue scenarios, the improved algorithm provides shorter routes, lower energy consumption, and more stable convergence, thereby ensuring both timeliness and reliability of rescue missions.

5.2.3. Ablation on Path-Repair Operator

To verify the effectiveness of the proposed repair operator, we conducted an ablation experiment comparing the complete EC-MOPSO algorithm with its variant that excludes the repair mechanism. Both algorithms were executed under the same mountainous emergency rescue scenario with identical initialization and parameter settings, differing only in whether the repair operator was applied to intermediate waypoints. Each algorithm was independently run 100 times, and the occurrence of terrain collisions was recorded. The results show that EC-MOPSO successfully avoided terrain collisions in all 100 runs, producing consistently smooth trajectories, whereas the variant without the repair operator experienced terrain penetration in 60 out of 100 runs, yielding a collision rate as high as 60%.

These findings clearly demonstrate that the repair operator plays a crucial role in UAV path planning for mountainous emergency rescue. By preventing collisions, maintaining the required safety clearance, and ensuring smooth trajectories, the repair mechanism not only enhances path safety and feasibility but also contributes to shorter routes and reduced energy consumption, thereby providing strong support for the timeliness and reliability of rescue mission.

6. Conclusions

This study investigates the UAV path planning problem in mountainous emergency rescue scenarios by simultaneously optimizing three conflicting objectives: path length, flight time, and energy consumption within a multi-objective optimization framework. An Enhanced Multi-Objective Particle Swarm Optimization (EC-MOPSO) algorithm was proposed, which integrates an adaptive parameter adjustment strategy and an external archive based on dominance and crowding distance. The proposed framework effectively balances convergence and diversity, improves population exploration, and ensures stable and feasible UAV trajectories through a repair operator and B-spline smoothing. Compared with four representative algorithms, namely MOPSO, NSGA-II, SPEA2, and MOBCA, EC-MOPSO achieves significant improvements in both convergence and solution quality. In terms of average path length (F1) and flight time (F2), EC-MOPSO achieves reductions of approximately 39.9%, 15.6%, 10.9%, and 42.3% compared with NSGA-II, MOPSO, SPEA2, and MOBCA, respectively, resulting in a smoother and more continuous Pareto front. The normalized hypervolume results show an average improvement of 23% to 30% and a standard deviation reduction of 20% to 25%, demonstrating enhanced convergence stability and robustness. In the ablation studies, the adaptive parameter mechanism shortens both the average path length and flight time by about 23.6%, and the dominance archive mechanism yields 9.9% improvements in both F1 and F2 while reducing the best-case energy consumption by 22.1% compared with the comparison algorithm. Overall, EC-MOPSO achieves faster convergence, generates more compact and higher-quality Pareto sets, and maintains strong stability across multiple independent runs. However, this study is limited by the assumption of a static and fully known environment, where terrain and obstacles remain unchanged during flight. External factors such as wind disturbance, dynamic obstacles, or communication delays were not considered, which may affect real-world adaptability.

In future work, the proposed framework will be extended to dynamic and uncertain mountainous environments, enabling UAVs to adapt online to moving obstacles, time-varying wind fields, and temporary no-fly zones using real-time environmental perception and predictive terrain modeling. Furthermore, multi-UAV cooperative planning will be explored, including distributed swarm coordination, communication-aware path sharing, and energy-based task allocation strategies to enhance large-scale coverage and mission efficiency. Additional research will focus on integrating online learning and reinforcement-based adaptation to enable continuous parameter self-tuning during flight. Moreover, to further evaluate the generalization capability of the proposed framework, future experiments will consider diverse operational environments, such as urban areas and desert regions, under varying weather conditions including strong winds, temperature fluctuations, and limited visibility. We also plan to incorporate real-world mountainous terrain data, such as digital elevation models (DEMs) obtained from remote sensing or LiDAR sources, to further validate the algorithm’s applicability under actual topographic conditions. These extensions aim to further enhance adaptability, robustness, and decision-making reliability in diverse and time-critical emergency rescue scenarios.