An Optimal Capacity Configuration Method for a Renewable Energy Integration-Transmission System Considering Economics and Reliability
Abstract
1. Introduction
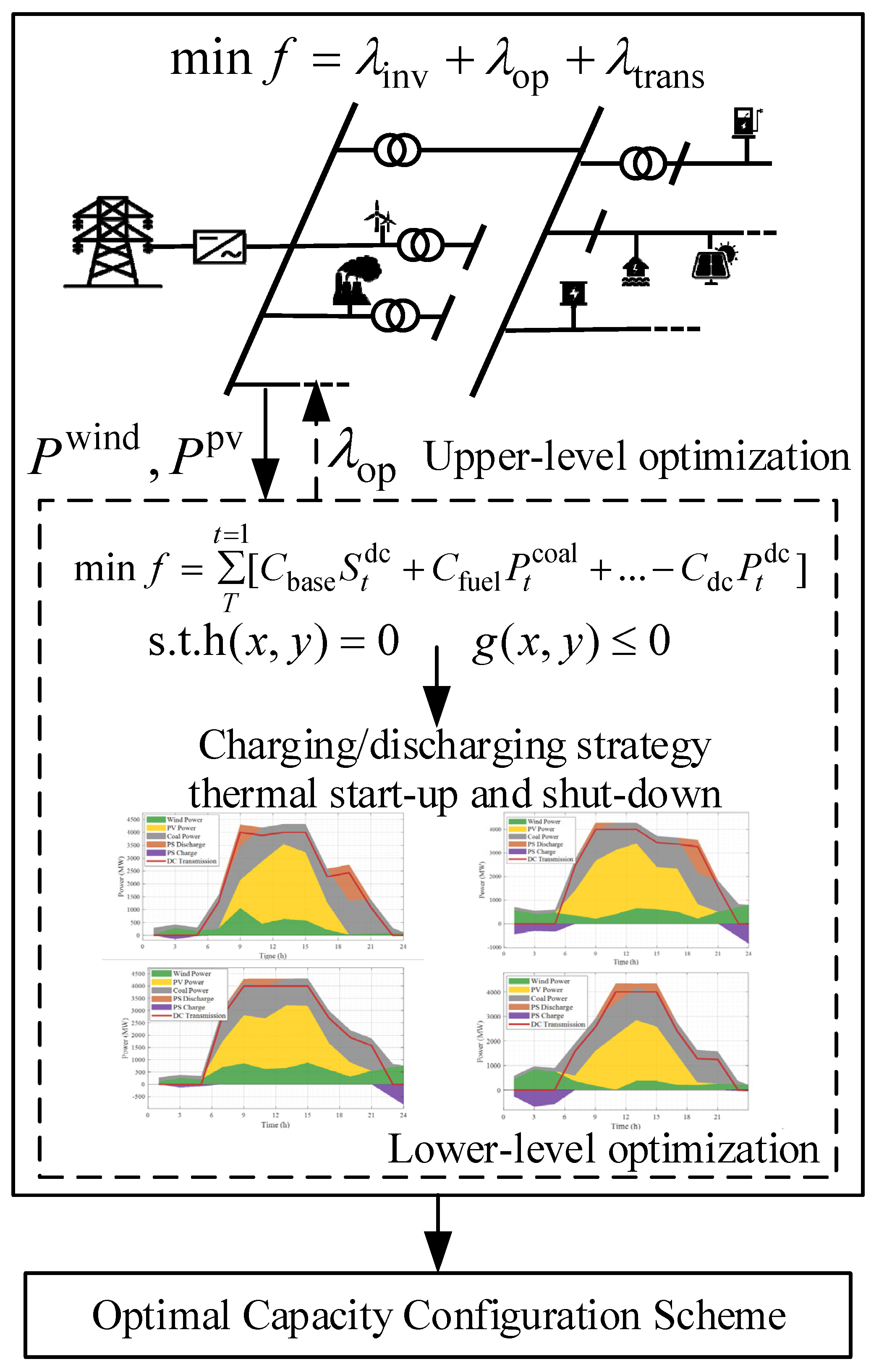
- A bilevel optimization framework is developed to co-optimize long-term capacity expansion and short-term operational scheduling for the IETS. This structure is computationally tractable and accommodates a full-year simulation, effectively accounting for the stochastic nature of wind and PV power. Specifically, the upper level determines the optimal capacity configuration. It achieves this with a single, market-driven objective: minimizing the delivered electricity price. This approach entirely avoids subjective trade-offs between conflicting goals. Meanwhile, the lower level minimizes the annual operational cost through the optimal dispatch of thermal units and pumped-storage operation. This is performed under system power supply reliability and renewable curtailment constraints, achieving an optimal balance between long-term market competitiveness and short-term operational security.
- A high-fidelity operational model is developed. This model precisely captures the operating characteristics of diverse power sources. This ensures that investment decisions are grounded in operational reality, not statistical simplification. The model explicitly represents the intermittency of renewables, the commitment decisions and ramping limits of thermal units, and the complex operational dynamics of the pumped-storage station.
- Carbon emission costs and HVDC utilization constraints are accounted for in the optimal capacity configuration. This approach provides a tool for assessing the interplay between decarbonization policies and the efficient utilization of transmission infrastructure. The model uses a carbon price to discourage fossil fuels. It also enforces a minimum HVDC utilization rate to guarantee transmission asset efficiency. This directly shapes the economic and operational trade-offs that determine the final optimal configuration.
2. The Model of Renewable Energy Generation and Evaluation Indices of Capacity Configuration
2.1. Generation Model of the Power Supply System
2.1.1. Model of Wind Power Generation Output
2.1.2. Model of PV Generation Output
2.1.3. Model of Pumped-Storage Station Output
2.2. Evaluation Indices for Capacity Configuration of IETS
2.2.1. Power Supply Reliability Rate
2.2.2. Renewable Generation Curtailment Rate
3. Configuration of IETS Considering Economics and Reliability
3.1. Framework of Bilevel Optimization Model
3.2. Objective Function of the Model
3.3. Constraints of the Model
- The constraints of system power balance, as given in Equation (15).where denotes the total renewable energy curtailment at time t, comprising curtailed hydro, wind, and PV.
- The output constraints of wind power generation and PV, as given in Equation (16).where and denote the maximum active-power outputs of the wind and PV, respectively.
- The constraints of thermal-unit output and ramp-rate, as given in Equation (17).where and are the maximum upward and downward ramp rates of thermal at time t, respectively.
- The output constraints of the pumped-storage unit, as given in Equation (18).where and are binary variables, taking values of 0 or 1, which indicate whether the pumped-storage unit is operating in generation or pumping mode. These two operational states are mutually exclusive. The unit cannot simultaneously generate and absorb power. When = 1 and = 0, the unit is in the generation mode and discharges stored energy to the grid; conversely, when = 0 and B = 1, it operates in the pumping mode, consuming electricity to store potential energy by elevating water. The combination = = 0 represents the idle state, while = = 1 is physically infeasible and therefore restricted by the constraint . and are the minimum and maximum power outputs in generation mode; and are the minimum and maximum power inputs in pumping mode;
- The water-balance constraints of the pumped-storage unit, as given in Equation (19).where and are the upper-reservoir storage volumes at time t and t + 1, respectively; and are the lower-reservoir storage volumes at time t and t + 1, respectively; and are the flow rates through the pumped-storage units in generation and pumping modes at time t, respectively.
- The initial–final water-level balance constraints of the pumped-storage unit, as given in Equation (20).where and are predefined parameters representing the minimum and maximum operational storage capacity of the upper reservoir. They define the lower and upper bounds for and are measured in cubic meters. and are predefined parameters representing the minimum and maximum operational storage capacity of the downstream reservoir. To ensure the physical safety and operational feasibility of the pumped-storage hydropower station, the stored volume cannot exceed the maximum effective capacity, nor can it fall below the minimum level required for safe operation. is the initial volume at hour 0 and is the water volume in the reservoir at the final hour of the simulation period. This constraint ensures that the water volume at the end of the scheduling horizon is close to its initial level, thereby maintaining the continuity of reservoir operation and avoiding long-term bias in storage utilization.
- The output-to-water conversion efficiency constraints of the pumped-storage unit, as given in Equation (21).where and are the generation and pumping efficiencies of pumped-storage, respectively; is the density of water; and h is the average hydraulic head of the pumped-storage plant.
- The constraints of HVDC export power, as given in Equation (22).where denotes the maximum transmission capacity of the HVDC transmission. In this paper, the power exported via HVDC is delivered in a stepped manner.
- The constraints of HVDC utilization duration, as given in Equation (23).where is a binary variable where = 1 if the HVDC transmission power is adjusted at hour t, and = 0 otherwise. denotes the minimum required duration for which the HVDC power must remain constant. These variables are introduced to represent the operational constraint that large-capacity HVDC systems cannot frequently adjust their power setpoints due to stability and coordination requirements. Equation (22) ensures that the power schedule is allowed to change at most once during the specified minimum adjustment period. Additionally, according to relevant national policies and existing research, the annual utilization duration of the HVDC corridor is set to 4400 h. This value corresponds to an annual utilization rate of approximately 50% (8760 × 0.5 ≈ 4380 h) and is consistent with planning targets reported in the recent literature.
- The constraint of HVDC power ramping, as given in Equation (24).where and denote the maximum upward and downward ramp rates of the HVDC export power, respectively.
- The constraints of and , as given in Equation (25).where denotes the minimum acceptable reliability level, which is set to 0.99 in this study; this constraint ensures that the system’s supplied energy satisfies a minimum reliability requirement. denotes the maximum allowable renewable generation curtailment rate, which is set to 0.05 in this study; this constraint limits the renewable energy curtailment within an acceptable range to enhance energy utilization efficiency.
3.4. Solution Method
4. Case Study
4.1. Analysis of the Lower-Level Optimization Results
4.2. Capacity Configuration Results for IETS Under the Lowest Delivered-Electricity Prices Comparative Analysis
4.3. Impact of HVDC Transmission Hours on Optimal Capacity Configuration and Electricity Price
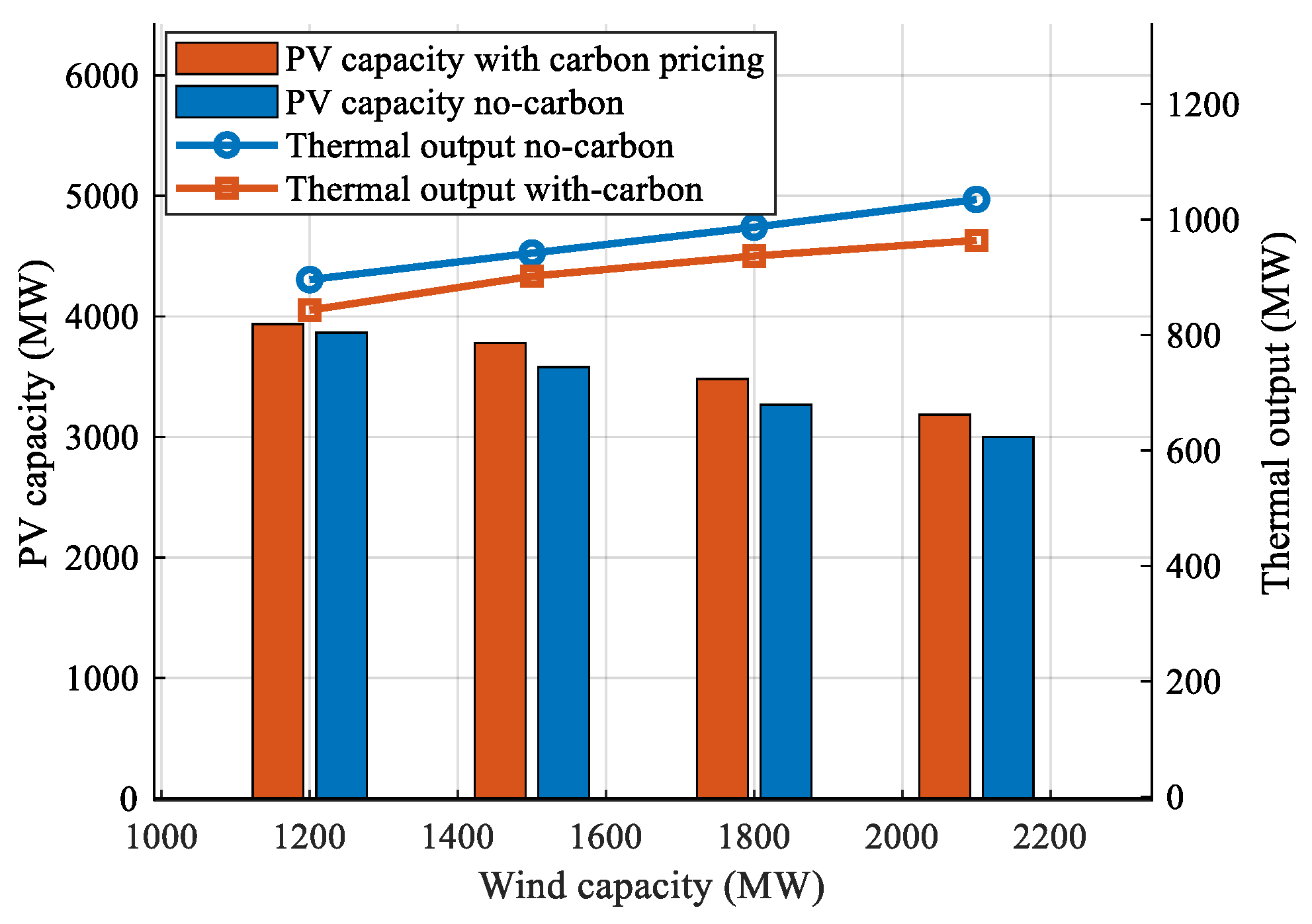
4.4. Carbon-Reduction Benefits Arising from the Imposition of Penalty Costs on Thermal Power Generation
5. Discussion
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| IETS | Integrated Energy Transmission System |
| PV | Photovoltaic |
| HVDC | High-Voltage Direct Current |
| ESS | Energy Storage System |
| DG | Distributed Generation |
| MILP | Mixed-Integer Linear Programming |
| MINLP | Mixed-Integer Nonlinear Programming |
References
- Dou, Z.; Ding, L.; Yan, S. Dynamic Integral-Event-Triggered Control of Photovoltaic Microgrids with Multimodal Deception Attacks. Symmetry 2025, 17, 838. [Google Scholar] [CrossRef]
- Lu, Y.; Wang, H.; Jin, X. An Efficient Traceable and Revocable Access Control Scheme for Smart Grids. Symmetry 2025, 17, 294. [Google Scholar] [CrossRef]
- Huang, Q.; Chen, P.; Zhou, L.; Zhang, H.; Huang, Z.; Wang, Y. Research on Green Construction Evaluation of Power Grid Construction under the Background of Dual Carbon. In Proceedings of the 2022 IEEE 5th International Electrical and Energy Conference (CIEEC), Nanjing, China, 27–29 May 2022. [Google Scholar] [CrossRef]
- Su, B.; Li, Y.; Liu, Z.; Li, K.-J.; Huang, Z.; Song, Y. On the Future of Micro Energy Control Unit (MECU) Integrated Grid. IEEE Trans. Ind. Appl. 2025, 61, 8866–8878. [Google Scholar] [CrossRef]
- Liu, J.; Zhang, W.; Zhou, R.; Zhong, J. Impacts of distributed renewable energy generations on smart grid operation and dispatch. In Proceedings of the IEEE Power and Energy Society General Meeting, San Diego, CA, USA, 22–26 July 2012. [Google Scholar] [CrossRef]
- Kong, L.; Tang, X.; Qi, Z. Study on Modified EMAP Model and Its Application in Collaborative Operation of Hybrid Distributed Power Generation System. In Proceedings of the International Conference on Sustainable Power Generation and Supply (SUPERGEN), Nanjing, China, 6–7 April 2009. [Google Scholar] [CrossRef]
- Liao, H.; Xu, C.; Song, J.; Yu, Y. Green power generation technology for distributed power supply. In Proceedings of the China International Conference on Electricity Distribution (CICED), Guangzhou, China, 10–13 December 2008. [Google Scholar] [CrossRef]
- Liu, B.; Li, M.; Chen, J. Projected waste and recycling potential of China’s photovoltaic industry. Waste Manag. 2025, 191, 264–273. [Google Scholar] [CrossRef]
- Shui, J.; Peng, D.; Song, Y. Optimal Scheduling Strategy of Virtual Power Plant with Carbon Emission and Carbon Penalty Considering Uncertainty of Wind Power and Photovoltaic Power. J. Syst. Simul. 2024, 36, 305–319. [Google Scholar] [CrossRef]
- Zhao, F.; Liu, X.; Zhao, X. Spatiotemporal distribution pattern and analysis of influencing factors of pumped storage power generation in China. J. Energy Storage 2024, 79, 110078. [Google Scholar] [CrossRef]
- Liu, L.-G.; Wei, K.; Ge, X.-N. GIC in Future Large-Scale Power Grids: An Analysis of the Problem. IEEE Electrif. Mag. 2015, 3, 52–59. [Google Scholar] [CrossRef]
- Li, X.; Fang, L. Research on economic dispatch of large power grid based on granular computing. In Proceedings of the 2016 IEEE PES Asia-Pacific Power and Energy Engineering Conference (APPEEC), Xi’an, China, 25–28 October 2016. [Google Scholar] [CrossRef]
- Guo, Z.; Zhang, Y. An enhanced model predictive control method for single-stage three-phase transformerless grid-connected photovoltaic inverter. Int. J. Electr. Power Energy Syst. 2025, 172, 111239. [Google Scholar] [CrossRef]
- Soroudi, A.; Siano, P. Optimal DR and ESS Scheduling for Distribution Losses Payments Minimization Under Electricity Price Uncertainty. IEEE Trans. Smart Grid 2016, 7, 261–272. [Google Scholar] [CrossRef]
- Yu, D.; Tang, R.; Pan, L. Optimal configuration of photovoltaic energy storage in DC distribution network based on interval linear programming. J. Energy Storage 2024, 85, 110981. [Google Scholar] [CrossRef]
- He, Y.; Zuo, Z.; Shen, K.; Gao, J.; Chen, Q.; Liu, J.; Liu, H. Sim-Geometry Modal Decomposition (SGMD)-Based Optimization Strategy for Hybrid Battery and Supercapacitor Energy Storage Frequency Regulation. Symmetry 2025, 17, 1356. [Google Scholar] [CrossRef]
- Xia, P. Study on Optimization Method of Energy and Power Path toward Dual Carbon Goal Considering Electricity-Heat-Hydrogen-Carbon Coupling. In Proceedings of the 2023 5th Asia Energy and Electrical Engineering Symposium (AEEES), Chengdu, China, 23–26 January 2023. [Google Scholar] [CrossRef]
- Bi, R.; Wang, J.; Chen, Y.; Nie, H.; Wang, A.; Liu, Y. Connotation and Functional Analysis of Integrated Energy Generation and Consumption Unit IECU. In Proceedings of the 2024 IEEE 8th Conference on Energy Internet and Energy System Integration (EI2), Shenyang, China, 29 November 2024. [Google Scholar] [CrossRef]
- Zhang, H.; Liu, J.; Zhou, W. Joint optimal operation and bidding strategy of scenic reservoir group considering energy storage sharing. J. Electr. Eng. Technol. 2024, 19, 61–71. [Google Scholar] [CrossRef]
- Das, B.K.; Hassan, R.; Tushar, M.S.H.K.; Zaman, F.; Hasan, M.; Das, P. Techno-economic and environmental assessment of a hybrid renewable energy system using multi-objective genetic algorithm: A case study for remote island in Bangladesh. Energy Convers. Manag. 2021, 230, 113823. [Google Scholar] [CrossRef]
- Li, Y.; Yang, Z.; Li, G. Optimal Scheduling of an Isolated Microgrid With Battery Storage Considering Load and Renewable Generation Uncertainties. IEEE Trans. Ind. Electron. 2019, 66, 1565–1575. [Google Scholar] [CrossRef]
- Zhao, Y.; Liu, Y.; Wu, Z.; Zhang, S.; Zhang, L. Improving Sparrow Search Algorithm for Optimal Operation Planning of Hydrogen-Electric Hybrid Microgrids Considering Demand Response. Symmetry 2023, 15, 919. [Google Scholar] [CrossRef]
- Cheng, J.; He, Y.; Cao, H.; Shi, H.; Hu, J.; Ding, T. Optimal Configuration of Distributed Generation for Improving Voltage Quality Based on Adaptive Weighted PSO. In Proceedings of the 2020 19th International Conference on Harmonics and Quality of Power (ICHQP), Dubai, United Arab Emirates, 6–7 July 2020. [Google Scholar] [CrossRef]
- Yu, D.X.; Zhang, J.H.; Wang, X.Y.; Gao, Y. Optimal capacity allocation of grid-connected wind–solar–storage hybrid generation system. J. Cent. South Univ. 2019, 31, 59–65. [Google Scholar] [CrossRef]
- Xie, X.; Ma, N.; Liu, W. Functions of energy storage in renewable energy dominated power systems: Review and prospect. Proc. CSEE 2023, 43, 158–169. [Google Scholar] [CrossRef]
- Li, P.; Han, P.; Liu, S. Capacity Coordinated Optimization of Battery, Thermal and Hydrogen Storage System for Multi-energy Complementary Power System. In Proceedings of the IEEE Conference on Energy, Beijing, China, 12–14 May 2023. [Google Scholar] [CrossRef]
- Xiao, Y.J.; Yu, Y.J.; Zhang, G.L. Optimal configuration of distributed power generation based on an improved sooty tern optimization algorithm. Power Syst. Prot. Control 2022, 50, 148–155. [Google Scholar] [CrossRef]
- Pesaran, M.H.A.; Nazari-Heris, M.; Mohammadi-Ivatloo, B. A hybrid genetic particle swarm optimization for distributed generation configuration in power distribution networks. Energy 2020, 209, 118218. [Google Scholar] [CrossRef]
- Li, L.; Ji, B.X.; Lim, M.K. Active distribution network operational optimization problem: A multi-objective tuna swarm optimization model. Appl. Soft Comput. 2024, 150, 111087. [Google Scholar] [CrossRef]
- Zhao, Y.; Yang, S.; Liu, S.; Zhang, S.; Zhong, Z. Optimal Economic Research of Microgrids Based on Multi-Strategy Integrated Sparrow Search Algorithm under Carbon Emission Constraints. Symmetry 2024, 16, 388. [Google Scholar] [CrossRef]
- Suman, G.K.; Guerrero, J.M.; Roy, O.P. Optimisation of solar/wind/bio-generator/diesel/battery based microgrids for rural areas: A PSO-GWO approach. Sustain. Cities Soc. 2021, 67, 102723. [Google Scholar] [CrossRef]
- Gholizadeh-Roshanagh, R.; Zare, K.; Marzband, M. An A-Posteriori Multi-Objective Optimization Method for MILP-Based Distribution Expansion Planning. IEEE Access 2020, 8, 60279–60292. [Google Scholar] [CrossRef]
- Liu, C.; Lee, C.; Chen, H.; Mehrotra, S. Stochastic Robust Mathematical Programming Model for Power System Optimization. IEEE Trans. Power Syst. 2016, 31, 821–822. [Google Scholar] [CrossRef]
- Poncelet, K.; Höschle, H.; Delarue, E.; Virag, A.; D’haeseleer, W. Selecting Representative Days for Capturing the Implications of Integrating Intermittent Renewables in Generation Expansion Planning Problems. IEEE Trans. Power Syst. 2017, 32, 1936–1948. [Google Scholar] [CrossRef]



| Items | Values |
|---|---|
| Thermal power installations | 1320 MW |
| Thermal minimum technical output | 10% |
| Thermal unit ramp rate | 80% h−1 |
| Pumped-storage installed installations | 1400 MW |
| HVDC transmission capacity | 4000 MW |
| Unit investment cost ci (wind/PV/thermal/pumped-storage) | 4.00/3.30/4.00/7.85 million CNY MW−1 |
| Discount rate r (wind–solar–thermal/pumped-storage) | 8%/6.5% |
| Lifetime n (wind–solar–thermal/pumped-storage) | 20 years/40 years |
| Coal fuel cost Cfuel | 130 CNY·MWh−1 |
| Curtailment penalty cost Ccurt | 200 CNY·MWh−1 |
| Carbon cost per ton | 70 CNY·tCO2−1 |
| Carbon emission factor | 0.5 tCO2·MWh−1 |
| Method | Wind Power Capacity (MW) | PV Capacity (MW) | Lowest Price (CNY MWh−1) | HVDC-Exported Energy (Billion kWh) | Thermal Output (MW) | fRPS | fAEP |
|---|---|---|---|---|---|---|---|
| M1 | 1200 | 3865 | 0.3788 | 17.577 | 896 | 99.29% | 1.24% |
| M2 | 4279 | 0.3831 | 18.214 | 931 | 99.34% | 1.71% | |
| M1 | 1500 | 3580 | 0.3826 | 17.592 | 942 | 99.32% | 1.62% |
| M2 | 4064 | 0.3881 | 18.230 | 967 | 99.38% | 2.13% | |
| M1 | 1800 | 3265 | 0.3866 | 17.606 | 987 | 99.35% | 2.07% |
| M2 | 3874 | 0.3939 | 18.244 | 1012 | 99.39% | 2.39% | |
| M1 | 2100 | 3000 | 0.3908 | 17.622 | 1035 | 99.39% | 2.23% |
| M2 | 3713 | 0.4001 | 18.261 | 1052 | 99.43% | 2.51% |
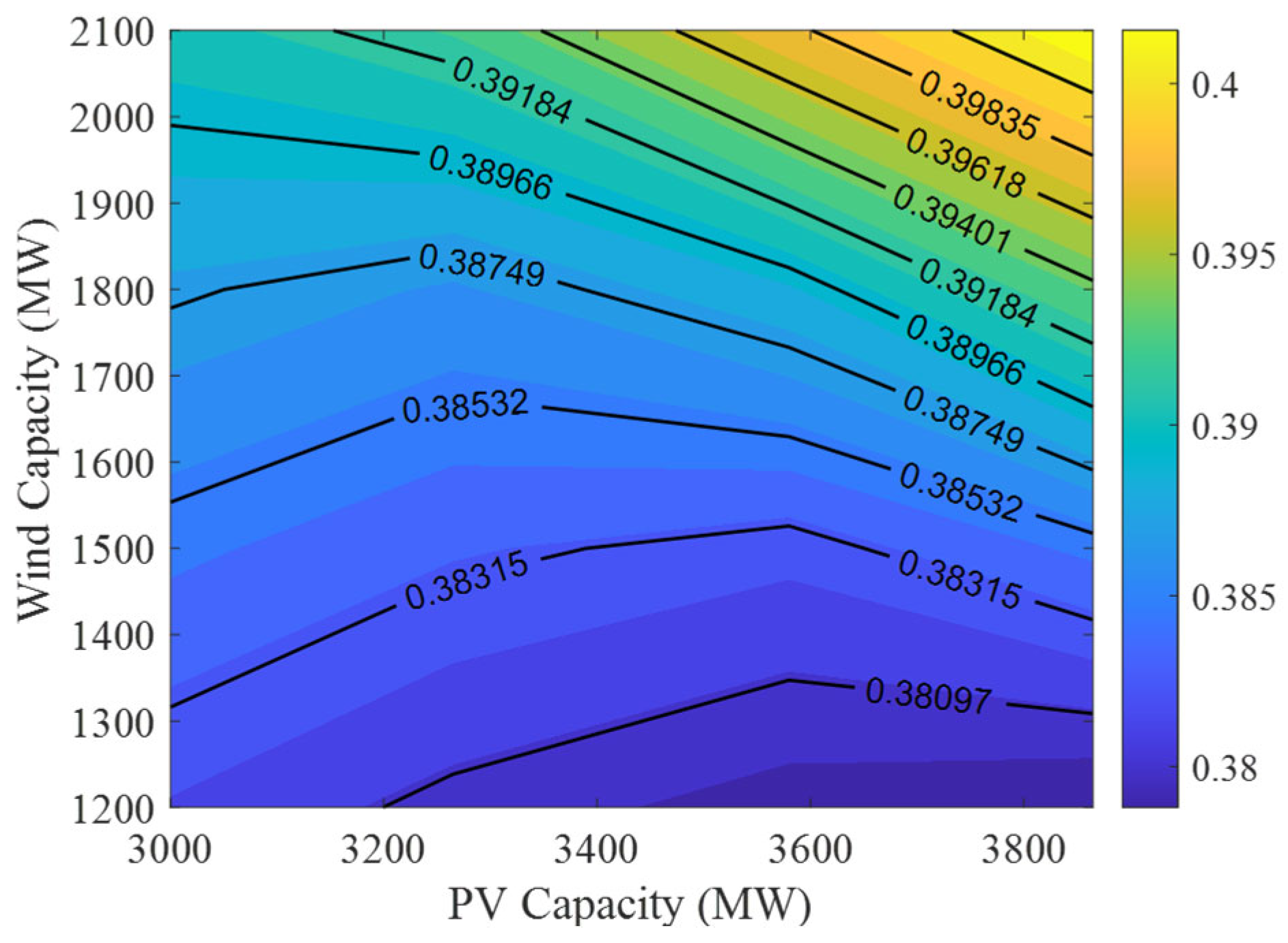
| Wind Power Capacity (MW) | PV Capacity (MW) | λinv (CNY MWh−1) | λop (CNY MWh−1) | λtrans (CNY MWh−1) | λtotal (CNY MWh−1) |
|---|---|---|---|---|---|
| 1200 | 3865 | 0.2564 | 0.0587 | 0.0637 | 0.3788 |
| 3580 | 0.2485 | 0.0672 | 0.0637 | 0.3794 | |
| 3265 | 0.2398 | 0.0771 | 0.0637 | 0.3806 | |
| 3000 | 0.2324 | 0.0860 | 0.0637 | 0.3921 | |
| 1500 | 3865 | 0.2665 | 0.0546 | 0.0637 | 0.3848 |
| 3580 | 0.2586 | 0.0603 | 0.0637 | 0.3826 | |
| 3265 | 0.2499 | 0.0700 | 0.0637 | 0.3835 | |
| 3000 | 0.2425 | 0.0786 | 0.0637 | 0.3848 | |
| 1800 | 3865 | 0.2766 | 0.0534 | 0.0637 | 0.3937 |
| 3580 | 0.2687 | 0.0565 | 0.0637 | 0.3889 | |
| 3265 | 0.2600 | 0.0629 | 0.0637 | 0.3866 | |
| 3000 | 0.2526 | 0.0714 | 0.0637 | 0.3877 | |
| 2100 | 3865 | 0.2867 | 0.0523 | 0.0637 | 0.4027 |
| 3580 | 0.2788 | 0.0555 | 0.0637 | 0.3980 | |
| 3265 | 0.2701 | 0.0588 | 0.0637 | 0.3926 | |
| 3000 | 0.2627 | 0.0644 | 0.0637 | 0.3908 |
| HVDC Transmission Utilization (h) | PV Capacity (MW) | Lowest Price (CNY MWh−1) | HVDC-Exported Energy (Billion kWh) | fRPS | fAEP |
|---|---|---|---|---|---|
| 4000 | 2850 | 0.3752 | 16.650 | 99.34% | 2.12% |
| 4200 | 3080 | 0.3813 | 17.128 | 99.35% | 2.09% |
| 4400 | 3265 | 0.3866 | 17.606 | 99.35% | 2.07% |
| 4600 | 3520 | 0.3955 | 18.084 | 99.37% | 2.04% |
| 4800 | 3785 | 0.4038 | 18.562 | 99.38% | 2.00% |
| 5000 | 3975 | 0.4090 | 19.871 | 99.38% | 1.98% |
| Wind Power Capacity (MW) | PV Capacity (MW) | Lowest Price (CNY MWh−1) | HVDC-Exported Energy (Billion kWh) | Thermal Output (MW) | fRPS | fAEP |
|---|---|---|---|---|---|---|
| 1200 | 3935 | 0.3933 | 17.478 | 843 | 99.24% | 0.97% |
| 1500 | 3780 | 0.3973 | 17.493 | 902 | 99.28% | 1.16% |
| 1800 | 3480 | 0.4014 | 17.507 | 937 | 99.35% | 1.43% |
| 2100 | 3185 | 0.4056 | 17.521 | 964 | 99.37% | 1.72% |
(CNY·tCO2−1) | PV Capacity (MW) | Lowest Price (CNY MWh−1) | Thermal Output (MW) | fRPS | fAEP |
|---|---|---|---|---|---|
| 50 | 3420 | 0.3972 | 951 | 99.35% | 1.62% |
| 60 | 3455 | 0.3994 | 944 | 99.35% | 1.52% |
| 70 | 3480 | 0.4014 | 937 | 99.35% | 1.43% |
| 80 | 3510 | 0.4035 | 929 | 99.34% | 1.33% |
| 90 | 3540 | 0.4053 | 922 | 99.34% | 1.24% |
| 100 | 3565 | 0.4075 | 915 | 99.34% | 1.15% |
(tCO2·MWh−1) | PV Capacity (MW) | Lowest Price (CNY MWh−1) | Thermal Output (MW) | fRPS | fAEP |
|---|---|---|---|---|---|
| 0.3 | 3395 | 967 | 0.3950 | 99.35% | 1.75% |
| 0.4 | 3440 | 944 | 0.3985 | 99.35% | 1.52% |
| 0.5 | 3480 | 937 | 0.4014 | 99.35% | 1.43% |
| 0.6 | 3520 | 925 | 0.4042 | 99.34% | 1.38% |
| 0.7 | 3565 | 921 | 0.4071 | 99.34% | 1.26% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sha, Z.; Cui, C.; Wang, Z.; Yu, F.; Yin, S.; Yang, Z.; Cao, C.; Huang, X.; Liu, Z. An Optimal Capacity Configuration Method for a Renewable Energy Integration-Transmission System Considering Economics and Reliability. Symmetry 2025, 17, 1880. https://doi.org/10.3390/sym17111880
Sha Z, Cui C, Wang Z, Yu F, Yin S, Yang Z, Cao C, Huang X, Liu Z. An Optimal Capacity Configuration Method for a Renewable Energy Integration-Transmission System Considering Economics and Reliability. Symmetry. 2025; 17(11):1880. https://doi.org/10.3390/sym17111880
Chicago/Turabian StyleSha, Zhicheng, Canyu Cui, Zhuodi Wang, Fei Yu, Shujian Yin, Zhishuo Yang, Chuanyu Cao, Xiaohan Huang, and Zhijie Liu. 2025. "An Optimal Capacity Configuration Method for a Renewable Energy Integration-Transmission System Considering Economics and Reliability" Symmetry 17, no. 11: 1880. https://doi.org/10.3390/sym17111880
APA StyleSha, Z., Cui, C., Wang, Z., Yu, F., Yin, S., Yang, Z., Cao, C., Huang, X., & Liu, Z. (2025). An Optimal Capacity Configuration Method for a Renewable Energy Integration-Transmission System Considering Economics and Reliability. Symmetry, 17(11), 1880. https://doi.org/10.3390/sym17111880





