A Robust Lagrangian Implicit Material Point Method for Accurate Large-Deformation Analysis
Abstract
1. Introduction
2. Traditional UL Formulation
Spatial Discretization of Equilibrium Equation for Traditional MPM
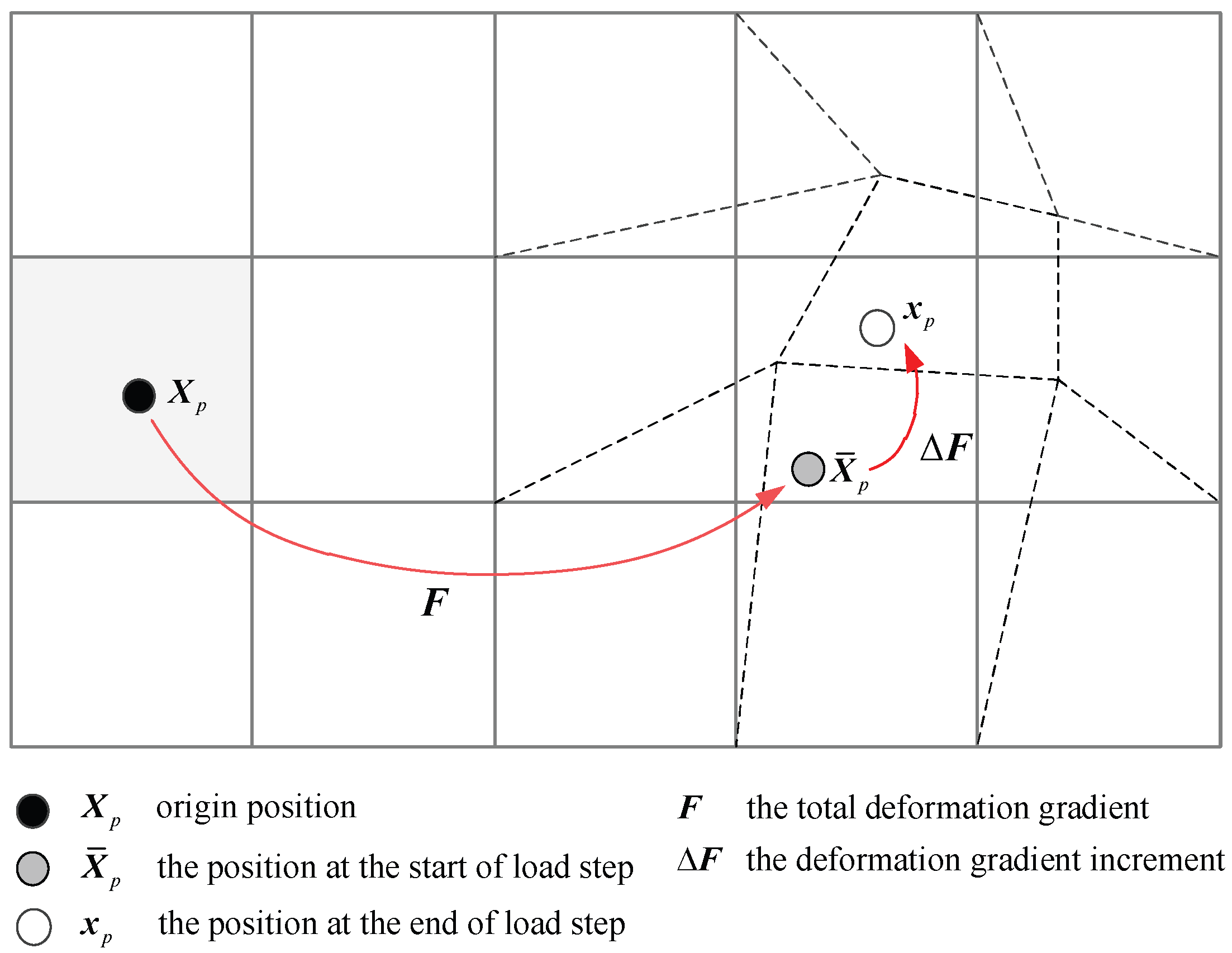
3. The Proposed Lagrangian Formulation
3.1. Equilibrium Equation for Proposed MPM
3.2. Spatial Discretization of Equilibrium Equation
4. Algorithm Implementation
| Algorithm 1 Implicit MPM computational framework (a load step process) | |
| 1. | Initialization stage |
| 1.1 | The motion and status variables of particles are initialized and the information is reset on the nodes |
| 1.2 | Calculate the number of nodes in the background grid occupied by each particle and store its number |
| 1.3 | The external load are mapped to the corresponding nodes |
| 2. | Updated Lagrangian stage |
| 2.1 | Loop iteration |
| 2.2 | Compute the linear and non-linear strain–displacement matrix BL and BNL, in each particle |
| 2.3 | Compute the material stiffness matrix and the geometry stiffness matrix |
| 2.4 | Solve governing equation |
| 2.5 | The increment deformation gradient, strain, and stress of each particle is evaluated |
| 2.6 | The internal force is updated by the increment stress |
| 2.7 | Compute residual vector Determine whether convergence or the number of iterations exceeds the allowed value |
| 2.8 | End Loop |
| 3. | Convection stage |
| 3.1 | Update volume of particles |
| 3.2 | Update position of particles |
- Remark 1.
- Remark 2.
- Remark 3.
5. Numerical Examples
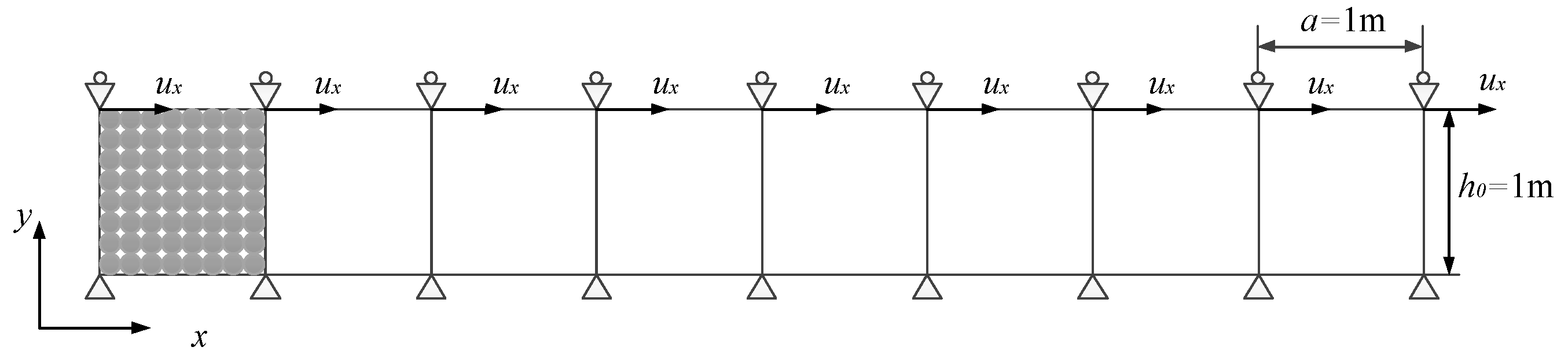
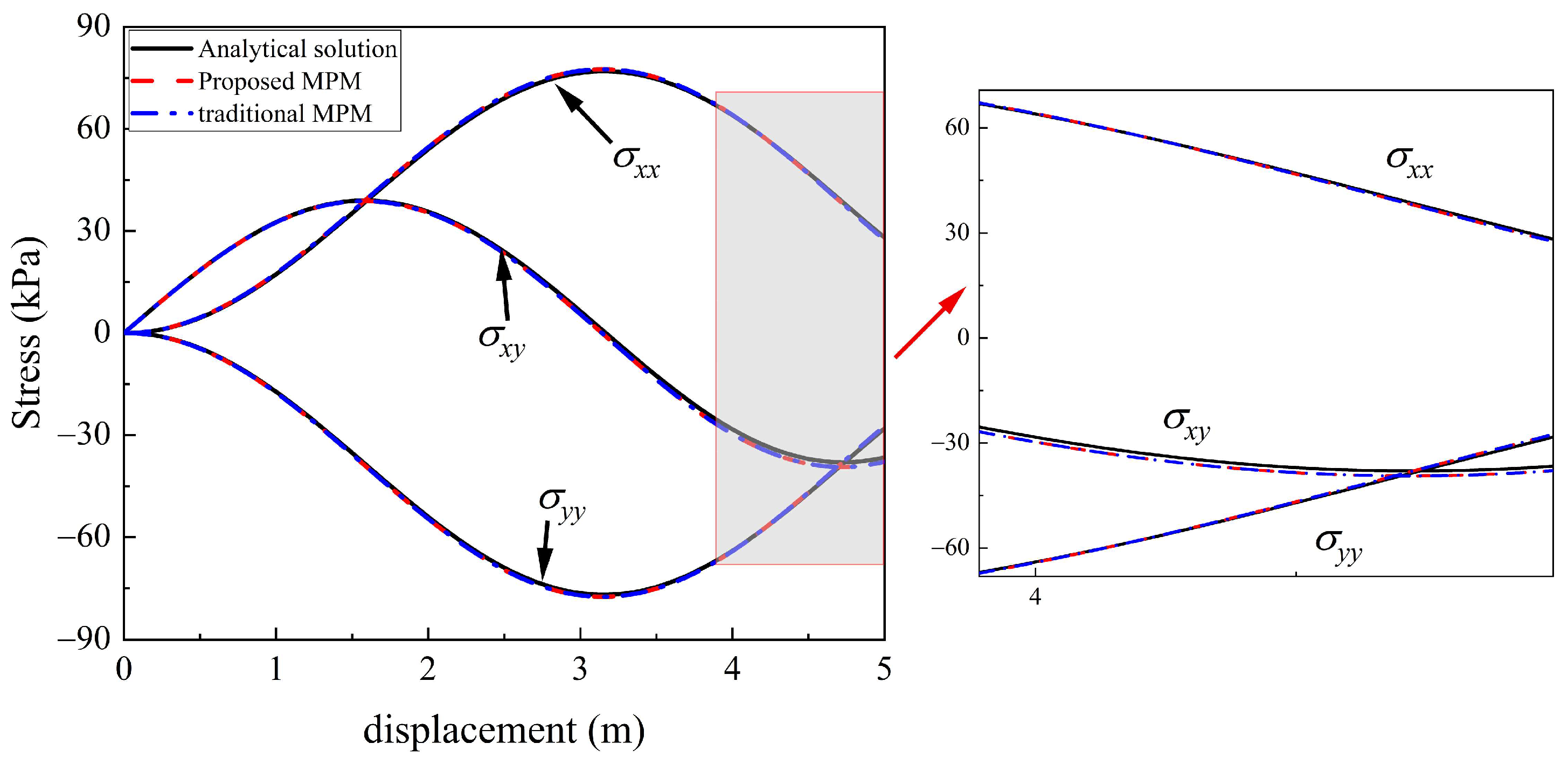
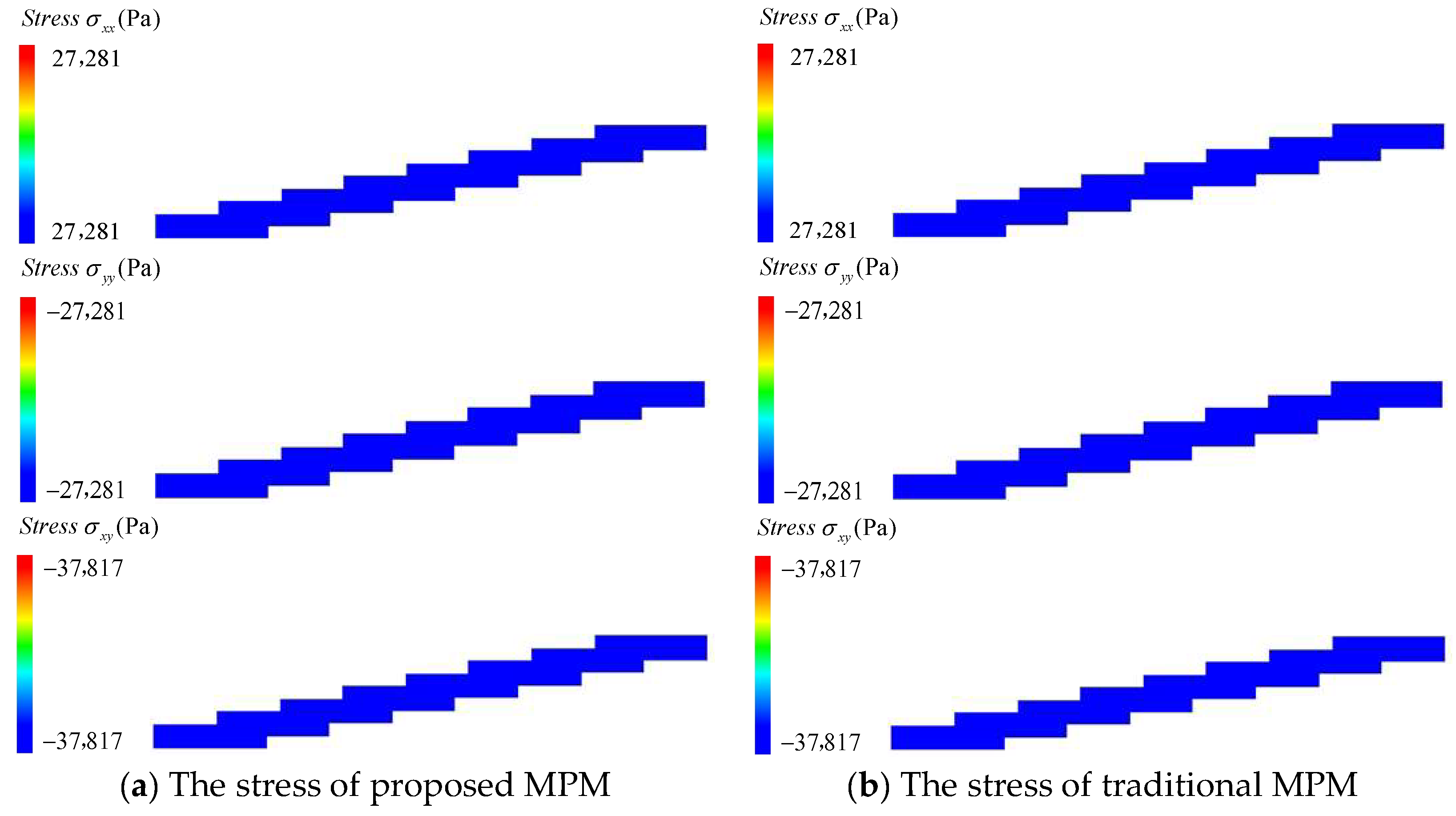
5.1. Simple Shear
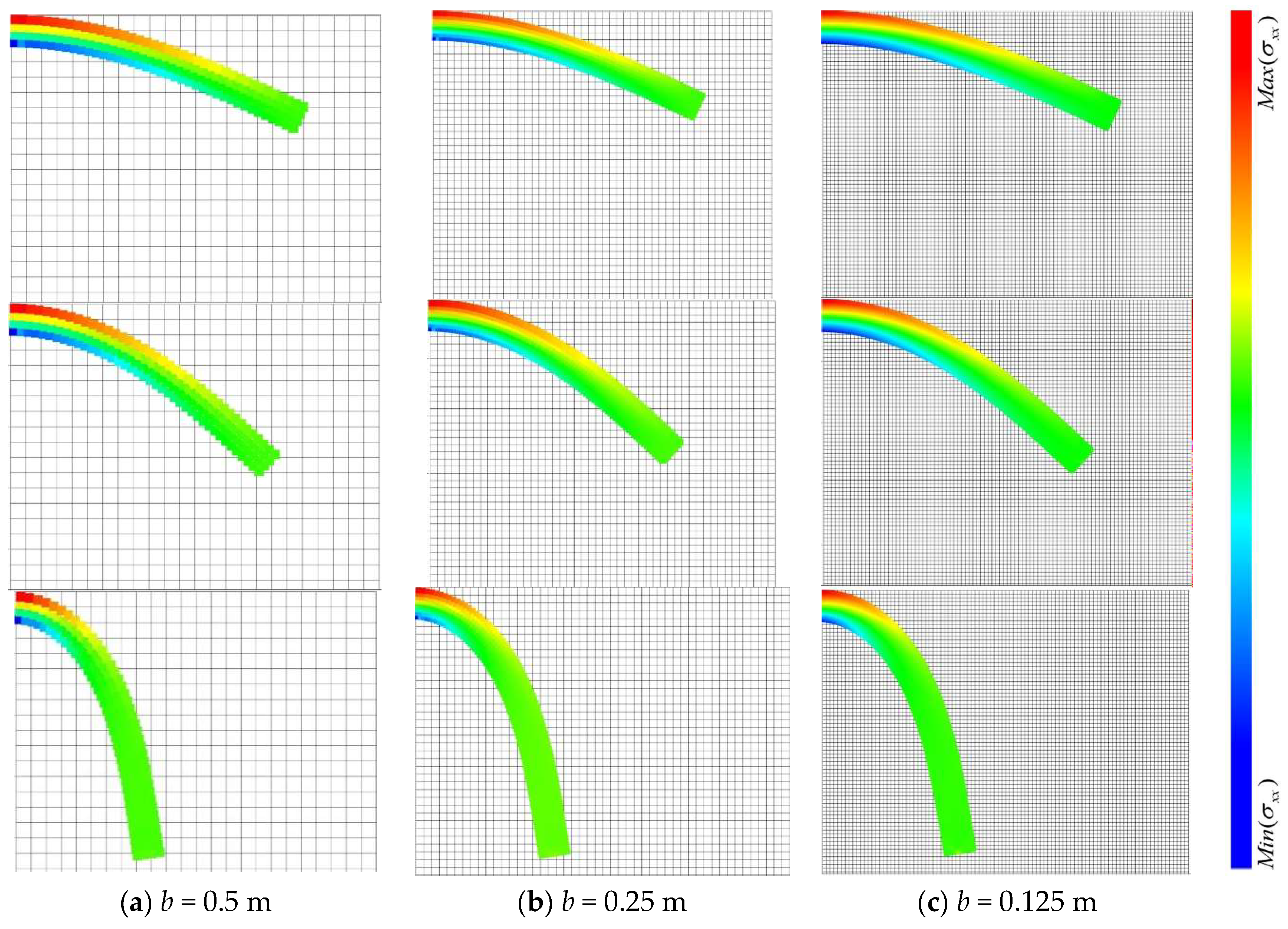
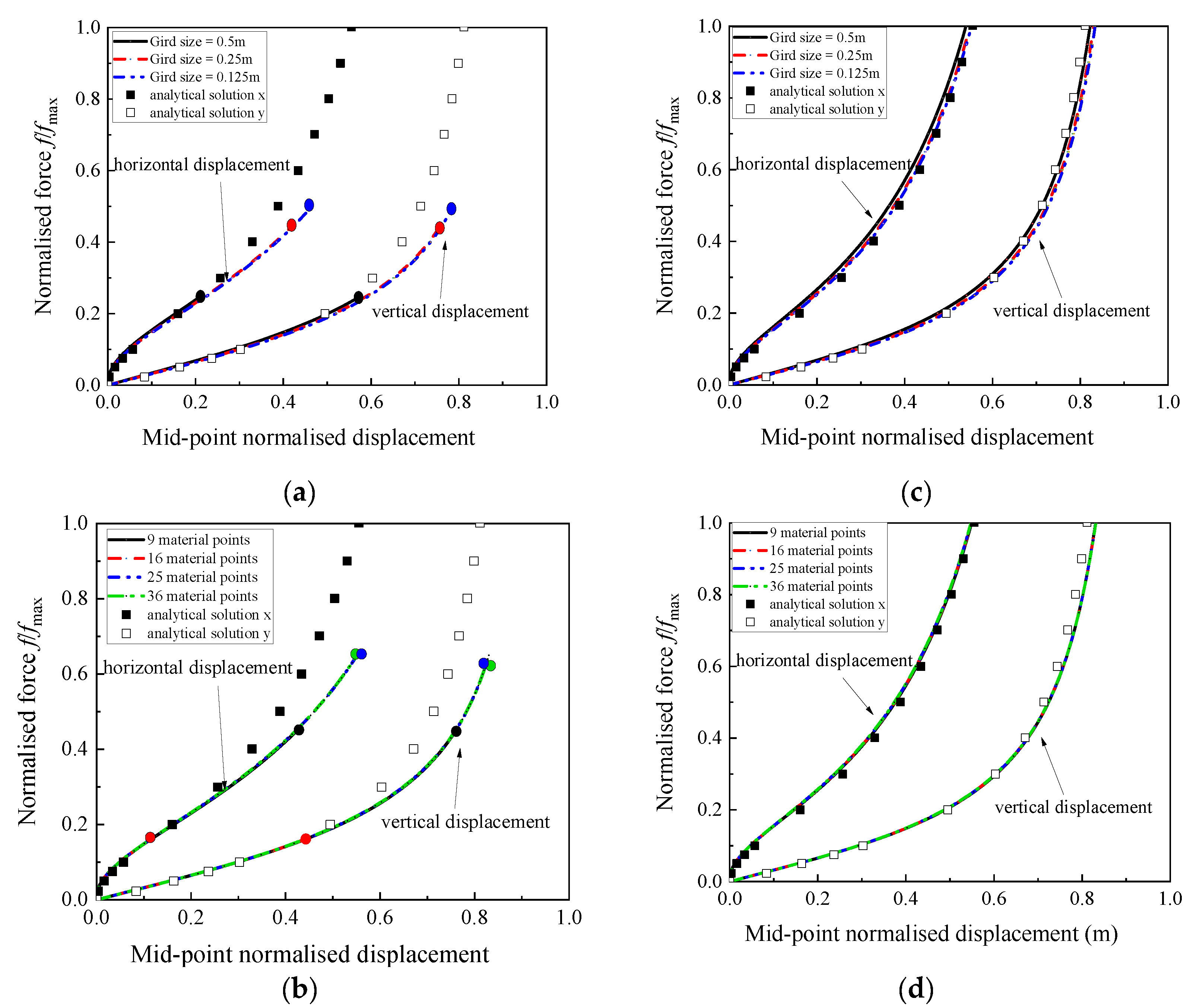
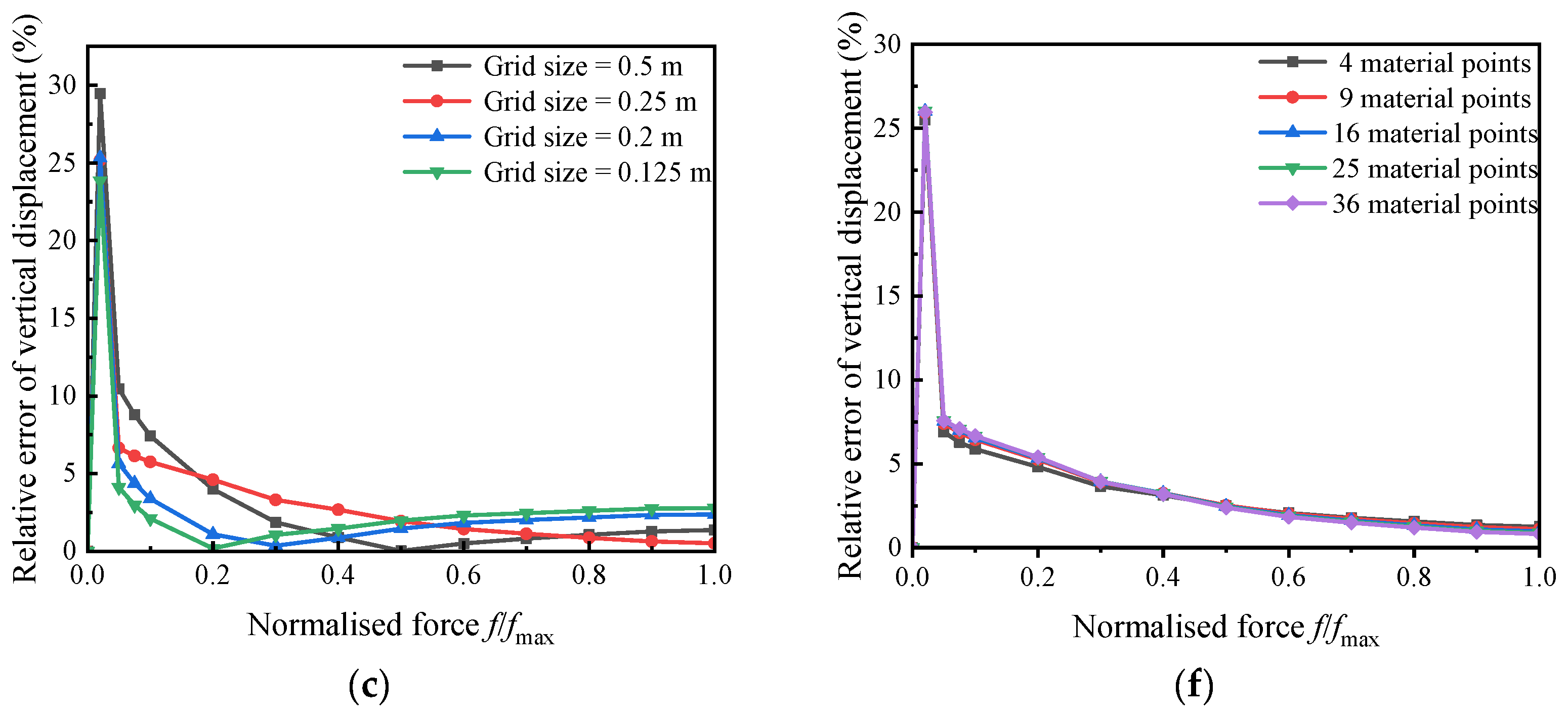
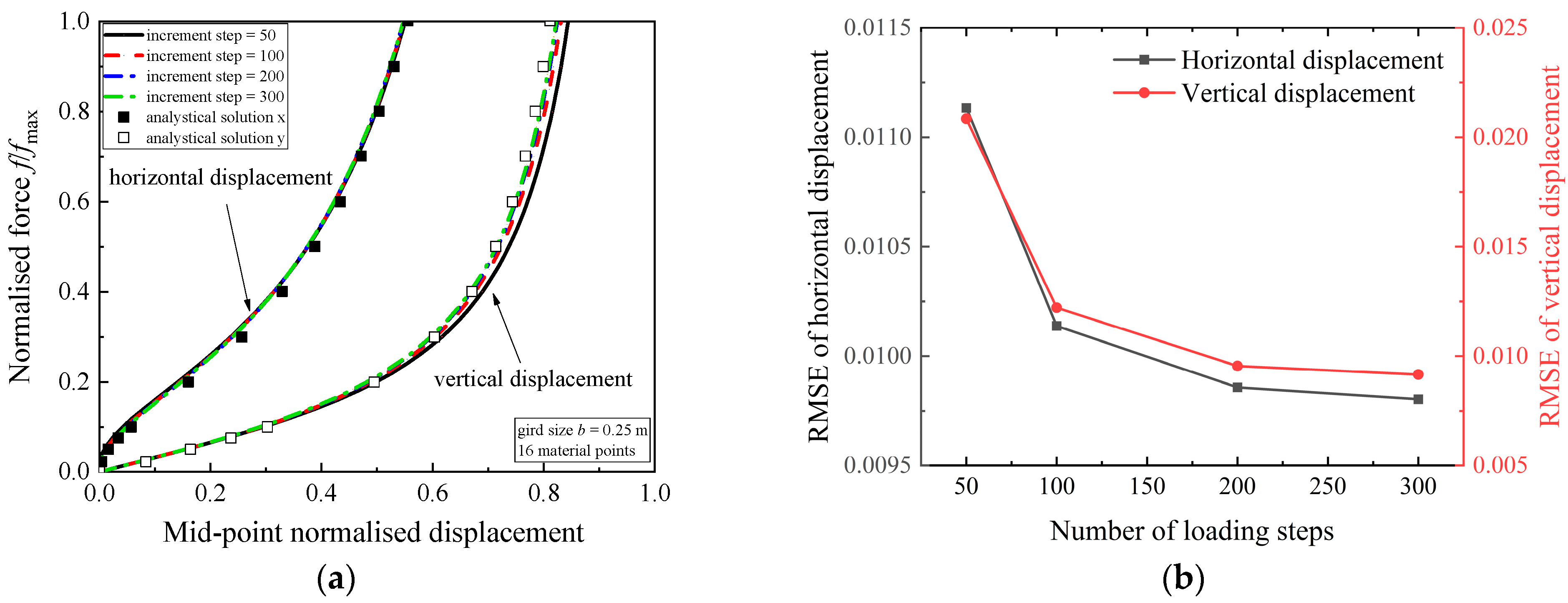
5.2. Elastic Cantilever Beam
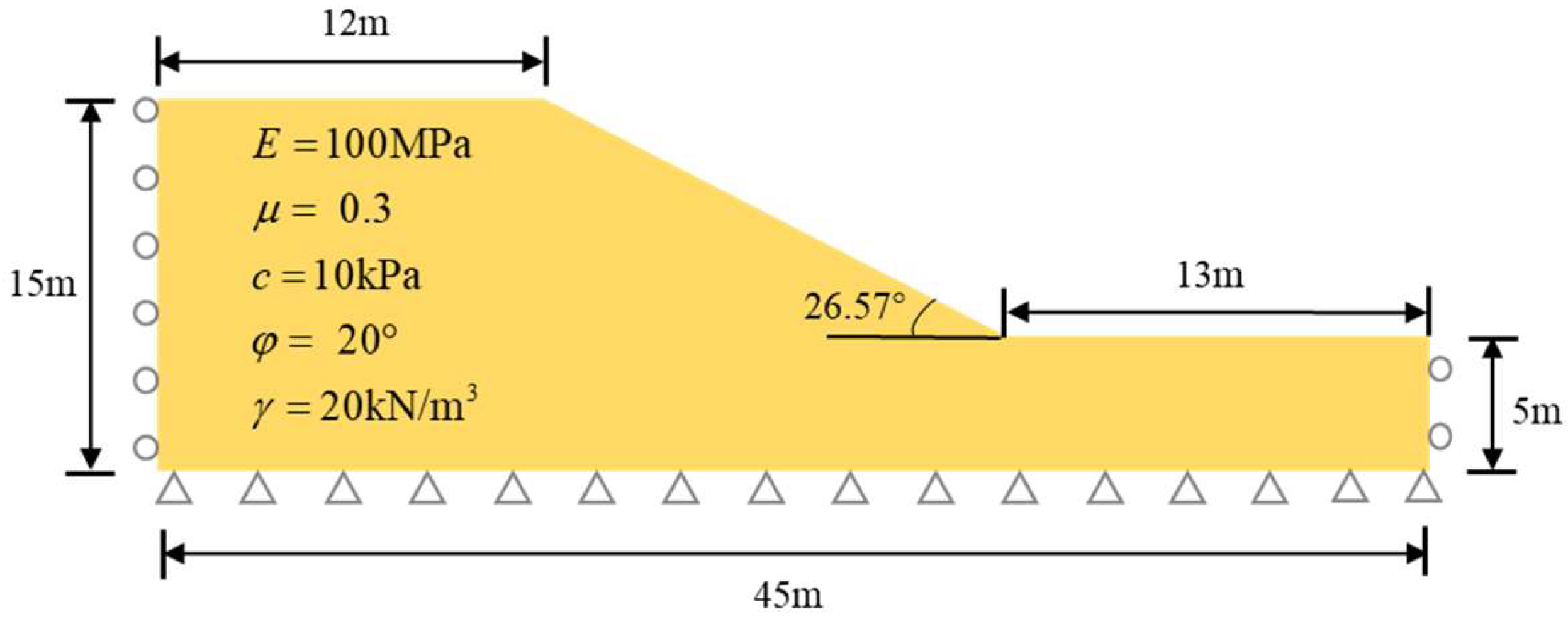
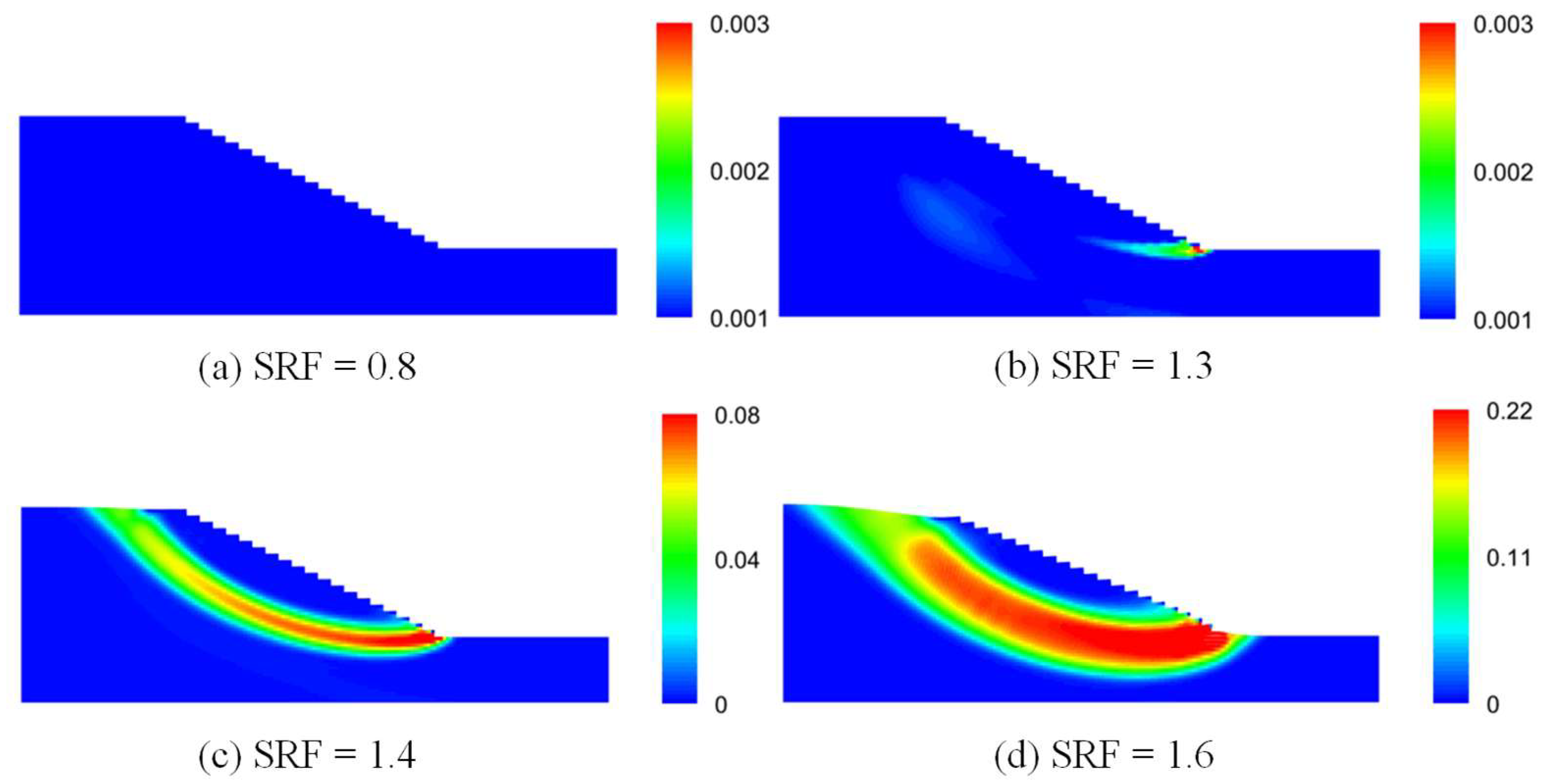
5.3. Slope Stability Analysis
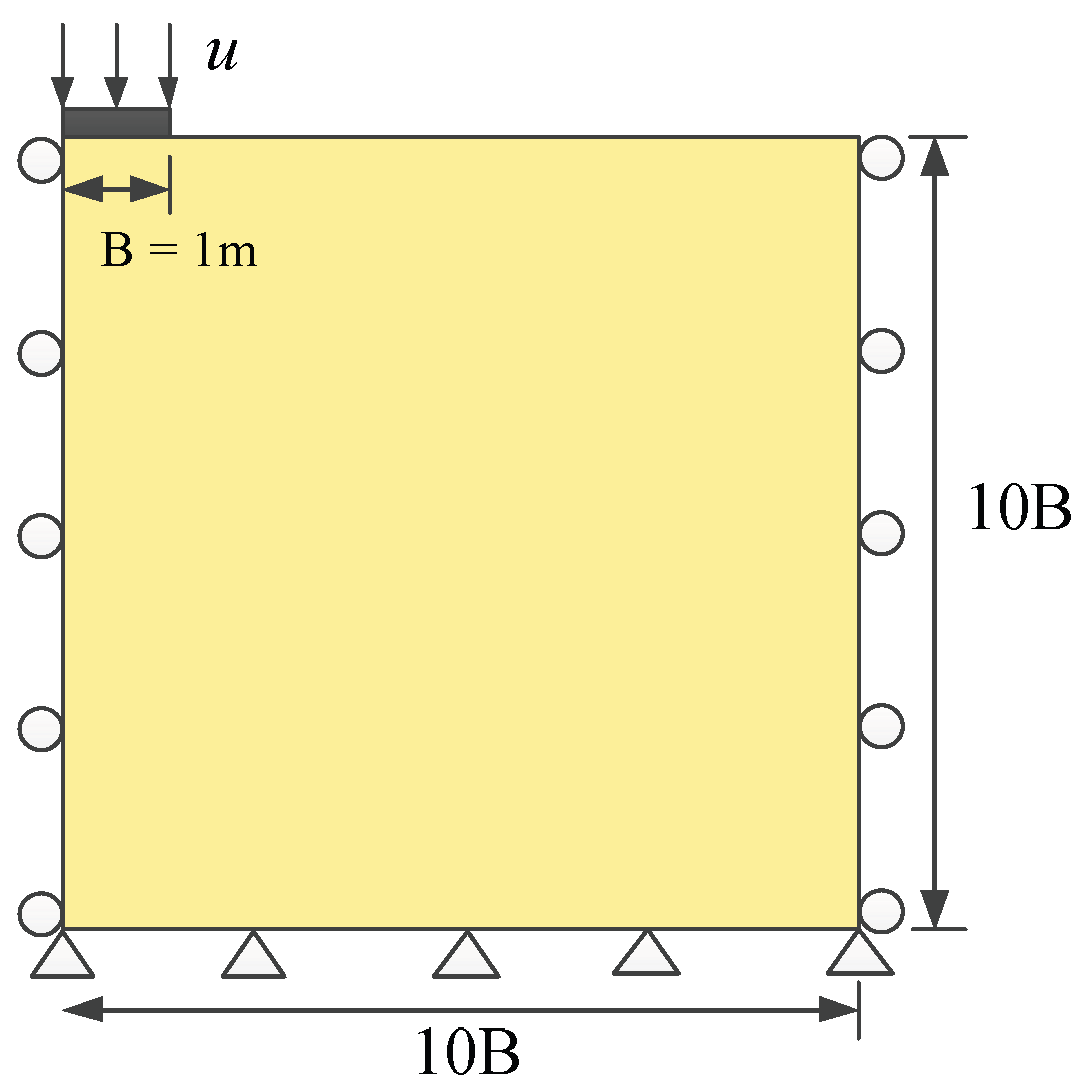
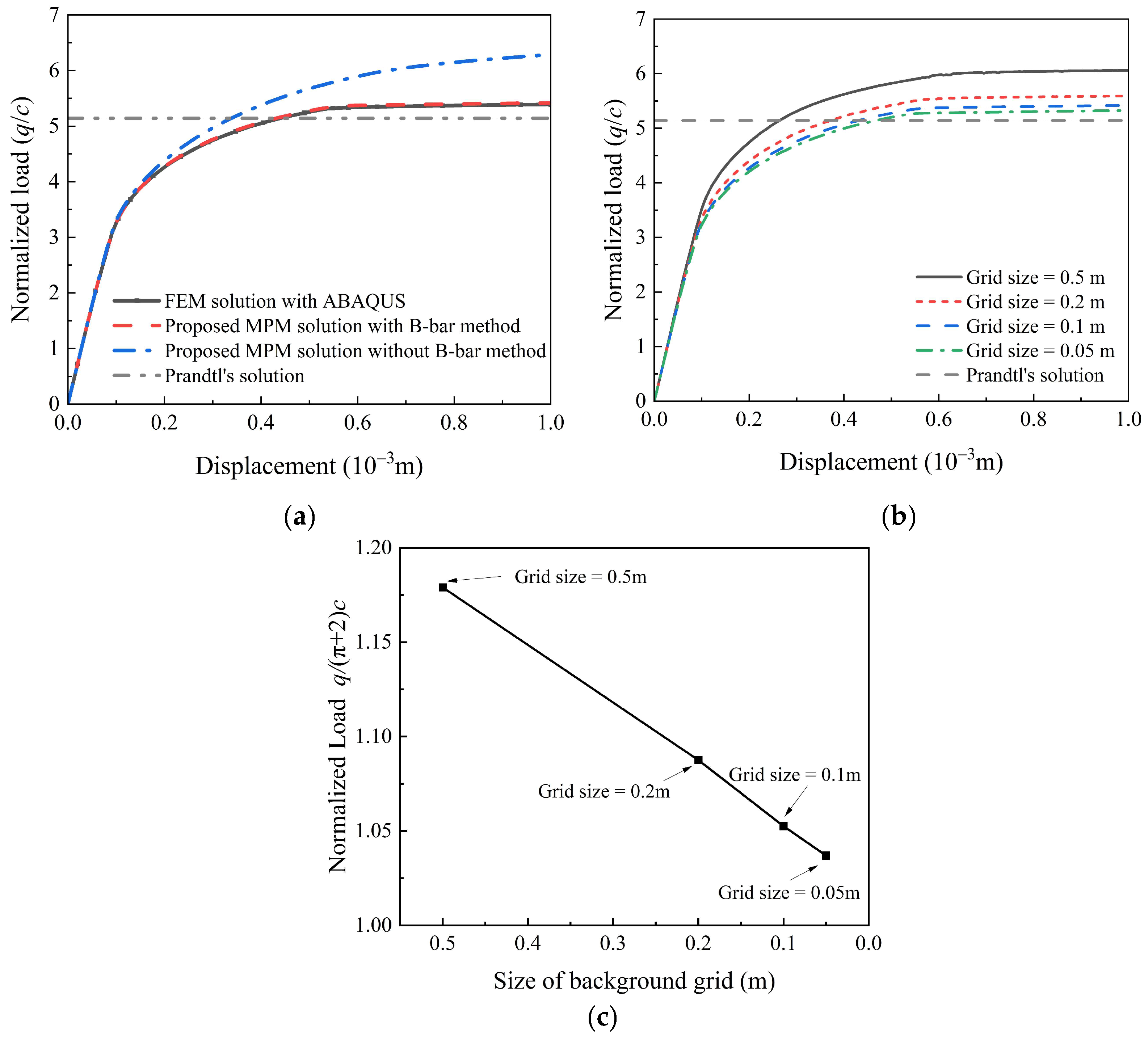
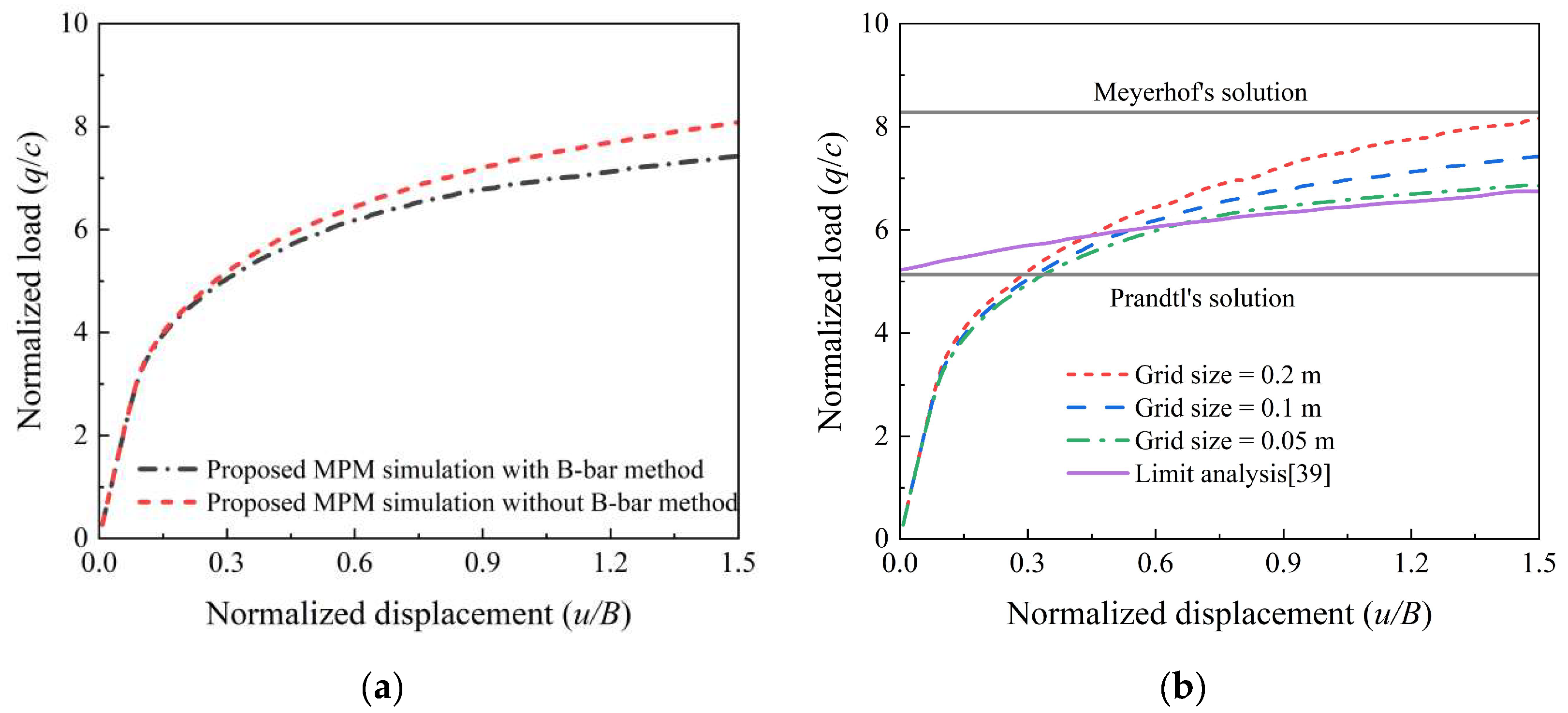
5.4. Strip Footing on Undrained Soil
- Small deformation;
- 2.
- Large deformation;
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| Symbol | Description |
| The second PK stress tensor at time t + Δt | |
| δε | The strain tensor corresponding to the virtual displacements |
| δu | the virtual displacement tensor |
| τ | Traction on the boundary surface |
| Γ | Boundary surface |
| b | Body load vector |
| V | Volume of continuity |
| C | Material stress–strain tensor |
| Δε | Incremental strain tensor |
| Linear strain tensor corresponding to the virtual displacements | |
| Nonlinear strain tensor corresponding to the virtual displacements | |
| C J | Tangent modulus matrix |
| Gradient of quantity | |
| Material stiffness matrix | |
| Geometric stiffness matrix | |
| BL | Linear strain–displacement matrix |
| BNL | Nonlinear strain–displacement matrix |
| Vp | Volume of material point |
| np | Number of material points |
| Stress matrix for geometric stiffness matrix | |
| fext | External load vector |
| Nip | Interpolation function |
| hp | Characteristic length of particle |
| δuk | Iterative displacement vector |
| k | Number iterative |
| Mass density | |
| Nominal stress tensor | |
| F | Deformation gradient tensor |
| J | Determinant of Jacobian matrix |
| q | Tractions vector |
| Δq | Tractions increment vector |
| Δb | Body force increment vector |
| t | Time |
| Δt | Increment time |
| Nominal stress rate at the current time t + Δt | |
| Virtual velocity tensor | |
| Cauchy stress rate tensor | |
| Cauchy stress tensor at time t | |
| Nonlinear strain–displacement matrix in the proposed framework | |
| Material matrix in the proposed framework | |
| Geometric matrix in the proposed framework | |
| L | Velocity gradient tensor |
| Deformation rate tensor | |
| Rotation tensor | |
| tr(·) | Trace of tensor |
| Jaumann stress rate tensor | |
| Stress tensor for geometric stiffness matrix | |
| External load on the nodes | |
| L2-norm of the entire residual vector | |
| ferror | Residual force vector |
| E | Young’s modulus |
| v | Poisson’s ratio |
| F | yield function |
| G | plastic potential function |
| c | Cohesion force |
| ϕ | Friction angle |
| φ | Dilatancy angle |
Appendix A. Transformation Process of Governing Equation
References
- Lucy, L.B. A Numerical Approach to the Testing of the Fission Hypothesis. Astron. J. 1977, 82, 1013. [Google Scholar] [CrossRef]
- Belytschko, T.; Gu, L.; Lu, Y.Y. Fracture and Crack Growth by Element Free Galerkin Methods. Model. Simul. Mater. Sci. Eng. 1994, 2, 519–534. [Google Scholar] [CrossRef]
- Oñate, E.; Idelsohn, S.R.; Del Pin, F.; Aubry, R. The particle finite element method—An overview. Int. J. Comput. Methods 2004, 1, 267–307. [Google Scholar] [CrossRef]
- Liu, S.; Tang, X.; Li, J. Extension of ALE Method in Large Deformation Analysis of Saturated Soil under Earthquake Loading. Comput. Geotech. 2021, 133, 104056. [Google Scholar] [CrossRef]
- Sulskya, D.; Chenb, Z.; Schreyer, H.L. A Particle Method for History-Dependent Materials. Comput. Methods Appl. Mech. Eng. 1994, 118, 179–196. [Google Scholar] [CrossRef]
- Jiang, C.; Schroeder, C.; Selle, A.; Teran, J.; Stomakhin, A. The Affine Particle-in-Cell Method. ACM Trans. Graph. 2015, 34, 1–10. [Google Scholar] [CrossRef]
- Brackbill, J.U.; Ruppel, H.M. FLIP: A Method for Adaptively Zoned, Particle-in-Cell Calculations of Fluid Flows in Two Dimensions. J. Comput. Phys. 1986, 65, 314–343. [Google Scholar] [CrossRef]
- Bardenhagen, S.G.; Kober, E.M. The Generalized Interpolation Material Point Method. Comput. Model. Eng. Sci. 2004, 5, 477–496. [Google Scholar]
- Steffen, M.; Kirby, R.M.; Berzins, M. Analysis and Reduction of Quadrature Errors in the Material Point Method (MPM). Int. J. Numer. Methods Eng. 2008, 76, 922–948. [Google Scholar] [CrossRef]
- Sadeghirad, A.; Brannon, R.M.; Burghardt, J. A Convected Particle Domain Interpolation Technique to Extend Applicability of the Material Point Method for Problems Involving Massive Deformations. Int. J. Numer. Methods Eng. 2011, 86, 1435–1456. [Google Scholar] [CrossRef]
- Zhang, D.Z.; Ma, X.; Giguere, P.T. Material Point Method Enhanced by Modified Gradient of Shape Function. J. Comput. Phys. 2011, 230, 6379–6398. [Google Scholar] [CrossRef]
- De Koster, P.; Tielen, R.; Wobbes, E.; Möller, M. Extension of B-Spline Material Point Method for Unstructured Triangular Grids Using Powell–Sabin Splines. Comput. Part Mech. 2021, 8, 273–288. [Google Scholar] [CrossRef]
- Hu, Y.; Fang, Y.; Ge, Z.; Qu, Z.; Zhu, Y.; Pradhana, A.; Jiang, C. A Moving Least Squares Material Point Method with Displacement Discontinuity and Two-Way Rigid Body Coupling. ACM Trans. Graph. 2018, 37, 1–14. [Google Scholar] [CrossRef]
- Sulsky, D.; Schreyer, H.L. Axisymmetric Form of the Material Point Method with Applications to Upsetting and Taylor Impact Problems. Comput. Methods Appl. Mech. Eng. 1996, 139, 409–429. [Google Scholar] [CrossRef]
- Dong, Y.; Wang, D.; Randolph, M.F. Quantification of Impact Forces on Fixed Mudmats from Submarine Landslides Using the Material Point Method. Appl. Ocean Res. 2020, 102, 102227. [Google Scholar] [CrossRef]
- Cui, X.X.; Zhang, X.; Zhou, X.; Liu, Y.; Zhang, F. A Coupled Finite Difference Material Point Method and Its Application in Explosion Simulation. Comput. Model. Eng. Sci. 2014, 98, 565–599. [Google Scholar]
- Wang, Y.; Beom, H.G.; Sun, M.; Lin, S. Numerical Simulation of Explosive Welding Using the Material Point Method. Int. J. Impact Eng. 2011, 38, 51–60. [Google Scholar] [CrossRef]
- Raymond, S.J.; Jones, B.D.; Williams, J.R. Fracture Shearing of Polycrystalline Material Simulations Using the Material Point Method. Comput. Part Mech. 2021, 8, 259–272. [Google Scholar] [CrossRef]
- Andersen, S.; Andersen, L. Modelling of Landslides with the Material-Point Method. Comput. Geosci. 2010, 14, 137–147. [Google Scholar] [CrossRef]
- Llano-Serna, M.A.; Farias, M.M.; Pedroso, D.M. An Assessment of the Material Point Method for Modelling Large Scale Run-out Processes in Landslides. Landslides 2016, 13, 1057–1066. [Google Scholar] [CrossRef]
- Shi, Y.H.; Guo, N.; Yang, Z.X. GeoTaichi: A Taichi-Powered High-Performance Numerical Simulator for Multiscale Geophysical Problems. Comput. Phys. Commun. 2024, 301, 109219. [Google Scholar] [CrossRef]
- Wang, B.; Vardon, P.J.; Hicks, M.A.; Chen, Z. Development of an Implicit Material Point Method for Geotechnical Applications. Comput. Geotech. 2016, 71, 159–167. [Google Scholar] [CrossRef]
- Yuan, W.; Wang, H.; Liu, K.; Zhang, W.; Wang, D.; Wang, Y. Analysis of Large Deformation Geotechnical Problems Using Implicit Generalized Interpolation Material Point Method. J. Zhejiang Univ.-Sci. A 2021, 22, 909–923. [Google Scholar] [CrossRef]
- Charlton, T.J.; Coombs, W.M.; Augarde, C.E. iGIMP: An Implicit Generalised Interpolation Material Point Method for Large Deformations. Comput. Struct. 2017, 190, 108–125. [Google Scholar] [CrossRef]
- Coombs, W.M.; Augarde, C.E.; Brennan, A.J.; Brown, M.J.; Charlton, T.J.; Knappett, J.A.; Ghaffari Motlagh, Y.; Wang, L. On Lagrangian Mechanics and the Implicit Material Point Method for Large Deformation Elasto-Plasticity. Comput. Methods Appl. Mech. Eng. 2020, 358, 112622. [Google Scholar] [CrossRef]
- Coombs, W.M.; Augarde, C.E. AMPLE: A Material Point Learning Environment. Adv. Eng. Softw. 2020, 139, 102748. [Google Scholar] [CrossRef]
- González Acosta, J.L.; Vardon, P.J.; Hicks, M.A. Development of an Implicit Contact Technique for the Material Point Method. Comput. Geotech. 2021, 130, 103859. [Google Scholar] [CrossRef]
- Li, S.; Zhang, Y.; Wu, J.; Yu, J.; Gong, X. Modeling of Crack Propagation with the Quasi-Static Material Point Method. Eng. Fract. Mech. 2021, 245, 107602. [Google Scholar] [CrossRef]
- Oka, F.; Yashima, A.; Shibata, T.; Kato, M.; Uzuoka, R. FEM-FDM Coupled Liquefaction Analysis of a Porous Soil Using an Elasto-Plastic Model. Appl. Sci. Res. 1994, 52, 209–245. [Google Scholar] [CrossRef]
- Flanagan, D.P.; Taylor, L.M. An Accurate Numerical Algorithm for Stress Integration with Finite Rotations. Comput. Methods Appl. Mech. Eng. 1987, 62, 305–320. [Google Scholar] [CrossRef]
- Dienes, J.K. On the Analysis of Rotation and Stress Rate in Deforming Bodies. Acta Mech. 1979, 32, 217–232. [Google Scholar] [CrossRef]
- Bishop, A.W.; Morgenstern, N. Stability Coefficients for Earth Slopes. Géotechnique 1960, 10, 129–153. [Google Scholar] [CrossRef]
- Sołowski, W.T.; Sloan, S.W. Evaluation of Material Point Method for Use in Geotechnics. Int. J. Numer. Anal. Methods Geomech. 2015, 39, 685–701. [Google Scholar] [CrossRef]
- Xie, M.; Navas, P.; López-Querol, S. An Implicit Locking-free B-spline Material Point Method for Large Strain Geotechnical Modelling. Int. J. Numer. Anal. Methods Geomech. 2023, 47, 2741–2761. [Google Scholar] [CrossRef]
- Ludwig Prandtl Über Die Härte Plastischer Körper. Nachrichten Von Ges. Wiss. Zu Gött. Math. Phys. Kl. 1921, 1, 15–20.
- Jin, Y.-F.; Yin, Z.-Y.; Li, J.; Dai, J.-G. A Novel Implicit Coupled Hydro-Mechanical SPFEM Approach for Modelling of Delayed Failure of Cut Slope in Soft Sensitive Clay. Comput. Geotech. 2021, 140, 104474. [Google Scholar] [CrossRef]
- Wang, Z.; Jin, Y.; Yin, Z.; Wang, Y. A Novel Coupled NS-PFEM with Stable Nodal Integration and Polynomial Pressure Projection for Geotechnical Problems. Int. J. Numer. Anal. Methods Geomech. 2022, 46, 2535–2560. [Google Scholar] [CrossRef]
- Meyerhof, G.G. The Ultimate Bearing Capacity of Foudations. Géotechnique 1951, 2, 301–332. [Google Scholar] [CrossRef]
- da Silva, M.V.; Krabbenhoft, K.; Lyamin, A.V.; Sloan, S.W. Rigid-plastic Large-deformation Analysis of Geotechnical Penetration Problems. Proceedings of 13th IACMAG conference. Comput Methods Geomech Front New Appl. 2011, 1, 42–47. [Google Scholar]
- Ye, B.; Ye, G.; Zhang, F.; Yashima, A. Experiment and Numerical Simulation of Repeated Liquefaction-Consolidation of Sand. Soils Found. 2007, 47, 547–558. [Google Scholar] [CrossRef]





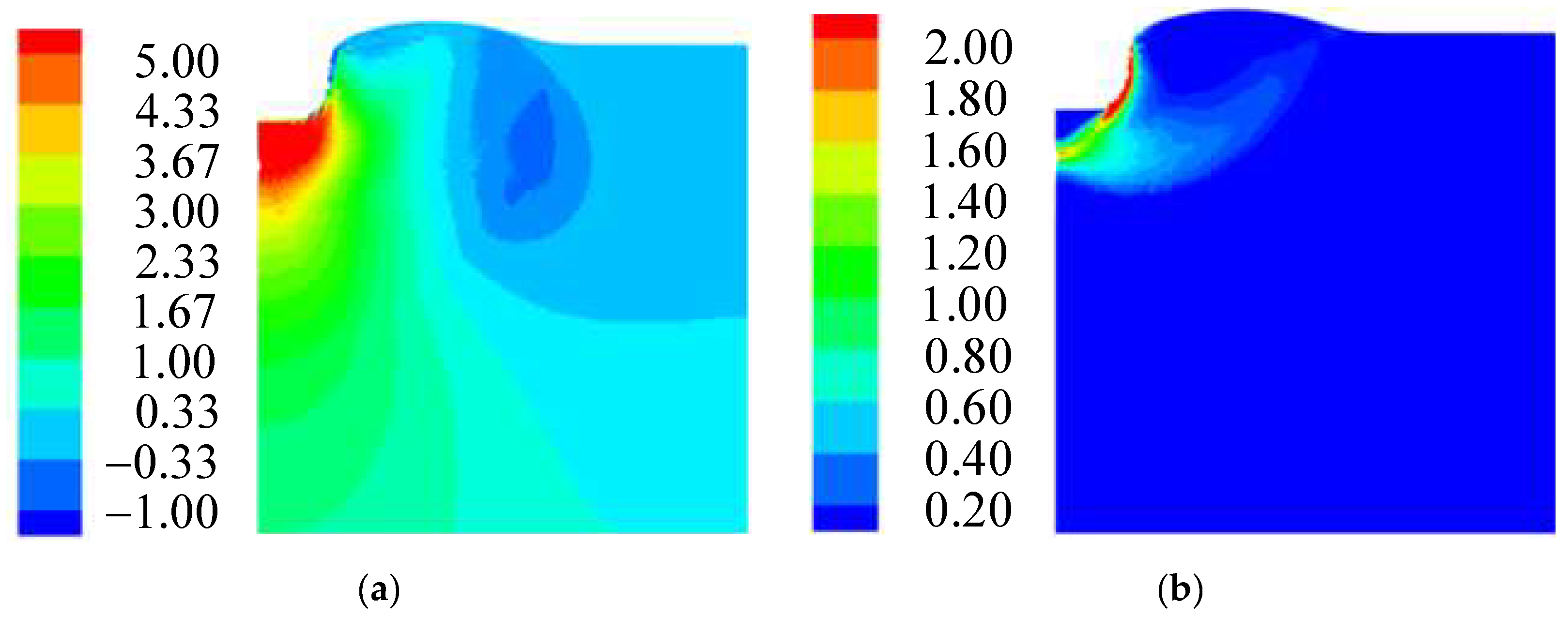
| Reference | Formulation | Basic Assumption | Objective Stress Rate | Configuration | Updated Interpolation Function Gradient |
|---|---|---|---|---|---|
| Wang et al. [22] | UL | Small strain | Jaumann stress rate | Current configuration | / |
| Yuan et al. [23] | UL | Small strain | Jaumann stress rate | Current configuration | / |
| Acosta et al. [27] | UL | Small strain | / | Current configuration | / |
| Li et al. [28] | UL | Small strain | / | Current configuration | / |
| Charlton et al. [24] | UL | Large strain | / | Current configuration | Mapping configuration method |
| Coombs et al. [26] | Novel Lagrangian | Large strain | / | Previous configuration | / |
| The proposed MPM | UL | Small strain | Jaumann stress rate | Previous configuration | Mapping configuration method |
| Calculation Process | Proposed MPM (ms) | Traditional MPM (ms) | Relative Error (%) |
|---|---|---|---|
| Initialization | 578.125 | 578.125 | 0.0 |
| Computational model | 6172.13 | 12,516.14 | 50.67 |
| Stiffness matrix calculation and assembly | 5250.25 | 10,671.88 | 50.80 |
| External and internal force | 406.25 | 828.63 | 50.97 |
| Linear solver | 515.63 | 1015.63 | 49.23 |
| Update the information of material point (e.g., displacement, deformation gradient, strain, stress and so on) | 1625.25 | 2812.50 | 42.21 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sang, Q.-Y.; Liu, Z.-G.; Xiong, Y.-L.; Wu, R.-X.; Yan, J.-H. A Robust Lagrangian Implicit Material Point Method for Accurate Large-Deformation Analysis. Symmetry 2025, 17, 1876. https://doi.org/10.3390/sym17111876
Sang Q-Y, Liu Z-G, Xiong Y-L, Wu R-X, Yan J-H. A Robust Lagrangian Implicit Material Point Method for Accurate Large-Deformation Analysis. Symmetry. 2025; 17(11):1876. https://doi.org/10.3390/sym17111876
Chicago/Turabian StyleSang, Qin-Yang, Zhi-Gang Liu, Yong-Lin Xiong, Rong-Xing Wu, and Jiang-Hua Yan. 2025. "A Robust Lagrangian Implicit Material Point Method for Accurate Large-Deformation Analysis" Symmetry 17, no. 11: 1876. https://doi.org/10.3390/sym17111876
APA StyleSang, Q.-Y., Liu, Z.-G., Xiong, Y.-L., Wu, R.-X., & Yan, J.-H. (2025). A Robust Lagrangian Implicit Material Point Method for Accurate Large-Deformation Analysis. Symmetry, 17(11), 1876. https://doi.org/10.3390/sym17111876






