An Online Reduced KPLS Data-Driven Method for Fault Diagnosis of Nonlinear Processes
Abstract
1. Introduction
2. Preliminaries
2.1. KPLS Principe
2.2. Reduced Form
2.2.1. RKPLS Formulation
| Algorithm 1: RKPLS algorithm |
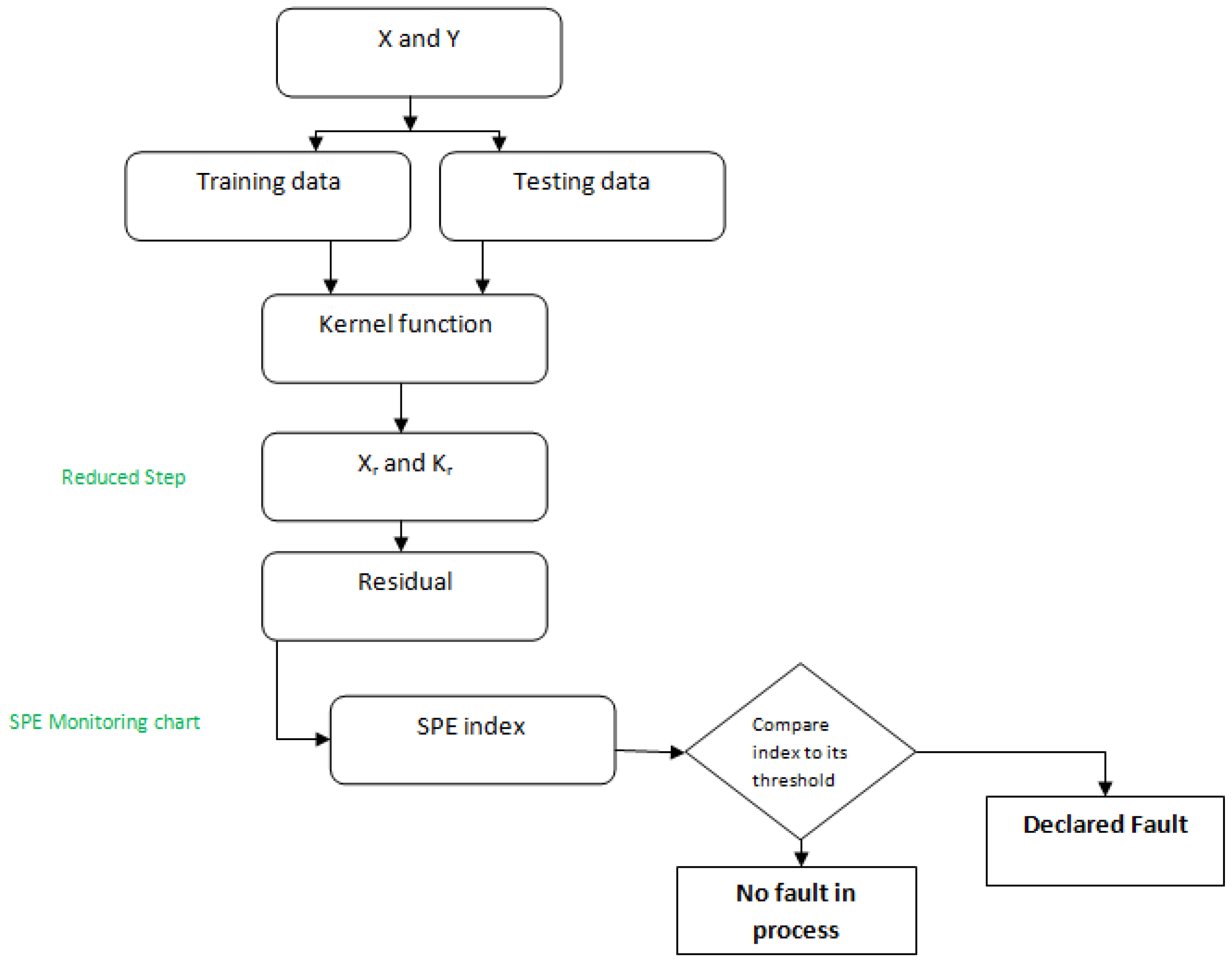
Training data 1-Determine an initial standardized block of training data entered in normal operating conditions. 2-Compute the kernel matrix K and scale it. 3-Estimate the reduced KPLS model. 4-Set control limit of the statistic monitoring. Testing data 1-Treat the testing data which represent a severe faults. 2-Project the on the component latent and select . 3-Evaluate the monitoring statistic using the kernel parameter with the same range. 4-Use the control limits to determine the fault detection performance (GDR and FAR). |
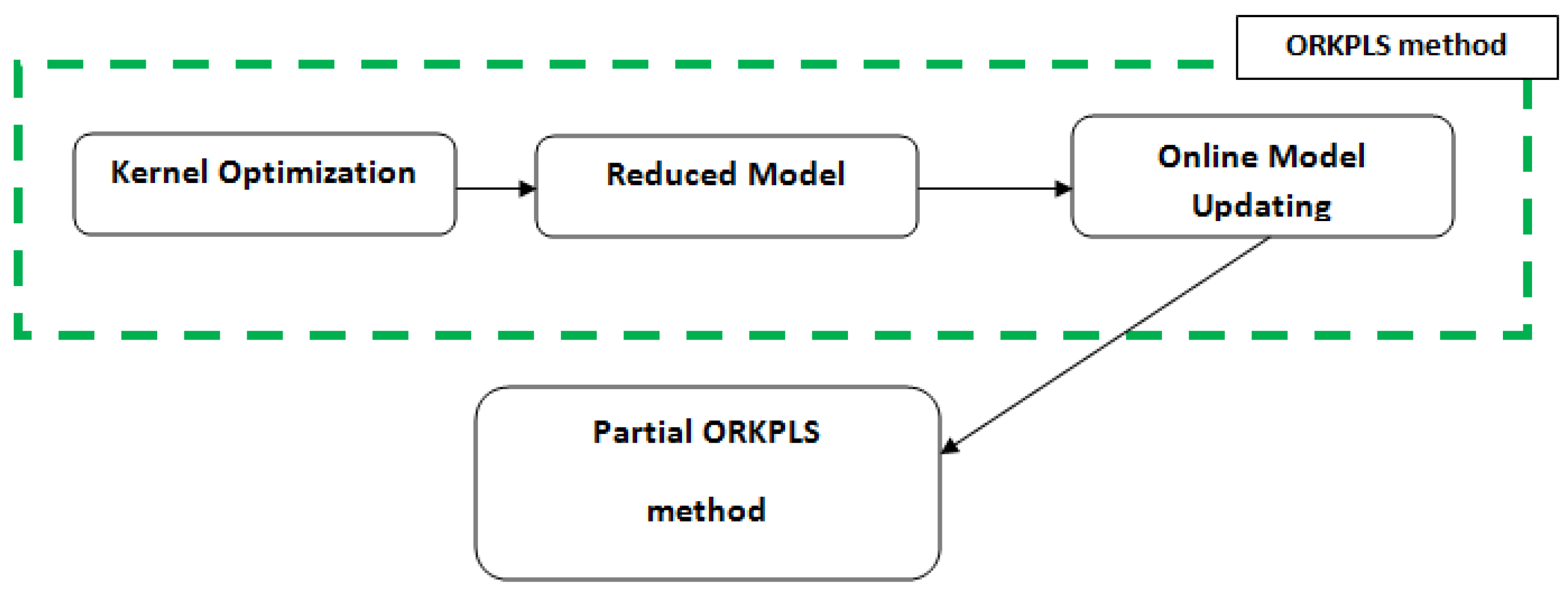
2.2.2. Online RKPLS for Fault Detection
- Offline reduced model: identificationIn this step, the initial data matrix (input, output) is set and also the reduced Gram matrix, as indicated Equations (13)–(15).Then, the updating phase is done by observation in the online part.
- Online fault detection: model updateThe update phase is based on two conditions:(a) A flawless observation (normal observation)(b) A rich observation of information on the system to be studied.When a new observation, at time k, is available, the SPE index can be tested, as shown Equation (16).where, is the new data, is the kernel vector, and is the score matrix of X. Indeed, if this observation is considered as flawless data, then its kernel vector is determined, and the kernel matrix is updated by adding a column and a row to the previous one.The reduced model, in this case, can be updated the reduced data matrix, the number of latent components and also the SPE index (thresholds).
| Algorithm 2: ORKPLS algorithm |
Offline phase: Initialized input and output matrix, reduced set of data, SPE index and the reduced Gram matrix. Online phase 1-For k ← k + 1. 2-For each new observation, calculate the index. 3-Check ; if satisfied go to next step, otherwise return to step 1. 4-If Equation (10) is satisfied, go to next step, otherwise, return to step 1. 5-Update the input/output data matrix. 6-Update the . 7-Update the SPE index and LVs. 8-Return to step 1. |
2.3. Fault Detection Based on SPE
2.4. Fault Detection Steps Based on RKPLS and ORKPLS
3. The Suggested Fault Isolation Methods
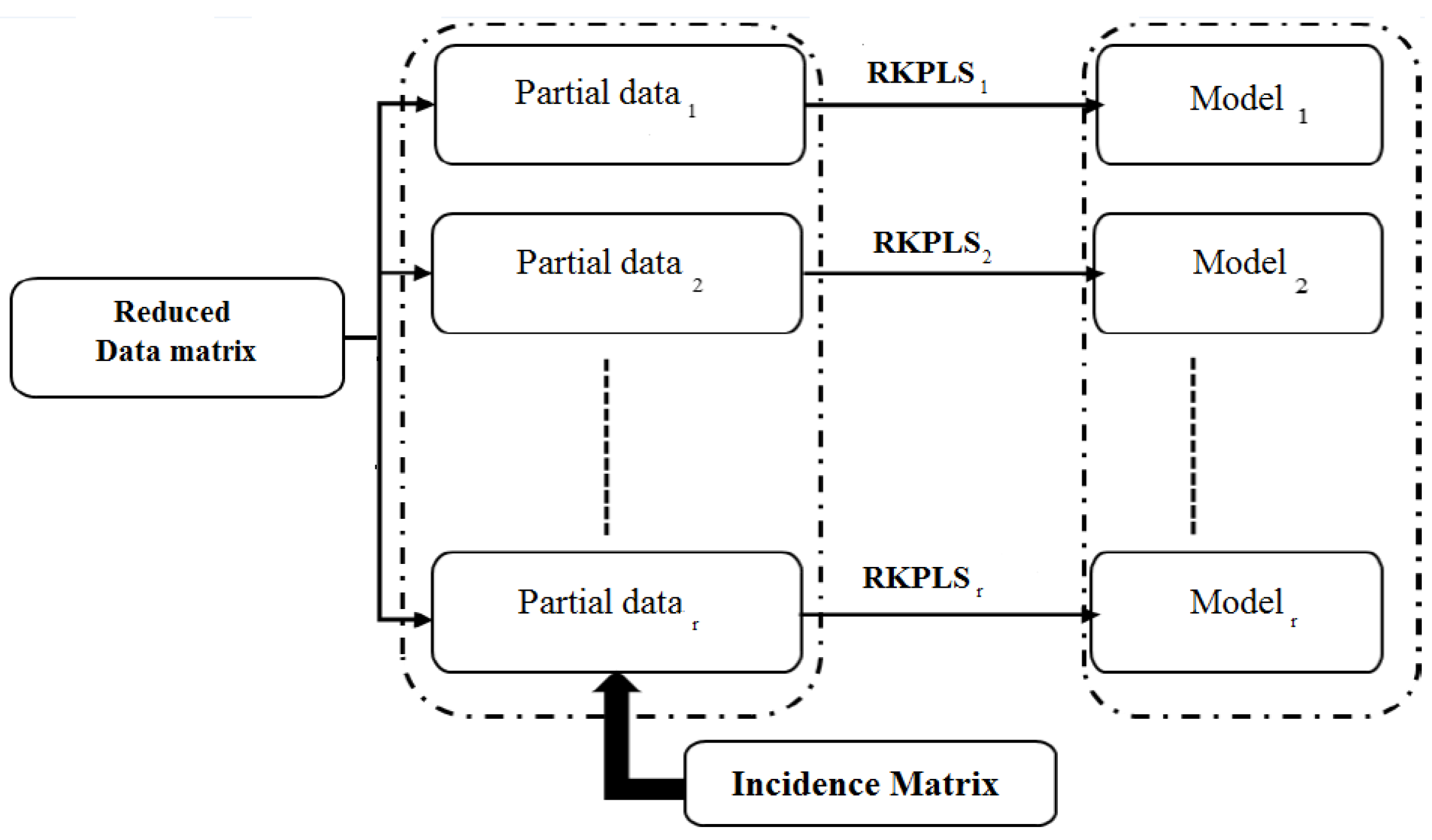
3.1. Fault Isolation Based on RKPLS
| Algorithm 3: Partial RKPLS localization algorithm |
1-Construct a highly interpretable incidence matrix. 2-Implement RKPLS on the data matrix. 3-Determine a partial RKPLS model set, as well as each corresponding to a row of the theoretical signature matrix. 4-Select the control thresholds. At each instant t 1-Calculate the indices for each of the partial RKPLS models. 2-Compare the indices to their appropriate confidence limits to determine the Experimental Signature (SE), as depicted in Equation (22). 3-Compare the experimental result with a column of the theoretical signature matrix to determine the location decision. |
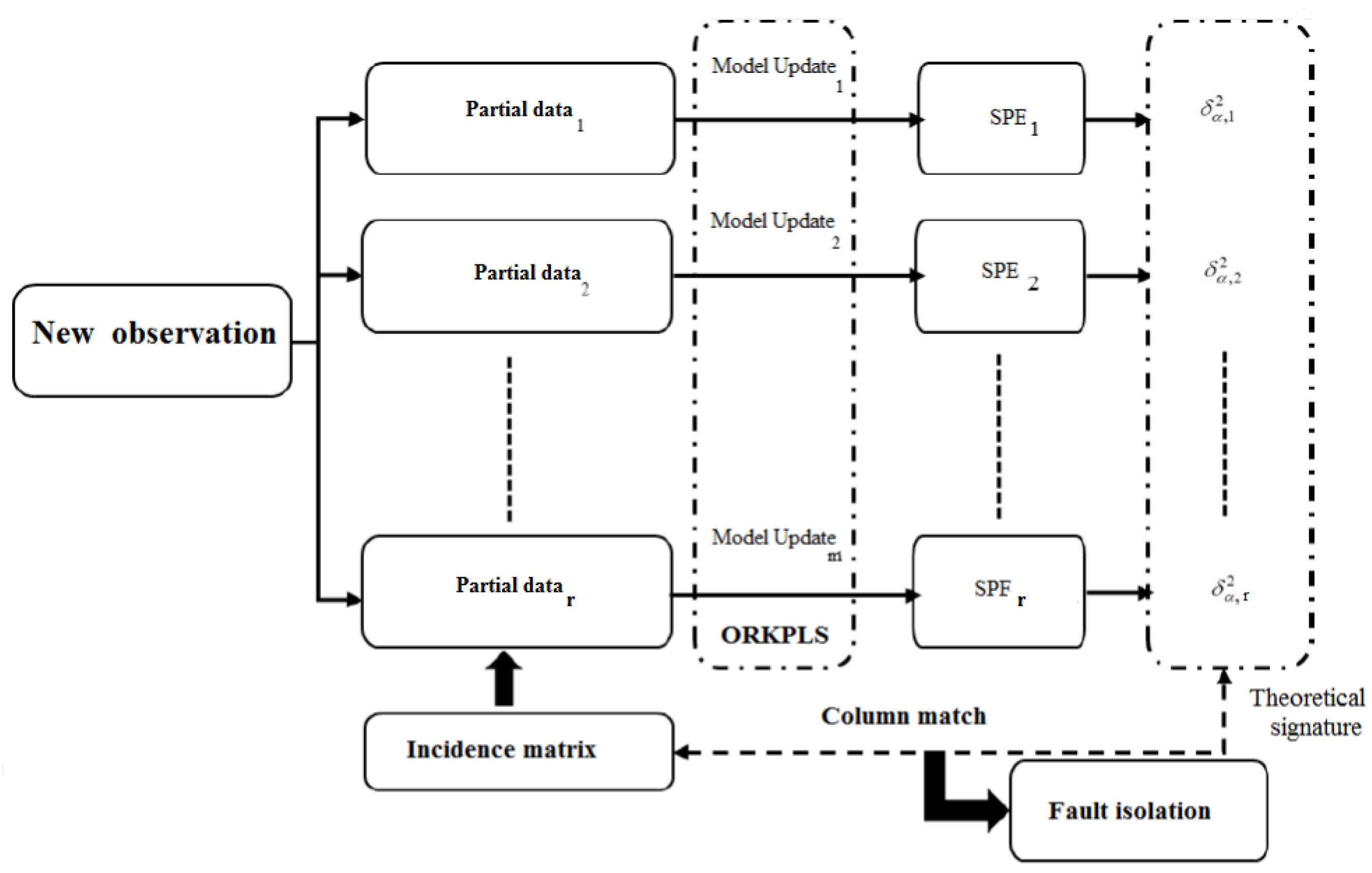
3.2. Online Fault Isolation Based on ORKPLS
- Use the principle of the method reduced to the data matrices.
- Determine an incidence matrix, in general, using strong isolation properties.
- Determine a set of partial data using the ORKPLS method, each implementing a row of the incidence matrix.
- Calculate, for each partial model, the with index and also its control limit , as depicted in Equation (20).
- Make a comparison between the threshold and the control limit.Then, is obtained.
- For each moment, compare the difference between the fault code and the columns of the incidence matrix to get an idea about the localization decision.
4. Experimental Results
4.1. Case Study on CSTR Process
4.1.1. Process Description
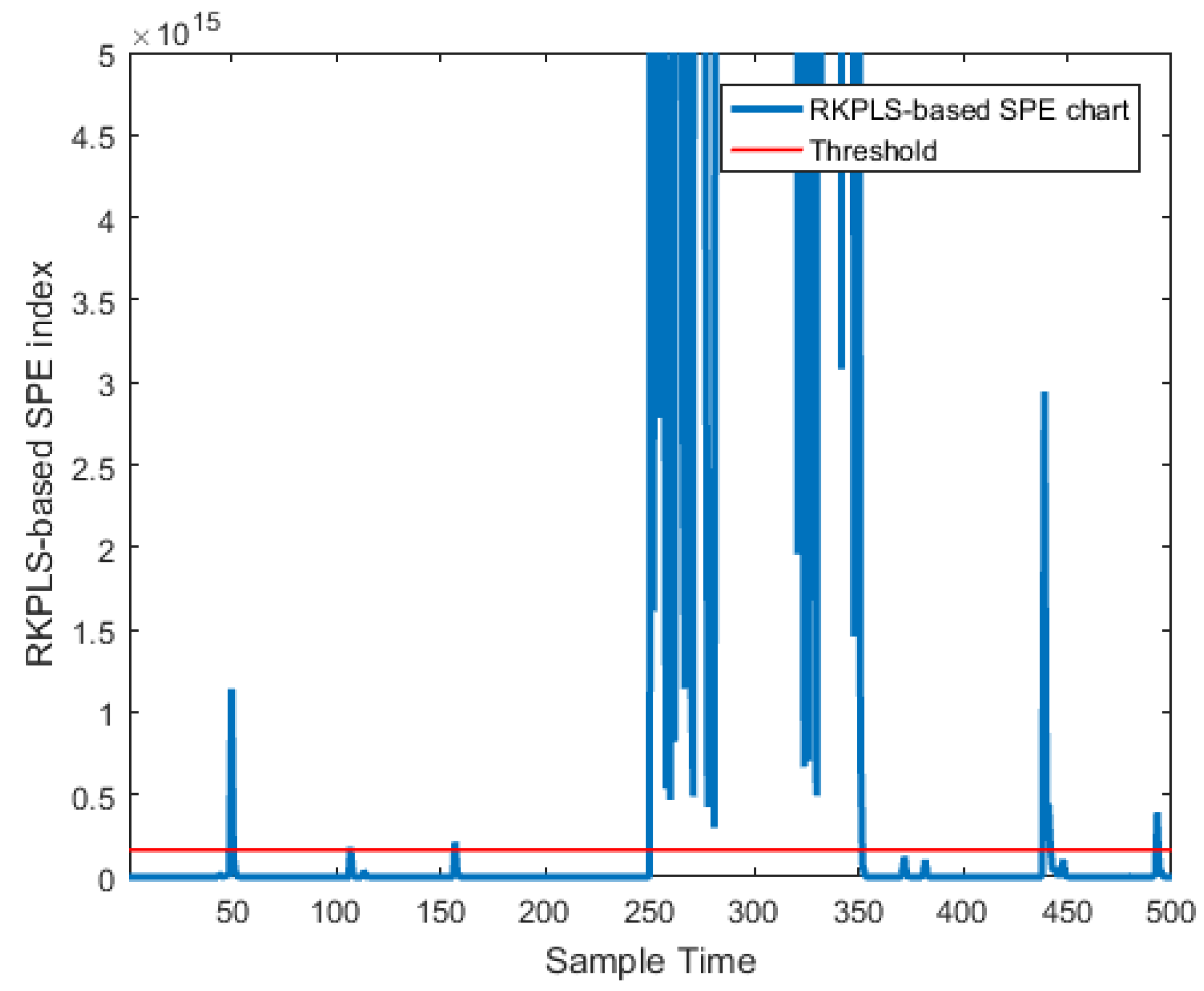
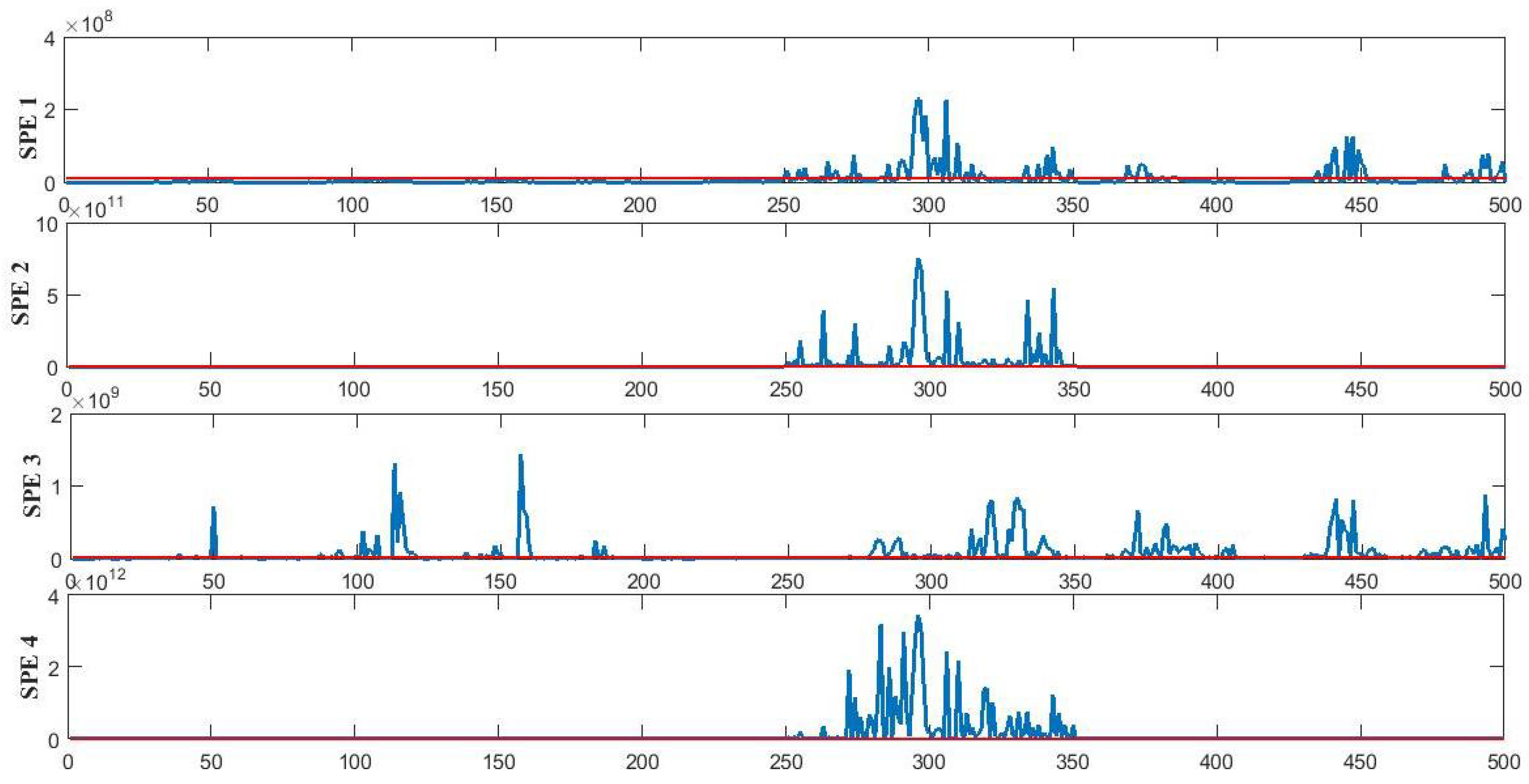
4.1.2. Simulation Results
4.2. Case Study on Air Quality Monitoring Network
4.2.1. Process Description
- Rural sites;
- Peri-urban sites;
- Urban sites.
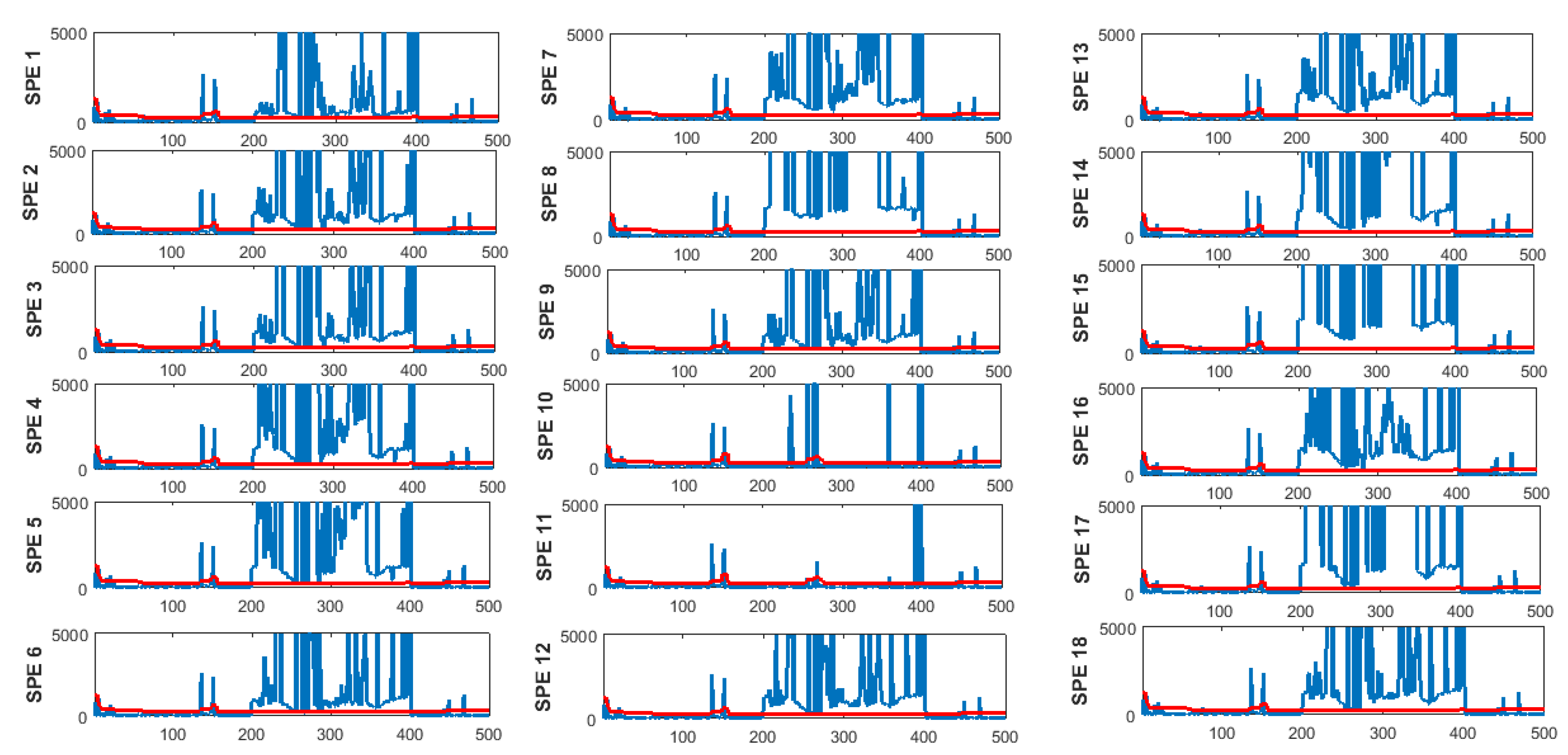
4.2.2. Simulation Results
5. Conclusions
- The RKPLS method uses only useful and relevant data for fault detection. Thus, the proposed partial RKPLS method is a useful approach for fault isolation.
- The reference model for the online method is updated if a new observation becomes available and satisfies the independence condition between variables in the feature space.
- Kernel Optimization: Select optimal kernel parameters using the Tabu search algorithm to improve the classical KPLS model.
- Reference Model Construction: Extract the most relevant observations to reduce computation time in feature space projections.
- Online Model Updating: Update the reference model when a new accurate observation satisfies independence conditions between variables.
- Online Fault Isolation: Develop ORKPLS-based approaches for real-time fault isolation.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Iulian, L.; Mihaiela, L. Machine Learning Techniques for Multi-Fault Analysis and Detection on a Rotating Test Rig Using Vibration Signal. Symmetry 2023, 15, 86. [Google Scholar]
- Seongjun, K.; Jihye, H.; Sang, K.; Sang, C.; Ohbyung, K. Leveraging Quantum Machine Learning to Address Class Imbalance: A Novel Approach for Enhanced Predictive Accuracy. Symmetry 2025, 17, 186. [Google Scholar] [CrossRef]
- Abid, A.; Khan, M.; Iqbal, J. A review on fault detection and diagnosis techniques: Basics and beyond. Artif. Intell. Rev. 2021, 54, 3639–3664. [Google Scholar] [CrossRef]
- Han, S.; Hua, Y.; Lin, Y.; Yao, L.; Wang, Z.; Zheng, Z.; Yang, J.; Zhao, C.; Zheng, C.; Gao, X. Fault diagnosis of regenerative thermal oxidizer system via dynamic uncertain causality graph integrated with early anomaly detection. Process Saf. Environ. Prot. 2023, 179, 724–734. [Google Scholar] [CrossRef]
- Muratbakeev, E.; Kozhubaev, Y.; Novak, D.; Ershov, R.; Wei, Z. Monitoring and Diagnostics of Mining Electromechanical Equipment Based on Machine Learning. Symmetry 2025, 17, 1548. [Google Scholar] [CrossRef]
- Taha, U.; Suhail, H.; Ahsen, U.; Ahmet, O.; Muhammad, R.; Daisuke, M. Machine Learning-Based Intrusion Detection for Achieving Cybersecurity in Smart Grids Using IEC 61850 GOOSE Messages. Symmetry 2021, 13, 826. [Google Scholar] [CrossRef]
- Kim, L.; Lee, J.D.; Lee, S.; Bang, H. Fault Detection for Re-initialization of Online Gaussian Process Regression Using Kernel Linear Independence Test. Int. J. Control Autom. Syst. 2024, 22, 3386–3395. [Google Scholar]
- Sun, Z.; Wang, X.; Han, T.; Wang, L.; Zhu, Z.; Huang, H.; Ding, J.; Wu, Z. Pipeline deformation prediction based on multi-source monitoring information and novel data-driven model. Eng. Struct. 2025, 337, 120461. [Google Scholar] [CrossRef]
- Sun, Z.; Wang, X.; Han, T.; Huang, H.; Huang, X.; Wang, L.; Wu, Z. Pipeline deformation monitoring based on long-gauge FBG sensing system: Missing data recovery and deformation calculation. J. Civ. Struct. Health Monit. 2025, 15, 2433–2453. [Google Scholar]
- Mohammed, K.; Abdelmalek, K.; Mohamed, H.; Abderazak, B.; Majdi, M. Data size reduction approach for nonlinear process monitoring refinement using Kernel PCA technique. Expert Syst. Appl. 2025, 274, 126975. [Google Scholar] [CrossRef]
- Kim, H.; Chang, H.; Shim, H. Evaluating MR-GPR and MR-NN: An Exploration of Data-driven Control Methods for Nonlinear Systems. Int. J. Control Autom. Syst. 2024, 22, 2934–2941. [Google Scholar] [CrossRef]
- Taqvi, S.A.; Zabiri, H.; Tufa, L.; Uddin, F.; Fatima, S.A.; Maulud, A.S. A review on data-driven learning approaches for fault detection and diagnosis in chemical processes. ChemBioEng Rev. 2021, 8, 239–259. [Google Scholar] [CrossRef]
- Ziyao, S.; Han, Z.; Jianfang, J. Data-Driven State of Health Interval Prediction for Lithium-Ion Batteries. Electronics 2024, 13, 3991. [Google Scholar]
- Hasnen, S.; Shahid, M.; Zabiri, H.; Taqvi, S. Semi-supervised adaptive PLS soft-sensor with PCA-based drift correction method for online valuation of NOx emission in industrial water-tube boiler. Process Saf. Environ. Prot. 2023, 172, 787–801. [Google Scholar] [CrossRef]
- Zhang, Y.; Ma, C. Fault diagnosis of nonlinear processes using multiscale KPCA and multiscale KPLS. Chem. Eng. Sci. 2011, 66, 64–72. [Google Scholar] [CrossRef]
- Silalahi, D.; Midi, H.; Arasan, J.; Mustafa, M.; Caliman, J. Kernel partial least square regression with high resistance to multiple outliers and bad leverage points on near-infrared spectral data analysis. Symmetry 2021, 13, 547. [Google Scholar] [CrossRef]
- Bennett, K.; Embrechts, M. An optimization perspective on kernel partial least squares regression. Nato Sci. Ser. Sub Ser. III Comput. Syst. Sci. 2003, 190, 227–250. [Google Scholar]
- Hu, W.; Wang, Y.; Li, Y.; Wan, X.; Gopaluni, R. A multi-feature-based fault diagnosis method based on the weighted timeliness broad learning system. Process Saf. Environ. Prot. 2024, 183, 231–243. [Google Scholar] [CrossRef]
- Tidriri, K.; Chatti, N.; Verron, S.; Tiplica, T. Bridging data-driven and model-based approaches for process fault diagnosis and health monitoring: A review of researches and future challenges. Annu. Rev. Control 2016, 42, 63–81. [Google Scholar] [CrossRef]
- Ge, Z. Review on data-driven modeling and monitoring for plant-wide industrial processes. Chemom. Intell. Lab. Syst. 2017, 171, 16–25. [Google Scholar] [CrossRef]
- Said, M.; Abdellafou, K.; Taouali, O.; Harkat, F. A new monitoring scheme of an air quality network based on the kernel method. Int. J. Adv. Manuf. Technol. 2019, 103, 153–163. [Google Scholar] [CrossRef]
- Lahdhiri, H.; Taouali, O. Reduced Rank KPCA based on GLRT chart for sensor fault detection in nonlinear chemical process. Measurement 2021, 169, 108342. [Google Scholar] [CrossRef]
- Mok, H.; Chan, C. Online fault detection and isolation of nonlinear systems based on neurofuzzy networks. Eng. Appl. Artif. Intell. 2008, 21, 171–181. [Google Scholar] [CrossRef]
- Chan, C.; Cheung, K.; Wang, Y.; Chan, W. Online fault detection and isolation of nonlinear systems. In Proceedings of the 1999 American Control Conference (Cat. No. 99CH36251), San Diego, CA, USA, 2–4 June 1999; Volume 6, pp. 3980–3984. [Google Scholar]
- Ellefsen, A.; Han, P.; Cheng, X.; Holmeset, F.; Vilmar, A.; Zhang, H. Online fault detection in autonomous ferries: Using fault-type independent spectral anomaly detection. IEEE Trans. Instrum. Meas. 2020, 69, 8216–8225. [Google Scholar] [CrossRef]
- Wahbe, R.; Lucco, S.; Anderson, T.; Graham, S. Efficient software-based fault isolation. In Proceedings of the Fourteenth ACM Symposium on Operating Systems Principles, Asheville, NC, USA, 5–8 December 1993; pp. 203–216. [Google Scholar]
- Laib, A.; Terriche, Y.; Melit, M.; Su, C.; Mutarraf, M.; Bouchekara, H.R.; Guerrero, J.M.; Boudjefdjouf, H. Enhanced artificial intelligence technique for soft fault localization and identification in complex aircraft microgrids. Eng. Appl. Artif. Intell. 2024, 127, 107289. [Google Scholar] [CrossRef]
- Yeu, T.; Kim, H.; Kawaji, S. Fault detection, isolation and reconstruction for descriptor systems. Asian J. Control 2005, 7, 356–367. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhou, H.; Qin, S.; Chai, T. Decentralized fault diagnosis of large-scale processes using multiblock kernel partial least squares. IEEE Trans. Ind. Inform. 2009, 6, 3–10. [Google Scholar] [CrossRef]
- Jia, Q.; Zhang, Y. Quality-related fault detection approach based on dynamic kernel partial least squares. Chem. Eng. Res. Des. 2016, 106, 242–252. [Google Scholar] [CrossRef]
- Rosipal, R.; Trejo, L.J. Kernel partial least squares regression in reproducing kernel hilbert space. J. Mach. Learn. Res. 2001, 2, 97–123. [Google Scholar]
- Zhang, Y.; Hu, Z. Multivariate process monitoring and analysis based on multi-scale KPLS. Chem. Eng. Res. Des. 2011, 89, 2667–2678. [Google Scholar] [CrossRef]
- Lindgren, F.; Geladi, P.; Wold, S. The kernel algorithm for PLS. J. Chemom. 1993, 7, 45–59. [Google Scholar] [CrossRef]
- Kim, K.; Lee, J.M.; Lee, I.B. A novel multivariate regression approach based on kernel partial least squares with orthogonal signal correction. Chemom. Intell. Lab. Syst. 2005, 79, 22–30. [Google Scholar] [CrossRef]
- Said, M.; Abdellafou, K.; Taouali, O. Machine learning technique for data-driven fault detection of nonlinear processes. J. Intell. Manuf. 2020, 31, 865–884. [Google Scholar] [CrossRef]
- Dunia, R.; Qin, S.J. Joint diagnosis of process and sensor faults using principal component analysis. Control Eng. Pract. 2005, 6, 457–469. [Google Scholar] [CrossRef]
- Jackson, J.E.; Mudholkar, G.S. Control procedures for residuals associated with principal component analysis. Technometrics 1979, 21, 341–349. [Google Scholar] [CrossRef]
- Navi, M.; Meskin, N.; Davoodi, M. Sensor fault detection and isolation of an industrial gas turbine using partial adaptive KPCA. J. Process Control 2018, 64, 37–48. [Google Scholar] [CrossRef]
- Zhang, X.; Deng, X.; Cao, Y.; Xiao, L. Nonlinear Predictable Feature Learning with Explanatory Reasoning for Complicated Industrial System Fault Diagnosis. Knowl.-Based Syst. 2024, 286, 111404. [Google Scholar] [CrossRef]
- Ben Abdellafou, K.; Hadda, H.; Korbaa, W. An improved tabu search meta-heuristic approach for solving scheduling problem with non-availability constraints. Arab. J. Sci. Eng. 2019, 44, 3369–3379. [Google Scholar] [CrossRef]
- Harkat, M.; Mourot, G.; Ragot, J. An improved PCA scheme for sensor FDI: Application to an air quality monitoring network. J. Process Control 2006, 16, 625–634. [Google Scholar] [CrossRef]
- Harkat, M.; Mourot, G.; Ragot, J. Sensor failure detection of air quality monitoring network. IFAC Proc. Vol. 2006, 33, 529–534. [Google Scholar] [CrossRef]



| Variables | Description | Value |
|---|---|---|
| The flow concentration of the inlet A | 1 (mol/L) | |
| The reaction rate constant | 4.11 (L/min·mol) | |
| E | Activation energy | 76,534 (J/mol) |
| The temperature of the inlet flow into the reactor | 350 (K) | |
| Coolant inlet temperature | 350 (K) | |
| The heat of reaction | 596,619 (J/mol) | |
| T | The temperature of the inlet stream | - |
| F | Flow in and out of the reactor | - |
| V | The volume of the reactor | 100 (L) |
| R | Real gas constant | 8.31451 (J/mol·K) |
| The density of the reactor contents and all streams | 1000 (J/L) | |
| Capacity of reactor contents and all streams | 4.25 (J/g·K) |
| 0 | 1 | 1 | 1 | |
| 1 | 0 | 1 | 1 | |
| 1 | 1 | 0 | 1 | |
| 1 | 1 | 1 | 0 |
| 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | |
| 1 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | |
| 1 | 1 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | |
| 1 | 1 | 1 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | |
| 1 | 1 | 1 | 1 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | |
| 1 | 1 | 1 | 1 | 1 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | |
| 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | |
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | |
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | |
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | |
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | |
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | |
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 1 | 1 | 1 | 1 | |
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 1 | 1 | 1 | |
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 1 | 1 | |
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 1 | |
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | |
| 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 |
| Computation Time (s) | AIRLOR | CSTR |
|---|---|---|
| KPLS | 1.104 | 0.87 |
| RKPLS | 0.98 | 0.69 |
| ORKPLS | 0.871 | 0.44 |
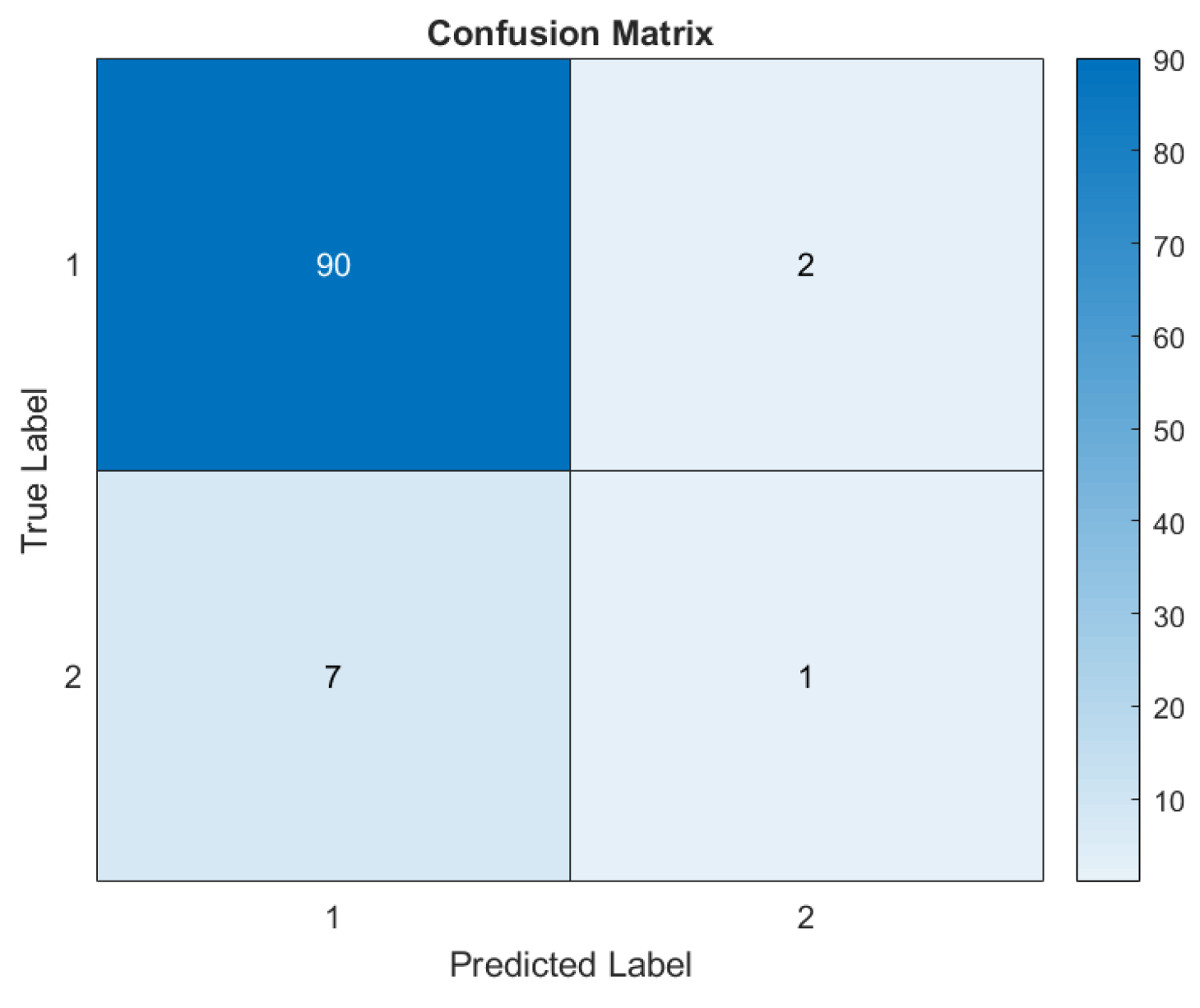
| Confusion Matrix | ||||||||
|---|---|---|---|---|---|---|---|---|
| FP | FN | TP | TN | Accuracy | Precision | Sensitivity | Total Events | |
| Modelo KNN | 90 | 7 | 2 | 1 | 91% | 92.86% | 97.83% | 100 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Said, M.; Taouali, O.; Zidi, K.; Ghaban, W. An Online Reduced KPLS Data-Driven Method for Fault Diagnosis of Nonlinear Processes. Symmetry 2025, 17, 1863. https://doi.org/10.3390/sym17111863
Said M, Taouali O, Zidi K, Ghaban W. An Online Reduced KPLS Data-Driven Method for Fault Diagnosis of Nonlinear Processes. Symmetry. 2025; 17(11):1863. https://doi.org/10.3390/sym17111863
Chicago/Turabian StyleSaid, Maroua, Okba Taouali, Kamel Zidi, and Wad Ghaban. 2025. "An Online Reduced KPLS Data-Driven Method for Fault Diagnosis of Nonlinear Processes" Symmetry 17, no. 11: 1863. https://doi.org/10.3390/sym17111863
APA StyleSaid, M., Taouali, O., Zidi, K., & Ghaban, W. (2025). An Online Reduced KPLS Data-Driven Method for Fault Diagnosis of Nonlinear Processes. Symmetry, 17(11), 1863. https://doi.org/10.3390/sym17111863






