Stabilization Method for nth-Order ODE by Distributed Control Function
Abstract
1. Introduction
2. Stabilization Problem Statement
3. Stabilization Method of -Order Ordinary Differential Equation by Control Function in the Form (2) in the Case of
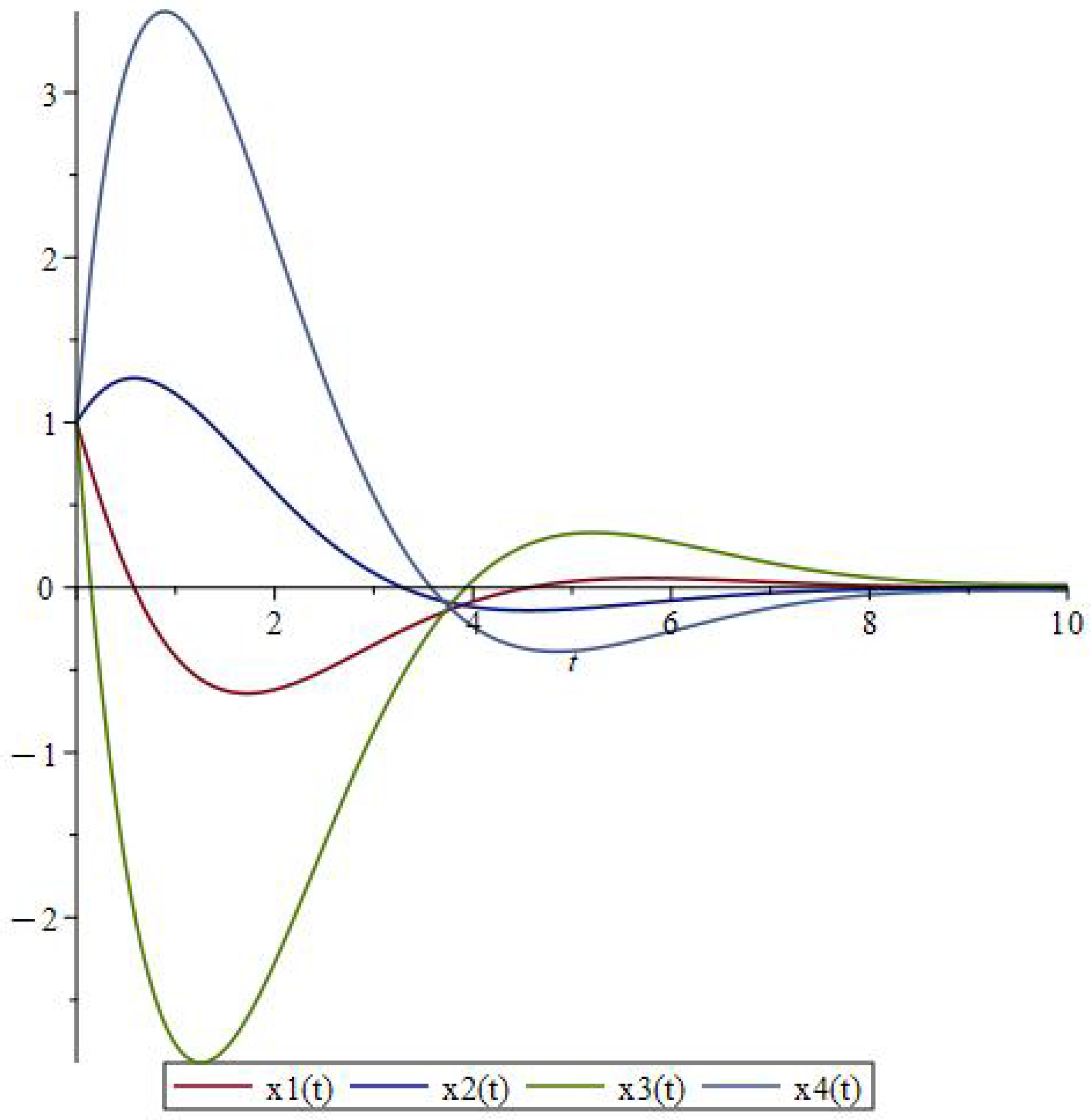
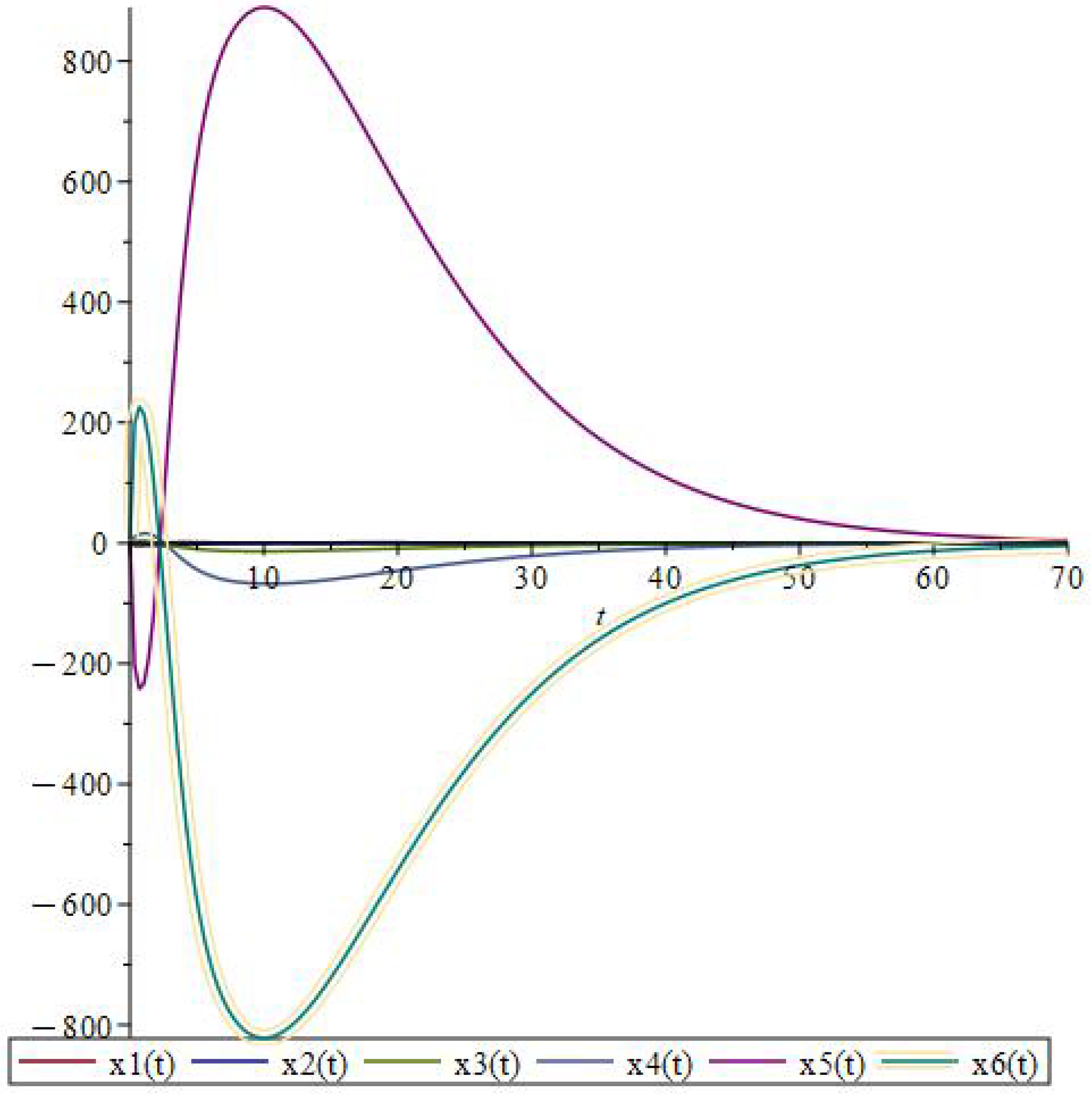
4. Examples
5. Conclusions
Funding
Data Availability Statement
Conflicts of Interest
References
- Bohner, M.; Domoshnitsky, A.; Kupervasser, O.; Sitkin, A. Floquet theory for first-order delay equations and an application to height stabilization of a drone’s flight. Electron. Res. Arch. 2025, 33, 2840–2861. [Google Scholar] [CrossRef]
- Domoshnitsky, A.; Volinsky, I.; Biton, S.; Steindorf, V. Estimates of Solutions for Integro-Differential Equations in Epidemiological Modeling. Math. Methods Appl. Sci. 2025, 48, 10533–10543. [Google Scholar] [CrossRef]
- Son, N.K.; Ngoc, L.V. Exponential stability analysis for a class of switched nonlinear time-varying functional differential systems. Nonlinear Anal. Hybrid Syst. 2022, 44, 101177. [Google Scholar] [CrossRef]
- Berezansky, L.; Braverman, E. Exponential stability of systems of vector delay differential equations with applications to second order equations. J. Math. Anal. Appl. 2021, 504, 125566. [Google Scholar] [CrossRef]
- Chalishajar, D.; Dhanalakshmi, K.; Ramkumar, K.; Ravikumar, K. Exponential Stability of Higher-Order Fractional Neutral Stochastic Differential Equation via Integral Contractors. Math. Methods Appl. Sci. 2025, 48, 6425–6446. [Google Scholar] [CrossRef]
- Linh, N.M.; Phat, V.N. Exponential stability of nonlinear time-varying differential equations and applications. Electron. J. Differ. Equ. 2001, 2001, 1–13. [Google Scholar]
- Li, X.; Fu, X. On the global exponential stability of impulsive functional differential equations with infinite delays or finite delays. Commun. Nonlinear Sci. Numer. Simul. 2014, 19, 442–447. [Google Scholar] [CrossRef]
- Mao, X.; Shah, A. Exponential stability of stochastic functional differential equations with infinite delay. Stochastics Stochastics Rep. 1998, 60, 135–153. [Google Scholar] [CrossRef]
- Berezansky, L.; Braverman, E. On exponential stability of a linear delay differential equation with an oscillating coefficient. Appl. Math. Lett. 2009, 22, 1833–1837. [Google Scholar] [CrossRef]
- Gao, L.; Wang, D.; Wang, G. Further results on exponential stability for impulsive switched nonlinear time-delay systems with delayed impulse effects. Appl. Math. Comput. 2015, 268, 186–200. [Google Scholar] [CrossRef]
- Singh, P.; Srivastava, S.; Kaur, K. Global Exponential Stability of Impulsive Functional Differential Equations with Effect of Delay at the Time of Impulses. Glob. J. Sci. Front. Res. 2015, 15. Available online: https://www.researchgate.net/publication/299410245 (accessed on 14 September 2025).
- Ding, M.; Zhu, B. Some results related to Hurwitz stability of combinatorial polynomials. Adv. Appl. Math. 2024, 152, 102591. [Google Scholar] [CrossRef]
- Markovsky, I.; Rao, S. Palindromic polynomials, time-reversible systems, and conserved quantities. In Proceedings of the 16th Mediterranean Conference on Control and Automation Congress Centre, Ajaccio, France, 25–27 June 2008. [Google Scholar]
- Domoshnitsky, A.; Volinsky, I.; Polonsky, A.; Sitkin, A. Stabilization by delay distributed feedback control. Math. Model. Nat. Phenom. 2017, 12, 91–105. [Google Scholar] [CrossRef]
- Domoshnitsky, A.; Volinsky, I.; Polonsky, A. Stabilization of third order differential equation by delay distributed feedback control with unbounded memory. Math. Slovaca 2019, 69, 1165–1175. [Google Scholar] [CrossRef]
- Domoshnitsky, A. Exponential stability of convolution integro-differential equations. Funct.-Differ. Equ. 1998, 5, 445–455. [Google Scholar]
- Domoshnitsky, A.; Goltser, Y. Approach to study of bifurcations and stability of integro-differential equations. Math. Comput. Model. 2002, 36, 663–678. [Google Scholar] [CrossRef]
- Kolmogorov, A.N.; Fomin, S.V. Elements of the Theory of Functions and Functional Analysis, Dover Books on Mathematics; Dover Publications: Mineola, NY, USA, 1999. [Google Scholar]
- Volinsky, I. A New Approach for Stabilization Criteria of n-Order Function Differential Equation by Distributed Control Function. Symmetry 2023, 15, 912. [Google Scholar] [CrossRef]
- Gantmacher, F.R. The Theory of Matrices; 2 Volumes; Matrix Theory; AMS Chelsea Publishing: New York, NY, USA, 1998. [Google Scholar]
- Medina, L.A.; Straub, A. On Multiple and Infinite Log-Concavity. Ann. Comb. 2016, 20, 125–138. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Volinsky, I. Stabilization Method for nth-Order ODE by Distributed Control Function. Symmetry 2025, 17, 1861. https://doi.org/10.3390/sym17111861
Volinsky I. Stabilization Method for nth-Order ODE by Distributed Control Function. Symmetry. 2025; 17(11):1861. https://doi.org/10.3390/sym17111861
Chicago/Turabian StyleVolinsky, Irina. 2025. "Stabilization Method for nth-Order ODE by Distributed Control Function" Symmetry 17, no. 11: 1861. https://doi.org/10.3390/sym17111861
APA StyleVolinsky, I. (2025). Stabilization Method for nth-Order ODE by Distributed Control Function. Symmetry, 17(11), 1861. https://doi.org/10.3390/sym17111861







