Dynamic Error Correction for Fine-Wire Thermocouples Based on CRBM-DBN with PINN Constraint
Abstract
1. Introduction
2. Principles and Methods
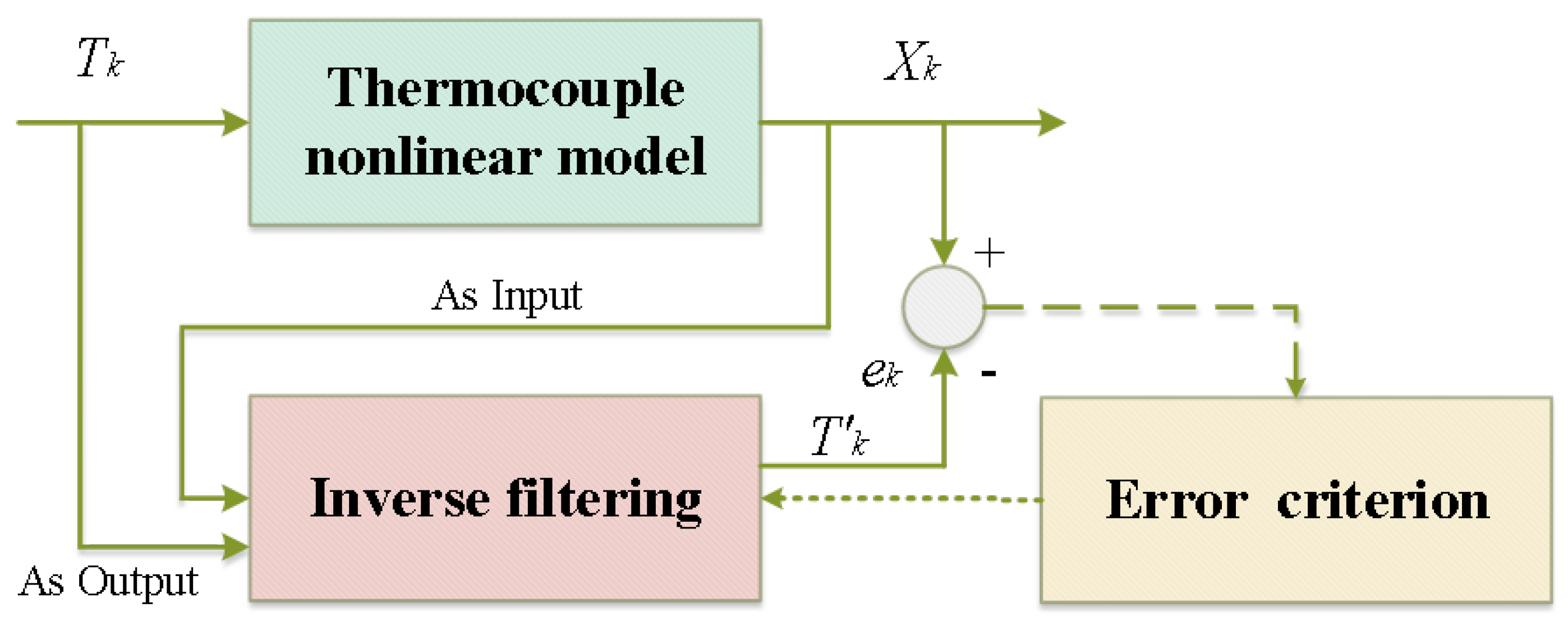
2.1. Principle of Thermocouple Dynamic Inverse Filtering
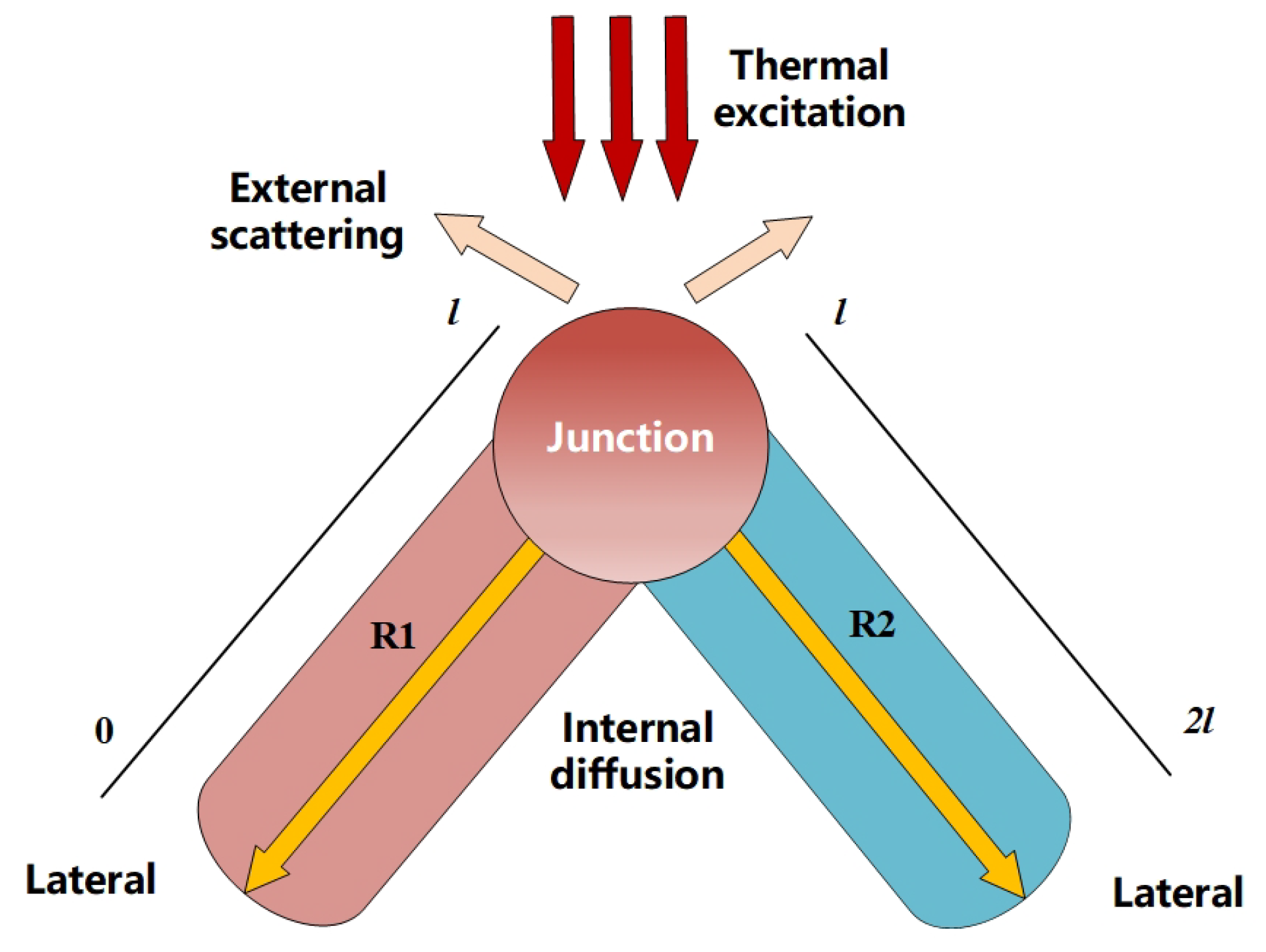
2.2. Inverse Problem Analysis
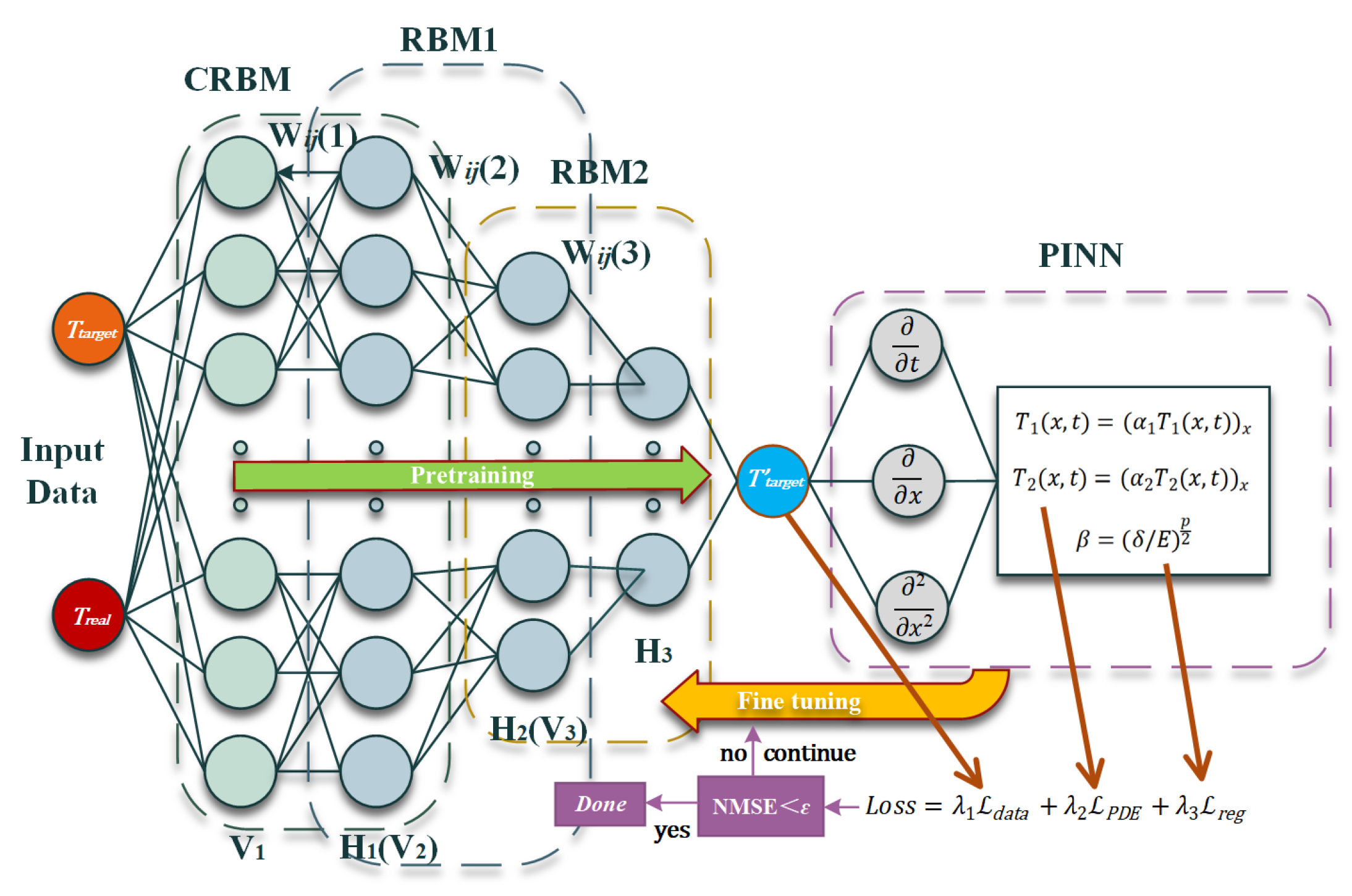
2.3. Improved CRBM-DBN-PINN Model
- 1.
- CRBM-DBN Initial Training: Employ laser pulse data to derive time-domain features using Adam optimization for initializing the weights of the PINN;
- 2.
- PINN Adjustment: Incorporate two layers of IHCP PDE constraints and refine hyperparameters via Bayesian optimization;
- 3.
- Solving Inverse Problems: The network generates the best solution , assessed through metrics like peak value and time constant, along with cross-validation and normalized mean square error (NMSE).
3. Experiment
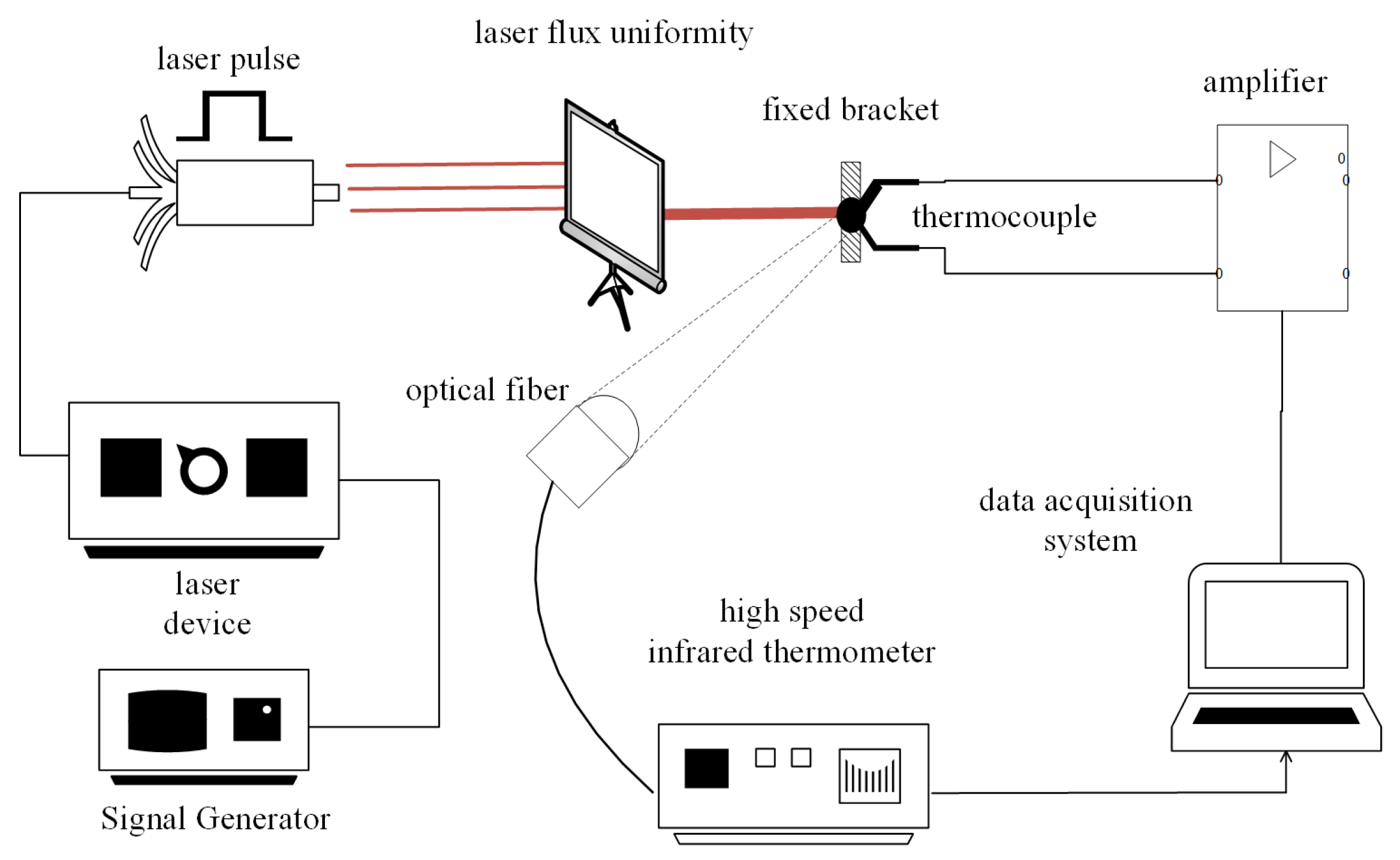
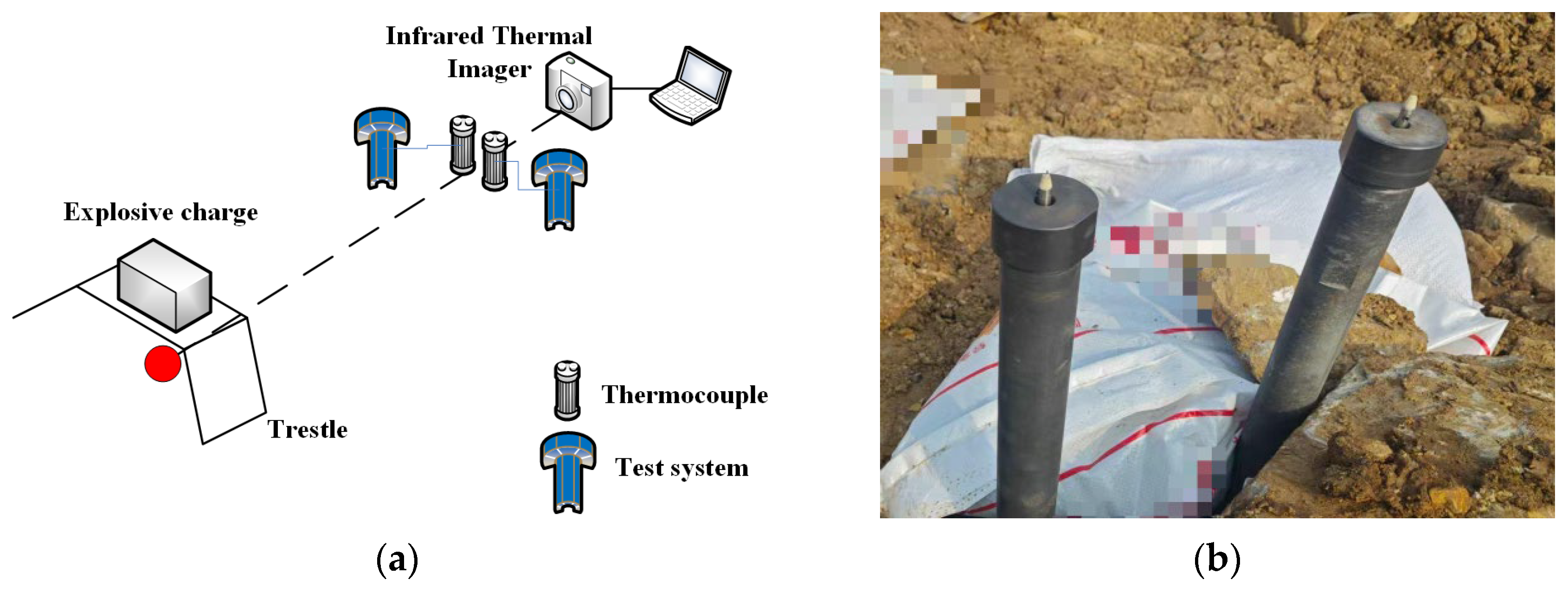
3.1. Laser Narrow Pulse Calibration Platform
3.2. Experimental Steps
4. Results and Analysis
4.1. Model Accuracy Analysis
4.2. Emission Sensitivity Analysis
4.3. Noise Sensitivity Analysis
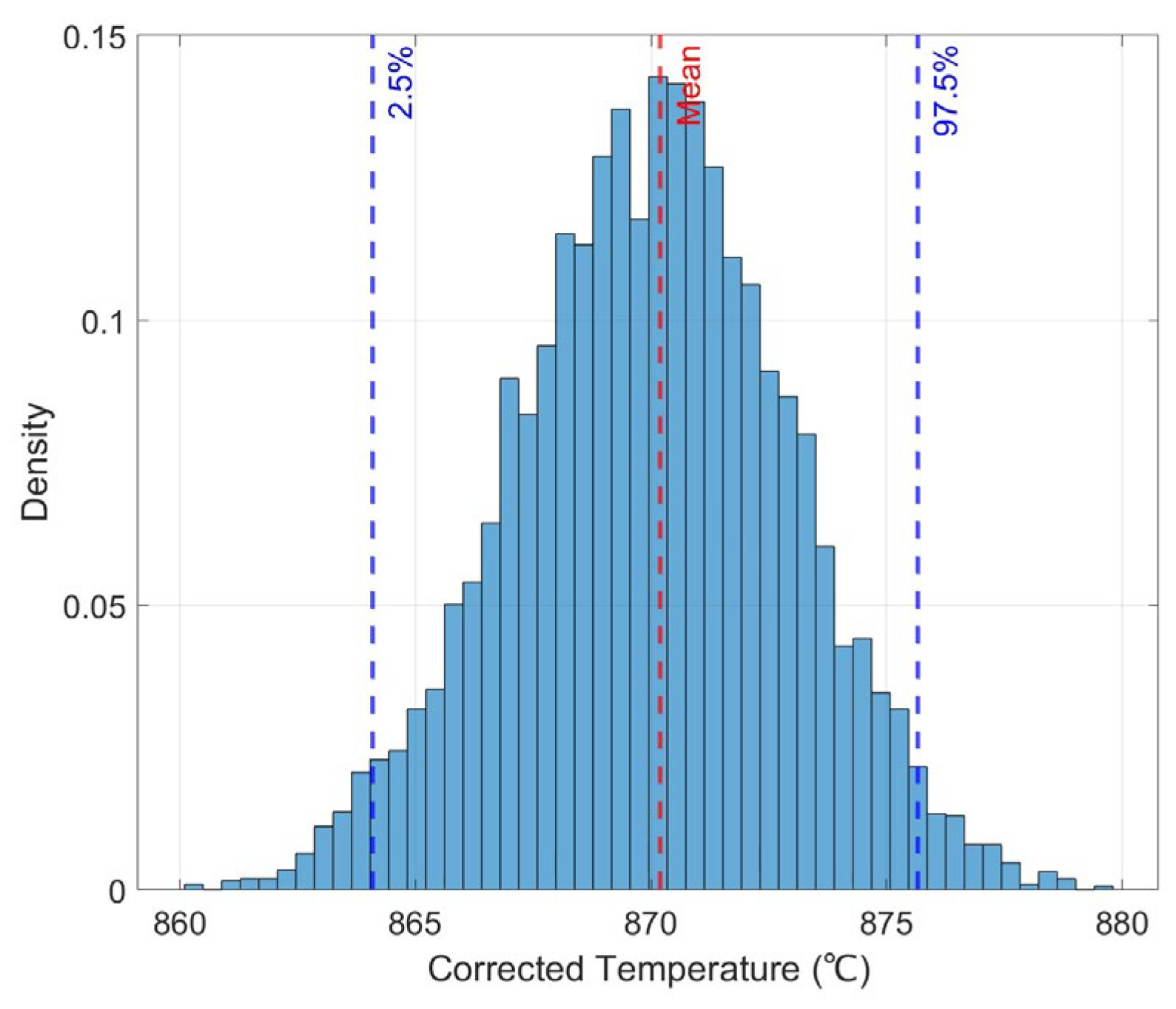
4.4. Uncertainty Quantitative Analysis
4.5. Blast Test and Result Analysis
5. Discussions
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Li, Z.L.; Wang, G.; Yin, J.P.; Xue, H.X.; Guo, J.Q.; Wang, Y.; Huang, M.G. Development and Performance Analysis of an Atomic Layer Thermopile Sensor for Composite Heat Flux Testing in an Explosive Environment. Electronics 2023, 12, 3582. [Google Scholar] [CrossRef]
- Cardillo, D.; Battista, F.; Gallo, G.; Mungiguerra, S.; Savino, R. Experimental Firing Test Campaign and Nozzle Heat Transfer Reconstruction in a 200 N Hybrid Rocket Engine with Different Paraffin-Based Fuel Grain Lengths. Aerospace 2023, 10, 546. [Google Scholar] [CrossRef]
- Liu, S.Y.; Huang, Y.; He, Y.; Zhu, Y.Q.; Wang, Z.H. Review of Development and Comparison of Surface Thermometry Methods in Combustion Environments: Principles, Current State of the Art, and Applications. Processes 2022, 10, 2528. [Google Scholar] [CrossRef]
- Tomczyk, K.; Benko, P. Analysis of the Upper Bound of Dynamic Error Obtained during Temperature Measurements. Energies 2022, 15, 7300. [Google Scholar] [CrossRef]
- Xu, S.Y.; Wang, Z.H.; Gui, L.J. Contact mode thermal sensors for ultrahigh-temperature region of 2000–3500 K. Rare Met. 2019, 38, 713–720. [Google Scholar] [CrossRef]
- Wang, F.X.; Lin, Z.Y.; Zhang, Z.J.; Li, Y.F.; Chen, H.Z.; Liu, J.Q.; Li, C. Fabrication and Calibration of Pt-Rh10/Pt Thin-Film Thermocouple. Micromachines 2023, 14, 4. [Google Scholar] [CrossRef]
- Kou, Z.H.; Wu, R.X.; Wang, Q.Y.; Li, B.B.; Li, C.Z.; Yin, X.Y. Heat transfer error analysis of high-temperature wall temperature measurement using thermocouple. Case Stud. Therm. Eng. 2024, 59, 104518. [Google Scholar] [CrossRef]
- Zhao, X.; Jin, K.Z.; Yan, M.Y.; Nan, P.Y.; Zhou, F.; Xin, G.G.; Lim, K.S.; Ahmad, H.; Zhang, Y.P.; Yang, H.Z. Inverse heat transfer for real-time thermal evaluation of aircraft thermal protection structure with embedded FBG sensors. Appl. Therm. Eng. 2025, 260, 124869. [Google Scholar] [CrossRef]
- Huang, Z.W.; Li, T.; Huang, K.X.; Ke, H.B.; Lin, M.; Wang, Q.W. Predictions of flow and temperature fields in a T-junction based on dynamic mode decomposition and deep learning. Energy 2022, 261, 125228. [Google Scholar] [CrossRef]
- Zeeshan, A.; Khalid, N.; Ellahi, R.; Khan, M.I.; Alamri, S.Z. Analysis of nonlinear complex heat transfer MHD flow of Jeffrey nanofluid over an exponentially stretching sheet via three phase artificial intelligence and Machine Learning techniques. Chaos Solitons Fractals 2024, 189, 115600. [Google Scholar] [CrossRef]
- Sulaiman, M.; Khan, N.A.; Alshammari, F.S.; Laouini, G. Performance of Heat Transfer in Micropolar Fluid with Isothermal and Isoflux Boundary Conditions Using Supervised Neural Networks. Mathematics 2023, 11, 1173. [Google Scholar] [CrossRef]
- Jaremkiewicz, M. Reduction of dynamic error in measurements of transient fluid temperature. Arch. Thermodyn. 2011, 32, 55–66. [Google Scholar] [CrossRef]
- Yang, Z.X.; Meng, X.F. Study on transient temperature generator and dynamic compensation technology. Appl. Mech. Mater. 2014, 511–512, 161–164. [Google Scholar] [CrossRef]
- Guo, Y.K.; Zhang, Z.J.; Li, Y.F.; Wang, W.Z. C-type two-thermocouple sensor design between 1000 and 1700 °C. Rev. Sci. Instrum. 2024, 95, 105119. [Google Scholar] [CrossRef] [PubMed]
- Chu, J.R.; Wang, S.L.; Gan, R.L.; Wang, W.H.; Li, B.R.; Yang, G. Dynamic compensation by coupled triple-thermocouples for temperature measurement error of high-temperature gas flow. Trans. Inst. Meas. Control 2024, 46, 952–961. [Google Scholar] [CrossRef]
- Woolley, J.W.; Woodbury, K.A. Thermocouple Data in the Inverse Heat Conduction Problem. Heat Transf. Eng. 2011, 32, 811–825. [Google Scholar] [CrossRef]
- Chen, Y.Y.; Frankel, J.I.; Keyhani, M. Nonlinear, rescaling-based inverse heat conduction calibration method and optimal regularization parameter strategy. J. Thermophys. Heat Transf. 2016, 30, 67–88. [Google Scholar] [CrossRef]
- Samadi, F.; Woodbury, K.; Kowsary, F. Optimal combinations of tikhonov regularization orders for ihcps. Int. J. Therm. Sci. 2021, 161, 106697. [Google Scholar] [CrossRef]
- Wang, F.; Zhang, P.; Wang, Y.; Sun, C.; Xia, X. Real-time identification of severe heat loads over external interface of lightweight thermal protection system. Therm. Sci. Eng. Prog. 2023, 37, 101583. [Google Scholar] [CrossRef]
- Frankel, J.I.; Chen, H. Analytical developments and experimental validation of a thermocouple model through an experimentally acquired impulse response function. Int. J. Heat Mass Transf. 2019, 141, 1301–1314. [Google Scholar] [CrossRef]
- Bauzin, J.G.; Cherikh, M.B.; Laraqi, N. Identification of thermal boundary conditions and the thermal expansion coefficient of a solid from deformation measurements. Int. J. Therm. Sci. 2021, 164, 106868. [Google Scholar] [CrossRef]
- Farahani, S.D.; Kisomi, M.S. Experimental estimation of temperature-dependent thermal conductivity coefficient by using inverse method and remote boundary condition. Int. Commun. Heat Mass Transf. 2020, 117, 104736. [Google Scholar] [CrossRef]
- Zhou, Z.-Y.; Ruan, B.; Jiang, G.-H.; Xu, B.-B.; Liu, H.-Y.; Zheng, Y.-T.; Jiang, W.-W.; Xu, F.-C.; Yang, K.; Gao, X.-W. A new method to identify non-steady thermal load based on element differential method. Int. J. Heat Mass Transf. 2023, 213, 124352. [Google Scholar] [CrossRef]
- Chen, G.H.; Zhou, B.; Li, T.; Mao, J.; Li, B.; Fu, Z.X. Research on thermal error compensation modeling for the machine tool integrated drive system based on energy consumption big data and an optimized bidirectional network. Precis. Eng.-J. Int. Soc. Precis. Eng. Nanotechnol. 2025, 94, 91–112. [Google Scholar] [CrossRef]
- Yu, Z.C.; Chen, H.C.; Qi, L.; Wu, Z. Calibration Method for Inverse Heat Conduction Problems Under Sensor Delay and Attenuation. J. Thermophys. Heat Transf. 2025, 39, 595–606. [Google Scholar] [CrossRef]
- Woodbury, K.A.; de Monte, F.; Najafi, H. Correcting temperature measurement Bias in experimental data. Int. Commun. Heat Mass Transf. 2025, 164, 108775. [Google Scholar] [CrossRef]
- Gautam, A.; Zafar, S. Ann based direct modelling of t type thermocouple for alleviating non linearity. In Communications in Computer and Information Science; Springer: Berlin/Heidelberg, Germany, 2020; Volume 1229. [Google Scholar] [CrossRef]
- Qiao, J.; Wang, L. Nonlinear system modeling and application based on restricted Boltzmann machine and improved BP neural network. Appl. Intell. 2021, 51, 37–50. [Google Scholar] [CrossRef]
- Dai, H.; Shang, S.P.; Lei, F.M.; Liu, K.; Zhang, X.N.; Wei, G.M.; Xie, Y.S.; Yang, S.; Lin, R.; Zhang, W.J. CRBM-DBN-based prediction effects inter-comparison for significant wave height with different patterns. Ocean Eng. 2021, 236, 109559. [Google Scholar] [CrossRef]
- Tian, F.; Yang, C. Deep belief network-hidden markov model based nonlinear equalizer for vcsel based optical interconnect. Sci. China (Inf. Sci.) 2020, 63, 155–163. [Google Scholar] [CrossRef]
- Wang, G.; Chen, Z.; Chen, H.; Mao, Z. Spatiotemporal-response-correlation-based model predictive control of heat conduction temperature field. J. Process Control 2024, 140, 103257. [Google Scholar] [CrossRef]
- Basir, S.; Senocak, I. Physics and equality constrained artificial neural networks: Application to forward and inverse problems with multi-fidelity data fusion. J. Comput. Phys. 2022, 463, 111301. [Google Scholar] [CrossRef]
- Moseley, B.; Markham, A.; Nissen-Meyer, T. Finite basis physics-informed neural networks (FBPINNs): A scalable domain decomposition approach for solving differential equations. Adv. Comput. Math. 2023, 49, 62. [Google Scholar] [CrossRef]
- Son, H.; Cho, S.W.; Hwang, H.J. Enhanced physics-informed neural networks with augmented Lagrangian relaxation method (AL-PINNs). Neurocomputing 2023, 548, 126424. [Google Scholar] [CrossRef]
- Bai, J.; Liu, G.-R.; Gupta, A.; Alzubaidi, L.; Feng, X.-Q.; Gu, Y. Physics-informed radial basis network (PIRBN): A local approximating neural network for solving nonlinear partial differential equations. Comput. Methods Appl. Mech. Eng. 2023, 415, 116290. [Google Scholar] [CrossRef]
- Costabal, F.S.; Pezzuto, S.; Perdikaris, P. Δ-PINNs: Physics-informed neural networks on complex geometries. Eng. Appl. Artif. Intell. 2024, 127, 107324. [Google Scholar] [CrossRef]
- Jiang, X.; Wang, X.; Wen, Z.; Li, E.; Wang, H. Practical uncertainty quantification for space-dependent inverse heat conduction problem via ensemble physics-informed neural networks. Int. Commun. Heat Mass Transf. 2023, 147, 106940. [Google Scholar] [CrossRef]
- Li, K.-Q.; Yin, Z.-Y.; Zhang, N.; Li, J. A PINN-based modelling approach for hydromechanical behaviour of unsaturated expansive soils. Comput. Geotech. 2024, 169, 106174. [Google Scholar] [CrossRef]
- Fang, B.L.; Wu, J.J.; Wang, S.; Wu, Z.J.; Li, T.Z.; Zhang, Y.; Yang, P.L.; Wang, J.G. Measurement method of metal surface absorptivity based on physics-informed neural network. Acta Phys. Sin. 2024, 73, 094301. [Google Scholar] [CrossRef]
- Wang, Y.; Ren, Q. A versatile inversion approach for space/temperature/time related thermal conductivity via deep learning. Int. J. Heat Mass Transf. 2022, 186, 122444. [Google Scholar] [CrossRef]
- Sun, J.Z.; Liu, B.D.; Xu, P.C.; Wang, P.Y. Influence of protection tube on thermocouple effect length. Case Stud. Therm. Eng. 2021, 26, 101178. [Google Scholar] [CrossRef]
- Zhao, C.; Zhang, Z. Inverse filtering method of bare thermocouple for transient high-temperature test with improved deep belief network. IEEE Access 2021, 9, 6706–6712. [Google Scholar] [CrossRef]
- Zhao, C.; Zhang, Z. Dynamic error correction of filament thermocouples with different structures of junction based on inverse filtering method. Micromachines 2020, 11, 44. [Google Scholar] [CrossRef]
- Liu, L.; Liang, Y.; Shang, Y.B.; Liu, D.H. Identification of ablation surface evolution using physics-informed neural network. Int. Commun. Heat Mass Transf. 2025, 167, 109310. [Google Scholar] [CrossRef]


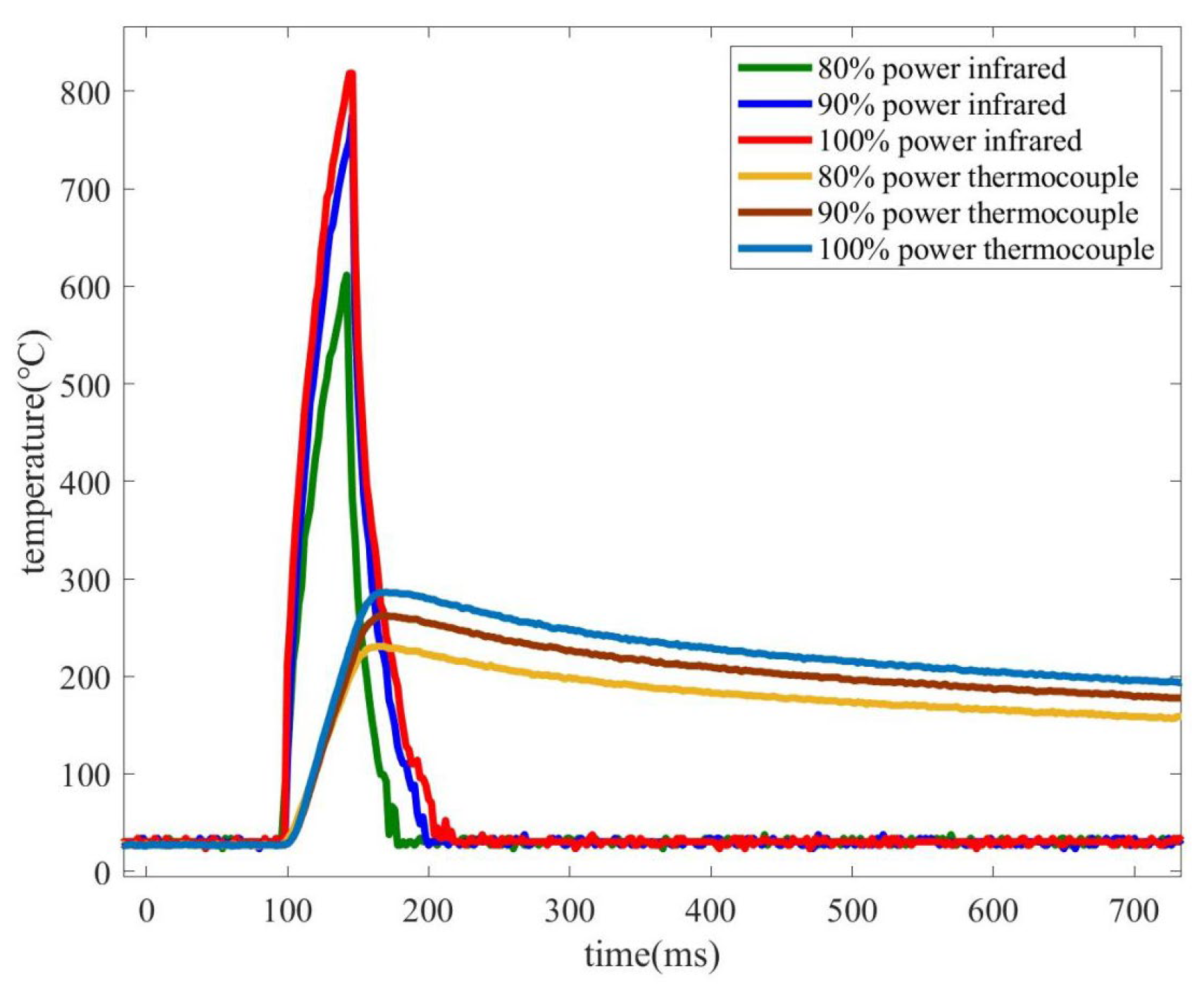
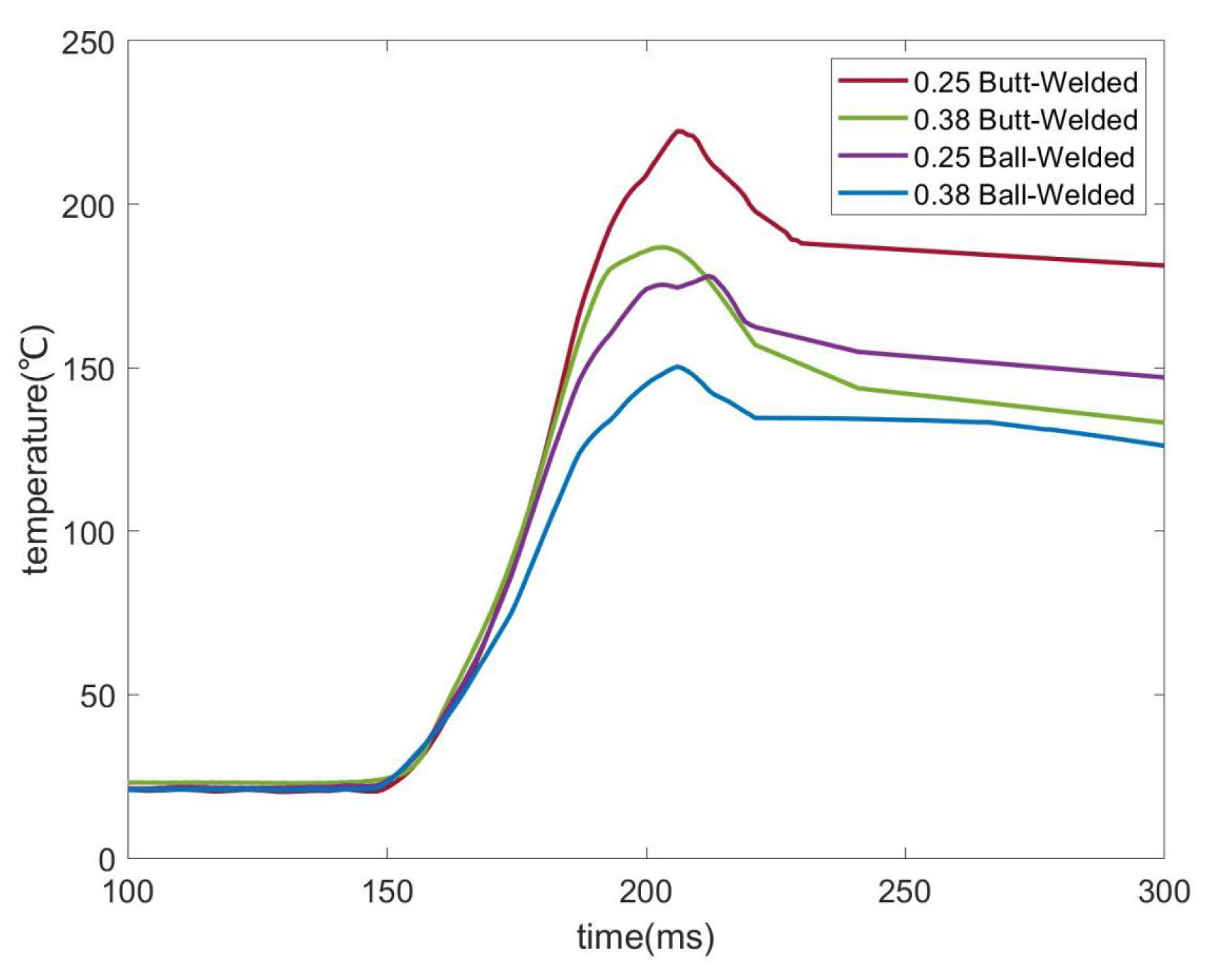
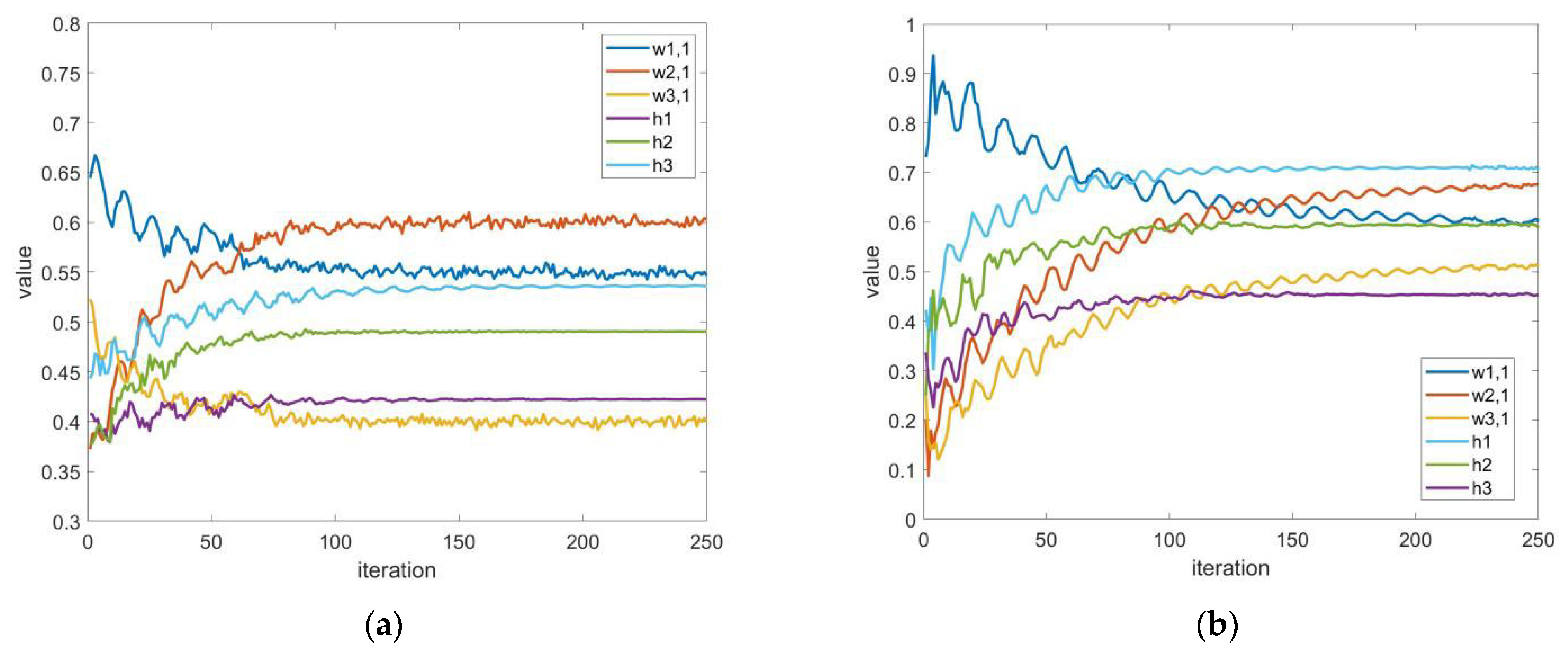
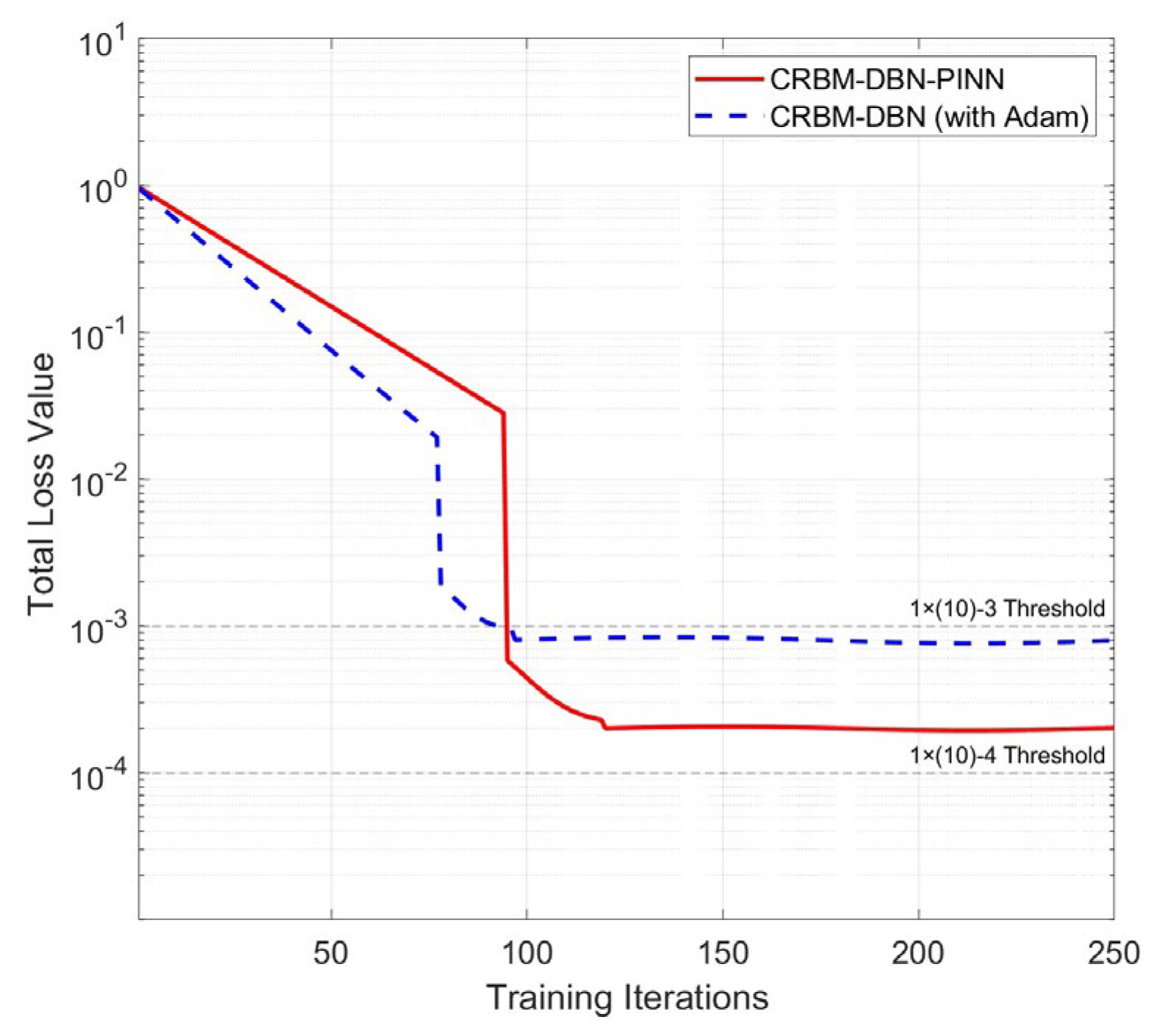
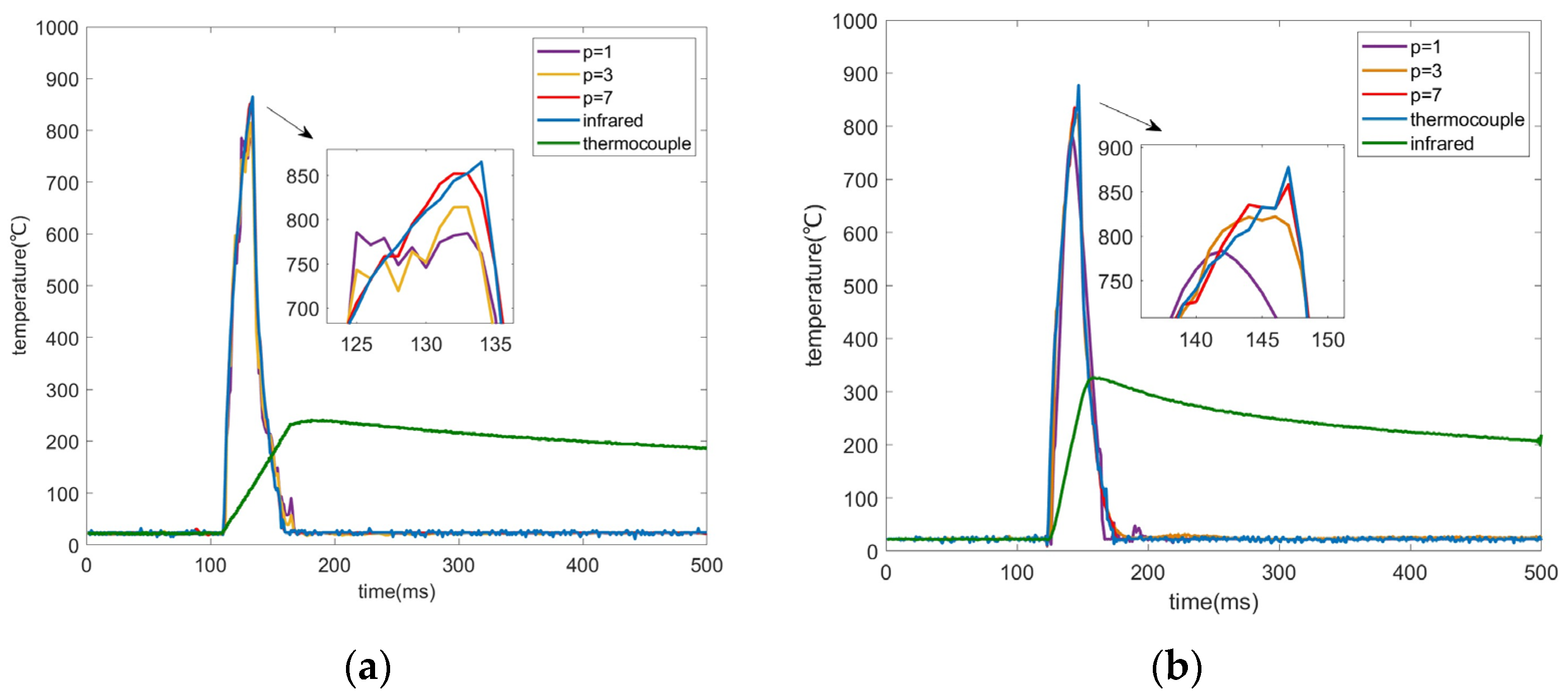



| Sobolev Order p | 0.25 mm Butt-Welded | 0.25 mm Ball-Welded | ||||
|---|---|---|---|---|---|---|
| Regularized Peak Value (°C) | Infrared Value (°C) | Relative Error (%) | Regularized Peak value (°C) | Infrared Value (°C) | Relative Error (%) | |
| 1 | 790.0 | 878.6 | 10.1 | 783.8 | 865.2 | 9.4 |
| 3 | 831.3 | 5.4 | 814.0 | 5.9 | ||
| 7 | 858.1 | 2.3 | 852.3 | 1.5 | ||
| Junction | Average Peak Temperature (°C) | Average Infrared Temperature (°C) | Peak Relative Error (%) | Rise Time Improved (ms) | R2 |
|---|---|---|---|---|---|
| 0.25 mm butt-welded | 858.4 | 864.9 | 0.75 | 11 | 0.947 |
| 0.25 mm ball-welded | 857.1 | 869.4 | 1.41 | 31 | 0.924 |
| 0.38 mm butt-welded | 847.1 | 859.8 | 2.06 | 11 | 0.925 |
| 0.38 mm ball-welded | 850.9 | 868.9 | 2.07 | 31 | 0.916 |
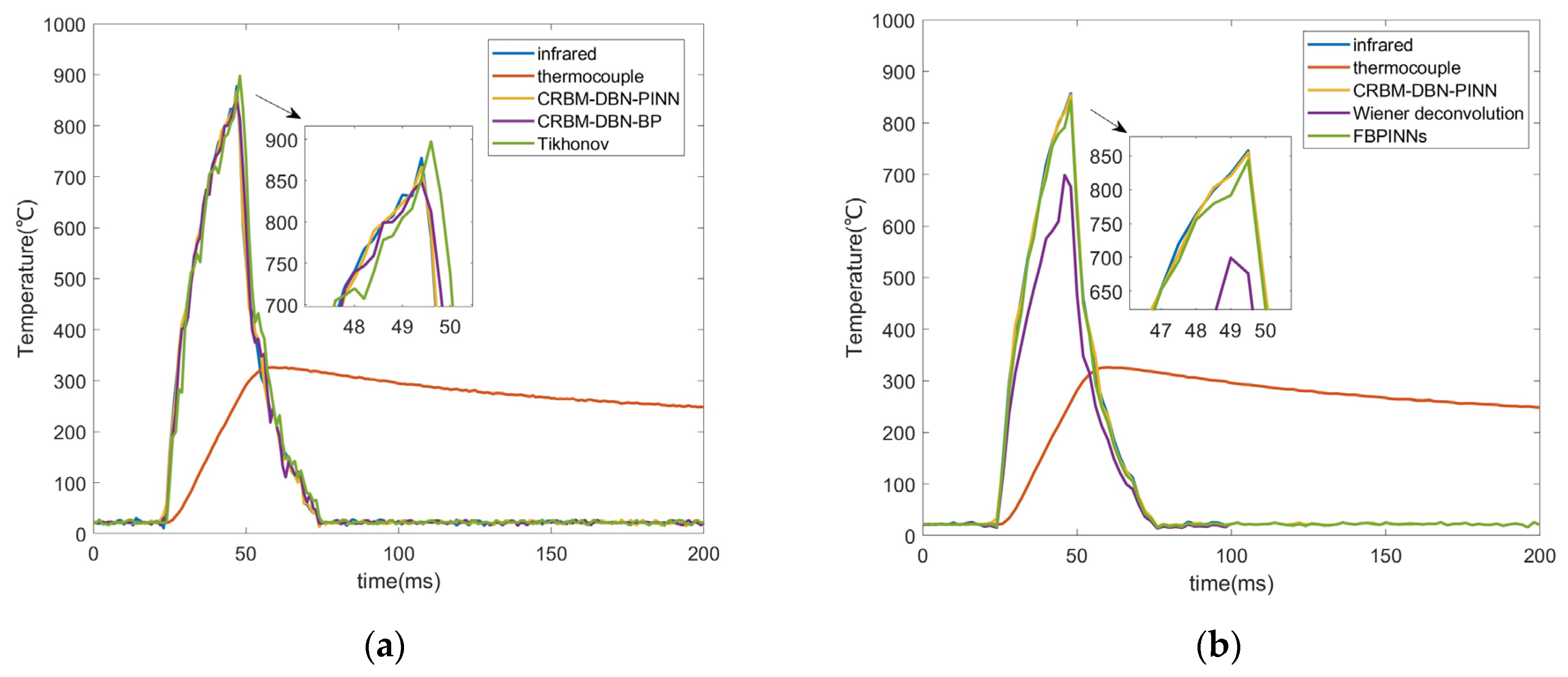
| Correction Algorithm | Average Peak Temperature (°C) | Average Infrared Temperature (°C) | Peak Relative Error (%) | Rise Time Improved (ms) | R2 |
|---|---|---|---|---|---|
| Tikhonov | 897.4 | 877.5 | −2.2 | 10 | 0.833 |
| Wiener | 698.5 | 20.40 | 8 | 0.662 | |
| FBPINNS | 865.2 | 1.40 | 12 | 0.908 | |
| CRBM-DBN-BP | 859.5 | 2.05 | 12 | 0.902 | |
| CRBM-DBN-PINN | 870.2 | 0.83 | 12 | 0.948 |
| Emissivity | Corrected Peak Temperature (°C) | Infrared Temperature (°C) | Peak Relative Error (%) | NMSE |
|---|---|---|---|---|
| 0.38 | 865.3 | 878.6 | 1.19 | 0.010 |
| 0.39 | 868.1 | 878.6 | 1.04 | 0.009 |
| 0.40 (Default) | 870.2 | 878.6 | 0.96 | 0.008 |
| 0.41 | 872.5 | 878.6 | 0.86 | 0.008 |
| 0.42 | 874.8 | 878.6 | 0.69 | 0.009 |
| Junction | Original Peak (°C) | Corrected Peak (°C) | Theoretical Peak (°C) | RE% (Original and Theoretical) | RE% (Revised and Theoretical) | Rise Time Improved (ms) |
|---|---|---|---|---|---|---|
| Ball-welded | 273.4 | 949.9 | 1103.1 | 75.2% | 13.7% | 26 |
| Butt-welded | 246.5 | 1045.7 | 77.7% | 5.1% | 6 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, C.; Zhou, G.; Zhang, J.; Zhang, Z.; Huang, G.; Xie, Q. Dynamic Error Correction for Fine-Wire Thermocouples Based on CRBM-DBN with PINN Constraint. Symmetry 2025, 17, 1831. https://doi.org/10.3390/sym17111831
Zhao C, Zhou G, Zhang J, Zhang Z, Huang G, Xie Q. Dynamic Error Correction for Fine-Wire Thermocouples Based on CRBM-DBN with PINN Constraint. Symmetry. 2025; 17(11):1831. https://doi.org/10.3390/sym17111831
Chicago/Turabian StyleZhao, Chenyang, Guangyu Zhou, Junsheng Zhang, Zhijie Zhang, Gang Huang, and Qianfang Xie. 2025. "Dynamic Error Correction for Fine-Wire Thermocouples Based on CRBM-DBN with PINN Constraint" Symmetry 17, no. 11: 1831. https://doi.org/10.3390/sym17111831
APA StyleZhao, C., Zhou, G., Zhang, J., Zhang, Z., Huang, G., & Xie, Q. (2025). Dynamic Error Correction for Fine-Wire Thermocouples Based on CRBM-DBN with PINN Constraint. Symmetry, 17(11), 1831. https://doi.org/10.3390/sym17111831





