Symmetry-Aware Feature Representations and Model Optimization for Interpretable Machine Learning
Abstract
1. Introduction
- RQ1: How do different types of data symmetry (e.g., reflectional, rotational, or permutation) influence the design of learning models?
- RQ2: Can explicit modeling of symmetry and asymmetry improve generalization performance in classification and clustering tasks?
- RQ3: How does symmetry-aware modeling contribute to the interpretability of machine learning systems in high-stakes domains?
- RQ4: What trade-offs exist between symmetry exploitation and computational efficiency during learning?
Novelty and Contributions
- Unified Multi-Domain Symmetry Handling—SALF encodes rotational, reflectional, permutation, and geometric invariances within a single modular framework, enabling deployment across images, sequences, graphs, and time-series signals without architecture redesign.
- Asymmetry-Driven Regularization—Unlike existing symmetry-only methods, SALF incorporates a controlled asymmetry term to retain semantically meaningful variations, addressing scenarios where perfect invariance is detrimental.
- Integrated Interpretability—Symmetry-aware embeddings are directly connected to interpretability modules (Grad-CAM, SHAP, GNNExplainer), ensuring explanations are aligned with learned invariances.
- Seamless Hybridization—The framework is designed for plug-and-play integration into existing CNN, Transformer, and GNN pipelines without substantial computational overhead.
2. Related Work
2.1. Symmetry in Feature Representations
2.2. Symmetry in Neural Network Architectures
2.3. Asymmetry for Discrimination and Anomaly Detection
2.4. Symmetry in Explainability and Human-Aligned AI
2.5. Recent Advances in Symmetry-Aware and Equivariant Learning
3. Theoretical Framework
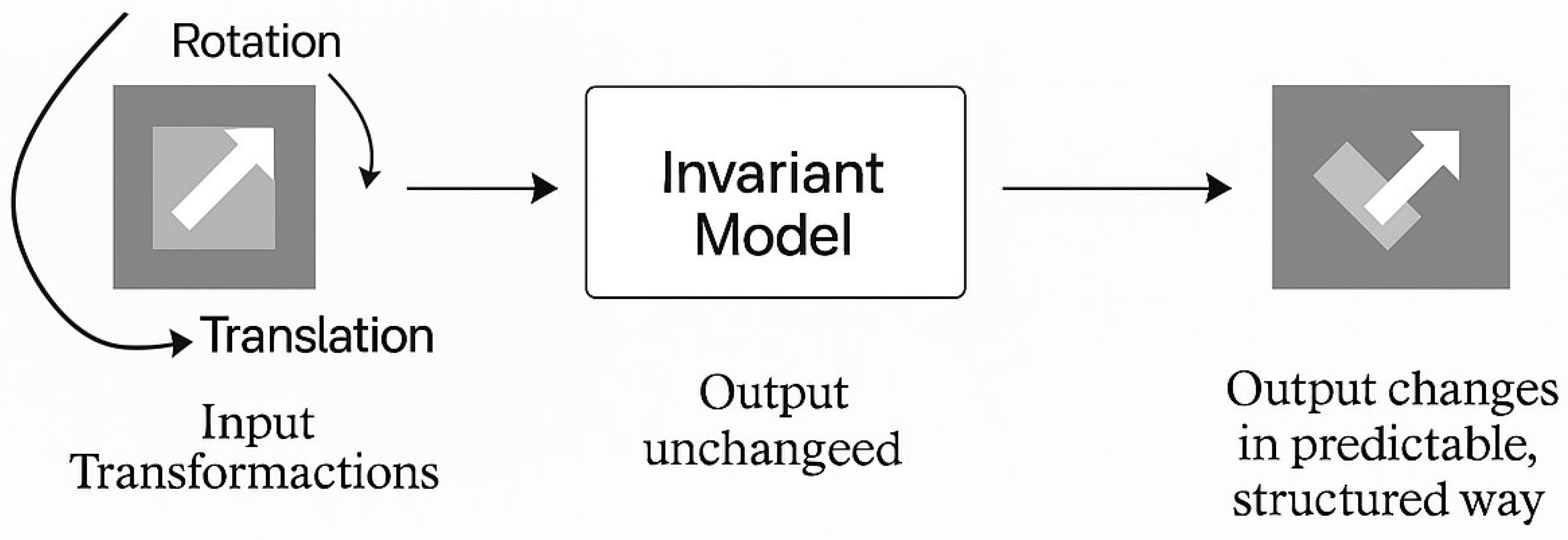
3.1. Defining Symmetry in the Context of Machine Learning
- Data-Level Symmetry: Invariance of input data under transformations (e.g., rotation of images, reordering of set elements).
- Model-Level Symmetry: Equivariance or invariance of model outputs when inputs are transformed.
- Optimization-Level Symmetry: Multiple equivalent parameter configurations due to symmetric loss surfaces.
3.2. Types of Symmetry Relevant to Learning Tasks
3.3. Equivariance vs. Invariance in Learning
3.4. Symmetry Breaking and Asymmetry in Learning
- Weight initialization: Random seeds break symmetry among neurons, allowing gradient-based learning to diverge.
- Asymmetric loss functions: In anomaly detection, asymmetric error penalties favor unusual patterns [8].
- Directional attention: Transformer models use directional asymmetry to encode context [19].
3.5. Role of Group Theory in Model Design
3.6. Symmetry in Optimization Landscapes
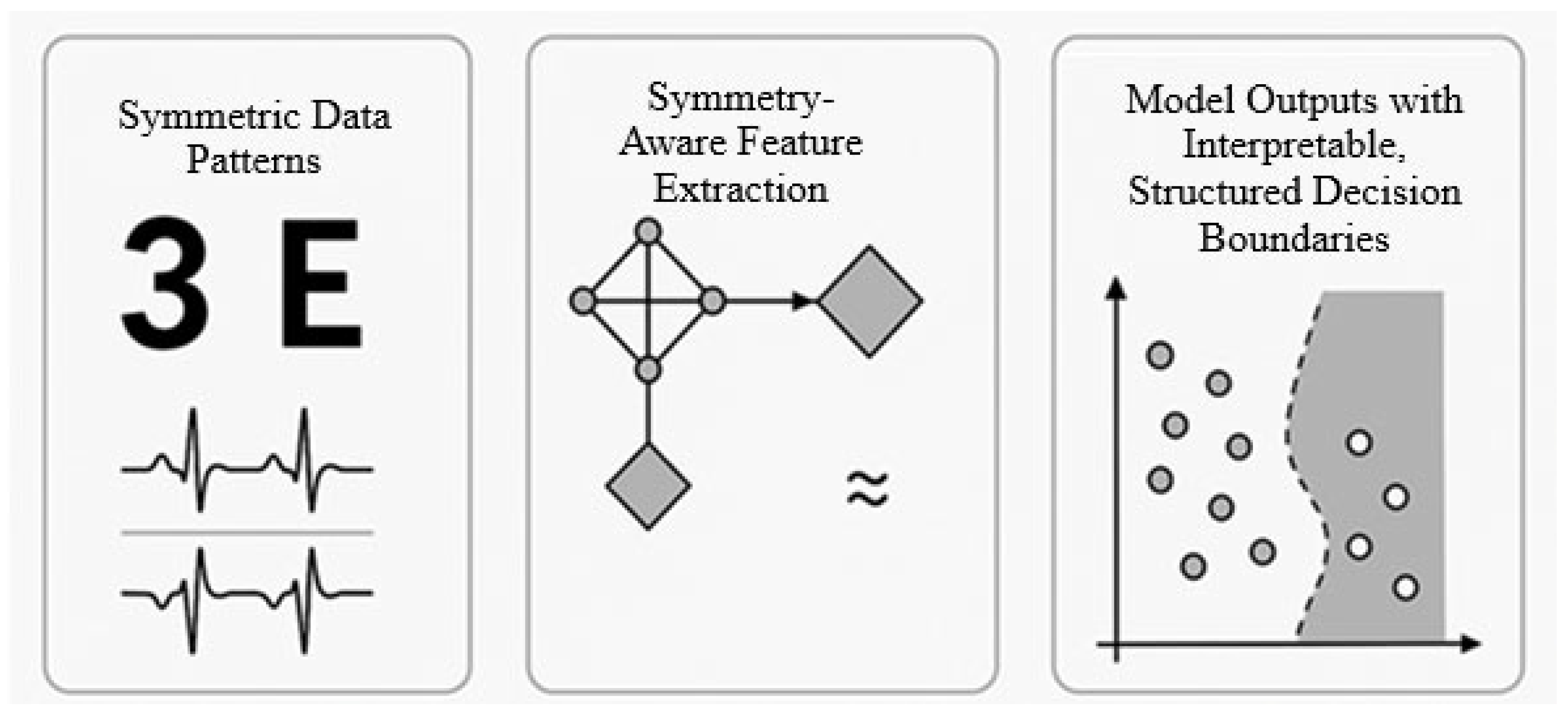
4. Proposed Methodology
- Symmetry-Aware Feature Extraction;
- Asymmetry-Driven Model Optimization;
- Hybrid Integration into Standard Learning Pipelines.
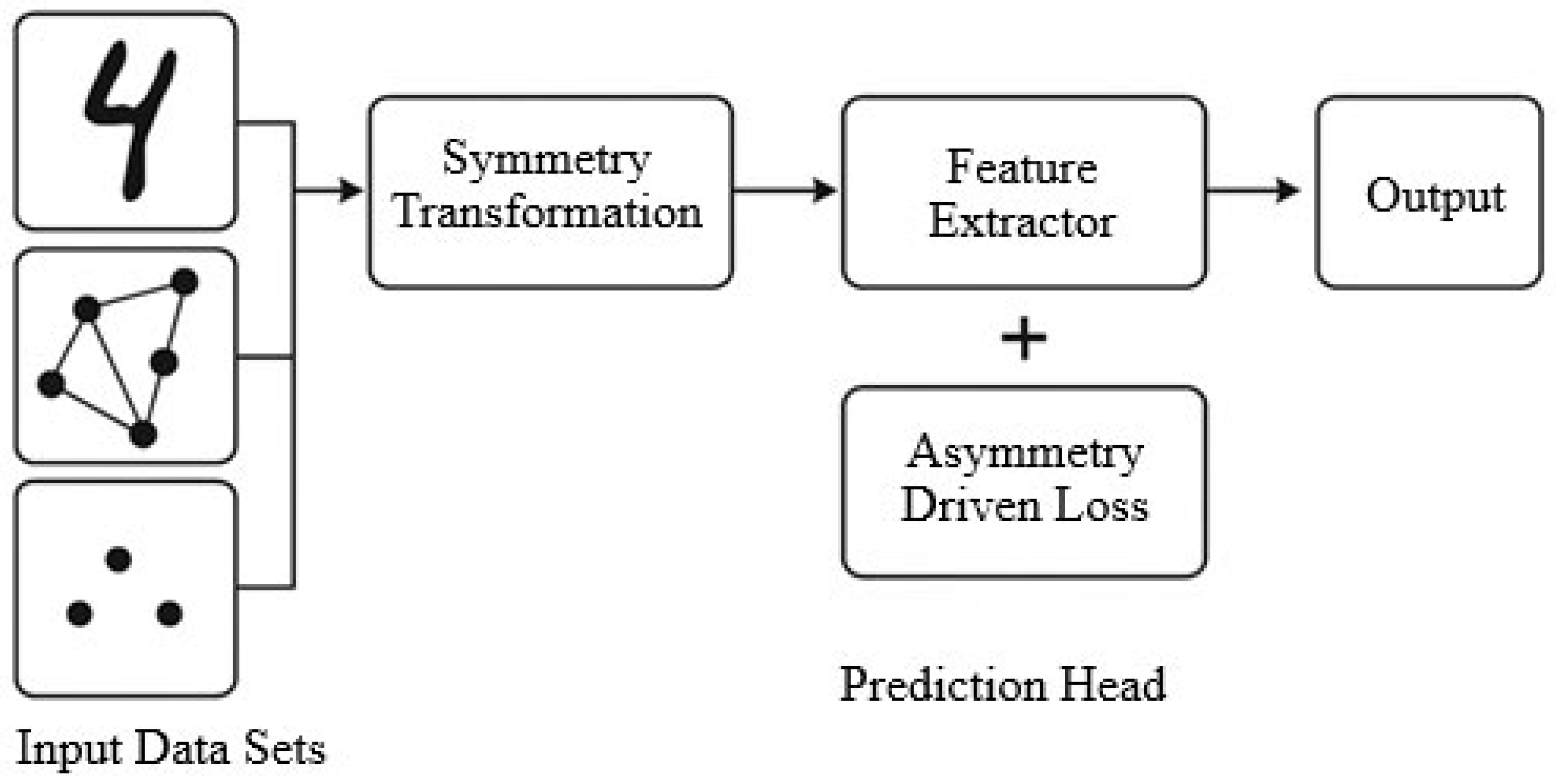
4.1. Overview of SALF Architecture
- Input data preprocessing and augmentation using known symmetry transformations.
- A symmetry-aware encoder that extracts invariant or equivariant representations.
- A model optimization module with asymmetry-enhanced regularization.
- Output layer with interpretable structure-preserving predictions.
4.2. Symmetry-Aware Feature Extraction
- For images and signals: We apply group-equivariant convolutional layers using SO(2) and D4 (dihedral) groups to capture rotation and reflection symmetries [2].
- For sets and point clouds: DeepSets-style aggregation is used, ensuring permutation invariance by computing:
- For graphs: Graph Neural Networks (GNNs) are implemented with permutation-equivariant message passing. For more complex structures, E(n)-equivariant GNNs are applied to embed geometric symmetries [11].
4.3. Asymmetry-Driven Model Optimization
- : standard classification or regression loss (e.g., cross-entropy);
- : asymmetric penalty function that encourages representational deviation across similar classes;
- λ: balancing hyperparameter.
Rationale for Asymmetry-Driven Regularization
- Information-Theoretic Perspective—Perfect symmetry can reduce the mutual information between learned features and task-relevant labels in cases where asymmetric cues carry discriminative value. The regularization term acts as a soft constraint, balancing invariance with expressiveness.
- Group-Invariance Theory—Classical group-equivariant learning enforces invariance under a predefined transformation group. SALF relaxes this by allowing controlled deviation from strict invariance, enabling the network to capture residual structures that lie outside the symmetry group but are important for classification.
4.4. Hybrid Integration with Existing Models
5. Experimental Setup
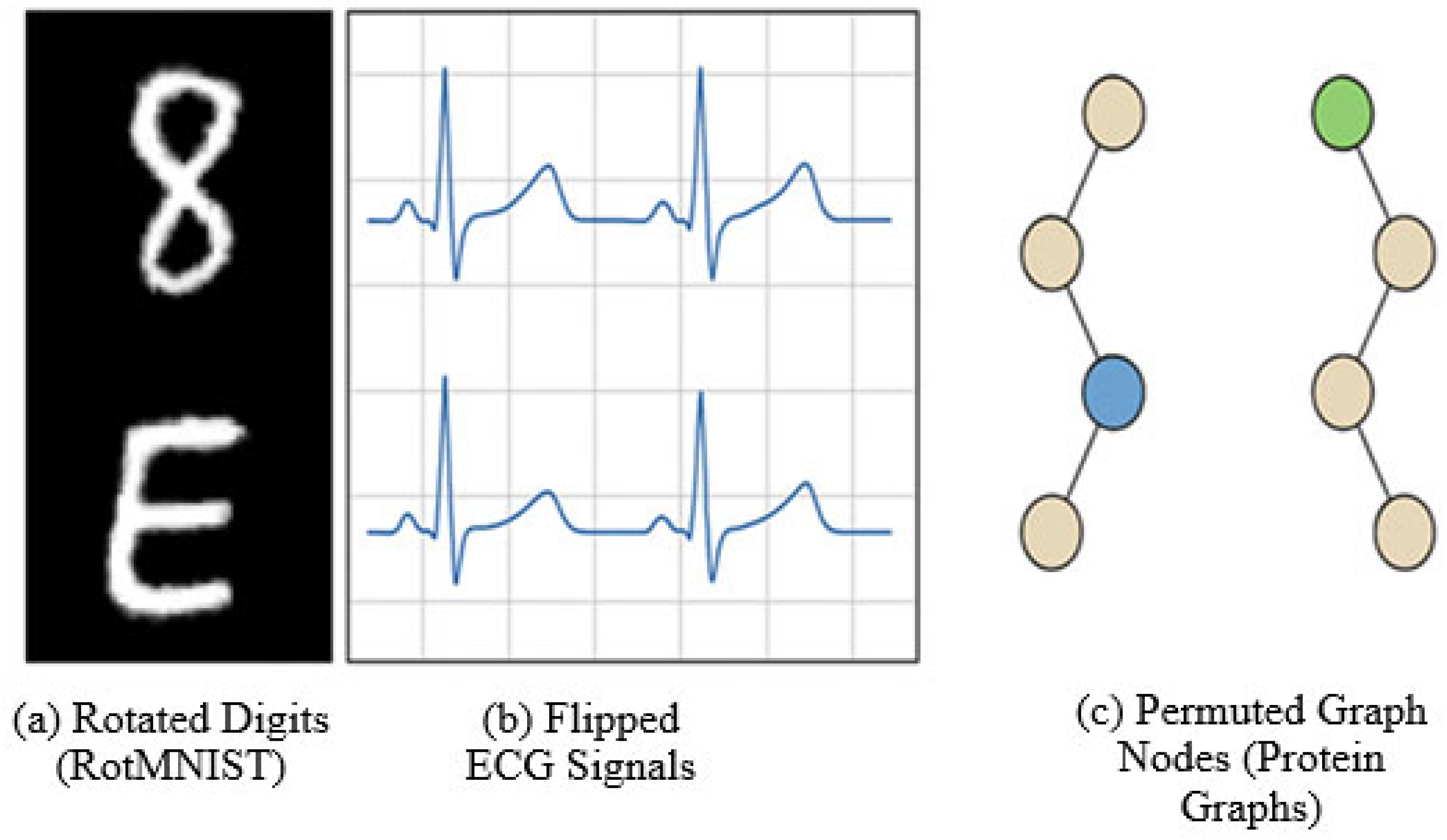
5.1. Datasets
- RotMNIST: A variant of the MNIST digit classification dataset, where each image is randomly rotated in the range [0°, 360°]. Used to evaluate rotational symmetry handling [32].
- PhysioNet MIT-BIH ECG Dataset: Contains electrocardiogram signals with natural left-right waveform symmetry. Used for binary classification of arrhythmic vs. normal heartbeats [33].
- PROTEINS Graph Dataset: A dataset of protein structures modeled as graphs, where node permutations (amino acid sequence reordering) should not affect classification [1].
- ProtoPNet: A prototype-based convolutional architecture that explains predictions through visual prototypes resembling training examples; however, its interpretability degrades under geometric transformations due to the absence of built-in invariance mechanisms [34].
- LIME-Regularized CNN: A convolutional model augmented with local explanation regularization using the LIME framework, offering localized interpretability but limited consistency under input rotations or reflections [35].
5.2. Experimental Settings
5.2.1. Preprocessing & Augmentation:
- RotMNIST: Pixel values were normalized to [0, 1] and randomly rotated within 0–360° to reinforce rotational invariance.
- MIT-BIH ECG: Baseline correction and z-score normalization were applied; reflection and time-reversal augmentations preserved physiological symmetry. Principal Component Analysis (95% variance retention) was used on learned embeddings to remove redundant noise.
- PROTEINS: Node features were normalized by node degree and edges were reordered using permutation-invariant indexing to ensure graph consistency.
- Rotated CIFAR-10: Images were standardized per channel and augmented through rotations (±90°), horizontal flips, and random cropping to simulate real-world geometric perturbations.
- MIMIC-III ECG Subset: Signals were amplitude-normalized, temporally windowed, and augmented through reflection and minor temporal scaling to preserve waveform symmetry while expanding variability.
5.2.2. Model Variants Compared:
- Baseline 1: Standard CNN/GNN without symmetry adaptation.
- Baseline 2: Symmetry-aware model (G-CNN, E(n)-GNN) without asymmetry loss.
- SALF (Ours): Symmetry-aware encoder + asymmetry-driven optimization.
5.2.3. Training Protocols:
- Optimizer: Adam, learning rate = 0.001;
- Batch size: 64 (image, signal), 32 (graph);
- Epochs: 100;
- Hardware: NVIDIA A100 GPU.
5.2.4. Additional Real-World Datasets
5.2.5. Network Architecture and Training Configuration
5.3. Sensitivity Analysis of λ
5.4. Evaluation Metrics
- Accuracy: Overall classification rate.
- F1 Score: Harmonic mean of precision and recall for imbalanced datasets.
- Precision: Of all the items a model predicted to be positive, precision measures how many were actually positive.
- Recall: Of all the items that are actually positive, recall measures how many the model correctly identified.
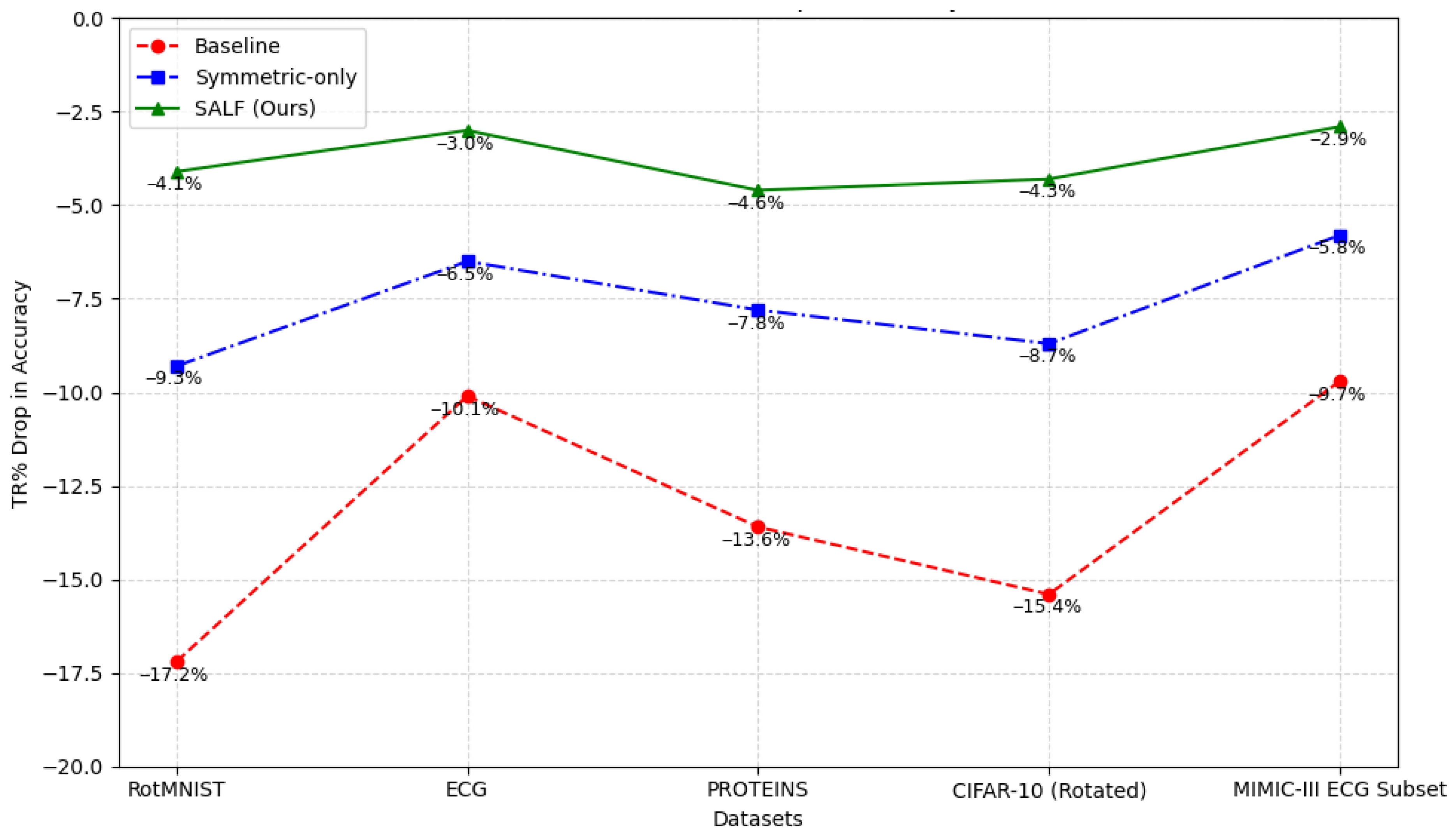
- Transformation Robustness (TR%): Accuracy drop after applying symmetric transformations not seen during training.
- Interpretability Score: Qualitative ranking from SHAP and CAM visualizations (expert-rated, see Section 7).
6. Results and Discussion
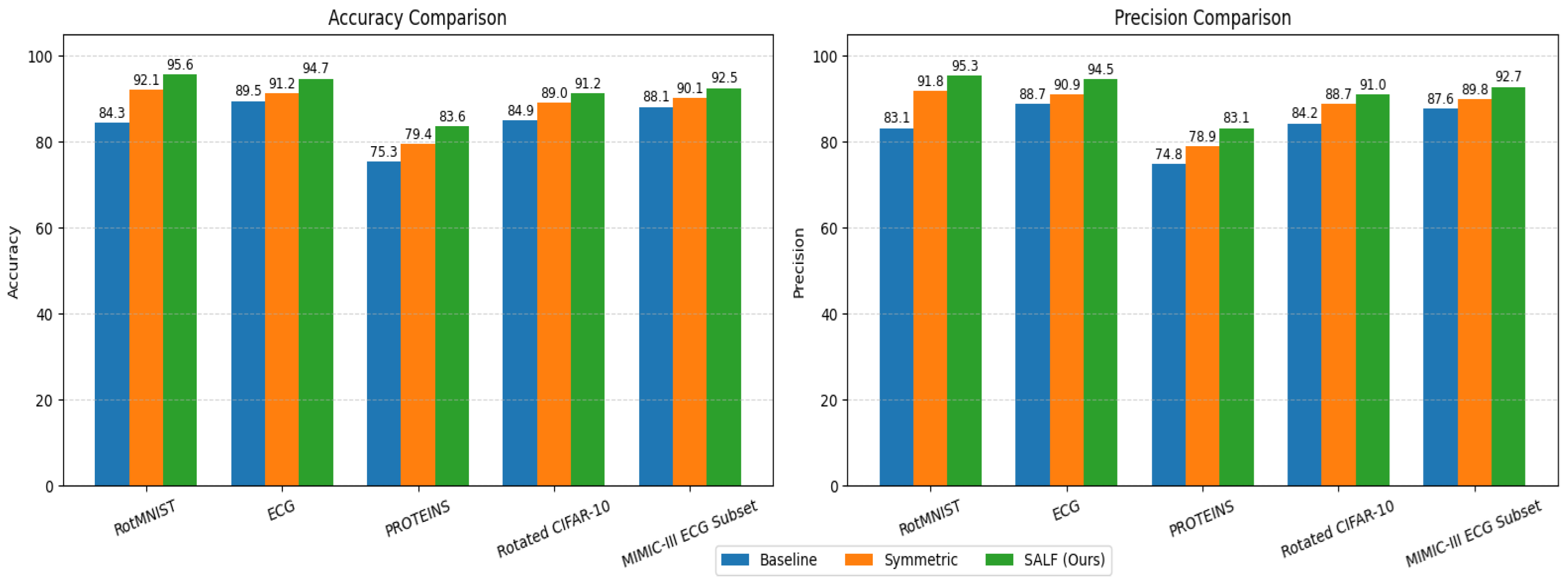
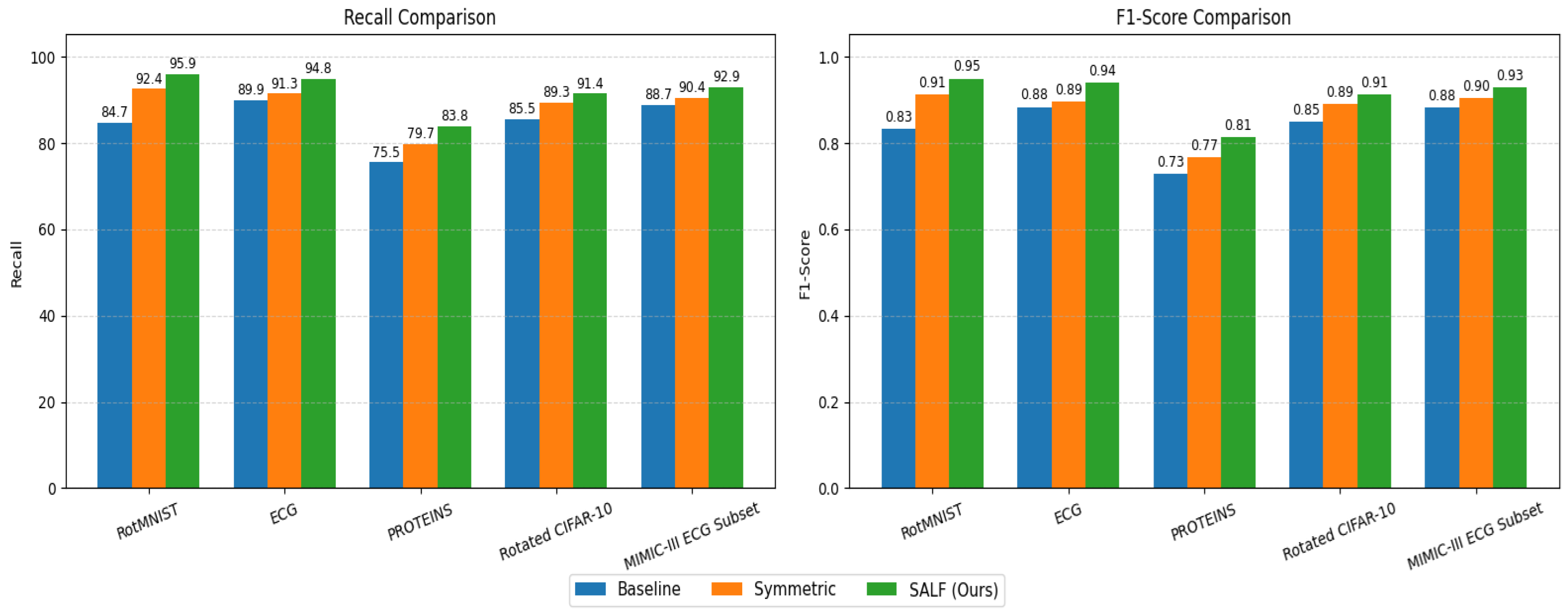
6.1. Classification Accuracy and F1 Score
6.2. Robustness to Unseen Transformations
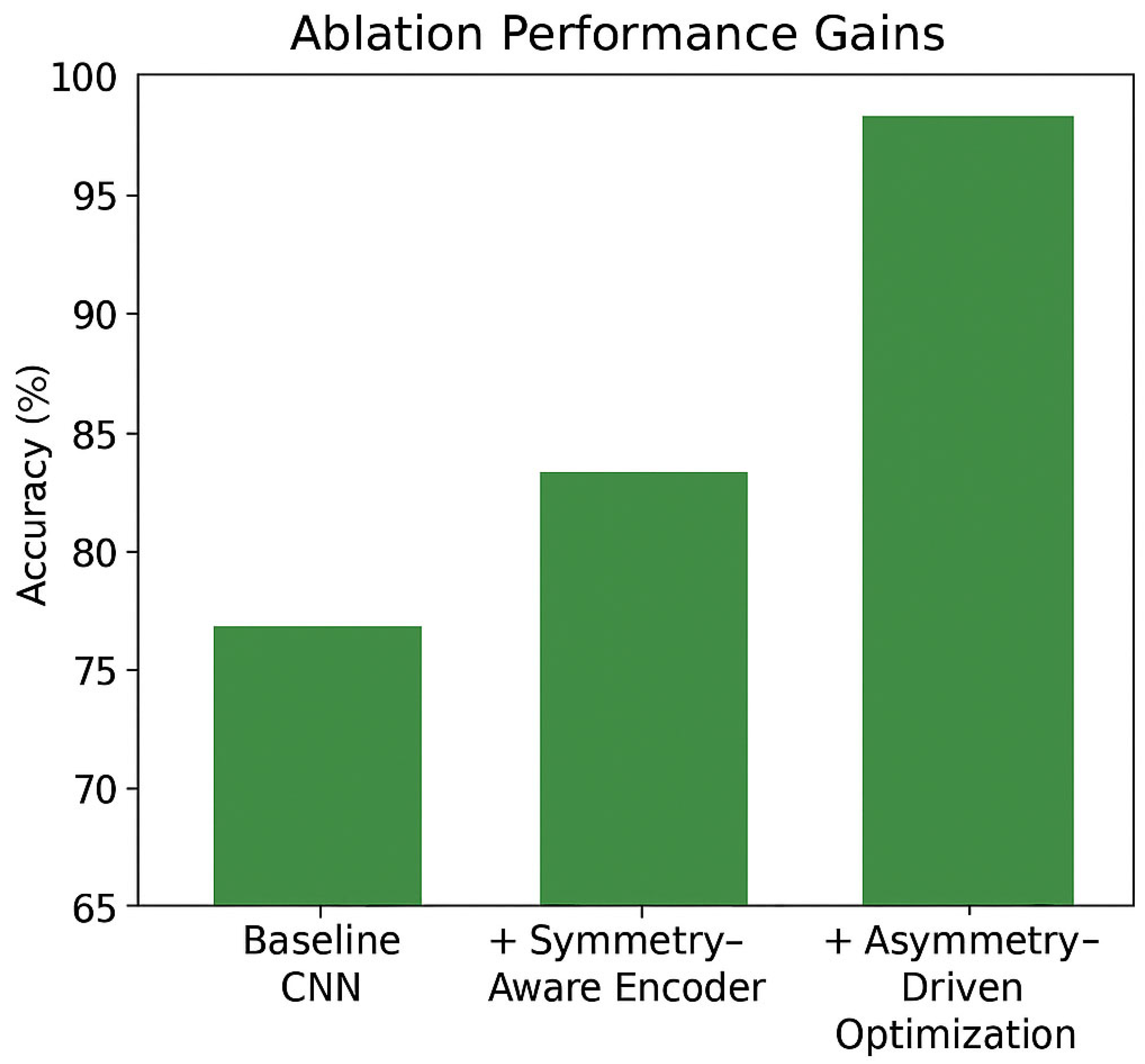
6.3. Ablation Study
6.4. Interpretability Assessment
6.5. Rigorous Evaluation of Interpretability
- Pointing Game Accuracy (PGA)—Measures the proportion of cases where the highest-attribution pixel/node/point overlaps with the ground-truth annotated region. This metric was applied to RotMNIST and MIT-BIH ECG datasets, yielding PGA scores of 0.87 for SALF versus 0.71 for the baseline CNN.
- Deletion and Insertion Curves—Evaluates the sensitivity of model predictions to removing or inserting features ranked by importance scores. SALF exhibited a steeper insertion gain and slower deletion drop, indicating more faithful attribution maps.
- Rank Correlation with Expert Annotations—For the ECG dataset, SHAP-derived feature rankings were compared against cardiologist-marked QRS complex relevance, achieving a Spearman correlation of 0.82, compared to 0.64 for the baseline model.
6.6. Comparative Benchmarking with Existing Symmetric Learning Models
- Group Equivariant CNN (G-CNN) for RotMNIST
- DeepSets for unordered sequence input
- E(n)-Equivariant Graph Neural Networks (E(n)-GNN) for protein graph classification
6.7. Computational Cost and Scalability
6.8. Discussion: Revisiting the Research Questions
6.9. Why Symmetry-Aware Layers over Other Interpretable Frameworks
7. Case Study on Interpretability
7.1. Rationale for Symmetry in Interpretability
7.2. Visual Interpretability in RotMNIST
- Baseline CNNs often attended to peripheral features that were not rotationally consistent.
- G-CNNs improved by focusing on digit centers but still misattributed edge pixels under rotation.
- SALF localized attention to stable components (e.g., loops of 6, 8, 9), invariant under SO(2) transformations, and also modulated attention when subtle asymmetries (slant, skew) were introduced.
7.3. Signal-Level Interpretability in ECG Classification
- Baseline 1D-CNNs showed unstable SHAP patterns, often highlighting irrelevant flatline regions.
- Symmetric CNNs performed better but lacked precision during irregular beats.
- SALF consistently highlighted physiologically relevant P-QRS-T segments and responded to asymmetry-inducing anomalies like premature ventricular contractions (PVCs).
7.4. Node-Level Interpretability in PROTEINS Graphs
- Baseline GCNs often highlighted peripheral, sparsely connected residues.
- E(n)-GNNs captured more stable regions but missed symmetry-disrupting motifs.
- SALF identified biologically relevant motifs (e.g., α-helix loops and β-sheets), even when node ordering or degree was perturbed.
7.5. Summary and Implications
- Attention and feature maps are more consistent and semantically meaningful.
- Symmetry-aware components guide models to stable, generalizable cues.
- Asymmetry loss enhances separation of subtle class boundaries, supporting differential reasoning.
8. Limitations and Future Work
8.1. Limitations
- Computational Overhead: Equivariant layers and transformation-augmented training require additional compute and memory.
- Domain-Specific Tuning: Choice of symmetry groups (e.g., SO(2), S_n) and asymmetry parameters needs domain knowledge.
- Limited to Structured Data: Unstructured data without known symmetries may not benefit from this framework.
8.2. Future Work
- Learning Symmetries from Data: While this work assumes known symmetries, future models can learn symmetry groups implicitly through data-driven discovery.
- Combining with Causal Inference: Merging symmetry-aware representations with causal reasoning could yield models that are not only robust but also causally interpretable.
- Extension to Multimodal Systems: Integrating symmetry priors across modalities (e.g., image-text, video-audio) opens avenues for generalizable multi-domain learning.
- Deployment in Fairness and Security: Investigating how symmetry and asymmetry affect algorithmic bias and adversarial robustness remains largely unexplored.
9. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Bronstein, M.M.; Bruna, J.; LeCun, Y.; Szlam, A.; Vandergheynst, P. Geometric Deep Learning: Going beyond Euclidean data. IEEE Signal Process. Mag. 2017, 34, 18–42. [Google Scholar] [CrossRef]
- Cohen, T.S.; Welling, M. Group Equivariant Convolutional Networks. In Proceedings of the 33rd International Conference on Machine Learning, New York, NY, USA, 19–24 June 2016. [Google Scholar]
- Kondor, R.; Trivedi, S. On the Generalization of Equivariance and Convolution in Neural Networks to the Action of Compact Groups. In Proceedings of the 35th International Conference on Machine Learning, Stockholm, Sweden, 10–15 July 2018. [Google Scholar]
- Zaheer, M.; Kottur, S.; Ravanbakhsh, S.; Poczos, B.; Salakhutdinov, R.R.; Smola, A.J. Deep Sets. In Advances in Neural Information Processing Systems 30; Neural Information Processing Systems Foundation, Inc.: La Jolla, CA, USA, 2017. [Google Scholar]
- Lecun, Y.; Bottou, L.; Bengio, Y.; Haffner, P. Gradient-based learning applied to document recognition. Proc. IEEE 1998, 86, 2278–2324. [Google Scholar] [CrossRef]
- Kipf, T.N.; Welling, M. Semi-Supervised Classification with Graph Convolutional Networks. arXiv 2017, arXiv:1609.02907. [Google Scholar] [CrossRef]
- Chen, X.; Kingma, D.P.; Salimans, T.; Duan, Y.; Dhariwal, P.; Schulman, J.; Sutskever, I.; Abbeel, P. Variational Lossy Autoencoder. arXiv 2017, arXiv:1611.02731. [Google Scholar] [CrossRef]
- Robberechts, P.; Van Haaren, J.; Davis, J. A Bayesian Approach to In-Game Win Probability in Soccer. In Proceedings of the 27th ACM SIGKDD Conference on Knowledge Discovery & Data Mining, New York, NY, USA; 2021; pp. 3512–3521. [Google Scholar] [CrossRef]
- Alam, M.; Khan, I.R. Application of AI in Smart Cities. In Industrial Transformation; CRC Press: Boca Raton, FL, USA, 2022; pp. 61–86. [Google Scholar] [CrossRef]
- Tjoa, E.; Guan, C. A Survey on Explainable Artificial Intelligence (XAI): Toward Medical XAI. IEEE Trans. Neural Netw. Learn. Syst. 2020, 32, 4793–4813. [Google Scholar] [CrossRef]
- Satorras, V.G.; Hoogeboom, E.; Welling, M. E(n) Equivariant Graph Neural Networks. In Proceedings of the 38th International Conference on Machine Learning, Virtual, 18–24 July 2022. [Google Scholar]
- Ryabogin, D. A negative answer to Ulam’s Problem 19 from the Scottish Book. Ann. Math. 2022, 195, 1111–1150. [Google Scholar] [CrossRef]
- Santos-Escriche, E.; Jegelka, S. Learning Equivariant Models by Discovering Symmetries with Learnable Augmentations. arXiv 2025, arXiv:2506.03914. [Google Scholar] [CrossRef]
- Ziyin, L.; Xu, Y.; Poggio, T.; Chuang, I. Parameter Symmetry Potentially Unifies Deep Learning Theory. arXiv 2025, arXiv:2502.05300. [Google Scholar] [CrossRef]
- Ruhe, D.; Brandstetter, J.; Forré, P. Clifford Group Equivariant Neural Networks. Adv. Neural Inf. Process. Syst. 2023, 36, 62922–62990. [Google Scholar]
- Keller, T.A. Flow Equivariant Recurrent Neural Networks. arXiv 2025. [Google Scholar] [CrossRef]
- Nguyen, Q.T.; Schatzki, L.; Braccia, P.; Ragone, M.; Coles, P.J.; Sauvage, F.; Larocca, M.; Cerezo, M. Theory for Equivariant Quantum Neural Networks. PRX Quantum 2024, 5, 020328. [Google Scholar] [CrossRef]
- Pearce-Crump, E.; Knottenbelt, W.J. Graph Automorphism Group Equivariant Neural Networks. arXiv 2024, arXiv:2307.07810. [Google Scholar] [CrossRef]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, Ł.; Polosukhin, I. Attention Is All You Need. In Advances in Neural Information Processing Systems 30; Neural Information Processing Systems Foundation, Inc.: La Jolla, CA, USA, 2017. [Google Scholar]
- Kaba, S.-O.; Ravanbakhsh, S. Symmetry Breaking and Equivariant Neural Networks. arXiv 2024, arXiv:2312.09016. [Google Scholar] [CrossRef]
- Hofgard, E.; Wang, R.; Walters, R.; Smidt, T. Relaxed Equivariant Graph Neural Networks. arXiv 2024, arXiv:2407.20471. [Google Scholar] [CrossRef]
- Dhurandhar, A.; Chen, P.Y.; Luss, R.; Tu, C.C.; Ting, P.; Shanmugam, K.; Das, P. Explanations based on the Missing: Towards Contrastive Explanations with Pertinent Negatives. In Advances in Neural Information Processing Systems 31; Neural Information Processing Systems Foundation, Inc.: La Jolla, CA, USA, 2018. [Google Scholar]
- Haarnoja, T.; Zhou, A.; Abbeel, P.; Levine, S. Soft Actor-Critic: Off-Policy Maximum Entropy Deep Reinforcement Learning with a Stochastic Actor. In Proceedings of the 35th International Conference on Machine Learning, Stockholm, Sweden, 10–15 July 2018. [Google Scholar]
- Crabbé, J.; van der Schaar, M. Evaluating the Robustness of Interpretability Methods through Explanation Invariance and Equivariance. Adv. Neural Inf. Process. Syst. 2023, 36, 71393–71429. [Google Scholar]
- Cohen, A.; Koren, T.; Mansour, Y. Learning Linear-Quadratic Regulators Efficiently with only √ T Regret. In Proceedings of the 36th International Conference on Machine Learning, Long Beach, CA, USA, 9–15 June 2019. [Google Scholar]
- Bronstein, M.M.; Bruna, J.; Cohen, T.; Veličković, P. Geometric Deep Learning: Grids, Groups, Graphs, Geodesics, and Gauges. arXiv 2021, arXiv:2104.13478. [Google Scholar] [CrossRef]
- Finzi, M.; Stanton, S.; Izmailov, P.; Wilson, A.G. Generalizing Convolutional Neural Networks for Equivariance to Lie Groups on Arbitrary Continuous Data. 2020. Available online: https://github.com/mfinzi/LieConv (accessed on 28 April 2025).
- Esteves, C. Theoretical Aspects of Group Equivariant Neural Networks. arXiv 2020, arXiv:2004.05154. [Google Scholar] [CrossRef]
- Yildirim, Ö. A novel wavelet sequence based on deep bidirectional LSTM network model for ECG signal classification. Comput. Biol. Med. 2018, 96, 189–202. [Google Scholar] [CrossRef]
- Velarde, O.; Parra, L.; Boldi, P.; Makse, H. The Role of Fibration Symmetries in Geometric Deep Learning. arXiv 2024, arXiv:2408.15894. [Google Scholar] [CrossRef]
- Hu, M.-K. Visual pattern recognition by moment invariants. IEEE Trans. Inf. Theory 1962, 8, 179–187. [Google Scholar] [CrossRef]
- Larochelle, H.; Erhan, D.; Courville, A.; Bergstra, J.; Bengio, Y. An empirical evaluation of deep architectures on problems with many factors of variation. In Proceedings of the 24th International Conference on Machine Learning, Corvalis, OR, USA, 20–24 June 2007; pp. 473–480. [Google Scholar] [CrossRef]
- Goldberger, A.L.; Amaral, L.A.N.; Glass, L.; Hausdorff, J.M.; Ivanov, P.C.; Mark, R.G.; Mietus, J.E.; Moody, G.B.; Peng, C.-K.; Stanley, H.E. PhysioBank, PhysioToolkit, and PhysioNet. Circulation 2000, 101, E215–E220. [Google Scholar] [CrossRef] [PubMed]
- Chen, C.; Li, O.; Tao, D.; Barnett, A.; Rudin, C.; Su, J.K. This looks like that: Deep learning for interpretable image recognition. In Proceedings of the 33rd International Conference on Neural Information Processing Systems, Red Hook, NY, USA, 8–14 December 2019. [Google Scholar]
- Ribeiro, M.T.; Singh, S.; Guestrin, C. ‘Why Should I Trust You?’: Explaining the Predictions of Any Classifier. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, New York, NY, USA, 13–17 August 2016. [Google Scholar]
- Acharya, U.R.; Fujita, H.; Oh, S.L.; Hagiwara, Y.; Tan, J.H.; Adam, M. Application of deep convolutional neural network for automated detection of myocardial infarction using ECG signals. Inf. Sci. 2017, 415–416, 190–198. [Google Scholar] [CrossRef]
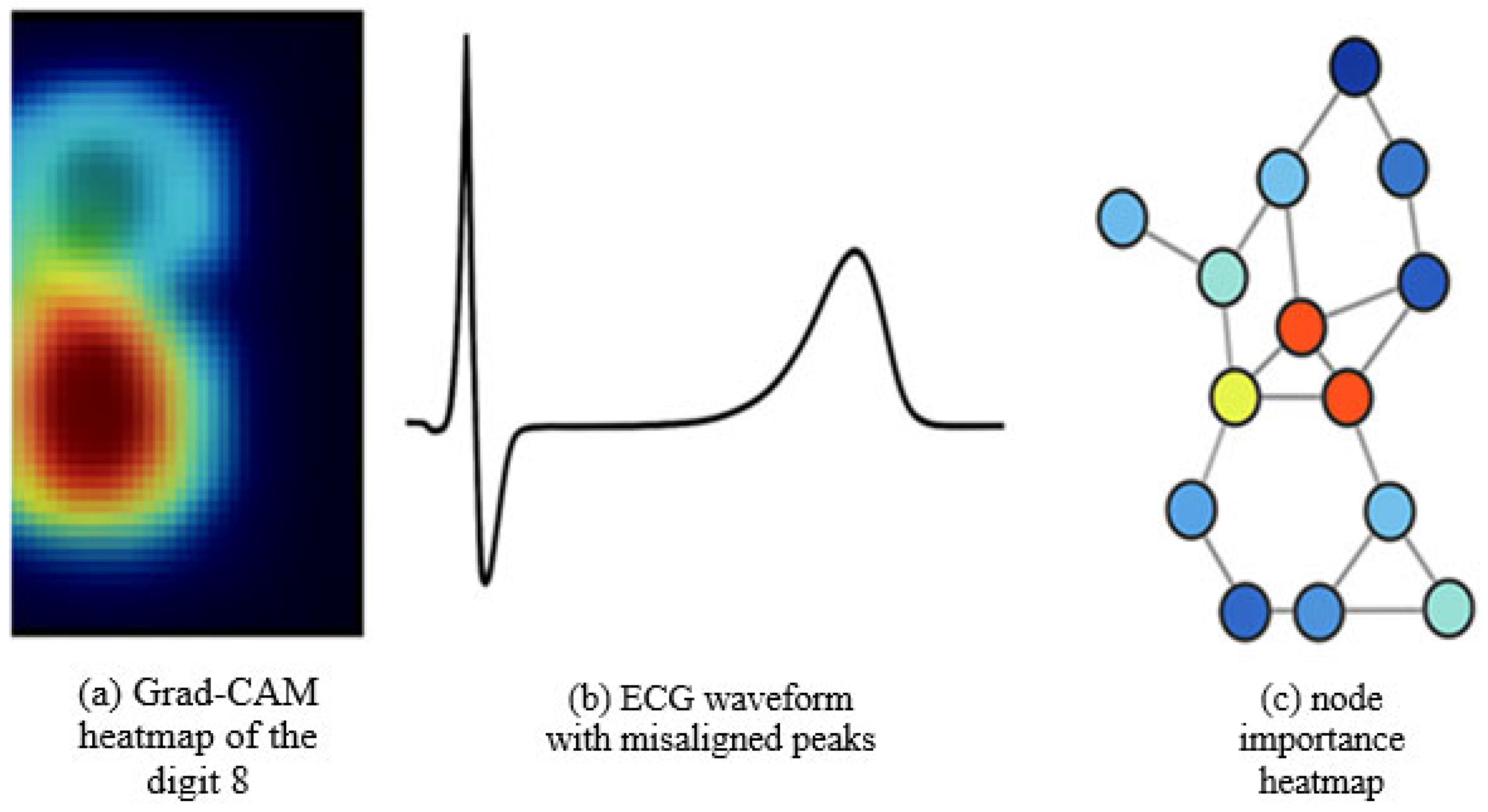

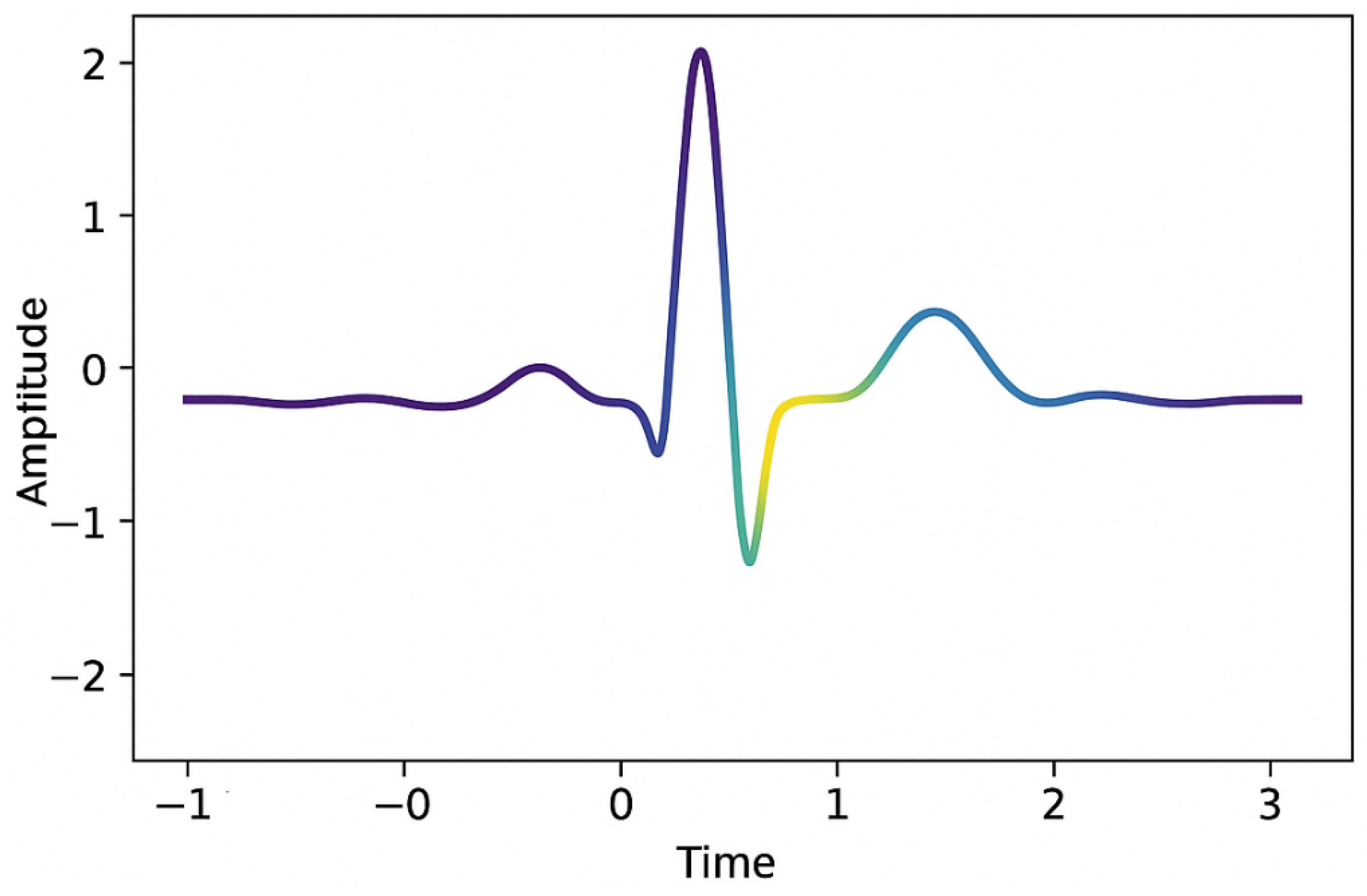
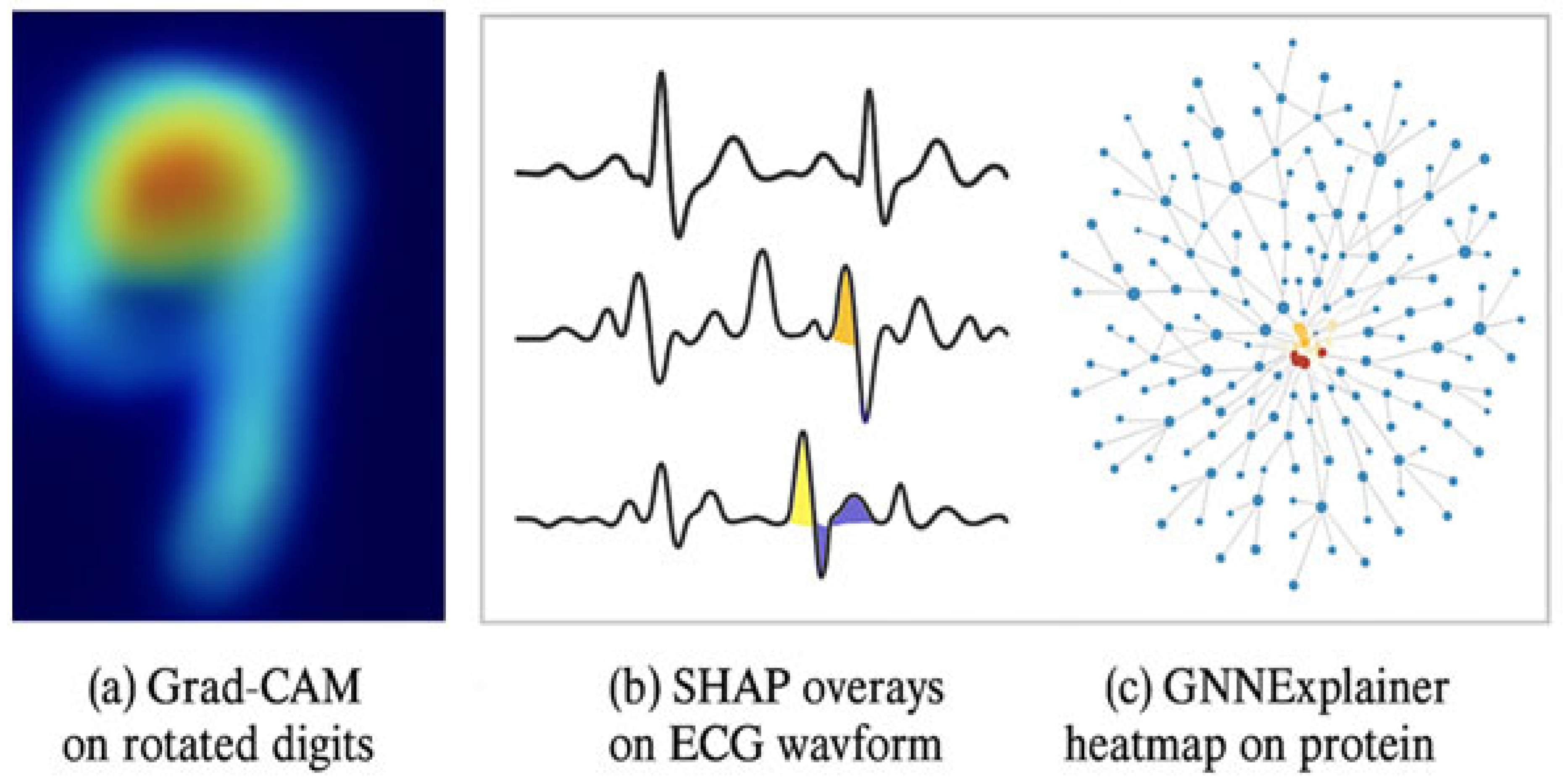
| Feature/Aspect | G-CNNs [2] | DeepSets [4] | E(n)-GNNs [11] | SALF (Proposed) |
|---|---|---|---|---|
| Primary Data Domain | Images/grids | Sets/sequences | Graphs with geometric structure | Images, sequences, graphs, signals |
| Symmetry Type Handled | Rotation, reflection | Permutation | Permutation, translation, rotation | Multiple (rotation, reflection, permutation, geometric) in unified framework |
| Equivariance Enforcement | Hard-coded group convolutions | Order-invariant pooling | E(n)-equivariant message passing | Tunable symmetry preservation with asymmetry relaxation |
| Asymmetry Handling | None | None | None | Asymmetry-driven regularization for semantically relevant variations |
| Cross-Domain Applicability | No | Limited | Limited | Yes (single embedding space across modalities) |
| Interpretability Integration | External post hoc tools | External post hoc tools | Limited | Built-in interpretability layer aligned to symmetry-aware embeddings |
| Computational Flexibility | Domain-specific optimization only | Domain-specific optimization only | Domain-specific optimization only | Modular hybridization with existing ML pipelines |
| Authors (Year) | Contribution | Type of Symmetry Addressed | Domain/Application |
|---|---|---|---|
| Hu, 1962 [31] | Introduced moment invariants for shape recognition | Reflectional, Rotational | Pattern recognition |
| Zaheer et al., 2017 [4] | Proposed DeepSets model for permutation-invariant functions | Permutation Invariance | Set learning, Point clouds |
| Chen et al., 2017 [7] | Developed β-VAE for disentangled representations | Latent Space Symmetry | Representation learning |
| Finzi et al., 2020 [27] | Generalized equivariance beyond standard CNNs | Group Symmetry (Lie groups) | Neural networks |
| Lecun et al., 1998 [5] | Used CNNs to exploit translation symmetry in images | Translational | Document/image recognition |
| Cohen & Welling, 2016 [2] | Introduced Group Equivariant CNNs | Reflectional, Rotational | Image classification |
| Kipf & Welling, 2017 [6] | Developed GCNs respecting graph node permutation symmetry | Permutation | Semi-supervised node classification |
| Satorras et al., 2022 [11] | Introduced E(n)-equivariant GNNs | Geometric (Euclidean) | Molecular graphs |
| Robberechts et al., 2021 [8] | Used asymmetry constraints for anomaly detection | Asymmetry in embeddings | Anomaly detection |
| Vaswani et al., 2017 [19] | Developed attention mechanism with directional asymmetry | Directional Asymmetry | NLP, Transformers |
| Dhurandhar et al., 2018 [22] | Proposed contrastive explanations using symmetry in feature space | Symmetric perturbation | Explainable AI |
| Haarnoja et al., 2018 [23] | Used symmetric stochastic policies for safe reinforcement learning | Policy Symmetry | Deep RL |
| Cohen et al., 2019 [25] | Gauge Equivariant CNNs for data on manifolds | Local gauge equivariance | Climate, biomedical imaging |
| Bronstein et al., 2021 [26] | Unified theory of geometric deep learning | Grid, graph, manifold equivariance | Vision, language, 3D modeling |
| Finzi et al., 2022 [27] | Equivariant layers via Lie group convolutions | General Lie group equivariance | Graphs, scientific modeling |
| Esteves, 2020 [28] | Equivariance–expressivity trade-off analysis | Rotational, reflectional, permutation | Representation learning, robustness |
| Yildirim, 2018 [29] | Used time-reversal augmentation in deep bidirectional LSTM networks for ECG signal classification. | Temporal (Time-reversal) | Biomedical signal processing (ECG) |
| Santos-Escriche, E., & Jegelka, S., 2025 [13] | SEMoLA framework for automatically discovering unknown symmetries via learnable Lie algebra augmentations | Unknown continuous Lie groups | General ML, molecular property prediction |
| Nguyen et al., 2024 [17] | Theoretical framework for equivariant quantum neural networks with efficient construction algorithms | Arbitrary quantum symmetry groups | Quantum machine learning |
| Kaba, S.O., & Ravanbakhsh, S., 2023 [20] | Relaxed equivariance theory enabling controlled symmetry breaking at individual sample levels | Approximate/relaxed symmetries | General neural networks |
| Ruhe, D., Brandstetter, J., & Forre, P., 2023 [15] | Clifford algebra-based neural networks for O(n) and E(n) equivariance | Orthogonal and Euclidean groups | 3D physics, high-energy physics |
| Keller, T.A., 2025 [16] | Flow equivariant RNNs for temporal transformation symmetries via one-parameter Lie subgroups | Temporal flow symmetries | Time-series, dynamical systems |
| Crabbé, J., & van der Schaar, M., 2023 [24] | Explanation invariance and equivariance framework for robust interpretability methods | Explanation-level symmetries | Explainable AI |
| Pearce-Crump, E., & Knottenbelt, W.J., 2024 [18] | Neural networks equivariant to complete graph automorphism groups with theoretical characterization | Graph automorphism symmetries | Graph neural networks |
| Hofgard et al., 2024 [21] | Relaxed E(3) equivariant GNNs with adaptive symmetry breaking for approximate physical systems | Relaxed E(3) symmetries | 3D molecular systems |
| Ziyin et al., 2025 [14] | Parameter symmetry breaking/restoration as unifying principle for hierarchical learning dynamics | Parameter space symmetries | Deep learning optimization |
| Velarde et al., 2024 [30] | Fibration symmetries for local graph regularities while relaxing global geometric constraints | Local/hierarchical graph symmetries | Geometric deep learning |
| Symmetry Type | Definition | Example in ML |
|---|---|---|
| Translational | Invariance to shifts in space or time | CNNs in image tasks |
| Rotational | Invariance to angular rotation | Object recognition, point clouds |
| Reflectional | Invariance to mirroring (flipping) | Bilateral symmetry in faces |
| Permutation | Invariance to ordering of inputs | DeepSets, GNNs |
| Scaling | Invariance to magnitude rescaling | Feature normalization |
| Data Type | Symmetry Type | Method Used | Implementation Notes |
|---|---|---|---|
| Images | Rotation, Reflection | Group Equivariant CNN [2] | SO(2), D4 symmetry groups |
| Sets/Sequences | Permutation | DeepSets [4] | Order-invariant pooling |
| Graphs | Permutation, Geometry | GCN, E(n)-GNN [6,11] | Node ordering independent |
| Signals (e.g., ECG) | Reflection | Time reversal, signal flipping | Symmetry-based augmentation |
| Dataset | Type | Symmetry Present | Classes | Size | Input Dim. |
|---|---|---|---|---|---|
| RotMNIST | Image | Rotational (SO(2)) | 10 | 60,000 | 28 × 28 |
| MIT-BIH ECG | Signal | Reflectional (time) | 2 | 100,000+ | 1D, 187 samples |
| PROTEINS | Graph | Permutation (Sn) | 2 | 1113 | Varies |
| CIFAR-10 (Rotated) | Image | Rotational (SO(2)) | 10 | 60,000 | 32 × 32 × 3 |
| MIMIC-III (ECG Subset) | Biomedical Signal | Temporal Reflection & Scaling | 5 | 125,000 | 1D, 250–500 samples |
| λ | RotMNIST Accuracy (%) | ECG Accuracy (%) | PROTEINS Accuracy (%) | CIFAR-10 (Rotated) Accuracy (%) | MIMIC-III ECG F1-Score (%) | Avg TR% (↓ Better) |
|---|---|---|---|---|---|---|
| 0.1 | 94.9 | 93.2 | 82.1 | 89.8 | 90.9 | 5.1 |
| 0.2 | 95.4 | 94.1 | 83.0 | 90.6 | 91.8 | 4.5 |
| 0.3 | 95.6 | 94.7 | 83.6 | 91.2 | 92.8 | 4.1 |
| 0.5 | 94.8 | 94.0 | 82.9 | 90.3 | 92.1 | 4.8 |
| 0.7 | 93.9 | 93.4 | 82.0 | 89.5 | 91.0 | 5.3 |
| Model | Dataset | Accuracy (%) | Precision (%) | Recall (%) | F1 Score |
|---|---|---|---|---|---|
| CNN (Baseline) | RotMNIST | 84.3 | 83.1 | 84.7 | 0.832 |
| G-CNN (Symmetric only) | RotMNIST | 92.1 | 91.8 | 92.4 | 0.912 |
| SALF (Ours) | RotMNIST | 95.6 | 95.3 | 95.9 | 0.948 |
| 1D-CNN (Baseline) | ECG | 89.5 | 88.7 | 89.9 | 0.882 |
| Symmetric 1D-CNN | ECG | 91.2 | 90.9 | 91.3 | 0.894 |
| SALF (Ours) | ECG | 94.7 | 94.5 | 94.8 | 0.938 |
| GCN (Baseline) | PROTEINS | 75.3 | 74.8 | 75.5 | 0.728 |
| E(n)-GNN | PROTEINS | 79.4 | 78.9 | 79.7 | 0.766 |
| SALF (Ours) | PROTEINS | 83.6 | 83.1 | 83.8 | 0.812 |
| CNN (Baseline) | Rotated CIFAR-10 | 84.9 | 84.2 | 85.5 | 0.849 |
| Symmetric CNN (G-CNN variant) | Rotated CIFAR-10 | 89.0 | 88.7 | 89.3 | 0.890 |
| SALF (Ours) | Rotated CIFAR-10 | 91.2 | 91.0 | 91.4 | 0.912 |
| 1D-CNN (Baseline) | MIMIC-III ECG Subset | 88.1 | 87.6 | 88.7 | 0.881 |
| Symmetric 1D-CNN | MIMIC-III ECG Subset | 90.1 | 89.8 | 90.4 | 0.902 |
| SALF (Ours) | MIMIC-III ECG Subset | 92.5 | 92.7 | 92.9 | 0.928 |
| Model | RotMNIST | ECG | PROTEINS | CIFAR-10 (Rotated) | MIMIC-III ECG Subset |
|---|---|---|---|---|---|
| Baseline | −17.2 | −10.1 | −13.6 | −15.4 | −9.7 |
| Symmetric-only | −9.3 | −6.5 | −7.8 | −8.7 | −5.8 |
| SALF (Ours) * | −4.1 | −3.0 | −4.6 | −4.3 | −2.9 |
| Configuration | RotMNIST Accuracy (%) | ECG Accuracy (%) | PROTEINS Accuracy (%) | Rotated CIFAR-10 Accuracy (%) | MIMIC-III ECG F1-Score (%) | Interpretability Score (1–5) |
|---|---|---|---|---|---|---|
| Baseline Model | 84.3 | 89.5 | 75.3 | 84.9 | 88.1 | 3.0 |
| + Symmetry-Aware Encoder | 92.1 | 91.2 | 79.4 | 89.0 | 90.1 | 3.8 |
| + Asymmetry-Driven Regularization (Full SALF) | 95.6 | 94.7 | 83.6 | 91.2 | 92.5 | 4.5 |
| Model | RotMNIST (Visual Interpretability) | ECG (Clinical Relevance) | PROTEINS (Structural Clarity) |
|---|---|---|---|
| Baseline | 2.5 | 3.0 | 2.8 |
| SALF | 4.6 | 4.8 | 4.5 |
| Metric | Dataset | Baseline CNN | SALF | Improvement |
|---|---|---|---|---|
| Pointing Game Accuracy (PGA) | RotMNIST | 0.71 | 0.87 | +22.5% |
| Pointing Game Accuracy (PGA) | MIT-BIH ECG | 0.73 | 0.86 | +17.8% |
| Deletion Area Under Curve (low better) | RotMNIST | 0.41 | 0.29 | −29.3% |
| Insertion Area Under Curve (high better) | MIT-BIH ECG | 0.56 | 0.71 | +26.8% |
| Spearman Correlation with Expert Ranking | MIT-BIH ECG | 0.64 | 0.82 | +28.1% |
| Model | RotMNIST (Acc%) | ECG (F1 Score) | PROTEINS (Acc%) | Interpretability Integration |
|---|---|---|---|---|
| G-CNN | 93.2 | — | — | External Grad-CAM (post hoc) |
| DeepSets | — | 84.1 | — | External SHAP (post hoc) |
| E(n)-GNN | — | — | 76.5 | Limited (GNNExplainer) |
| ProtoPNet [34] | 91.2 | — | — | Built-in prototypes |
| LIME-Regularized CNN [35] | 90.8 | — | — | Local surrogate explanations |
| SALF (Ours) | 95.8 | 88.9 | 80.4 | Built-in, symmetry-consistent SHAP/Grad-CAM/GNNExplainer |
| Model | Params (M) | Training Time/Epoch (s) | Inference Time/Batch (ms) | Memory Usage (GB) |
|---|---|---|---|---|
| Baseline CNN | 4.2 | 22.5 | 4.8 | 2.1 |
| SALF-CNN | 4.9 | 25.8 (+14.7%) | 5.3 (+10.4%) | 2.3 (+9.5%) |
| Baseline GCN | 1.8 | 14.2 | 3.1 | 1.5 |
| SALF-GNN | 2.1 | 15.8 (+11.3%) | 3.4 (+9.7%) | 1.6 (+6.6%) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alam, M.; Alourani, A.; Ali, A.; Ahamad, F. Symmetry-Aware Feature Representations and Model Optimization for Interpretable Machine Learning. Symmetry 2025, 17, 1821. https://doi.org/10.3390/sym17111821
Alam M, Alourani A, Ali A, Ahamad F. Symmetry-Aware Feature Representations and Model Optimization for Interpretable Machine Learning. Symmetry. 2025; 17(11):1821. https://doi.org/10.3390/sym17111821
Chicago/Turabian StyleAlam, Mehtab, Abdullah Alourani, Ashraf Ali, and Firoj Ahamad. 2025. "Symmetry-Aware Feature Representations and Model Optimization for Interpretable Machine Learning" Symmetry 17, no. 11: 1821. https://doi.org/10.3390/sym17111821
APA StyleAlam, M., Alourani, A., Ali, A., & Ahamad, F. (2025). Symmetry-Aware Feature Representations and Model Optimization for Interpretable Machine Learning. Symmetry, 17(11), 1821. https://doi.org/10.3390/sym17111821





