3D Laser Point Cloud-Based Identification of Lining Defects in Symmetric Tunnel Structures
Abstract
1. Introduction
2. Methodology
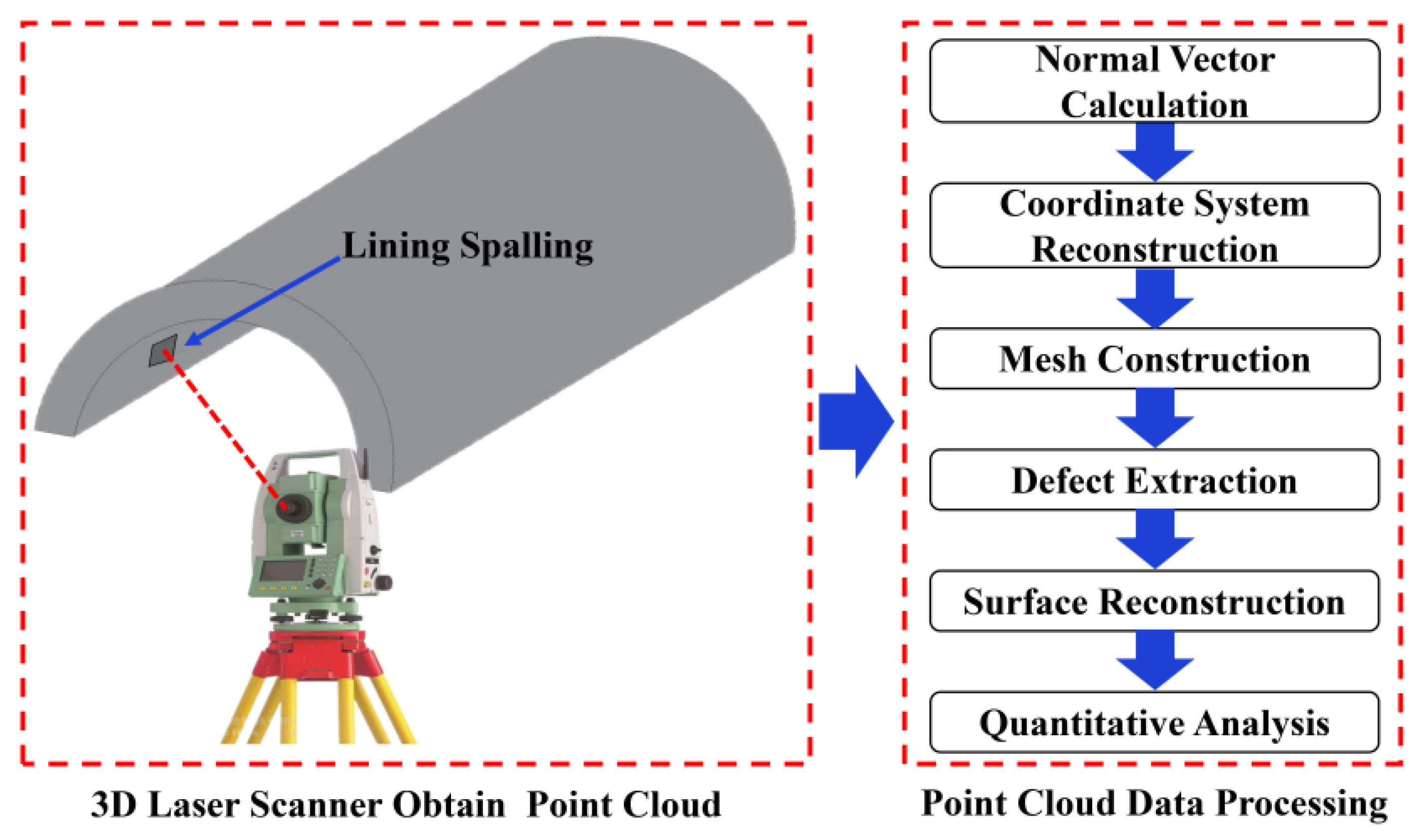
2.1. Implementation Procedure
- Acquisition of Point Cloud
- Input: Tunnel lining surface (physical reality).
- Process: A 3D laser scanner is employed to obtain the spatial coordinates of the tunnel lining surface, generating the raw point cloud data.
- Output: Raw point cloud P0 of the tunnel lining, which includes both intact surfaces and potential defect regions.
- 2.
- Normal Vector Calculation
- Input: Raw point cloud P0.
- Process: A set of representative points is selected from the intact regions of P0. The ith surface normal vectors vi for these points are computed by performing Principal Component Analysis (PCA) on their local neighborhoods.
- Output: A set of local surface normal vectors vi, which encode the local geometry of the intact lining.
- 3.
- Tunnel Axis Determination
- Input: The set of computed surface normal vectors vi.
- Process: The axial direction vector u of the tunnel’s central axis is estimated using the Sequential Quadratic Programming (SQP) algorithm, optimizing for orthogonality between u and the normal vectors. The quasi-Newton method is then applied to iteratively refine the spatial position, determining the precise central axis vector w.
- Output: The accurately determined central axis w of the tunnel.
- 4.
- Coordinate System Reconstruction and Outlier Removal
- Input: Raw point cloud P0 and the central axis w.
- Process: The identified tunnel axis w is used as the polar axis to reconstruct the coordinate system. The distance (polar radius) from each point in P0 to this axis is calculated. A threshold based on the nominal tunnel radius is applied to filter out distant interference points (e.g., vehicle interference).
- Output: Cleaned and axis-aligned point cloud P1.
- 5.
- Mesh Construction and Defect Extraction
- Input: Cleaned point cloud P1.
- Process: A triangulated mesh is generated from the point cloud P1 to establish surface connectivity. The variance of the curvature radius between adjacent mesh elements is computed. A predefined variation threshold is applied to segment and extract regions with high curvature variance, which correspond to spalling defects.
- Output: The segmented defective point cloud region P2.
- 6.
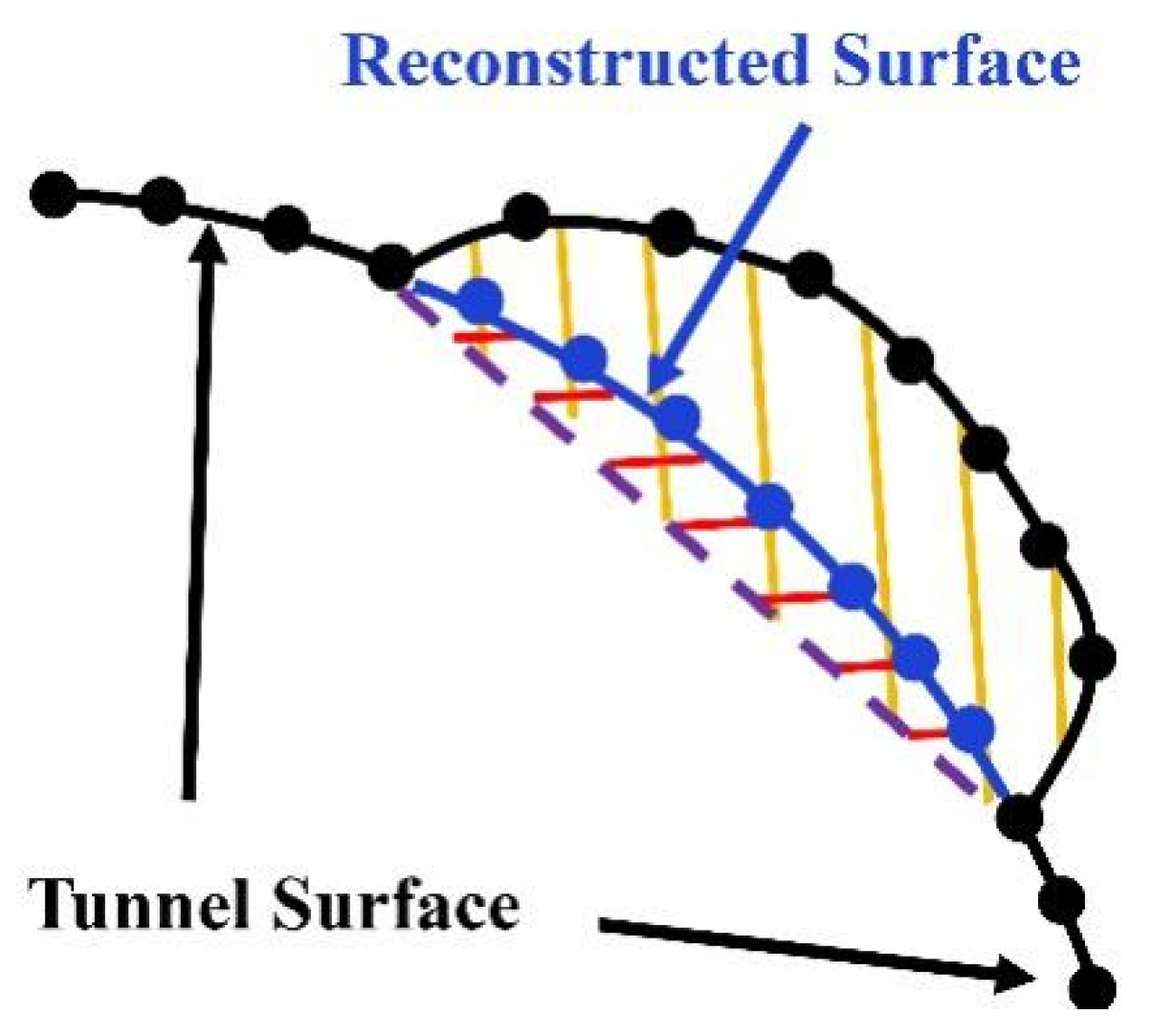
- Surface Reconstruction and Quantitative Analysis:
- Input: Defect point cloud P2 and the central axis w.
- Process: The intact lining surface is reconstructed along the boundary of the defect region P2, based on the known tunnel radius derived from axis w. The spalling volume, area, and depth are then calculated by comparing the defective surface (from P2) and the reconstructed intact surface.
- Output: Quantitative defect parameters: Spalling Depth, Area, and Volume.
2.2. Fundamental Principles
2.2.1. Estimation of Tunnel Central Axis
2.2.2. Removal of Outlier Points
2.2.3. Extraction of Lining Spalling
2.3. Evaluation Metrics
- (1)
- Thickness indicator
- (2)
- Area indicator
- (3)
- Volume indicator
3. Evaluation of the Proposed Method in the Laboratory
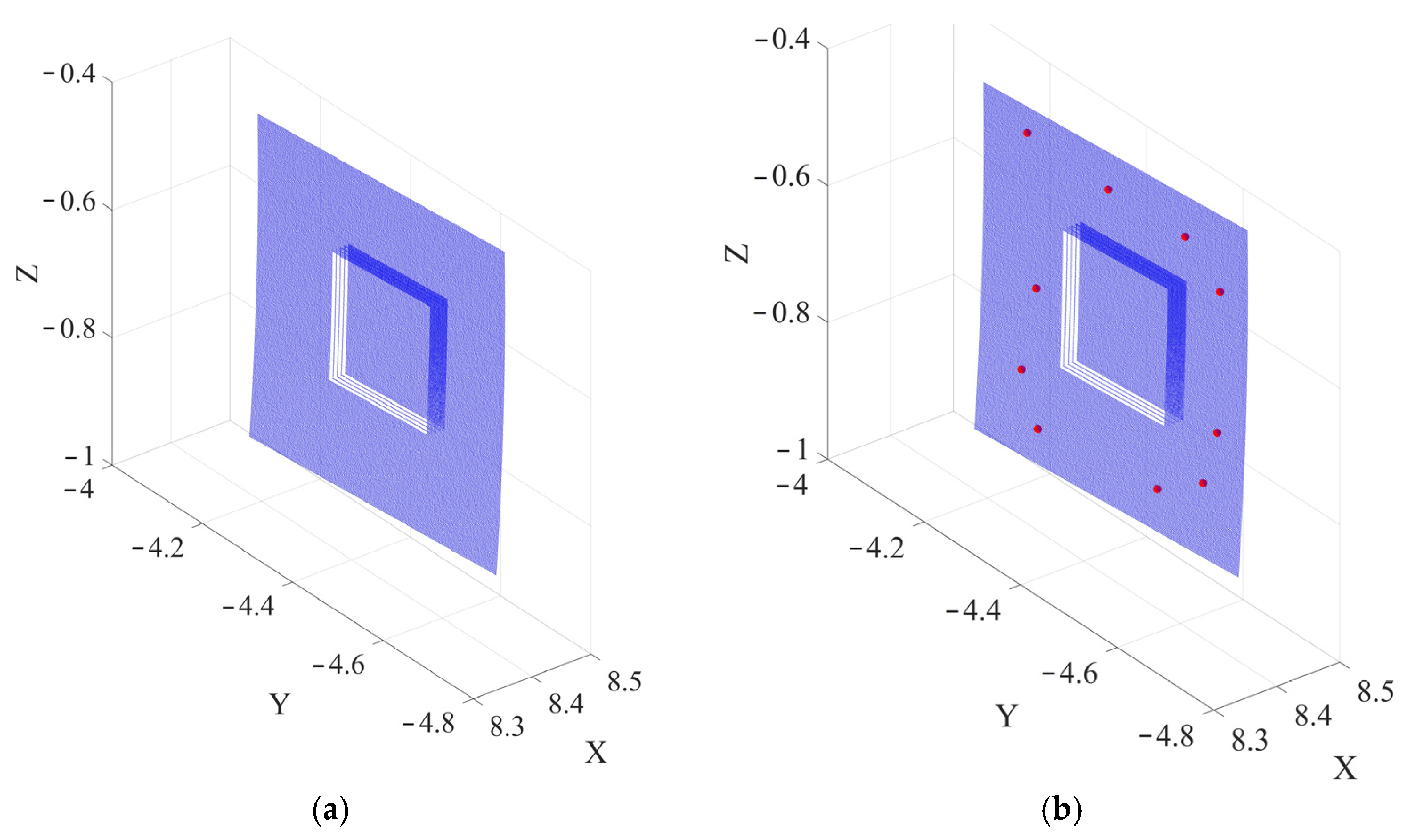
3.1. Experiments in an Experimental Tunnel Environment
3.2. Point Cloud Processing in a Controlled Tunnel Environment
3.2.1. Central Axis Calculation of the Tunnel
3.2.2. Coordinate System Reconstruction and Mesh Generation
3.2.3. Defect Extraction and Surface Reconstruction
3.3. Evaluation of Method Effectiveness
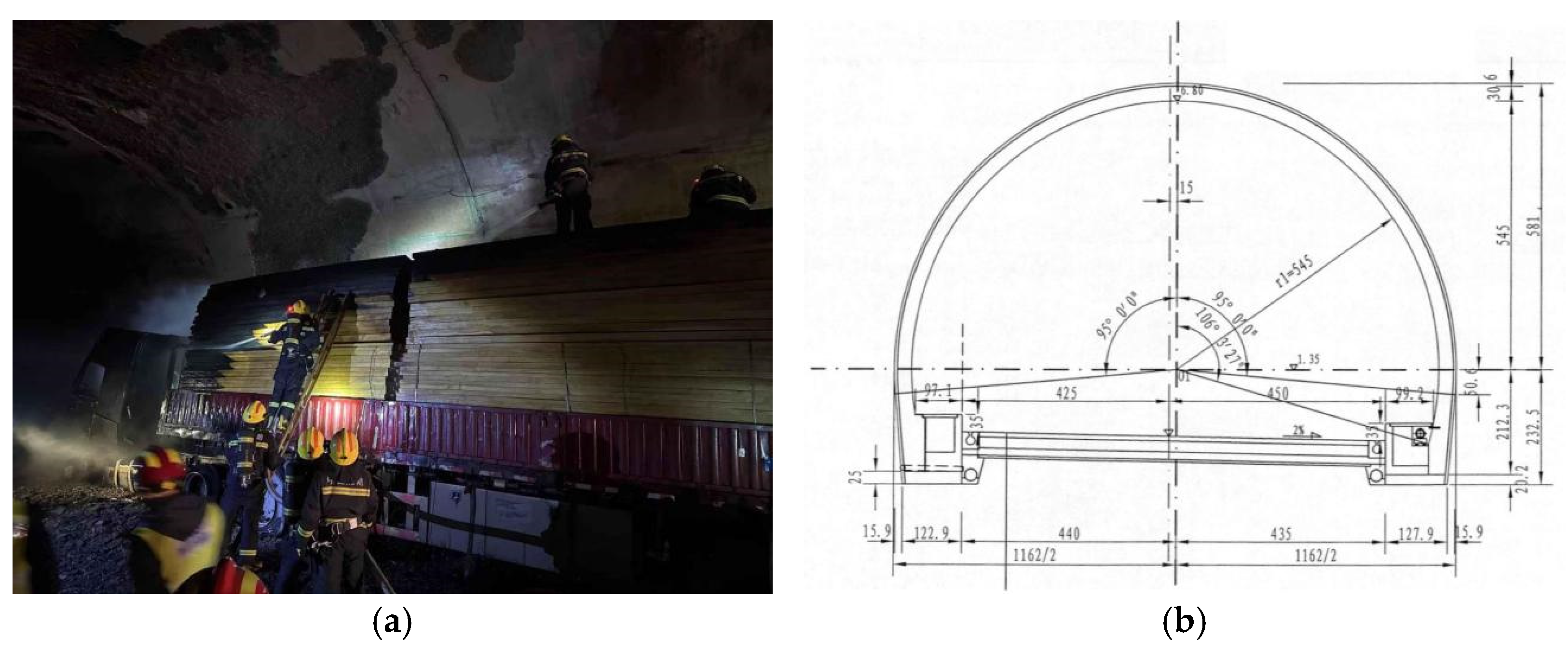
4. Case Study on Actual Operating Tunnel
5. Discussion
5.1. Interpretation of Experimental Results
5.2. Influence of Scanning Parameters
5.3. Comparison with Existing Methods
5.4. Practical Implications
6. Conclusions
- Fundamental Principle Validated: The geometrical deviation caused by spalling creates a distinct and measurable signature in the point cloud, which is most effectively captured not by simple radial distance, but by the variance of local curvature within triangulated meshes. This principle proves to be a reliable indicator for precise defect boundary extraction.
- Practical Accuracy Achieved: The method delivers parameter estimates with an average error of approximately 9.70% for depth, 9.39% for area, and 8.17% for volume in real-world conditions, a level of accuracy that is fully acceptable for practical engineering assessments and post-incident safety evaluations.
- Operational Advantage Established: Compared to traditional manual inspection and 2D image-based methods, this approach is immune to poor lighting conditions and reduces subjective error. Furthermore, unlike some complex surface reconstruction techniques, it requires only a limited set of points from the intact lining near the defect, resulting in lower computational cost and faster processing, which is crucial for time-sensitive assessments.
- Despite its effectiveness, the proposed method has certain limitations. First, the accuracy of volume estimation is sensitive to the scanning angle, as non-perpendicular angles may cause occlusions and incomplete data acquisition. Second, the method assumes that the tunnel cross-section consists of symmetrical circular arcs, which may not fully represent tunnels with irregular or non-standard geometries. Third, the computational efficiency of the mesh-based curvature analysis may decrease with very large-scale point clouds.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Sjölander, A.; Belloni, V.; Ansell, A.; Nordström, E. Towards automated inspections of tunnels: A review of optical inspections and autonomous assessment of concrete tunnel linings. Sensors 2023, 23, 3189. [Google Scholar] [CrossRef]
- Zhu, A.; Wang, B.; Xie, J.; Ma, C. MFF-YOLO: An accurate model for detecting tunnel defects based on multi-scale feature fusion. Sensors 2023, 23, 6490. [Google Scholar] [CrossRef]
- Attard, L.; Debono, C.J.; Valentino, G.; Di Castro, M. Tunnel inspection using photogrammetric techniques and image processing: A review. ISPRS-J. Photogramm. Remote Sens. 2018, 144, 180–188. [Google Scholar] [CrossRef]
- Liu, J.; Song, M.; Shu, H.; Peng, W.; Wei, L.; Wang, K. A novel FBG placement optimization method for tunnel monitoring based on WOA and deep Q-network. Symmetry 2024, 16, 1400. [Google Scholar] [CrossRef]
- Ye, F.; Qin, N.; Liang, X.; Ouyang, A.; Qin, Z.; Su, E. Analyses of the defects in highway tunnels in China. Tunn. Undergr. Space Technol. 2021, 107, 103658. [Google Scholar] [CrossRef]
- Li, S.; Qiu, Y.; Jiang, J.; Wang, H.; Nan, Q.; Sun, L. Identification of Abnormal Vibration Signal of Subway Track Bed Based on Ultra-Weak FBG Sensing Array Combined with Unsupervised Learning Network. Symmetry 2022, 14, 1100. [Google Scholar] [CrossRef]
- Xu, W.; Cheng, M.; Xu, X.; Chen, C.; Liu, W. Deep learning method on deformation prediction for large-section tunnels. Symmetry 2022, 14, 2019. [Google Scholar] [CrossRef]
- Bentz, D.P. Fibers, percolation, and spalling of high-performance concrete. Mater. J. 2000, 97, 351–359. [Google Scholar]
- Hertz, K.D. Limits of spalling of fire-exposed concrete. Fire Saf. J. 2003, 38, 103–116. [Google Scholar] [CrossRef]
- Xiong, H.; An, B.; Sun, B.; Lu, J. An improved synchrosqueezing S-transform and its application in a GPR detection task. Sensors 2024, 24, 2981. [Google Scholar] [CrossRef]
- Wang, T.; Shi, B.; Zhu, Y. Structural monitoring and performance assessment of shield tunnels during the operation period, based on distributed optical-fiber sensors. Symmetry 2019, 11, 940. [Google Scholar] [CrossRef]
- Wang, K.; Zhang, Z.; Wu, X.; Zhang, L. Multi-class object detection in tunnels from 3D point clouds: An auto-optimized lazy learning approach. Adv. Eng. Inform. 2022, 52, 101543. [Google Scholar] [CrossRef]
- Ren, Z.; Fang, F.; Yan, N.; Wu, Y. State of the art in defect detection based on machine vision. Int. J. Precis. Eng. Man-Green Technol. 2022, 9, 661–691. [Google Scholar] [CrossRef]
- Li, T.; Wang, H.; Pan, D.; Tan, J.; Hou, J.; Kong, L.; Liu, J. A machine vision approach with temporal fusion strategy for concrete vibration quality monitoring. Appl. Soft. Comput. 2024, 160, 111684. [Google Scholar] [CrossRef]
- Beskopylny, A.N.; Stel’makh, S.A.; Shcherban’, E.M.; Razveeva, I.; Kozhakin, A.; Meskhi, B.; Chernil’nik, A.; Elshaeva, D.; Ananova, O.; Girya, M. Computer vision method for automatic detection of microstructure defects of concrete. Sensors 2024, 24, 4373. [Google Scholar] [CrossRef]
- Golewski, G.L. The phenomenon of cracking in cement concretes and reinforced concrete structures: The mechanism of cracks formation, causes of their initiation, types and places of occurrence, and methods of detection—A review. Buildings 2023, 13, 765. [Google Scholar] [CrossRef]
- Hsieh, Y.A.; Tsai, Y.J. Machine learning for crack detection: Review and model performance comparison. J. Comput. Civil. Eng. 2020, 34, 04020038. [Google Scholar] [CrossRef]
- Cha, Y.J.; Choi, W.; Suh, G.; Mahmoudkhani, S.; Büyüköztürk, O. Autonomous structural visual inspection using region-based deep learning for detecting multiple damage types. Comput.-Aided Civil Infrastruct. Eng. 2018, 33, 731–747. [Google Scholar] [CrossRef]
- Huang, H.; Li, Q. Image recognition for water leakage in shield tunnel based on deep learning. Chin. J. Rock Mech. Eng. 2017, 36, 2861–2871. [Google Scholar]
- Xue, Y.; Li, Y. A fast detection method via region-based fully convolutional neural networks for shield tunnel lining defects. Comput.-Aided Civil Infrastruct. Eng. 2018, 33, 638–654. [Google Scholar] [CrossRef]
- Xue, Y.; Cai, X.; Shadabfar, M.; Shao, H.; Zhang, S. Deep learning-based automatic recognition of water leakage area in shield tunnel lining. Tunn. Undergr. Space Technol. 2020, 104, 103524. [Google Scholar] [CrossRef]
- Jang, A.; Jeong, S.; Cho, H.; Jung, D.; Ju, Y.K.; Kim, J.S.; Jung, D. Geometric and structural assessment and reverse engineering of a steel-framed building using 3D laser scanning. Comput. Concr. 2024, 33, 595–603. [Google Scholar]
- Alkadri, M.F.; Alam, S.; Santosa, H.; Yudono, A.; Beselly, S.M. Investigating surface fractures and materials behavior of cultural heritage buildings based on the attribute information of point clouds stored in the tls dataset. Remote Sens. 2022, 14, 410. [Google Scholar] [CrossRef]
- Fujita, Y.; Kobayashi, I.; Chanseawrassamee, W.; Hoshino, Y. Application of attributed road surface point cloud data in road maintenance. Jpn. Soc. Civ. Eng. Ser. F3 Civil Eng. Inform. 2014, 70, 185–192. [Google Scholar] [CrossRef]
- Alkadri, M.F.; Turrin, M.; Sariyildiz, S. A computational workflow to analyse material properties and solar radiation of existing contexts from attribute information of point cloud data. Build. Environ. 2019, 155, 268–282. [Google Scholar] [CrossRef]
- Wang, C.; Han, R.; Zhang, Y.; Wang, Y.; Zi, Y.; Zhao, J. Defect detection method based on sparse scanning with laser ultrasonics. Sci. Rep. 2025, 15, 13175. [Google Scholar] [CrossRef]
- Tang, Y.; Wang, Q.; Wang, H.; Li, J.; Ke, Y. A novel 3D laser scanning defect detection and measurement approach for automated fibre placement. Meas. Sci. Technol. 2021, 32, 075201. [Google Scholar] [CrossRef]
- Zhou, G.; Zhang, Z.; Yin, W.; Chen, H.; Wang, L.; Wang, D.; Ma, H. Characterization and depth detection of internal delamination defects in CFRP based on line laser scanning infrared thermography. Struct. Health Monit. 2024, 23, 3195–3210. [Google Scholar] [CrossRef]
- Maru, M.B.; Lee, D.; Cha, G.; Park, S. Beam deflection monitoring based on a genetic algorithm using lidar data. Sensors 2020, 20, 2144. [Google Scholar] [CrossRef]
- Liu, X.; He, J.; Cheng, Q.; Yang, S.; Li, M. Surface defect identification based on broadband laser-generated Rayleigh wave with wavenumber filtering. Meas. Sci. Technol. 2023, 34, 125205. [Google Scholar] [CrossRef]
- Dai, K.; Li, A.; Zhang, H.; Chen, S.E.; Pan, Y. Surface damage quantification of postearthquake building based on terrestrial laser scan data. Struct. Control. Health Monit. 2018, 25, e2210. [Google Scholar] [CrossRef]
- Ham, N.; Lee, S.H. Empirical study on structural safety diagnosis of large-scale civil infrastructure using laser scanning and BIM. Sustainability 2018, 10, 4024. [Google Scholar] [CrossRef]
- Wei, Z.; Wang, Y.; Weng, W.; Zhou, Z.; Li, Z. Research on tunnel construction monitoring method based on 3D laser scanning technology. Symmetry 2022, 14, 2065. [Google Scholar] [CrossRef]
- Jun, Z.L. Markerless point cloud matching algorithm based on 3d feature extraction. Int. J. Eng. Contin. 2023, 2, 38–47. [Google Scholar] [CrossRef]
- Yang, H.J.; Chen, J.W.; Zhang, Y.C.; Xu, X.D. Surface feature extraction based on curvelet transform from point cloud data. Appl. Mech. Mater. 2015, 719, 1236–1243. [Google Scholar] [CrossRef]
- Chen, H.; Liang, M.; Liu, W.; Wang, W.; Liu, P.X. An approach to boundary detection for 3D point clouds based on DBSCAN clustering. Pattern Recognit. 2022, 124, 108431. [Google Scholar] [CrossRef]
- Mineo, C.; Pierce, S.G.; Summan, R. Novel algorithms for 3D surface point cloud boundary detection and edge reconstruction. J. Comput. Des. Eng. 2019, 6, 81–91. [Google Scholar] [CrossRef]
- Qi, C.R.; Su, H.; Nießner, M.; Dai, A.; Yan, M.; Guibas, L.J. Volumetric and multi-view cnns for object classification on 3D data. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 5648–5656. [Google Scholar]
- Heqiang, T.; Xiaoqing, D.; Jihu, W.; Dongmei, W. Registration method for three-dimensional point cloud in rough and fine registrations based on principal component analysis and iterative closest point algorithm. Trait. Signal 2017, 34, 57. [Google Scholar]
- Li, X.; Ma, X.; Liang, N.; Deng, F. 3D reconstruction of ancient structures assisted by terrestrial laser scanning technology. In Proceedings of the 2nd International Forum on Management, Education and Information Technology Application (IFMEITA 2017), Shenzhen, China, 16–17 October 2017; Atlantis Press: Dordrecht, The Netherlands, 2018; pp. 481–485. [Google Scholar]
- Lawani, K.; Sadeghineko, F.; Tong, M.; Bayraktar, M. Methodology for retrospectively developing a BIM model from point cloud scans using ongoing building project as case study. J. Eng. Des. Technol. 2025, 23, 1243–1261. [Google Scholar] [CrossRef]
- Chithra, P.; Lakshmi Bala, S. Physics-driven neural network for geometrical compression of lidar 3D point cloud data. In International Conference on Data Analytics and Management; Springer: Singapore, 2024; pp. 171–185. [Google Scholar]
- Zhou, Y.; Shen, S.; Hu, Z. Detail preserved surface reconstruction from point cloud. Sensors 2019, 19, 1278. [Google Scholar] [CrossRef]
- Liu, W.; Cheung, Y.; Sabouri, P.; Arai, T.J.; Sawant, A.; Ruan, D. A continuous surface reconstruction method on point cloud captured from a 3D surface photogrammetry system. Med. Phys. 2015, 42, 6564–6571. [Google Scholar] [CrossRef]
- He, Y.; Kang, S.H.; Liu, H. Curvature regularized surface reconstruction from point clouds. SIAM J. Imaging Sci. 2020, 13, 1834–1859. [Google Scholar] [CrossRef]
- Fliege, J.; Vaz, A.I.F. A method for constrained multi-objective optimization based on SQP techniques. SIAM J. Optim. 2016, 26, 2091–2119. [Google Scholar] [CrossRef]
- Byrd, R.H.; Hansen, S.L.; Nocedal, J.; Singer, Y. A stochastic Quasi-Newton method for large-scale optimization. SIAM J. Optim. 2016, 26, 1008–1031. [Google Scholar] [CrossRef]
- Liu, B.Z.; Zheng, C.X.; Xu, X.M.; Xu, C.; Zhang, H.D.; He, S.F. Rotation-adaptive point cloud domain generalization via intricate orientation learning. IEEE Trans. Pattern Anal. Mach. Intell. 2025, 47, 4232–4239. [Google Scholar] [CrossRef]


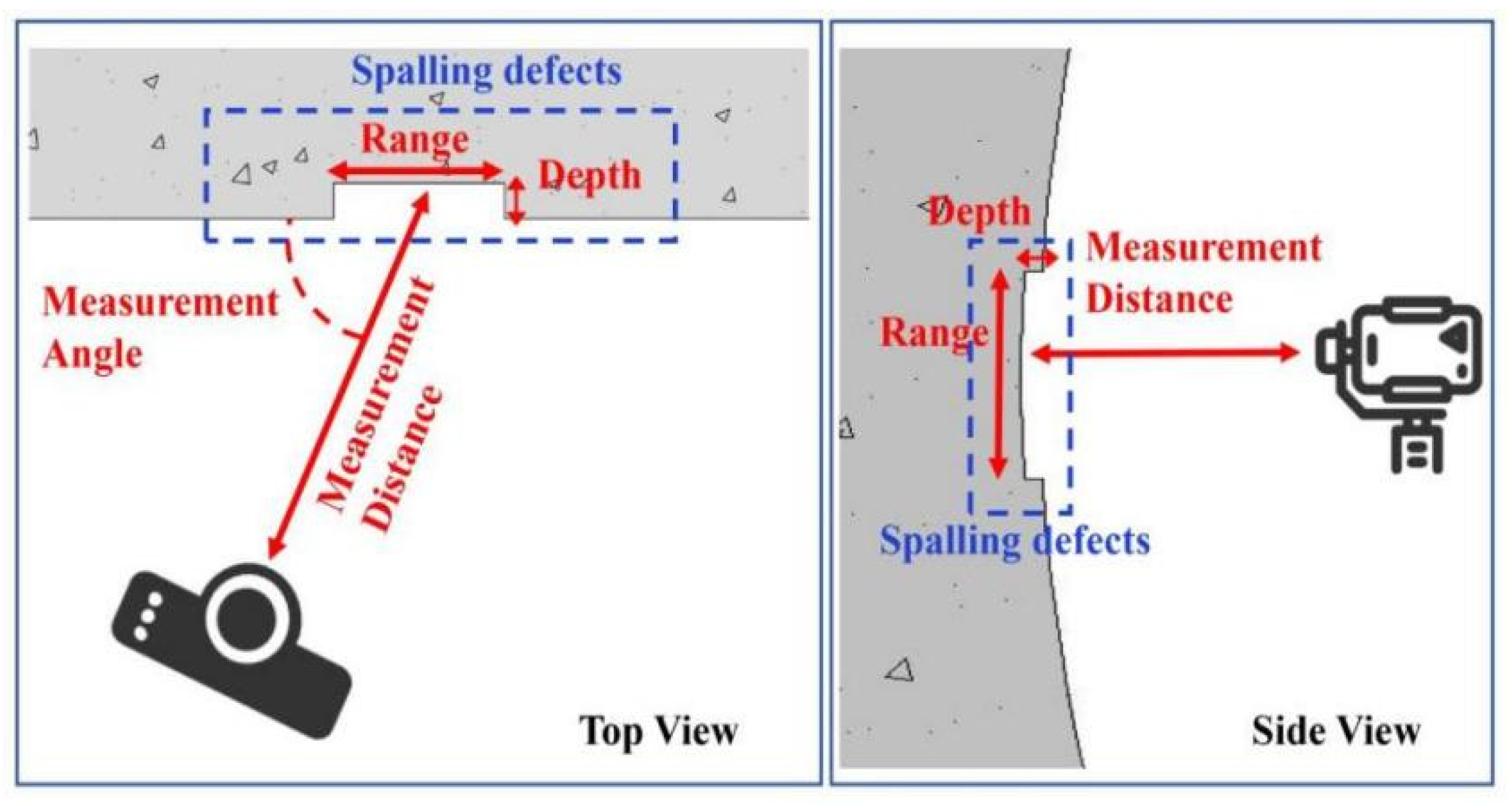



| Condition | Range (cm) | Depth (cm) | Measurement Distance (m) | Measurement Angle |
|---|---|---|---|---|
| Condition A1 | 5 × 5 | 3 | 8 | 90° |
| Condition A2 | 10 × 10 | 3 | 8 | 90° |
| Condition A3 | 20 × 20 | 3 | 8 | 90° |
| Condition A4 | 30 × 30 | 3 | 8 | 90° |
| Condition A5 | 40 × 40 | 3 | 8 | 90° |
| Condition B1 | 20 × 20 | 1 | 8 | 90° |
| Condition B2 | 20 × 20 | 2 | 8 | 90° |
| Condition B3 | 20 × 20 | 4 | 8 | 90° |
| Condition B4 | 20 × 20 | 5 | 8 | 90° |
| Condition C1 | 20 × 20 | 3 | 2 | 90° |
| Condition C2 | 20 × 20 | 3 | 4 | 90° |
| Condition C3 | 20 × 20 | 3 | 6 | 90° |
| Condition C4 | 20 × 20 | 3 | 10 | 90° |
| Condition D1 | 20 × 20 | 3 | 8 | 30° |
| Condition D2 | 20 × 20 | 3 | 8 | 45° |
| Condition D3 | 20 × 20 | 3 | 8 | 60° |
| Condition D4 | 20 × 20 | 3 | 8 | 75° |
| Condition | Depth (cm) | Area (cm2) | Volume (cm3) | ||||||
|---|---|---|---|---|---|---|---|---|---|
| CV | MV | ER | CV | MV | ER | CV | MV | ER | |
| Condition A1 | 2.93 | 3 | 2.33% | 24.74 | 25 | 1.04% | 72.37 | 75 | 3.51% |
| Condition A2 | 2.97 | 3 | 1.00% | 97.61 | 100 | 2.39% | 304.04 | 300 | 1.35% |
| Condition A3 | 3.03 | 3 | 1.00% | 397.10 | 400 | 0.72% | 1250.58 | 1200 | 4.21% |
| Condition A4 | 2.98 | 3 | 0.67% | 915.79 | 900 | 1.75% | 2589.46 | 2700 | 4.09% |
| Condition A5 | 2.97 | 3 | 1.00% | 1593.69 | 1600 | 0.39% | 5019.85 | 4800 | 4.58% |
| Condition B1 | 0.99 | 1 | 1.00% | 413.57 | 400 | 3.39% | 406.29 | 400 | 1.57% |
| Condition B2 | 1.98 | 2 | 1.00% | 388.62 | 400 | 2.85% | 771.71 | 800 | 3.54% |
| Condition B3 | 3.97 | 4 | 0.75% | 409.50 | 400 | 2.38% | 1625.25 | 1600 | 1.58% |
| Condition B4 | 5.03 | 5 | 0.60% | 391.28 | 400 | 2.18% | 2013.21 | 2000 | 0.66% |
| Condition C1 | 2.98 | 3 | 0.67% | 400.04 | 400 | 0.01% | 1147.65 | 1200 | 4.36% |
| Condition C2 | 2.95 | 3 | 1.67% | 400.43 | 400 | 0.11% | 1158.37 | 1200 | 3.47% |
| Condition C3 | 2.95 | 3 | 1.67% | 395.17 | 400 | 1.21% | 1140.92 | 1200 | 4.92% |
| Condition C4 | 2.92 | 3 | 2.67% | 390.12 | 400 | 2.47% | 1175.46 | 1200 | 2.05% |
| Condition D1 | 2.93 | 3 | 2.33% | 413.85 | 400 | 3.46% | 1055.90 | 1200 | 12.01% |
| Condition D2 | 2.94 | 3 | 2.00% | 411.87 | 400 | 2.97% | 1073.98 | 1200 | 10.50% |
| Condition D3 | 3.05 | 3 | 1.67% | 408.09 | 400 | 2.02% | 1112.46 | 1200 | 7.30% |
| Condition D4 | 3.03 | 3 | 1.00% | 405.31 | 400 | 1.33% | 1134.80 | 1200 | 5.43% |
| Condition | Depth (cm) | Area (cm2) | Volume (cm3) | ||||||
|---|---|---|---|---|---|---|---|---|---|
| CV | MV | ER | CV | MV | ER | CV | MV | ER | |
| Defect 1 | 2.95 | 3.04 | 3.06% | 7150 | 7510 | 5.03% | 2742 | 2966 | 8.17% |
| Defect 2 | 1.22 | 1.27 | 4.10% | 22,770 | 24,348 | 6.93% | 3610 | 3751 | 3.91% |
| Defect 3 | 0.78 | 0.81 | 3.39% | 5134 | 5288 | 2.99% | 1154 | 1199 | 3.91% |
| Defect 4 | 4.22 | 4.58 | 8.42% | 3413 | 3435 | 0.63% | 2501 | 2646 | 5.79% |
| Defect 5 | 3.54 | 3.69 | 4.38% | 4876 | 5325 | 9.22% | 2762 | 2845 | 3.03% |
| Defect 6 | 4.25 | 4.39 | 3.32% | 1716 | 1874 | 9.23% | 1823 | 1965 | 7.78% |
| Defect 7 | 11.78 | 12.92 | 9.70% | 631,257 | 690,511 | 9.39% | 1,338,517 | 1,446,659 | 8.08% |
| Defect 8 | 5.15 | 5.63 | 9.36% | 3517 | 3523 | 0.16% | 5434 | 5657 | 4.11% |
| Defect 9 | 3.65 | 3.83 | 4.96% | 1478 | 1580 | 6.87% | 1133 | 1173 | 3.58% |
| Defect 10 | 7.82 | 8.32 | 6.38% | 16,358 | 17,069 | 4.35% | 33,259 | 35,927 | 8.02% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, Z.; Jin, Y.; Sun, X.; Huo, L.; Yu, M.; Zhang, H.; Xu, J.; Xu, R. 3D Laser Point Cloud-Based Identification of Lining Defects in Symmetric Tunnel Structures. Symmetry 2025, 17, 1822. https://doi.org/10.3390/sym17111822
Yang Z, Jin Y, Sun X, Huo L, Yu M, Zhang H, Xu J, Xu R. 3D Laser Point Cloud-Based Identification of Lining Defects in Symmetric Tunnel Structures. Symmetry. 2025; 17(11):1822. https://doi.org/10.3390/sym17111822
Chicago/Turabian StyleYang, Zhuodong, Ye Jin, Xingliang Sun, Linsheng Huo, Mu Yu, Hanwen Zhang, Jianda Xu, and Rongqiao Xu. 2025. "3D Laser Point Cloud-Based Identification of Lining Defects in Symmetric Tunnel Structures" Symmetry 17, no. 11: 1822. https://doi.org/10.3390/sym17111822
APA StyleYang, Z., Jin, Y., Sun, X., Huo, L., Yu, M., Zhang, H., Xu, J., & Xu, R. (2025). 3D Laser Point Cloud-Based Identification of Lining Defects in Symmetric Tunnel Structures. Symmetry, 17(11), 1822. https://doi.org/10.3390/sym17111822







