Abstract
The flow of a two-dimensional incompressible hybrid nanofluid over a stretching cylinder containing microorganisms with parallel effect of inclined magnetohydrodynamic was examined in the current study in relation to chemical reactions, heat source effect, nonlinear heat radiation, and multiple convective boundaries. The main objective of this research is the optimization of heat transfer with inclined MHD and variation in different physical parameters. The governing partial differential equations are transformed into a set of ordinary differential equations by applying the appropriate similarity transformations. The Runge–Kutta method is recognized for using shooting as a technique. Surface plots, graphs, and tables have been used to illustrate how various parameters affect the local Nusselt number, mass transfer, and heat transmission. It is demonstrated that when the chemical reaction parameter rises, the concentration and motile concentration profiles drop. The least responsive is the rate of heat transfer to changes in the inclined magnetic field and most associated with changes in the Biot number and radiation parameter shown in contour plot. The streamline graph illustrates the way fluid flow is affected simultaneously by the magnetic parameter M and an angled magnetic field. Local Nusselt number and local skin friction are improved by the curvature parameter and mixed convection parameter. The contours highlight the intricate interactions between restricted magnetic field, significant radiation, and substantial convective condition factors by displaying the best heat transfer. The three-dimensional surface, scattered graph, pie chart, and residual plotting demonstrate the statistical analysis of the heat transfer. The results support their use in sophisticated energy, healthcare, and industrial systems and enhance our theoretical knowledge of hybrid nanofluid dynamics.
1. Introduction
Enhancements to heat transfer include adding manufactured surface roughness, applying a magnetic flux, making surfaces elastic, attaching fins, and putting in barriers. Over the past few decades, researchers have been working hard to create novel nanofluids that would enhance performance. Nanofluids are produced by suspending metallic or non-metallic nanoparticles in traditional heat transfer fluids to significantly enhance their thermal performance. The thermal conductivity of the nanofluid with copper nanophase materials was investigated, and the findings showed that one benefit of employing nanofluids is a significant decrease in heat exchanger pumping power. A nanofluid that contains two or more nanoparticles is called a hybrid nanofluid. In comparison to single nanoparticles, hybrid nanoparticles had a significant effect on thermal distribution.
They used a stretching cylinder to examine the flow of the mixture of and with hybrid nanoparticles [1]. They tested bio-convection, the impact of fluctuating thermal viscosity, the two-fold diffusion effect, and a magneto-hydrodynamic boundary layer flow. They also found taht a higher Péclet number boosts the motile microorganism profile [2]. The motile density stratification and chemical reaction variables have an impact on the microorganism density number. In a magnetic field environment, the drag coefficient increases with increasing electric field parameter values and decreases with decreasing electric field parameter values [3]. Nanofluid bioconvection has an extensive list of possible uses in the medical sciences, according to Saranya and Radha [4]. Using a 2-D laminar bioconvective barrier, the flow of an MHD bioconvective micropolar nanofluid containing microorganisms is investigated [5]. Incorporating velocity, thermal, and mass slips affects heat and mass transfer rates as well as reduces boundary layer thickness (Yahaya et al. [6]). The bvp4c solver and Runge–Kutta integration are two methods commonly used to solve the set of ODE numerically (Khan et al. [7]).
The converted nonlinear equations are derived from the governing thermal field and flow equations and are numerically solved using the Runge–Kutta methodology and a boundary value conversion method incorporated into an iterative solution scheme [8]. The impacts of the input variables on skin friction and heat transfer rate with nonlinear radiation and an angled magnetic field are analyzed for the magnetohydrodynamic flow of an engineered fluid past a stretching cylinder [9].
Heat radiation, microorganism motility, and other flow characteristics are examined in the magnetohydrodynamic flow of metal oxide and graphene oxide hybrid nanofluids in a permeable rotating system as they interact. Utilizing and hybrid nanofluids, investigates how velocity, temperature, solutal, and motile microbe profiles are affected by magnetic fields, inclination angle, and porous media [10,11,12].
Inayat Ullah et al. [13] investigated the thermal and magnetic field interactions of inclined MHD mixed convection of a Bingham fluid in a lid-driven square cavity with an embedded wavy cylinder and found Ri is a measure of increased buoyant forces that can improve fluid motion and heat transmission. Kumbhakar et al. [14] examined the stagnation point flow of a hybrid nanofluid over a convectively heated stretching cylinder surrounded by an inclined magnetic field. Using velocity slip and convective boundary conditions, Riaz et al. [15] investigated mixed convection of , and hybrid nanofluids in water over a moving vertical cylinder.
Haq et al. [16] studied the transfer of heat and stagnation flow of a hybrid nanofluid in the direction of a stretched cylinder while subjected to mixed convection and a magnetic field. The impacts of Soret and Dufour have been used for investigating the 2-D radiative heat transfer of second-grade fluid flow across a stretched cylinder [17]. They observe that concurrent fluctuations of Soret and Dufour have an inverse correlation with heat and mass transfer rates. Using the Soret-Dufour parameter, Ramzan et al. [18] examine a permeable stretched cylinder. Activation energy and mobile motile microorganisms are described in relation to the bioconvection incompressible flow of nanofluid. Additionally, Brownian motion and thermophoresis parameters are being studied [19].
The impact of heat transfer on nanofluid flow on stretched cylinder has been examined by the authors of [20]. They demonstrate that as rises the porosity parameter decreases the drag force coefficient and the Nusselt number. Hayat et al. [21] described the fluid flow of the third-grade magnetohydrodynamics through a stretching cylinder. Research on Williamson hybrid nanofluid flow over a spinning cylinder containing gyrotactic microorganisms revealed that higher nanoparticle volume fractions were associated with higher Sherwood numbers and local skin friction coefficients (Reddy et al. [22]). Shilpa et al. [23] investigated magneto-convection and Cattaneo–Christov heat transport in a magnetically driven porous cylinder and discovered that increasing the magnetic force parameter suppresses fluid motion by lowering the generated magnetic field. The nanofluid and hybrid nanofluids, as well as nonlinear mixed convective hybrid nanofluid flow with different slip conditions, were also investigated, showing enhanced mass and heat transport rates with greater nanoparticle volume fractions (Xia et al. [24]).
The thermal conductivity is taken to be a linear function of temperature in magnetohydrodynamic (MHD) boundary layer viscous fluid with variable thermal conductivity and mass transfer over a stretching cylinder [25]. The nanofluids in thermal energy transfer through a cylinder involving heat generation and joule heating are presented by Islam et al. [26]. The combined effects of heat radiation and convection movement of a nanofluid over a stretched cylinder in a porous medium, along with viscous dissipation and slip conditions, were studied [27]. Using suction/injection, heat source, nanoparticle shape, stagnation point flow, and heat transfer coefficient, the flow dynamics of nanofluid over stretching cylinders was investigated [28]. The shape of nanoparticles is revealed by a hybrid nanofluid flow of /water toward a horizontal stretching shrinking cylinder and it was studied by Rashid et al. [29] using three different forms of and . The flow of a mixed convection nanofluid based on Arrhenius activation energy across a porous medium involves binary chemical processes, buoyancy effects, thermal radiation, and heat absorption/generation [30]. Williamson nanofluid mixed convective three-dimensional flow with chemical reactions [31].
Even with these developments, there are still some research restrictions. The simultaneous examination of numerous phenomena, such as inclined magnetic fields, nonlinear thermal conductivity, and bio-convection in hybrid nanofluids, has received attention, whereas many studies concentrate on particular boundary conditions or isolated physical effects.
This study focuses on optimizing the rate of heat transfer in an inclined MHD bioconvective flow of a hybrid nanofluid under the influence of multiple thermal convections and a variable thermal conductivity heat source. Specifically, it examines the flow of a two-dimensional inclined MHD hybrid nanofluid across a stretching cylinder in a different environment. After converting the PDE into ODEs using a similarity function, the Ranga–Kutta method and Newton–Raphson methodology are used to obtain numerical solutions. The mathematical combination for , , , and is shown when various features are applied to the applicable parameters. Particularly in applications requiring heat generation, chemical processes, and microorganism dynamics, these constraints underscore the necessity of conducting more thorough studies into coupled multiphysics systems.
2. Physical Interpretation
Figure 1 illustrates motion across the cylinder leads proposed flow with cartesian coordinates. The flow of a two-dimensional incompressible hybrid nanofluid featuring microorganisms and chemically reactive species has been considered to flow over cylinder having radius R and free stream velocity . The study and independent of pressure gradient assumption are taken. This work includes the effects of the variable thermal conductivity, inclined MHD, heat source, mixed convection parameter, chemical reaction, and convective boundary condition. With a being a positive constant, let , the free stream velocity, flow across the cylinder. The coordination system takes into account both r in the axial direction and the x-axis along the cylinder’s surface. The surface temperature, represented by T, and thermal efficiency, represented by , are the results of convective heating from a hot fluid. The fluid with the wall is characterised as . Additionally, the Cattaneo–Christov heat flux prototype has been considered and we obtain the following governing equations using the following assumptions [9,32,33].
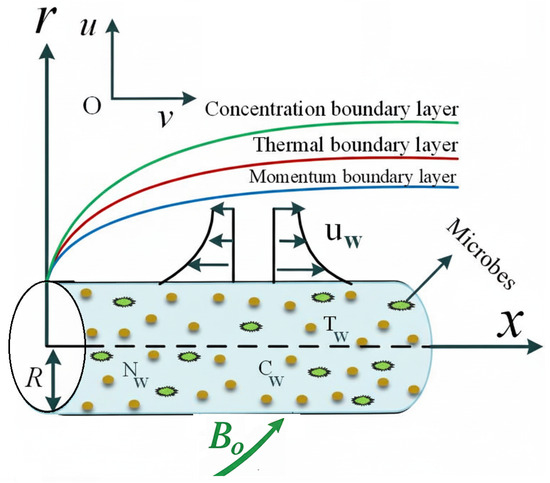
Figure 1.
Graphical representation of the model.
Fundamental conservation laws in tensor form for governing equations with the above assumption:
The Cartesian form of these equations are
The boundary conditions can be categorized into the following kinds based on the structure of the problem [34].
The magnetic field intensity is denoted , thermal relaxation is , and the chemical reaction parameter is . Maximum swimming speed of microorganisms in hybrid nanofluids and their diffusivity maintain constant properties, with the exception of density variations that produce a thermal buoyancy force.
In Table 1, the subscript represents fluid. The elaborated problem’s complexity can be decreased by including the following nondimensional variables:

Table 1.
Hybrid nanofluid’s thermophysical characteristics [35,36].
The stream functions and are dimensionless, and the stream function typically satisfies Equation (1). Employing the previously indicated similarity vectors (7), the nonlinear partial differential Equations (2)–(5) are transformed as follows:
Additionally, the following are the updated boundary conditions of the model:
The thermos-physical factors are explained.
3. Physical Quantities
Equations (8)–(13) contain many relevant parameters. The classic Lewis number , Reynolds number, Lewis number , Prandtl number , mixed convection parameter , magnetic parameter , and The curvature parameter , the thermally stratified variable , the chemical reaction parameter , the microorganisms difference parameter , and the Péclet number .
4. Engineering Quantities
Engineering requirements include the skin friction coefficient , local Sherwood number , local Nusselt number , and local motile microorganism . The following categories
can be computed using the transformations (7):
where is the local Reynold’s number.
Numerical Methodology
The system of nonlinear ordinary differential equations (ODEs) that resulted from applying the proper similarity transformations to the governing partial differential equations was numerically solved in this study using the Runge–Kutta method. In general, the converted ODEs can be expressed as follows:
where f represents the dimensionless velocity, the dimensionless temperature, the nanoparticle concentration, and N the motile microorganism density. The boundary conditions are given at the surface () and far from the surface () as
The Newton–Raphson iteration was used to develop the shooting method in order to meet the boundary criteria at infinity. By estimating unknown starting slopes (such as , and ) and iteratively improving them until the boundary requirements at are satisfied within a certain tolerance, this turns the boundary value problem into an initial value problem. The ODEs were numerically integrated using MATLAB 2021 adaptive RK approach, which dynamically changed the step size to preserve accuracy and stability:
Sensitivity to initial assumptions, possible numerical instability in stiff systems, and higher computational costs for highly nonlinear instances are some of the limitations. To provide a thorough parametric analysis of the hybrid nanofluid system, the method was successfully used to calculate velocity, temperature, concentration, and microorganism profiles under a variety of conditions, including chemical reaction rates, convective boundary effects, and inclined magnetohydrodynamic influences [37]. To achieve this, we first consider: the following
are estimated using the Newton-Raphson procedure with a suitable initial guess. The Table 1 and Table 2 show thermo physical and physical properties, and during validation, the numerical method (Runge-Kutta) displayed substantial agreement, as shown in Table 3.

Table 2.
Physical properties [38,39].

Table 3.
Verification of .
5. Results and Discussion
The influence on the thermal distribution , momentum profile , the concentration distribution , and motile profile with skin coefficient, , , and are shown using graphs and tables. Figure 2a,b describe the fluctuation of velocity profile with magnetic parameter M and mixed convection parameter with simultaneous effect of . The fluid’s velocity profile decreases in the case of the magnetic parameter, whereas improves it. Physically, the mixed convection parameter is the ratio of buoyant to inertial forces; hence, a greater indicates a higher thermal buoyancy force, which improves velocity profiles. Also when rises, the dimensionless velocity decreases. This is due to the fact that the Lorentz force, a resistive force to fluid flow, is connected to the magnetic parameter, and the magnetic effect gets stronger as rises. The velocity decreases as the magnetic parameter rises because greater resistive force is applied.
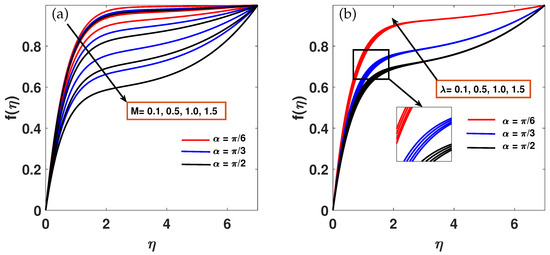
Figure 2.
(a,b) The variation of the velocity profile against over a range of and M values for .
Figure 3a,b show how the curvature parameter affects the temperature and velocity profiles with parallel effect of . The velocity profile rises with increasing distance from the stretching surface and falls with increasing distance. This is physically justified by higher curvature values, which reduce the cylinder radius and, consequently, its contact area with the fluid, increasing fluid velocity and lowering surface resistance. Also when we approach the stretched surface, the temperature profile drops, but as we go farther away, it starts to rise. As increases, the thickness of the thermal barrier layer increases, slowing down the transfer of heat and raising the temperature profile. Additionally, the graph above shows that as increases, so does the dimensionless temperature profile. This is because the magnetic effect becomes stronger as increases. The transverse magnetic field reduces the fluid’s velocity and significantly slows down the transmission rate. This is because the magnetic effect gets stronger as rises. By decreasing the fluid’s velocity, the transverse magnetic field significantly slows down the transmission rate. As the Lorentz force increases with M, the flow resistance increases as well.
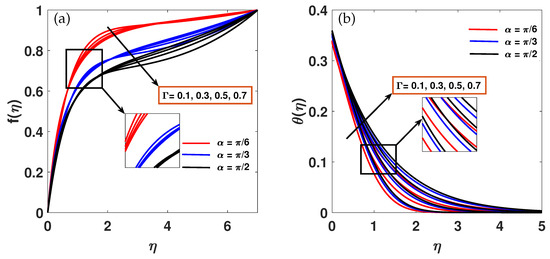
Figure 3.
(a,b) The temperature distribution and velocity profile fluctuates against for a variety of values at .
Figure 4a,b show the inspiration of radiation factor and Prandtl number alongside acting concurrently on hybrid nanofluid fluid temperature profile. The increasing incidence in the nanofluid temperature profile demonstrated in Figure 4a can be seen by an increase in the radiation factor . From a physical perspective, when the radiation parameter increases, the fluid discharges heat energy from the flow area, enhancing the nanofluid’s temperature and cooling the system. Heat is added to the system as the radiation parameter increases, and more heat is added when the thermal boundary layer is thicker. Since the mean absorption coefficient falls as K1 rises, the thermal field rises as well. Therefore, in order to cool more effectively, heat radiation should be minimized. The effect of the Prandtl number on the temperature of nanoparticles is seen in Figure 4b. The ratio of two numbers, momentum and thermal diffusivity, is known as the Prandtl number, which is a non-dimensional quantity. As increases, thermal diffusivity decreases, resulting in a further decrease in the temperature and thickness of the boundary layer.
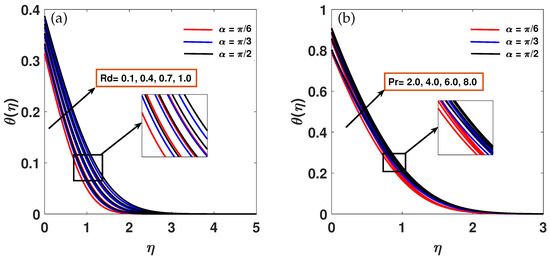
Figure 4.
(a,b) Variability of the temperature distribution against across a wide range of and values at .
Figure 5a,b demonstrate that an increase in the Biot number and the wall temperature parameter leads to a rise in the nanofluid temperature profile with a simultaneous effect of MHD. Physically, higher Bi indicates a greater ratio of convective heat transfer to thermal conductivity, leading to elevated temperature within the fluid. When the Biot number is low, the internal thermal resistance of the solid is negligible compared to surface resistance, resulting in a nearly uniform solid temperature and making enhancements to surface convection the most effective design strategy. When the Biot number is high, internal thermal resistance dominates, causing significant temperature gradients within the solid and making it essential to enhance internal thermal conductivity. Additionally, as increases, the temperature profile continues to rise, a trend consistently observed across all inclination angles .
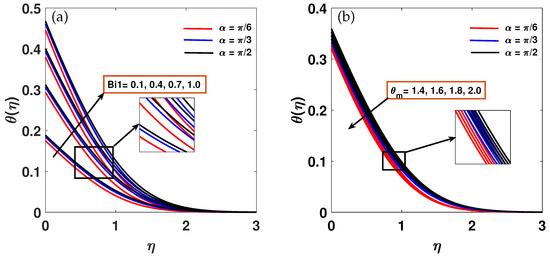
Figure 5.
(a,b) Temperature distribution variation against over an interval of and values for .
The consequences of the chemical reaction and convective parameter on concentration profile with a parallel effect of is shown in Figure 6a,b. High values cause the reaction rate and molecular diffusivity to rise, which lowers the concentration profiles of nanoparticles. Higher chemical reaction parameter values are associated with a drop in the concentration profile, while the concentration profile is enhanced by the concentration convective parameter . Figure 7a,b depicts the features of the motile profile involving the chemical reaction parameter and motile concentration convective parameter with simultaneous effect of inclination MHD. As increases, motile concentration falls, as shown in Figure 8a. However, the motile concentration profile rises together with the convective parameter parameter. Physically, the strength of chemical reactions that can change local concentration gradients and either increase or decrease microbe activity is represented by the parameter . Due to stronger response consumption, a higher typically results in a lower motile density. In the meantime, convective mass transfer at the boundary is characterized by , where a higher improves the movement of microorganisms from the fluid’s surface. These factors work together to control the dispersion of microorganisms and the stability of bioconvection.
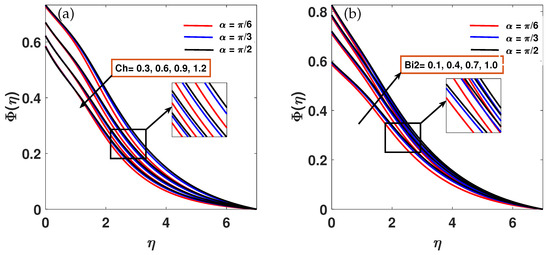
Figure 6.
(a,b) The variation of the concentration profile against for a set of and values at .
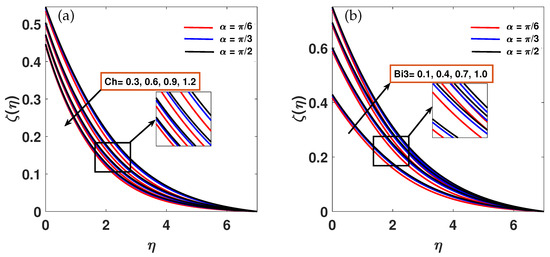
Figure 7.
(a,b) Motile concentration profile variation against for a range of and values at .
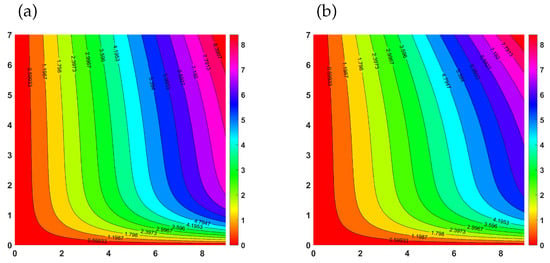
Figure 8.
(a,b) Streamline graph for M = 0.0 at and .
The different profiles of velocity and temperature show the fluctuation in velocity, temperature, and concentration profiles for various values of the inclination angle (). As the inclination angle () increases, the thickness of the velocity boundary layer decreases. This is because the fluid’s velocity impedes in the fluid area as the values of () increase. An increase in the plate inclination angle () is thought to increase the thickness of the thermal boundary layer by resisting the fluid’s motion. The streamline graph illustrate the way fluid flow is affected simultaneously by the magnetic parameter M and an angled magnetic field shown in Figure 8 and Figure 9. Asymmetric streamline patterns are produced when the flow direction gets skewed due to magnetic field inclination. The flow is redirected and the boundary layer thickens on one side as a result of the inclination’s alteration of the inertial and magnetic force balance. The flow field is smoothed, velocity is decreased, and damping effects are enhanced with higher M values. In MHD flow management and heat transfer optimization, the combined effect of magnetic strength and angle regulates flow behavior.
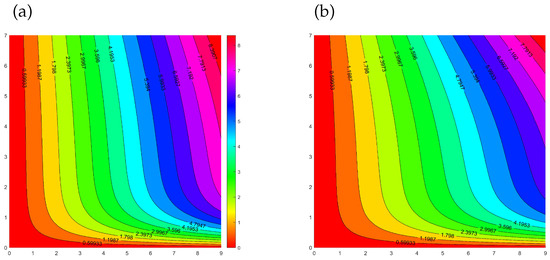
Figure 9.
(a,b) Streamline graph for M = 0.5 at and .
The Nusselt number distribution in a hybrid nanofluid as impacted by the parameters , , and , as shown in a pie chart in Figure 10. The figure illustrates the combined effects of these parameters on the efficiency of heat transmission in hybrid nanofluids, with different sections highlighting their respective contributions to improved thermal performance in engineering applications. A residual plot of the Nusselt number distribution in AlO3-Cu/water hybrid nanofluids is shown in Figure 11. The distribution indicates improved convective heat transfer, with Nu rising above base fluids as a result of boundary layer thinning and thermal conductivity increases brought on by nanoparticles. In Figure 12 the contour map shows how the radiation parameter Rd, Biot number Bi, and inclined MHD interact collectively to affect the local Nusselt number, which is the measure of heat transport at the surface. Heat transport decreases as magnetic damping increases with magnetic field strength and inclination. The Nusselt number is raised by higher Rd values because they increase temperature gradients and thermal radiation. Heat transport is also improved by a higher Bi, which indicates stronger convective surface heating.
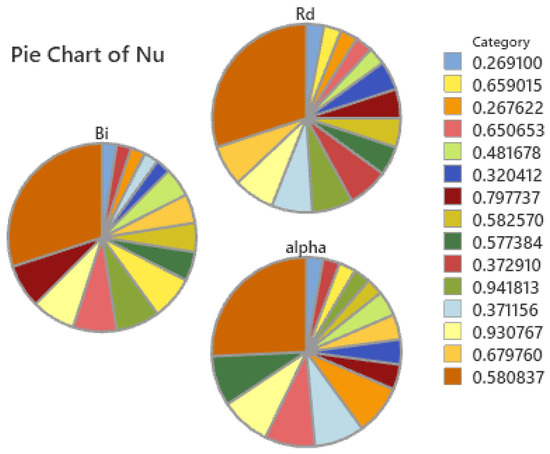
Figure 10.
Pie chart of for different values of Rd, Bi and .
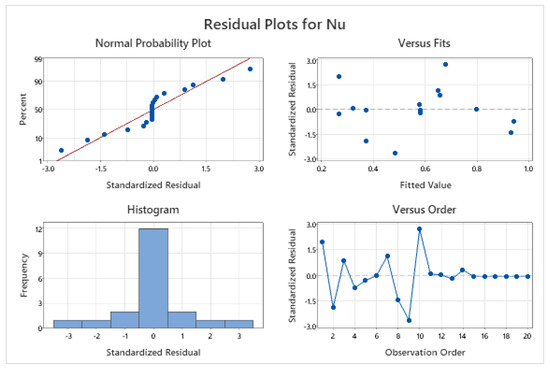
Figure 11.
Residual versus fitted value of .
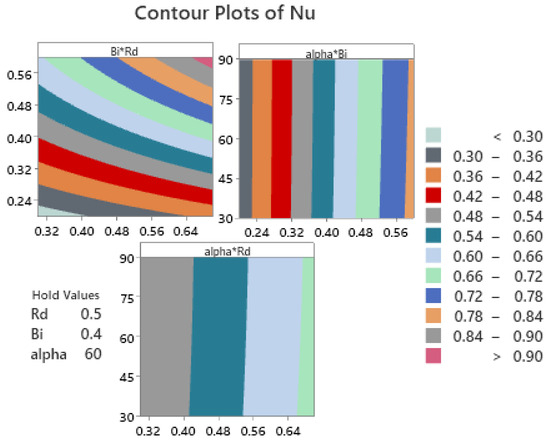
Figure 12.
Contour plots for .
Figure 13 illustrates the heat transfer response using 3D surface plots and scatter graphs, taking into consideration the effects of the inclined magnetic field, Biot number (Bi), and radiation parameter (Rd). The complex interactions between the parameters are highlighted by these figures, which display both constant and fluctuating patterns of heat transmission. The surface plots show the overall response patterns, while the scatter graphs show the data’s variability and dispersion. Together, they provide comprehensive understandings of the reliability and unpredictability of heat transfer performance in various contexts. This section presents the numerical results for the skin frictions and Nusselt number in relation to different parameters and inclination (). Table 4 shows the calculated numerical results for skin frictions and Nusselt number, respectively. Skin friction decreases as the radiation parameter (Rd) increases from . Higher radiation causes more energy to be transferred by radiation in forced convection, thickening the thermal boundary layer. The buoyant driving force decreases with increasing inclination from , which slows fluid motion near the surface and lowers wall shear stress, which reduces skin friction. Increasing the inclination from causes the surface gravity component to decrease, which weakens the flow and lowers the Nusselt number and convective heat transfer in both active and passive scenarios. Greater heat transfer and a higher Nusselt number result from stronger surface convection as opposed to interior conduction, which is indicated by a higher Biot number. Nusselt number values increase for both when the radiation parameter is increased from Rd and Pr .
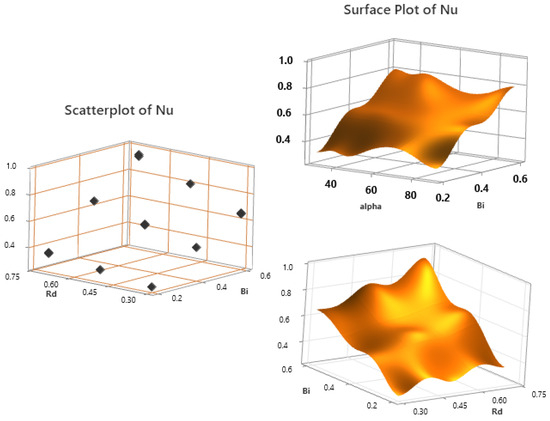
Figure 13.
Scatter plot and surface plots depicting for different values of Rd, Bi and .

Table 4.
The change in and for varying values of while other parameters remain fixed in active and passive case.
6. Concluding Remarks
The current work examined an inclined MHD analysis of a two-dimensional incompressible hybrid nanofluid Cu-Ag/water flow across a stretching cylinder containing gyrotactic microorganisms in the presence of chemically reactive substances. The influence of the source of heat, mixed convection parameter, chemical reaction, and numerous convective boundary conditions were all investigated. By using similarity transformations, ODEs were derived from the controlling PDEs. The Runge–Kutta–Fehlberg approach is employed to determine the numerical results with shooting proficiency. When applying different characteristics to the necessary parameters, the mathematical combination for the local Sherwood number, local skin friction, and local Nusselt number is displayed. Three-dimensional graphs show how physical quantities and effective attributes can have an impact at the same time.
- 1.
- Velocity distribution is a decline with magnetic parameter as a function of () and Prandtl parameter.
- 2.
- The thermal profile, concentration distribution, and the motile profiles reduce near a stretching surface but increase as we move further away from the surface when the curvature parameter increases.
- 3.
- A higher Soret number decreases the Sherwood number, while curvature parameter , mixed convection parameter , and Biot number increase the local Nusselt number and local skin friction.
- 4.
- The concentration distribution and motile concentration profile decrease with the chemical reaction parameter.
- 5.
- The streamline graph illustrates the way fluid flow is affected simultaneously by the magnetic parameter M and an angled magnetic field.
- 6.
- The three-dimensional surface, scattered graph, pie chart, and residual plotting demonstrate the statistical analysis of the heat of heat transfer response.
- 7.
- The contours highlight the intricate interactions between restricted magnetic field, significant radiation, and substantial convective condition factors by display the best heat transmission.
- 8.
- The framework for maximizing hybrid nanofluid performance in practical applications where effective heat and mass transmission are essential is provided by a comprehension of magnetic and convective phenomena.
This study’s focus is limited to numerical simulations of an incompressible model in two dimensions. Three-dimensional turbulent models with experimental support may be included in the scope of future research. Further optimization of thermal performance may be achieved by examining various nanoparticle geometries and hybrid combinations.
Author Contributions
Conceptualization, S. and M.A.; Methodology, S. and P.K.; Software, P.K. and P.S.M.; Validation, S. and P.K.; Formal analysis, M.A. and P.K.; Investigation, P.S.M.; Writing—original draft, S. and M.A.; Writing—review & editing, M.A., P.K. and P.S.M.; Supervision, P.K. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported and funded by the Deanship of Scientific Research at Imam Mohammad Ibn Saud Islamic University (IMSIU) (grant number IMSIU-DDRSP2502).
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding author.
Acknowledgments
The School of Basic and Applied Sciences at KR Mangalam University in India is gratefully acknowledged by the first author for their technical support.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Hosseinzadeh, K.; Asadi, A.; Mogharrebi, A.; Ermia Azari, M.; Ganji, D. Investigation of mixture fluid suspended by hybrid nanoparticles over vertical cylinder by considering shape factor effect. J. Therm. Anal. Calorim. 2021, 143, 1081–1095. [Google Scholar] [CrossRef]
- Basir, M.; Faisal, M.; Kumar, R.; Sarojamma, G.; Narayana, P.; Raza, J.; Mahmood, A. Exploration of thermal-diffusion and diffusion-thermal effects on the motion of temperature-dependent viscous fluid conveying microorganism. Arab. J. Sci. Eng. 2019, 44, 8023–8033. [Google Scholar] [CrossRef]
- Areekara, S.; Sabu, A.S.; Mathew, A.; Saravanan, B. Statistical analysis on the stratification effects of bioconvective EMHD nanofluid flow past a stretching sheet: Application in theranostics. Heat Transf. 2021, 50, 6680–6702. [Google Scholar] [CrossRef]
- Saranya, S.; Radha, K. Review of nanobiopolymers for controlled drug delivery. Polym.-Plast. Technol. Eng. 2014, 53, 1636–1646. [Google Scholar] [CrossRef]
- Ali, L.; Liu, X.; Ali, B.; Mujeed, S.; Abdal, S. Finite element simulation of multi-slip effects on unsteady MHD bioconvective micropolar nanofluid flow over a sheet with solutal and thermal convective boundary conditions. Coatings 2019, 9, 842. [Google Scholar] [CrossRef]
- Yahaya, R.I.; Arifin, N.M.; Ali, F.M.; Isa, S. Hybrid Nanofluid Flow with multiple slips over a Permeable Stretching/Shrinking sheet embedded in a porous medium. J. Adv. Res. Fluid Mech. Therm. Sci. 2023, 106, 143–152. [Google Scholar] [CrossRef]
- Khan, Z.H.; Khan, W.A.; Ibrahim, S.M.; Swain, K.; Huang, Z. Impact of multiple slips and thermal radiation on heat and mass transfer in MHD Maxwell hybrid nanofluid flow over porous stretching sheet. Case Stud. Therm. Eng. 2024, 61, 104906. [Google Scholar] [CrossRef]
- Cherala, S.S.; Gajjela, N.; Reddy, G.S.; Thumma, T. Mixed convective hydromagnetic radiative flow of ferro-hybrid nanofluid over an inclined elongating cylinder with heat generation and variable properties: Heat transfer analysis. J. Therm. Anal. Calorim. 2025, 1–18. [Google Scholar] [CrossRef]
- Sulaiman Basha, M.I.; Anthony, D.M.G. Numerical investigation of non-linear radiative flow of hybrid nanofluid past a stretching cylinder with inclined magnetic field. Numer. Heat Transf. Part B Fundam. 2024, 85, 842–866. [Google Scholar] [CrossRef]
- Alam, M.M.; Arshad, M.; Alharbi, F.M.; Al-Essa, L.A.; Galal, A.M. Heat and mass transmission for hybrid nanofluid flow in rotating system: Effects of microorganism motility. J. Therm. Anal. Calorim. 2025, 1–15. [Google Scholar] [CrossRef]
- Pattnaik, P.; Panda, S.; Mishra, S.; Baithalu, R. Enhanced heat transfer in micropolar fluids with inclined magnetic field and chemical reaction used in solar and geothermal energy systems: A comparative solution with semi-analytical approaches. Chaos Solitons Fractals 2025, 198, 116566. [Google Scholar] [CrossRef]
- Galal, A.M.; Zeemam, M.; Imran, M.; Basit, M.A.; Tahir, M.; Akram, S.; Younis, J. Numerical exploration of bioconvection in optimizing nanofluid flow through heated stretched cylinder in existence of magnetic field. Multidiscip. Model. Mater. Struct. 2025, 21, 425–447. [Google Scholar] [CrossRef]
- Ullah, I.; Ullah, H.; Nadeem, S.; Alzabut, J.; Saleem, S.; Alblawi, A. Inclined MHD mixed convection of a Bingham fluid in a lid-driven square cavity with an embedded wavy cylinder: Thermal and magnetic field interactions. J. Therm. Anal. Calorim. 2025, 150, 10105–10126. [Google Scholar] [CrossRef]
- Kumbhakar, B.; Nandi, S.; Chamkha, A.J. Unsteady hybrid nanofluid flow over a convectively heated cylinder with inclined magnetic field and viscous dissipation: A multiple regression analysis. Chin. J. Phys. 2022, 79, 38–56. [Google Scholar] [CrossRef]
- Riaz, A.; Abbasi, A.; Al-Khaled, K.; Gulzar, S.; Khan, S.U.; Farooq, W.; El-Din, E.M.T. A numerical analysis of the transport of modified hybrid nanofluids containing various nanoparticles with mixed convection applications in a vertical cylinder. Front. Phys. 2022, 10, 1018148. [Google Scholar] [CrossRef]
- Haq, F.; Khan, M.I.; Chu, Y.M.; Khan, N.B.; Kadry, S. Non-magnetized mixed convective viscous flow submerged in titanium oxide and aluminum titanium oxide hybrid nanoparticles towards a surface of cylinder. Int. Commun. Heat Mass Transf. 2021, 120, 105027. [Google Scholar] [CrossRef]
- Shojaei, A.; Amiri, A.J.; Ardahaie, S.S.; Hosseinzadeh, K.; Ganji, D. Hydrothermal analysis of Non-Newtonian second grade fluid flow on radiative stretching cylinder with Soret and Dufour effects. Case Stud. Therm. Eng. 2019, 13, 100384. [Google Scholar] [CrossRef]
- Ramzan, M.; Farooq, M.; Hayat, T.; Alsaedi, A.; Cao, J. MHD stagnation point flow by a permeable stretching cylinder with Soret-Dufour effects. J. Cent. South Univ. 2015, 22, 707–716. [Google Scholar] [CrossRef]
- Waqas, H.; Imran, M.; Bhatti, M. Influence of bioconvection on Maxwell nanofluid flow with the swimming of motile microorganisms over a vertical rotating cylinder. Chin. J. Phys. 2020, 68, 558–577. [Google Scholar] [CrossRef]
- Pandey, A.K.; Kumar, M. Boundary layer flow and heat transfer analysis on Cu-water nanofluid flow over a stretching cylinder with slip. Alex. Eng. J. 2017, 56, 671–677. [Google Scholar] [CrossRef]
- Hayat, T.; Shafiq, A.; Alsaedi, A. MHD axisymmetric flow of third grade fluid by a stretching cylinder. Alex. Eng. J. 2015, 54, 205–212. [Google Scholar] [CrossRef]
- Sreedevi, P.; Reddy, P.S. Williamson hybrid nanofluid flow over swirling cylinder with Cattaneo–Christov heat flux and gyrotactic microorganism. Waves Random Complex Media 2024, 34, 2767–2794. [Google Scholar] [CrossRef]
- Shilpa, B.; Badruddin, I.A.; Kamangar, S.; Zuber, M.; Mahmoud, E.R. Magneto-Convection and Cattaneo–Christov Heat Transport in a magnetically driven porous cylinder. Case Stud. Therm. Eng. 2025, 75, 107044. [Google Scholar] [CrossRef]
- Xia, W.F.; Ahmad, S.; Khan, M.N.; Ahmad, H.; Rehman, A.; Baili, J.; Gia, T.N. Heat and mass transfer analysis of nonlinear mixed convective hybrid nanofluid flow with multiple slip boundary conditions. Case Stud. Therm. Eng. 2022, 32, 101893. [Google Scholar] [CrossRef]
- Dey, D.; Borah, R.; Mahanta, B. Boundary layer flow and its dual solutions over a stretching cylinder: Stability analysis. In Emerging Technologies in Data Mining and Information Security: Proceedings of IEMIS 2020, Kolkata, India, 2–4 July 2020; Springer: Berlin/Heidelberg, Germany, 2021; Volume 1, pp. 27–38. [Google Scholar]
- Islam, S.; Khan, A.; Kumam, P.; Alrabaiah, H.; Shah, Z.; Khan, W.; Zubair, M.; Jawad, M. Radiative mixed convection flow of maxwell nanofluid over a stretching cylinder with joule heating and heat source/sink effects. Sci. Rep. 2020, 10, 17823. [Google Scholar] [CrossRef]
- Pandey, A.K.; Kumar, M. Natural convection and thermal radiation influence on nanofluid flow over a stretching cylinder in a porous medium with viscous dissipation. Alex. Eng. J. 2017, 56, 55–62. [Google Scholar] [CrossRef]
- Sulochana, C.; Sandeep, N. Stagnation point flow and heat transfer behavior of Cu–water nanofluid towards horizontal and exponentially stretching/shrinking cylinders. Appl. Nanosci. 2016, 6, 451–459. [Google Scholar] [CrossRef]
- Rashid, U.; Liang, H.; Ahmad, H.; Abbas, M.; Iqbal, A.; Hamed, Y. Study of (Ag and TiO2)/water nanoparticles shape effect on heat transfer and hybrid nanofluid flow toward stretching shrinking horizontal cylinder. Results Phys. 2021, 21, 103812. [Google Scholar] [CrossRef]
- Khan, N.S.; Kumam, P.; Thounthong, P. Second law analysis with effects of Arrhenius activation energy and binary chemical reaction on nanofluid flow. Sci. Rep. 2020, 10, 1226. [Google Scholar] [CrossRef]
- Hayat, T.; Kiyani, M.; Alsaedi, A.; Khan, M.I.; Ahmad, I. Mixed convective three-dimensional flow of Williamson nanofluid subject to chemical reaction. Int. J. Heat Mass Transf. 2018, 127, 422–429. [Google Scholar] [CrossRef]
- Wang, Y.; Yu, L.; Nazir, F.; Ahmed, J.; Mohamed, A.; Khan, I.; Elseesy, I.E. Heat transfer in transient motion of thin film coatings with copper (Cu), aluminium oxide (Al2O3) and molybdenum disulfide (MoS2) nanoparticles over a stretching cylinder. Case Stud. Therm. Eng. 2025, 69, 105951. [Google Scholar] [CrossRef]
- Kumar, P.; Poonia, H.; Ali, L.; Areekara, S.; Mathew, A. Effects of different nanoparticles Cu, TiO2, and Ag on fluid flow and heat transfer over cylindrical surface subject to non-fourier heat flux model. Numer. Heat Transf. Part B Fundam. 2024, 85, 325–343. [Google Scholar] [CrossRef]
- Khan, A.; Iqbal, Z.; Ahammad, N.A.; Sidi, M.O.; Elattar, S.; Awad, S.; Yousef, E.S.; Eldin, S.M. Bioconvection Maxwell nanofluid flow over a stretching cylinder influenced by chemically reactive activation energy surrounded by a permeable medium. Front. Phys. 2023, 10, 1065264. [Google Scholar] [CrossRef]
- Ali, B.; Naqvi, R.A.; Ali, L.; Abdal, S.; Hussain, S. A comparative description on time-dependent rotating magnetic transport of a water base liquid H2O with hybrid nano-materials Al2O3-Cu and Al2O3-TiO2 over an extending sheet using Buongiorno model: Finite element approach. Chin. J. Phys. 2021, 70, 125–139. [Google Scholar] [CrossRef]
- Yashkun, U.; Zaimi, K.; Ishak, A.; Pop, I.; Sidaoui, R. Hybrid nanofluid flow through an exponentially stretching/shrinking sheet with mixed convection and Joule heating. Int. J. Numer. Methods Heat Fluid Flow 2021, 31, 1930–1950. [Google Scholar] [CrossRef]
- Kiusalaas, J. Numerical Methods in Engineering with MATLAB®; Cambridge University Press: Cambridge, UK, 2005. [Google Scholar]
- Ali, L.; Liu, X.; Ali, B.; Mujeed, S.; Abdal, S.; Mutahir, A. The Impact of Nanoparticles Due to Applied Magnetic Dipole in Micropolar Fluid Flow Using the Finite Element Method. Symmetry 2020, 12, 520. [Google Scholar] [CrossRef]
- Oztop, H.F.; Abu-Nada, E. Numerical study of natural convection in partially heated rectangular enclosures filled with nanofluids. Int. J. Heat Fluid Flow 2008, 29, 1326–1336. [Google Scholar] [CrossRef]
- Merkin, J. Mixed convection from a horizontal circular cylinder. Int. J. Heat Mass Transf. 1977, 20, 73–77. [Google Scholar] [CrossRef]
- El-Zahar, E.; Rashad, A.; Saad, W.; Seddek, L. Magneto-hybrid nanofluids flow via mixed convection past a radiative circular cylinder. Sci. Rep. 2020, 10, 10494. [Google Scholar]
- Nazar, R.; Amin, N.; Pop, I. Mixed convection boundary-layer flow from a horizontal circular cylinder in micropolar fluids: Case of constant wall temperature. Int. J. Numer. Methods Heat Fluid Flow 2003, 13, 86–109. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).