Multi-Armed Bandit Optimization for Explainable AI Models in Chronic Kidney Disease Risk Evaluation
Abstract
1. Introduction
- A unified adaptive bandit approach that merges XGBoost with Upper Confidence Bound exploration for intelligent hyperparameter search, achieving 0.9-fold to 9.7-fold time efficiency improvement over four hyperparameter optimization methods;
- Advanced imbalance handling through BorderlineSMOTE with conservative balancing strategy preventing over-synthesis while preserving original data distribution characteristics;
- Rigorous statistical validation through extensive empirical evaluation across 30 repeated experiments against 16 baseline algorithms with Bonferroni-corrected significance testing, demonstrating consistent superiority (p < 0.001) across all performance metrics;
- Comprehensive explainability integration through dual SHAP-LIME framework resolving interpretability deficits of ensemble architectures while preserving clinical utility.
2. Related Works
3. Preliminary
3.1. Data Overview
3.2. Preliminary Data Investigation
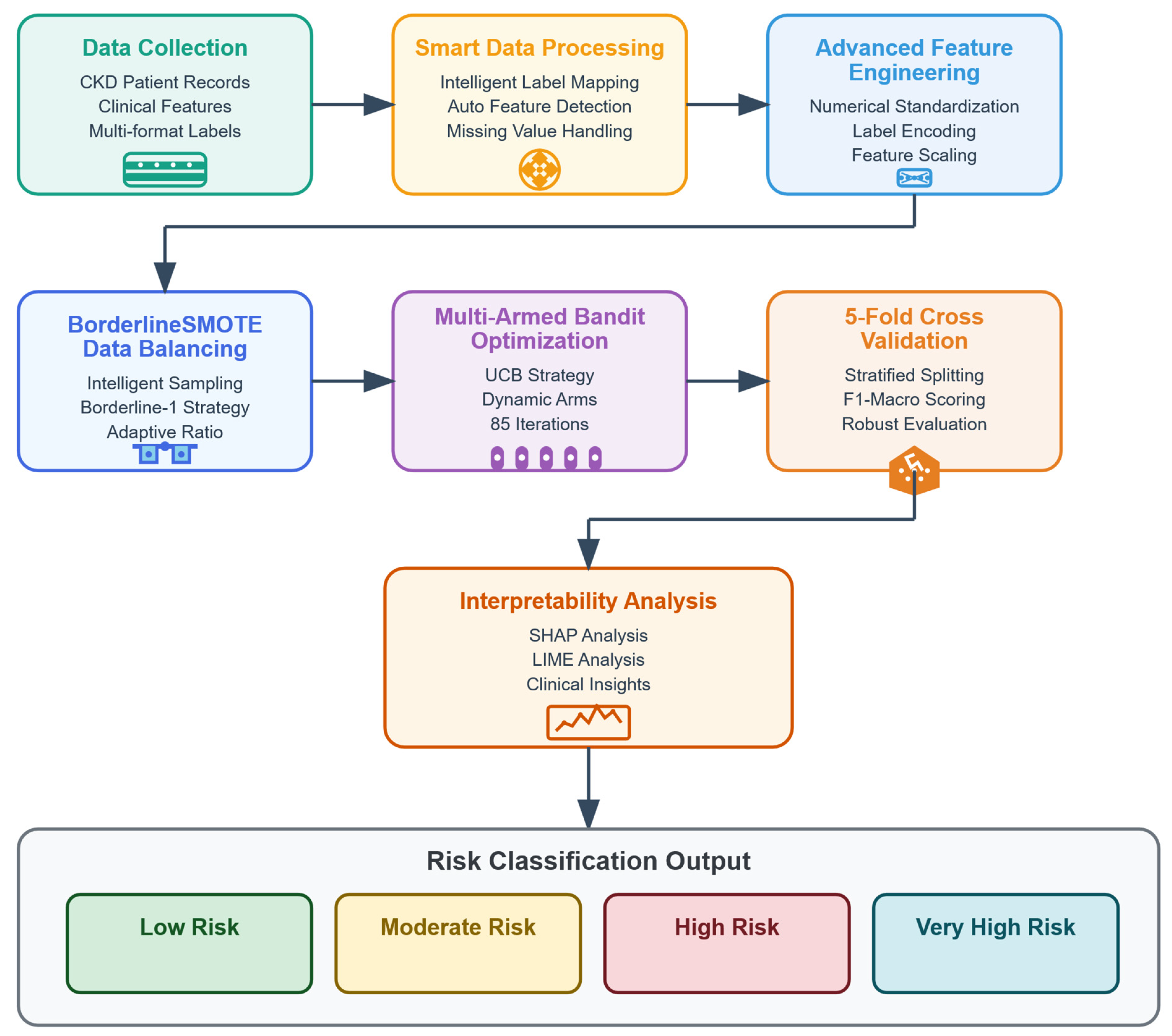
3.3. Data Processing
4. Methodology
4.1. XGBoost
4.2. Multi-Armed Bandit Optimization
| Algorithm 1 Multi-Armed Bandit XGBoost Hyperparameter Optimization | |
| 1: | def sample_arm(): |
| 2: | params = { |
| 3: | n_estimators: random.choice(range(300, 801, 25)), |
| 4: | max_depth: random.choice(range(5, 10)), |
| 5: | learning_rate: exp(uniform(log(0.01), log(0.05))), |
| 6: | subsample: uniform(0.7, 0.9), |
| 7: | colsample_bytree: uniform(0.8, 1.0), |
| 8: | reg_alpha: uniform(0.1, 1.0), |
| 9: | reg_lambda: uniform(3.0, 8.0) } |
| 10: | return params |
| 11: | def evaluate_arm(arm_params): |
| 12: | model = XGBClassifier(**arm_params) |
| 13: | cv_scores = cross_val_score(model, X, y, cv = 5, scoring = ‘f1_macro’) |
| 14: | return cv_scores.mean() |
| 15: | def select_arm_ucb(t): |
| 16: | if t < len(arms): return t |
| 17: | ucb_values = [arm_means[i] + c*sqrt(log(t)/arm_counts[i]) for i in range(len(arms))] |
| 18: | return argmax(ucb_values) |
| 19: | for t in range(T): |
| 20: | arm_idx = select_arm_ucb(t) |
| 21: | reward = evaluate_arm(arms[arm_idx]) |
| 22: | update_arm_statistics(arm_idx, reward) |
| 23: | if t % 20 == 0 and len(arms) < max_arms: |
| 24: | arms.append(sample_arm()) |
| 25: | best_arm_idx = argmax(arm_means) |
| 26: | final_model = XGBClassifier(**arms[best_arm_idx]).fit(X_train, y_train) |
| 27: | predictions = final_model.predict(X_test) |
| Return: final_model, arms[best_arm_idx], evaluate_metrics(y_test, predictions) | |
4.3. BorderlineSMOTE
4.4. Model Validation Strategy
5. Experiment
5.1. Implementation Environment and Settings
5.2. Performance Metrics
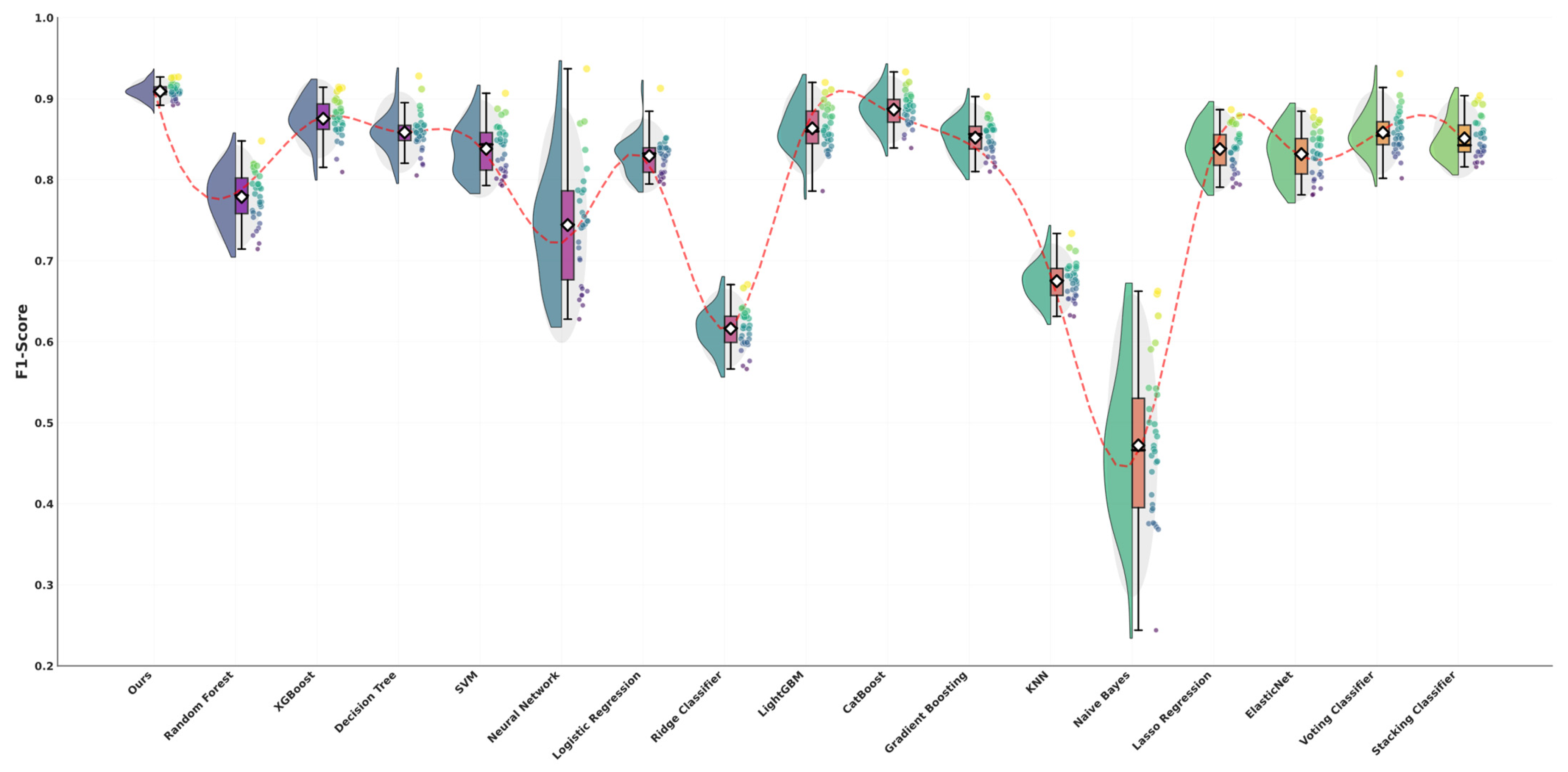
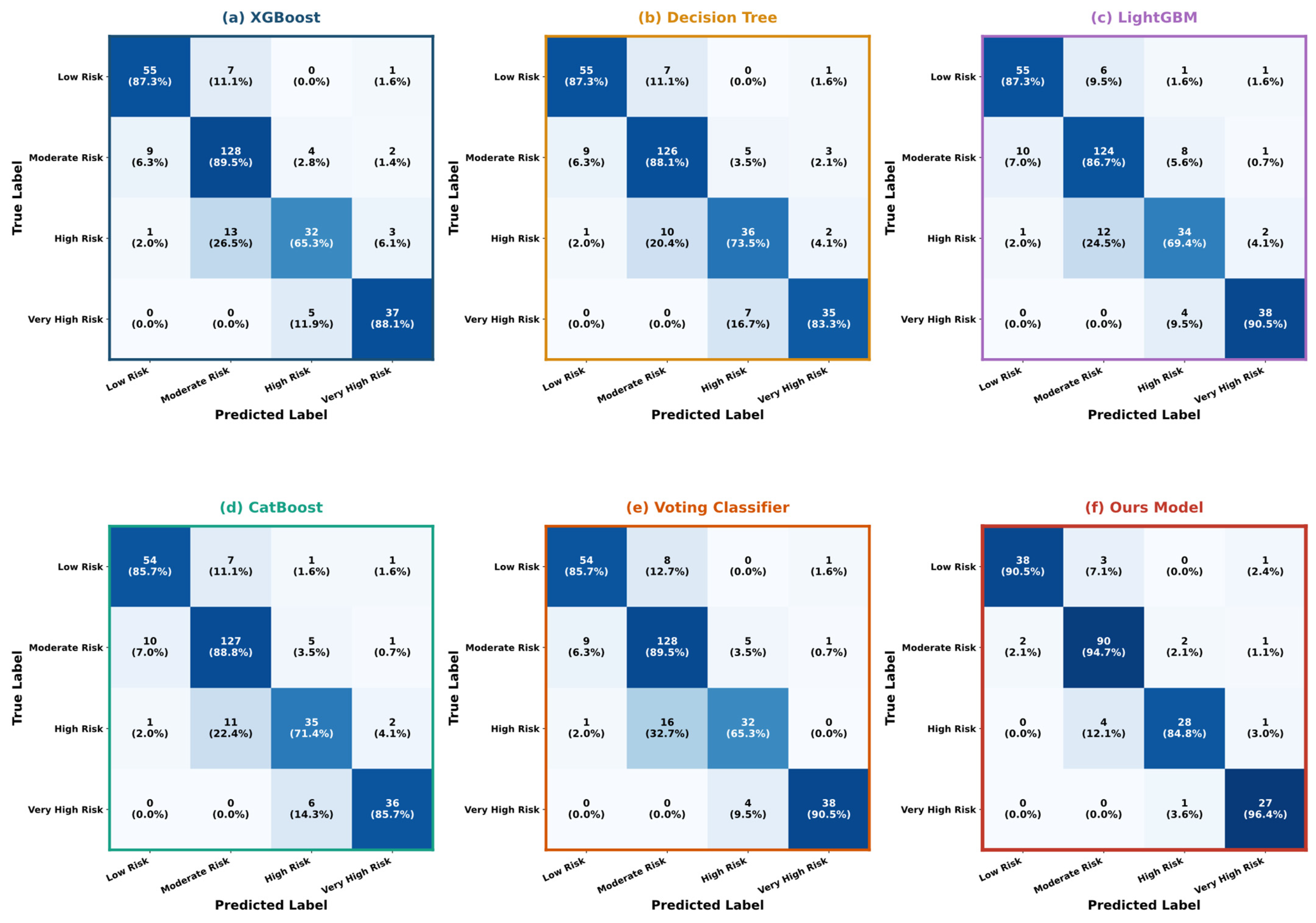
5.3. Performance Evaluation and Comparative Assessment
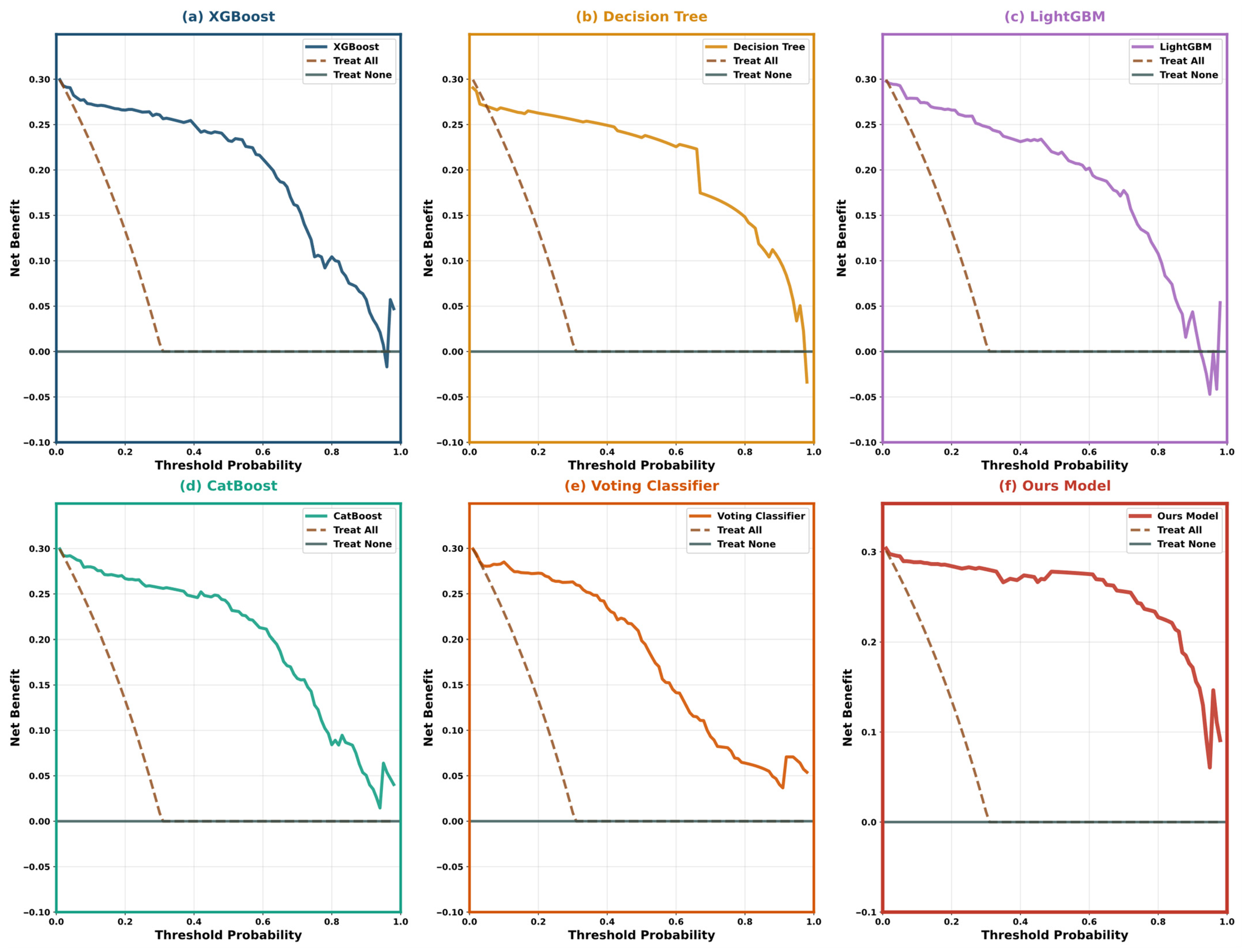
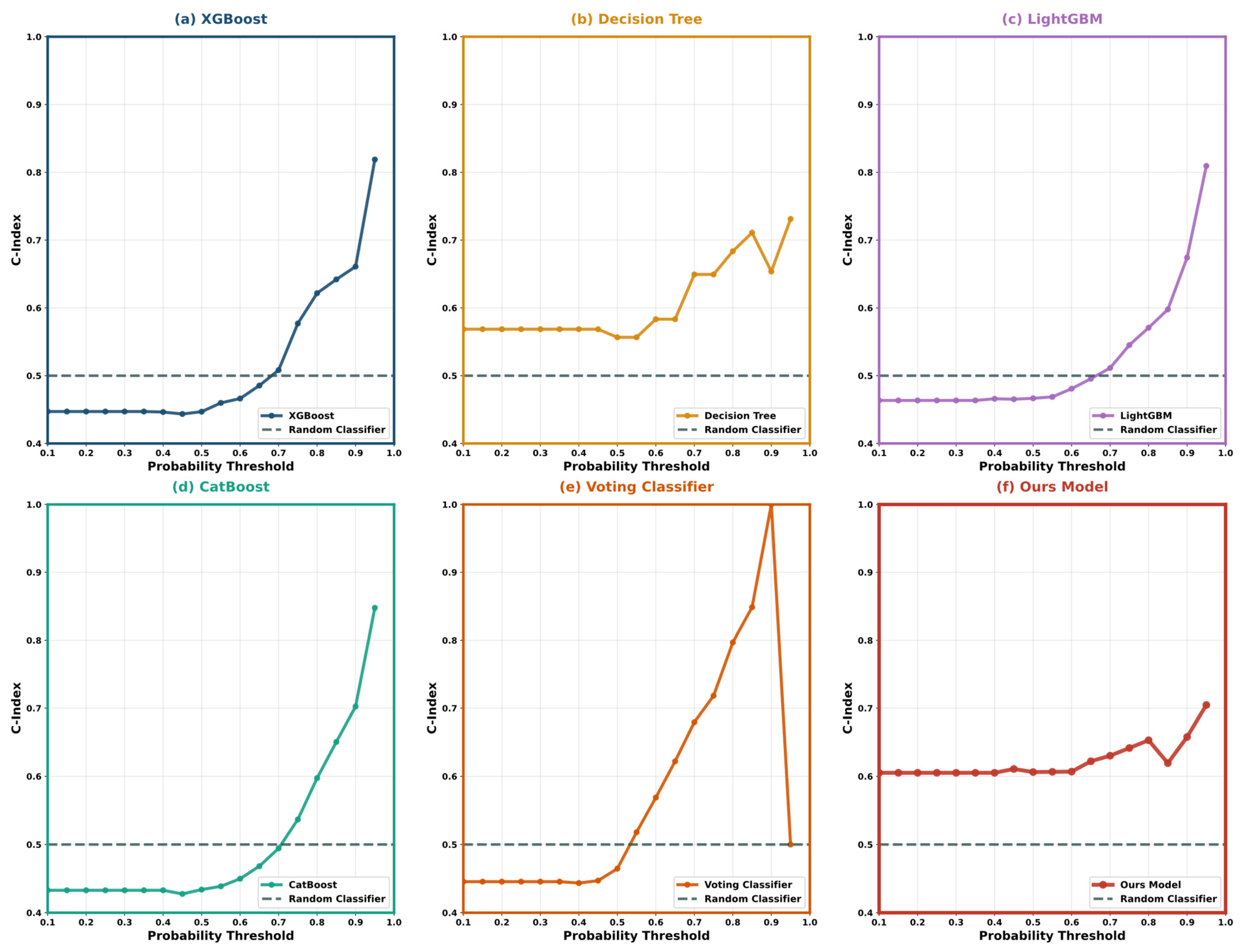
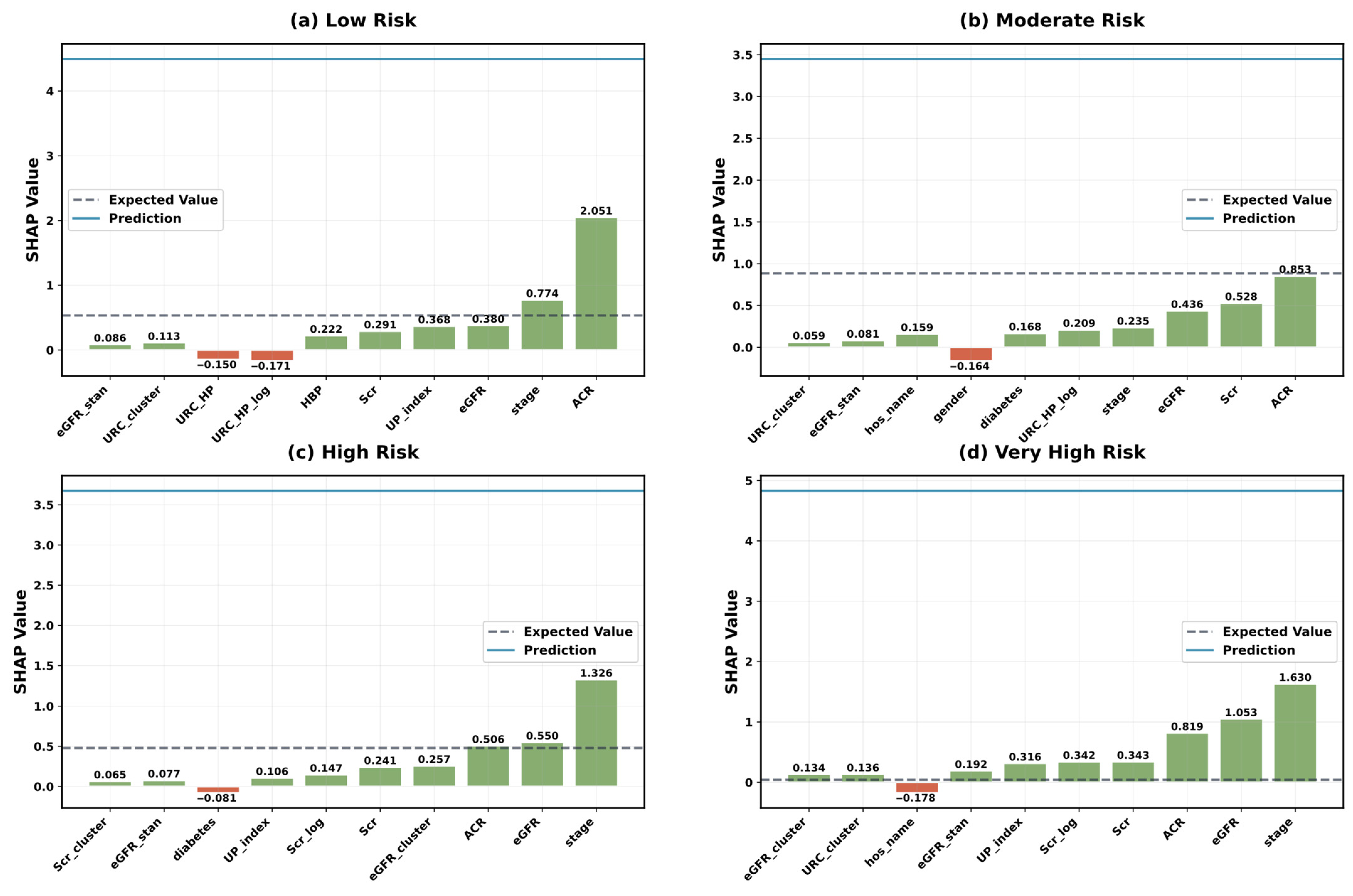
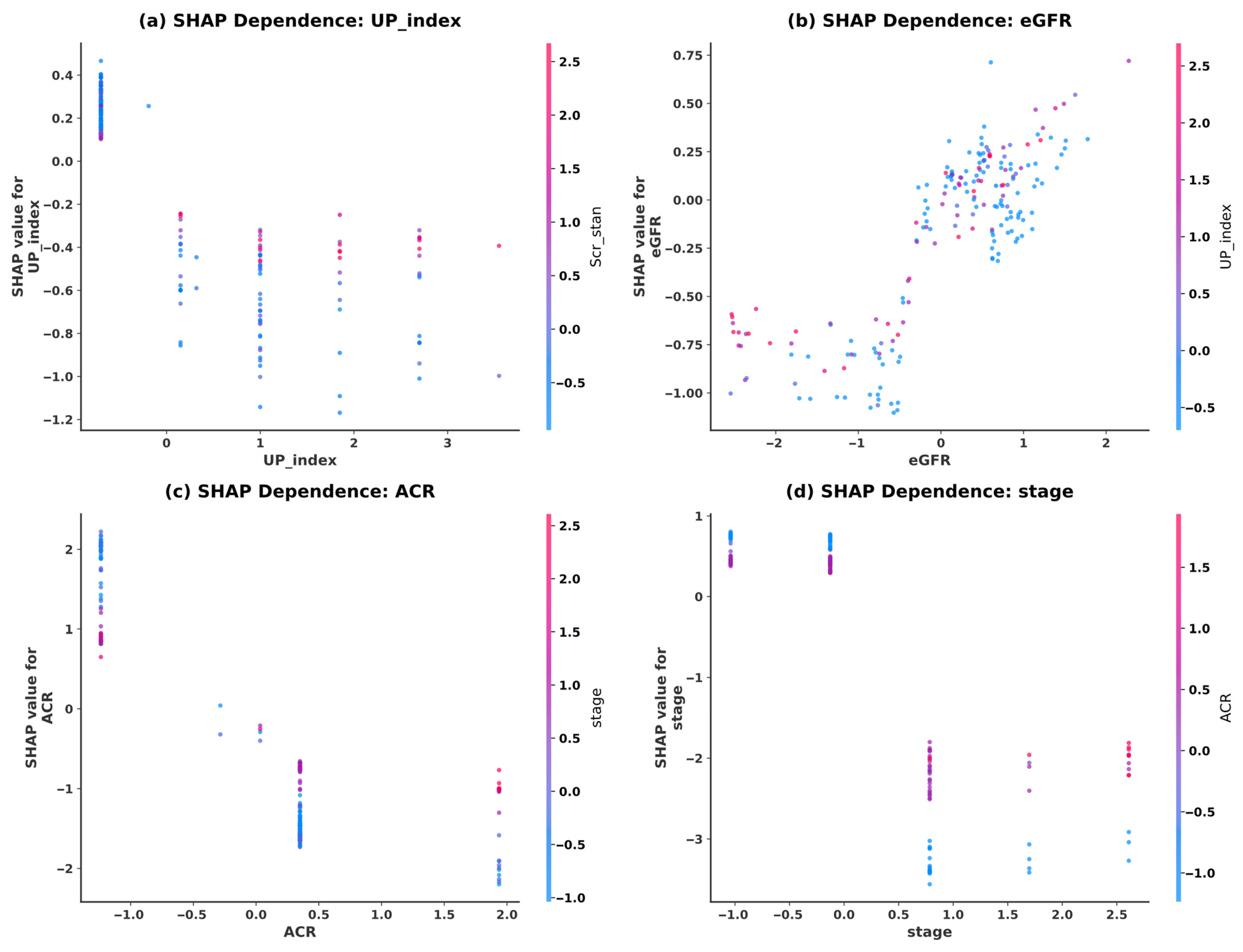
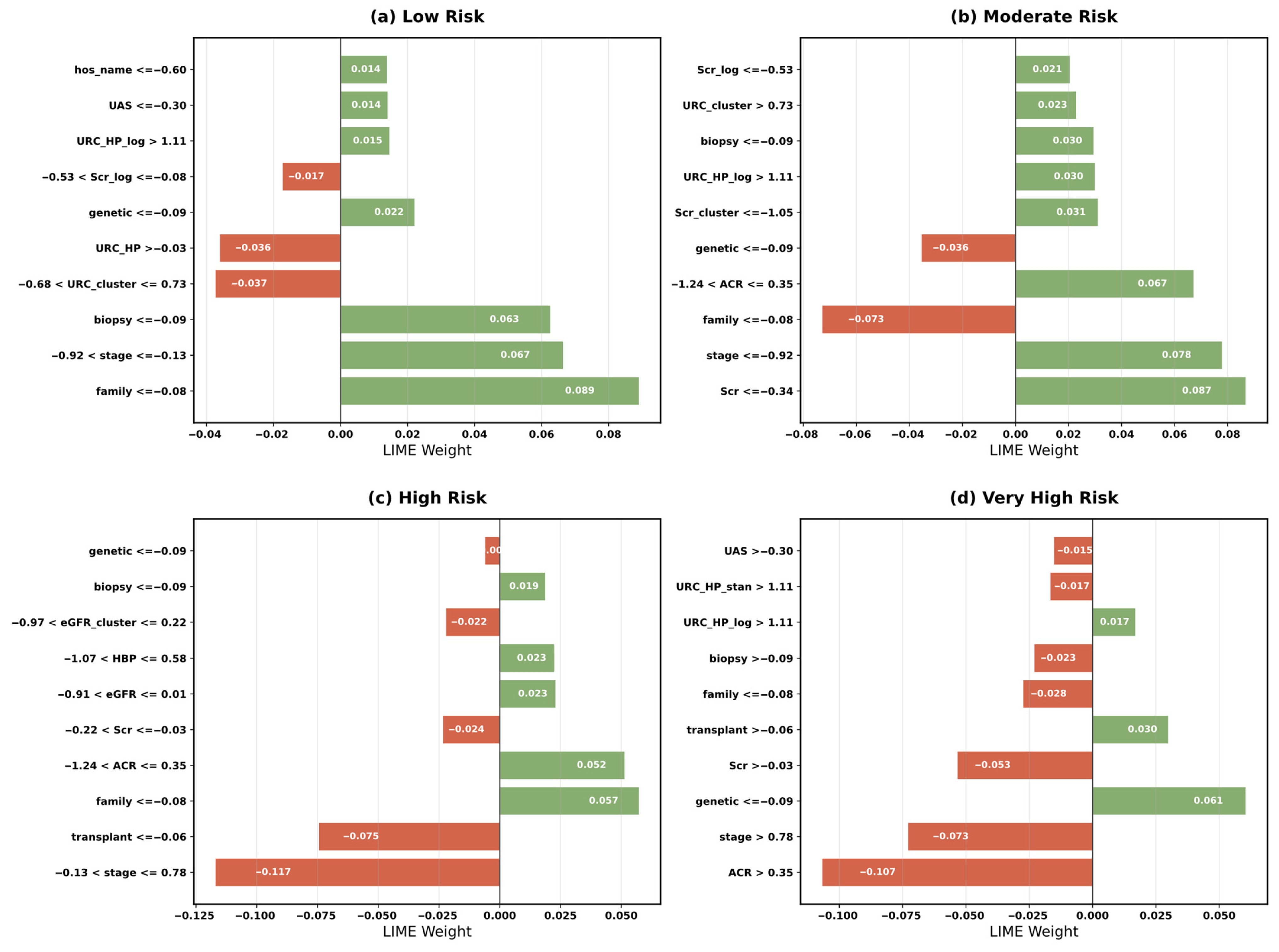
5.4. Model Interpretability Analysis
5.5. MAB Optimization and Algorithm Performance
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Ahmed, K.; Dubey, M.K.; Kajal; Dubey, S.; Pandey, D.K. Chronic Kidney Disease: Causes, Treatment, Management, and Future Scope. In Computational Intelligence for Genomics Data; Elsevier: Amsterdam, The Netherlands, 2025; pp. 99–111. ISBN 978-0-443-30080-6. [Google Scholar]
- Gogoi, P.; Valan, J.A. Machine Learning Approaches for Predicting and Diagnosing Chronic Kidney Disease: Current Trends, Challenges, Solutions, and Future Directions. Int. Urol. Nephrol. 2024, 57, 1245–1268. [Google Scholar] [CrossRef]
- Simeri, A.; Pezzi, G.; Arena, R.; Papalia, G.; Szili-Torok, T.; Greco, R.; Veltri, P.; Greco, G.; Pezzi, V.; Provenzano, M.; et al. Artificial Intelligence in Chronic Kidney Diseases: Methodology and Potential Applications. Int. Urol. Nephrol. 2024, 57, 159–168. [Google Scholar] [CrossRef] [PubMed]
- Francis, A.; Harhay, M.N.; Ong, A.C.M.; Tummalapalli, S.L.; Ortiz, A.; Fogo, A.B.; Fliser, D.; Roy-Chaudhury, P.; Fontana, M.; Nangaku, M.; et al. Chronic Kidney Disease and the Global Public Health Agenda: An International Consensus. Nat. Rev. Nephrol. 2024, 20, 473–485. [Google Scholar] [CrossRef]
- Bello, A.K.; Okpechi, I.G.; Levin, A.; Ye, F.; Damster, S.; Arruebo, S.; Donner, J.-A.; Caskey, F.J.; Cho, Y.; Davids, M.R.; et al. An Update on the Global Disparities in Kidney Disease Burden and Care across World Countries and Regions. Lancet Glob. Health 2024, 12, e382–e395. [Google Scholar] [CrossRef]
- Lee, P.-H.; Huang, S.M.; Tsai, Y.-C.; Wang, Y.-T.; Chew, F.Y. Biomarkers in Contrast-Induced Nephropathy: Advances in Early Detection, Risk Assessment, and Prevention Strategies. Int. J. Mol. Sci. 2025, 26, 2869. [Google Scholar] [CrossRef]
- Talaat, F.M.; Aly, W.F. Toward Precision Cardiology: A Transformer-Based System for Adaptive Prediction of Heart Disease. Neural Comput. Appl. 2025, 37, 13547–13571. [Google Scholar] [CrossRef]
- Montalescot, L.; Dorard, G.; Speyer, E.; Legrand, K.; Ayav, C.; Combe, C.; Stengel, B.; Untas, A. Patient Perspectives on Chronic Kidney Disease and Decision-Making about Treatment. Discourse of Participants in the French CKD-REIN Cohort Study. J. Nephrol. 2022, 35, 1387–1397. [Google Scholar] [CrossRef]
- Wen, F.; Wang, J.; Yang, C.; Wang, F.; Li, Y.; Zhang, L.; Pagán, J.A. Cost-Effectiveness of Population-Based Screening for Chronic Kidney Disease among the General Population and Adults with Diabetes in China: A Modelling Study. Lancet Reg. Health—West. Pac. 2025, 56, 101493. [Google Scholar] [CrossRef]
- Rane, N.; Choudhary, S.P.; Rane, J. Ensemble Deep Learning and Machine Learning: Applications, Opportunities, Challenges, and Future Directions. Stud. Med. Health Sci. 2024, 1, 18–41. [Google Scholar] [CrossRef]
- Shivahare, B.D.; Singh, J.; Ravi, V.; Chandan, R.R.; Alahmadi, T.J.; Singh, P.; Diwakar, M. Delving into Machine Learning’s Influence on Disease Diagnosis and Prediction. Open Public Health J. 2024, 17, e18749445297804. [Google Scholar] [CrossRef]
- Sanmarchi, F.; Fanconi, C.; Golinelli, D.; Gori, D.; Hernandez-Boussard, T.; Capodici, A. Predict, Diagnose, and Treat Chronic Kidney Disease with Machine Learning: A Systematic Literature Review. J. Nephrol. 2023, 36, 1101–1117. [Google Scholar] [CrossRef] [PubMed]
- Li, C.; Liu, J.; Fu, P.; Zou, J. Artificial Intelligence Models in Diagnosis and Treatment of Kidney Diseases: Current Status and Prospects. Kidney Dis. 2025, 11, 501–517. [Google Scholar] [CrossRef] [PubMed]
- Ramu, K.; Patthi, S.; Prajapati, Y.N.; Ramesh, J.V.N.; Banerjee, S.; Rao, K.B.V.B.; Alzahrani, S.I.; Ayyasamy, R. Hybrid CNN-SVM Model for Enhanced Early Detection of Chronic Kidney Disease. Biomed. Signal Process. Control. 2025, 100, 107084. [Google Scholar] [CrossRef]
- Iliyas, I.I.; Boukari, S.; Gital, A.Y. Recent Trends in Prediction of Chronic Kidney Disease Using Different Learning Approaches: A Systematic Literature Review. J. Med. Artif. Intell. 2025, 8, 62. [Google Scholar] [CrossRef]
- Delrue, C.; De Bruyne, S.; Speeckaert, M.M. Application of Machine Learning in Chronic Kidney Disease: Current Status and Future Prospects. Biomedicines 2024, 12, 568. [Google Scholar] [CrossRef]
- Silveira, A.C.M.D.; Sobrinho, Á.; Silva, L.D.D.; Costa, E.D.B.; Pinheiro, M.E.; Perkusich, A. Exploring Early Prediction of Chronic Kidney Disease Using Machine Learning Algorithms for Small and Imbalanced Datasets. Appl. Sci. 2022, 12, 3673. [Google Scholar] [CrossRef]
- Dhanka, S.; Sharma, A.; Kumar, A.; Maini, S.; Vundavilli, H. Advancements in Hybrid Machine Learning Models for Biomedical Disease Classification Using Integration of Hyperparameter-Tuning and Feature Selection Methodologies: A Comprehensive Review. Arch. Computat. Methods Eng. 2025. [Google Scholar] [CrossRef]
- Agrawal, R.; Agrawal, R. Explainable AI in Early Autism Detection: A Literature Review of Interpretable Machine Learning Approaches. Discov. Ment. Health 2025, 5, 98. [Google Scholar] [CrossRef]
- Arjmandmazidi, S.; Heidari, H.R.; Ghasemnejad, T.; Mori, Z.; Molavi, L.; Meraji, A.; Kaghazchi, S.; Mehdizadeh Aghdam, E.; Montazersaheb, S. An In-Depth Overview of Artificial Intelligence (AI) Tool Utilization across Diverse Phases of Organ Transplantation. J. Transl. Med. 2025, 23, 678. [Google Scholar] [CrossRef]
- Hossain, M.I.; Zamzmi, G.; Mouton, P.R.; Salekin, M.S.; Sun, Y.; Goldgof, D. Explainable AI for Medical Data: Current Methods, Limitations, and Future Directions. ACM Comput. Surv. 2025, 57, 1–46. [Google Scholar] [CrossRef]
- Goktas, P.; Grzybowski, A. Shaping the Future of Healthcare: Ethical Clinical Challenges and Pathways to Trustworthy AI. J. Clin. Med. 2025, 14, 1605. [Google Scholar] [CrossRef] [PubMed]
- Hooshyar, D.; Yang, Y. Problems with SHAP and LIME in Interpretable AI for Education: A Comparative Study of Post-Hoc Explanations and Neural-Symbolic Rule Extraction. IEEE Access 2024, 12, 137472–137490. [Google Scholar] [CrossRef]
- Shah, P.; Shukla, M.; Dholakia, N.H.; Gupta, H. Predicting Cardiovascular Risk with Hybrid Ensemble Learning and Explainable AI. Sci. Rep. 2025, 15, 17927. [Google Scholar] [CrossRef] [PubMed]
- Li, M.; Sun, H.; Huang, Y.; Chen, H. Shapley Value: From Cooperative Game to Explainable Artificial Intelligence. Auton. Intell. Syst. 2024, 4, 2. [Google Scholar] [CrossRef]
- Khan, N.; Nauman, M.; Almadhor, A.S.; Akhtar, N.; Alghuried, A.; Alhudhaif, A. Guaranteeing Correctness in Black-Box Machine Learning: A Fusion of Explainable AI and Formal Methods for Healthcare Decision-Making. IEEE Access 2024, 12, 90299–90316. [Google Scholar] [CrossRef]
- Asri, B.; Qassimi, S.; Rakrak, S. Active Learning-Based Multi-Armed Bandits for Recommendation Systems. Knowl. Inf. Syst. 2025, 67, 9253–9275. [Google Scholar] [CrossRef]
- Xia, H.; Li, C.; Tan, Q.; Zeng, S.; Yang, S. Learning to Search Promising Regions by Space Partitioning for Evolutionary Methods. Swarm Evol. Comput. 2024, 91, 101726. [Google Scholar] [CrossRef]
- Baheri, A. Multilevel Constrained Bandits: A Hierarchical Upper Confidence Bound Approach with Safety Guarantees. Mathematics 2025, 13, 149. [Google Scholar] [CrossRef]
- Nie, X.; Ahmad, F.S. Dynamic Reward Systems and Customer Loyalty: Reinforcement Learning-Optimized Personalized Service Strategies. Future Technol. 2025, 4, 259–268. [Google Scholar] [CrossRef]
- Ni, Y.; Yang, D. Health Consulting Services Recommendation Considering Patients’ Decision-Making Behaviors: A CNN and Multiarmed Bandit Approach. IEEE Trans. Eng. Manag. 2025, 72, 2341–2355. [Google Scholar] [CrossRef]
- Keerthika, K.; Kannan, M.; Saravanan, T. Clinical Intelligence: Deep Reinforcement Learning for Healthcare and Biomedical Advancements. In Deep Reinforcement Learning and Its Industrial Use Cases; Mahajan, S., Raj, P., Pandit, A.K., Eds.; Wiley: Hoboken, NJ, USA, 2024; pp. 137–150. ISBN 978-1-394-27255-6. [Google Scholar]
- Nasarian, E.; Alizadehsani, R.; Acharya, U.R.; Tsui, K.-L. Designing Interpretable ML System to Enhance Trust in Healthcare: A Systematic Review to Proposed Responsible Clinician-AI-Collaboration Framework. Inf. Fusion 2024, 108, 102412. [Google Scholar] [CrossRef]
- Salmi, M.; Atif, D.; Oliva, D.; Abraham, A.; Ventura, S. Handling Imbalanced Medical Datasets: Review of a Decade of Research. Artif. Intell. Rev. 2024, 57, 273. [Google Scholar] [CrossRef]
- Song, R. Optimizing Decision-Making in Uncertain Environments through Analysis of Stochastic Stationary Multi-Armed Bandit Algorithms. Appl. Comput. Eng. 2024, 68, 93–113. [Google Scholar] [CrossRef]
- Khan, N.; Raza, M.A.; Mirjat, N.H.; Balouch, N.; Abbas, G.; Yousef, A.; Touti, E. Unveiling the Predictive Power: A Comprehensive Study of Machine Learning Model for Anticipating Chronic Kidney Disease. Front. Artif. Intell. 2024, 6, 1339988. [Google Scholar] [CrossRef] [PubMed]
- Metherall, B.; Berryman, A.K.; Brennan, G.S. Machine Learning for Classifying Chronic Kidney Disease and Predicting Creatinine Levels Using At-Home Measurements. Sci. Rep. 2025, 15, 4364. [Google Scholar] [CrossRef]
- Rahman, M.M.; Al-Amin, M.; Hossain, J. Machine Learning Models for Chronic Kidney Disease Diagnosis and Prediction. Biomed. Signal Process. Control 2024, 87, 105368. [Google Scholar] [CrossRef]
- Ghosh, S.K.; Khandoker, A.H. Investigation on Explainable Machine Learning Models to Predict Chronic Kidney Diseases. Sci. Rep. 2024, 14, 3687. [Google Scholar] [CrossRef]
- Dharmarathne, G.; Bogahawaththa, M.; McAfee, M.; Rathnayake, U.; Meddage, D.P.P. On the Diagnosis of Chronic Kidney Disease Using a Machine Learning-Based Interface with Explainable Artificial Intelligence. Intell. Syst. Appl. 2024, 22, 200397. [Google Scholar] [CrossRef]
- Saif, D.; Sarhan, A.M.; Elshennawy, N.M. Early Prediction of Chronic Kidney Disease Based on Ensemble of Deep Learning Models and Optimizers. J. Electr. Syst. Inf. Technol. 2024, 11, 17. [Google Scholar] [CrossRef]
- Zhu, H.; Qiao, S.; Zhao, D.; Wang, K.; Wang, B.; Niu, Y.; Shang, S.; Dong, Z.; Zhang, W.; Zheng, Y.; et al. Machine Learning Model for Cardiovascular Disease Prediction in Patients with Chronic Kidney Disease. Front. Endocrinol. 2024, 15, 1390729. [Google Scholar] [CrossRef]
- Shanmugarajeshwari, V.; Ilayaraja, M. Intelligent Decision Support for Identifying Chronic Kidney Disease Stages: Machine Learning Algorithms. Int. J. Intell. Inf. Technol. 2023, 20, 1–22. [Google Scholar] [CrossRef]
- Singamsetty, S.; Ghanta, S.; Biswas, S.; Pradhan, A. Enhancing Machine Learning-Based Forecasting of Chronic Renal Disease with Explainable AI. PeerJ Comput. Sci. 2024, 10, e2291. [Google Scholar] [CrossRef] [PubMed]
- Saputra, A.G.; Purwanto, P.; Pujiono, P. Hyperparameter Tuning Decision Tree and Recursive Feature Elimination Technique for Improved Chronic Kidney Disease Classification. Sci. J. Inform. 2024, 11, 821–830. [Google Scholar] [CrossRef]
- Liu, Y.; Chen, J.; Wang, M. BO–FTT: A Deep Learning Model Based on Parameter Tuning for Early Disease Prediction from a Case of Anemia in CKD. Electronics 2025, 14, 2471. [Google Scholar] [CrossRef]
- Gogoi, P.; Valan, J.A. Interpretable Machine Learning for Chronic Kidney Disease Prediction: A SHAP and Genetic Algorithm-Based Approach. Biomed. Mater. Devices 2025, 3, 1384–1402. [Google Scholar] [CrossRef]
- Gokiladevi, M.; Santhoshkumar, S. Henry Gas Optimization Algorithm with Deep Learning Based Chronic Kidney Disease Detection and Classification Model. Int. J. Intell. Eng. Syst. 2024, 17, 645–655. [Google Scholar] [CrossRef]
- Priyadharshini, M.; Murugesh, V.; Samkumar, G.V.; Chowdhury, S.; Panigrahi, A.; Pati, A.; Sahu, B. A Population Based Optimization of Convolutional Neural Networks for Chronic Kidney Disease Prediction. Sci. Rep. 2025, 15, 14500. [Google Scholar] [CrossRef]
- Awad Yousif, S.M.; Halawani, H.T.; Amoudi, G.; Osman Birkea, F.M.; Almunajam, A.M.R.; Elhag, A.A. Early Detection of Chronic Kidney Disease Using Eurygasters Optimization Algorithm with Ensemble Deep Learning Approach. Alex. Eng. J. 2024, 100, 220–231. [Google Scholar] [CrossRef]
- Nayyem, M.N.; Sharif, K.S.; Raju, M.A.H.; Al Rakin, A.; Arafin, R.; Khan, M.M. Optimized Ensemble Learning for Chronic Kidney Disease Prognostication: A Stratified Cross-Validation Approach. In Proceedings of the 2024 IEEE International Conference on Computing (ICOCO), Kuala Lumpur, Malaysia, 12 December 2024; pp. 553–558. [Google Scholar]
- Mohamad Tabish, H.A.; Arbaz, S.M.; Agarwal, M.; Sinha, A. Early Prediction and Risk Identification of Chronic Kidney Disease Using Deep Learning Technique. In Proceedings of the 2024 15th International Conference on Computing Communication and Networking Technologies (ICCCNT), Kamand, India, 24 June 2024; pp. 1–9. [Google Scholar]
- Tawsik Jawad, K.M.; Verma, A.; Amsaad, F.; Ashraf, L. A Study on the Application of Explainable AI on Ensemble Models for Predictive Analysis of Chronic Kidney Disease. IEEE Access 2025, 13, 23312–23330. [Google Scholar] [CrossRef]
- Jawad, K.M.T.; Verma, A.; Amsaad, F.; Ashraf, L. AI-Driven Predictive Analytics Approach for Early Prognosis of Chronic Kidney Disease Using Ensemble Learning and Explainable AI. arXiv 2024, arXiv:2406.06728. [Google Scholar] [CrossRef]
- Jafar, A.; Lee, M. Enhancing Kidney Disease Diagnosis Using ACO-Based Feature Selection and Explainable AI Techniques. Appl. Sci. 2025, 15, 2960. [Google Scholar] [CrossRef]
- Huang, M.; Zhang, X.S.; Bhatti, U.A.; Wu, Y.; Zhang, Y.; Yasin Ghadi, Y. An Interpretable Approach Using Hybrid Graph Networks and Explainable AI for Intelligent Diagnosis Recommendations in Chronic Disease Care. Biomed. Signal Process. Control 2024, 91, 105913. [Google Scholar] [CrossRef]
- Reddy, S.; Roy, S.; Choy, K.W.; Sharma, S.; Dwyer, K.M.; Manapragada, C.; Miller, Z.; Cheon, J.; Nakisa, B. Predicting Chronic Kidney Disease Progression Using Small Pathology Datasets and Explainable Machine Learning Models. Comput. Methods Programs Biomed. Update 2024, 6, 100160. [Google Scholar] [CrossRef]
- Nguycharoen, N. Explainable Machine Learning System for Predicting Chronic Kidney Disease in High-Risk Cardiovascular Patients. arXiv 2024, arXiv:2404.11148. [Google Scholar] [CrossRef]
- Huang, J.; Li, L.; Hou, M.; Chen, J. Bayesian Optimization Meets Explainable AI: Enhanced Chronic Kidney Disease Risk Assessment. Mathematics 2025, 13, 2726. [Google Scholar] [CrossRef]
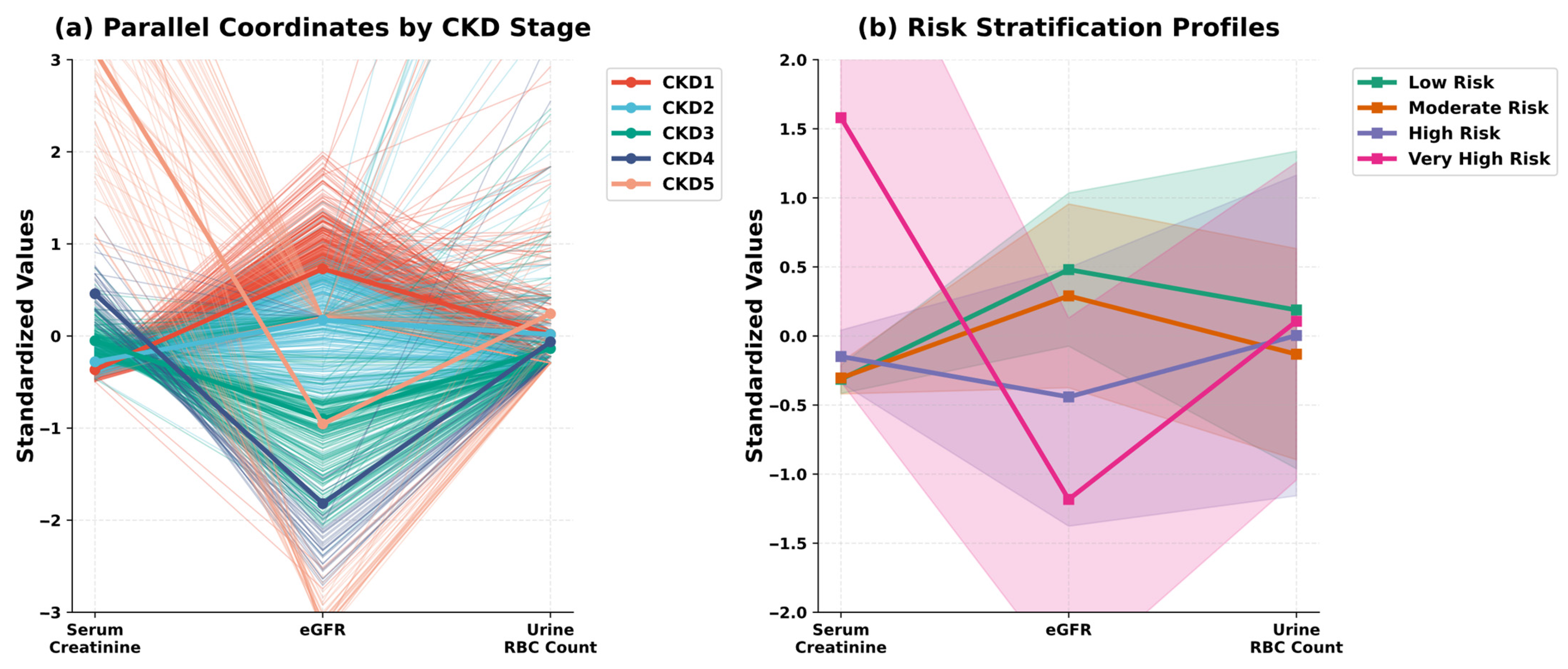
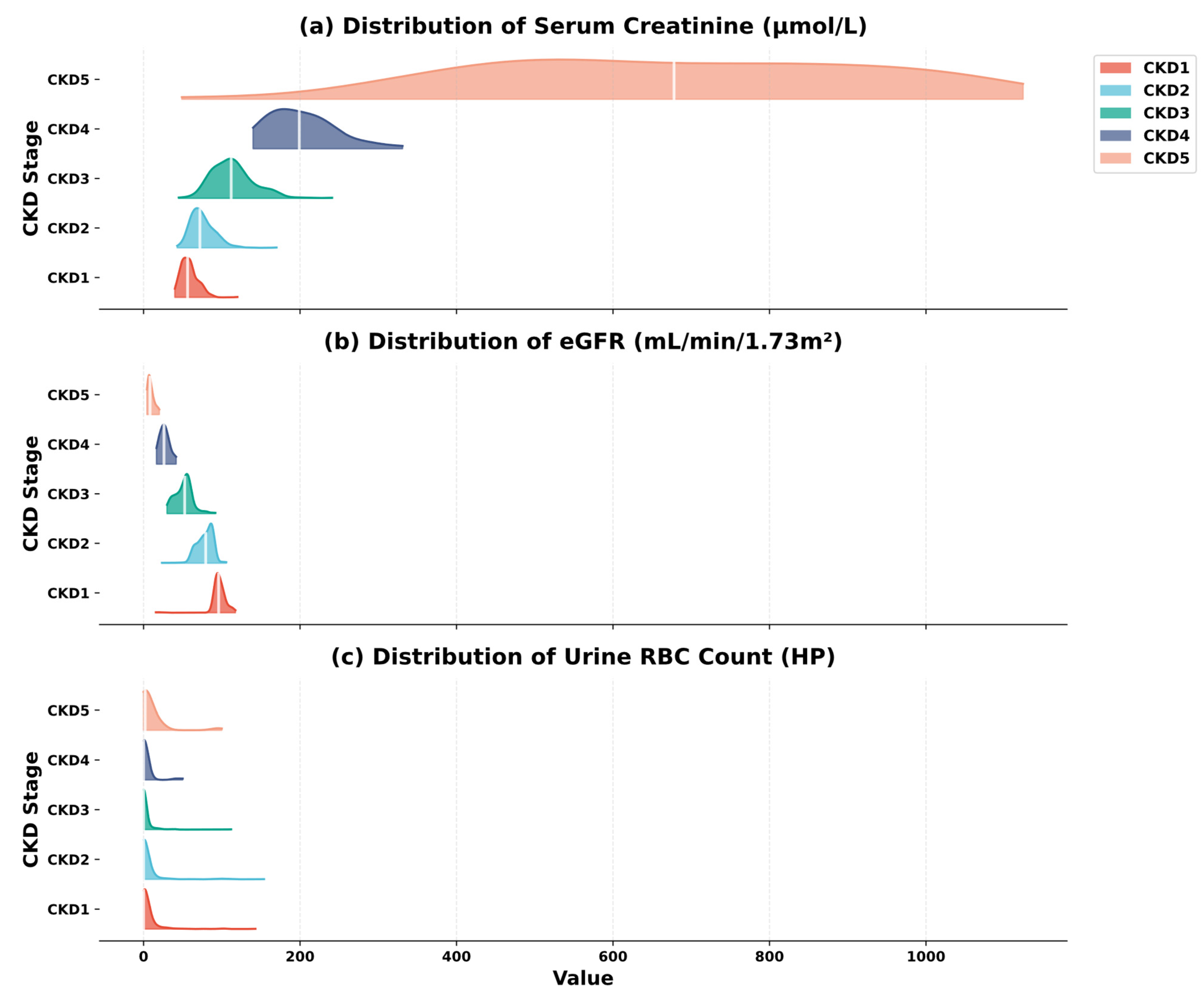
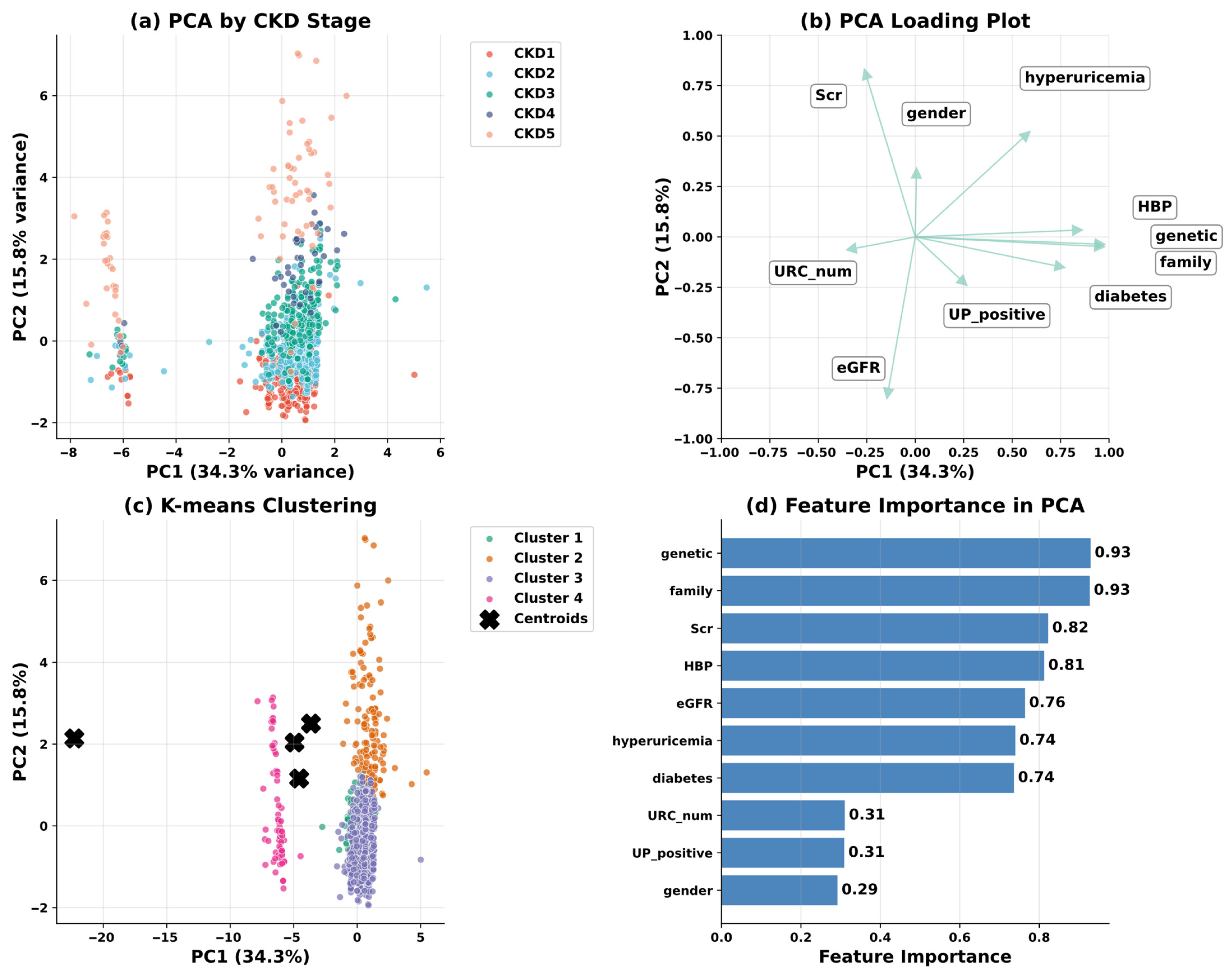
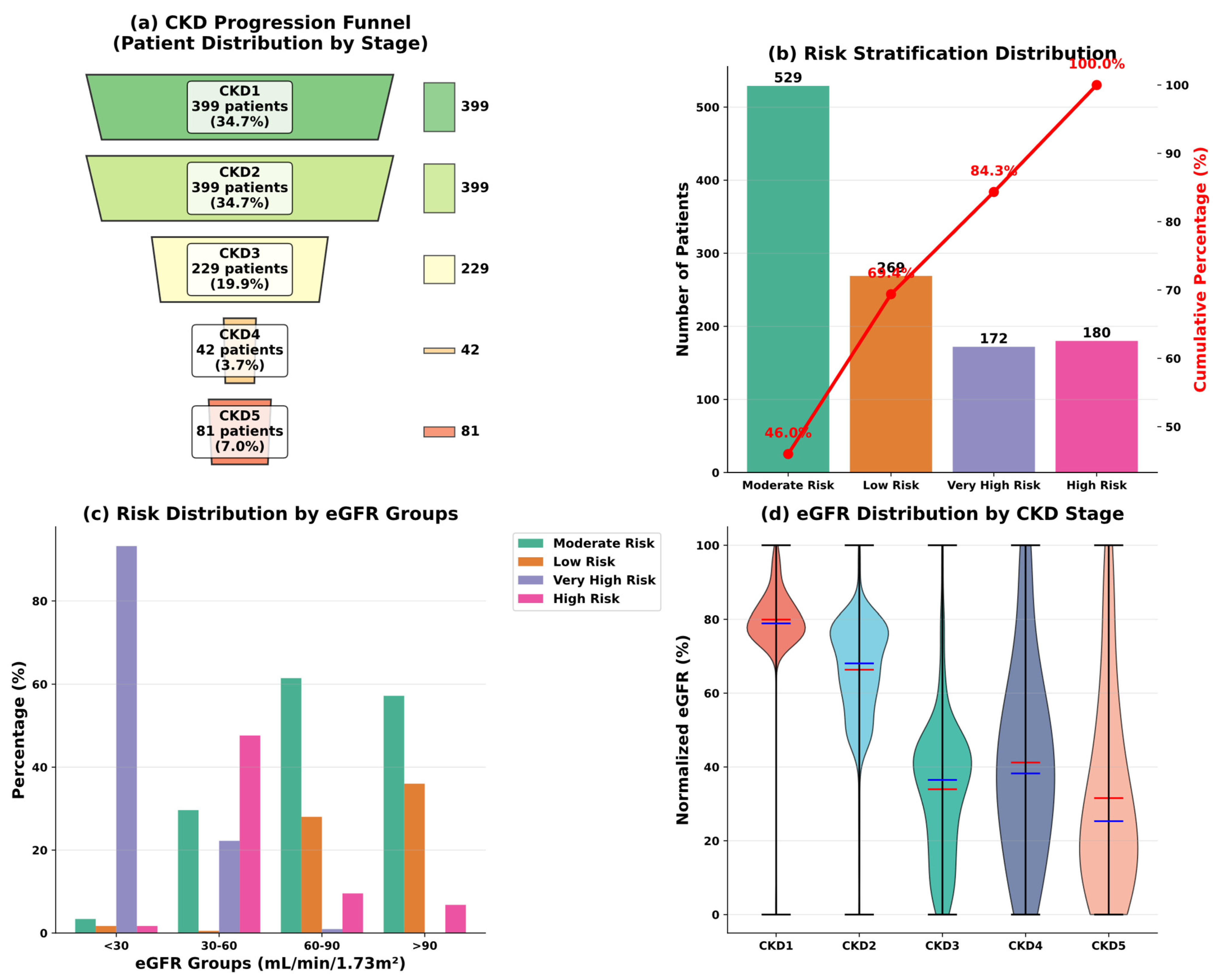







| Variable Name | Description | Values/Range |
|---|---|---|
| hos_id | Hospital ID | 7 hospitals |
| hos_name | Hospital Name | Hospital names |
| gender | Gender | Male/Female |
| genetic | Hereditary Kidney Disease | Yes/No |
| family | Family History of Chronic Nephritis | Yes/No |
| transplant | Kidney Transplant History | Yes/No |
| biopsy | Renal Biopsy History | Yes/No |
| HBP | Hypertension History | Yes/No |
| diabetes | Diabetes Mellitus History | Yes/No |
| hyperuricemia | Hyperuricemia | Yes/No |
| UAS | Urinary Anatomical Structure Abnormality | None/No/Yes |
| ACR | Albumin-to-Creatinine Ratio | <30/30–300/>300 mg/g |
| UP_positive | Urine Protein Test | Negative/Positive |
| UP_index | Urine Protein Index | ±(0.1–0.2 g/L) +(0.2–1.0) 2 + (1.0–2.0) 3 + (2.0–4.0) 5 + (>4.0) |
| URC_unit | Urine RBC Unit | HP—per high power field μL—per microliter |
| URC_num | Urine RBC Count | 0–93.9 Different units |
| Scr | Serum Creatinine | 0/27.2–85,800 μmol/L |
| eGFR | Estimated Glomerular Filtration Rate | 2.5–148 mL/min/1.73 m2 |
| date | Diagnosis Date | 13 December 2016 to 27 January 2018 |
| rate | CKD Risk Stratification | Low Risk/Moderate Risk High Risk/Very High Risk |
| stage | CKD Stage | CKD Stage 1–5 |
| Model | F1-Score | Accuracy | Precision | Recall | ROC AUC | F1 Overfitting Gap | Accuracy Overfitting Gap | p Value | 95% CI | Effect Size |
|---|---|---|---|---|---|---|---|---|---|---|
| Ours | 0.911 ± 0.010 | 0.919 ± 0.009 | 0.913 ± 0.014 | 0.911 ± 0.007 | 0.978 ± 0.001 | 0.024 | 0.017 | — | — | — |
| Random Forest | 0.783 ± 0.035 | 0.819 ± 0.026 | 0.823 ± 0.038 | 0.763 ± 0.033 | 0.940 ± 0.013 | 0.056 | 0.042 | <0.001 | [0.113, 0.140] | 4.849 |
| XGBoost | 0.875 ± 0.025 | 0.884 ± 0.024 | 0.883 ± 0.024 | 0.869 ± 0.026 | 0.957 ± 0.012 | 0.037 | 0.032 | <0.001 | [0.026, 0.046] | 1.833 |
| Decision Tree | 0.859 ± 0.028 | 0.872 ± 0.026 | 0.866 ± 0.028 | 0.855 ± 0.029 | 0.942 ± 0.017 | 0.04 | 0.033 | <0.001 | [0.040, 0.062] | 2.356 |
| SVM | 0.841 ± 0.030 | 0.856 ± 0.027 | 0.853 ± 0.032 | 0.833 ± 0.029 | 0.951 ± 0.013 | 0.052 | 0.043 | <0.001 | [0.057, 0.080] | 3.005 |
| Neural Network | 0.722 ± 0.079 | 0.766 ± 0.057 | 0.763 ± 0.065 | 0.709 ± 0.076 | 0.908 ± 0.030 | 0.057 | 0.045 | <0.001 | [0.157, 0.219] | 3.32 |
| Logistic Regression | 0.828 ± 0.022 | 0.842 ± 0.021 | 0.848 ± 0.026 | 0.815 ± 0.021 | 0.938 ± 0.013 | 0.032 | 0.027 | <0.001 | [0.073, 0.091] | 4.597 |
| Ridge Classifier | 0.615 ± 0.024 | 0.714 ± 0.023 | 0.703 ± 0.078 | 0.633 ± 0.022 | 0.000 ± 0.000 | 0.031 | 0.02 | <0.001 | [0.286, 0.305] | 15.732 |
| LightGBM | 0.867 ± 0.025 | 0.877 ± 0.023 | 0.876 ± 0.025 | 0.861 ± 0.028 | 0.955 ± 0.013 | 0.079 | 0.069 | <0.001 | [0.033, 0.053] | 2.161 |
| CatBoost | 0.884 ± 0.023 | 0.894 ± 0.022 | 0.893 ± 0.021 | 0.878 ± 0.025 | 0.961 ± 0.011 | 0.024 | 0.018 | <0.001 | [0.016, 0.035] | 1.416 |
| Gradient Boosting | 0.844 ± 0.028 | 0.858 ± 0.024 | 0.857 ± 0.027 | 0.835 ± 0.030 | 0.950 ± 0.012 | 0.059 | 0.048 | <0.001 | [0.055, 0.076] | 3.026 |
| KNN | 0.682 ± 0.035 | 0.720 ± 0.030 | 0.726 ± 0.035 | 0.658 ± 0.036 | 0.871 ± 0.020 | 0.1 | 0.085 | <0.001 | [0.215, 0.240] | 8.647 |
| Naive Bayes | 0.450 ± 0.097 | 0.431 ± 0.119 | 0.489 ± 0.113 | 0.542 ± 0.065 | 0.857 ± 0.022 | 0.01 | 0.007 | <0.001 | [0.423, 0.495] | 6.671 |
| Lasso Regression | 0.837 ± 0.027 | 0.851 ± 0.024 | 0.857 ± 0.031 | 0.825 ± 0.026 | 0.943 ± 0.012 | 0.028 | 0.023 | <0.001 | [0.063, 0.082] | 3.52 |
| ElasticNet | 0.833 ± 0.025 | 0.846 ± 0.022 | 0.853 ± 0.029 | 0.819 ± 0.024 | 0.941 ± 0.012 | 0.03 | 0.026 | <0.001 | [0.067, 0.087] | 3.933 |
| Voting Classifier | 0.857 ± 0.024 | 0.869 ± 0.022 | 0.878 ± 0.025 | 0.843 ± 0.024 | 0.958 ± 0.011 | 0.045 | 0.038 | <0.001 | [0.043, 0.062] | 2.771 |
| Stacking Classifier | 0.856 ± 0.025 | 0.866 ± 0.023 | 0.867 ± 0.026 | 0.849 ± 0.025 | 0.952 ± 0.012 | 0.05 | 0.044 | <0.001 | [0.044, 0.063] | 2.69 |
| Hyperparameter | Ours | Grid Search | Random Search | Genetic Algorithm | Bayes Search |
|---|---|---|---|---|---|
| n_estimators | 300–800 | [400, 600, 800] | 300–800 | 300–800 | 300–800 |
| max_depth | 5–8 | [6, 8] | 5–8 | 5–8 | 5–8 |
| learning_rate | exp (0.01–0.05) | [0.02, 0.03, 0.04] | 0.01–0.05 | exp (0.01–0.05) | 0.01–0.05 |
| subsample | 0.7–0.9 | [0.8, 0.9] | 0.7–0.9 | 0.7–0.9 | 0.7–0.9 |
| colsample_bytree | 0.8–1.0 | [0.9, 1.0] | 0.8–1.0 | 0.8–1.0 | 0.8–1.0 |
| reg_alpha | 0.1–1.0 | [0.1, 0.5] | 0.1–1.0 | 0.1–1.0 | 0.1–1.0 |
| reg_lambda | 3.0–8.0 | [5.0, 8.0] | 3.0–8.0 | 3.0–8.0 | 3.0–8.0 |
| min_child_weight | [1, 2, 3] | [2, 3] | 1–3 | [1, 2, 3] | 1–3 |
| gamma | 0.1–1.0 | [0.1, 0.5] | 0.1–1.0 | 0.1–1.0 | 0.1–1.0 |
| scale_pos_weight | [2, 3, 4] | [2, 3] | 2–4 | [2, 3, 4] | 2–4 |
| Method | F1 Score | Accuray | Precision | Recall | ROC AUC | Time (s) | Evaluations |
|---|---|---|---|---|---|---|---|
| Ours | 0.9140 | 0.9242 | 0.9201 | 0.9113 | 0.9785 | 158.52 | 85 |
| Grid Search | 0.9092 | 0.9192 | 0.9122 | 0.9086 | 0.9758 | 1539.93 | 2304 |
| Random Search | 0.9092 | 0.9192 | 0.9122 | 0.9086 | 0.9764 | 137.79 | 100 |
| Genetic Algorithm | 0.9044 | 0.9141 | 0.9048 | 0.9060 | 0.9752 | 415.93 | 100 |
| Bayes Search | 0.8998 | 0.9091 | 0.8978 | 0.9034 | 0.9727 | 598.24 | 100 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, J.; Li, L.; Chen, J. Multi-Armed Bandit Optimization for Explainable AI Models in Chronic Kidney Disease Risk Evaluation. Symmetry 2025, 17, 1808. https://doi.org/10.3390/sym17111808
Huang J, Li L, Chen J. Multi-Armed Bandit Optimization for Explainable AI Models in Chronic Kidney Disease Risk Evaluation. Symmetry. 2025; 17(11):1808. https://doi.org/10.3390/sym17111808
Chicago/Turabian StyleHuang, Jianbo, Long Li, and Jia Chen. 2025. "Multi-Armed Bandit Optimization for Explainable AI Models in Chronic Kidney Disease Risk Evaluation" Symmetry 17, no. 11: 1808. https://doi.org/10.3390/sym17111808
APA StyleHuang, J., Li, L., & Chen, J. (2025). Multi-Armed Bandit Optimization for Explainable AI Models in Chronic Kidney Disease Risk Evaluation. Symmetry, 17(11), 1808. https://doi.org/10.3390/sym17111808







