Abstract
Cardiac medical image segmentation can advance healthcare and embedded vision systems. In this paper, a symmetric semantic segmentation architecture for cardiac magnetic resonance (MR) images based on a symmetric multiscale detail-guided attention network is presented. Detailed information and multiscale attention maps can be exploited more efficiently in this model. A symmetric encoder and decoder are used to generate high-dimensional semantic feature maps and segmentation masks, respectively. First, a series of densely connected residual blocks is introduced for extracting high-dimensional semantic features. Second, an asymmetric detail-guided module is proposed. In this module, a feature pyramid is used to extract detailed information and generate detailed feature maps as part of the detail guidance of the model during the training phase, which are used to extract deep features of multiscale information and calculate a detail loss with specific encoder semantic features. Third, a series of multiscale upsampling attention blocks symmetrical to the encoder is introduced in the decoder of the model. For each upsampling attention block, feature fusion is first performed on the previous-level low-resolution features and the symmetric skip connections of the same layer, and then spatial and channel attention are used to enhance the features. Image gradients of the input images are also introduced at the end of the decoder. Finally, the predicted segmentation masks are obtained by calculating a detail loss and a segmentation loss. Our method demonstrates outstanding performance on the public cardiac MR image dataset, which can achieve significant results for endocardial and epicardial segmentation of the left ventricle (LV).
1. Introduction
In the process of the development of healthcare industries and embedded vision systems, cardiac image segmentation can promote and benefit them effectively. Image semantic segmentation aims at pixel-level semantic classification in a given image. It distinguishes meaningful objects (such as individual objects and regions of interest) by determining ground-truth boundary information. Traditionally, methods based on filtering [1], clustering [2], region [3,4], histograms [5], graphs [6,7], thresholds [8], the energy function [9,10,11], edges [12], and decomposition [13,14] are convenient for inputting various types of knowledge, but these types of methods have drawbacks, such as the simplicity of the image data to be segmented, insufficient use of public datasets, a low degree of automation, and limitations in terms of the effectiveness and segmentation of objects. Convolutional neural networks have overcome these problems and have been successful in many fields, such as image quality assessment [15,16,17,18,19,20,21,22,23,24,25], fault diagnosis [26,27], 3D point cloud analysis [28,29,30], video coding [31,32,33,34,35] and transmission [36,37], and image retrieval [38,39] The field of cardiac image segmentation is no exception. Cardiac magnetic resonance (MR) images have become the standard for noninvasive assessment of various cardiovascular functions. Therefore, cardiac MR image segmentation is crucial in the diagnosis and treatment process. In the image segmentation model, the context information and spatial resolution are particularly important and can correlate between pixels and retain the detailed information of the object. In cardiac MR image segmentation tasks, previous methods based on convolutional neural networks have attempted to preserve context information or spatial resolution to obtain higher accuracy [40,41,42,43,44,45,46,47,48].
However, detailed information, such as boundary and corner information, has not been exploited effectively, as the distinction between the boundary of cardiac MR images and surrounding pixels is not high, the shape changes greatly and is relatively fuzzy, and the grayscale and texture are relatively similar. Furthermore, the segmentation model needs to be more effective in understanding features of detailed information and contextual information. Moreover, contextual and detailed information, such as boundary and corner information, need to be fused further. In this work, a symmetric semantic segmentation architecture for cardiac magnetic resonance (MR) images based on a symmetric multiscale detail-guided attention network, which is an end-to-end trainable architecture, is presented. Detailed information and multiscale attention maps can be exploited more efficiently in this model. First, a series of densely connected residual blocks is introduced for extracting high-dimensional semantic features. Second, a detail-guided module is proposed. In this module, a feature pyramid is used to extract detailed information and generate detailed feature maps as part of the detail guidance of the model during the model training process, which are used to extract deep features of multiscale information and calculate a detail loss with semantic features. Third, multiscale upsampling blocks symmetrical to the encoder are employed in the decoder of the model. For each upsampling block, feature fusion is first performed on the previous-level low-resolution features and the symmetrical skip connections of the same layer, and then spatial and channel attention are used to enhance the features. A feature aggregation module and image gradients of the input images are also introduced at the top of the model and the end of the upsampling attention block, respectively. Finally, the predicted segmentation masks are obtained by calculating a detail loss and a segmentation loss. Our main contributions are as follows:
- We propose a semantic segmentation architecture that effectively extracts multiscale context and detailed features.
- We introduce a detail-guided module to extract detailed information and generate detailed feature maps in the encoder as part of the detail guidance of the model.
- We introduce a series of multiscale upsampling blocks that utilize spatial and channel attention, a feature aggregation module, and image gradients to extract multiscale and multilevel context.
2. Related Work
2.1. Resolution Preservation
The spatial resolution is preserved by an encoder–decoder architecture in these methods. Long et al. [49] proposed fully convolutional networks (FCNs) [49] that combine coarse and fine features. In DeconvNet [50] and SegNet [51], the resolution is preserved by a symmetrical network, and the fully connected layers are removed in SegNet to reduce the model parameters. LRR, proposed by Ghiasi et al. [52], performs upsampling operations on feature maps instead of score maps. In U-Net [53] and SPGNet [54], skip connections between the same level were added. Cheng et al. [55] proposed HigherHRNet, in which convolutional flows of different resolutions are connected with multiscale fusion across resolutions. Yu et al. [56] proposed BiSeNet, which uses convolution with more channels and reduces downsampling times to preserve resolution. Yan et al. [57,58] used Multi-Branch-CNN to maintain feature resolution. Zhang et al. [59] proposed a spatiotemporal video super-resolution network to reconstruct high-resolution images.
2.2. Context Embedding
Context methods include multilayer and multiscale context embedding methods. The multilayer context was extracted from the FCN, U-Net, and SPGNet. For the multiscale context, several segmentation models [60,61,62] have been introduced to extract the multiscale context via multiscale analysis. In the works of [63,64], dilated convolution was integrated to obtain representations of multiscale context. Both the DeepLab series proposed by Chen et al. [65,66,67] and the Denseaspp proposed by Yang et al. [68] applied the atrous spatial pyramid pooling module (ASPP) to increase receptive fields while maintaining high resolution. In DDRNets [69], proposed by Pan et al., deep aggregation pyramid pooling was used to enhance contextual information.
2.3. Attention Aggregation
Attention aggregation methods calculate the similarities of images, which can dynamically adjust the weights of different positions according to the content in the image so that the model can better automatically capture the information of interest. Zhao et al. [70] proposed PSANet, aggregating contextual information from all locations through similarity to generate dense pixel-level information, which introduced a spatial attention network to obtain attention context. Hu et al. [71] presented SENet, in which a squeeze-and-excitation unit was introduced to obtain the attention context. Jetley et al. [72] used spatial attention to enhance attention maps. Wang et al. [73] presented a nonlocal operation for capturing long-range dependencies. In addition, OCNet [74], DANet [75], CFNet [76], and CCNet [77] are also representative attention aggregation methods. Similarly, attention aggregations are also applied in image enhancement [78,79] and object detection tasks [80,81,82,83,84,85,86].
3. Proposed Method
A symmetric multiscale detail-guided attention network is presented for cardiac MR image semantic segmentation. An overview of our symmetric multiscale detail-guided attention network is shown in Figure 1. The input images are first sent to densely connected residual blocks after preprocessing. A detail-guided module is then employed on the corresponding labels to extract deep features of multiscale information, in which a feature pyramid is used to generate detailed feature maps, and a detail loss is calculated with semantic features. Next, a series of multiscale upsampling blocks symmetrical to the encoder is introduced to fuse the previous-level low-resolution features and the corresponding symmetrical skip connections and to enhance features via spatial and channel attention. Finally, the predicted segmentation masks are obtained via a multitask loss function, which calculates a detail loss and a segmentation loss.
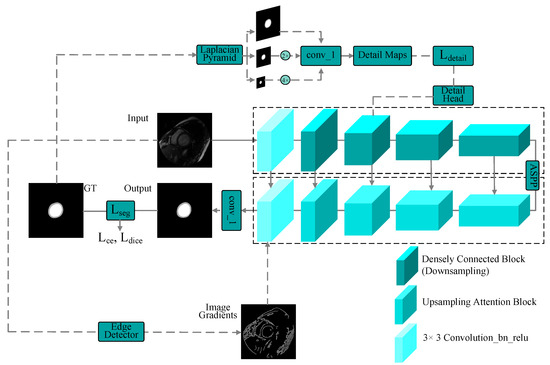
Figure 1.
Overview of the proposed method.
3.1. CNN Architecture
To extract context information efficiently, a CNN architecture with multiscale context extraction is designed. We use densely connected residual blocks [87] to obtain semantic features. We introduce an ASPP module to extract multiscale context at the top of the encoder and decoder. For the decoder, multiscale upsampling attention blocks are integrated. To aggregate the multilevel features of the encoder, the outputs of ASPP and each upsampling attention block are concatenated with the cropped skip connection feature in the encoder. At the end of the upsampling attention block, image gradients of the input images are also introduced, followed by a normalized 3 × 3 convolution with batch normalization and ReLU activation . In this hierarchical structure, the features of each level of the encoder have different scale perception capabilities, so effectively aggregating multilayer and multiscale information between levels helps to accurately segment objects of different sizes.
3.2. Detail-Guided Module
In our densely connected blocks, spatial detail information needs to be further extracted, so we use an asymmetric detail guidance module to extract spatial detail information in the encoder. The Laplacian image pyramid is used to process the ground-truth mask and utilize multiple levels of detail at different scales to generate detail feature maps. The segmentation head and densely connected block are then introduced to calculate a detail loss to guide the learning of spatial detail features. We use the detail guidance module to extract deep features of multiscale spatial detail information to fuse with the semantic features extracted in the encoder and pass them to the decoder through the downsampled densely connected blocks and corresponding skip connections. The detail feature maps on the ground truth G are computed as follows:
where denotes the Laplacian convolution on G and s denotes the stride. ·) is a bilinear upsampling function. denotes the channelwise concatenation. is a normalized 1 × 1 convolution layer performed after the concatenation.
3.3. Multiscale Upsampling Attention Block
Multiscale upsampling attention blocks are introduced in the decoder of the model, which are symmetrical to the encoder. A diagram of the multiscale upsampling attention block is shown in Figure 2. For each upsampling block, the previous lower-resolution features are first upsampled via transposed convolution. Then, feature fusion is performed on the previous-level low-resolution features and the symmetrical skip connections of the same level from the densely connected residual blocks. After , spatial and channel attention are used to enhance the ability to extract contextual and spatial information.
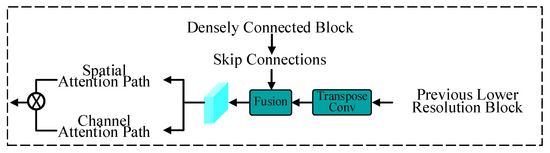
Figure 2.
Diagram of the multiscale upsampling attention block.
In the spatial attention path, two consecutive normalized 1 × 1 convolution layers are used to reduce the number of channels to 1, and a sigmoid function is applied to rescale the feature values of each channel attention map to the interval [0, 1]. The spatial attention mechanism can be formulated as follows:
where denotes all the channels in the combined feature maps, which means stacking channelwise for matching output dimensions.
In the channel attention path, the squeeze-and-excitation module [71] is employed for channel weight adaptation. The module generates a scaling factor in [0, 1] for each channel of the input features and scales the channel according to this factor to obtain the output .
The output of the upsampling attention block is as follows:
where ⊙ denotes an elementwise product.
3.4. Loss Function
We apply a multitask loss for our multiscale detail-guided attention network, which combines detail loss and segmentation loss organically for these two tasks and performs well in our experiments. The total loss is given by
For detail loss, the detail maps obtained by the detail-guided module are binary feature maps, and the proportion of details in all the pixels is small. Therefore, we use binary cross-entropy and Dice loss as detail loss to jointly optimize learning to align the spatial detail features extracted by the encoder with the detail ground truth. The detail loss is as follows:
where are the ground-truth detail label and predicted detail, respectively. All the pixels are in the domain with height h and width w. is composed of a binary cross-entropy loss and a Dice loss , which are as follows:
where N represents the domain with height h and width w. i is the i-th pixel of N, and and are the ground-truth detail label and predicted detail of the i-th pixel, respectively.
where is a smoothing item. Here, we set = 1.
The segmentation loss is composed of and :
where y and are the ground-truth coding and the predicted matrix, respectively. and . and are the i-th pixel ground truth and prediction of category k. is set to 1 × 10 −7 for the numerical stability of the denominator.
4. Experiments
4.1. Implementation Details
Our method is tested on a public magnetic resonance image segmentation dataset—the Sunnybrook Left Ventricle Segmentation Challenge dataset [88]. The Sunnybrook dataset contains short-axis cine MR images of 45 subjects: hypertrophic (HYP), heart failure without/with infarction (HF-NI/HF-I), and healthy (N). It contains 15 cases each in the training set, validation set, and online set. The resolution is 256 × 256 for each slice, and all the training images are augmented through centre cropping, random rotation, and random horizontal/vertical flipping. We present the experimental results of the model implemented via PyTorch1.9 and trained on an NVIDIA 4090 GPU and an Intel® CoreTM i9–13900K CPU, which was trained independently for 100 epochs with a batch size of 4 and the RAdam optimizer. The initial learning rate of the model was 0.001, which was exponentially decayed with a coefficient of 0.9. In the final stage, the loss curve gradually stabilizes.
4.2. Quantitative Results
The Jaccard coefficient, Dice similarity coefficient (DSC), and pixel accuracy are the evaluation metrics for our segmentation:
The DSCs for the endocardium and epicardium of other works and our method are given in Table 1. The best metric for each category is marked in bold. The top eight reported accuracies of previous works are listed. These previously proposed methods are fully automatic segmentation methods. Table 1 demonstrates the superiority of our multiscale detail-guided attention network, which can achieve the best DSC in the endocardium and epicardium compared with other methods. Our model can achieve DSC improvements of 0.69% and 1.02% in Dice scores of the endocardium and epicardium, respectively, over the second-ranked method.

Table 1.
Dice scores of different methods.
For different cardiac phases (end-diastolic (ED) and end-systolic (ES)), the pixel accuracy and Jaccard and Dice scores for the endocardium and epicardium are presented in Table 2. Notably, only the contour of the endocardium is labeled in the ES phase in the dataset. As shown in Table 2, the endocardium segmentation in the ES phase is better than that in the ED phase. Some visualizations of segmentations in the ED and ES phases are given in Figure 3, which demonstrates the performance of our method in every subject group. HYP-06, HF-NI-11, HF-I-05, and SC-N-05 represent cavity hypertrophy subject No. 6, heart failure without infarction subject No. 11, heart failure with infarction subject No. 5, and normal subject No. 5, respectively.

Table 2.
Pixel accuracy and Jaccard and Dice scores in the ED and ES cardiac phases.
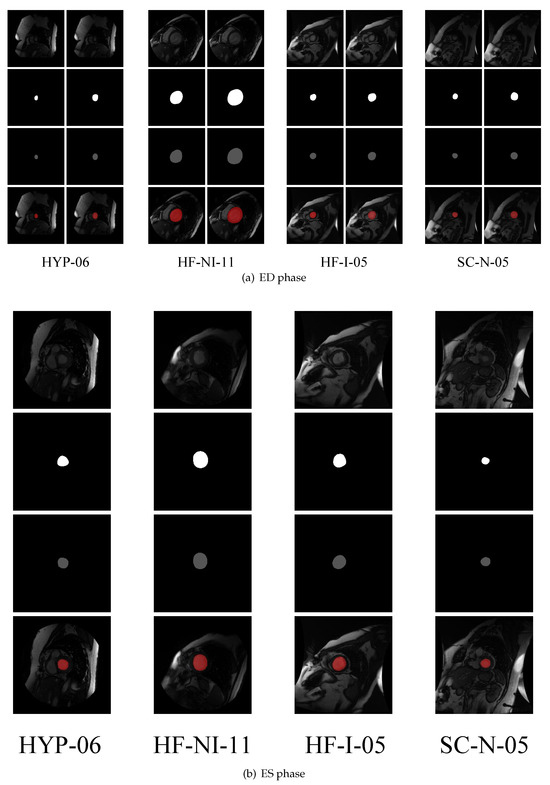
Figure 3.
Visualizations of segmentations in the ED and ES phases. In each subfigure, the top row shows the input images of each patient, the second row shows the ground truths, the third row shows the predicted segmentation results output by our model, and the bottom row shows the predicted segmentation results on their input images. In each instance of (a), the first and second columns are the endocardial and epicardial segmentation instances, respectively.
4.3. Ablation Experiments
The baseline of our experiments is a basic model whose encoder consists of densely connected residual blocks and whose decoder consists mainly of transposed convolutions. The Jaccard and DSC for the endocardium and epicardium with different settings of ablation studies are presented in Table 3, Table 4, Table 5 and Table 6.

Table 3.
Ablation studies on the detail-guided module.

Table 4.
Ablation studies on the pooling operation.

Table 5.
Ablation studies on the multiscale upsampling attention block.

Table 6.
Ablation studies on image gradients.
For the detail-guided module (DG) component, Table 3 shows that, compared with the method without detail guidance, the method with detail guidance achieves average performance improvements of 1.33% and 0.73%, respectively, in terms of the Jaccard and DSC.
The pooling operation component is applied at the top of the model to extract the multiscale context. We apply PPM and ASPP modules. Table 4 demonstrates that the method with the ASPP module attained average performance improvements of 1.55% and 0.86% in terms of the Jaccard and DSC, respectively, compared with the baseline. Compared with the method using the PPM module, the method using the ASPP module attained average performance improvements of 0.26% and 0.14% in terms of the Jaccard and DSC, respectively.
For the multiscale upsampling attention block (UA) component, it is applied as a part of the decoder of the model for further extracting context. Table 5 shows that the method with the UA module attained average performance improvements of 3.65% and 2.01% in terms of the Jaccard and DSC, respectively, compared with the baseline.
For the image gradient component, we perform methods without/with image gradients generated by a Sobel/Canny edge detector at the end of the upsampling attention block separately. Table 6 demonstrates that Canny performs better, and the method with the Canny image gradients attained average performance improvements of 4.54% and 2.48% in terms of the Jaccard and DSC, respectively, compared with the baseline.
5. Conclusions
A symmetric multiscale detail-guided attention network for cardiac MR image segmentation, which can extract context and detailed features effectively, is presented in this paper. In the encoder, a detail-guided module was introduced to extract detailed information and generate detailed feature maps, which were combined with semantic features from the densely connected residual blocks as part of the detail guidance of the model. An ASPP module was also applied to extract multiscale context. To aggregate multilayer and multiscale information between levels effectively, a series of upsampling blocks was also introduced in the decoder of the model. Moreover, a feature aggregation module and image gradients of the input images are also integrated to extract multiscale and multilevel context. Our method was tested on the public cardiac MR image dataset. Our method achieved favourable performance for endocardial and epicardial segmentation of the left ventricle. In future work, if context from different directions can be better integrated and the adaptive weight selection is performed based on the high-, medium-, and low frequency regions of cardiac medical images, then valuable pixel regions can be integrated, and the accuracy will be further improved.
Author Contributions
Conceptualization, H.H.; Methodology, H.H.; Software, X.W.; Formal analysis, B.F. and B.D.; Investigation, J.Y.; Resources, W.X.; Data curation, D.L.; Writing—original draft, H.H.; Writing—review & editing, H.H.; Visualization, X.W.; Supervision, D.L.; Project administration, B.F.; Funding acquisition, H.H. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The data presented in this study are openly available in Sunnybrook Left Ventricle Segmentation Challenge dataset, at https://midasjournal.org/browse/publication/658 (accessed on 1 September 2024), reference number [88].
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Lu, Z.; Li, J.; Liu, Z.; Cao, Q.; Tian, T.; Wang, X.; Huang, Z. Semi-Supervised Retinal Vessel Segmentation Based on Pseudo Label Filtering. Symmetry 2025, 17, 1462. [Google Scholar] [CrossRef]
- Zhu, Y.; Zhang, D.; Lin, Y.; Feng, Y.; Tang, J. Merging Context Clustering With Visual State Space Models for Medical Image Segmentation. IEEE Trans. Med. Imaging 2025, 44, 2131–2142. [Google Scholar] [PubMed]
- Orbe-Trujillo, E.; Novillo, C.J.; Pérez-Ramírez, M.; Vazquez-Avila, J.L.; Pérez-Ramírez, A. Fast Treetops Counting Using Mathematical Image Symmetry, Segmentation, and Fast K-Means Classification Algorithms. Symmetry 2022, 14, 532. [Google Scholar] [CrossRef]
- Zhou, M.; Hu, H.M.; Zhang, Y. Region-based intra-frame rate-control scheme for high efficiency video coding. In Proceedings of the Signal and Information Processing Association Annual Summit and Conference (APSIPA), 2014 Asia-Pacific, Siem Reap, Cambodia, 9–12 December 2014; pp. 1–4. [Google Scholar]
- Kheirkhah, F.M.; Mohammadi, H.R.S.; Shahverdi, A. Modified histogram-based segmentation and adaptive distance tracking of sperm cells image sequences. Comput. Methods Programs Biomed. 2018, 154, 173–182. [Google Scholar] [CrossRef]
- Long, J.; Feng, X.; Zhu, X.; Zhang, J.; Gou, G. Efficient superpixel-guided interactive image segmentation based on graph theory. Symmetry 2018, 10, 169. [Google Scholar] [CrossRef]
- Shen, W.; Zhou, M.; Luo, J.; Li, Z.; Kwong, S. Graph-represented distribution similarity index for full-reference image quality assessment. IEEE Trans. Image Process. 2024, 33, 3075–3089. [Google Scholar]
- Dey, N.; Rajinikanth, V.; Ashour, A.S.; Tavares, J.M.R. Social group optimization supported segmentation and evaluation of skin melanoma images. Symmetry 2018, 10, 51. [Google Scholar] [CrossRef]
- Liu, R.; Liao, J.; Liu, X.; Liu, Y.; Chen, Y. LSRL-Net: A level set-guided re-learning network for semi-supervised cardiac and prostate segmentation. Biomed. Signal Process. Control 2025, 110, 108062. [Google Scholar]
- Zhu, Z.; Hou, J.; Liu, H.; Zeng, H.; Hou, J. Learning efficient and effective trajectories for differential equation-based image restoration. IEEE Trans. Pattern Anal. Mach. Intell. 2025, 47, 9150–9168. [Google Scholar]
- Hasan, A.M.; Meziane, F.; Aspin, R.; Jalab, H.A. Segmentation of brain tumors in MRI images using three-dimensional active contour without edge. Symmetry 2016, 8, 132. [Google Scholar] [CrossRef]
- Pratondo, A.; Chui, C.K.; Ong, S.H. Robust edge-stop functions for edge-based active contour models in medical image segmentation. IEEE Signal Process. Lett. 2015, 23, 222–226. [Google Scholar]
- Minaee, S.; Wang, Y. An ADMM approach to masked signal decomposition using subspace representation. IEEE Trans. Image Process. 2019, 28, 3192–3204. [Google Scholar] [CrossRef]
- Zhou, M.; Leng, H.; Fang, B.; Xiang, T.; Wei, X.; Jia, W. Low-light image enhancement via a frequency-based model with structure and texture decomposition. ACM Trans. Multimed. Comput. Commun. Appl. 2023, 19, 187. [Google Scholar] [CrossRef]
- Lang, S.; Liu, X.; Zhou, M.; Luo, J.; Pu, H.; Zhuang, X.; Wang, J.; Wei, X.; Zhang, T.; Feng, Y.; et al. A full-reference image quality assessment method via deep meta-learning and conformer. IEEE Trans. Broadcast. 2023, 70, 316–324. [Google Scholar] [CrossRef]
- Liao, X.; Wei, X.; Zhou, M.; Kwong, S. Full-reference image quality assessment: Addressing content misalignment issue by comparing order statistics of deep features. IEEE Trans. Broadcast. 2023, 70, 305–315. [Google Scholar] [CrossRef]
- Xian, W.; Zhou, M.; Fang, B.; Liao, X.; Ji, C.; Xiang, T.; Jia, W. Spatiotemporal feature hierarchy-based blind prediction of natural video quality via transfer learning. IEEE Trans. Broadcast. 2022, 69, 130–143. [Google Scholar] [CrossRef]
- Liao, X.; Wei, X.; Zhou, M.; Li, Z.; Kwong, S. Image quality assessment: Measuring perceptual degradation via distribution measures in deep feature spaces. IEEE Trans. Image Process. 2024, 33, 4044–4059. [Google Scholar] [CrossRef]
- Shen, W.; Zhou, M.; Chen, Y.; Wei, X.; Feng, Y.; Pu, H.; Jia, W. Image Quality Assessment: Investigating Causal Perceptual Effects with Abductive Counterfactual Inference. In Proceedings of the Computer Vision and Pattern Recognition Conference, Nashville, TN, USA, 11–15 June 2025; pp. 17990–17999. [Google Scholar]
- Zhou, Z.; Zhou, M.; Luo, J.; Pu, H.; U, L.H.; Wei, X.; Jia, W. VideoGNN: Video Representation Learning via Dynamic Graph Modelling. Acm Trans. Multimed. Comput. Commun. Appl. 2025. [Google Scholar] [CrossRef]
- Wei, X.; Li, J.; Zhou, M.; Wang, X. Contrastive distortion-level learning-based no-reference image-quality assessment. Int. J. Intell. Syst. 2022, 37, 8730–8746. [Google Scholar] [CrossRef]
- Xian, W.; Zhou, M.; Fang, B.; Kwong, S. A content-oriented no-reference perceptual video quality assessment method for computer graphics animation videos. Inf. Sci. 2022, 608, 1731–1746. [Google Scholar] [CrossRef]
- Zhou, M.; Wang, H.; Wei, X.; Feng, Y.; Luo, J.; Pu, H.; Zhao, J.; Wang, L.; Chu, Z.; Wang, X.; et al. HDIQA: A hyper debiasing framework for full reference image quality assessment. IEEE Trans. Broadcast. 2024, 70, 545–554. [Google Scholar] [CrossRef]
- Lan, X.; Xian, W.; Zhou, M.; Yan, J.; Wei, X.; Luo, J.; Jia, W.; Kwong, S. No-Reference Image Quality Assessment: Exploring Intrinsic Distortion Characteristics via Generative Noise Estimation with Mamba. IEEE Trans. Circuits Syst. Video Technol. 2025. Early Access. [Google Scholar] [CrossRef]
- Lang, S.; Zhou, M.; Wei, X.; Yan, J.; Feng, Y.; Jia, W. Image Quality Assessment: Exploring the Similarity of Deep Features via Covariance-Constrained Spectra. IEEE Trans. Broadcast. 2025. Early Access. [Google Scholar]
- Gao, T.; Sheng, W.; Zhou, M.; Fang, B.; Zheng, L. MEMS inertial sensor fault diagnosis using a cnn-based data-driven method. Int. J. Pattern Recognit. Artif. Intell. 2020, 34, 2059048. [Google Scholar] [CrossRef]
- Gao, T.; Sheng, W.; Zhou, M.; Fang, B.; Luo, F.; Li, J. Method for fault diagnosis of temperature-related mems inertial sensors by combining Hilbert–Huang transform and deep learning. Sensors 2020, 20, 5633. [Google Scholar] [PubMed]
- Zhang, Y.; Hou, J.; Ren, S.; Wu, J.; Yuan, Y.; Shi, G. Self-supervised learning of lidar 3d point clouds via 2d-3d neural calibration. IEEE Trans. Pattern Anal. Mach. Intell. 2025, 47, 9201–9216. [Google Scholar] [CrossRef]
- Ren, S.; Hou, J.; Chen, X.; Xiong, H.; Wang, W. DDM: A Metric for Comparing 3D Shapes Using Directional Distance Fields. IEEE Trans. Pattern Anal. Mach. Intell. 2025, 47, 6631–6646. [Google Scholar] [CrossRef]
- Zhang, Q.; Hou, J.; Qian, Y.; Zeng, Y.; Zhang, J.; He, Y. Flattening-net: Deep regular 2d representation for 3d point cloud analysis. IEEE Trans. Pattern Anal. Mach. Intell. 2023, 45, 9726–9742. [Google Scholar] [CrossRef]
- Zhou, M.; Wei, X.; Wang, S.; Kwong, S.; Fong, C.K.; Wong, P.H.; Yuen, W.Y. Global rate-distortion optimization-based rate control for HEVC HDR coding. IEEE Trans. Circuits Syst. Video Technol. 2019, 30, 4648–4662. [Google Scholar] [CrossRef]
- Zhou, M.; Wei, X.; Ji, C.; Xiang, T.; Fang, B. Optimum quality control algorithm for versatile video coding. IEEE Trans. Broadcast. 2022, 68, 582–593. [Google Scholar] [CrossRef]
- Wei, X.; Zhou, M.; Wang, H.; Yang, H.; Chen, L.; Kwong, S. Recent advances in rate control: From optimization to implementation and beyond. IEEE Trans. Circuits Syst. Video Technol. 2023, 34, 17–33. [Google Scholar] [CrossRef]
- Zhou, M.; Zhang, Y.; Li, B.; Hu, H.M. Complexity-based intra frame rate control by jointing inter-frame correlation for high efficiency video coding. J. Vis. Commun. Image Represent. 2017, 42, 46–64. [Google Scholar]
- Zhou, M.; Zhang, Y.; Li, B.; Lin, X. Complexity correlation-based CTU-level rate control with direction selection for HEVC. ACM Trans. Multimed. Comput. Commun. Appl. (TOMM) 2017, 13, 53. [Google Scholar] [CrossRef]
- Wei, X.; Zhou, M.; Kwong, S.; Yuan, H.; Jia, W. A hybrid control scheme for 360-degree dynamic adaptive video streaming over mobile devices. IEEE Trans. Mob. Comput. 2021, 21, 3428–3442. [Google Scholar] [CrossRef]
- Wei, X.; Zhou, M.; Kwong, S.; Yuan, H.; Wang, S.; Zhu, G.; Cao, J. Reinforcement learning-based QoE-oriented dynamic adaptive streaming framework. Inf. Sci. 2021, 569, 786–803. [Google Scholar]
- Shen, Y.; Feng, Y.; Fang, B.; Zhou, M.; Kwong, S.; Qiang, B.h. DSRPH: Deep semantic-aware ranking preserving hashing for efficient multi-label image retrieval. Inf. Sci. 2020, 539, 145–156. [Google Scholar]
- Zhao, L.; Shang, Z.; Tan, J.; Zhou, M.; Zhang, M.; Gu, D.; Zhang, T.; Tang, Y.Y. Siamese networks with an online reweighted example for imbalanced data learning. Pattern Recognit. 2022, 132, 108947. [Google Scholar] [CrossRef]
- Romaguera, L.V.; Romero, F.P.; Costa Filho, C.F.F.; Costa, M.G.F. Myocardial segmentation in cardiac magnetic resonance images using fully convolutional neural networks. Biomed. Signal Process. Control 2018, 44, 48–57. [Google Scholar] [CrossRef]
- Trinh, M.N.; Tran, T.T.; Pham, V.T.; Tran, T.T. A modified FCN-based method for Left Ventricle endocardium and epicardium segmentation with new block modules. In Proceedings of the 2021 8th NAFOSTED Conference on Information and Computer Science (NICS), Hanoi, Vietnam, 21–22 December 2021; pp. 392–397. [Google Scholar]
- Sun, J.; Darbehani, F.; Zaidi, M.; Wang, B. Saunet: Shape attentive u-net for interpretable medical image segmentation. In Proceedings of the International Conference on Medical Image Computing and Computer-Assisted Intervention, Lima, Peru, 4–8 October 2020; Springer: Cham, Switzerland, 2020; pp. 797–806. [Google Scholar]
- Le, D.H.; Le, N.M.; Le, K.H.; Pham, V.T.; Tran, T.T. DR-Unet++: An Approach for Left Ventricle Segmentation from Magnetic Resonance Images. In Proceedings of the 2022 6th International Conference on Green Technology and Sustainable Development (GTSD), Nha Trang City, Vietnam, 29–30 July 2022; pp. 1048–1052. [Google Scholar]
- Tran, T.T.; Tran, T.T.; Ninh, Q.C.; Bui, M.D.; Pham, V.T. Segmentation of left ventricle in short-axis MR images based on fully convolutional network and active contour model. In Computational Intelligence Methods for Green Technology and Sustainable Development, Proceedings of the International Conference GTSD2020 5, Da Nang City, Vietnam, 27–28 November 2020; Springer: Cham, Switzerland, 2021; pp. 49–59. [Google Scholar]
- Isensee, F.; Jaeger, P.F.; Kohl, S.A.A.; Petersen, J.; Maier-Hein, K.H. nnU-Net: A self-configuring method for deep learning-based biomedical image segmentation. Nat. Methods 2021, 18, 203–211. [Google Scholar] [PubMed]
- Zhou, H.Y.; Guo, J.; Zhang, Y.; Han, X.; Yu, L.; Wang, L.; Yu, Y. nnFormer: Volumetric Medical Image Segmentation via a 3D Transformer. IEEE Trans. Image Process. 2023, 32, 4036–4045. [Google Scholar] [CrossRef]
- Cao, H.; Wang, Y.; Chen, J.; Jiang, D.; Zhang, X.; Tian, Q.; Wang, M. Swin-unet: Unet-like pure transformer for medical image segmentation. In Proceedings of the ECCV 2022 Workshops, Tel Aviv, Israel, 23–27 October 2022; Springer: Cham, Switzerland, 2023; pp. 205–218. [Google Scholar]
- Liu, J.; Yang, H.; Zhou, H.Y.; Xi, Y.; Yu, L.; Li, C.; Liang, Y.; Shi, G.; Yu, Y.; Zhang, S.; et al. Swin-umamba: Mamba-based unet with imagenet-based pretraining. In Proceedings of the International Conference on Medical Image Computing and Computer-Assisted Intervention, Marrakesh, Morocco, 6–10 October 2024; Springer: Cham, Switzerland, 2024; pp. 615–625. [Google Scholar]
- Long, J.; Shelhamer, E.; Darrell, T. Fully convolutional networks for semantic segmentation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015; pp. 3431–3440. [Google Scholar]
- Noh, H.; Hong, S.; Han, B. Learning deconvolution network for semantic segmentation. In Proceedings of the IEEE International Conference on Computer Vision, Santiago, Chile, 7–13 December 2015; pp. 1520–1528. [Google Scholar]
- Badrinarayanan, V.; Kendall, A.; Cipolla, R. Segnet: A deep convolutional encoder-decoder architecture for image segmentation. IEEE Trans. Pattern Anal. Mach. Intell. 2017, 39, 2481–2495. [Google Scholar] [PubMed]
- Ghiasi, G.; Fowlkes, C.C. Laplacian pyramid reconstruction and refinement for semantic segmentation. In Proceedings of the Computer Vision—ECCV 2016: 14th European Conference, Amsterdam, The Netherlands, 11–14 October 2016; Proceedings, Part III 14. Springer: Cham, Switzerland, 2016; pp. 519–534. [Google Scholar]
- Ronneberger, O.; Fischer, P.; Brox, T. U-net: Convolutional networks for biomedical image segmentation. In Proceedings of the International Conference on Medical Image Computing and Computer-Assisted Intervention, Munich, Germany, 5–9 October 2015; Springer: Cham, Switzerland, 2015; pp. 234–241. [Google Scholar]
- Cheng, B.; Chen, L.C.; Wei, Y.; Zhu, Y.; Huang, Z.; Xiong, J.; Huang, T.S.; Hwu, W.M.; Shi, H. Spgnet: Semantic prediction guidance for scene parsing. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Seoul, Republic of Korea, 27 October–2 November 2019; pp. 5218–5228. [Google Scholar]
- Cheng, B.; Xiao, B.; Wang, J.; Shi, H.; Huang, T.S.; Zhang, L. Higherhrnet: Scale-aware representation learning for bottom-up human pose estimation. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 13–19 June 2020; pp. 5386–5395. [Google Scholar]
- Yu, C.; Gao, C.; Wang, J.; Yu, G.; Shen, C.; Sang, N. Bisenet v2: Bilateral network with guided aggregation for real-time semantic segmentation. Int. J. Comput. Vis. 2021, 129, 3051–3068. [Google Scholar] [CrossRef]
- Yan, J.; Zhang, B.; Zhou, M.; Kwok, H.F.; Siu, S.W. Multi-Branch-CNN: Classification of ion channel interacting peptides using multi-branch convolutional neural network. Comput. Biol. Med. 2022, 147, 105717. [Google Scholar] [CrossRef]
- Yan, J.; Zhang, B.; Zhou, M.; Campbell-Valois, F.X.; Siu, S.W. A deep learning method for predicting the minimum inhibitory concentration of antimicrobial peptides against Escherichia coli using Multi-Branch-CNN and Attention. mSystems 2023, 8, e00345-23. [Google Scholar] [CrossRef]
- Zhang, W.; Zhou, M.; Ji, C.; Sui, X.; Bai, J. Cross-frame transformer-based spatio-temporal video super-resolution. IEEE Trans. Broadcast. 2022, 68, 359–369. [Google Scholar]
- Ding, H.; Jiang, X.; Shuai, B.; Liu, A.Q.; Wang, G. Context contrasted feature and gated multi-scale aggregation for scene segmentation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 2393–2402. [Google Scholar]
- He, J.; Deng, Z.; Qiao, Y. Dynamic multi-scale filters for semantic segmentation. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Seoul, Republic of Korea, 27 October–2 November 2019; pp. 3562–3572. [Google Scholar]
- He, J.; Deng, Z.; Zhou, L.; Wang, Y.; Qiao, Y. Adaptive pyramid context network for semantic segmentation. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; pp. 7519–7528. [Google Scholar]
- Yu, F.; Koltun, V.; Funkhouser, T. Dilated residual networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 472–480. [Google Scholar]
- Li, Z.; Peng, C.; Yu, G.; Zhang, X.; Deng, Y.; Sun, J. Detnet: Design backbone for object detection. In Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018; pp. 334–350. [Google Scholar]
- Chen, L.C.; Papandreou, G.; Kokkinos, I.; Murphy, K.; Yuille, A.L. Semantic image segmentation with deep convolutional nets and fully connected crfs. arXiv 2014, arXiv:1412.7062. [Google Scholar]
- Chen, L.C.; Papandreou, G.; Kokkinos, I.; Murphy, K.; Yuille, A.L. Deeplab: Semantic image segmentation with deep convolutional nets, atrous convolution, and fully connected crfs. IEEE Trans. Pattern Anal. Mach. Intell. 2017, 40, 834–848. [Google Scholar] [CrossRef]
- Chen, L.C.; Papandreou, G.; Schroff, F.; Adam, H. Rethinking atrous convolution for semantic image segmentation. arXiv 2017, arXiv:1706.05587. [Google Scholar] [CrossRef]
- Yang, M.; Yu, K.; Zhang, C.; Li, Z.; Yang, K. Denseaspp for semantic segmentation in street scenes. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 3684–3692. [Google Scholar]
- Pan, H.; Hong, Y.; Sun, W.; Jia, Y. Deep Dual-Resolution Networks for Real-Time and Accurate Semantic Segmentation of Traffic Scenes. IEEE Trans. Intell. Transp. Syst. 2023, 24, 3448–3460. [Google Scholar] [CrossRef]
- Zhao, H.; Zhang, Y.; Liu, S.; Shi, J.; Loy, C.C.; Lin, D.; Jia, J. Psanet: Point-wise spatial attention network for scene parsing. In Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018; pp. 267–283. [Google Scholar]
- Hu, J.; Shen, L.; Sun, G. Squeeze-and-excitation networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 7132–7141. [Google Scholar]
- Jetley, S.; Lord, N.A.; Lee, N.; Torr, P.H. Learn to Pay Attention. In Proceedings of the International Conference on Learning Representations, Vancouver, BC, Canada, 30 April–3 May 2018. [Google Scholar]
- Wang, X.; Girshick, R.; Gupta, A.; He, K. Non-local neural networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 7794–7803. [Google Scholar]
- Yuan, Y.; Huang, L.; Guo, J.; Zhang, C.; Chen, X.; Wang, J. Ocnet: Object context network for scene parsing. arXiv 2018, arXiv:1809.00916. [Google Scholar]
- Fu, J.; Liu, J.; Tian, H.; Li, Y.; Bao, Y.; Fang, Z.; Lu, H. Dual attention network for scene segmentation. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; pp. 3146–3154. [Google Scholar]
- Zhang, H.; Zhang, H.; Wang, C.; Xie, J. Co-occurrent features in semantic segmentation. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; pp. 548–557. [Google Scholar]
- Huang, Z.; Wang, X.; Wei, Y.; Huang, L.; Shi, H.; Liu, W.; Huang, T.S. CCNet: Criss-Cross Attention for Semantic Segmentation. IEEE Trans. Pattern Anal. Mach. Intell. 2023, 45, 6896–6908. [Google Scholar] [CrossRef]
- Zhou, M.; Han, S.; Luo, J.; Zhuang, X.; Mao, Q.; Li, Z. Transformer-Based and Structure-Aware Dual-Stream Network for Low-Light Image Enhancement. ACM Trans. Multimed. Comput. Commun. Appl. 2025, 21, 293. [Google Scholar] [CrossRef]
- Guo, Q.; Zhou, M. Progressive domain translation defogging network for real-world fog images. IEEE Trans. Broadcast. 2022, 68, 876–885. [Google Scholar] [CrossRef]
- Song, J.; Zhou, M.; Luo, J.; Pu, H.; Feng, Y.; Wei, X.; Jia, W. Boundary-aware feature fusion with dual-stream attention for remote sensing small object detection. IEEE Trans. Geosci. Remote Sens. 2024, 63, 5600213. [Google Scholar] [CrossRef]
- Zhou, M.; Li, Y.; Yang, G.; Wei, X.; Pu, H.; Luo, J.; Jia, W. COFNet: Contrastive Object-aware Fusion using Box-level Masks for Multispectral Object Detection. IEEE Trans. Multimed. 2025. Early Access. [Google Scholar] [CrossRef]
- Zheng, Z.; Zhou, M.; Shang, Z.; Wei, X.; Pu, H.; Luo, J.; Jia, W. GAANet: Graph Aggregation Alignment Feature Fusion for Multispectral Object Detection. IEEE Trans. Ind. Inform. 2025, 21, 8282–8292. [Google Scholar] [CrossRef]
- Zhou, M.; Zhao, X.; Luo, F.; Luo, J.; Pu, H.; Xiang, T. Robust rgb-t tracking via adaptive modality weight correlation filters and cross-modality learning. ACM Trans. Multimed. Comput. Commun. Appl. 2023, 20, 95. [Google Scholar] [CrossRef]
- Li, Y.l.; Feng, Y.; Zhou, M.l.; Xiong, X.c.; Wang, Y.h.; Qiang, B.h. DMA-YOLO: Multi-scale object detection method with attention mechanism for aerial images. Vis. Comput. 2024, 40, 4505–4518. [Google Scholar] [CrossRef]
- Zhou, M.; Li, J.; Wei, X.; Luo, J.; Pu, H.; Wang, W.; He, J.; Shang, Z. AFES: Attention-Based Feature Excitation and Sorting for Action Recognition. IEEE Trans. Consum. Electron. 2025, 71, 5752–5760. [Google Scholar] [CrossRef]
- Cheng, S.; Song, J.; Zhou, M.; Wei, X.; Pu, H.; Luo, J.; Jia, W. Ef-detr: A lightweight transformer-based object detector with an encoder-free neck. IEEE Trans. Ind. Inform. 2024, 20, 12994–13002. [Google Scholar] [CrossRef]
- Huang, G.; Liu, Z.; Van Der Maaten, L.; Weinberger, K.Q. Densely connected convolutional networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 4700–4708. [Google Scholar]
- Radau, P.; Lu, Y.; Connelly, K.; Paul, G.; Dick, A.J.; Wright, G.A. Evaluation framework for algorithms segmenting short axis cardiac MRI. MIDAS J. 2009. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).