Secure Quantum Teleportation of Squeezed Thermal States

Abstract

Quantum teleportation is a fundamental protocol in quantum information science. It represents a critical resource for quantum communication and distributed quantum computing. We derive an analytical expression of the fidelity of teleportation of an input squeezed thermal state using for teleportation a bipartite Gaussian resource state shared between Alice and Bob. Each mode of the resource state is susceptible to the influence of the environment. We employ the characteristic function approach in conjunction with the covariance matrix formalism. The fidelity of teleportation is expressed in terms of input and resource state covariance matrices. We investigate, as an example, the feasibility of secure quantum teleportation of a squeezed thermal state using a two-mode resource state whose modes are placed in separate thermal baths. A successful quantum teleportation requires meeting two criteria: the presence of two-way quantum steering and a teleportation fidelity exceeding the classical threshold. The quantum steering is by nature asymmetric and has found applications in quantum cryptography and secure quantum teleportation. Weak squeezing and a high number of average thermal photons in the input states lead to an increase in the fidelity of teleportation. Generally, steering disappears much faster than the fidelity of teleportation decreases below its classical limit.

1. Introduction

Quantum teleportation represents a process in which Alice, the sender, transmits to Bob, the receiver, an arbitrary quantum state employing quantum correlations and a classical communication channel [1,2]. Quantum teleportation is a crucial process for applications such as quantum communication for secure quantum transfer (important for quantum key distribution [3,4]) and long-distance quantum networks (essential for the manufacture of quantum repeaters [5]). It also enables distributed quantum computing [6], quantum cryptography [7], quantum sensors and metrology [8].

In this way, quantum teleportation is the key technology that will be able to facilitate Quantum Internet [9]. On the Classical Internet, eavesdroppers can secretly intercept the transfer of information without altering it, allowing them to access sensitive data (such as credit card details, private files, passwords, and messages) without being detected. Quantum Internet, on the other hand, can enable secure voting [10], secure communication [11], blind quantum computation (that will allow users to keep hidden input, algorithm, and outcome while using a quantum server) [12], synchronization of clocks for extremely high precision [13], and longer baseline of telescope [14].

Quantum information can be encoded using discrete-variable (DV) or continuous-variable (CV) systems, depending on the nature of the physical system and the information processing task. Each system (DV or CV) has essential advantages and limitations that make it preferable for certain tasks over others in quantum technologies. CV systems generally allow deterministic generation of quantum states (especially coherent and squeezed Gaussian states) employing laser sources, optical parametric amplifiers and modulators [15,16,17]. In DV systems most common are probabilistic single-photon sources that are of low efficiency or exhibit random emission timing [18].

In addition, CV systems employ homodyne and heterodyne detectors that manifest very high efficiency (up to $99\%$) and work at room temperature [19]. In contrast, DV systems use superconducting detectors, which require cryogenic cooling, suffer from reduced quantum efficiency, and are expensive [20]. CV systems can be transmitted through standard optical fiber, indicating its suitability for quantum communication and quantum key distribution (QKD) over geographically distant locations [21,22]. CV systems still face some challenges, for example, increased susceptibility to noise and loss [23], and limitations in fault-tolerant error correction [24].

Recent advancement in CV teleportation includes the teleportation of optical modes over fiber channels [25]. In this study, the deterministic teleportation of a coherent state was implemented via a fiber link at a distance of $6.0$ km. The measured fidelity of $0.62\pm 0.03$ is greater than the classical limit, making the teleportation successful. Moreover, in study [26] a quantum photonic platform was proposed for machine learning purposes based on CV cluster states and quantum teleportation. Authors presented a design for measurement-based quantum reservoir computing that substantially enhances photonic utility in computational tasks. A heralded quantum teleportation scheme [27] that mitigates thermal decoherence effects, enabling higher fidelities and longer-distance operation via noiseless linear amplification was proposed. However, this protocol operates probabilistically, sacrificing full determinism. The use of measurement-based noiseless amplification enhances (under specific conditions) the accuracy of estimating the coherent displacement of the teleported state based on CV Bell measurement outcomes [28].

It is crucial to consider squeezed thermal states for a more realistic depiction of CV teleportation process. Squeezed states are generated through nonlinear optical processes. Due to optical losses, detection inefficiencies, or phase noise, squeezed vacuum states are transformed into squeezed thermal states [29]. The teleportation of a thermal state was presented in the paper [30]. In this article, we make a step forward, deriving a general formula for the quantum fidelity of teleportation for an input squeezed thermal state using as a resource two entangled Gaussian modes interacting with a general environment. This study represents a more general case compared to our previous work. In Ref. [30], we investigated the teleportation of a thermal state, derived an analytical expression for the quantum fidelity in the general case, and analyzed a specific scenario in which the two modes of the resource state are coupled to a common thermal bath. In contrast, the present study focuses on the secure teleportation of a squeezed thermal input state. Secure teleportation has broader practical applications, and squeezed thermal states provide a more realistic description of experimentally accessible systems. As an illustrative example, we consider the case in which the two resource modes are coupled to different thermal baths. The scheme of the teleportation protocol is presented in Figure 1. We also verify the teleportation to be secure [31,32,33,34] by checking the conditions: the fidelity of quantum teleportation needs to be higher than the upper classical limit and two-way quantum steering has to be present in the system. We also estimate the quantum fidelity of teleportation, upper and lower classical limit of the fidelity of teleportation and quantum steering for the case when the two modes are embedded each one in their own thermal environment.

The remainder of this article is organized in the following manner: in Section 2 we deduce the analytical expression of the fidelity of quantum teleportation of an input squeezed thermal state and describe the steering temporal evolution.

To check whether the quantum teleportation is secure we discuss the classical limit of the fidelity of teleportation and the two-way quantum steering between the resource state modes. We also describe the evolution of the two-mode Gaussian resource state in the two-reservoir model using the Gorini-Kossakowski-Lindblad-Sudarshan quantum Markovian master equation. In Section 3 we assess the success of secure teleporting a squeezed thermal state utilizing an entangled two-mode resource state, subject to independent thermal baths.

The Section 4 offers a comprehensive summary and interpretation of the obtained main results.

2. Criteria for Successful Secure Quantum Teleportation

In this section we deduce the expression for the fidelity of quantum teleportation of a squeezed thermal state and the classical limit of fidelity. We also describe the quantum steering between the modes of the resource state and its temporal evolution.

2.1. Teleportation of a Squeezed Thermal State

The derivation of the fidelity of teleportation formula for a squeezed thermal state is carried out through the following key steps:

• Expressing the analytical formula for the fidelity of teleportation in terms of the covariance matrices of the input and output states.
• Writing the characteristic function of the output state in terms of its covariance matrix and mean displacement vector.
• Expressing the characteristic function of the output state in terms of the characteristic functions of the input state and the resource state at time t.
• Deriving the formula for the covariance matrix of the output state based on the two previous expressions.

The detailed formula derivation is provided below.

The general expression for the fidelity of teleportation has the form [35]:

$$F({\varrho }_{in},{\varrho }_{out})={\left[\mathrm{Tr}\sqrt{\sqrt{{\varrho }_{out}}{\varrho }_{in}\sqrt{{\varrho }_{out}}}\right]}^2,$$

(1)

where ${\varrho }_{in}$ and ${\varrho }_{out}$ are the density matrices of the input and output states. We compare the input squeezed thermal state (STS) and the output state by means of fidelity of teleportation. For unimodal states, it is given by [36,37]:

$$F({\varrho }_{in},{\varrho }_{out})={\displaystyle \frac{exp\left[-\frac{1}{2}{(\overline{X_{out}}-\overline{X_{in}})}^{\top }{({\sigma }_{in}+{\sigma }_{out})}^{-1}(\overline{X_{out}}-\overline{X_{in}})\right]}{\sqrt{\Delta +\mathsf{\Theta }}-\sqrt{\mathsf{\Theta }}}},$$

(2)

where ${\sigma }_{in}$ is the covariance matrix of the input state, ${\sigma }_{out}$ is the covariance matrix of the output one, the average values for the input and output state are given by $\overline{X_k}=\mathrm{Tr}\left[{\varrho }_k{(X,P)}^{\top }\right]$, where $X,P$ are the position and momentum operators and $k=\{in,out\}$. We introduce the notations:

$$\begin{array}{c}\Delta =det({\sigma }_{in}+{\sigma }_{out})\ge 1,\hfill \\ \mathsf{\Theta }=4det\left({\sigma }_{in}+{\displaystyle \frac{i}{2}}\right)det\left({\sigma }_{out}+{\displaystyle \frac{i}{2}}J\right),\hfill \end{array}$$

(3)

where $J=\left(\begin{array}{cc}0& 1\\ -1& 0\end{array}\right).$

The input state is a STS with the covariance matrix [29]:

$${\sigma }_{in}={\displaystyle \frac{2N_S+1}{2}}\left(\begin{array}{cc}cosh2\rho +sinh2\rho cos\theta & -sinh2\rho sin\theta \\ -sinh2\rho sin\theta & cosh2\rho -sinh2\rho cos\theta \end{array}\right),$$

(4)

where $N_S$ is the average number of thermal photons, $\rho$ is the squeezing parameter and $\theta$ is the phase of the input state.

To obtain a detailed description of the output state, we will use the characteristic function approach. The bimodal Gaussian state ${\varrho }_{AB}^t,$ initially entangled and shared between Alice and Bob, and used as the resource for teleportation has the following characteristic function at moment t [38]:

$${\chi }_{AB}^t({\lambda }_A,{\lambda }_B)=exp\left\{-{\displaystyle \frac{1}{2}}{\mathsf{\Lambda }}^{\top }{\sigma }_{AB}^t\mathsf{\Lambda }-i{\mathsf{\Lambda }}^{\top }{\overline{X_{AB}}}^t\right\},$$

(5)

with ${\lambda }_A=-{\displaystyle \frac{i}{\sqrt{2}}}(x_A+i{p}_A)$, ${\lambda }_B=-{\displaystyle \frac{i}{\sqrt{2}}}(x_B+i{p}_B)$ and $\mathsf{\Lambda }={(x_A,p_A,x_B,p_B)}^{\top }$, where $x_A,p_A,x_B,p_B$ are the position and momentum variables of the two modes. The position and momentum operators are $X_j={\displaystyle \frac{1}{\sqrt{2}}}(a_j+a_j^{†})$ and $P_j=-{\displaystyle \frac{i}{\sqrt{2}}}(a_j-a_j^{†})$, where $a_j$ and $a_j^{†}$ ($j=A,B$) are the annihilation and creation operators ($\hslash =1$).

We write the covariance matrix of the resource state, shared between Alice and Bob in the form

$${\sigma }_{AB}^t=\left(\begin{array}{cc}{A}_t& C_t\\ C_t^{\top }& B_t\end{array}\right),$$

(6)

where $A_t=\left(\begin{array}{cc}{A}_{11}& A_{12}\\ A_{12}& A_{22}\end{array}\right)$ represents the covariance matrix of Alice mode, $B_t=\left(\begin{array}{cc}{B}_{11}& B_{12}\\ B_{12}& B_{22}\end{array}\right)$ is the covariance matrix of Bob mode, and $C_t=\left(\begin{array}{cc}{C}_{11}& C_{12}\\ C_{21}& C_{22}\end{array}\right)$ depicts the correlations between the two modes.

We denote the average values as:

$${\overline{X_{AB}}}^t=\mathrm{Tr}\left[{\varrho }_{AB}^t{(X_A,P_A,X_B,P_B)}^{\top }\right]\equiv {(s_1,q_1,s_2,q_2)}^{\top }.$$

(7)

The characteristic function of the output state is given by [38]:

$$\begin{array}{c}{\chi }_{out}\left({\lambda }_{out}\right)={\chi }_{in}\left({\lambda }_{out}\right){\chi }_{AB}^t({\lambda }_{out}^{*},{\lambda }_{out})\\ ={\chi }_{in}(x_{out},p_{out}){\chi }_{AB}^t(x_{out},p_{out},-x_{out},p_{out}),\end{array}$$

(8)

where ${\chi }_{in}$ is the characteristic function of the input state. Writing the characteristic function of the input (output) state with $k=\{in,out\}$ as

$${\chi }_k(x,p)=exp\left\{-{\displaystyle \frac{1}{2}}{\mathsf{\Lambda }}_k^{\top }{\sigma }_k{\mathsf{\Lambda }}_k-i{\mathsf{\Lambda }}_k^{\top }\overline{X_k}\right\}$$

(9)

and making use of Equations (5), (8) and (9), we obtain:

$$-{\displaystyle \frac{1}{2}}{\mathsf{\Lambda }}_{out}^{\top }{\sigma }_{out}{\mathsf{\Lambda }}_{out}-i{\mathsf{\Lambda }}_{out}^{\top }\overline{X_{out}}=-{\displaystyle \frac{1}{2}}{\mathsf{\Lambda }}_{out}^{\top }{\sigma }_{in}{\mathsf{\Lambda }}_{out}-i{\mathsf{\Lambda }}_{out}^{\top }\overline{X_{in}}-{\displaystyle \frac{1}{2}}{\mathsf{\Lambda }}_o^{\top }{\sigma }_{AB}^t{\mathsf{\Lambda }}_o-i{\mathsf{\Lambda }}_o^{\top }{\overline{X_{AB}}}^t,$$

(10)

where $\overline{X_{in}}={(\overline{x_{in}},\overline{p_{in}})}^{\top }$ are the average values of the canonical variables of the input state, ${\mathsf{\Lambda }}_{in}={(x_{in},p_{in})}^{\top }$, ${\mathsf{\Lambda }}_{out}={(x_{out},p_{out})}^{\top }$ and ${\mathsf{\Lambda }}_o={(x_{out},p_{out},-x_{out},p_{out})}^{\top }$. The covariance matrix has all of its elements real, therefore Equation (10) can be separated:

$$\left\{\begin{array}{c}{\mathsf{\Lambda }}_{out}^{\top }{\sigma }_{out}{\mathsf{\Lambda }}_{out}={\mathsf{\Lambda }}_{out}^{\top }{\sigma }_{in}{\mathsf{\Lambda }}_{out}+{\mathsf{\Lambda }}_o^{\top }{\sigma }_{AB}^t{\mathsf{\Lambda }}_o,\hfill \\ {\mathsf{\Lambda }}_{out}^{\top }\overline{X_{out}}={\mathsf{\Lambda }}_{out}^{\top }\overline{X_{in}}+{\mathsf{\Lambda }}_o^{\top }{\overline{X_{AB}}}^t.\hfill \end{array}\right.$$

(11)

The average value of the output state is obtained as

$$\overline{X_{out}}={(\overline{x_{in}}+s_1-s_2,\overline{p_{in}}+q_1+q_2)}^{\top }.$$

(12)

We can determine the elements of the covariance matrix of the output state using the first equality of (11):

$${\mathsf{\Lambda }}_{out}^{\top }\left({\sigma }_{out}-{\sigma }_{in}\right){\mathsf{\Lambda }}_{out}={\mathsf{\Lambda }}_o^{\top }{\sigma }_{AB}^t{\mathsf{\Lambda }}_o.$$

(13)

We obtain:

$$\begin{array}{c}\hfill (A_{11}+B_{11}-2C_{11})x_{out}^2+2(A_{12}-B_{12}+C_{12}-C_{21})x_{out}{p}_{out}+(A_{22}+B_{22}+2C_{22})p_{out}^2=\\ \hfill \left({\sigma }_{{out}_{11}}-{\sigma }_{{in}_{11}}\right)x_{out}^2+2\left({\sigma }_{{out}_{12}}-{\sigma }_{{in}_{12}}\right)x_{out}{p}_{out}+\left({\sigma }_{{out}_{22}}-{\sigma }_{{in}_{22}}\right)p_{out}^2.\end{array}$$

(14)

The general expression of the covariance matrix of the output state after the teleportation becomes:

$${\sigma }_{out}=\left(\begin{array}{cc}{A}_{11}+B_{11}-2C_{11}+{\sigma }_{{in}_{11}}& A_{12}-B_{12}+C_{12}-C_{21}+{\sigma }_{{in}_{12}}\\ A_{12}-B_{12}+C_{12}-C_{21}+{\sigma }_{{in}_{12}}& A_{22}+B_{22}+2C_{22}+{\sigma }_{{in}_{22}}\end{array}\right).$$

(15)

For the case of an input STS it becomes:

$$\begin{array}{c}{\sigma }_{out}=\left(\begin{array}{cc}{A}_{11}+B_{11}-2C_{11}& A_{12}-B_{12}+C_{12}-C_{21}\\ A_{12}-B_{12}+C_{12}-C_{21}& A_{22}+B_{22}+2C_{22}\end{array}\right)\hfill \\ +{\displaystyle \frac{2N_S+1}{2}}\left(\begin{array}{cc}cosh2\rho +sinh2\rho cos\theta & -sinh2\rho sin\theta \\ -sinh2\rho sin\theta & cosh2\rho -sinh2\rho cos\theta \end{array}\right).\hfill \end{array}$$

(16)

Let us assume that $\overline{X_{out}}-\overline{X_{in}}={(0,0)}^{\top }$. Then the expression (2) for the fidelity of teleportation becomes:

$$F({\varrho }_{in},{\varrho }_{out})={\displaystyle \frac{1}{\sqrt{\Delta +\mathsf{\Theta }}-\sqrt{\mathsf{\Theta }}}}.$$

(17)

2.2. Classical Limit for Squeezed Thermal State Teleportation

For quantum teleportation to take place, the quantum fidelity has to be greater than the classical fidelity threshold (CFT). This threshold fidelity value is determined as the best fidelity value when the two parties use only classical communication and measurements, but do not have the capacity to directly transmit quantum systems or share entanglement [39].

The fidelity between two squeezed thermal states described by covariance matrices ${\sigma }_{\rho ,N_S}$ and ${\sigma }_{\rho +\delta ,N_S}$, for any given value of $N_S$ is given by [37,40]:

$$F_{\delta ,N_S}={\displaystyle \frac{2}{\left(-4N_S-4N_S^2+\sqrt{1+2{(1+2N_S)}^{2}cosh2\delta +{(1+2N_S)}^4}\right)}}$$

(18)

In the case of the phase-free squeezed states, the classical fidelity threshold can be estimated by numerical integration:

$$F_{\mathrm{sq}(N_S=0)}^{\mathrm{cl}}=\int d\delta p_0^{\mathrm{opt}}\left(\delta \right)F_{\delta ,N_S=0},$$

(19)

where $p_0^{\mathrm{opt}}\left(\delta \right)$ is the probability distribution peaked around $\delta =0$ of an optimal measurement to estimate a completely unknown squeezing transformation $\widehat{U}\left(r\right)$ acting on a single-mode state $|\psi \rangle$ (for a squeezed state):

$$p_0^{\mathrm{opt}}={\left|{\int }_{-\infty }^{+\infty }{\displaystyle \frac{e^{-i\nu \delta }}{{\left(2\pi \right)}^{5/4}}}\left|\mathsf{\Gamma }\left({\displaystyle \frac{1}{4}}+{\displaystyle \frac{i\nu }{2}}\right)\right|d\nu \right|}^2,$$

(20)

where $\mathsf{\Gamma }\left(z\right)$ is the Euler gamma function. This leads to classical fidelity limit of about $F_{\mathrm{sq}(N_S=0)}^{\mathrm{cl}}\approx 81.5\%$ [40].

In the case of input squeezed thermal states ${\varrho }_{N_S,r}^{\mathrm{in}}$ with a given number of thermal photons $N_S$ (related to experimental losses) and an unknown degree of squeezing $r,$ upper and lower bounds of classical fidelity limit have been estimated [40]. The thermal state of interest can be represented as a mixture of Fock states. For all measurements performed on this state, the probability distribution becomes:

$$p_{th}\left(\delta \right)=(1-S)\sum _{n=0}^{\infty }{S}^n{p}_n\left(\delta \right),$$

(21)

where $S={\displaystyle \frac{N_S}{N_S+1}}$ and $p_n\left(\delta \right)$ is the probability distribution obtained when performing the exact same measurement on the squeezed Fock state defined by $\widehat{U}\left(r\right)|n\rangle$ for different values of n.

The value of classical limit of fidelity of teleportation for a squeezed thermal state is given by:

$${\overline{F}}_{\mathrm{sq}{N}_S}^{\mathrm{cl}}={\int }_{-\infty }^{+\infty }{\tilde{p}}_{th}\left(\delta \right){\mathcal{F}}_{\delta ,N_S}d\delta .$$

(22)

For $n>0$, ${\tilde{p}}_{th}\left(\delta \right)\le p_{th}\left(\delta \right)$ is the probability distribution for a specific measurement and its form depends on the measurement operator. The classical fidelity threshold will change for different measurement operators.

The value of the classical limit for the selected setup $F_{cl}$ is restricted by two extreme cases corresponding to specific measurement operators: upper and lower bounds of CFT $F_{lower}\le F_{cl}\le F_{upper}$. In the case of a thermal input state the measurement is performed over an ensemble of squeezed states that makes the final result less predictable. The upper bound occurs if the selected measurement operator ensures the optimal probability distribution for the $n^{th}$ Fock state. This is an asymptotic case for a thermal input state with $N_S>0$, because the measurement operator is applied on a random squeezed state from the Fock ensemble. The classical limit of the fidelity of teleportation belongs to the lower bound if the Lüder measurement of the parity is carried out, and the selected measurements ensure an optimal distribution for vacuum and one-photon states from the Fock ensemble.

The upper and lower limits of classical fidelity are shown in Figure 2. They are given by approximate formulas [40]:

$$\left\{\begin{array}{cc}\hfill & F_{lower}={\displaystyle \frac{163+4N_S\left[321+2N_S\left(477+598N_S+288N_S^2\right)\right]}{200{(1+2N_S)}^4}},\hfill \\ \hfill & F_{upper}={\displaystyle \frac{163+4N_S\left\{321+4N_S\left[240+N_S\left(314+179N_S\right)\right]\right\}}{200{(1+2N_S)}^4}}.\hfill \end{array}\right.$$

(23)

2.3. Quantum Steering of the Resource State

Quantum steering is a stronger quantum correlation compared to entanglement and can be present if the state of the system is entangled. Unlike entanglement and Bell nonlocality quantum steering is inherently directional and therefore asymmetric, therefore it may be possible for Alice to steer Bob state, and not for Bob to steer Alice state. However, for a symmetric initial bipartite Gaussian squeezed thermal state and when the temperatures of the thermal baths are equal, then the quantum steering is symmetric relative to the two parts of Alice and Bob, that is quantum steering $A\to B$ and $B\to A$ are equal. Quantum steering has found useful applications in quantum cryptography, for example one-sided device independent quantum key distribution (QKD) [41].

The operational definition of steering [42] includes two parties, Alice and Bob. Alice can arrange a bipartite quantum state multiple times and can send one part to Bob. Her goal is to convince Bob that the state they share is entangled. Bob checks if the correlations in their state can be explained by local hidden variable (LHV) theory [43]. If these correlations cannot be described by LHV, then the state they share is entangled and Alice can steer Bob’s state. It may be possible for Alice to steer Bob’s state, and not for Bob to steer Alice’s.

Alice, during the quantum teleportation protocol, performs on her mode local Gaussian measurements represented by a positive operator with covariance matrix ${\mathsf{\Gamma }}^{R_A}$ satisfying the condition:

$${\mathsf{\Gamma }}^{R_A}+{\displaystyle \frac{i}{2}}{\mathsf{\Omega }}_A\ge 0,{\mathsf{\Omega }}_A=\left(\begin{array}{cc}0& 1\\ -1& 0\end{array}\right).$$

(24)

Symplectic transformations and homodyne detection [44] are necessary to validate these measurements. The Bob conditional state, obtained as the result of the Alice measurement on her part, is represented by the covariance matrix $B_t-C_t{(A_t+{\mathsf{\Gamma }}^{R_A})}^{-1}{C}_t^{\top }$.

Quantum steering from Alice to Bob is present if and only if the following condition is violated [42,45]:

$${\sigma }_{AB}^t+{\displaystyle \frac{i}{2}}\left(0_A\oplus {\mathsf{\Omega }}_B\right)\ge 0,$$

(25)

or, equivalently,

$$A_t>0,\mathrm{and}{\Delta }_{\sigma }^B+{\displaystyle \frac{i}{2}}{\mathsf{\Omega }}_B\ge 0,$$

(26)

where ${\Delta }_{\sigma }^B=B_t-C_t{A}_t^{-1}{C}_t^{\top }$ is the Schur complement of $A_t$. The condition $A_t>0$ in ${\sigma }_{AB}^t$ holds at all times. Alice cannot steer Bob state if ${\Delta }_{\sigma }^B$ is a covariance matrix. We can test this by applying the Williamson theorem for ${\Delta }_{\sigma }^B$ with the appropriate symplectic transformation $S^{\top }{\Delta }_{\sigma }^{B}S=\mathrm{Diag}({\nu }^B,{\nu }^B)$ and checking the nonsteerability condition ${\nu }^B\ge {\displaystyle \frac{1}{2}}$. Therefore, the presence of quantum steering from Alice to Bob can be quantified by:

$$G^{A\to B}\left({\sigma }_{AB}^t\right):=\max \{0,-ln2{\nu }^B\}.$$

(27)

Alice can steer Bob state if $G^{A\to B}$ is positive. In a similar manner, the quantum steering from Bob to Alice can be determined. Alice and Bob have each one mode of the resource state, therefore the condition for steering can be simplified [46]:

$$G^{A\to B}\left({\sigma }_{AB}^t\right)=\max \left\{0,{\displaystyle \frac{1}{2}}ln{\displaystyle \frac{det{A}_t}{4det{\sigma }_{AB}^t}}\right\}.$$

(28)

2.4. Evolution of a Two-Mode Gaussian State in the Two-Reservoir Model

To gain deeper insight into the physics of teleporting a squeezed thermal state, we consider a bimodal open system, for which the environment consists of two thermal baths, each one embedding a Gaussian mode.

We employ the formalism of completely positive quantum dynamical semigroups, in which the evolution in time of the Gaussian bimodal state is given by the Gorini-Kossakowski-Lindblad-Sudarshan Markovian master equation [47,48]:

$${\displaystyle \frac{d\varrho \left(t\right)}{dt}}=-{\displaystyle \frac{i}{\hslash }}[H,\varrho \left(t\right)]+{\displaystyle \frac{1}{2\hslash }}\sum _j(2V_j\varrho \left(t\right)V_j^{†}-{\{\varrho \left(t\right),V_j^{†}{V}_j\}}_{+}),$$

(29)

where $\varrho \left(t\right)$ is the density operator, H is a Hamiltonian of the system, and the operators $V_j,$ which are taken polynomials of first degree in coordinates $X_A$, $X_B$ and momenta $P_A$, $P_B,$ describe a weak interaction with the environment.

In the case of a single bosonic mode the evolution is described by the associated covariance matrix:

$$s\left(t\right)=\left(\begin{array}{cc}{\sigma }_{x_A{x}_A}& {\sigma }_{x_A{p}_A}\\ {\sigma }_{p_A{x}_A}& {\sigma }_{p_A{p}_A}\end{array}\right),$$

(30)

where the elements are ${\sigma }_{ij}=\langle R_i{R}_j+R_j{R}_i\rangle /2,i,j=1,2,$ and $\mathit{R}=\{X_A,P_A\}\equiv \{R_1,R_2\}$ is the vector of position and momentum quadratures. The Hamiltonian in this case is:

$$H_A={\displaystyle \frac{1}{2}}{X}_A^2+{\displaystyle \frac{{\omega }_1^2}{2}}{P}_A^2,$$

(31)

where ${\omega }_1$ is the frequency of the mode.

The evolution in time of the covariance matrix is given by [48,49,50]:

$${\displaystyle \frac{ds\left(t\right)}{dt}}=Z_{1}s\left(t\right)+s\left(t\right)Z_1^{\top }+2D_1,$$

(32)

where $Z_1=\left(\begin{array}{cc}-{\lambda }_1& 1\\ -{\omega }_1^2& -{\lambda }_1\end{array}\right)$ and $D_1$ is the matrix of diffusion coefficients:

$$D_1={\displaystyle \frac{{\lambda }_1}{2}}\left(\begin{array}{cc}{\displaystyle \frac{1}{{\omega }_1}}coth{\displaystyle \frac{{\omega }_1}{2k{T}_1}}& 0\\ 0& {\omega }_{1}coth{\displaystyle \frac{{\omega }_1}{2k{T}_1}}\end{array}\right).$$

(33)

Here ${\lambda }_1$ is the dissipation constant and $T_1$ is the temperature of the thermal bath that the mode is coupled to (we set $\hslash =1$). The frequency of the modes is measured in [${\omega }_0$] units, time in [$1/{\omega }_0$] units and temperature in [$T_0$] units. The ${\omega }_0$ is the characteristic frequency of the source of the modes. For example, for optical modes the ${\omega }_0=2\pi c/\zeta$, where c is the speed of light and $\zeta$ is wavelength of the light. The unit of temperature is $T_0=\hslash \tilde{\nu }/k_B$, where $\tilde{\nu }$ is the characteristic frequency of the environment. $\tilde{\nu }$ denotes the frequency of the thermal photons generated in the environment.

Equation (32) yields the solution [50]:

$$s\left(t\right)=X_1\left(t\right)[s\left(0\right)-s(\infty )]X_1^{\top }\left(t\right)+s(\infty ),$$

(34)

where $X_1=exp\left(Z_{1}t\right)$. Its value asymptotically approaches zero as time tends to infinity. Equivalently the solution can be written as:

$$s\left(t\right)=X_1\left(t\right)s\left(0\right)X_1^{\top }\left(t\right)+Y_1\left(t\right),$$

(35)

with

$$\left\{\begin{array}{c}{X}_1=e^{-{\lambda }_{1}t}\left(\begin{array}{cc}cos\left({\omega }_{1}t\right)& {\displaystyle \frac{1}{{\omega }_1}}sin\left({\omega }_{1}t\right)\\ -{\omega }_{1}sin\left({\omega }_{1}t\right)& cos\left({\omega }_{1}t\right)\end{array}\right),\hfill \\ Y_1\left(t\right)=-X_1\left(t\right)s(\infty )X_1^{\top }\left(t\right)+s(\infty ).\hfill \end{array}\right.$$

(36)

The solution to the equation:

$$Z_{1}s(\infty )+s(\infty )Z_1^{\top }=-2D_1$$

(37)

provides the covariance matrix in the limit of asymptotic time:

$$s(\infty )={\displaystyle \frac{1}{2}}\left(\begin{array}{cc}{\displaystyle \frac{1}{{\omega }_1}}coth{\displaystyle \frac{{\omega }_1}{2k{T}_1}}& 0\\ 0& {\omega }_{1}coth{\displaystyle \frac{{\omega }_1}{2k{T}_1}}\end{array}\right).$$

(38)

The resource state shared by Alice and Bob is a two-mode Gaussian state, each mode being put in contact with its own thermal bath. It is characterized by the covariance matrix (6), whose evolution is given by the equation:

$${\sigma }_{AB}^t=(X_1\left(t\right)\oplus X_2\left(t\right))\sigma \left(0\right){(X_1\left(t\right)\oplus X_2\left(t\right))}^{\top }+(Y_1\left(t\right)\oplus Y_2\left(t\right)),$$

(39)

where $X_1$ and $Y_1$ are given by Equation (36) and similarly for $X_2$ and $Y_2,$ with frequencies ${\omega }_{1,2},$ dissipation coefficients ${\lambda }_{1,2}$ and temperatures $T_{1,2}$, respectively.

The initial state is a squeezed thermal state with the covariance matrix [51]:

$${\sigma }_{STS}=\left(\begin{array}{cccc}{a}_I& 0& c_I& 0\\ 0& a_{II}& 0& c_{II}\\ c_I& 0& b_I& 0\\ 0& c_{II}& 0& b_{II}\end{array}\right),$$

(40)

with

$$\begin{array}{cc}\hfill & a_I={\displaystyle \frac{1}{{\omega }_1}}\left(n_1{cosh}^{2}r+n_2{sinh}^{2}r+{\displaystyle \frac{1}{2}}cosh2r\right),\hfill \\ \hfill & a_{II}={\omega }_1\left(n_1{cosh}^{2}r+n_2{sinh}^{2}r+{\displaystyle \frac{1}{2}}cosh2r\right),\hfill \\ \hfill & b_I={\displaystyle \frac{1}{{\omega }_2}}\left(n_1{sinh}^{2}r+n_2{cosh}^{2}r+{\displaystyle \frac{1}{2}}cosh2r\right),\hfill \\ \hfill & b_{II}={\omega }_2\left(n_1{sinh}^{2}r+n_2{cosh}^{2}r+{\displaystyle \frac{1}{2}}cosh2r\right),\hfill \\ \hfill & c_I={\displaystyle \frac{1}{2\sqrt{{\omega }_1{\omega }_2}}}(n_1+n_2+1)sinh2r,\hfill \\ \hfill & c_{II}=-{\displaystyle \frac{\sqrt{{\omega }_1{\omega }_2}}{2}}(n_1+n_2+1)sinh2r,\hfill \end{array}$$

(41)

where $n_{1,2}$ stands for the average thermal photon number of mode 1 or 2, respectively. The number of thermal photons associated with a temperature is $n_{\mathrm{therm}}=coth(\tilde{\nu }/\left(2T\right))/2-1/2$. The thermal photon number of the resource state modes is determined by the physical temperature of the source of the modes and its characteristic frequency. The squeezing parameter r between the two modes has to meet the requirement for entanglement presence $r>r_s,$ where

$${cosh}^2{r}_s={\displaystyle \frac{(n_1+1)(n_2+1)}{n_1+n_2+1}}.$$

(42)

3. Main Results

We use Wolfram Mathematica 11.0.4 [52] to evaluate the dependence of fidelity of quantum teleportation given by Equation (17) and quantum steering between the modes given by Equations (28). We compare the fidelity of teleportation with the upper and lower classical limits given by Equation (23). The explicit parameters used during numerical simulation are presented in

Table 1. Parameters used in numerical simulation for each figure.

Figure	Value	${\mathit{N}}_{\mathit{S}}$	$\mathit{\rho }$	$\mathit{\theta }$	${\mathit{\omega }}_1/{\mathit{\omega }}_0$	${\mathit{\omega }}_2/{\mathit{\omega }}_0$	$\mathit{t}{\mathit{\omega }}_0$	${\mathit{T}}_1/{\mathit{T}}_0$	${\mathit{T}}_2/{\mathit{T}}_0$	r	${\mathit{n}}_1$	${\mathit{n}}_2$
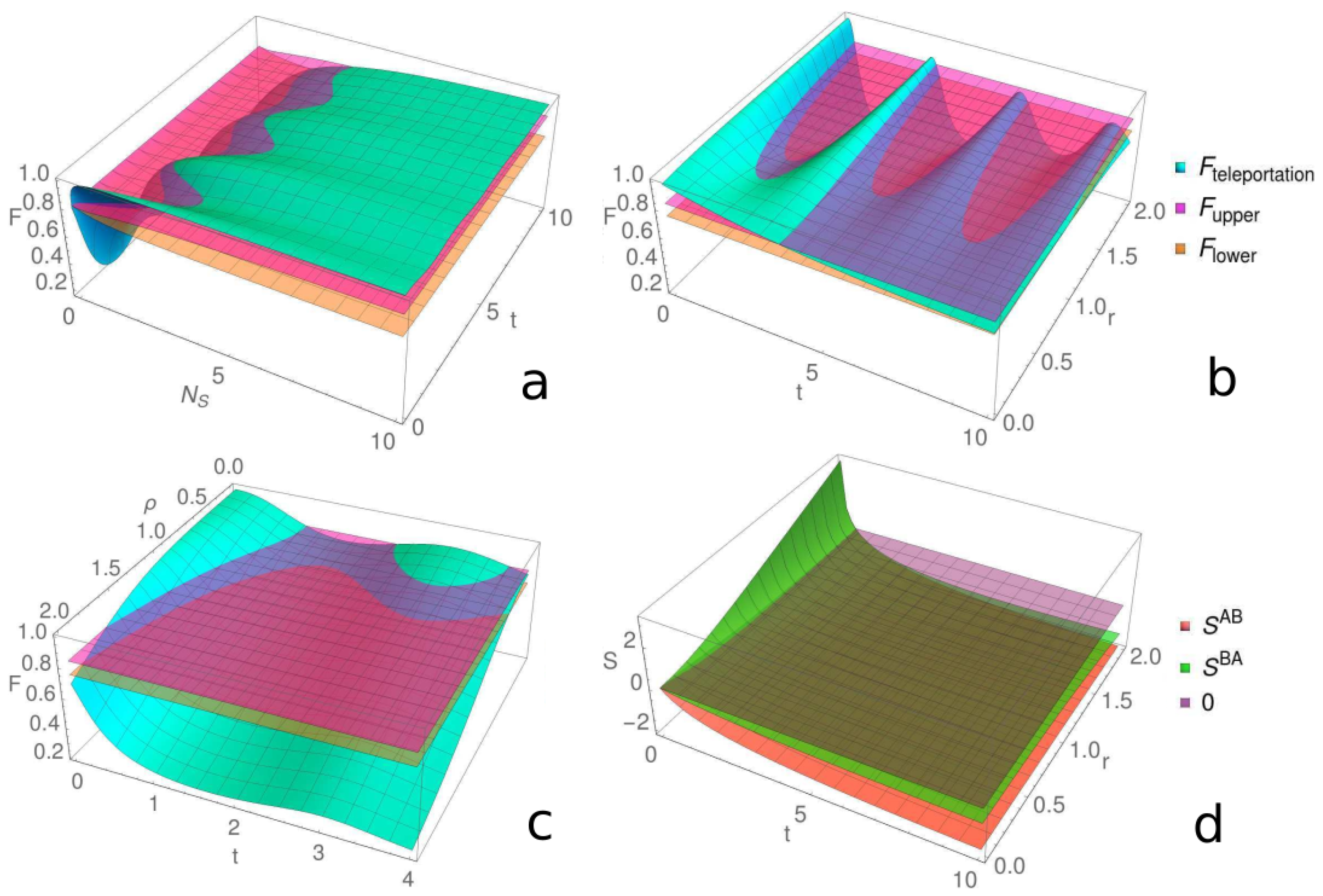
Figure 3a	F	$N_S$	$0.2$	0	1	1	t	1	4	$0.7$	0	0
Figure 3b	F	2	$0.2$	0	1	1	t	1	4	r	0	0
Figure 3c	F	2	$\rho$	0	1	1	t	1	4	$0.7$	0	0
Figure 3d	$S^{AB}$,$S^{BA}$	−	−	−	1	1	t	1	4	r	0	0
Figure 4a	$F_{secure}$	$N_S$	$0.7$	0	1	1	$0.2$	$T_1$	5	$0.7$	0	0
Figure 4b	$F_{secure}$	$N_S$	$0.7$	0	${\omega }_1$	1	$0.2$	1	5	$0.7$	0	0
Figure 4c	$F_{secure}$	1	$\rho$	0	${\omega }_1$	1	$0.2$	1	5	$0.7$	0	0
Figure 4d	$F_{secure}$	1	$0.7$	0	${\omega }_1$	${\omega }_2$	$0.2$	1	5	$0.7$	0	0
Figure 5a	$F_{secure}$	$N_S$	$0.2$	0	1	1	t	1	4	$0.7$	0	0
Figure 5b	$F_{secure}$	1	$\rho$	0	1	1	t	1	4	$0.7$	0	0
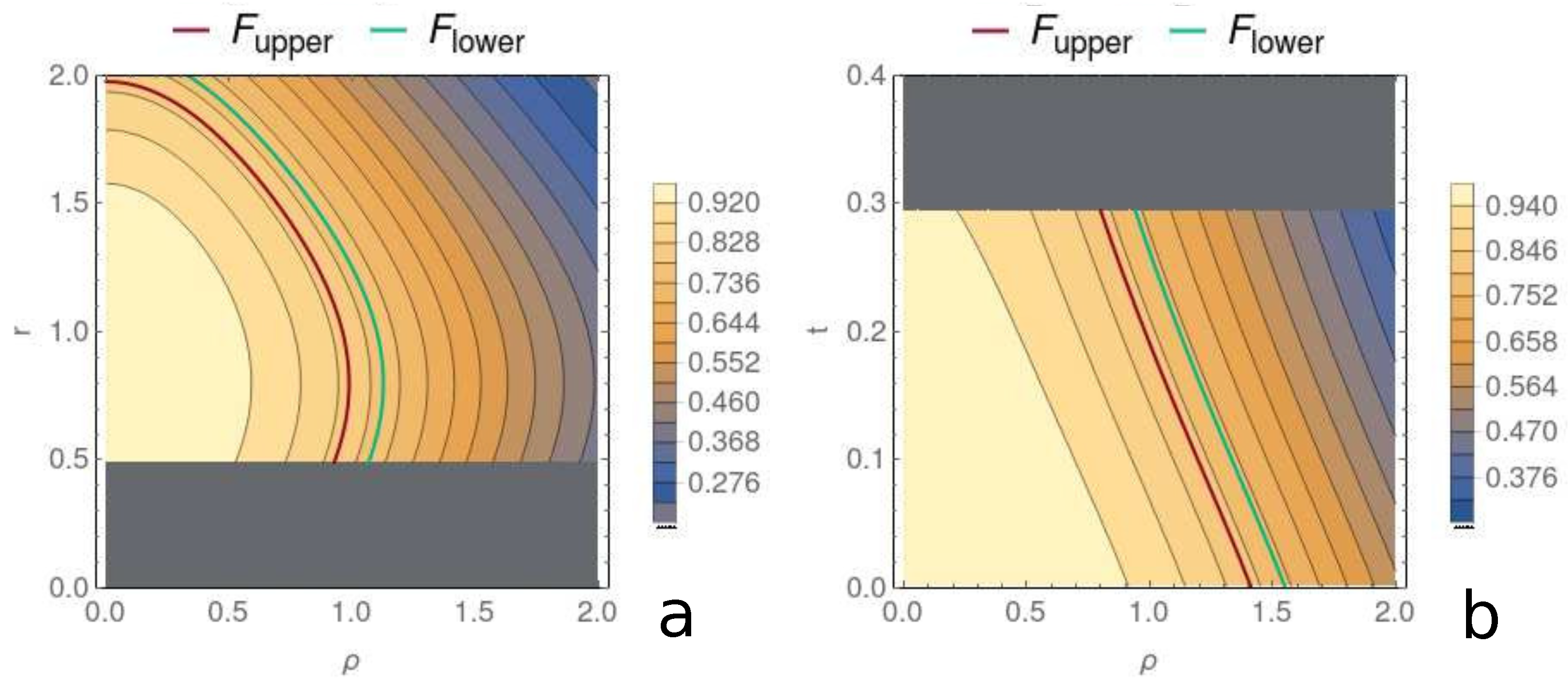
Figure 6a,b	$F_{secure}$,F	1	$0.7$	0	1	1	$0.2$	$T_1$	$T_2$	$0.7$	0	0
Figure 6c,d	$S^{AB}$,$S^{BA}$	−	−	−	1	1	$0.2$	$T_1$	$T_2$	$0.7$	0	0
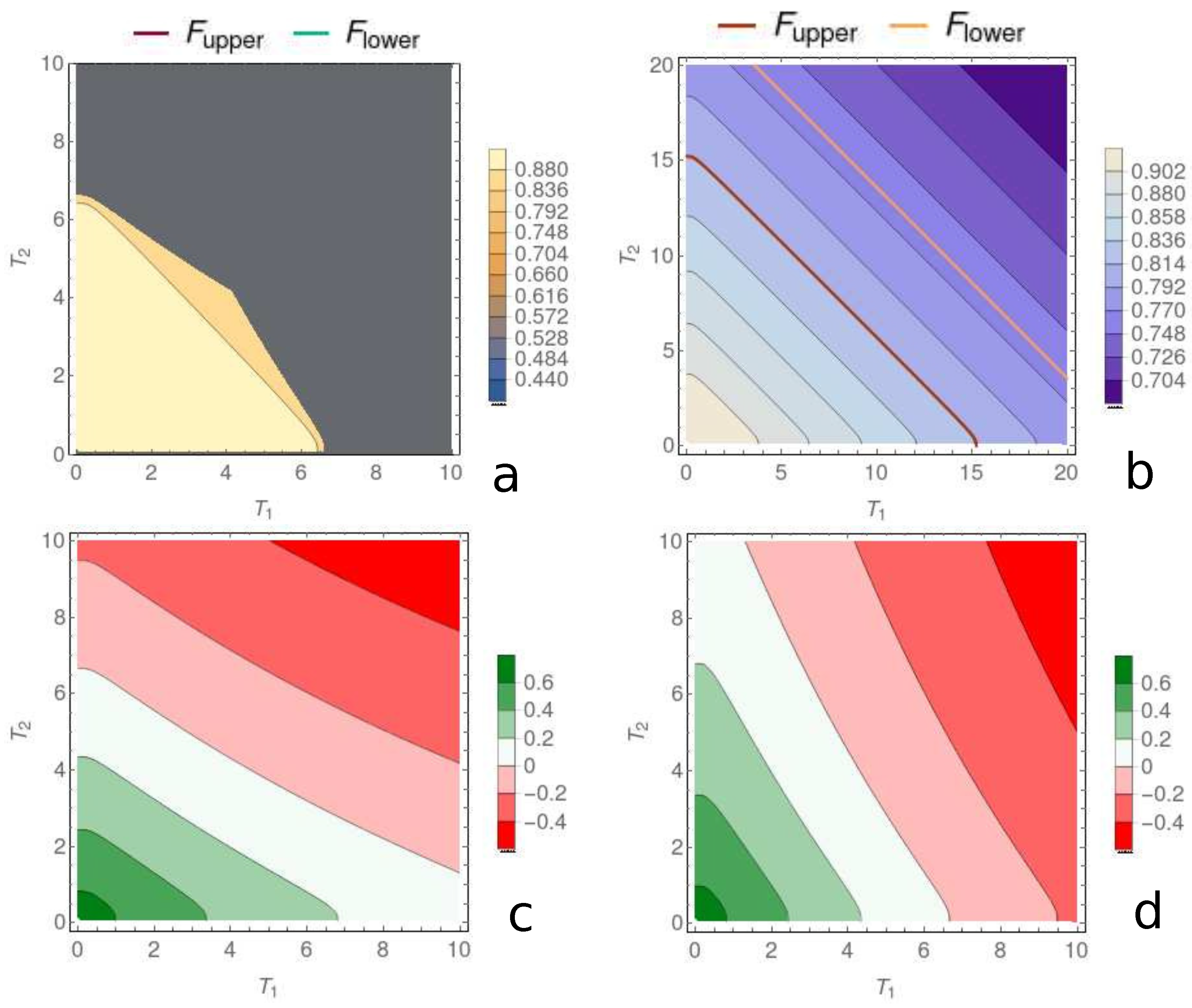
Figure 7a,b	$F_{secure}$,F	1	$0.7$	0	1	1	$0.02$	1	5	$0.7$	$n_1$	$n_2$
Figure 7c,d	$S^{AB}$,$S^{BA}$	−	−	−	1	1	$0.02$	1	5	$0.7$	$n_1$	$n_2$

The values of dissipation parameters are ${\lambda }_1={\lambda }_2=0.1$.

.

The dependence on time of the quantities determining the success of secure quantum teleportation is presented in Figure 3. In Figure 3a we examine the evolution of the fidelity of quantum teleportation with time t and the number of thermal photons $N_S$ of the input state. There are also shown upper $F_{upper}$ and lower $F_{lower}$ classical fidelities of teleportation with magenta and orange planes, respectively. For a quantum fidelity higher than the upper classical fidelity ($F>F_{upper}$), the secure quantum teleportation is possible if the two-way quantum steering is present. For a quantum fidelity $F\in (F_{lower},F_{upper})$, a successful quantum teleportation is strongly dependent on the type of the measurement operator, together with the presence of the two-way steering. For $F<F_{lower}$ the quantum teleportation is impossible.

We observe that the fidelity of quantum teleportation increases with the average number of thermal photons of the input state. Starting with a certain number of thermal photons it exceeds the upper limit of fidelity of classical teleportation, which is the threshold required for the process to successfully be carried out. The fidelity of teleportation decreases in time with weak oscillations. However, for secure teleportation, we need two-way steering between the resource state modes. The behaviour of quantum steering is shown in Figure 3d. The steering rapidly decreases in time, and its sudden death occurs, making teleportation impossible for large times.

The dependence of fidelity of teleportation on the mode squeezing r has a complex form shown in Figure 3b. The fidelity of teleportation decreases with the increase of r for most values of time. However, it increases with r for the moments of time when the fidelity presents local peaks. For these times, the fidelity of teleportation is larger than the upper classical limit for relatively high values of r. However, due to the quantum steering sudden death (Figure 3d), only the first maximum could be relevant for technological applications.

The fidelity of teleportation decreases by increasing the squeezing of the input state for all times, as depicted in Figure 3c and it exhibits a damped oscillatory behavior over time. Distinct islands, corresponding to secondary maxima of the teleportation fidelity above the classical bound, are observed. However, in those cases, the quantum steering sudden death has already been occurred, so that only the first maximum could be relevant.

For an easier analysis of the conditions required for a secure teleportation process, we introduce quantity $F_{secure}$, defined as:

$$F_{secure}=\left\{\begin{array}{c}F,\mathrm{if}{G}^{A\to B}>0,G^{B\to A}>0,\hfill \\ 0,\mathrm{otherwise}.\hfill \end{array}\right.$$

(43)

Figure 4a depicts the evolution of the fidelity of secure teleportation of a squeezed thermal state with the average number of photons $N_S$ of the input state and the temperature $T_1$ of the first bath. We observe that the fidelity of teleportation decreases by increasing the temperature. However, steering sudden death occurs for relatively small temperatures ($T_1>2.88$ for the parameters given in Table 1). The secure fidelity $F_{secure}$ increases with the average photon number of the input state.

The evolution of the fidelity of secure teleportation with the average thermal photon number $N_S$ of the input state and the first mode frequency ${\omega }_1$ is shown in Figure 4b. For small values of the mode frequency, teleportation is impossible due to the absence of the steering. For high values of the first mode frequency, the fidelity of teleportation decreases below the classical limit. Therefore, the most favorable case for secure quantum teleportation is for high values of $N_S$ and relatively small frequency ${\omega }_1$ (between $0.5$ and 1 for the computation parameters specified in Table 1).

In Figure 4c is presented the dependence of fidelity of secure teleportation on squeezing $\rho$ of the input state and the frequency of the first mode ${\omega }_1$. For small values of the frequency, secure teleportation is impossible due to the absence of quantum steering. Optimal values of frequency are in the range $[0.5,1]$ employing the parameter values from Table 1. The fidelity of secure teleportation decreases with the increase of the squeezing of the input state for all values of frequency.

The dependence of the fidelity of secure teleportation on both frequencies ${\omega }_1$, ${\omega }_2$ of the resource state modes is illustrated in Figure 4d. Two-way quantum steering is absent for a wider range of second mode frequencies ${\omega }_2$ than for first mode frequencies ${\omega }_1$. The optimal values of the second mode frequency are found in the range $[0.95,1.9]$, while the optimal values of the first mode frequency are in the range $[0.4,1.9]$ (for the computation parameters specified in Table 1). This unevenness in the range of values can be explained by the asymmetric behavior of quantum steering, due to different temperatures of the thermal baths.

The impact of the squeezing $\rho$ of the input state on the fidelity of secure teleportation is presented in Figure 5. The fidelity of teleportation generally decreases by increasing the squeezing of the input state. The two-way steering is absent for the squeezing r of the resource state mode less than $0.5$ for the computation parameters specified in Table 1, as can be observed in Figure 5a. The optimal fidelity of teleportation of the squeezed thermal state is encompassed by the red curve, corresponding to the upper limit of classical fidelity of teleportation. The steering sudden death occurs abruptly, making secure teleportation unfeasible (Figure 5b).

The evolution of the fidelity of secure teleportation with the temperatures of both baths is shown in Figure 6. Once again, we observe the importance of the two-way steering. Even though the fidelity of teleportation is over the upper limit of classical teleportation (Figure 6b), we observe that the secure quantum teleportation is not possible for high temperatures (Figure 6a), due to the sudden death of the quantum steering, as can be seen in Figure 6c,d. Quantum steering $A\to B$ (Figure 6c) and $B\to A$ (Figure 6d) are asymmetric, however, we observe that the fidelity of secure quantum teleportation exhibits a symmetry line when the temperatures of the baths are equal $T_1=T_2$.

A similar picture can be observed while examining the fidelity of secure teleportation evolution (Figure 7a) with the average number of thermal photons $n_1$ and $n_2$ of the resource modes. In Figure 7b is depicted the dependence of the fidelity of teleportation on $n_1$ and $n_2$. We observe that for $n_1,n_2<3$ the fidelity of teleportation is higher than the upper classical limit. However, as can be seen from Figure 7c,d, the steering sudden death occurs for $n_1,n_2>1.14$ (for the parameters specified in Table 1).

4. Discussion

In this article, we investigated the secure quantum teleportation of a squeezed thermal state using as the teleportation resource a bipartite Gaussian state shared between two parties, Alice and Bob. First, we deduced the analytical expression of the fidelity of quantum teleportation using the characteristic function approach together with the covariance matrix formalism. We have shown that the fidelity of teleportation is determined by the parameters of the two resource state modes interacting with the environment and by the parameters of the input state to be teleported (squeezing, thermal photon number and phase).

Next we studied the secure quantum teleportation in the case when each mode of the resource state is embedded in its own thermal bath. The evolution of the two resource modes in the two-reservoir model was investigated by using the Gorini-Kossakowski-Lindblad-Sudarshan quantum Markovian master equation. The two crucial conditions for a successful secure quantum teleportation are the presence of the two-way quantum steering and the fidelity of teleportation to exceed the classical threshold.

We described the dependence of the fidelity of teleportation and of the quantum steering on time and the parameters characterizing the resource state and the thermal baths. The fidelity of quantum teleportation increases with the input state thermal number and, therefore, squeezed thermal states are more convenient for teleportation than squeezed vacuum states. The low squeezing of the input state and a higher average number of the thermal photons associated with the input state favor quantum teleportation. In most cases, the success of quantum teleportation is determined by the steering presence during the experiment, due to the fact that the fidelity is still larger than the upper classical threshold when the quantum steering already disappeared. Indeed, the steering between the modes of the resource state decreases rapidly over time, and by increasing the temperature of the reservoirs and the average thermal photon numbers of the resource state modes. Besides cooling the reservoirs or the source of the modes, the temperature of the reservoirs can be reduced by increasing their characteristic frequencies.

The most convenient result for teleportation was observed for strongly squeezed, near-resonant resource states with a low number of thermal photons. To enhance the performance of the quantum teleportation protocol additional techniques could be used, in order to increase the survival time of the quantum steering. Such techniques include steering distillation [53] and reservoir engineering or auxiliary reservoir coupling [54].

Our theoretical model predicts the classical limit for the fidelity of teleportation to be approximately $0.75$. This is in good agreement with recent experimental studies of teleportation using continuous-variable systems, where the authors obtained fidelities above $0.75$ [55,56] for continuous-variable quantum teleportation. Furthermore, a previous study [57] reported a decrease in the fidelity of teleportation with increasing squeezing of the input state. Similarly, another study [58] found that an increase in the number of thermal photons enhances the fidelity of cloning. This supports the conclusions of the present work and our previous study [30], in which we observed that the fidelity of teleportation increases with the number of thermal photons in the input state.