An Efficient and Effective Model for Preserving Privacy Data in Location-Based Graphs
Abstract
1. Introduction
2. Motivation
- Dataset attributes are separated into explicit identifier, quasi-identifier, and sensitive attribute(s).
- All values in every explicit identifier attribute must be removed.
- The re-identifiable quasi-identifier values are suppressed or generalized by their less specific values to be indistinguishable.
- In addition, some privacy preservation models (e.g., l-diversity and t-closeness) further consider the characteristics of sensitive values in terms of their privacy preservation constraints.
3. Model and Notation
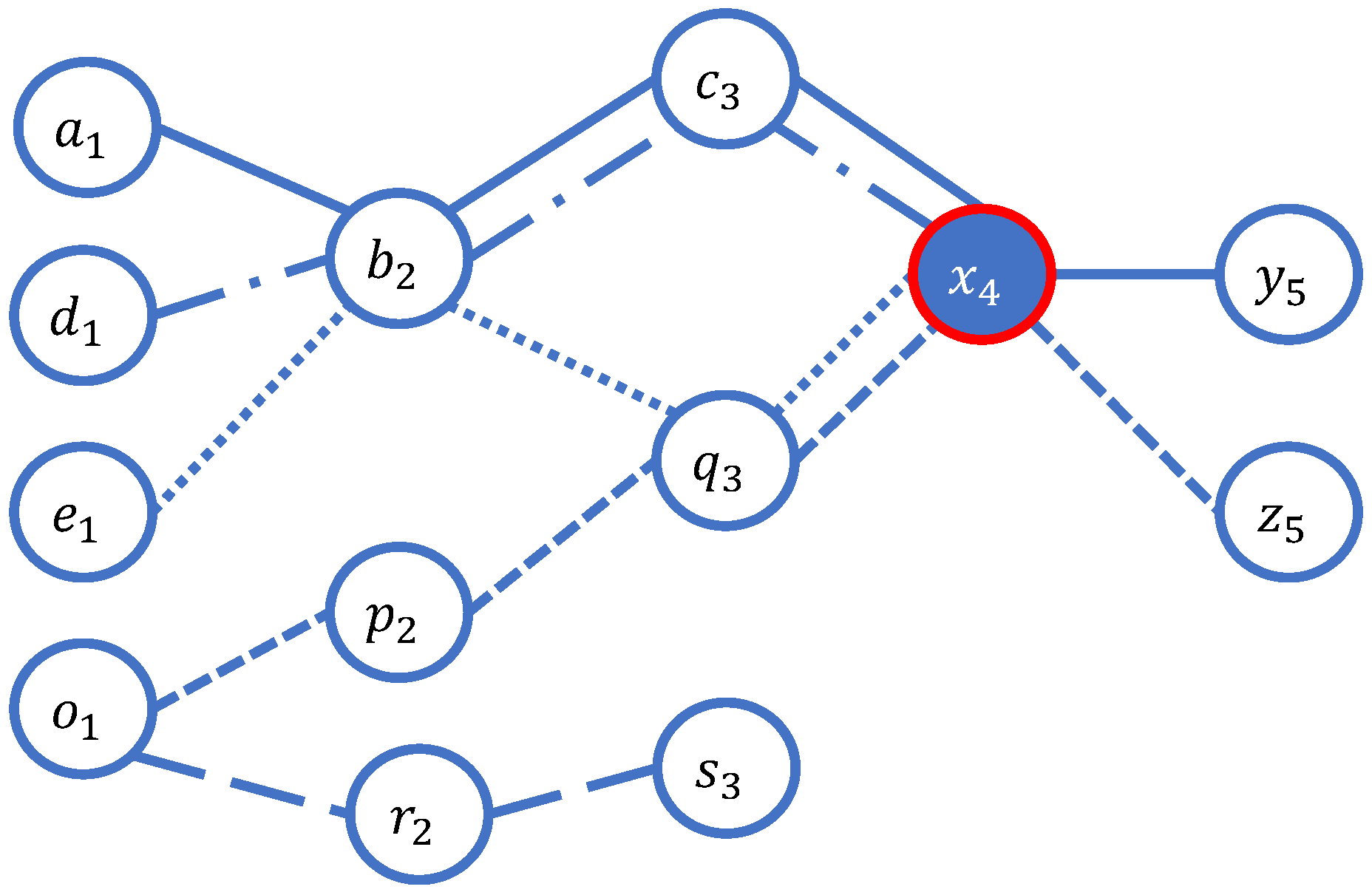
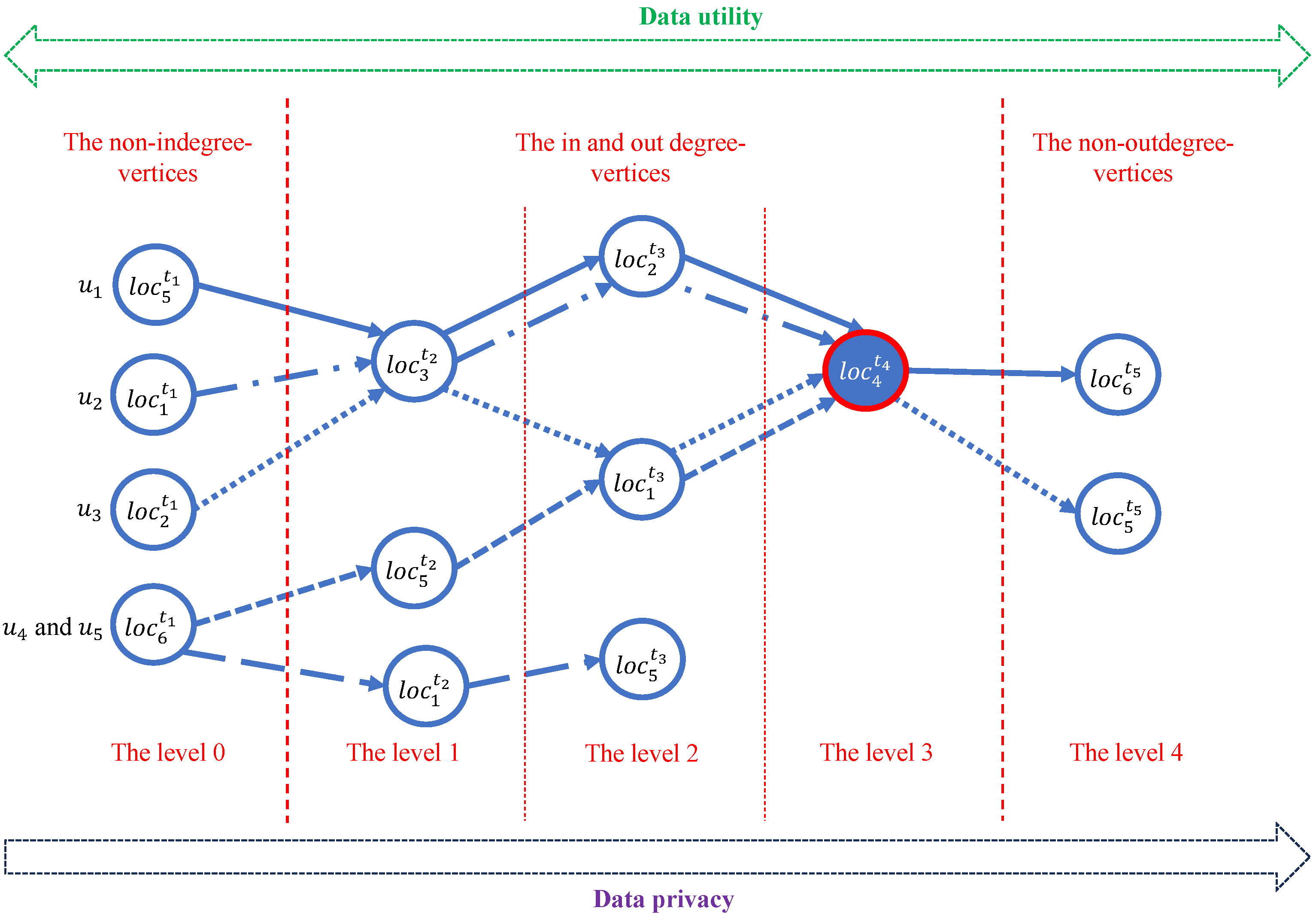
3.1. The Graph of Users’ Visited Sequence Locations
- Let vertex connect to vertex .
- Moreover, let vertex connect to vertex .
- Therefore, the timestamp of the vertices , . must be, according to the property, .
3.2. The Type of Vertices
3.3. Data Sliding Windows [58,59,60,61]
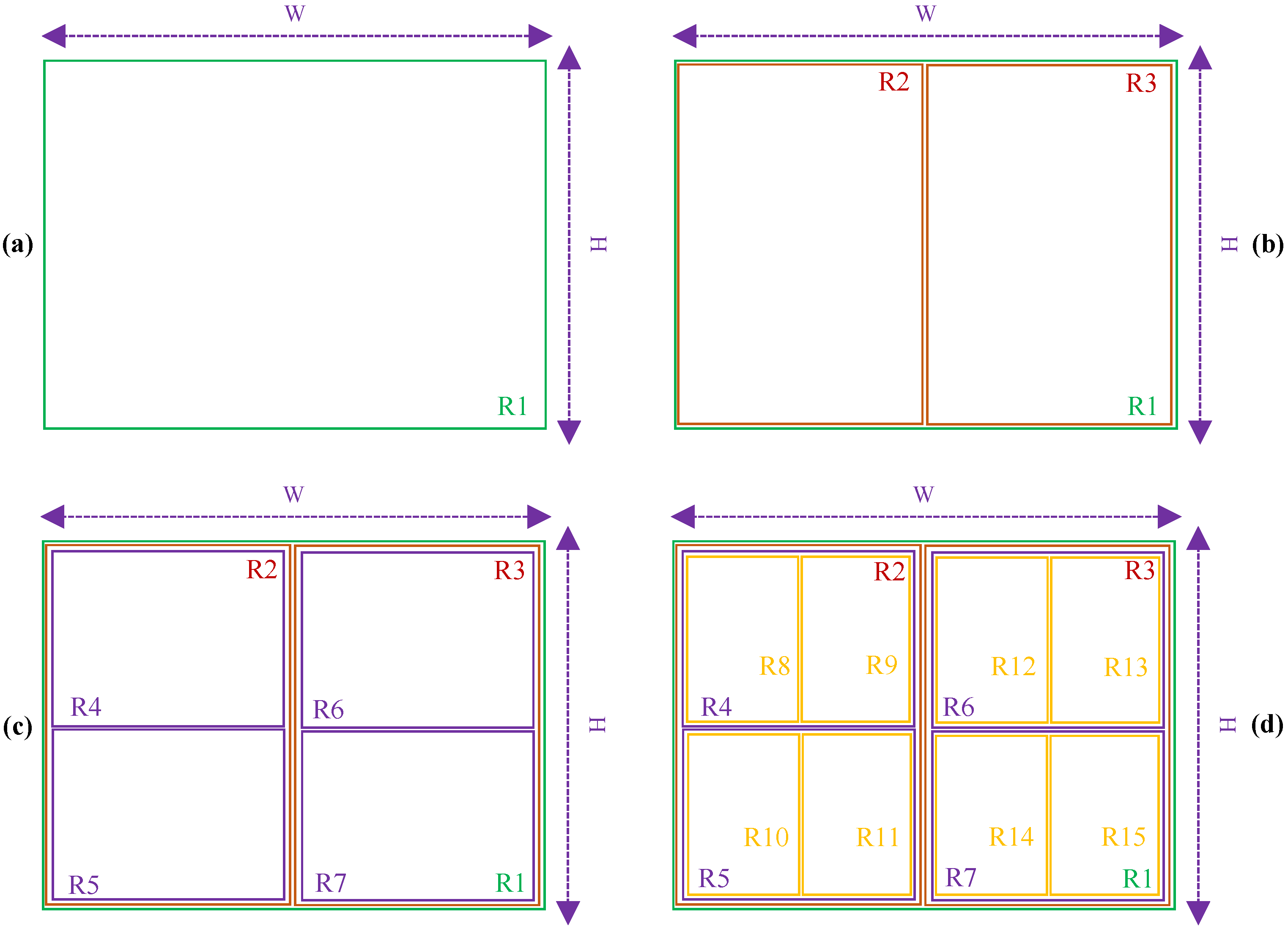
3.4. Location Hierarchy
3.4.1. Dynamic Location Hierarchy
- The bounding rectangle is not covered by others; it is the root of R.
- The child of is every that is only covered by and is not covered by others.
- The label of each vertex in the tree is represented by .
3.4.2. Manual Location Hierarchy
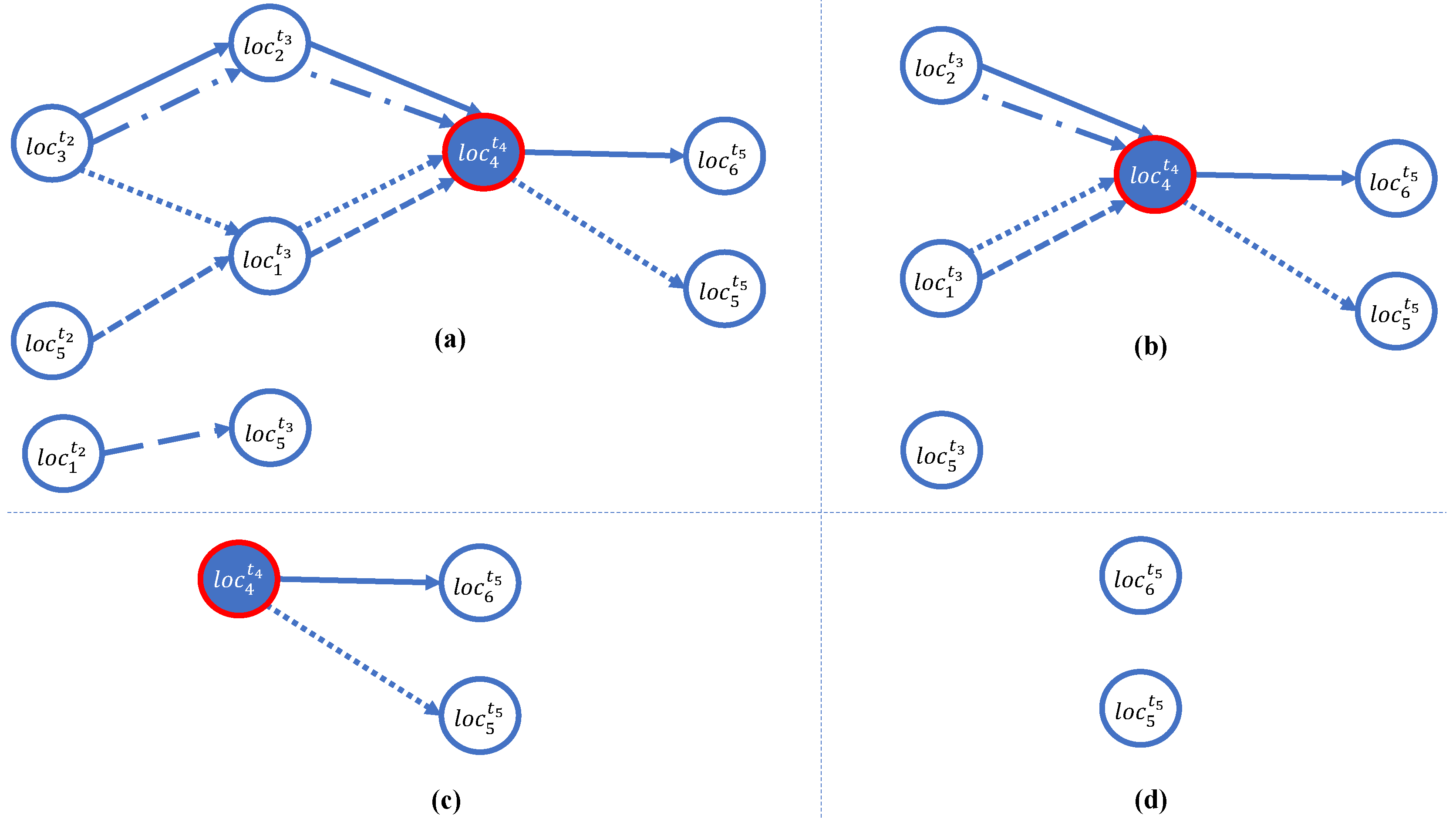
3.5. Data Suppression
- .
- ∪…∩∪…∪=∅ such that is the set of the vertices in level l of , where .
- ∪…∪∪…∪=.
3.6. Data Generalization
3.7. The Proposed Privacy Preservation Model
3.7.1. Problem Statement
3.7.2. The Privacy Preservation Algorithm
| Algorithm 1, , , , , , )-privacy |
|
- is the level of suppressed vertices.
- is the number of paths that are available in .
- n is the number of locations that each user visit in .
- is the number of sensitive locations that must be protected in .
- is the number of paths that are available in of .
- l is the high of or .
- are the forest graphs of .
3.7.3. Utility Measurement
- is the number of paths in .
- is the number of vertices in .
- is the number of suppressed vertices in .
- represents the generalization level of the vertex .
- is the highest of .
- v is the original query result.
- is that of the related experiment query.
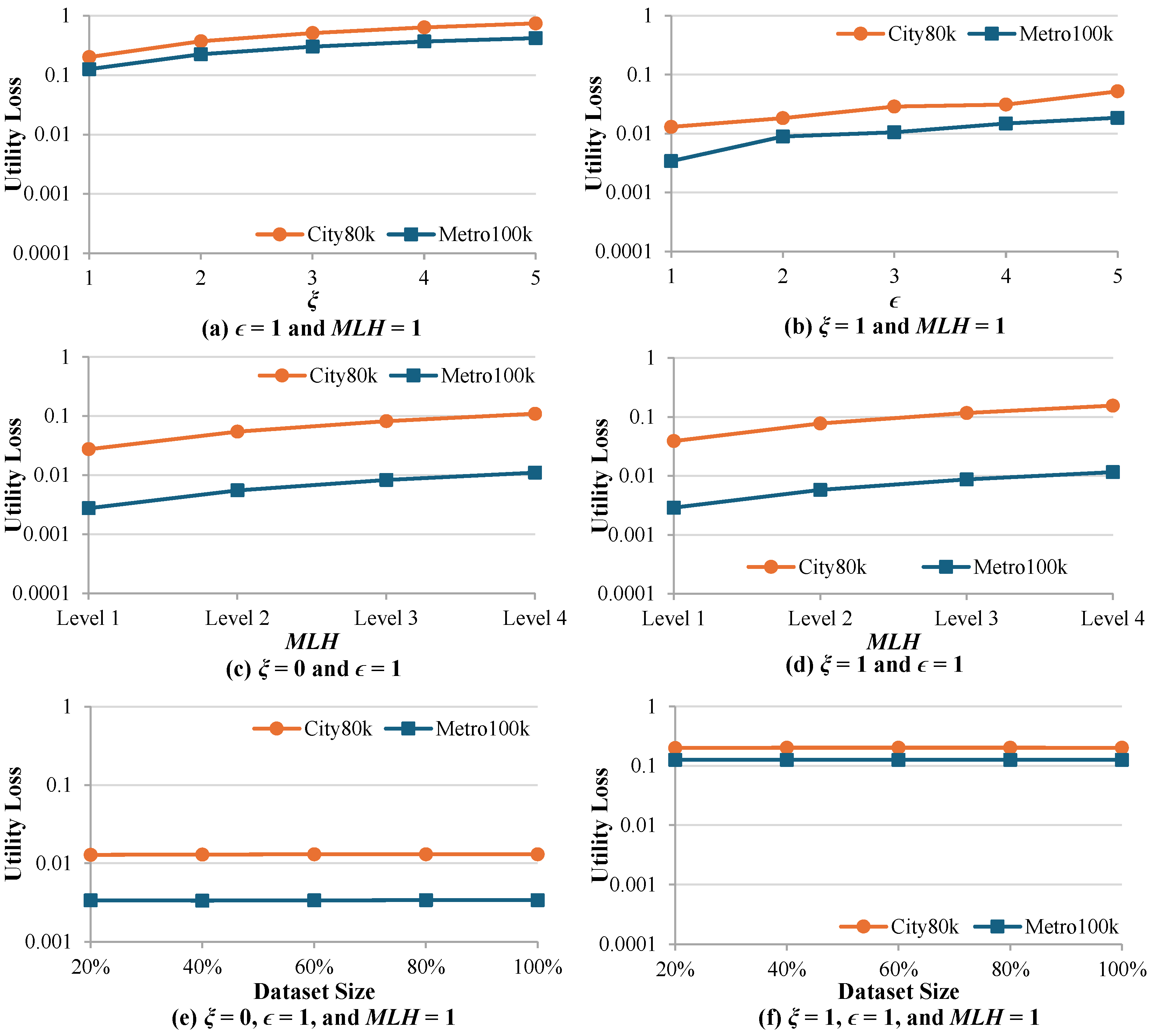
4. Experiment
4.1. Experimental Setup
4.1.1. Effectiveness
4.1.2. Efficiency
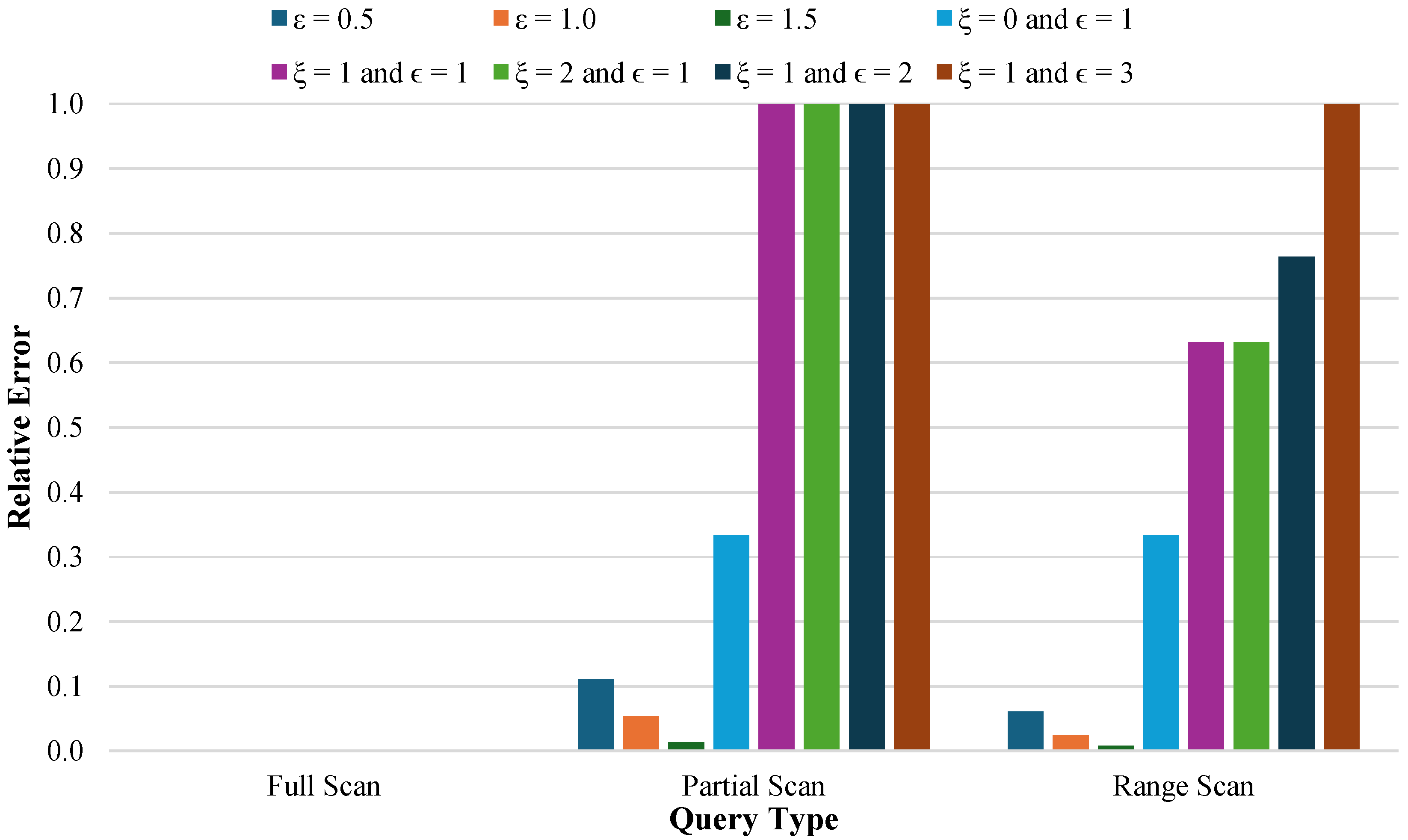
4.2. Relative Error Across Query Types
4.2.1. Full Scan Queries
4.2.2. Partial Scan Queries
4.2.3. Multi-Timestamp Scan Queries
5. Conclusions
6. Future Work
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Cummins, C.; Orr, R.; O’Connor, H.; West, C. Global positioning systems (GPS) and microtechnology sensors in team sports: A systematic review. Sport Med. 2013, 43, 1025–1042. [Google Scholar] [CrossRef] [PubMed]
- Enge, P.K. The global positioning system: Signals, measurements, and performance. Int. J. Wirel. Inf. Netw. 1994, 1, 83–105. [Google Scholar] [CrossRef]
- Grewal, M.S.; Weill, L.R.; Andrews, A.P. Global Positioning Systems, Inertial Navigation, and Integration; John Wiley & Sons: Hoboken, NJ, USA, 2007. [Google Scholar]
- Lee, H.-S.; Kim, G.-H.; Ju, H.-S.; Mun, H.-S.; Oh, J.-H.; Shin, B.-S. Global Navigation Satellite System/Inertial Navigation System-Based Autonomous Driving Control System for Forestry Forwarders. Forests 2025, 4, 647. [Google Scholar] [CrossRef]
- Li, R.; Zheng, S.; Wang, E.; Chen, J.; Feng, S.; Wang, D.; Dai, L. Advances in BeiDou Navigation Satellite System (BDS) and satellite navigation augmentation technologies. Satell. Navig. 2020, 1, 12, Erratum in Satell. Navig. 2020, 1, 13. https://doi.org/10.1186/s43020-020-00015-x. [Google Scholar] [CrossRef]
- Yang, Y.; Gao, W.; Guo, S.; Mao, Y.; Yang, Y. Introduction to BeiDou-3 navigation satellite system. Navigation 2019, 66, 7–18. [Google Scholar] [CrossRef]
- Noone, R. Location Awareness in the Age of Google Maps; Taylor & Francis: Abingdon, UK, 2024. [Google Scholar]
- Pramanik, M.A.; Rahman, M.M.; Anam, A.I.; Ali, A.A.; Amin, M.A.; Rahman, A.M. Modeling traffic congestion in developing countries using google maps data. In Proceedings of the Advances in Information and Communication: Proceedings of the 2021 Future of Information and Communication Conference (FICC), Virtual, 29–30 April 2021; Springer: Berlin/Heidelberg, Germany, 2021; Volume 1, pp. 513–531. [Google Scholar]
- Zhao, Q.; Yu, L.; Li, X.; Peng, D.; Zhang, Y.; Gong, P. Progress and trends in the application of Google Earth and Google Earth Engine. Remote Sens. 2021, 13, 3778. [Google Scholar] [CrossRef]
- Yang, L.; Driscol, J.; Sarigai, S.; Wu, Q.; Chen, H.; Lippitt, C.D. Google Earth Engine and artificial intelligence (AI): A comprehensive review. Remote Sens. 2022, 14, 3253. [Google Scholar] [CrossRef]
- Herfort, B.; Lautenbach, S.; Porto de Albuquerque, J.; Anderson, J.; Zipf, A. A spatio-temporal analysis investigating completeness and inequalities of global urban building data in OpenStreetMap. Nat. Commun. 2023, 14, 3985. [Google Scholar] [CrossRef]
- Biljecki, F.; Chow, Y.S.; Lee, K. Quality of crowdsourced geospatial building information: A global assessment of OpenStreetMap attributes. Build. Environ. 2023, 237, 110295. [Google Scholar] [CrossRef]
- Wojtusiak, J.; Nia, R.M. Location prediction using GPS trackers: Can machine learning help locate the missing people with dementia? Internet Things 2021, 13, 100035. [Google Scholar] [CrossRef]
- Cullen, A.; Mazhar, M.K.A.; Smith, M.D.; Lithander, F.E.; Ó Breasail, M.; Henderson, E.J. Wearable and portable GPS solutions for monitoring mobility in dementia: A systematic review. Sensors 2022, 22, 3336. [Google Scholar] [CrossRef]
- Yadav, S.P.; Zaidi, S.; Nascimento, C.D.S.; de Albuquerque, V.H.C.; Chauhan, S.S. Analysis and Design of automatically generating for GPS Based Moving Object Tracking System. In Proceedings of the 2023 International Conference on Artificial Intelligence and Smart Communication (AISC), Greater Noida, 27–29 January 2023; pp. 1–5. [Google Scholar]
- McFedries, P.; McFedries, P. Protecting Your Device. In Troubleshooting iOS: Solving iPhone and iPad Problems; Apress: New York, NY, USA, 2017; pp. 91–109. [Google Scholar]
- Heinrich, A.; Bittner, N.; Hollick, M. AirGuard-protecting android users from stalking attacks by apple find my devices. In Proceedings of the 15th ACM Conference on Security and Privacy in Wireless and Mobile Networks, Washington DC, USA, 16–19 May 2022; pp. 26–38. [Google Scholar]
- Chen, Y.; Huang, Z.; Ai, H.; Guo, X.; Luo, F. The impact of GIS/GPS network information systems on the logistics distribution cost of tobacco enterprises. Transp. Res. Part Logist. Transp. Rev. 2021, 149, 102299. [Google Scholar] [CrossRef]
- Feng, Z.; Li, G.; Wang, W.; Zhang, L.; Xiang, W.; He, X.; Zhang, M.; Wei, N. Emergency logistics centers site selection by multi-criteria decision-making and GIS. Int. J. Disaster Risk Reduct. 2023, 96, 103921. [Google Scholar] [CrossRef]
- Zhang, X.; Liu, X. A two-stage robust model for express service network design with surging demand. Eur. J. Oper. Res. 2022, 299, 154–167. [Google Scholar] [CrossRef]
- Wang, L.; Garg, H.; Li, N. Pythagorean fuzzy interactive Hamacher power aggregation operators for assessment of express service quality with entropy weight. Soft Comput. 2021, 25, 973–993. [Google Scholar] [CrossRef]
- Xu, S.X.; Guo, R.Y.; Zhai, Y.; Feng, J.; Ning, Y. Toward a positive compensation policy for rail transport via mechanism design: The case of China Railway Express. Transp. Policy 2024, 146, 322–342. [Google Scholar] [CrossRef]
- Dalal, S.; Chiem, N.; Karbassi, N.; Liu, Y.; Monroy-Hernández, A. Understanding Human Intervention in the Platform Economy: A Case Study of an Indie Food Delivery Service; Association for Computing Machinery: New York, NY, USA, 2023. [Google Scholar] [CrossRef]
- Hasegawa, Y.; Ido, K.; Kawai, S.; Kuroda, S. Who took gig jobs during the COVID-19 recession? Evidence from Uber Eats in Japan. Transp. Res. Interdiscip. Perspect. 2022, 13, 100543. [Google Scholar] [CrossRef]
- Panigrahi, A.K. A case study on Zomato–The online Foodking of India. J. Manag. Res. Anal. 2020, 7, 25–33. [Google Scholar] [CrossRef]
- Galati, A.; Crescimanno, M.; Vrontis, D.; Siggia, D. Contribution to the sustainability challenges of the food-delivery sector: Finding from the Deliveroo Italy case study. Sustainability 2020, 12, 7045. [Google Scholar] [CrossRef]
- Pourrahmani, E.; Jaller, M.; Fitch-Polse, D.T. Modeling the online food delivery pricing and waiting time: Evidence from Davis, Sacramento, and San Francisco. Transp. Res. Interdiscip. Perspect. 2023, 21, 100891. [Google Scholar] [CrossRef]
- Yeo, S.F.; Tan, C.L.; Teo, S.L.; Tan, K.H. The role of food apps servitization on repurchase intention: A study of FoodPanda. Int. J. Prod. Econ. 2021, 234, 108063. [Google Scholar] [CrossRef]
- Coifman, B.; Li, L. A critical evaluation of the Next Generation Simulation (NGSIM) vehicle trajectory dataset. Transp. Res. Part Methodol. 2017, 105, 362–377. [Google Scholar] [CrossRef]
- Ivanovic, B.; Song, G.; Gilitschenski, I.; Pavone, M. trajdata: A unified interface to multiple human trajectory datasets. Adv. Neural Inf. Process. Syst. 2024, 36, 27582–27593. [Google Scholar]
- Huang, X.; Yin, Y.; Lim, S.; Wang, G.; Hu, B.; Varadarajan, J.; Zheng, S.; Bulusu, A.; Zimmermann, R. Grab-posisi: An extensive real-life gps trajectory dataset in southeast asia. In Proceedings of the 3rd ACM SIGSPATIAL international workshop on prediction of human mobility, Chicago, IL, USA, 5 November 2019; pp. 1–10. [Google Scholar]
- Jiang, W.; Zhu, J.; Xu, J.; Li, Z.; Zhao, P.; Zhao, L. A feature based method for trajectory dataset segmentation and profiling. World Wide Web 2017, 20, 5–22. [Google Scholar] [CrossRef]
- Mohammed, N.; Fung, B.C.M.; Hung, P.C.K.; Debbabi, M. Anonymizing RFID Data: Preserving Privacy and Utility. In Privacy and Anonymity in Information Society; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2009; Volume 5479, pp. 373–389. [Google Scholar]
- Peng, T.; Liu, Q.; Wang, G.; Xiang, Y.; Chen, S. Multidimensional privacy preservation in location-based services. Future Gener. Comput. Syst. 2019, 93, 312–326. [Google Scholar] [CrossRef]
- Shaham, S.; Ding, M.; Liu, B.; Dang, S.; Lin, Z.; Li, J. Privacy preservation in location-based services: A novel metric and attack model. IEEE Trans. Mob. Comput. 2020, 20, 3006–3019. [Google Scholar] [CrossRef]
- Sun, G.; Cai, S.; Yu, H.; Maharjan, S.; Chang, V.; Du, X.; Guizani, M. Location privacy preservation for mobile users in location-based services. IEEE Access 2019, 7, 87425–87438. [Google Scholar] [CrossRef]
- Yang, X.; Gao, L.; Zheng, J.; Wei, W. Location privacy preservation mechanism for location-based service with incomplete location data. IEEE Access 2020, 8, 95843–95854. [Google Scholar] [CrossRef]
- Liao, D.; Huang, X.; Anand, V.; Sun, G.; Yu, H. k-DLCA: An efficient approach for location privacy preservation in location-based services. In Proceedings of the 2016 IEEE International Conference on Communications (ICC), Kuala Lumpur, Malaysia, 22–27 May 2016; pp. 1–6. [Google Scholar]
- Riyana, S.; Riyana, N. A privacy preservation model for rfid data-collections is highly secure and more efficient than lkc-privacy. In Proceedings of the 12th International Conference on Advances in Information Technology, Bangkok, Thailand, 29 June–1 July 2021; pp. 1–11. [Google Scholar]
- Rafiei, M.; Wagner, M.; van der Aalst, W.M. TLKC-privacy model for process mining. In Proceedings of the International Conference on Research Challenges in Information Science, Limassol, Cyprus, 12–14 May 2021; Springer: Berlin/Heidelberg, Germany, 2020; pp. 398–416. [Google Scholar]
- Liu, P.; Wu, D.; Shen, Z.; Wang, H. Trajectory privacy data publishing scheme based on local optimisation and R-tree. Connect. Sci. 2023, 35, 2203880. [Google Scholar] [CrossRef]
- Hemkumar, D.; Ravichandra, S.; Somayajulu, D. Impact of prior knowledge on privacy leakage in trajectory data publishing. Eng. Sci. Technol. Int. J. 2020, 23, 1291–1300. [Google Scholar] [CrossRef]
- Aïmeur, E.; Brassard, G.; Rioux, J. CLiKC: A privacy-mindful approach when sharing data. In Proceedings of the Risks and Security of Internet and Systems: 11th International Conference, CRiSIS 2016, Roscoff, France, 5–7 September 2016; Revised Selected Papers 11. Springer: Berlin/Heidelberg, Germany, 2017; pp. 3–10. [Google Scholar]
- Sweeney, L. Achieving k-anonymity privacy protection using generalization and suppression. Int. J. Uncertain. Fuzziness Knowl.-Based Syst. 2002, 10, 571–588. [Google Scholar] [CrossRef]
- Sweeney, L. k-anonymity: A model for protecting privacy. Int. J. Uncertain. Fuzziness -Knowl.-Based Syst. 2002, 10, 557–570. [Google Scholar] [CrossRef]
- Machanavajjhala, A.; Kifer, D.; Gehrke, J.; Venkitasubramaniam, M. l-diversity: Privacy beyond k-anonymity. ACM Trans. Knowl. Discov. Data (TKDD) 2007, 1, 3-es. [Google Scholar] [CrossRef]
- Li, N.; Li, T.; Venkatasubramanian, S. t-closeness: Privacy beyond k-anonymity and l-diversity. In Proceedings of the 2007 IEEE 23rd International Conference on Data Engineering, Istanbul, Turkey, 15 April 2006–20 April 2007; pp. 106–115. [Google Scholar]
- Wang, R.; Zhu, Y.; Chen, T.S.; Chang, C.C. Privacy-preserving algorithms for multiple sensitive attributes satisfying t-closeness. J. Comput. Sci. Technol. 2018, 33, 1231–1242. [Google Scholar] [CrossRef]
- Casas-Roma, J.; Herrera-Joancomartí, J.; Torra, V. k-Degree anonymity and edge selection: Improving data utility in large networks. Knowl. Inf. Syst. 2017, 50, 447–474. [Google Scholar] [CrossRef]
- Lu, D.; Kate, A. Rpm: Robust anonymity at scale. Proc. Priv. Enhancing Technol. 2023, 2023, 347–360. [Google Scholar] [CrossRef]
- Dorri, A.; Kanhere, S.S.; Jurdak, R.; Gauravaram, P. LSB: A Lightweight Scalable Blockchain for IoT security and anonymity. J. Parallel Distrib. Comput. 2019, 134, 180–197. [Google Scholar] [CrossRef]
- Bojja Venkatakrishnan, S.; Fanti, G.; Viswanath, P. Dandelion: Redesigning the bitcoin network for anonymity. Proc. ACM Meas. Anal. Comput. Syst. 2017, 1, 1–34. [Google Scholar] [CrossRef]
- Temuujin, O.; Ahn, J.; Im, D.H. Efficient L-diversity algorithm for preserving privacy of dynamically published datasets. IEEE Access 2019, 7, 122878–122888. [Google Scholar] [CrossRef]
- Parameshwarappa, P.; Chen, Z.; Koru, G. Anonymization of daily activity data by using l-diversity privacy model. ACM Trans. Manag. Inf. Syst. (TMIS) 2021, 12, 1–21. [Google Scholar] [CrossRef]
- Dwork, C. Differential privacy. In Proceedings of the International Colloquium on Automata, Languages, and Programming; Springer: Berlin/Heidelberg, Germany, 2006; pp. 1–12. [Google Scholar]
- Wang, B.; Li, H.; Ren, X.; Guo, Y. An Efficient Differential Privacy-Based Method for Location Privacy Protection in Location-Based Services. Sensors 2023, 23, 5219. [Google Scholar] [CrossRef]
- Yan, L.; Li, L.; Mu, X.; Wang, H.; Chen, X.; Shin, H. Differential Privacy Preservation for Location Semantics. Sensors 2023, 23, 2121. [Google Scholar] [CrossRef] [PubMed]
- Tao, Y.; Papadias, D. Maintaining sliding window skylines on data streams. IEEE Trans. Knowl. Data Eng. 2006, 18, 377–391. [Google Scholar] [CrossRef]
- Braverman, V.; Ostrovsky, R.; Zaniolo, C. Optimal sampling from sliding windows. In Proceedings of the Twenty-Eighth ACM SIGMOD-SIGACT-SIGART Symposium on Principles of Database Systems, Providence, RI, USA, 19 June 19–1 July 2009; pp. 147–156. [Google Scholar]
- Yang, L.; Shami, A. A lightweight concept drift detection and adaptation framework for IoT data streams. IEEE Internet Things Mag. 2021, 4, 96–101. [Google Scholar] [CrossRef]
- Nguyen, T.D.; Shih, M.H.; Srivastava, D.; Tirthapura, S.; Xu, B. Stratified random sampling from streaming and stored data. Distrib. Parallel Databases 2021, 39, 665–710. [Google Scholar] [CrossRef]
- Qiao, J.; Feng, G.; Yao, G.; Li, C.; Tang, Y.; Fang, B.; Zhao, T.; Hong, Z.; Jing, X. Research progress on the principle and application of multi-dimensional information encryption based on metasurface. Opt. Laser Technol. 2024, 179, 111263. [Google Scholar] [CrossRef]
- McCabe, M.C.; Lee, J.; Chowdhury, A.; Grossman, D.; Frieder, O. On the design and evaluation of a multi-dimensional approach to information retrieval. In Proceedings of the 23rd Annual International ACM SIGIR Conference on Research and Development in Information Retrieval, Athens, Greece, 24–28 July 2000; pp. 363–365. [Google Scholar]
- Guttman, A. R-trees: A dynamic index structure for spatial searching. In Proceedings of the 1984 ACM SIGMOD International Conference on Management of Data, Boston, MA, USA, 18–21 June 1984; pp. 47–57. [Google Scholar]
- Riyana, S.; Natwichai, J. Privacy preservation for recommendation databases. Serv. Oriented Comput. Appl. 2018, 12, 259–273. [Google Scholar] [CrossRef]
- Chen, R.; Fung, B.C.; Mohammed, N.; Desai, B.C.; Wang, K. Privacy-preserving trajectory data publishing by local suppression. Inf. Sci. 2013, 231, 83–97. [Google Scholar] [CrossRef]
- Jin, F.; Hua, W.; Francia, M.; Chao, P.; Orlowska, M.E.; Zhou, X. A Survey and Experimental Study on Privacy-Preserving Trajectory Data Publishing. IEEE Trans. Knowl. Data Eng. 2023, 35, 5577–5596. [Google Scholar] [CrossRef]
- Harnsamut, N.; Natwichai, J.; Riyana, S. Privacy preservation for trajectory data publishing by look-up table generalization. In Proceedings of the Australasian Database Conference. Springer International Publishing Cham, Gold Coast, QLD, Australia, 24–27 May 2018; pp. 15–27. [Google Scholar]
- Harnsamut, N.; Natwichai, J. Privacy-aware trajectory data publishing: An optimal efficient generalisation algorithm. Int. J. Grid Util. Comput. 2023, 14, 632–643. [Google Scholar] [CrossRef]



| Path | Diagnosis | |
|---|---|---|
| HIV | ||
| Food poisoning | ||
| Leukemia | ||
| Gerd | ||
| Cancer | ||
| Flu | ||
| Diabetes | ||
| Tuberculosis | ||
| Conjunctiva | ||
| Flu |
| Path | Diagnosis | |
|---|---|---|
| HIV | ||
| Food poisoning | ||
| Leukemia | ||
| Gerd | ||
| Cancer | ||
| Flu | ||
| Diabetes | ||
| Tuberculosis | ||
| Conjunctiva | ||
| Flu |
| Model | Sensitive Location Handling | Duplicate Trajectories | Unique Location Handling | Released Data Version |
|---|---|---|---|---|
| k-anonymity | × | × | × | ✓ |
| l-diversity | × | × | × | ✓ |
| t-closeness | × | × | × | ✓ |
| Differential privacy | ✓ | ✓ | × | × |
| (, )-privacy (the proposed model) | ✓ | ✓ | ✓ | ✓ |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Riyana, S.; Harnsamut, N. An Efficient and Effective Model for Preserving Privacy Data in Location-Based Graphs. Symmetry 2025, 17, 1772. https://doi.org/10.3390/sym17101772
Riyana S, Harnsamut N. An Efficient and Effective Model for Preserving Privacy Data in Location-Based Graphs. Symmetry. 2025; 17(10):1772. https://doi.org/10.3390/sym17101772
Chicago/Turabian StyleRiyana, Surapon, and Nattapon Harnsamut. 2025. "An Efficient and Effective Model for Preserving Privacy Data in Location-Based Graphs" Symmetry 17, no. 10: 1772. https://doi.org/10.3390/sym17101772
APA StyleRiyana, S., & Harnsamut, N. (2025). An Efficient and Effective Model for Preserving Privacy Data in Location-Based Graphs. Symmetry, 17(10), 1772. https://doi.org/10.3390/sym17101772






