Optimal Function Study of One-Cycle Control with Embedded Composite Function for Boost Converters

Abstract

One-cycle control (OCC) is prized in power converter applications for its rapid dynamic response and effective disturbance suppression. While its core principle relies on the symmetry of the volt-second value of the inductor in each cycle, recent research shows that embedding a composite function can significantly expand the stable parameter domain of conventional OCC. This paper seeks to identify the optimal function for this enhancement. The logarithmic and arc-tangent functions are selected based on the required characteristics and analyzed using a state-space average model. Analysis of the stability boundaries demonstrates that with $ln(u+1)$ embedded, the stability region of $u_{\mathrm{r}\mathrm{e}\mathrm{f}}$ is effectively enlarged to more than $4u_{in}$. With ${\mathit{tan}}^{-1}u$ embedded, the stability region of $u_{\mathrm{r}\mathrm{e}\mathrm{f}}$ is effectively enlarged to infinity. Therefore, embedding ${\mathit{tan}}^{-1}u$ can achieve optimal results, so it is considered the optimal function. This conclusion is conclusively validated by both simulation and experimental results.

1. Introduction

One-cycle control (OCC) offers significant advantages in power electronics, primarily due to its ability to reject input voltage disturbances and achieve exceptional dynamic response within a single switching cycle. Therefore, it plays an important role in applications such as DC-DC converters, inverters, and power factor correction [1,2,3]. Due to the high frequency action of the switch, OCC converters exhibit bifurcation and other nonlinear behaviors, similar to converters based on other control methods. These nonlinear behaviors, such as Hopf bifurcation, period-doubling bifurcation, and even chaos, can significantly impact the stability and performance of converters. Therefore, the nonlinear characteristics of converters should be thoroughly analyzed, and an effective method to control the bifurcation and chaotic phenomena needs to be explored.

Over the past few decades, along with the development of nonlinear dynamic theory and analytic procedures, the existence of different dynamic behaviors, such as Hopf bifurcation, sub-harmonic oscillation, and chaos, have been confirmed to appear in converters, and a set of control strategies has been developed to control them. In [4], a constant on-time one-cycle-controlled boost converter operating in continuous conduction mode was analyzed using the discrete-time model. It was found that Neimark–Sacker bifurcation occurs as the constant on-time value increases. Moreover, based on stability analysis, an additional current loop was developed, extending the stable region. Under certain operating and parameters conditions, it was confirmed that bifurcation and chaotic nonlinear phenomena occur in buck–boost converters [5]. Based on a time-domain mathematical model of buck converters, a discrete iterative mapping model was established, and the chaotic behaviors of the system were studied [6]. In [7], hybrid-scale bifurcation evolutionary phenomena in OCC single-inductor dual-output (SIDO) buck DC–DC converters were investigated, and the underlying mechanism of these hybrid-scale bifurcations was explained in detail. In [8], one-cycle-controlled boost converters were confirmed to lose stability via a supercritical Hopf bifurcation.

Such bifurcations and other nonlinear behaviors are usually undesirable in power converters. Since they have been detected in power converters, researchers have tried to weaken or completely suppress such bifurcations and other nonlinear behaviors in their harmful state. Generally, feedback and non-feedback control strategies are addressed. Many are widely adopted, including the OGY method (a chaos control method proposed by E. Ott, C. Grelogi, and J. A. Yorke) [9,10], occasional proportional feedback (OPF) [11], and time delay feedback (TDF) [12,13]. These feedback methods require measurement of the system variables. In [14], the bifurcation behavior of boost converters was analyzed, and a segmented pole configuration method based on feedback was proposed to suppress it. Filters are used to improve the stability of the system; however, the addition of filters increases the number of control parameters that need to be determined [8,15,16], thus increasing the computational complexity. Compared with the feedback methods, in non-feedback control methods, such as resonant parametric perturbation [17], ramp compensation [18], and weak periodic perturbation [19], no specific periodic orbit is determined and there is no need to measure system variables.

Recently, in [20], the energy balance control method (EBC) was confirmed to effectively suppress unstable behaviors, such as Hopf bifurcation, oscillation, and even chaos, and extend the stable parameter domain of the systems. Moreover, a novel OCC with an embedded composite function was proposed in [21]. By embedding composite function $\sqrt{u}$, the eigenvalue distribution of the system was optimized, thus delaying the emergence of the bifurcation point. This means that the parameter stability domain of the converter is significantly broadened. Here, the sqrt function $\sqrt{u}$ was chosen; however, various commonly used functions, such as the logarithmic function and the arc-tangent function, can also be used as the embedded composite function. It is possible that embedding these functions can obtain a wider parameter stability domain.

Based on the exploration of the required embedded function features in [21], the main contributions of this manuscript are as follows: (1) the arc-tangent function is identified as the optimal embedding function, providing the boost converter with infinite stable parameter domains; and (2) the characteristics of functions that are suitable for embedding are summarized and confirmed: they should be positive, monotonically increasing, and have a zero initial value. Based on the symmetry concept, the control method in this paper is to keep the balance of absorbing and releasing electrical energy in each cycle. This paper is organized as follows: Section 2 presents the average model of a boost converter. Section 3 introduces converters using the proposed OCC with embedded logarithmic and arc-tangent functions and analyzes their stability using average models. The nonlinear stability theoretical analysis results are confirmed through calculation, simulation, and experiments in Section 4 and Section 5. Section 6 concludes this article.

2. Average Model of the Boost Converter

This section develops the average model of a boost converter to analyze its stability using the OCC method proposed in [21], with different embedded composite functions.

The structure of a boost converter is shown in Figure 1, where u_in and U_in represent the instantaneous and average values of the input voltage; i_L and I_L represent the instantaneous and average values of the inductor current, respectively; i_c and I_c represent the instantaneous and average values of the current across the capacitor; i_o and I_o represent the instantaneous and average values of the current of the load; u and U represent the instantaneous and average values of the output voltage. According to [21], under CCM, such a boost converter is described as follows:

$$\left\{\begin{array}{c}{\displaystyle \frac{\mathrm{d}i}{\mathrm{d}t}}={\displaystyle \frac{u_{\mathrm{i}\mathrm{n}}}{L}}-{\displaystyle \frac{1-s}{L}}u\\ {\displaystyle \frac{\mathrm{d}u}{\mathrm{d}t}}=-{\displaystyle \frac{u}{RC}}+i{\displaystyle \frac{1-s}{C}}\end{array}\right.$$

(1)

where s = 1 denotes that S is in the on-state, and s = 0 denotes that S is in the off-state [21].

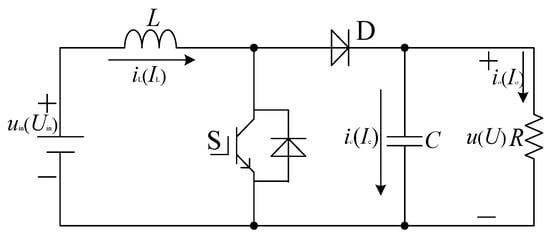
Figure 1. The structure of a boost converter.

3. Stability Analysis of the Boost Converter Using the Proposed OCC with Composite Functions $\mathit{ln}(\mathit{u}+1)$ and ${\mathit{tan}}^{-1}\mathit{u}$ Embedded

According to [21], a composite function can be embedded in the conventional OCC to change the eigenvalue locations of the system. Figure 2 shows the structure of the proposed OCC with a composite function embedded. With the embedding of a composite function, the control equation of the proposed OCC is written as follows:

$${\int }_{(n-1)T_{\mathrm{s}}}^{(n-1)T_{\mathrm{s}}+t_{\mathrm{o}\mathrm{n}}\left(n\right)}{u}_{\mathrm{r}\mathrm{e}\mathrm{f}}\phi \left(u\right)\mathrm{d}t=(u_{\mathrm{r}\mathrm{e}\mathrm{f}}-u_{\mathrm{i}\mathrm{n}})\phi \left(u_{\mathrm{r}\mathrm{e}\mathrm{f}}\right)T_{\mathrm{s}}$$

(2)

where $\mathrm{\phi }(u)={\displaystyle \frac{u}{u_{\mathrm{r}\mathrm{e}\mathrm{f}}}}$. This is a dimensionless coefficient that is positive and increases from zero. When this function is embedded, the system can converge on the same equilibrium point as the conventional OCC, as long as $\phi (u)$ is a positive and strictly increasing function. Therefore, $\phi \left(u\right)$ can be the sqrt function [21], the logarithmic function, the arc-tangent function, etc.

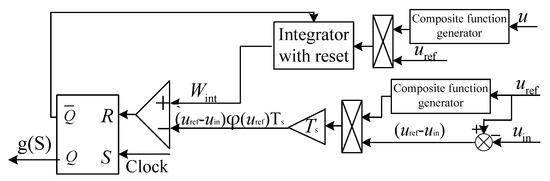
Figure 2. The structure of the boost converter using the proposed OCC with a composite function embedded.

3.1. Embedding the Logarithmic Function

Here, $\phi \left(u\right)$ is chosen as $\phi \left(u\right)=ln(u+1)$. This function is positive and increases from zero. Then, (2) is rewritten as (3):

$${\int }_{(n-1)T_{\mathrm{s}}}^{(n-1)T_{\mathrm{s}}+t_{on}\left(n\right)}{u}_{\mathrm{r}\mathrm{e}\mathrm{f}}ln(u+1)\mathrm{d}t=(u_{\mathrm{r}\mathrm{e}\mathrm{f}}-u_{in})ln(u_{\mathrm{r}\mathrm{e}\mathrm{f}}+1)T_{\mathrm{s}}$$

(3)

The average model of (3) is obtained as follows:

$$U_{\mathrm{r}\mathrm{e}\mathrm{f}}ln(U+1)D=(U_{\mathrm{r}\mathrm{e}\mathrm{f}}-U_{in})ln(U_{\mathrm{r}\mathrm{e}\mathrm{f}}+1)$$

(4)

And the duty cycle D is derived as follows:

$$D={\displaystyle \frac{(U_{\mathrm{r}\mathrm{e}\mathrm{f}}-U_{in})ln(U_{\mathrm{r}\mathrm{e}\mathrm{f}}+1)}{U_{\mathrm{r}\mathrm{e}\mathrm{f}}ln(U+1)}}$$

(5)

Replacing s in (1) with D derived in (5), the average state-space model of the boost converter using OCC with $ln(U+1)$ embedded is derived as follows:

$$\left\{\begin{array}{c}{\displaystyle \frac{\mathrm{d}I}{\mathrm{d}t}}={\displaystyle \frac{U_{\mathrm{i}\mathrm{n}}}{L}}-{\displaystyle \frac{U}{L}}[1-{\displaystyle \frac{{(U}_{\mathrm{r}\mathrm{e}\mathrm{f}}-U_{\mathrm{i}\mathrm{n}}\left)ln\right(U_{\mathrm{r}\mathrm{e}\mathrm{f}}+1)}{u_{\mathrm{r}\mathrm{e}\mathrm{f}}ln(U+1)}}]\\ {\displaystyle \frac{\mathrm{d}\mathrm{U}}{\mathrm{d}t}}=-{\displaystyle \frac{U}{RC}}+{\displaystyle \frac{I}{C}}[1-{\displaystyle \frac{{(U}_{\mathrm{r}\mathrm{e}\mathrm{f}}-U_{\mathrm{i}\mathrm{n}}\left)ln\right(U_{\mathrm{r}\mathrm{e}\mathrm{f}}+1)}{U_{\mathrm{r}\mathrm{e}\mathrm{f}}ln(U+1)}}]\end{array}\right.$$

(6)

Setting ${\displaystyle \frac{\mathrm{d}I}{\mathrm{d}t}}$ and ${\displaystyle \frac{\mathrm{d}U}{\mathrm{d}t}}$ in (6) to zero, the equilibrium point can be obtained as follows:

$$\left\{\begin{array}{c}U=U_{\mathrm{r}\mathrm{e}\mathrm{f}}\\ I={\displaystyle \frac{U_{\mathrm{r}\mathrm{e}\mathrm{f}}^2}{U_{\mathrm{i}\mathrm{n}}R}}\end{array}\right.$$

(7)

Then, the Jacobian matrix evaluated at this equilibrium point is obtained as follows:

$$J=\left(\begin{array}{cc}0& -{\displaystyle \frac{1}{L}}+{\displaystyle \frac{{(U}_{\mathrm{r}\mathrm{e}\mathrm{f}}-U_{\mathrm{i}\mathrm{n}}\left)ln\right(U_{\mathrm{r}\mathrm{e}\mathrm{f}}+1)}{L{U}_{\mathrm{r}\mathrm{e}\mathrm{f}}}}{\displaystyle \frac{\left[ln\right(U+1)-U/(U+1\left)\right]}{{\left[ln\right(U+1\left)\right]}^2}}\\ {\displaystyle \frac{1}{C}}\left[1-{\displaystyle \frac{{(U}_{\mathrm{r}\mathrm{e}\mathrm{f}}-U_{\mathrm{i}\mathrm{n}})ln{U}_{\mathrm{r}\mathrm{e}\mathrm{f}}}{U_{\mathrm{r}\mathrm{e}\mathrm{f}}lnU}}\right]& -{\displaystyle \frac{1}{RC}}+{\displaystyle \frac{I(U_{\mathrm{r}\mathrm{e}\mathrm{f}}-u_{\mathrm{i}\mathrm{n}})ln(U_{\mathrm{r}\mathrm{e}\mathrm{f}}+1)}{U_{\mathrm{r}\mathrm{e}\mathrm{f}}}}{\displaystyle \frac{1}{{(U+1)\left[ln\right(U+1\left)\right]}^2}}\end{array}\right)$$

(8)

Substituting (7) into the Jacobian matrix (8) gives

$$J=\left(\begin{array}{cc}0& -{\displaystyle \frac{1}{L}}{\displaystyle \frac{U_{\mathrm{i}\mathrm{n}}}{U_{\mathrm{r}\mathrm{e}\mathrm{f}}}}-{\displaystyle \frac{U_{\mathrm{r}\mathrm{e}\mathrm{f}}-U_{\mathrm{i}\mathrm{n}}}{L(U_{\mathrm{r}\mathrm{e}\mathrm{f}}+1)ln(U_{\mathrm{r}\mathrm{e}\mathrm{f}}+1)}}\\ {\displaystyle \frac{U_{\mathrm{i}\mathrm{n}}}{{CU}_{\mathrm{r}\mathrm{e}\mathrm{f}}}}& -{\displaystyle \frac{1}{RC}}+{\displaystyle \frac{U_{\mathrm{r}\mathrm{e}\mathrm{f}}{(U}_{\mathrm{r}\mathrm{e}\mathrm{f}}-U_{\mathrm{i}\mathrm{n}})}{\mathrm{R}\mathrm{C}{U}_{\mathrm{i}\mathrm{n}}ln(U_{\mathrm{r}\mathrm{e}\mathrm{f}}+1)(U_{\mathrm{r}\mathrm{e}\mathrm{f}}+1)}}\end{array}\right)$$

(9)

According to det [λI − J] = 0 and the second-order Padé approximation, the characteristic quasi-polynomial equation can be written as follows:

$$\mathrm{f}(\lambda )=a_2{\lambda }^2+a_1\lambda +a_0$$

(10)

where $a_2=1$, $a_1={\displaystyle \frac{1}{RC}}(1-{\displaystyle \frac{U_{\mathrm{r}\mathrm{e}\mathrm{f}}{(U}_{\mathrm{r}\mathrm{e}\mathrm{f}}-U_{\mathrm{i}\mathrm{n}})}{U_{\mathrm{i}\mathrm{n}}ln(U_{\mathrm{r}\mathrm{e}\mathrm{f}}+1)(U_{\mathrm{r}\mathrm{e}\mathrm{f}}+1)}})$, and $a_0=[{\displaystyle \frac{U_{\mathrm{i}\mathrm{n}}}{L{U}_{\mathrm{r}\mathrm{e}\mathrm{f}}}}+{\displaystyle \frac{U_{\mathrm{r}\mathrm{e}\mathrm{f}}-U_{\mathrm{i}\mathrm{n}}}{L(U_{\mathrm{r}\mathrm{e}\mathrm{f}}+1)ln(U_{\mathrm{r}\mathrm{e}\mathrm{f}}+1)}}]{\displaystyle \frac{U_{\mathrm{i}\mathrm{n}}}{{LU}_{\mathrm{r}\mathrm{e}\mathrm{f}}}}$.

From (10), it is obvious that $a_2>0$. Since in a boost converter, $U_{\mathrm{r}\mathrm{e}\mathrm{f}}>U_{\mathrm{i}\mathrm{n}}$ always holds, and since $U_{\mathrm{r}\mathrm{e}\mathrm{f}}+1\ge 1$, $ln(U_{\mathrm{r}\mathrm{e}\mathrm{f}}+1)\ge 0$ is obtained, then $a_0>0$ is established. Therefore, if $a_1>0$ is obtained, the stability condition of the OCC with $ln(u+1)$ embedded can be obtained.

To obtain the condition of $a_1>0$, let f1($U_{\mathrm{r}\mathrm{e}\mathrm{f}}$) = $U_{\mathrm{r}\mathrm{e}\mathrm{f}}{(U}_{\mathrm{r}\mathrm{e}\mathrm{f}}-5)$ and f2($U_{\mathrm{r}\mathrm{e}\mathrm{f}}$) = $5ln(U_{\mathrm{r}\mathrm{e}\mathrm{f}}+1)(U_{\mathrm{r}\mathrm{e}\mathrm{f}}+1)$. The values of f1 and f2 were plotted against $U_{\mathrm{r}\mathrm{e}\mathrm{f}}$ changes for comparison, and the results are shown in Figure 3. As illustrated, both f1($U_{\mathrm{r}\mathrm{e}\mathrm{f}}$) and f2($U_{\mathrm{r}\mathrm{e}\mathrm{f}}$) exhibit monotonically increasing behavior, intersecting at $U_{\mathrm{r}\mathrm{e}\mathrm{f}}$ = 21, which is their sole intersection point. This means that when $U_{\mathrm{r}\mathrm{e}\mathrm{f}}$ < 21, f1($U_{\mathrm{r}\mathrm{e}\mathrm{f}}$) < f2($U_{\mathrm{r}\mathrm{e}\mathrm{f}}$); otherwise, f1($U_{\mathrm{r}\mathrm{e}\mathrm{f}}$) > f2($U_{\mathrm{r}\mathrm{e}\mathrm{f}}$).

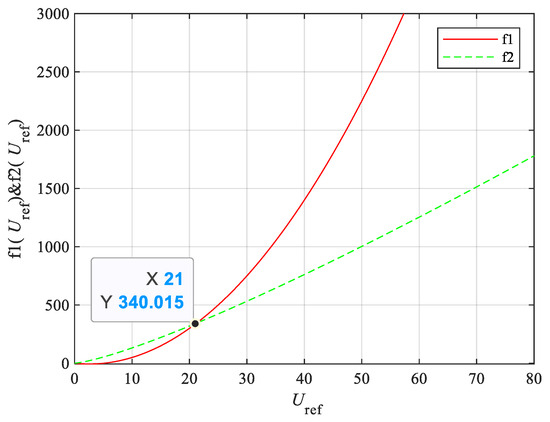
Figure 3. Diagram of bifurcation points of the boost converter using the proposed OCC with composite function $ln(u+1)$ embedded.

According to the figure and analysis, with the parameters in Table 1, if $U_{\mathrm{r}\mathrm{e}\mathrm{f}}<21$ is satisfied, which is more than 4$U_{\mathrm{i}\mathrm{n}}$, then $a_1>0$ is obtained. Compared with the conventional OCC (2$U_{\mathrm{i}\mathrm{n}}$) and the OCC with $\sqrt{u}$ embedded (3$U_{\mathrm{i}\mathrm{n}}$), it can be seen that embedding $ln(u+1)$ extends the stable parameter domain further.

Table 1. The circuit parameters of the boost converter.

Parameter	uin	L	C	R	fs
Value	5 V	3000 µH	460 µF	30 Ω	5000 Hz

3.2. Embedding the Arc-Tangent Function

Here, φ(u) is chosen as $\mathrm{\phi }\left(u\right)={\mathit{tan}}^{-1}u$. Then, (2) is rewritten as (11):

$${\int }_{(n-1)T_{\mathrm{s}}}^{(n-1)T_{\mathrm{s}}+t_{\mathrm{o}\mathrm{n}}\left(n\right)}{u}_{\mathrm{r}\mathrm{e}\mathrm{f}}{\mathit{tan}}^{-1}u\mathrm{d}t=(u_{\mathrm{r}\mathrm{e}\mathrm{f}}-u_{\mathrm{i}\mathrm{n}}){\mathit{tan}}^{-1}{u}_{\mathrm{r}\mathrm{e}\mathrm{f}}{T}_{\mathrm{s}}$$

(11)

Then, the average model of (11) is obtained as follows:

$$U_{\mathrm{r}\mathrm{e}\mathrm{f}}{\mathit{tan}}^{-1}UD=(U_{\mathrm{r}\mathrm{e}\mathrm{f}}-U_{\mathrm{i}\mathrm{n}}){\mathit{tan}}^{-1}{U}_{\mathrm{r}\mathrm{e}\mathrm{f}}$$

(12)

D is derived as follows:

$$D={\displaystyle \frac{\left(U_{\mathrm{r}\mathrm{e}\mathrm{f}}U{u}_{\mathrm{i}\mathrm{n}}\right){\mathit{tan}}^{-1}{U}_{\mathrm{r}\mathrm{e}\mathrm{f}}}{U_{\mathrm{r}\mathrm{e}\mathrm{f}}{\mathit{tan}}^{-1}U}}$$

(13)

Replacing s in (1) with D derived in (13), the average state-space model of the boost converter using OCC with ${\tan }^{-1}\mathrm{u}$ embedded is derived as follows:

$$\left\{\begin{array}{c}{\displaystyle \frac{\mathrm{d}I}{\mathrm{d}t}}={\displaystyle \frac{U_{\mathrm{i}\mathrm{n}}}{L}}-{\displaystyle \frac{U}{L}}[1-{\displaystyle \frac{(U_{\mathrm{r}\mathrm{e}\mathrm{f}}-U_{\mathrm{i}\mathrm{n}}){\mathit{tan}}^{-1}{U}_{\mathrm{r}\mathrm{e}\mathrm{f}}}{U_{\mathrm{r}\mathrm{e}\mathrm{f}}{\tan }^{-1}U}}]\\ {\displaystyle \frac{\mathrm{d}U}{\mathrm{d}t}}=-{\displaystyle \frac{U}{RC}}+{\displaystyle \frac{I}{C}}[1-{\displaystyle \frac{(U_{\mathrm{r}\mathrm{e}\mathrm{f}}-{\mathrm{U}}_{\mathrm{i}\mathrm{n}}){\mathit{tan}}^{-1}{U}_{\mathrm{r}\mathrm{e}\mathrm{f}}}{U_{\mathrm{r}\mathrm{e}\mathrm{f}}{\mathit{tan}}^{-1}U}}]\end{array}\right.$$

(14)

Setting ${\displaystyle \frac{\mathrm{d}I}{\mathrm{d}t}}$ and ${\displaystyle \frac{\mathrm{d}U}{\mathrm{d}t}}$ in (14) as zero, the equilibrium point can be obtained as follows:

$$\left\{\begin{array}{c}U=U_{\mathrm{r}\mathrm{e}\mathrm{f}}\\ I={\displaystyle \frac{U_{\mathrm{r}\mathrm{e}\mathrm{f}}^2}{U_{\mathrm{i}\mathrm{n}}R}}\end{array}\right.$$

(15)

Then, the Jacobian matrix evaluated at this equilibrium point is obtained as follows:

$$J=\left(\begin{array}{cc}0& -{\displaystyle \frac{1}{L}}+{\displaystyle \frac{{(U}_{\mathrm{r}\mathrm{e}\mathrm{f}}-U_{\mathrm{i}\mathrm{n}}){\mathit{tan}}^{-1}{U}_{\mathrm{r}\mathrm{e}\mathrm{f}}}{L{U}_{\mathrm{r}\mathrm{e}\mathrm{f}}}}\left[{\displaystyle \frac{({\mathit{tan}}^{-1}U-\frac{U}{1+U^2})}{{\left({\mathit{tan}}^{-1}U\right)}^2}}\right]\\ {\displaystyle \frac{1}{C}}\left[1-{\displaystyle \frac{{(U}_{\mathrm{r}\mathrm{e}\mathrm{f}}-U_{\mathrm{i}\mathrm{n}}){\mathit{tan}}^{-1}{U}_{\mathrm{r}\mathrm{e}\mathrm{f}}}{U_{\mathrm{r}\mathrm{e}\mathrm{f}}{\mathit{tan}}^{-1}U}}\right]& -{\displaystyle \frac{1}{RC}}+{\displaystyle \frac{I(U_{\mathrm{r}\mathrm{e}\mathrm{f}}-U_{\mathrm{i}\mathrm{n}}){\mathit{tan}}^{-1}{U}_{\mathrm{r}\mathrm{e}\mathrm{f}}}{C{U}_{\mathrm{r}\mathrm{e}\mathrm{f}}}}{\displaystyle \frac{1}{{(1+U^2)\left({\mathit{tan}}^{-1}U\right)}^2}}\end{array}\right)$$

(16)

Substituting (15) into the Jacobian matrix (16) gives

$$J=\left(\begin{array}{cc}0& -{\displaystyle \frac{1}{L}}{\displaystyle \frac{U_{\mathrm{i}\mathrm{n}}}{U_{\mathrm{r}\mathrm{e}\mathrm{f}}}}-{\displaystyle \frac{U_{\mathrm{r}\mathrm{e}\mathrm{f}}-U_{\mathrm{i}\mathrm{n}}}{L{\mathit{tan}}^{-1}{U}_{\mathrm{r}\mathrm{e}\mathrm{f}}(1+{U_{\mathrm{r}\mathrm{e}\mathrm{f}}}^2)}}\\ {\displaystyle \frac{U_{\mathrm{i}\mathrm{n}}}{{CU}_{\mathrm{r}\mathrm{e}\mathrm{f}}}}& -{\displaystyle \frac{1}{RC}}+{\displaystyle \frac{U_{\mathrm{r}\mathrm{e}\mathrm{f}}(U_{\mathrm{r}\mathrm{e}\mathrm{f}}-U_{\mathrm{i}\mathrm{n}})}{RC{U}_{\mathrm{i}\mathrm{n}}{\mathit{tan}}^{-1}{U}_{\mathrm{r}\mathrm{e}\mathrm{f}}(1+{U_{\mathrm{r}\mathrm{e}\mathrm{f}}}^2)}}\end{array}\right)$$

(17)

According to det [λI − J] = 0 and the second-order Padé approximation, the characteristic quasi-polynomial equation can be written as follows:

$$\mathrm{f}(\lambda ) = a_2{\lambda }^2+a_1\lambda +a_0$$

(18)

where $a_2=1,a_1={\displaystyle \frac{1}{RC}}(1-{\displaystyle \frac{U_{\mathrm{r}\mathrm{e}\mathrm{f}}(U_{\mathrm{r}\mathrm{e}\mathrm{f}}-U_{\mathrm{i}\mathrm{n}})}{U_{\mathrm{i}\mathrm{n}}{\mathit{tan}}^{-1}{U}_{\mathrm{r}\mathrm{e}\mathrm{f}}(1+{U_{\mathrm{r}\mathrm{e}\mathrm{f}}}^2)}}),$ $a_0=[{\displaystyle \frac{U_{\mathrm{i}\mathrm{n}}}{L{U}_{\mathrm{r}\mathrm{e}\mathrm{f}}}}+{\displaystyle \frac{(U_{\mathrm{r}\mathrm{e}\mathrm{f}}-U_{in})}{L{\mathit{tan}}^{-1}{U}_{\mathrm{r}\mathrm{e}\mathrm{f}}(1+{U_{\mathrm{r}\mathrm{e}\mathrm{f}}}^2)}}]{\displaystyle \frac{U_{\mathrm{i}\mathrm{n}}}{{LU}_{\mathrm{r}\mathrm{e}\mathrm{f}}}}$.

From (18), it is obvious that ${ a}_2=1>0$. Since in a boost converter, $U_{\mathrm{r}\mathrm{e}\mathrm{f}}>U_{in}$ always holds, and when $U_{\mathrm{r}\mathrm{e}\mathrm{f}}$ > 0, ${\mathit{tan}}^{-1}{U}_{\mathrm{r}\mathrm{e}\mathrm{f}}$ > 0 can be obtained, then $a_0>0$ is established. Therefore, if $a_1>0$ is obtained, the stability condition of OCC with the arc-tangent function embedded can be obtained. Again, the graph method was used to determine the condition $a_1>0$.

From $a_1={\displaystyle \frac{1}{RC}}(1-{\displaystyle \frac{U_{\mathrm{r}\mathrm{e}\mathrm{f}}(U_{\mathrm{r}\mathrm{e}\mathrm{f}}-U_{\mathrm{i}\mathrm{n}})}{U_{\mathrm{i}\mathrm{n}}{\mathit{tan}}^{-1}{U}_{\mathrm{r}\mathrm{e}\mathrm{f}}(1+{U_{\mathrm{r}\mathrm{e}\mathrm{f}}}^2)}})$, it can be seen that as long as $U_{\mathrm{r}\mathrm{e}\mathrm{f}}(U_{\mathrm{r}\mathrm{e}\mathrm{f}}-5)$ is smaller than (5${\mathit{tan}}^{-1}{U}_{\mathrm{r}\mathrm{e}\mathrm{f}}$)$(1+{U_{\mathrm{r}\mathrm{e}\mathrm{f}}}^2)$, $a_1>0$ will be guaranteed. Let ${\mathrm{f}1\left(U_{\mathrm{r}\mathrm{e}\mathrm{f}}\right)=U}_{\mathrm{r}\mathrm{e}\mathrm{f}}(U_{\mathrm{r}\mathrm{e}\mathrm{f}}-5)$ and $\mathrm{f}2\left(U_{\mathrm{r}\mathrm{e}\mathrm{f}}\right)=\left(5{\tan }^{-1}{U}_{\mathrm{r}\mathrm{e}\mathrm{f}}\right)(1+{U_{\mathrm{r}\mathrm{e}\mathrm{f}}}^2)$. The values of f1 and f2 were plotted against $U_{\mathrm{r}\mathrm{e}\mathrm{f}}$ changes for comparison, and the results are shown in Figure 4. As illustrated, both f1($U_{\mathrm{r}\mathrm{e}\mathrm{f}}$) and f2($U_{\mathrm{r}\mathrm{e}\mathrm{f}}$) exhibited monotonically increasing behavior, with no intersecting points. This means that, regardless of parameter changes, the stability condition of OCC with ${\mathit{tan}}^{-1}u$ embedded is always met, demonstrating an infinite stable parameter domain.

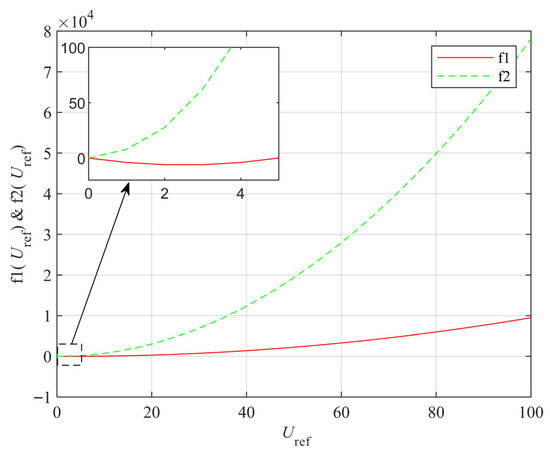
Figure 4. Diagram of bifurcation points of the boost converter using the proposed OCC with embedded composite function ${\mathit{tan}}^{-1}u$.

According to the figure and analysis, with the parameters in Table 1, compared with the conventional OCC (2$U_{\mathrm{i}\mathrm{n}}$) and the OCC with $\sqrt{u}$ embedded (3$U_{\mathrm{i}\mathrm{n}}$), it can be seen that embedding ${\mathit{tan}}^{-1}u$ infinitely extends the stable parameter domain.

4. Calculation Verification

Taking $u_{\mathrm{r}\mathrm{e}\mathrm{f}}$ as the variable parameter to verify the results of the above theoretical analysis, bifurcation diagrams of the proposed OCC with different composite functions embedded are shown in Figure 5. Figure 5a,b show the bifurcation diagrams of the conventional OCC and the proposed OCC with composite function $\sqrt{u}$ embedded [21]. The results show that with $\sqrt{u}$ embedded, the instability point is delayed from 10 V to about 15 V.

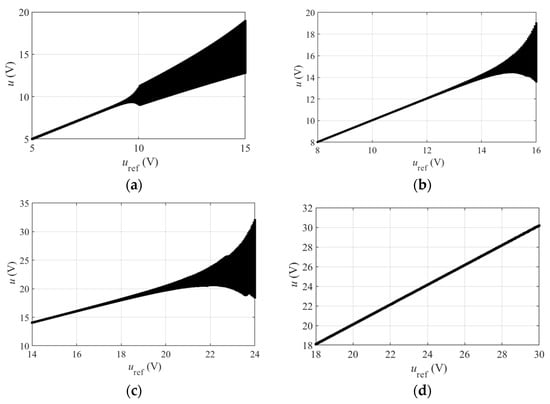
Figure 5. The bifurcation diagram of the boost converter: (a) conventional OCC [21]; (b) proposed OCC with composite function $\sqrt{u}$ embedded [21]; (c) proposed OCC with composite function $ln(u+1)$ embedded; (d) proposed OCC with composite function ${\mathit{tan}}^{-1}u$ embedded.

Figure 5c shows the bifurcation diagram of the proposed OCC with $ln(u+1)$ embedded. It can be seen that as $u_{\mathrm{r}\mathrm{e}\mathrm{f}}$ varies from 10 to 30 V, the bifurcation diagram of the proposed OCC with $ln(u+1)$ embedded loses its stability when $u_{\mathrm{r}\mathrm{e}\mathrm{f}}$ increases to about 21 V. Figure 5d shows the bifurcation diagram of the proposed OCC with ${\mathit{tan}}^{-1}u$ embedded. It can be seen that even when $u_{\mathrm{r}\mathrm{e}\mathrm{f}}$ increases to 30 V, the boost converter using the proposed OCC with ${\tan }^{-1}\mathrm{u}$ embedded remains stable throughout. The results show that compared with $\sqrt{u}$, with $ln(u+1)$ and ${\mathit{tan}}^{-1}u$ embedded, the boost converter with an embedded composite function has a wider parameter stability domain. Moreover, the results show that ${\mathit{tan}}^{-1}u$ is the optimal embedding function for OCC boost converters.

The calculation results indicate that different embedding functions improve the stability of the system in different ways. The comparison results are listed in Table 2, showing that embedding ${\mathit{tan}}^{-1}u$ can achieve the optimal results, so it can be considered the optimal function.

Table 2. Comparison results.

Embedded Function	$\mathit{u}/{\mathit{u}}_{\mathbf{r}\mathbf{e}\mathbf{f}}$	$\sqrt{\mathit{u}}$	$\mathit{l}\mathit{n}(\mathit{u}+1)$	${\mathit{tan}}^{-1}\mathit{u}$
Value of unstable point	10 V	15 V	21 V	∞

5. Simulation and Experimental Verification

According to the circuit parameters listed in Table 1, the stability of the boost converter was tested through simulations and experiments under varying $u_{\mathrm{r}\mathrm{e}\mathrm{f}}$. The simulation results are shown in Figure 6 and Figure 7. Figure 8 displays the experimental setup, and the experimental results are shown in Figure 9 and Figure 10.

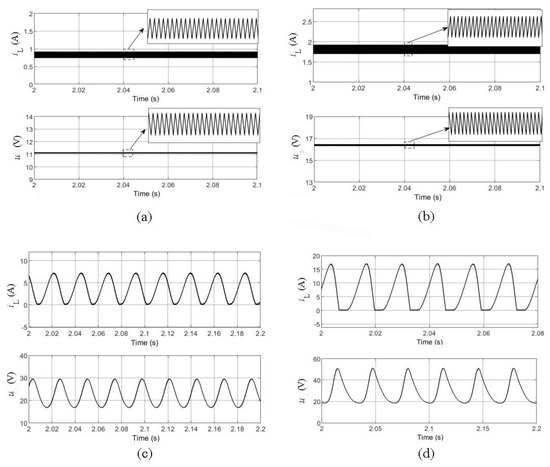
Figure 6. Simulation results of the proposed OCC with $ln(u+1)$ embedded. (a) u_ref = 11 V; (b) u_ref = 16 V; (c) u_ref = 22 V; (d) u_ref = 28 V.

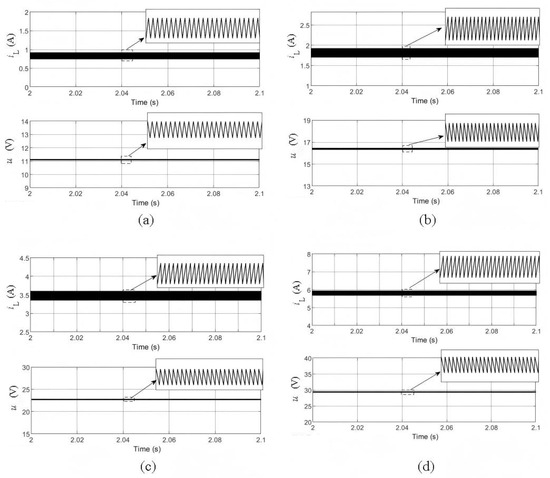
Figure 7. Simulation results of the OCC with composite function ${\mathit{tan}}^{-1}u$ embedded. (a) u_ref = 11 V; (b) u_ref = 16 V; (c) u_ref = 22 V; (d) u_ref = 28 V.

Figure 8. Experimental setup.

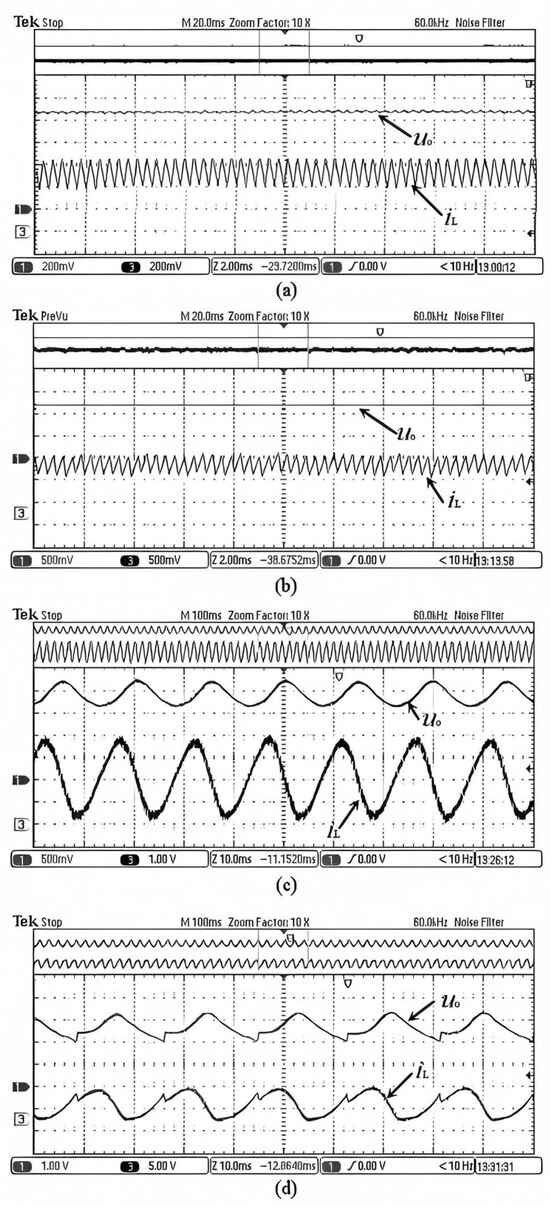
Figure 9. Experimental results of the proposed OCC with composite function $ln(u+1)$ embedded (Channel 1 is the value of $u_{\mathrm{o}1}$; Channel 3 is the value of $u_{\mathrm{s}}$). (a) u_ref = 11 V; (b) u_ref = 16 V; (c) u_ref = 22 V; (d) u_ref = 28 V.

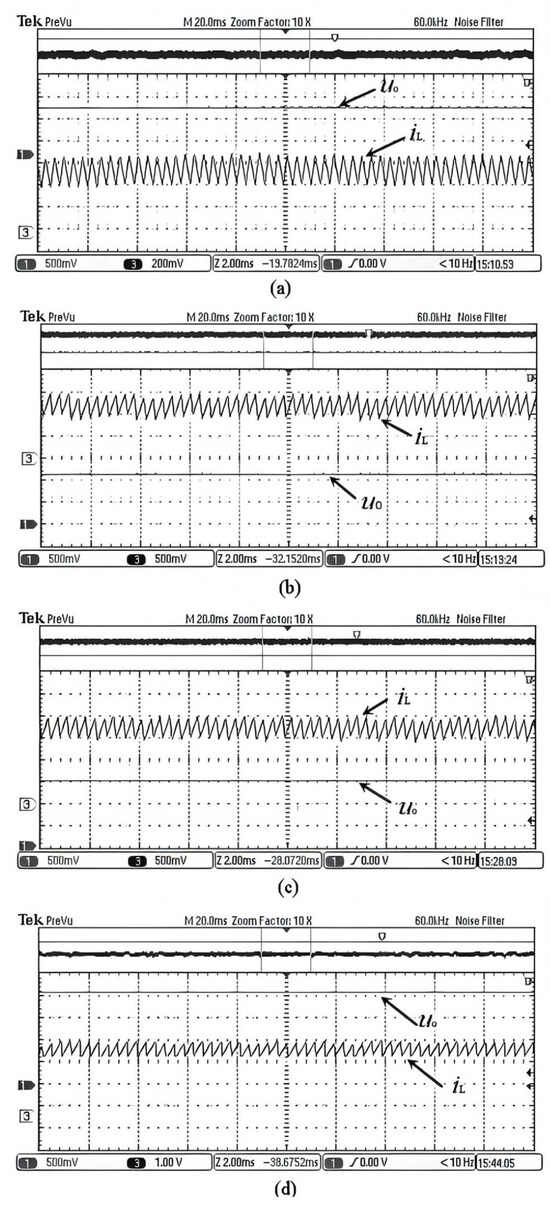
Figure 10. Experimental results of the proposed OCC with composite function ${\mathit{tan}}^{-1}u$ embedded. (Channel 1 is the value of $u_{\mathrm{o}1}$; Channel 3 is the value of $u_{\mathrm{s}}$). (a) u_ref = 11 V; (b) u_ref = 16 V; (c) u_ref = 22 V; (d) u_ref = 28 V.

5.1. Simulation Results

Figure 6 displays the results of the boost converter with the proposed OCC with $ln(u+1)$ embedded. From the results, it can be seen that under $u_{ref}=$ 11 V and $u_{ref}=$ 16 V, the boost converter can operate stably with this control method, and no bifurcation or other nonlinear phenomena occurs. However, when $u_{ref}$ increases to 22 V, bifurcation occurs (Figure 6c), which means that the system using the proposed OCC with $ln(u+1)$ embedded loses its stability. Figure 6d shows that when $u_{ref}$ continues increasing to 28 V, the bifurcation becomes increasingly severe.

Figure 7 displays the simulation results of the boost converter using the proposed OCC with ${\mathit{tan}}^{-1}u$ embedded. The results show that under $u_{ref}=$ 11 V, $u_{ref}=$ 16 V, $u_{ref}=$ 22 V, and even $u_{ref}=$ 28 V, the boost converter can maintain stable operation without any bifurcation or other nonlinear phenomena, as shown in Figure 7. The results show that the simulation results are consistent with the calculation results.

5.2. Experimental Results

Figure 8 shows the experimental prototype and control platform. As in [21], the MOSFET IRF640N switch and the BYW29-200 fast recovery diode were used in the experimental prototype. Control was implemented using the STM32H7 microcontroller.

In the experimental prototype, a sampling resistor R_s = 0.5 Ω was used to measure the inductor current i_L. The resulting voltage u_s across R_s was monitored using an oscilloscope, which was then processed and sent to the controller to restore it to i_L. The output voltage uₒ was regulated using a voltage divider consisting of two series resistors: R₁ = 30 Ω and R₂ = 370 Ω. The voltage u_o1 across R₁ was measured using the oscilloscope, which was then processed and sent to the controller to restore it to u. The relationships between u_s and i_L and between u_o1 and u are as follows:

$${\displaystyle \frac{u_{\mathrm{s}}}{i_{\mathrm{L}}}}=R_{\mathrm{s}}=0.5$$

(19)

$${\displaystyle \frac{u_{\mathrm{o}1}}{u}}={\displaystyle \frac{R_1}{R_1+R_2}}={\displaystyle \frac{30}{400}}={\displaystyle \frac{3}{40}}$$

(20)

Figure 9 and Figure 10 display the experimental results. The results illustrate that the experimental results are consistent with the simulation results. By using the proposed OCC with embedded composite function $ln(u+1)$, the system maintains stable operation under $u_{\mathrm{r}\mathrm{e}\mathrm{f}}=$ 11 V and $u_{\mathrm{r}\mathrm{e}\mathrm{f}}=$ 16 V, and no bifurcation or other nonlinear phenomena occur. However, under $u_{\mathrm{r}\mathrm{e}\mathrm{f}}$= 22 V, the system loses stability, and bifurcation occurs (Figure 9c). The bifurcation becomes more severe when $u_{\mathrm{r}\mathrm{e}\mathrm{f}}$ continues to increase, as shown in Figure 9d. As shown in Figure 10, by embedding ${\mathit{tan}}^{-1}u$, the boost converter can work stably under $u_{\mathrm{r}\mathrm{e}\mathrm{f}}=$ 11 V, $u_{\mathrm{r}\mathrm{e}\mathrm{f}}=$ 16 V, $u_{\mathrm{r}\mathrm{e}\mathrm{f}}=$ 22 V, and even $u_{\mathrm{r}\mathrm{e}\mathrm{f}}=$ 28 V.

Thus, the simulation and experimental results are mostly in agreement with the presented theories, demonstrating that different embedding functions can improve the stability of the system in different ways. Among them, embedding ${\mathit{tan}}^{-1}u$ achieves optimal results, so it can be considered the optimal function.

6. Conclusions

Building upon the foundational work of [21], this study investigates selected embedding functions, specifically the logarithmic and arc-tangent functions, for enhancing the stability of one-cycle-controlled converters. Through state-space averaging and Jacobian matrix analysis, the stability boundaries and parameter domains were determined. Simulations and experiments consistently validated these theoretical findings. First, during the research process, it was found that for logarithmic functions, ln(u+1) rather than lnu should be used as the embedding function to broaden the parameter stability domain. The results further clarify that the embedding function should be a positive, monotonic function that starts at zero. The analytic results indicate that the stability region of u_ref is enlarged to more than $4u_{\mathrm{i}\mathrm{n}}$ when $ln(u+1)$ is embedded and the stability region of u_ref is enlarged to infinity with ${\mathit{tan}}^{-1}u$. This means that embedding ${\mathit{tan}}^{-1}u$ results in no bifurcation or other nonlinear phenomena as parameters vary. Therefore, the arc-tangent function is the optimal function, providing the boost converter with an infinite stable parameter domain.

While the arc-tangent function is identified as the optimal choice, it is likely not unique. Therefore, future work will focus on generalizing the essential characteristics that define an optimal embedding function to guide the selection of other potential candidates. Furthermore, a comprehensive evaluation of the boost converter’s efficiency under different load conditions will be conducted to further validate the practical efficacy of the proposed method.