1. Introduction
The M/G/1 queue model is widely applied across various fields due to its straightforward solution methodology. The M/G/1 model represents a system in which arrivals follow a Markovian (Poisson) process with parameter
, and the service time follows a non-exponential probability distribution. The exact solution of the M/G/1 model was first developed by Pollaczek–Khinchine (P-K). To derive performance metrics, the service-time distribution must conform to a theoretical distribution and its variance must be known [
1]. However, when distribution-fitting tests are performed on heterogeneous datasets, it is often observed that these data do not conform to any theoretical distribution. In such cases, rather than directly using an empirical distribution, it can be tested whether the dataset fits a mixture distribution.
Mixture distributions are often applied to represent heterogeneous populations composed of multiple hidden but internally homogeneous subgroups [
2]. Such models, also referred to as latent class models or as forms of unsupervised learning, have seen increasing use in recent years across numerous fields. A batch process monitoring approach based on Gaussian mixture models was introduced, outperforming conventional methods in fault detection [
3]. The connection between theoretical advances in mixture modeling and practical applications in medical and health sciences has been demonstrated through extensive real-world examples [
4]. A new claim number distribution was introduced by mixing a negative binomial distribution with a Gamma distribution, and its performance was evaluated [
5]. Wiper et al. [
6] also applied mixture models through a Bayesian density estimation approach to the M/G/1 queueing model. Bosch-Domènech et al. [
7] introduced a mixture model based on the Beta distribution to analyze Beauty-Contest data, providing better fit and more precise insights into common reasoning patterns than Gaussian-based mixture models. Finite mixture models (FMMs) were applied for Danish fire insurance losses, and Gamma mixture density networks have been applied to motor insurance claim dataset, improving both risk assessment and the prediction of claim severities [
8,
9]. FMMs combining Gamma, Weibull, and Lognormal distributions have been applied to model the length of hospital stay within diagnosis-related groups, addressing skewness and improving estimation [
10]. Gaussian mixture modeling, combined with manifold learning and data augmentation, has been applied to predict the flow of water in coal mines, significantly improving predictive precision, interpretability and applicability under complex geological conditions [
11]. Time-course gene expression analysis was conducted by Hefemeister et al. [
12] to identify co-expressed genes, predict treatment responses, and classify novel toxic compounds.
Mixture models have been widely studied for their ability to handle heterogeneous data, particularly in large datasets essential for scientific and practical applications [
13]. Mixture distributions consist of two or more component distributions. If all distributions belong to the same distribution family but have different parameter sets, they are called pure mixture distributions. If at least one of them is different from the others, they are referred to as convoluted mixture distributions. In convoluted mixture distributions, the calculations are somewhat more complex. Therefore, pure mixture distributions are more commonly used in practice. Among pure mixture distributions, the Gaussian mixture distribution is the most widely used in the literature, as it is formed by combining several Gaussian distributions with distinct parameters. A key property of the Gaussian distribution is its symmetry. Symmetry plays a fundamental role in statistical theory, since in symmetric distributions the sample mean and variance are uncorrelated. The Gaussian mixture distribution comprises multiple component distributions, each of which is symmetric.
Estimation of mixture distribution parameters represents a critical methodological challenge with wide-ranging applications in statistics, machine learning, and data analysis [
14]. Several methods exist for estimating the parameters of a mixture distribution, each with its advantages and limitations. Rao [
15] was the first to introduce the Maximum Likelihood Estimation (MLE) approach to the problem of normal mixtures, proposing an iterative solution for the case of two components with equal standard deviations using Fisher’s scoring method. This approach was extended to more complex cases with more than two components and unequal variances [
16,
17]. The use of MLE was generalized to mixtures of multivariate normal distributions and the first computer program enabling their routine application was developed [
18,
19]. Wolfe’s method for solving MLEs is an early example of the EM (Expectation Maximization) algorithm, which was later generalized by Dempster [
20]. Bermudez et al. [
21] introduced finite mixtures of multiple Poisson and multiple negative binomial models, estimating them through the EM algorithm on an empirical dataset. The results indicated that the finite mixture of multiple Poisson models fit the data better in terms of EM parameters than the negative binomial model for the dataset concerning the number of days of work disability resulting from motor vehicle accidents. Several researchers have also applied Bayesian analysis for mixture models. Diebolt et al. [
22] described the Bayes estimators with Gibbs sampling and compared them with MLE results. Roberts and Rezek [
23] presented a Bayesian approach for parameter estimation of a Gaussian mixture model, while Tsionas [
24] and Bouguila et al. [
25] applied it to the Gamma mixture model and the Beta mixture model, respectively.
Although Gaussian-based finite mixtures have traditionally dominated discussions and applications, various other mixture distributions have found practical use in specific domains. In cases of failure or survival, the observed times may fit mixture distributions due to the presence of multiple causes [
26]. The components of these mixtures may consist of distributions such as the negative exponential, Weibull, and others. Elmahdy and Aboutahoun [
27] employed finite mixtures of Weibull distributions to simulate lifetime data for systems with failure modes. This involves estimating the unknown parameters, which constitutes crucial statistical work, particularly for reliability analysis and life testing. Instead of representing the length of hospital stay (LOS) with a single distribution, Ickowicz and Sparks [
28] modeled it using convolutive mixture distributions and employed MLE and EM for parameter estimation.
In addition to parameter estimation, evaluating how well the system reacts to changes in its parameters provides a means of assessing the reliability of the approximation methods in M/G/1 mixture models. Among the most notable contributions to the adaptation of mixture distributions to M/G/1 systems is the study by Mohammadi and Salahi [
29]. Their work considers the case where a certain proportion of customers require re-service, assuming that both the initial service time and the re-service time follow a truncated normal mixture distribution. Based on this assumption, they derived closed-form expressions for the system parameters within a Bayesian framework. In a subsequent study, the same authors extended their analysis to the case where the initial service time and the re-service times of customers follow a Gamma mixture distribution, once again deriving the corresponding system parameters using a Bayesian approach [
30].
The main distinction of this study from the aforementioned works lies in the estimation of system parameters for an M/G/1 queueing model where customers receive service only once, and the service-time distribution follows
k-component Gaussian, Gamma, or Beta mixture distributions. A major contribution of this study is the derivation of lower- and upper-bound formulations for the mean waiting time in the queue, separately for each of the three systems under consideration. When the service-time distribution consists of pure (non-mixture) distributions, the determination of the upper bound of the mean waiting time in an M/G/1 system was first introduced by Marchal [
31]. In Marchal’s study, it was demonstrated that the upper bound of the mean waiting time in the queue is equal to the exact solution obtained from the P-K formula for the same parameter. In this study, the analysis of the lower and upper bound formulations for the mean waiting time—derived and presented in detail in the subsequent sections—shows that, for all three mixture distributions considered, both the simulation results and the derived formulations for the mean waiting time closely approximate the upper bound. This consistency provides strong evidence supporting the validity of the proposed formulations and constitutes one of the key contributions of this work.
In the M/G/c system, when the service-time distribution consists of pure distributions, no exact solution for the system parameters has yet been established. However, several studies have proposed approximate solutions [
32,
33,
34]. Morozov et al. [
35] conducted a sensitivity analysis of the system parameters in an M/G/c model with a two-component Pareto mixture service-time distribution, employing the regenerative perfect simulation method. Since the M/G/c system does not have an exact solution, they evaluated approximate solutions with simulation. In this study, an approximate solution is proposed for the M/G/1 model when the service-time distribution consists of a pure mixture distribution. The rationale for deriving the approximate formula is based on the ability to compute the variance of certain pure mixture distributions. By substituting this variance into the P-K equation, we obtain an approximate formula for the M/G/1 queue. The approximate formula has been adapted for service-time distributions consisting of two components, including the Gamma, Gaussian, and Beta mixture distributions. To measure the effectiveness of the proposed approximate formula, an M/G/1 system was simulated using random numbers generated from mixture distributions. The results indicate that the proposed approximate formula yields outcomes very close to those of the simulation, particularly for Gaussian mixture distributions.
The remainder of this paper is organized as follows.
Section 2 introduces mixture distributions and describes both exact and approximate solution approaches. In
Section 3, the approximate formulas for M/G/1 queueing models with mixture distributions are presented.
Section 4 outlines the experimental design framework used to analyze different model parameters.
Section 5 reports the numerical results along with performance graphs. Finally,
Section 6 concludes the paper.
2. Mixture Distributions
In recent years, the growing prevalence of heterogeneous datasets in real-life applications has necessitated the use of efficient data modeling techniques to uncover the valuable information they contain. Within this framework, finite mixture distributions have emerged as prominent statistical tools, grounded in solid theoretical foundations, for modeling complex data structures, identifying latent subpopulations, and revealing hidden patterns within the data. A mixture distribution is a probability distribution typically expressed as a convex linear combination of probability density functions (PDFs).
The PDF of a finite mixture distribution can be defined as a weighted combination of
k component distributions as in Equation (
1).
where the mixing proportions satisfy
Here, denotes the PDF of the j-th component distribution with parameter vector (e.g., mean and variance in the case of a Gaussian distribution). The full parameter set of the mixture model is denoted by for , where is the mixing proportion of the j-th component.
2.1. Parameter Estimation
In the analysis of FMMs, various methodologies are employed to estimate the parameters of the mixture distribution and to determine the optimal number of components. The most common approaches include the method of moments, minimum distance methods, MLE, and Bayesian techniques. Among these alternatives, MLE has gained particular prominence due to its broad applicability.
2.1.1. Maximum Likelihood Estimation
Given a random sample of observations
generated from the mixture distribution in Equation (
1), the likelihood function of a FMM with
k components is given in Equation (
3).
denotes the likelihood of the observed data given the set of parameters . Here, denotes the mixing proportion of the j-th component, and is the PDF of the i-th observation under the j-th component with parameter . The likelihood is computed as the product over all observations of the sum of the weighted component densities.
In Equation (
4),
refers to the log-likelihood function associated with the sample data, obtained by applying the logarithm to the summation of weighted probability densities for all observations. Such a transformation is beneficial, as it changes the product form in the likelihood expression into an additive form, thereby simplifying the mathematical formulation, particularly in the maximization step for estimating the parameter
.
The likelihood and log-likelihood functions play a fundamental role in the statistical analysis of mixture distributions and constitute the foundation for parameter estimation techniques, including MLE which corresponds to the set of parameters that maximizes the log-likelihood function
. It can be obtained by computing the gradient of the log-likelihood, as shown in Equations (
5) and (
6). Solving these equations yields the MLEs of the component parameters
and the mixing proportions
.
Since closed-form solutions for the MLE of mixture distributions are typically intractable, the EM algorithm, originally proposed by Dempster et al. [
20], is commonly employed to estimate the parameters of such models.
2.1.2. Expectation Maximization Algorithm
The EM algorithm is an iterative computational procedure used to obtain either maximum likelihood estimates or maximum a posteriori estimates of the parameters within statistical models. It works by introducing missing or latent data, representing unobserved information that simplifies the model and its likelihood function. The application of the EM algorithm to mixture distributions has been extensively described in the literature [
2].
Consider an independent and identically distributed (i.i.d.) sample
generated from the mixture distribution introduced in Equation (
1). In practice, it is more convenient to employ the log-likelihood function, denoted by
and presented in Equation (
7).
We can define the missing data as a binary variable
.
for
and
and
.
Let
complete data where
. In this case, the complete likelihood function of augmented data can be written as
Since the latent variables are not observable, the MLE of cannot be obtained in closed form. To address this limitation, the EM algorithm is employed, which iteratively alternates between two stages: the Expectation (E) step and the Maximization (M) step.
In the E-step, the log-likelihood is replaced by its conditional expectation given the observed data, thereby incorporating the contribution of the unobserved components.The expected value of the complete-data log-likelihood is evaluated, given the observed data and the current parameter estimates. This expectation can be expressed as follows:
where
represents the parameter estimates obtained in the
m-th iteration. Since the complete-data log-likelihood
is linear in latent variables
, these unobserved indicators are replaced with their conditional expectations, also called responsibilities. Accordingly, the conditional probability that the
i-th observation belongs to the
j-th component is given by Equation (
11).
represents the posterior probability (responsibility) that the
i-th observation belongs to the
j-th component, based on the estimates of the current parameters
. In this context,
can be viewed as the estimator of the latent indicator
. Subsequently, these probabilities are utilized in the M-step to estimate the model parameters, thereby guiding the iterative process of the EM algorithm toward convergence. In the M-step, Equations (
12) and (
13) describe a constrained optimization problem.
subject to
This problem can be reformulated by introducing the Lagrange multiplier (
) in Equation (
14).
By substituting the likelihood and log-likelihood expressions (given in Equations (
7)–(
9)) into the probability structure of the mixture model, the Lagrangian for the constrained maximization problem can be explicitly written as
By taking the partial derivatives of the Lagrangian in Equation (
15) with respect to
,
, and
, and equating them to zero, the parameter estimators can be derived as follows:
The solution of Equations (
16)–(
19) provides estimates of the parameters
and
for
in each iteration [
36]. The relation between
and
can be expressed as follows.
The steps of the EM algorithm are explained in Algorithm 1.
| Algorithm 1 EM Algorithm |
Initialize the parameters with starting values and iterate the steps until the algorithm converges. E-step: Estimate the responsibility that observation belongs to j-th component according to Equation ( 21). M-step: Update the parameter estimates by maximizing the expected complete-data log-likelihood, using the responsibilities from the E-step as in Equations ( 22) and ( 23).
|
2.1.3. Identifying the Number of Components
To identify the best-fitting model, we use the Akaike Information Criterion (AIC) and the Bayesian Information Criterion (BIC), which are statistical tools commonly applied in model selection. These criteria are defined as follows:
where
k denotes the number of parameters,
L is the likelihood function, and
n represents the sample size. Both AIC and BIC include penalty terms that account for the complexity of the model, reflecting the number of parameters. However, BIC imposes a stricter penalty than AIC, rendering it more conservative when it comes to selecting overly complex models. AIC generally favors models that fit the data more closely, but this can sometimes result in overfitting, especially with large datasets. In contrast, BIC reduces the risk of overfitting by applying a stronger penalty, making it a more appropriate choice when striking a balance between model complexity and goodness of fit is important [
37]. The model selection is based on a comparison of AIC and BIC values, with the model producing the lowest criterion value considered the most suitable for representing the dataset.
2.2. The Gaussian Mixture Distribution
Let
for
where
denotes the parameters of the
j-th component, with
representing the mean and
the variance. Then, the density function of the Gaussian mixture distribution can be expressed as
By substituting the Gaussian mixture distribution given in Equation (
26) in place of PDF in Equation (
21), we obtain the following expression:
Given the following equation,
Therefore, the parameter estimates of the Gaussian mixture distribution are obtained using the following equations.
2.3. The Gamma Mixture Distribution
The PDF of the gamma-mixture distribution is defined as follows:
where
for
denotes the set of parameters of the components of the gamma mixture.
and
represent the shape and scale parameters of the
j-th gamma distribution, respectively.
denotes the mixing proportion of the
j-th component, satisfying
for all
k and
.
The PDF of the gamma distribution denoted by
and the gamma function
for the
j-th component are defined in Equations (
33) and (
34), respectively.
The mean and variance of the
j-th gamma distribution are denoted by Equations (
35) and (
36), respectively.
The EM algorithm, widely used for estimating the parameters of the Gamma mixture distribution [
38], completes its E-step by applying Equation (
37).
Subsequently, these probabilities are employed in the M-step of the algorithm to update the parameter estimates.
In the M-step, the parameters of the gamma mixture distribution are substituted into the log-likelihood function, and the constrained optimization problem is solved using the Lagrange multiplier
. To estimate the scale parameters of the gamma mixture distribution, the partial derivatives of the log-likelihood with respect to the parameters
and
are calculated. The estimation of the parameter
is given in Equation (
38).
It is observed that the estimation of the scale parameter
depends on the shape parameter
. Since
cannot be obtained in closed form, its estimation is carried out by exploiting the iterative and gradient-based nature of the EM algorithm. During each iteration, the parameters are updated by performing a positive projection along the gradient of the log-likelihood function with respect to the model parameters. Consequently, the shape parameter
is updated in the gradient direction with a step size
as in Equations (
39) and (
40).
The digamma function, represented by the symbol
, is defined in Equation (
41). Since the digamma function does not have a closed-form solution, particularly for
, an approximate representation is provided in Equation (
42).
Consequently, the parameter
can be computed iteratively by using Equation (
43).
For a gamma mixture distribution, in which each component follows a Gamma(
) distribution with mixing proportion
(
), the mean
and variance
can be expressed as follows:
2.4. The Beta Mixture Distribution
The PDF of the beta mixture distribution with
k components is given by
where
represents the parameter space of the mixture distribution, with each component defined as
for
. Here,
refers to the shape parameter of the
j-th component, while
represents the scale parameter of the
j-th component and takes positive real values.
denotes the mixing proportion of the
j-th component, where
for all
j and the weights satisfy the constraint
. In this framework,
defines the density of the
j-th beta component, which is scaled by its corresponding proportion
, as expressed below:
where
is the Gamma function, as given in Equation (
48).
For the Beta mixture distribution, the log-likelihood function is given in Equation (
49).
If we substitute the PDF of the Beta mixture distribution into Equation (
49), we obtain Equation (
50).
The Lagrange function for the beta mixture distribution is
By differentiating the Lagrangian function with respect to
and
and equating the results to zero, the following equations are obtained.
where
(.) is the digamma function and is expressed as
. The following equations are obtained.
Since there is no exact solution for these equations, approximate solutions can be obtained using the Newton–Raphson method [
39,
40].
3. Incorporating Mixture Distributions into M/G/1 Queueing System
The exact results of the M/G/1 queueing system were first derived by Pollaczek and Khintchine. When the interarrival times of customers follow an exponential distribution and the mean and variance of the service time distribution are known, the corresponding equations for the parameters defined below are presented in Equations (
56)–(
60).
Under the stability condition
,
where
The mean and variance of the Gaussian mixture distribution, with each component parameterized by
for
, are expressed in Equations (
61) and (
62).
where
In the M/G/1 queueing system, if the service time distribution is modeled as a
k-component Gaussian mixture distribution with the parameters defined above, let the average waiting time in the queue be denoted by
. Then, by substituting
and
, as defined in Equations (
61) and (
62), in place of
and
in Equation (
58), the expression for
given in Equation (
63) can be obtained.
In this system, let the expected waiting time of a customer in the system be denoted by
. When Equation (
59) is reformulated using the parameters of the Gaussian mixture distribution, the equality given in Equation (
64) is obtained.
Let the average number of customers in the queue and in the system be denoted by
and
, respectively. When the equalities given in Equations (
56) and (
60) are adapted using the parameters of the Gaussian mixture distribution, the expressions in Equations (
65)–(
67) are obtained.
If the service-time distribution is modeled as a
k-component Gamma mixture with the parameter set
,
, the mean (
) and variance of the distribution (
) can be expressed as in Equations (
68) and (
69).
In such a system, if the average waiting time of a customer in the queue and in the system is denoted by
and
, respectively, then the utilization factor
is given by Equation (
70).
By substituting the Gamma mixture distribution parameters defined in Equations (
68) and (
69) into Equations (
58) and (
59), the expressions for
and
given in Equations (
71) and (
72) are obtained:
By adapting the distribution parameters of the Gamma mixture to Equations (
56) and (
60),
and
are obtained as given in Equations (
73) and (
74):
Finally, when the service-time distribution follows a
k-component Beta mixture distribution, with each component parameterized by
,
, let the mean and variance of the Beta mixture distribution be denoted by
and
, respectively, with their formulas given in Equations (
75) and (
76).
By performing the same steps as those applied in the Gaussian and Gamma mixture distributions, and employing the Beta mixture distribution parameters defined in Equations (
75) and (
76), the corresponding formulations for
,
,
, and
are derived, as presented in Equations (
77)–(
80).
The corresponding performance measures for the Gaussian, Gamma, and Beta mixture distributions are summarized in
Table 1.
Determination of Lower and Upper Bounds for the Mean Waiting Time in the Queue
In the analysis of G/G/1 queueing systems, where both the interarrival and service times follow a general distribution, Marchal [
31] and Kingman [
41] established the lower and upper bounds of the
for a customer, as given in Equations (
81) and (
82), in order to assess the consistency of the results [
42].
where
For the M/G/1 model, the upper bound value was derived by [
31], particularly as
, employing the quotient presented in Equation (
83):
This was chosen to make the approximation exact for the M/G/1 queue. The resulting approximation for
, obtained by multiplying the upper bound in Equation (
84) by the quotient given in Equation (
82), is expressed as
Since the interarrival time of the M/G/1 system follows an exponential distribution, its variance can be expressed as
. Accordingly, the relation in Equation (
85) is obtained for
:
As can be observed from Equation (
85), the upper bound of
coincides with the exact solution of
in the P-K formula. In this part of the study, for the M/G/1 queueing system where the service-time distribution follows a Gaussian mixture distribution, the lower and upper bounds of
are determined. For a Gaussian mixture distribution with
k components, defined by the mean
and the variance
, and with the utilization of the system given by
, the upper bound of
is obtained as in Equation (
86).
By performing the necessary simplifications in Equation (
86), Equation (
87) is obtained.
Based on the parameters of the Gaussian mixture distribution, the upper bound given in Equation (
87) can be expressed as shown in Equation (
88):
By denoting the lower bound of this system as
, and substituting the relevant parameters into the equality in Equation (
82), the lower bound presented in Equation (
89) is derived:
Furthermore, by rearranging and simplifying the numerator of Equation (
89), Equations (
90) and (
91) are obtained:
Moreover, it can be expressed as in Equation (
92), depending on the parameters of the Gaussian mixture distribution.
When the service-time distribution is modeled by a Gamma mixture distribution, the upper bound of the mean waiting time in the queue can be determined by substituting its mean and variance, as defined in Equations (
68) and (
69), into Equation (
81). Accordingly, the upper bound is initially formulated in Equation (
85), and upon performing the required simplifications, the expressions in Equations (
93)–(
95) are obtained, provided that
.
By substituting the parameters of the Gamma mixture distribution into Equation (
68), the upper bound can be expressed as in Equation (
96).
In a similar manner, by denoting the lower bound as
and substituting the parameters of the Gamma mixture distribution into Equation (
82), the expressions for the lower bound given in Equations (
97) and (
98) are derived.
Within the M/G/1 model, assuming that the service time is characterized by a mixture of
k Beta distributions, the mean
and variance
of
j-th Beta mixture distribution are presented above in Equations (
75) and (
76), respectively.
By applying the same procedure used for the Gaussian and Gamma mixture distributions to the Beta mixture distribution, the upper bound can be derived as shown in Equation (
99), whereas the lower bound is obtained as presented in Equation (
100).
4. Experimental Design
In M/G/1 queueing systems with mixture service time distributions, a simulation model (illustrated in
Figure 1) has been developed to test the effectiveness of the proposed approximate solutions for system parameters.
In the first stage of the simulation model, 10,000 entities were generated so that the interarrival time distribution follows the exponential distribution. In the second stage, these entities were routed according to the parameters of the mixture proportions, and a service time was assigned to each entity based on the parameters of the corresponding mixture distribution in the selected route. At this stage, each entity that proceeded to the server was assigned a service time generated from the mixture distribution of the respective component determined in the previous step.
When the processing times in the process stage are considered collectively, it is evident that their distribution follows a
k component mixture distribution. The simulation model illustrated in the flow diagram above was developed using Arena 13.0, which is particularly suitable for modeling discrete-event systems [
43]. In each simulation run, the number of replications was set to 10 using the sequential method to improve the consistency of the results [
44]. The simulation model used in this study, together with the datasets constructed according to the model parameters provided in
Table A2, was employed for the analysis.
In the experimental design for the M/G/1 queueing model, it was assumed that the number of components (
k) was 2 for each of the Gaussian, Gamma, and Beta mixture distributions. The parameters of the first and second components were hypothetically determined by setting the average service time of the first component to
, and by increasing it by
for the second component, i.e.,
. Based on these parameters, ten distinct samples were constructed, and for each sample, nine test groups were generated under M/G/1 queueing models with interarrival times corresponding to traffic intensities (
) ranging from
to
. The data are given at
Table A1 and
Table A2. In addition, the Gaussian distribution parameters, along with the shape parameters
and
for the Gamma and Beta distributions are provided in
Table A3.
The approximate solutions for these test groups were obtained by integrating the formulas for the mixture distribution parameters into the P-K equation. To evaluate the accuracy of the proposed approximation across all distributions, discrete-event simulation models were developed and executed for each sample, from which the corresponding approximate values were then obtained.
5. Results and Discussion
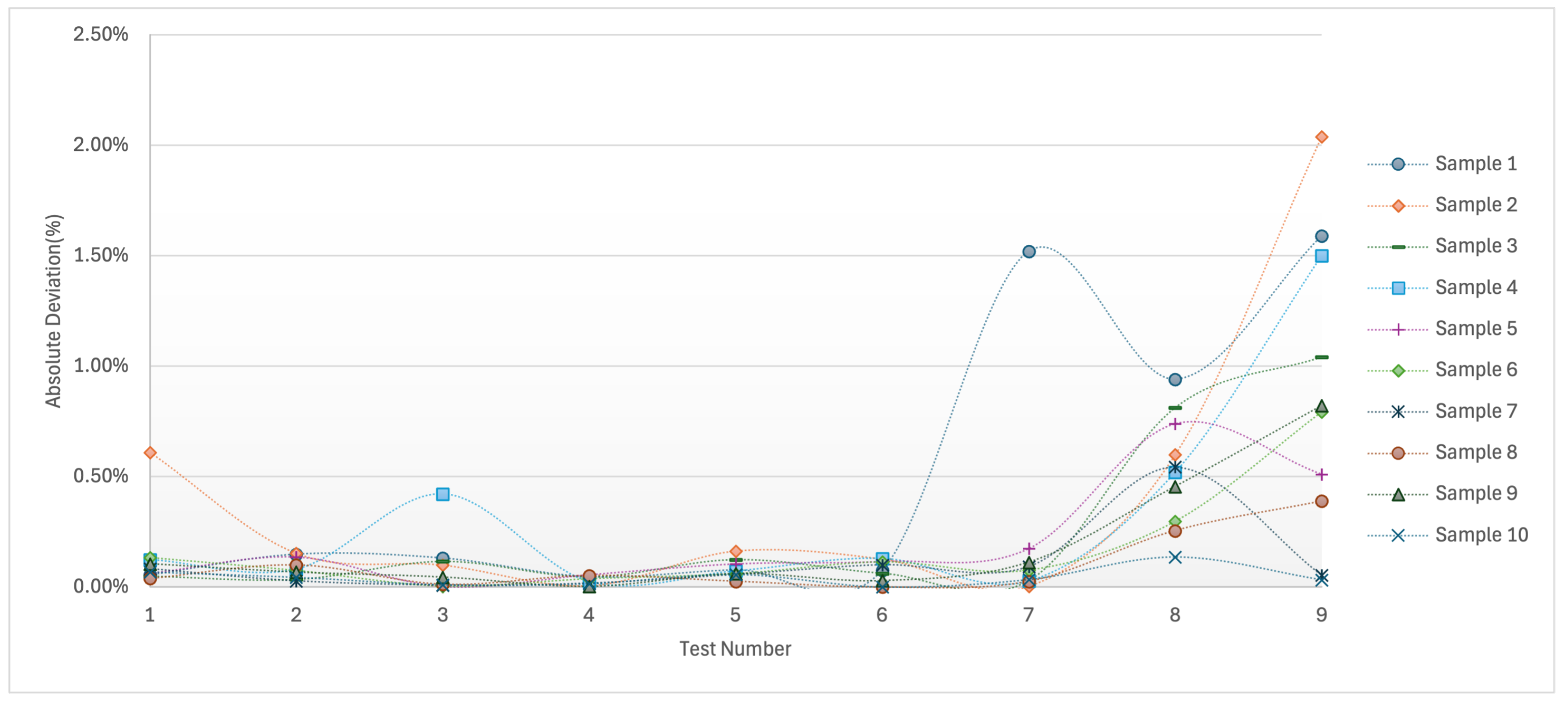
In the case of the Gaussian distribution in
Figure 2, the absolute deviation between the simulation and the approximation method remains relatively small at lower traffic intensities, typically below
. Nevertheless, at higher intensities, irregular increases occur, with certain samples (e.g., Sample 1, Sample 2, and Sample 4) exhibiting pronounced fluctuations. This pattern suggests that while the approximation retains stable in the initial range, its accuracy deteriorates at higher intensities in a sample-dependent manner.
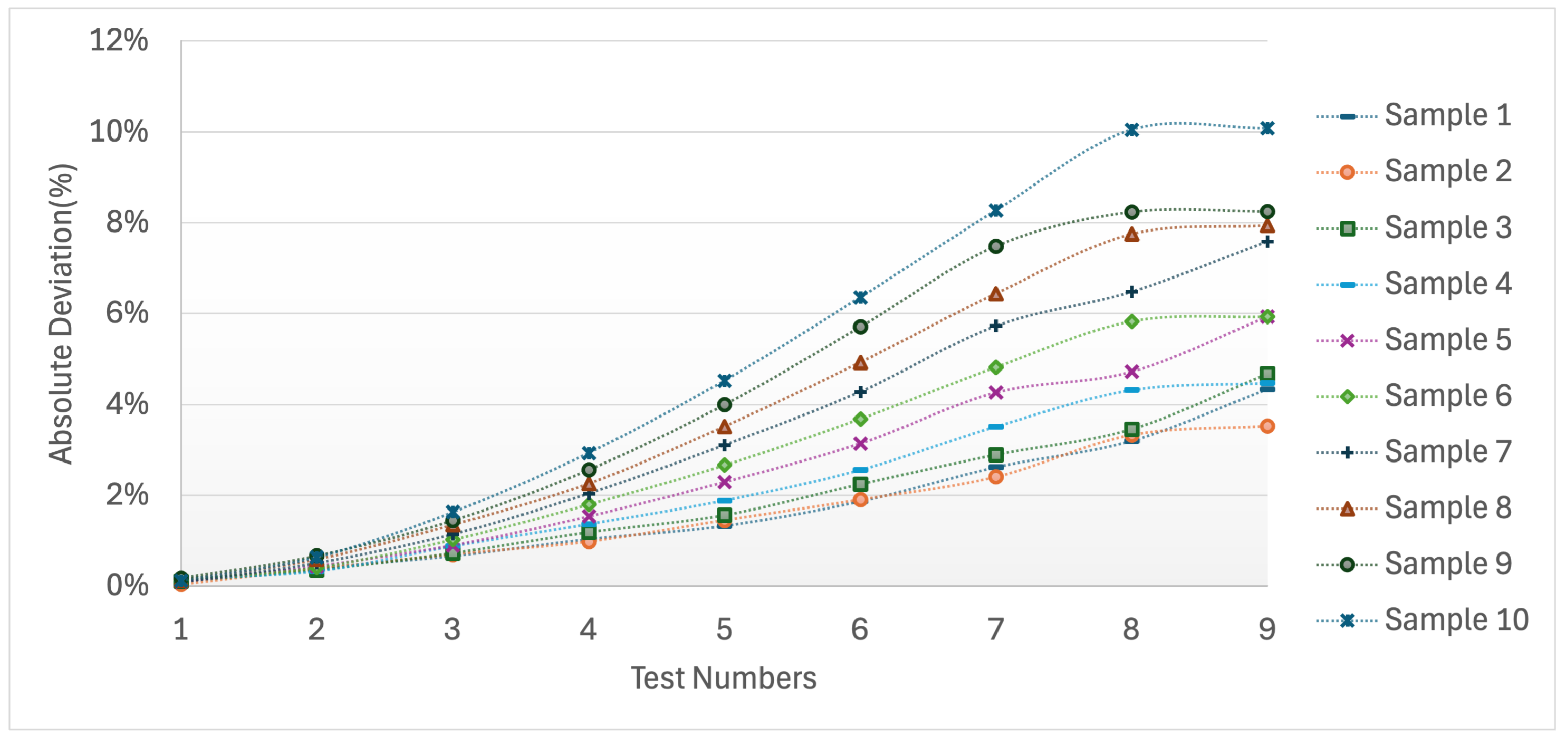
For the Gamma distribution in
Figure 3, the deviations follow a more systematic trajectory. Starting close to zero, they increase gradually with traffic intensity, exceeding
for several samples at higher traffic intensities. Unlike the irregular pattern observed in the Gaussian case, the Gamma distribution results reveal a smoother and more consistent upward trend across samples, suggesting that the approximation exhibits a cumulative bias rather than stochastic variability.
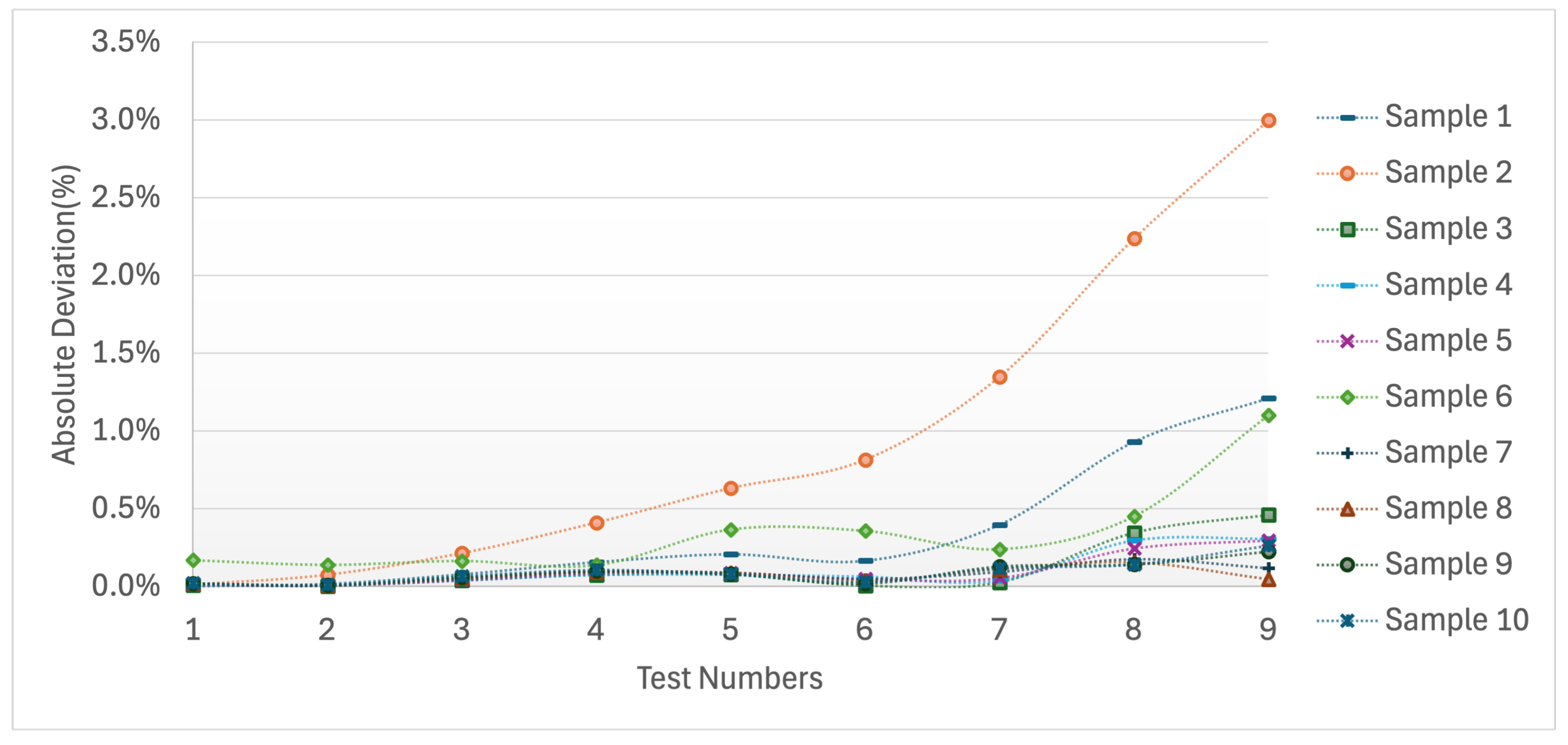
For the Beta distribution in
Figure 4, deviations are markedly lower in magnitude compared to both the Gaussian and Gamma cases. Almost all values remain well below
, with only a limited number of samples exhibiting minor increases at higher intensities. This indicates that the Beta-based approximation yields the most robust performance among the three distributions, while maintaining stability and minimizing errors across the entire range of tests.
Overall, these results highlight that the accuracy of the approximated method is distribution-dependent. While the Gaussian case suffers from irregular fluctuations and the Gamma case from systematic error growth, the Beta distribution consistently provides superior approximation quality with negligible deviations.
The expected waiting times in the queue for Gaussian, Gamma, and Beta mixture distributions had been determined in Equation (
63), Equation (
68), and Equation (
85), respectively. In addition, the approximate formulas for the lower and upper bounds of the queue waiting times were presented in Equations (
88) and (
92) for the Gaussian mixture distribution, in Equations (
96) and (
98) for the Gamma mixture distribution, and in Equations (
99) and (
100) for the Beta mixture distribution. To evaluate the effectiveness of these approximation formulas,
Figure 5,
Figure 6 and
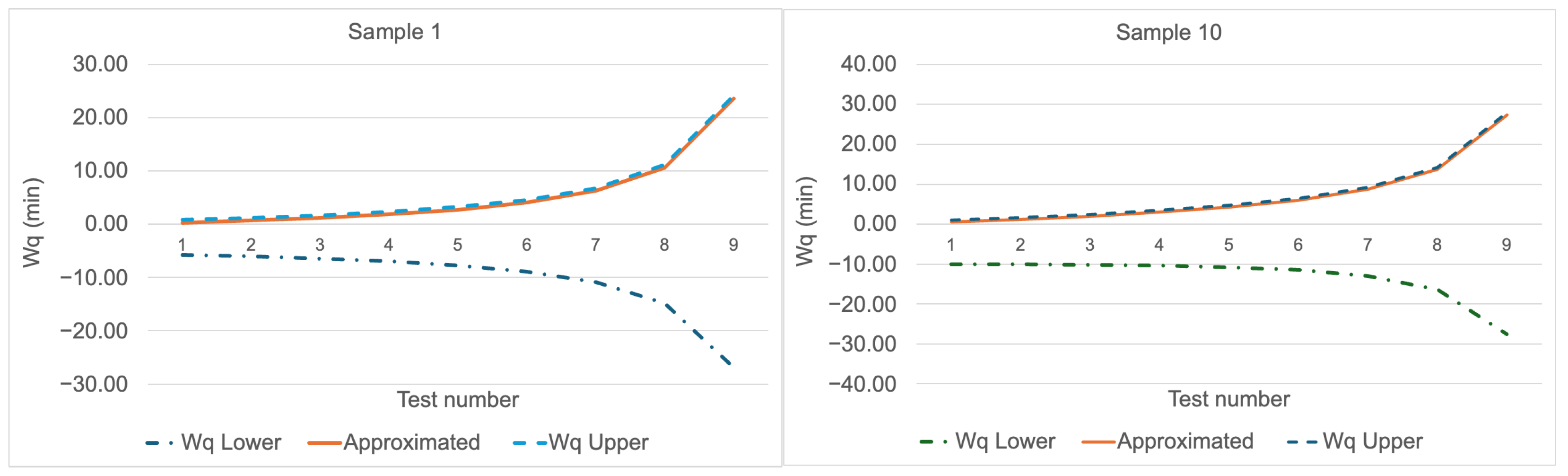
Figure 7 illustrate the comparative plots of the lower and upper bound values obtained from the two-component mixture distributions, whose parameters are given in
Table A1–
Table A3, together with the
values calculated using Equation (
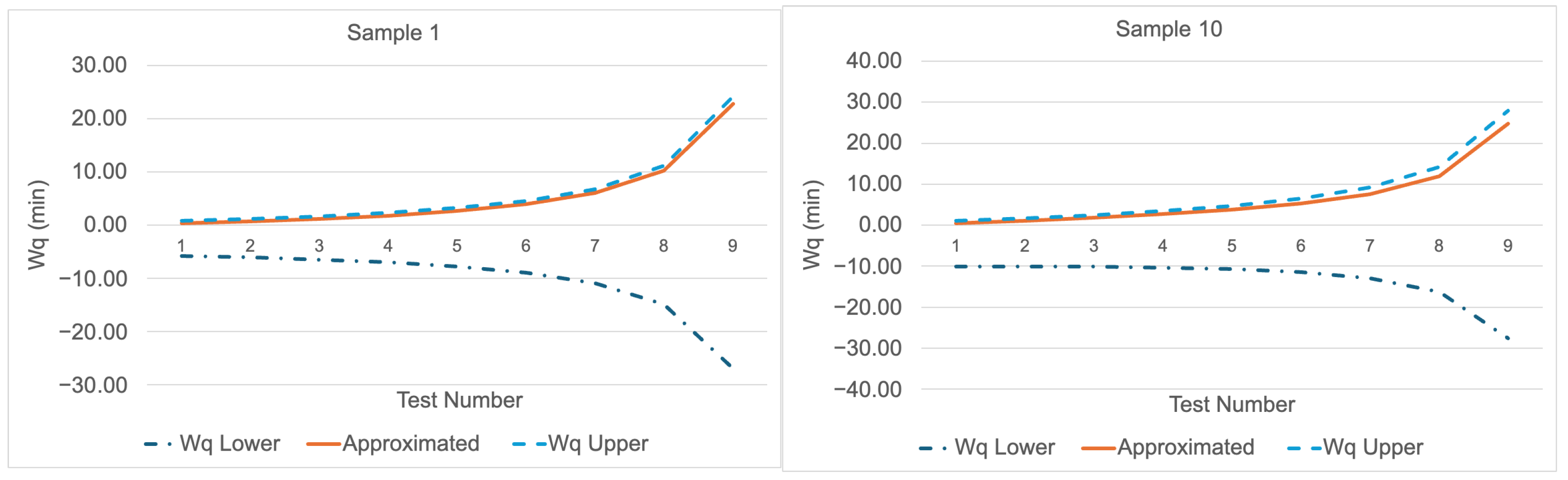
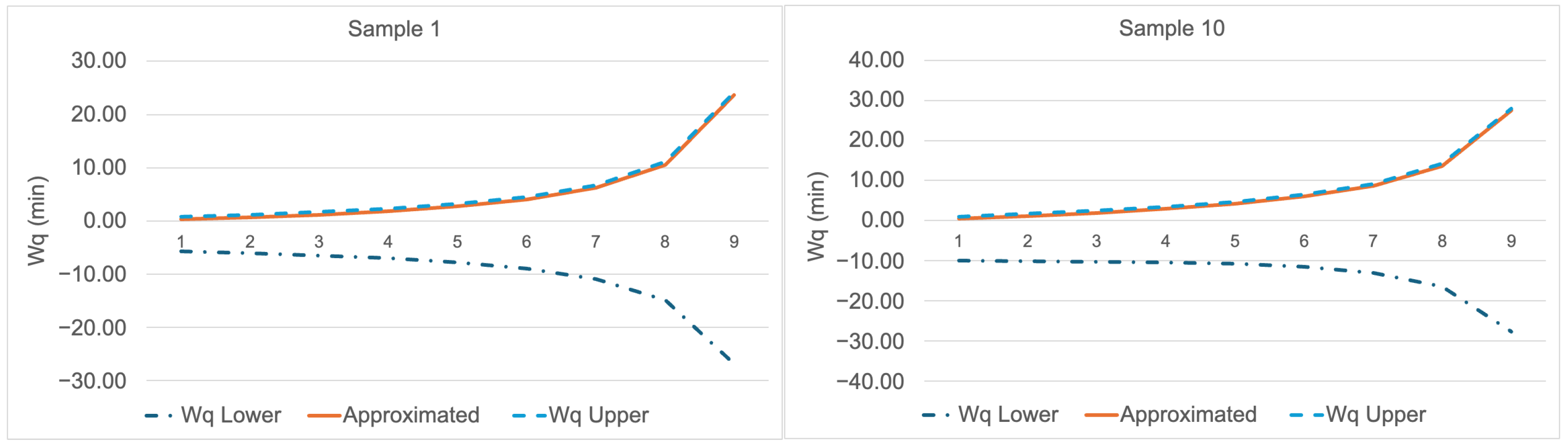
63) and (
68) for Sample 1 and Sample 10. The means of the first components are set to 5 for all three distributions, with their variances adjusted to 1, while the means of the second components are set to 5.5 and 10 respectively for all three distributions, with their variances likewise set to 1. For all three mixture distributions, it is observed that the
values are close to the upper bound. This finding is consistent with Marchal’s [
31], in which the upper bound of the
in the M/G/1 model coincides with the
value obtained from the P-K formula. Consequently,
Figure 5,
Figure 6 and
Figure 7 provide graphical evidence supporting that the lower and upper bounds derived for
yield reliable results.
Across the six plots comparing the Gaussian (
Figure 5), Gamma (
Figure 6), and Beta (
Figure 7) distributions, the approximated results generally follow a consistent trend, although subtle differences emerge among the distributions. For the Gaussian distribution, both under small sample size (Sample 1) and larger sample size (Sample 10), the approximation curve remains closely aligned with the upper and lower bounds, indicating a high level of accuracy. In contrast, for the Gamma distribution, while the approximation maintains a reasonable fit under small samples, deviations become more evident as the sample size increases, particularly at higher traffic intensities where the curve tends to align more closely with the lower bound. Finally, for the Beta distribution, the approximation values also show good agreement with the bounds, though a slightly wider gap appears in larger samples, suggesting that the sensitivity of the approximation to distributional shape becomes more pronounced in this case. Overall, these comparisons highlight that while the approximation method is robust across different distributions, its precision is highest for Gaussian, moderately reliable for Beta, and relatively less accurate for Gamma as the traffic intensity increases.
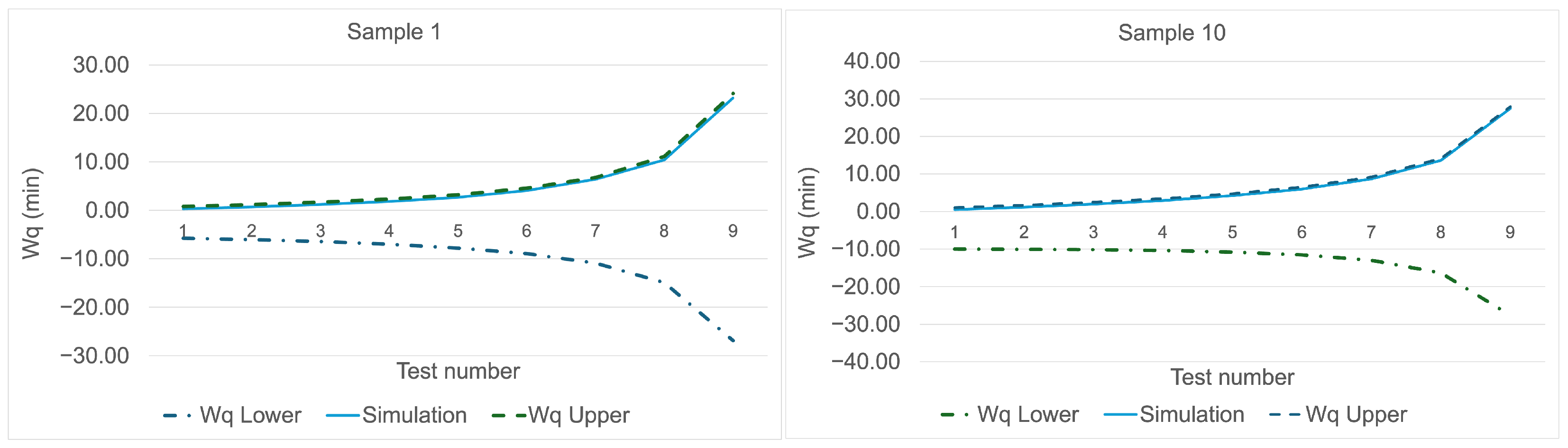
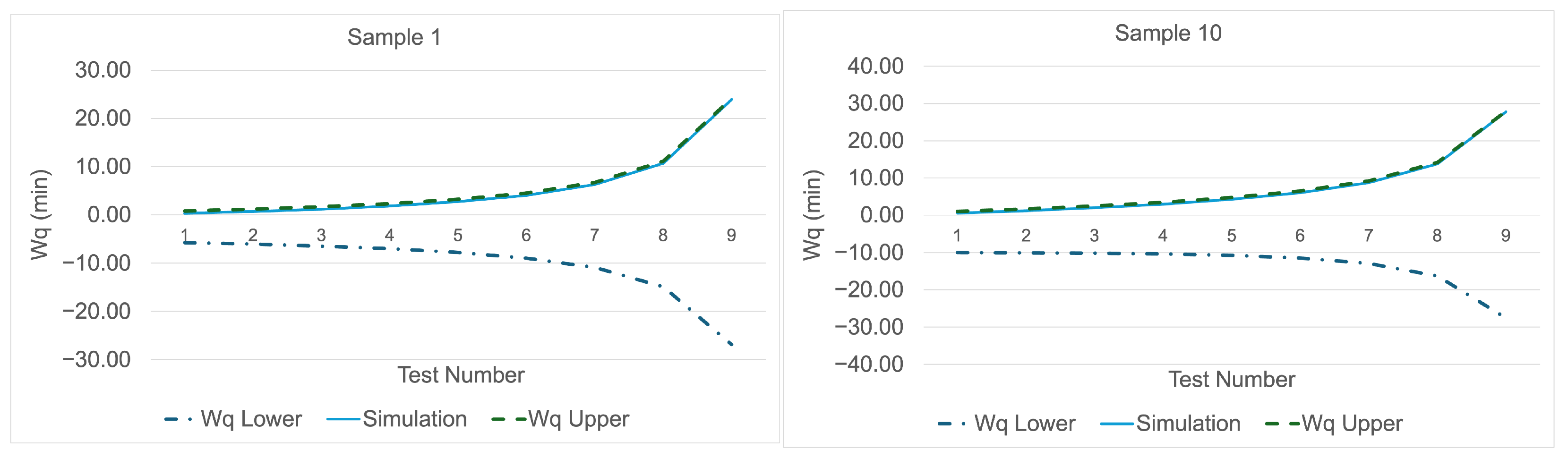
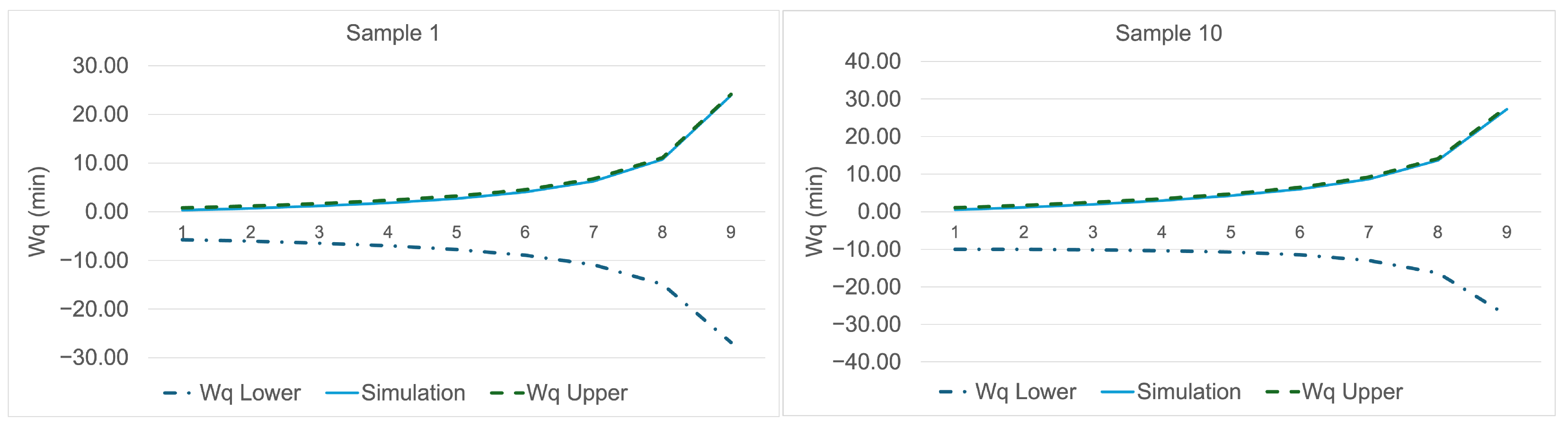
Using the parameters described above, when the system was simulated with the model presented in
Figure 1, the comparative graphs of the lower and upper bound values together with the
values obtained from the simulation model are shown in
Figure 8,
Figure 9 and
Figure 10. For all three mixture distributions, it was observed that the
values obtained from the simulation model were also close to the upper bound. This finding can be interpreted as an indication that the approximation formulas for the lower and upper bounds yield reliable results.