Numerical Solutions for Fractional Bagley–Torvik Equation with Integral Boundary Conditions
Abstract
1. Introduction
2. Fredholm–Hammerstein Integral Equations
3. Uniqueness of the Solution
4. A New Numerical Method
4.1. Formulation of the Approximate Solution
4.2. Convergence Analysis and Error Estimation
5. Numerical Results
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Notation
| Riemann–Liouville fractional derivative of order | |
| Gamma function | |
| Closed interval | |
| Space of continuous functions on the closed interval | |
| Space of n-times continuously differentiable functions on | |
| Space of integrable (Lebesgue integrable) functions on | |
| Space of n-th power integrable functions on , | |
| Space of real-valued n-th power integrable functions on | |
| Infinity (uniform) norm, | |
| Operator norm induced by the infinity norm, | |
| dimensional real vector space | |
| Inverse operator of , assumed to be linear and bounded |
References
- Sabir, Z.; Bhat, S.; Wahab, H.; Camargo, M.; Abildinova, G.; Zulpykhar, Z. A bio inspired learning scheme for the fractional order kidney function model with neural networks. Chaos Solitons Fractals 2024, 180, 114562. [Google Scholar] [CrossRef]
- Zhang, Y.; Li, J.; Zhu, S.; Ma, Z. Harmonic resonance and bifurcation of fractional Rayleigh oscillator with distributed time delay. Math. Comput. Simul. 2024, 221, 281–297. [Google Scholar] [CrossRef]
- Zhang, Y.; Li, J.; Zhu, S.; Zhao, H. Chaos detection and control of a fractional piecewise-smooth system with nonlinear damping. Chin. J. Phys. 2024, 90, 885–900. [Google Scholar] [CrossRef]
- Li, X.; Shao, H. Investigation of bio-thermo-mechanical responses based on nonlocal elasticity theory and fractional Pennes equation. Appl. Math. Model. 2024, 125, 390–401. [Google Scholar] [CrossRef]
- Din, Q. Controlling chaos and codimension-two bifurcation in a discrete fractional-order Brusselator model. J. Vib. Control 2015, 31, 2963–2988. [Google Scholar] [CrossRef]
- Qing, J.; Zhou, S.; Wu, J.; Shao, M.; Tang, J. Parametric resonance of an axially accelerating viscoelastic membrane with a fractional model. Commun. Nonlinear Sci. Numer. Simul. 2024, 130, 107691. [Google Scholar] [CrossRef]
- Chaturvedi, E.; Roy, P.; Upadhyay, R.; Chowdhury, P. Enhanced yield and production of aromatics rich fractions in bio-oil through co-pyrolysis of waste biomass and plastics. J. Anal. Appl. Pyrolysis 2024, 178, 106379. [Google Scholar] [CrossRef]
- Sui, P.; Shen, Y.; Gao, C.; Jing, W. Mechanical mechanism and parameter optimization of a tuned inerter damper with delayed fractional-order PID. Nonlinear Dyn. 2024, 112, 13903–13925. [Google Scholar] [CrossRef]
- Torvik, P.; Bagley, R. On the appearance of the fractional derivative in the behavior of real materials. J. Appl. Mech. 1984, 51, 294–298. [Google Scholar] [CrossRef]
- Yadav, P.; Jahan, S.; Nisar, K. Solving fractional Bagley-Torvik equation by fractional order Fibonacci wavelet arising in fluid mechanics. Ain Shams Eng. J. 2024, 15, 102299. [Google Scholar] [CrossRef]
- Webb, J.; Lan, K. Fractional differential equations of Bagley-Torvik and Langevin type. Fract. Calc. Appl. Anal. 2024, 27, 1639–1669. [Google Scholar] [CrossRef]
- Wu, Z.; Zhang, X.; Wang, J.; Zeng, X. Applications of fractional differentiation matrices in solving Caputo fractional differential equations. Fractal Fract. 2023, 7, 374. [Google Scholar] [CrossRef]
- Guirao, J.; Sabir, Z.; Raja, M. Design of neuro-swarming computational solver for the fractional Bagley–Torvik mathematical model. Eur. Phys. J. Plus 2022, 137, 245. [Google Scholar] [CrossRef]
- Wei, H.; Zhong, X.; Huang, Q. Uniqueness and approximation of solution for fractional Bagley–Torvik equations with variable coefficients. Int. J. Comput. Math. 2017, 94, 1542–1561. [Google Scholar] [CrossRef]
- Wang, H.; Li, F. Explicit solution for the Bagley–Torvik equation with variable coefficients. Math. Methods Appl. Sci. 2025, 48, 10008–10015. [Google Scholar] [CrossRef]
- Arqub, O.; Rabah, A.; Momani, S. A spline construction scheme for numerically solving fractional Bagley–Torvik and Painlevé models correlating initial value problems concerning the Caputo–Fabrizio derivative ap-proach. Int. J. Mod. Phys. C 2023, 34, 2350115. [Google Scholar] [CrossRef]
- Yassin, N.; Aly, E.; Atta, A. Novel approach by shifted Schröder polynomials for solving the fractional Bagley-Torvik equation. Phys. Scr. 2024, 100, 015242. [Google Scholar] [CrossRef]
- Wang, L.; Liang, H. Analysis of direct piecewise polynomial collocation methods for the Bagley–Torvik equation. BIT Numer. Math. 2024, 64, 41. [Google Scholar] [CrossRef]
- Wang, Z.; Wang, X. General solution of the Bagley–Torvik equation with fractional-order derivative. Commun. Nonlinear Sci. Numer. Simul. 2010, 15, 1279–1285. [Google Scholar] [CrossRef]
- Staněk, S. Fractional-order harmonic resonance in a multi-frequency excited fractional Duffing oscil-lator with distributed time delay. Open Math. 2013, 11, 574–593. [Google Scholar]
- Zhong, X.; Huang, Q. Approximate solution of three-point boundary value problems for second-order ordinary differential equations with variable coefficients. Appl. Math. Comput. 2014, 247, 18–29. [Google Scholar] [CrossRef]
- Lv, X.; Zhao, K. Study of Stability and Simulation for Nonlinear (k, ψ)-Fractional Differential Coupled Laplacian Equations with Multi-Point Mixed (k, ψ)-Derivative and Symmetric Integral Boundary Con-ditions. Symmetry 2025, 17, 472. [Google Scholar] [CrossRef]
- Al-Khateeb, A.; Zureigat, H.; Abuasbeh, K.; Fadhal, E. Leray–Schauder Alternative for the Existence of Solutions of a Modified Coupled System of Caputo Fractional Differential Equations with Two Point’s In-tegral Boundary Conditions. Symmetry 2023, 15, 863. [Google Scholar] [CrossRef]
- Yao, N.; Liu, X.; Jia, M. Solvability for Riemann-Stieltjes integral boundary value problems of Bagley-Torvik equations at resonance. J. Appl. Anal. Comput. 2020, 10, 1937–1953. [Google Scholar] [CrossRef]
- Tamilselvan, A. Second order spline method for fractional Bagley-Torvik equation with variable coefficients and Robin boundary conditions. J. Math. Model. 2023, 11, 117–132. [Google Scholar]
- Buranay, S.; Chin, M.; Mahmudov, N. A highly accurate numerical method for solving boundary value problem of generalized Bagley-Torvik equation. Math. Methods Appl. Sci. 2024, 1–23. [Google Scholar] [CrossRef]
- Ali, H.; Kamrujjaman, M.; Shirin, A. Numerical solution of a fractional-order Bagley–Torvik equation by quadratic finite element method. J. Appl. Math. Comput. 2021, 66, 351–367. [Google Scholar] [CrossRef]
- Saw, V.; Kumar, S. Numerical solution of fraction Bagley–Torvik boundary value problem based on Cheby-shev collocation method. Int. J. Appl. Comput. Math. 2019, 5, 68. [Google Scholar] [CrossRef]
- Huang, Q.; Zhong, X.; Guo, B. Approximate solution of Bagley–Torvik equations with variable coefficients and three-point boundary-value conditions. Int. J. Appl. Comput. Math. 2016, 2, 327–347. [Google Scholar] [CrossRef]
- Hamou, A.; Hammouch, Z.; Azroul, E.; Agarwal, P. Monotone iterative technique for solving finite difference systems of time fractional parabolic equations with initial/periodic conditions. Appl. Numer. Math. 2022, 181, 561–593. [Google Scholar] [CrossRef]
- Zhang, X.; Zeng, S. Time-space fractional porous medium equations with nonlocal nonlinear terms. Evol. Equations Control Theory 2025, 14, 1678–1695. [Google Scholar] [CrossRef]
- Gülsu, M.; Öztürk, Y.; Anapali, A. Numerical solution the fractional Bagley–Torvik equation arising in fluid mechanics. Int. J. Comput. Math. 2017, 94, 173–184. [Google Scholar] [CrossRef]
- Podlubny, I. Fractional Differential Equations; Academic Press: New York, NY, USA, 1998. [Google Scholar]
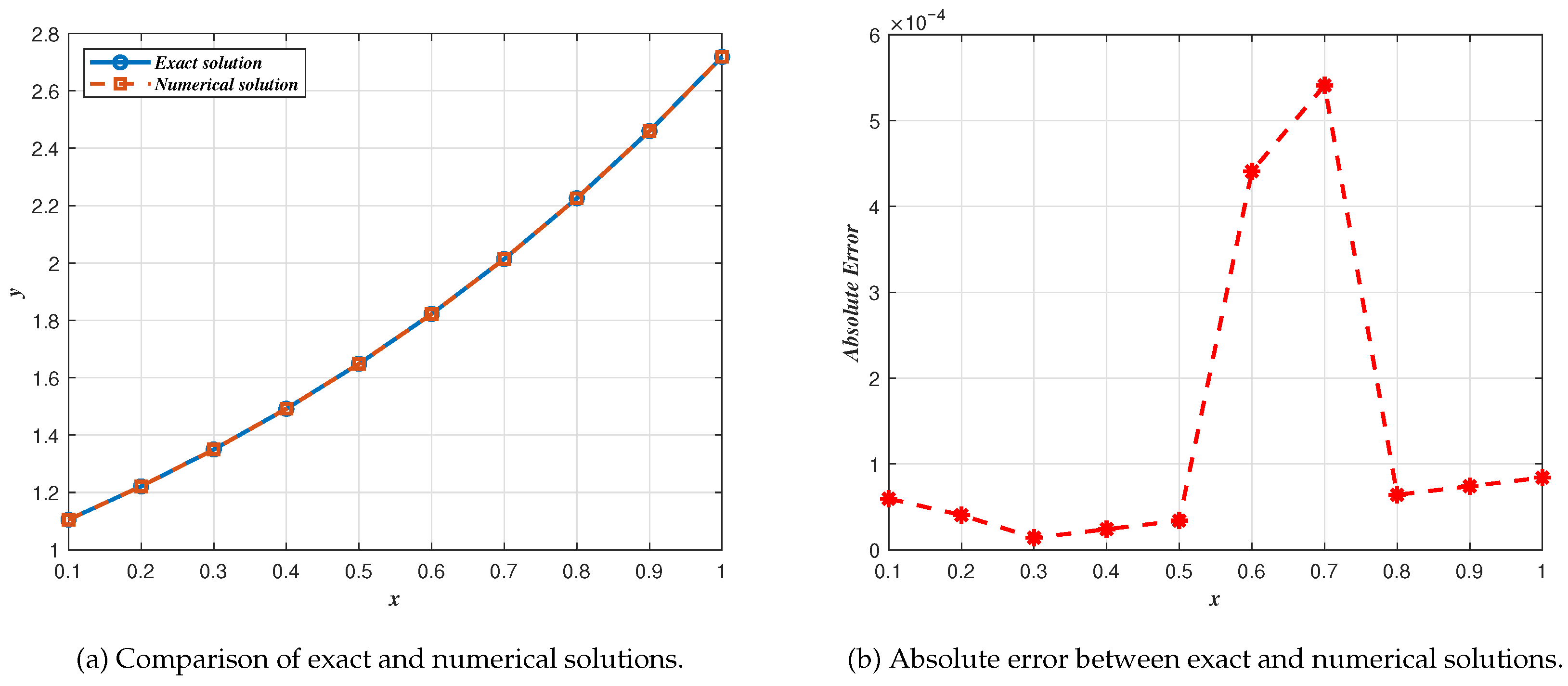
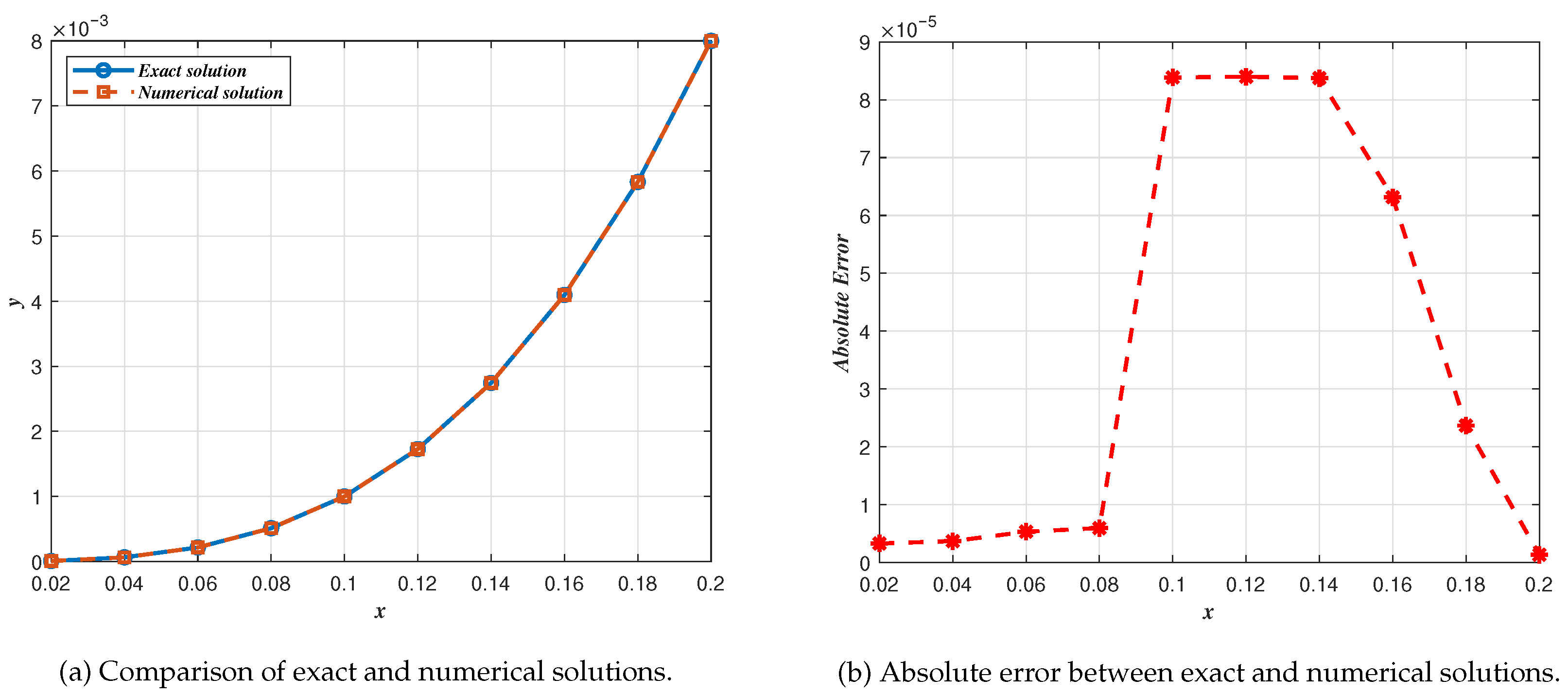
| x | ||||||
|---|---|---|---|---|---|---|
| x | ||||||
|---|---|---|---|---|---|---|
| : The Present Method | : The Difference Method | |||||
|---|---|---|---|---|---|---|
| 0.0006999 | 0.0001596 | 0.0001560 | 0.0001017 | 0.0001693 | 0.0001002 | |
| 0.0005007 | 0.0004051 | 0.0004404 | 0.0004003 | 0.0004205 | 0.0004003 | |
| 0.0010001 | 0.0009141 | 0.0009140 | 0.0009021 | 0.0009582 | 0.0009002 | |
| 0.0018402 | 0.0016241 | 0.0016240 | 0.0016093 | 0.0016703 | 0.0016005 | |
| 0.0028403 | 0.0025341 | 0.0025340 | 0.0025079 | 0.0025863 | 0.0025006 | |
| 0.0077538 | 0.0040408 | 0.0036440 | 0.0036094 | 0.0036955 | 0.0036062 | |
| 0.0100049 | 0.0054500 | 0.0049539 | 0.0049063 | 0.0049763 | 0.0049005 | |
| 0.0070407 | 0.0064641 | 0.0064063 | 0.0064006 | 0.0064271 | 0.0064010 | |
| 0.0088409 | 0.0081741 | 0.0081740 | 0.0081109 | 0.0081648 | 0.0081017 | |
| 0.0108411 | 0.0100842 | 0.0100008 | 0.0100006 | 0.0102180 | 0.0100002 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, X.; Huang, J.; Li, J.; Zhang, Y. Numerical Solutions for Fractional Bagley–Torvik Equation with Integral Boundary Conditions. Symmetry 2025, 17, 1755. https://doi.org/10.3390/sym17101755
Liu X, Huang J, Li J, Zhang Y. Numerical Solutions for Fractional Bagley–Torvik Equation with Integral Boundary Conditions. Symmetry. 2025; 17(10):1755. https://doi.org/10.3390/sym17101755
Chicago/Turabian StyleLiu, Xueling, Jing Huang, Junlin Li, and Yufeng Zhang. 2025. "Numerical Solutions for Fractional Bagley–Torvik Equation with Integral Boundary Conditions" Symmetry 17, no. 10: 1755. https://doi.org/10.3390/sym17101755
APA StyleLiu, X., Huang, J., Li, J., & Zhang, Y. (2025). Numerical Solutions for Fractional Bagley–Torvik Equation with Integral Boundary Conditions. Symmetry, 17(10), 1755. https://doi.org/10.3390/sym17101755






