Controlling Spiral Wave Solutions in the Barkley System Using a Proportional Feedback Control
Abstract
1. Introduction
2. Research Methodology
3. The Model
3.1. Nonlinear System for the Barkley Model
3.2. Linear System for Nonlinear Barkley Model
3.3. Adjoint Linear System for the Barkley Model
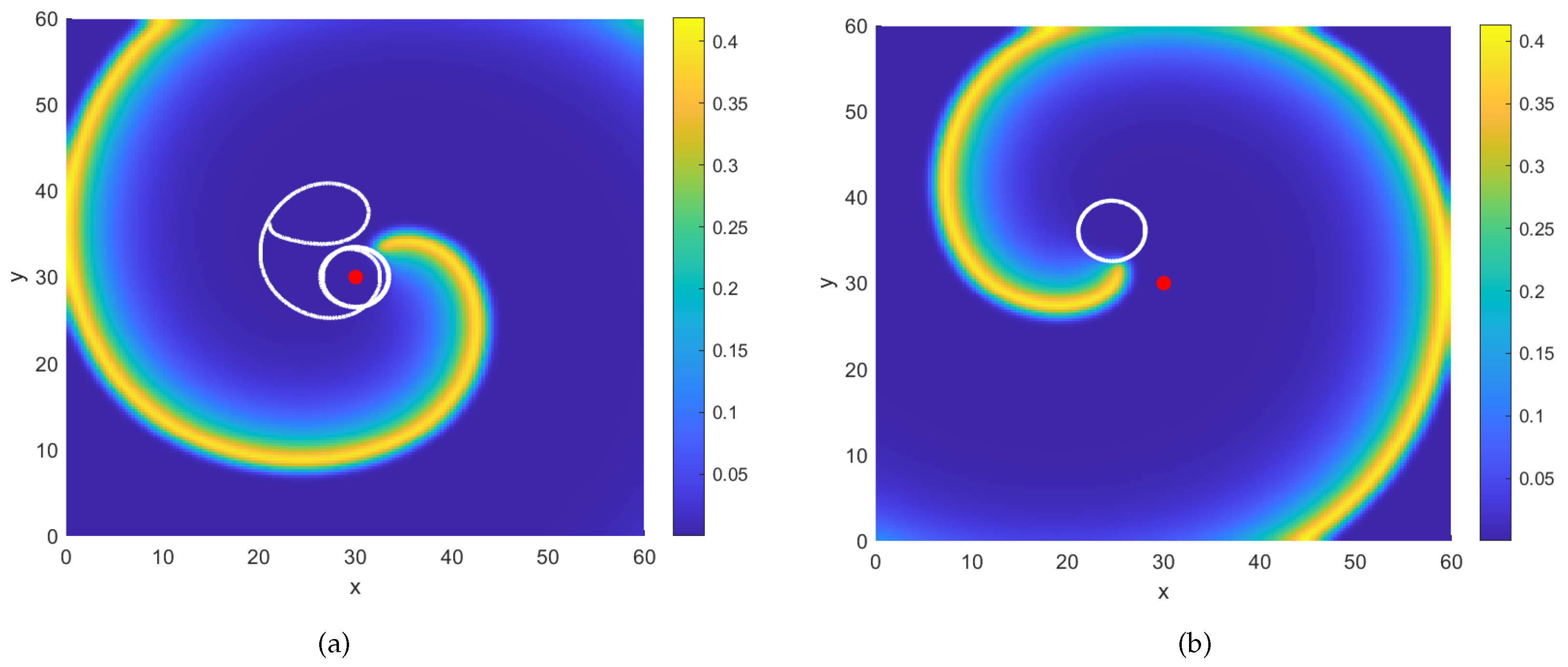
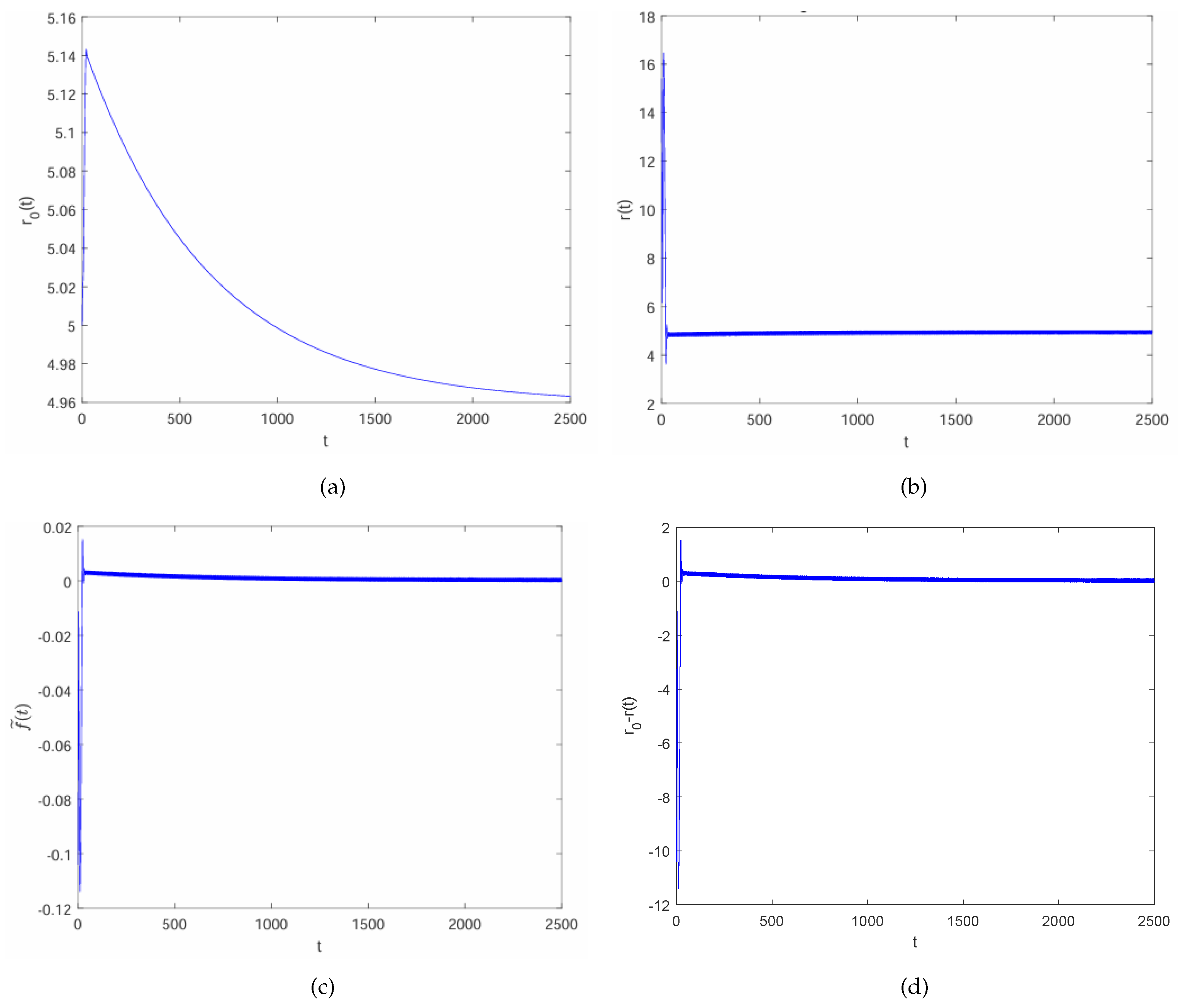
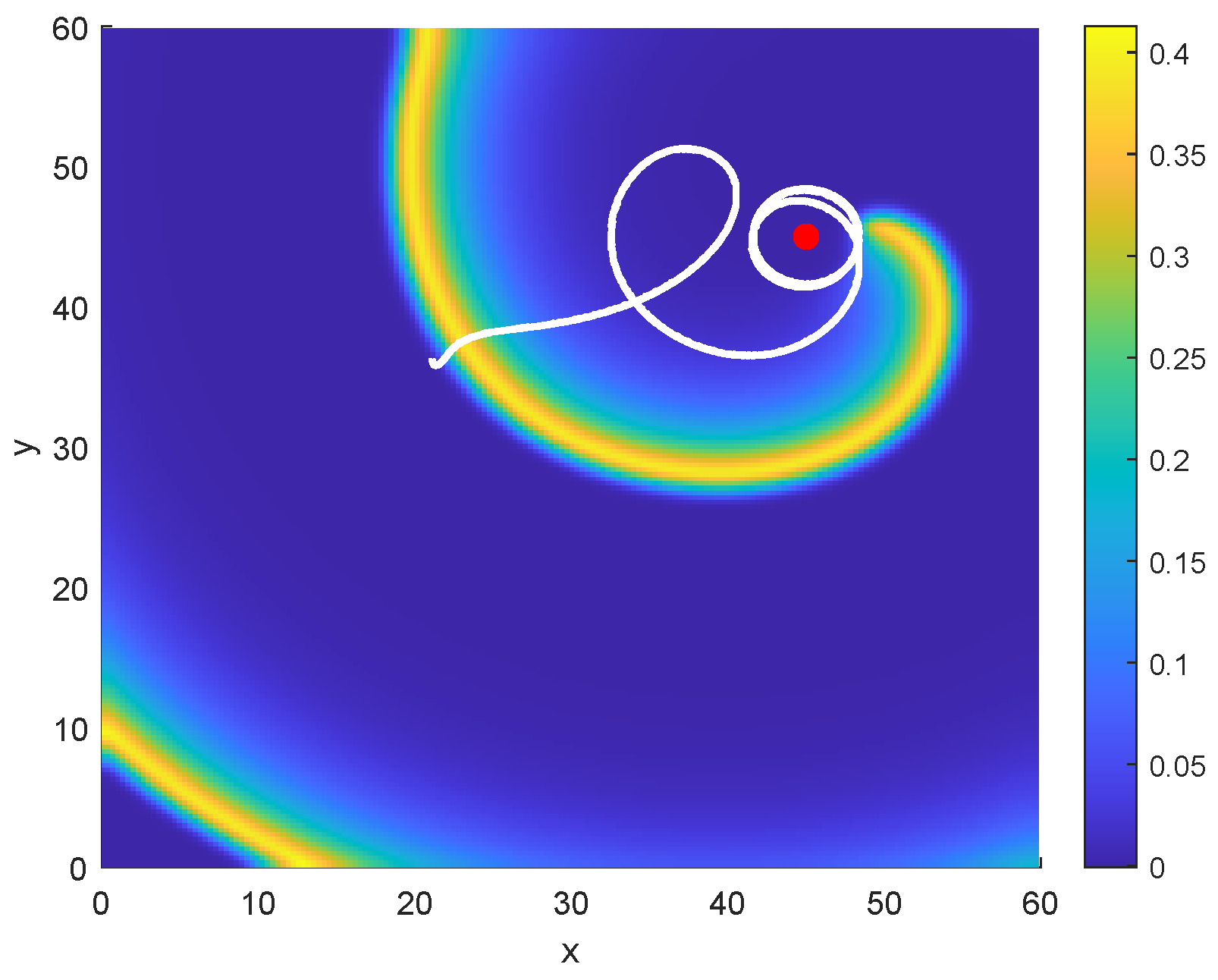
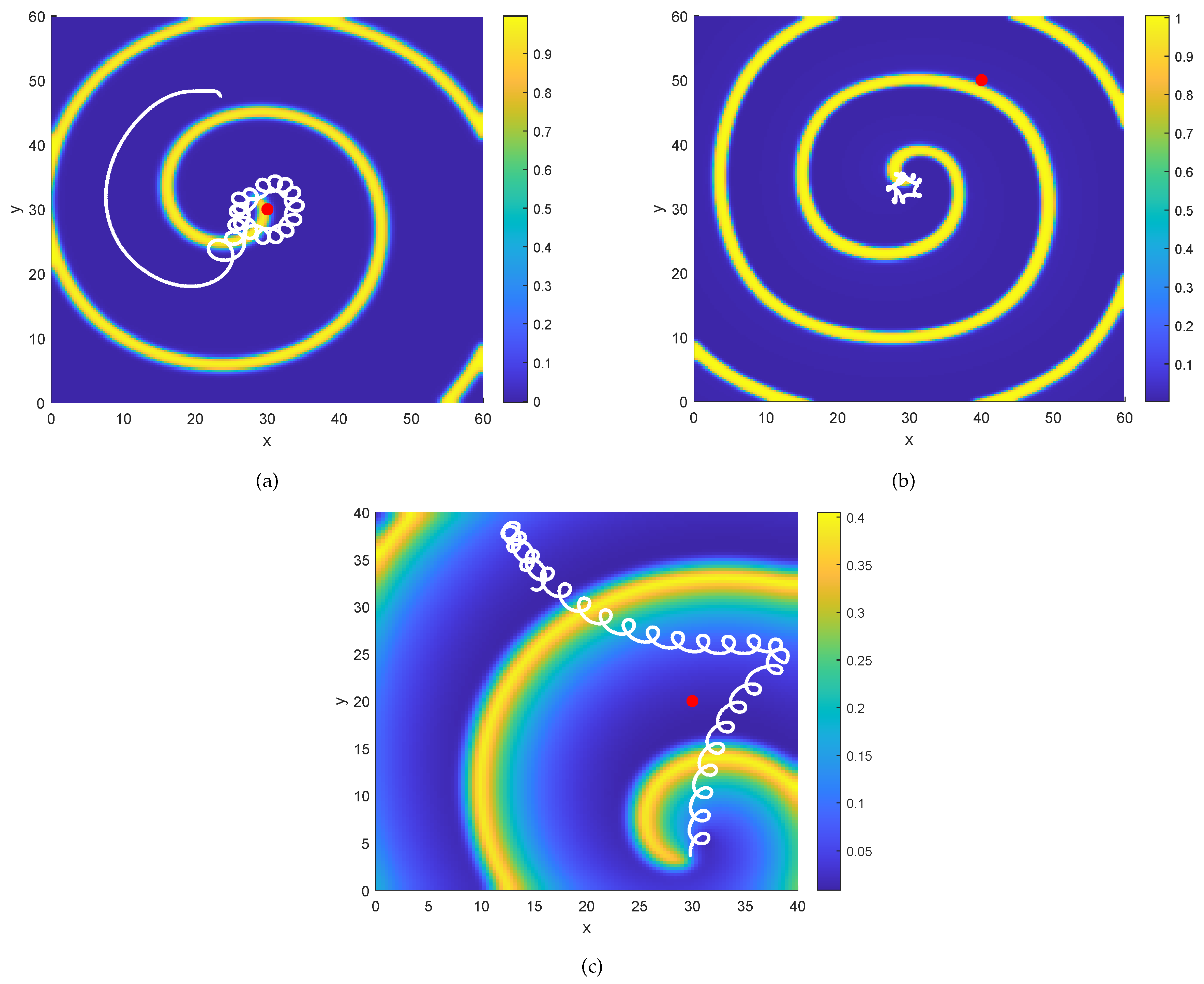
4. The Stability of Spiral Wave and Numerical Results
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Bishop, R.C. An Introduction to Chaotic Dynamics: Classical and Quantum; IOP Publishing: Bristol, UK, 2025. [Google Scholar]
- Almuaddi, S.M. Control of Spiral Waves in Reaction-Diffusion Systems Using Response Function; University of Exeter (United Kingdom): Exeter, UK, 2019. [Google Scholar]
- Tyree, T.J.; Reiss, M.; Rappel, W.-J. Particle model of creation and annihilation captures termination dynamics of spiral defect chaos. Chaos Interdiscip. J. Nonlinear Sci. 2025, 35, 9. [Google Scholar]
- Taher, P.M.; Farhad, T.; Behrouz, D.; Hamzeh, S.S.; Sadat, R.F.; Ebrahim, P. A comparison of Barkley’s behavioral inhibition model (1997) with Barkley’s updated executive functioning model in predicting adult ADHD symptoms: A preliminary report using structural equation modeling. Appl. Neuropsychol. Adult 2025, 32, 140–152. [Google Scholar]
- Tarpan, M.; Achal, J.; Pushpita, G. Programmable Spiral Wave Dynamics: Instability Cascades Driven by Temporal Modulation in a Reaction-Diffusion System. J. Chem. Theory Comput. 2025. [CrossRef]
- Parvej, K.; Sumana, D. Controlling spiral wave dynamics of the BZ system in a modified Oregonator model: From suppression to turbulence. Chaos Interdiscip. J. Nonlinear Sci. 2025, 35, 1. [Google Scholar]
- Zou, Y.; Shi, W.; Lu, C.; Hu, B.; Qiu, F.; Liu, Y. An improved design of high-signal-to-noise ratio spiral-coil EMAT for high-temperature defect detection. Nondestruct. Test. Eval. 2025, 40, 2982–3003. [Google Scholar]
- Meletti, G.; Abide, S.; Viazzo, S.; Curbelo, J.; Harlander, U. Wave-like Spiral Interactions and the Emergence of Quasi-Biennial Oscillations in Strato-Rotational Flows. arXiv 2025, arXiv:2509.06691. [Google Scholar]
- De Coster, T.; Nobacht, A.; Oostendorp, T.; de Vries, A.A.; Coronel, R.; Pijnappels, D.A. Monitoring and modulating cardiac bioelectricity: From Einthoven to End-user. Europace 2025, 27, euae300. [Google Scholar]
- Ferreira, M.; Geraldes, V.; Felix, A.C.; Oliveira, M.; Laranjo, S.; Rocha, I. Advancing Atrial Fibrillation Research: The Role of Animal Models, Emerging Technologies and Translational Challenges. Biomedicines 2025, 13, 307. [Google Scholar] [CrossRef]
- Wang, J.; Liu, H.; Zou, Q.; Hu, J. Experimental Study on Spatiotemporal Evolution Mechanisms of Roll Waves and Their Impact on Particle Separation Behavior in Spiral Concentrators. Separations 2025, 12, 245. [Google Scholar] [CrossRef]
- Perov, G.A.; Kasatkin, A.D.; Presnyakov, S.A.; Kravchenko, N.P. Investigation of Modified Designs of Helix Slowwave Structures for Millimetre and Submillimetre Ranges. In Proceedings of the 2025 Systems of Signal Synchronization, Generating and Processing in Telecommunications (SYNCHROINFO), Tyumen, Russia, 30 June–3 July 2025; pp. 1–5. [Google Scholar]
- Babu, V.K.; Pandit, R. Deep Neural Networks can eliminate Spiral-wave Turbulence in Cardiac Tissue Models. arXiv 2025, arXiv:2509.09806. [Google Scholar] [CrossRef]
- Blackburne, G.; McAlpine, R.G.; Fabus, M.; Liardi, A.; Kamboj, S.K.; Mediano, P.A.M.; Skipper, J.I. Complex slow waves in the human brain under 5-MeO-DMT. Cell Rep. 2025, 44, 8. [Google Scholar] [CrossRef]
- de Groot, N.M.; Kleber, A.; Narayan, S.M.; Ciaccio, E.J.; Doessel, O.; Bernus, O.; Berenfeld, O.; Callans, D.; Fedorov, V.; Hummel, J.; et al. Atrial fibrillation nomenclature, definitions, and mechanisms: Position paper from the international Working Group of the Signal Summit. Heart Rhythm. 2025, 22, 1480–1491. [Google Scholar]
- Anichur, R.; Dipanjali, K.; Tanoy, D.; Muaz, R.; Kanti, D.U.; Musa, M.A.S.; Ghulam, M. From AI to the Era of Explainable AI in Healthcare 5.0: Current State and Future Outlook. Expert Syst. 2025, 42, e70060. [Google Scholar] [CrossRef]
- Ding, Q.; Wu, Y.; Huang, W.; Hu, Y.; Xie, Y.; Jia, Y. Adaptive electric shocks control and elimination of spiral waves using dynamic learning based techniques. Nonlinear Dyn. 2025, 113, 10425–10443. [Google Scholar]
- Emanuele, Z.; Brambley, E.J.; Dwight, B. Deep-water closure model for surface waves on axisymmetric swirling flows. Phys. Rev. Fluids 2025, 10, 024801. [Google Scholar] [CrossRef]
- Shumba, K.B.; Simbarashe, N.; Kenneth, S.; Tinsley, M.R. Tunable photochemical properties of silica gel Belousov–Zhabotinsky micro-reactors: Synthesis and temperature characterization. Chaos Interdiscip. J. Nonlinear Sci. 2025, 35, 6. [Google Scholar]
- Yiğit, O. Novel Spiral Antenna for GNSS Applications. Microw. Opt. Technol. Lett. 2025, 67, e70192. [Google Scholar]
- Wang, H.; Chen, H.; Sun, K.; Zhu, W.; Yao, Z. Spatiotemporal dynamics and synchronization in a memristive Chialvo neural network. Nonlinear Dyn. 2025, 113, 10365–10377. [Google Scholar] [CrossRef]
- Xu, H.; Wu, W.; Pan, D. Localized transient conduction block to suppress and eliminate spiral wave doppler instability: A numerical simulation study. Chaos Solitons Fractals 2025, 193, 116140. [Google Scholar]
- Xu, Y.; McInnes, A.; Kao, C.H.; D’Rozario, A.; Feng, J.; Gong, P. Spatiotemporal dynamics of sleep spindles form spiral waves that predict overnight memory consolidation and age-related memory decline. Commun. Biol. 2025, 8, 1014. [Google Scholar] [CrossRef]
- Dipa, G.; Tanisha, C.; Sarthok, S. IMPLICIT–EXPLICIT TIME INTEGRATION METHOD FOR FRACTIONAL ADVECTION–DIFFUSION-REACTION EQUATIONS. Anziam J. 2025, 67, e2. [Google Scholar]
- Alfifi, H.Y.; Almuaddi, S.M. Stability Analysis and Hopf Bifurcation for the Brusselator Reaction–Diffusion System with Gene Expression Time Delay. Mathematics 2024, 12, 1170. [Google Scholar] [CrossRef]
- Shi, S.; Xu, H.; Ma, L.; Kang, K.; Pang, Y.; Wang, Z.; Hu, J. A high sensitivity and wide frequency band vector hydrophone using PZT-based four spiral beam structure. Measurement 2025, 242, 115840. [Google Scholar]
- Mulimani, M.K.; Echeverria-Alar, S.; Reiss, M.; Rappel, W.J. Prediction of excitable wave dynamics using machine learning. Chaos Solitons Fractals 2025, 192, 115990. [Google Scholar]
- Simon, S.; Ceyhun, Ö.; Heiko, G.; Karsten, U.; Bernd, G. Stability and Instability of Time-Domain Boundary Element Methods for the Acoustic Neumann Problem. Proc. Appl. Math. Mech. 2025. [Google Scholar]
- He, L.; Yang, Y.; Wei, Y. Mechanism of the zigzag and spiral bubble ascension: The alternating steering and continuous chase effects of the side reflux on the bottom surface. Int. J. Heat Fluid Flow 2025, 116, 109980. [Google Scholar] [CrossRef]
- Zhuang, L.; Wang, Z.; Jiang, H.; Shi, X.; Xu, W.; Huang, J. The dynamics of a memristive neuron model and the elimination of spiral waves in neural networks composed of such models. Eur. Phys. J. Spec. Top. 2025, 1–19. [Google Scholar] [CrossRef]
- Kumar, M.M.; Rappel, W.-J. Spiral defect chaos with intermittency increases mean termination time. Phys. Rev. E 2025, 112, 034203. [Google Scholar] [CrossRef]
- Russo, A.M.; Desai, M.Y.; Do, M.M.; Butler, J.; Chung, M.K.; Epstein, A.E.; Guglin, M.E.; Levy, W.C.; Piccini, J.P.; Bhave, N.M.; et al. ACC/AHA/ASE/HFSA/HRS/SCAI/SCCT/SCMR 2025 Appropriate Use Criteria for Implantable Cardioverter-Defibrillators, Cardiac Resynchronization Therapy, and Pacing. J. Am. Coll. Cardiol. 2025, 85, 1213–1285. [Google Scholar]
- Stefano, M. Precision cardiac electrophysiology: Toward digital twins and beyond. J. Precis. Med. Health Dis. 2025, 2, 100009. [Google Scholar]
- Pravdin, S.F.; Alexander, V.P. Role of myocardial ischemia components in overdrive pacing of spiral waves. Chaos Solitons Fractals 2025, 196, 116332. [Google Scholar]
- Christian, K.; Pascal, S. Stability of N-front and N-back solutions in the Barkley model. GAMM-Mitteilungen 2025, 48, e70001. [Google Scholar]
- Gao, J.; Xu, B.; Shen, C. Period-doubled spiral waves without line defects in oscillatory systems. Phys. Rev. E 2025, 112, 014203. [Google Scholar]
- Xue, Y.; Yuan, G.; Guo, F.; Shen, W. Dynamics of spiral wave chimeras subjected to a local feedback control. Commun. Nonlinear Sci. Numer. Simul. 2025, 148, 108859. [Google Scholar] [CrossRef]
- Khaothong, K.; Chanchang, V.; Osaklung, J.; Sutthiopad, M.; Kijamnajsuk, P.; Luengviriya, J.; Luengviriya, C. Effect of Electric Field on Partially Pinned Scroll Waves in Excitable Chemical Media. ACS Omega 2025, 10, 35293–35300. [Google Scholar] [CrossRef] [PubMed]
- Benedetti, L.; Fan, R.; Weigel, A.V.; Moore, A.S.; Houlihan, P.R.; Kittisopikul, M.; Park, G.; Petruncio, A.; Hubbard, P.M.; Pang, S.; et al. Periodic ER-plasma membrane junctions support long-range Ca2+ signal integration in dendrites. Cell 2025, 188, 484–500. [Google Scholar]
- Chen, D.; Wang, F.; Liu, Y.; Lyu, W.; Zhao, X.; Fang, R.; Chen, L.; Li, Y. Selective Electroreduction of CO2 to CO over Ultrawide Potential Window via Implanting Active Site with Long-Range P Regulation on Periodic Pores. Angew. Chem. 2025, 137, e202421149. [Google Scholar] [CrossRef]
- Alfifi, H.Y. Effects of Diffusion and Delays on the Dynamic Behavior of a Competition and Cooperation Model. Mathematics 2025, 13, 1026. [Google Scholar] [CrossRef]
- Kai, G. Emergence and regulation of spiral waves in a neuronal network with adaptive synaptic current. Eur. Phys. J. Spec. Top. 2025, 234, 1051–1061. [Google Scholar]
- Speights, J.C.; Aust, V.; Lu, Q. Spiral Density Waves in the Multiple-armed Galaxy NGC 628. Astrophys. J. 2025, 981, 115. [Google Scholar] [CrossRef]
- Eriksson, L.E.J.; Yang, C.-C.; Armitage, P.J. Particle fragmentation inside planet-induced spiral waves. Mon. Not. R. Astron. Soc. Lett. 2025, 537, L26–L32. [Google Scholar] [CrossRef]
- Kolesnikov, I.D.; Bukh, A.V.; Muni, S.S.; Ram, J.S. Impact of Lévy noise on spiral waves in a lattice of Chialvo neuron map. Chaos Solitons Fractals 2025, 190, 115759. [Google Scholar] [CrossRef]
- Garcia-Azpeitia, C.; Ghanem, Z.; Krawcewicz, W. Global Bifurcation of Spiral Wave Solutions to the Complex Ginzburg-Landau Equation. arXiv 2025, arXiv:2507.15098. [Google Scholar] [CrossRef]
- Wang, J.; Chang, Z.; Liu, T.; Chen, L. A review of linear and nonlinear vibration analysis of composite laminated structures by computational approaches: 2015–2024. Nonlinear Dyn. 2025, 113, 10839–10859. [Google Scholar] [CrossRef]
- Du, K.; Fan, J.-J. GP-CMRH: An inner product free iterative method for block two-by-two nonsymmetric linear systems. arXiv 2025, arXiv:2509.11272. [Google Scholar]
- Qiao, W.; Liu, Y.; Jiao, J.; Chen, X.; Zhang, H. Spatiotemporal Analysis and Characterization of Multilayer Buried Cracks in Rails Using Swept-Frequency Eddy-Current-Pulsed Thermal Tomography. Appl. Sci. 2025, 15, 9069. [Google Scholar] [CrossRef]
- Eisenberg, R.S. Current Flow in Nerves and Mitochondria: An Electro-Osmotic Approach. Biomolecules 2025, 15, 1063. [Google Scholar] [CrossRef] [PubMed]
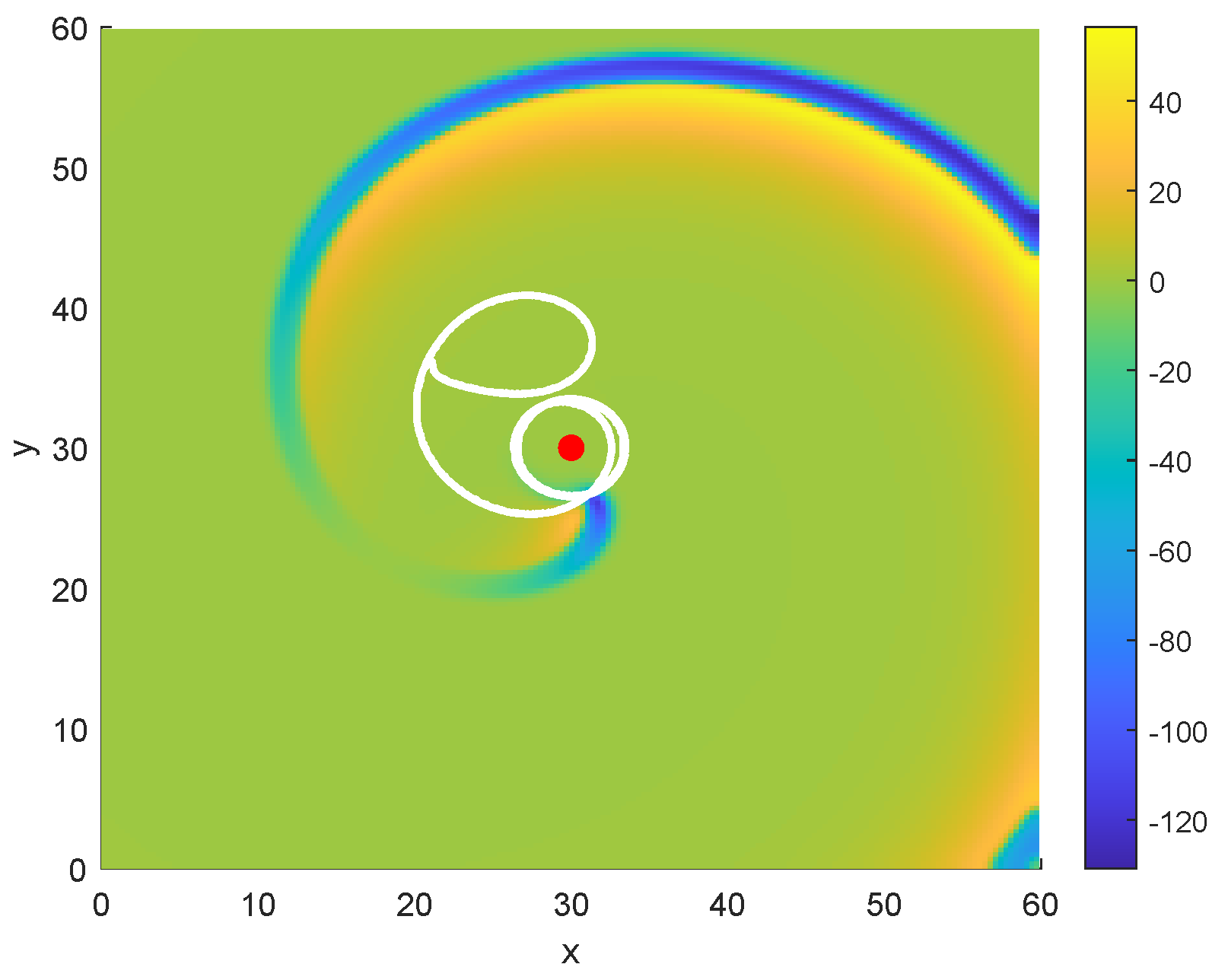

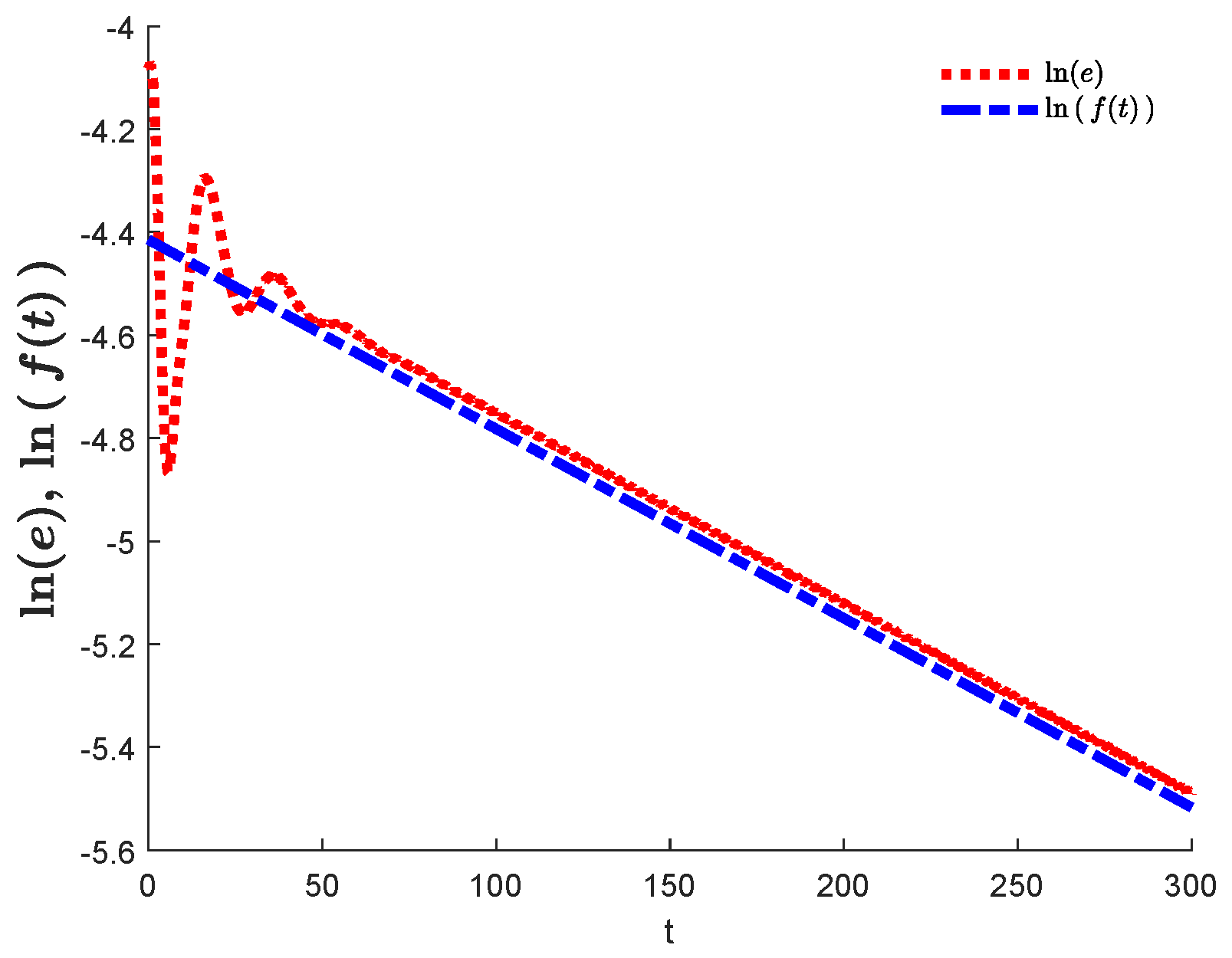
| Iteration Number m | Angular Velocity Estimate |
|---|---|
| 1 | |
| 2 | |
| 3 | |
| 4 | |
| 5 | |
| 6 | |
| 7 | |
| 8 | |
| 9 | |
| 10 | |
| 11 | |
| 12 | |
| 13 | |
| 14 | |
| 15 | |
| 16 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Almuaddi, S.M.; Alfifi, H.Y. Controlling Spiral Wave Solutions in the Barkley System Using a Proportional Feedback Control. Symmetry 2025, 17, 1721. https://doi.org/10.3390/sym17101721
Almuaddi SM, Alfifi HY. Controlling Spiral Wave Solutions in the Barkley System Using a Proportional Feedback Control. Symmetry. 2025; 17(10):1721. https://doi.org/10.3390/sym17101721
Chicago/Turabian StyleAlmuaddi, Saad M., and H. Y. Alfifi. 2025. "Controlling Spiral Wave Solutions in the Barkley System Using a Proportional Feedback Control" Symmetry 17, no. 10: 1721. https://doi.org/10.3390/sym17101721
APA StyleAlmuaddi, S. M., & Alfifi, H. Y. (2025). Controlling Spiral Wave Solutions in the Barkley System Using a Proportional Feedback Control. Symmetry, 17(10), 1721. https://doi.org/10.3390/sym17101721





