Thermo-Fluid Dynamic Performance of Self-Similar Dendritic Networks: CFD Analysis of Structural Isomers
Abstract
1. Introduction
- (1)
- Do flow asymmetries in branched structures with heat transfer differ from those without it?
- (2)
- Can heat transfer amplify or mitigate these asymmetric effects?
- (3)
- Are thermal performance markers effective for identifying fluid dynamic asymmetries?
2. Methods
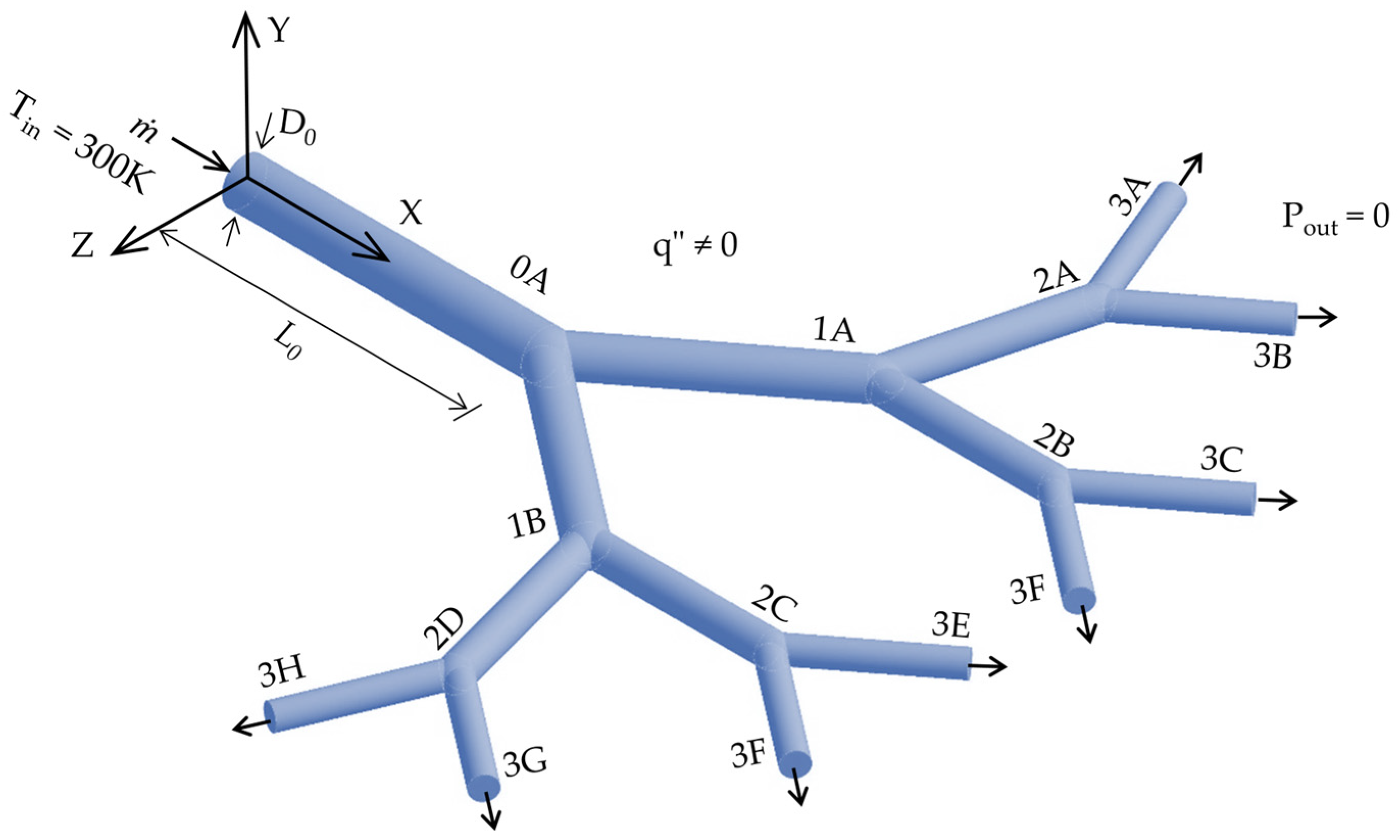
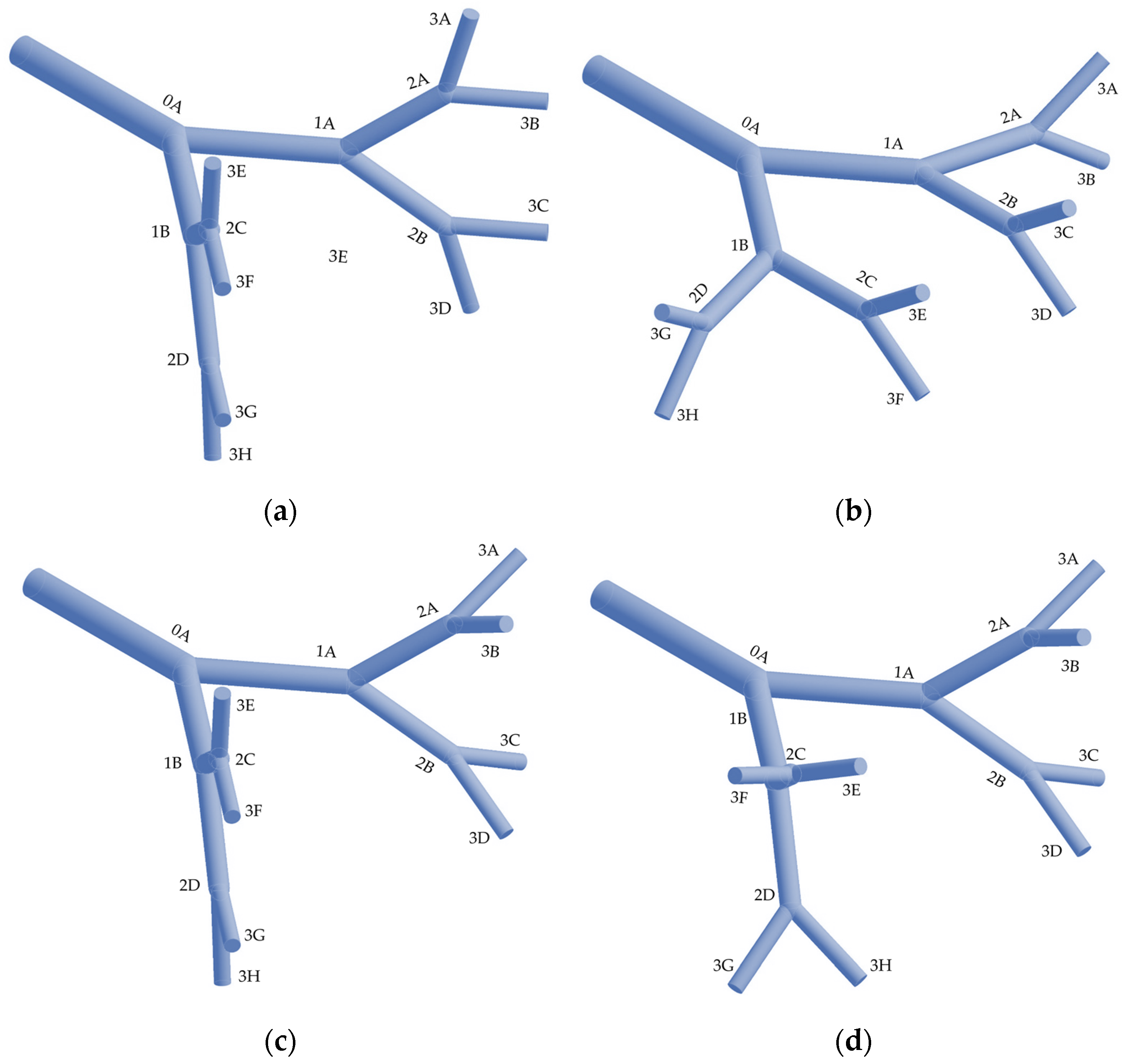
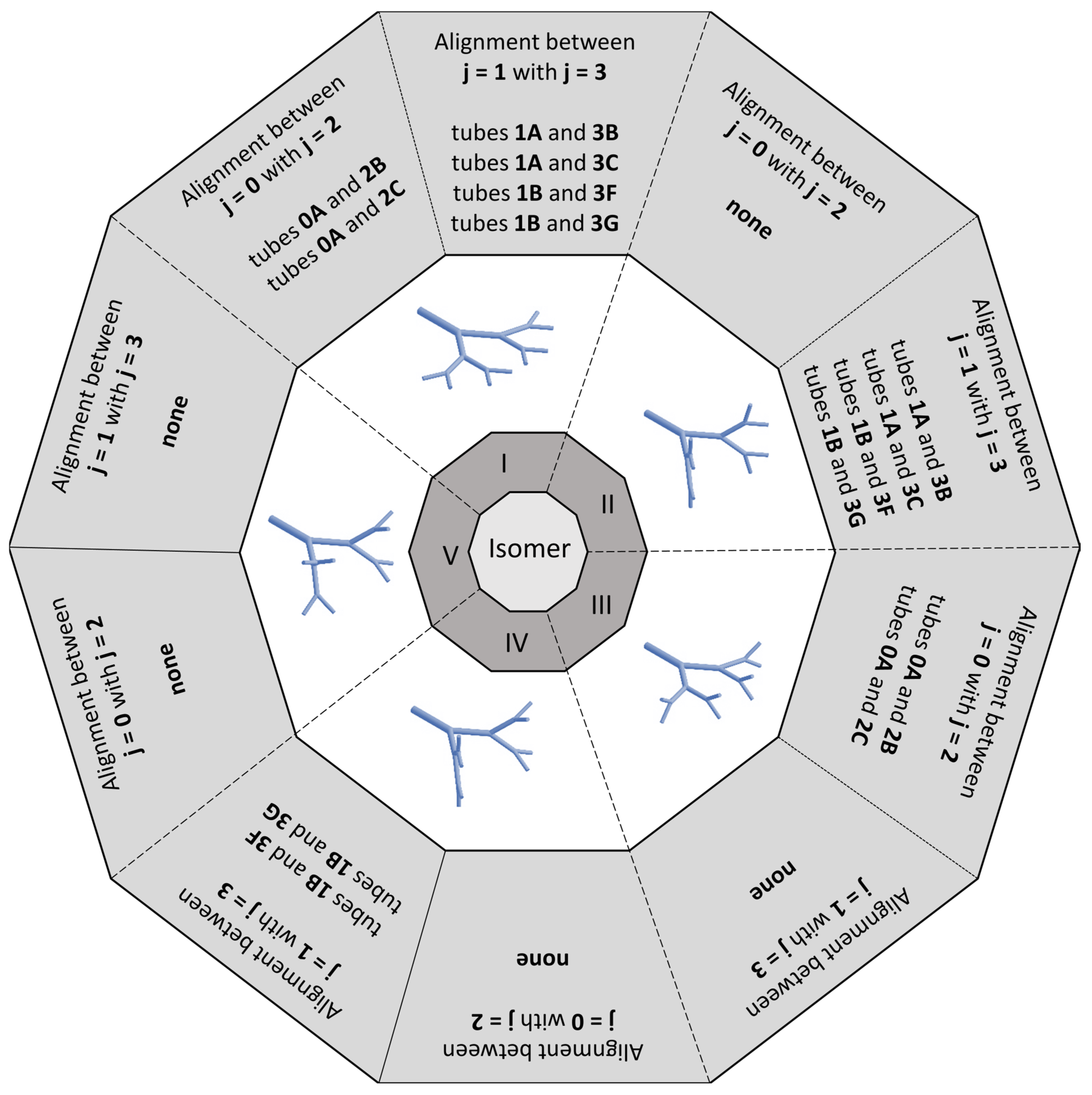
2.1. Geometrical Modeling
2.2. Mathematical and Numerical Modeling
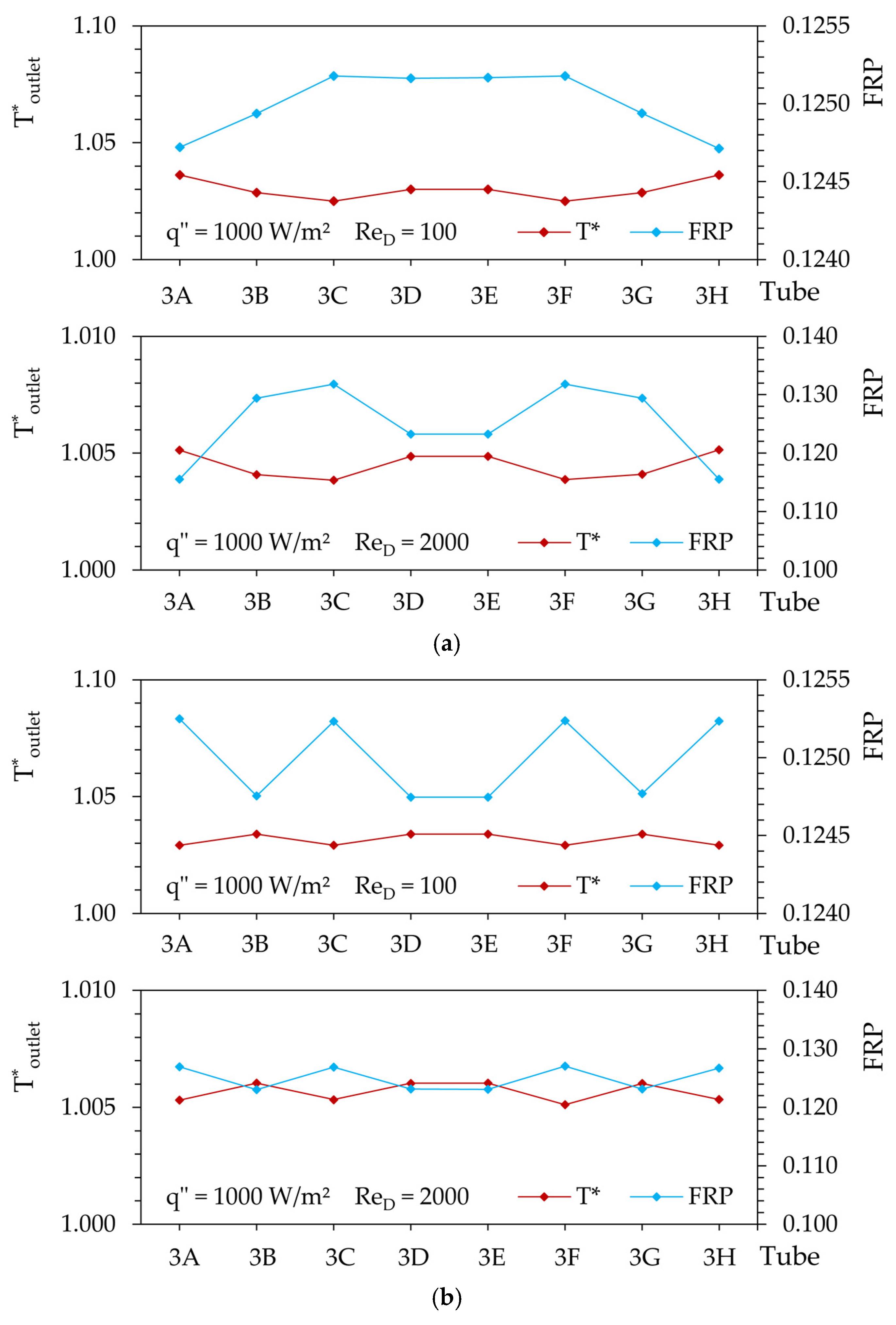
2.3. Network Thermo-Fluid Dynamic Performance
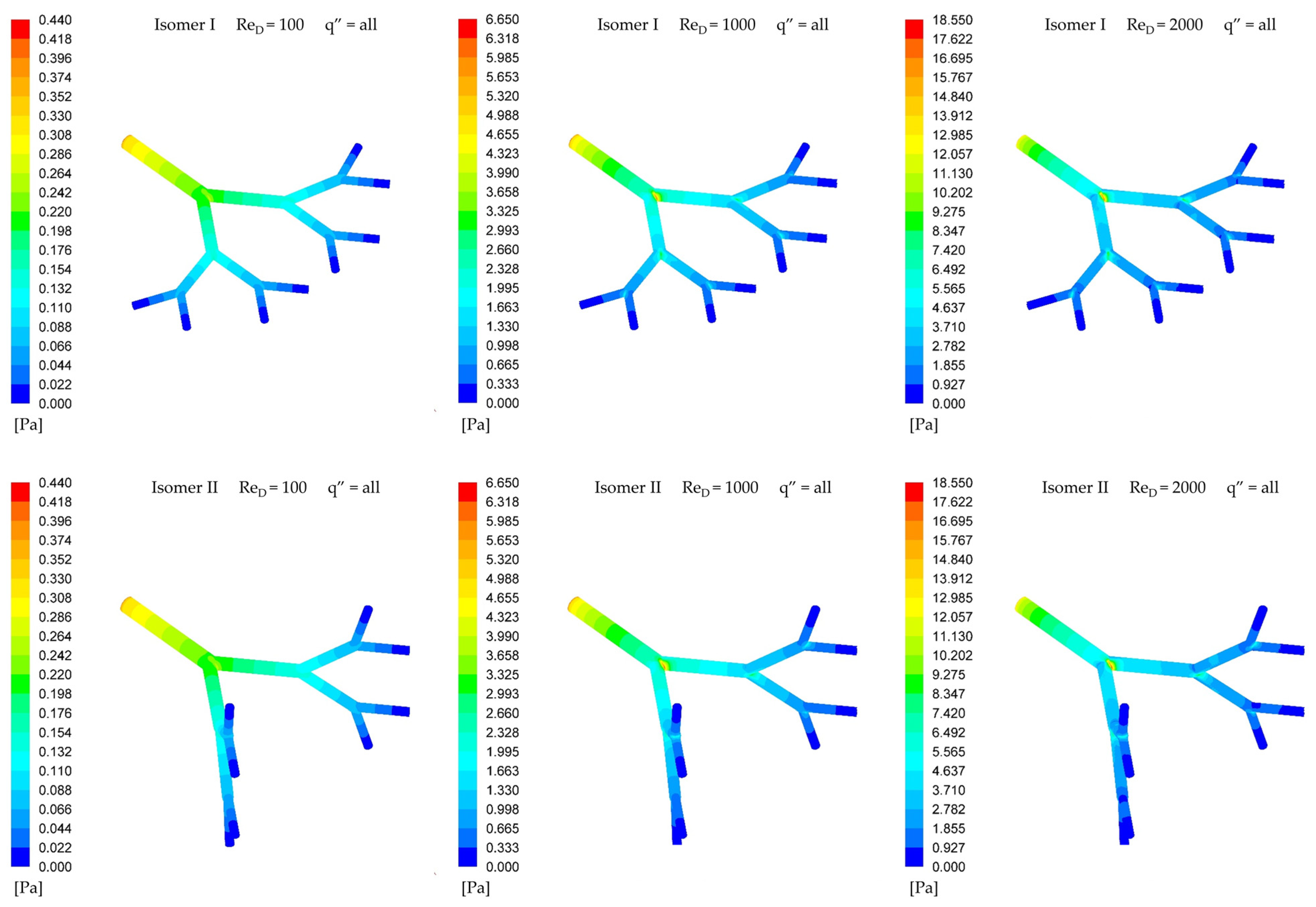
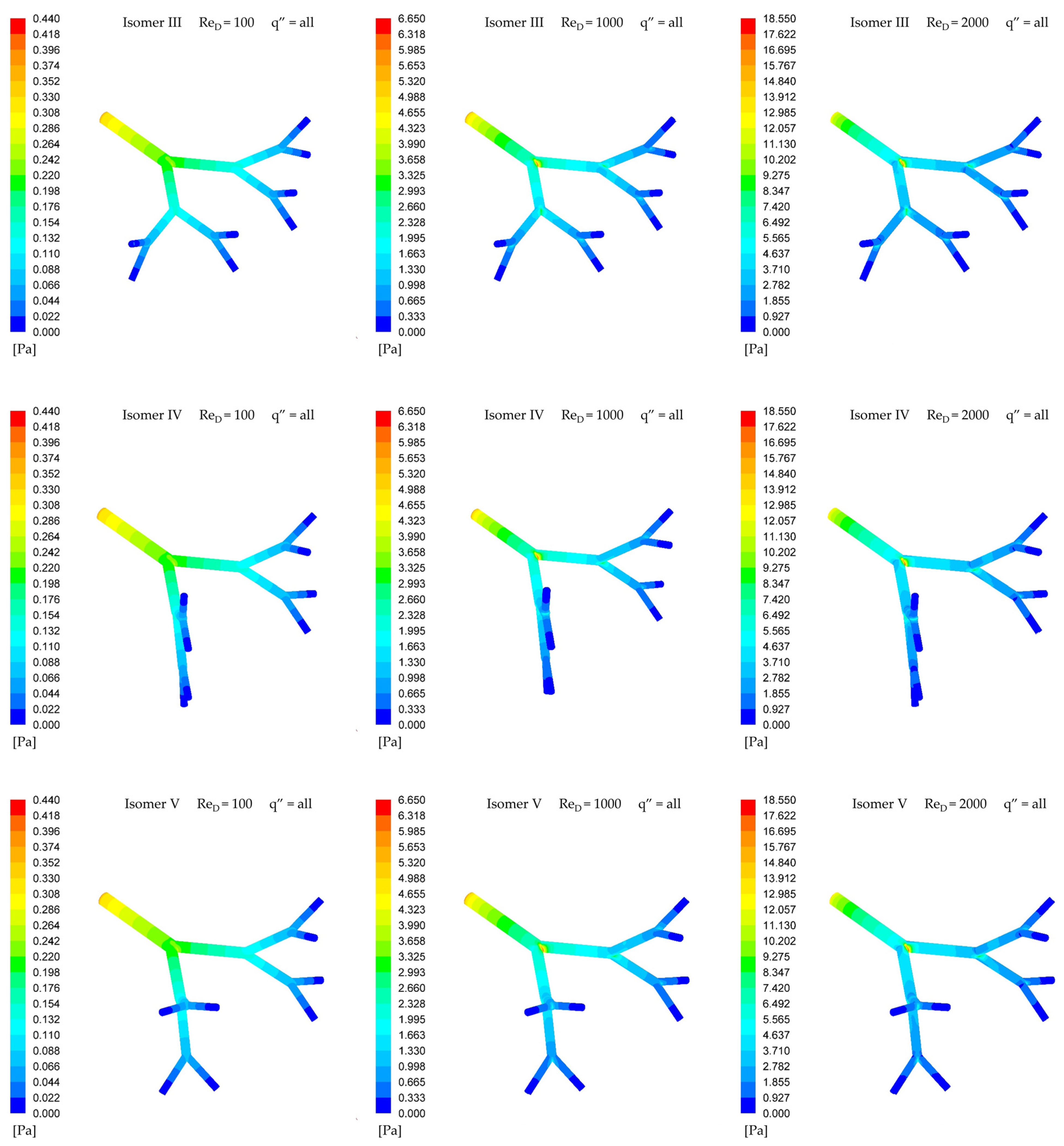
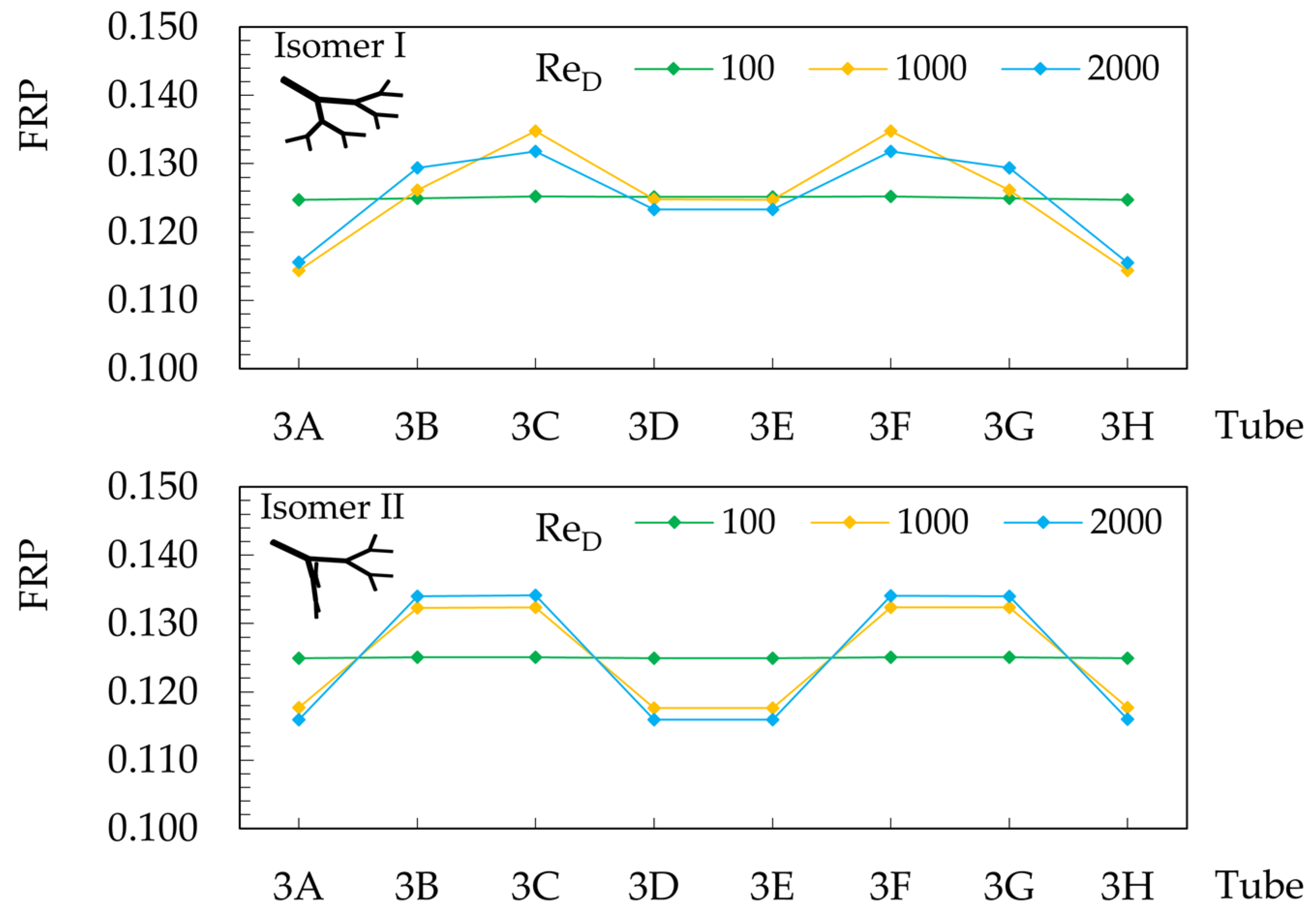
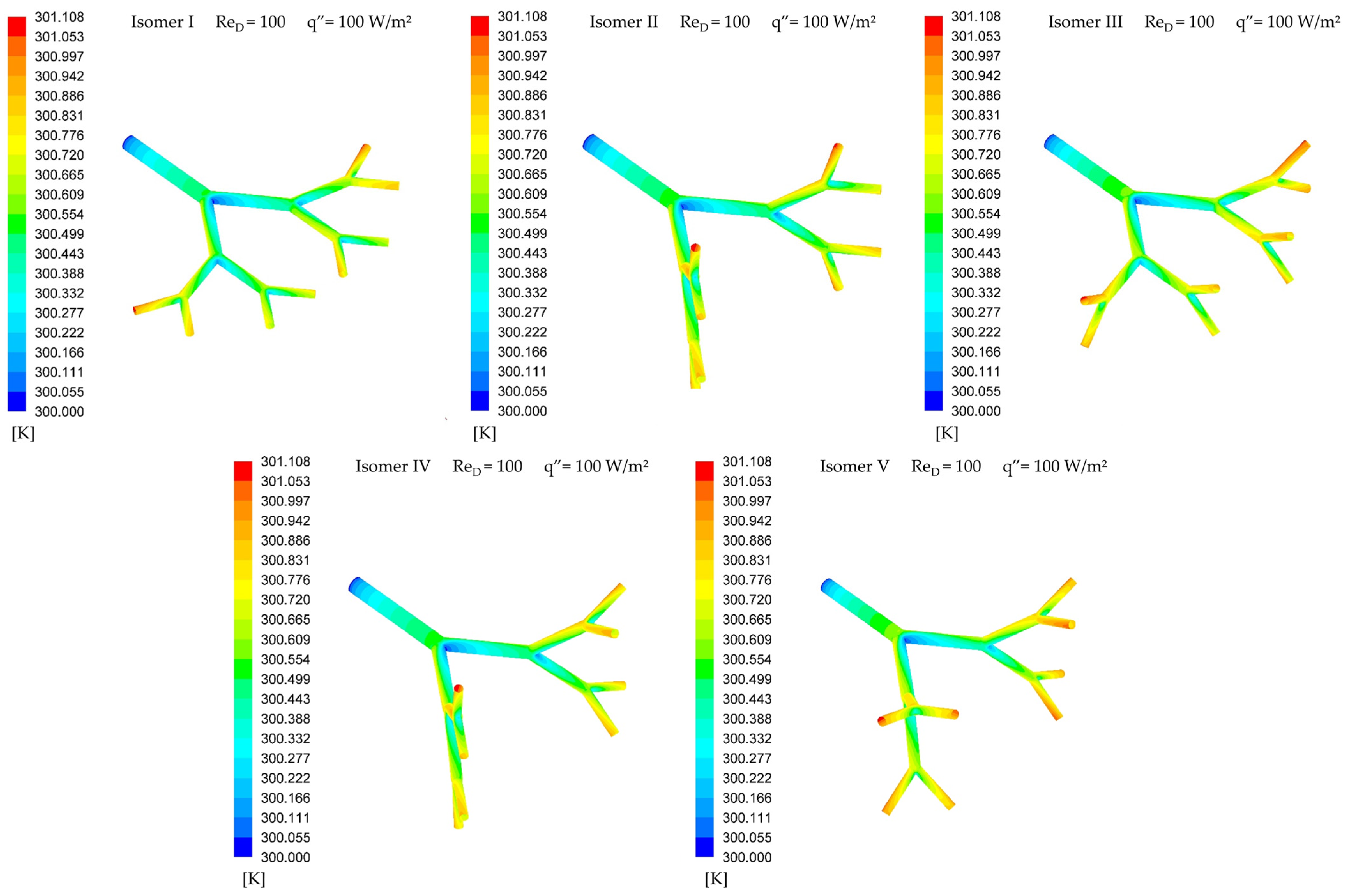
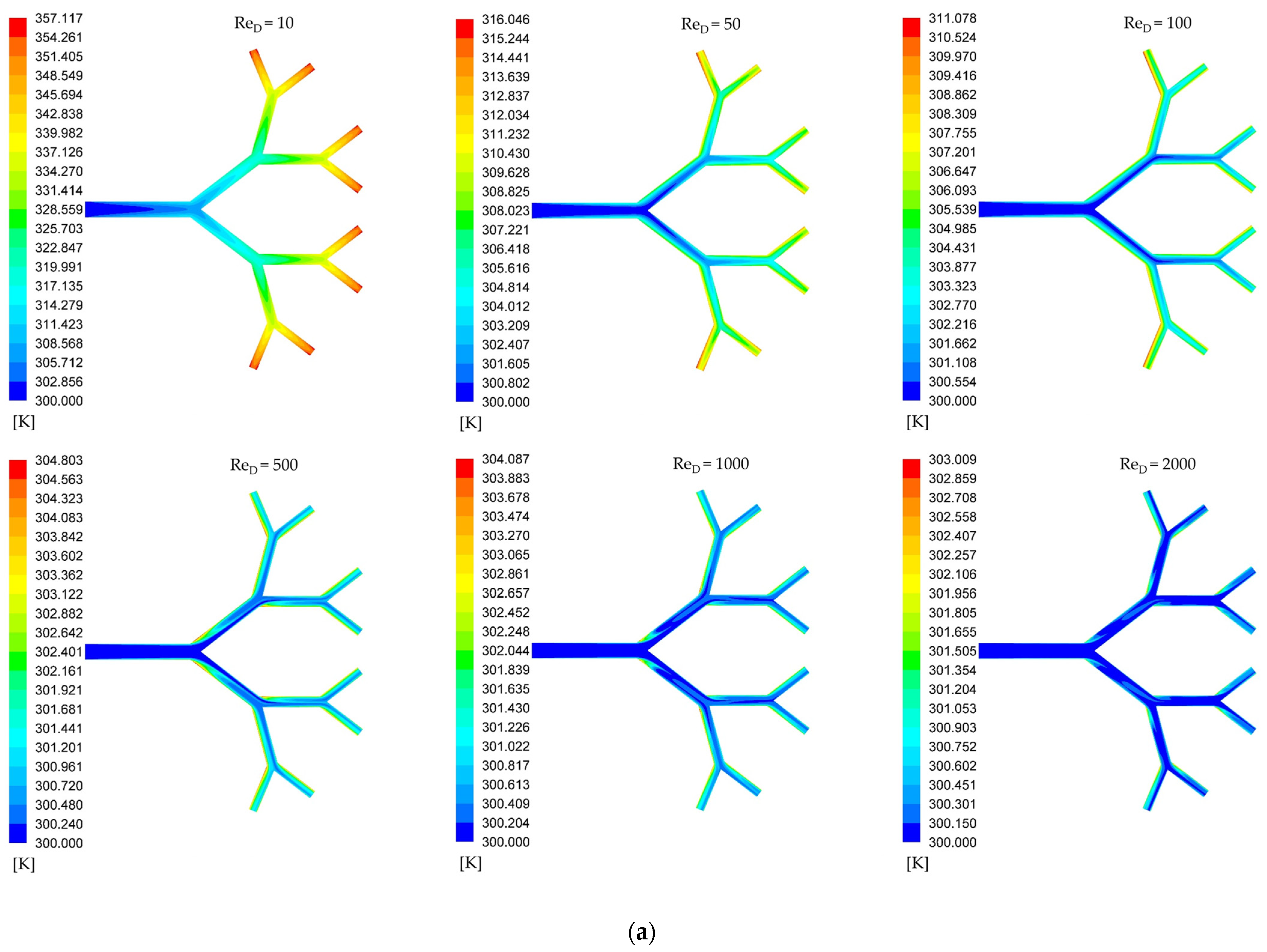
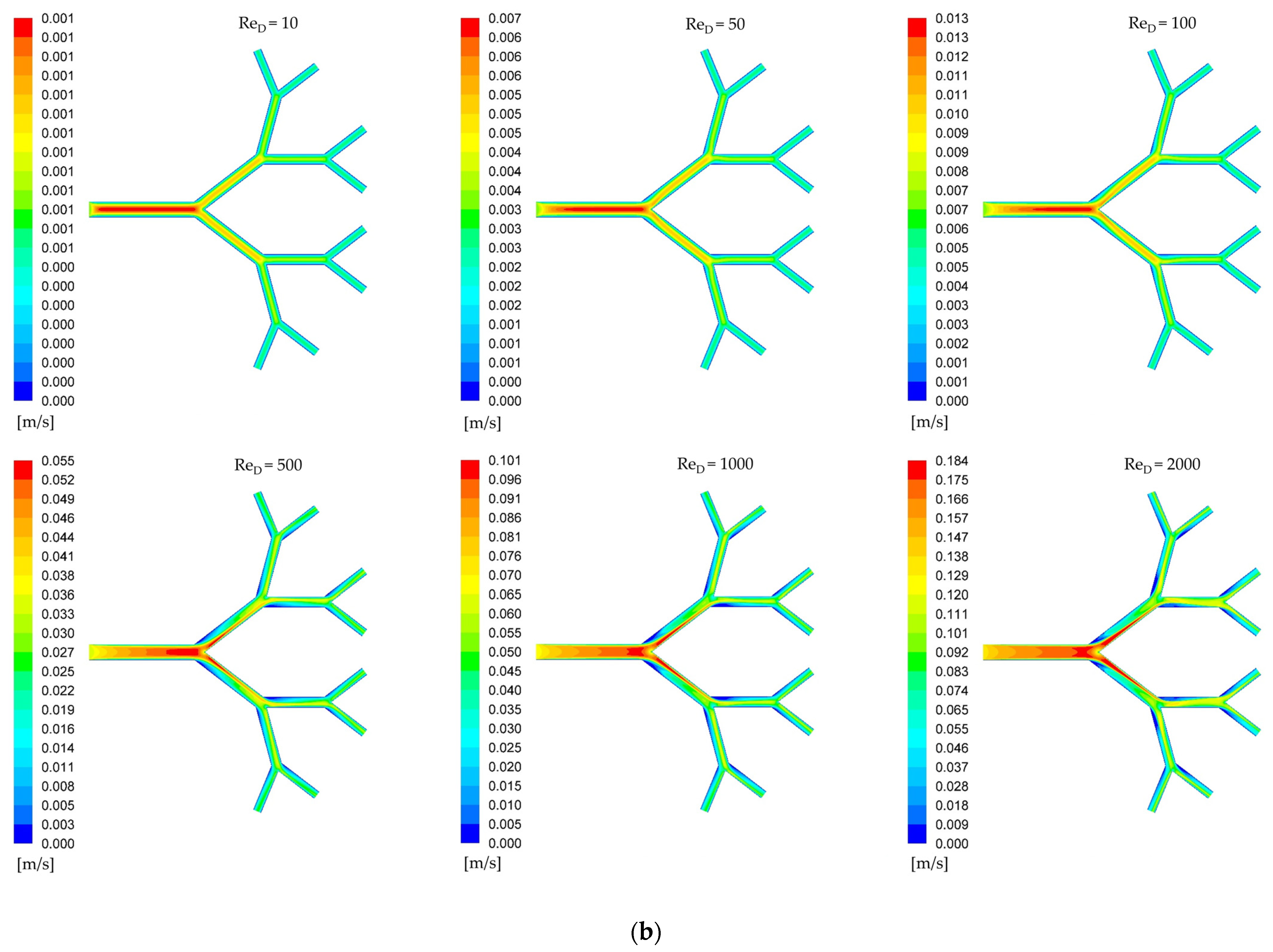
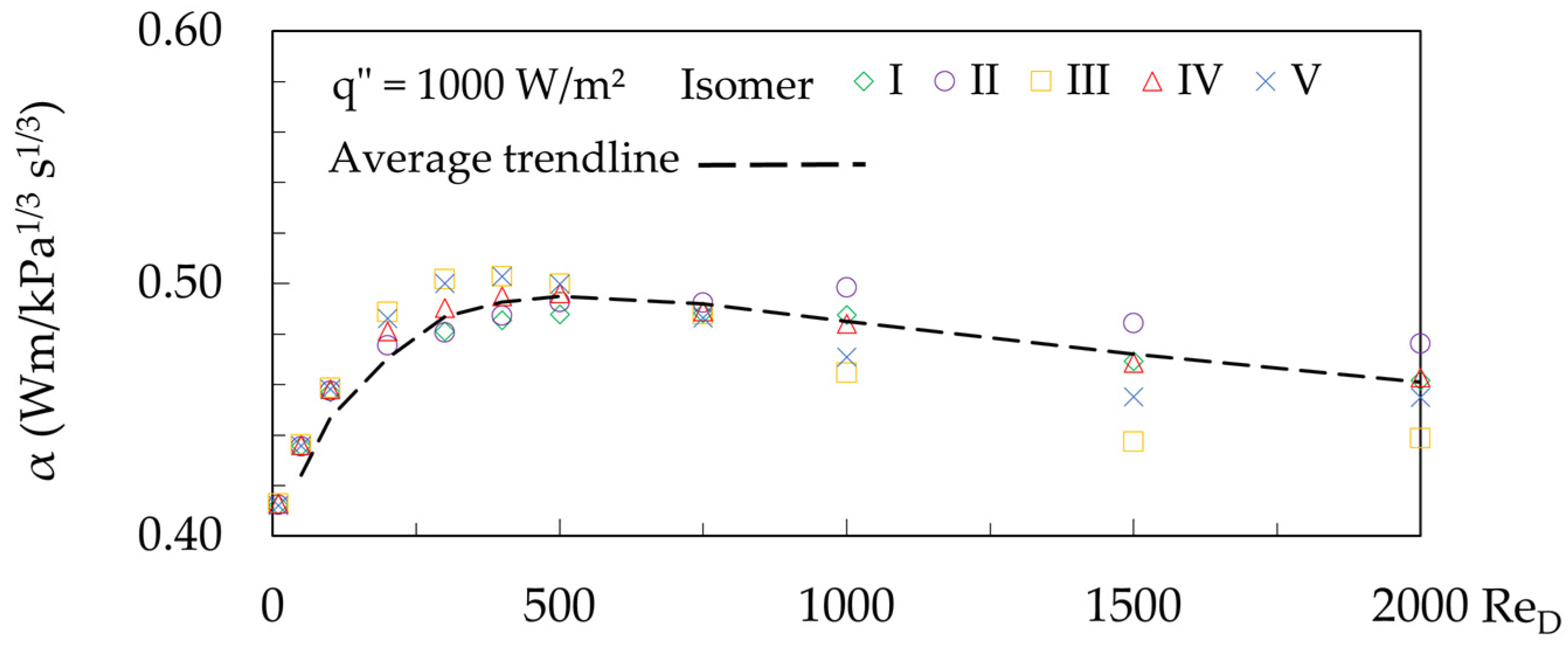
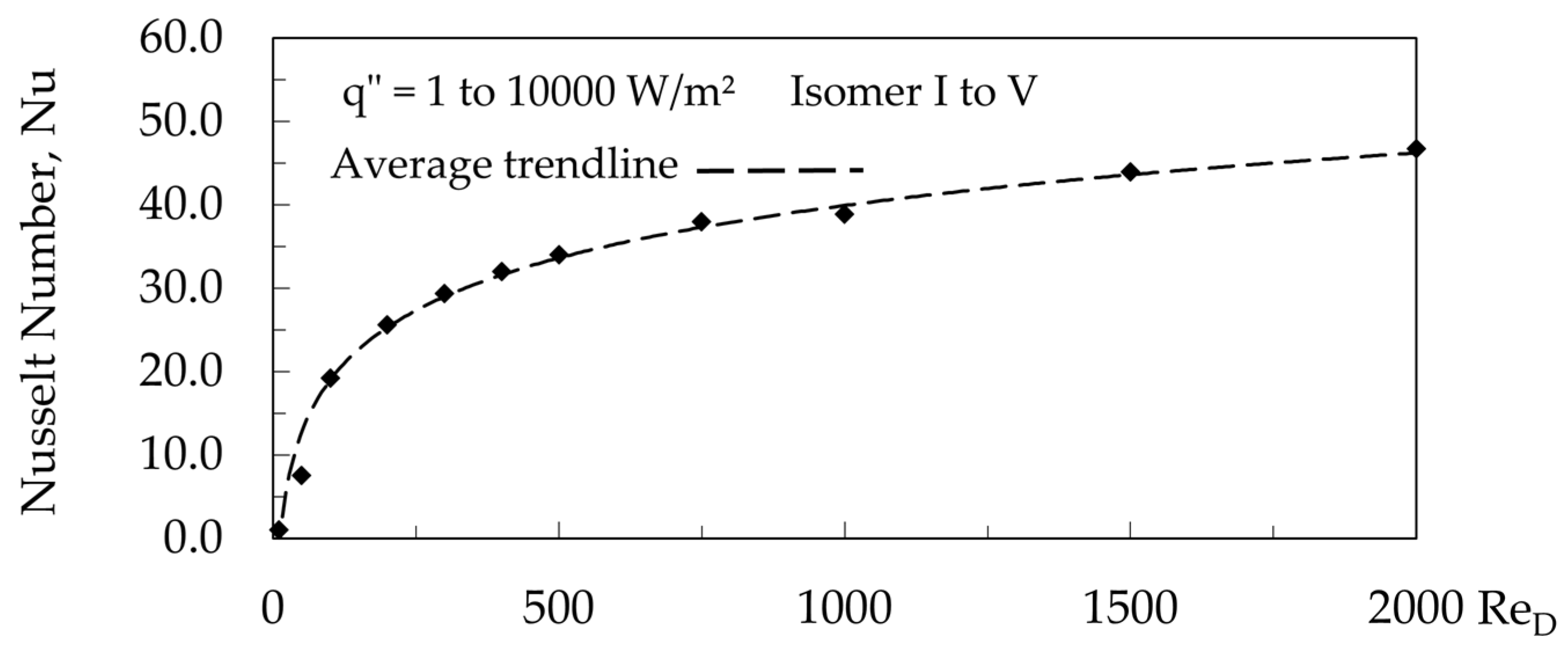
3. Results and Discussion
Pressure Drop Characteristics
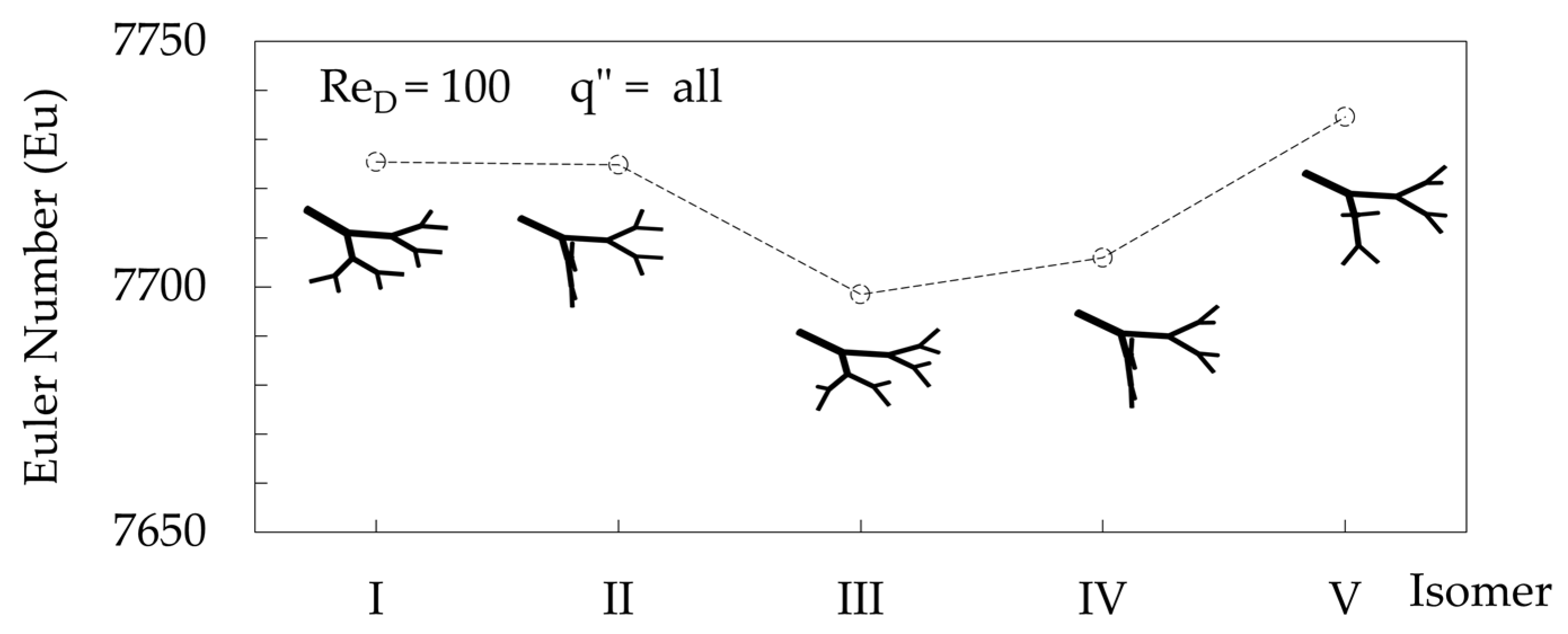
4. Conclusions
- The structure that has the lowest pressure drop (i.e., isomer I) does not correspond to the structure that best distributes the flow symmetrically (i.e., isomer V). This result is obtained with and without heat transfer on the walls.
- Changing the planes that contain the branching levels is not sufficient to correct asymmetries in symmetrical structures.
- Heat transfer from the wall to the fluid generates insignificant effects on the flow asymmetry; that is, it does not amplify or attenuate asymmetric effects.
- For the assessment of asymmetry in complex structures, thermal effects directly correlate with fluid dynamic effects. The use of heat transfer as a diagnostic tool is effective for identifying fluid dynamic asymmetries.
- The response of thermal effects is more sensitive than that of fluid dynamic effects for low Reynolds numbers.
- The trade-off between the pressure drop that increases pumping work and the positive effects on heat transfer was more significant in the range 200 ≤ ReD ≤ 500.
- According to constructal law, the symmetrical structure that best achieves the objective is the isomer V.
Upcoming Studies
- Explore and evaluate tree-shaped networks with more than three levels of branching;
- Examine how homothetic relationships affect structures with asymmetrical bifurcations and their requirements for symmetric flows;
- Explore the asymmetry of dimensional scales for applications with extremely high heat transfer density;
- Explore engineering metrics like global and local Nusselt Number and pumping power per heat removed.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A. Geometric Parameters
| V0 (m3) | V1 (m3) | V2 (m3) | V3 (m3) |
|---|---|---|---|
| 0.0000176714586764426 | 0.0000176714586764426 | 0.0000176714586764426 | 0.0000176714586764426 |
| aDi | L0 (m) | L1 (m) | L2 (m) | L3 (m) | D0 (m) | D1 (m) | D2 (m) | D3 (m) |
|---|---|---|---|---|---|---|---|---|
| 0.8 | 0.10000 | 0.07813 | 0.06104 | 0.04768 | 0.01500 | 0.01200 | 0.00960 | 0.00768 |
Appendix B. Svelteness Factor or Svelteness Number
| aDi | A (m2) | VT (m3) | Sv |
|---|---|---|---|
| 0.8 | 0.0746311108520472 | 0.0000706858347057704 | 6.6 |
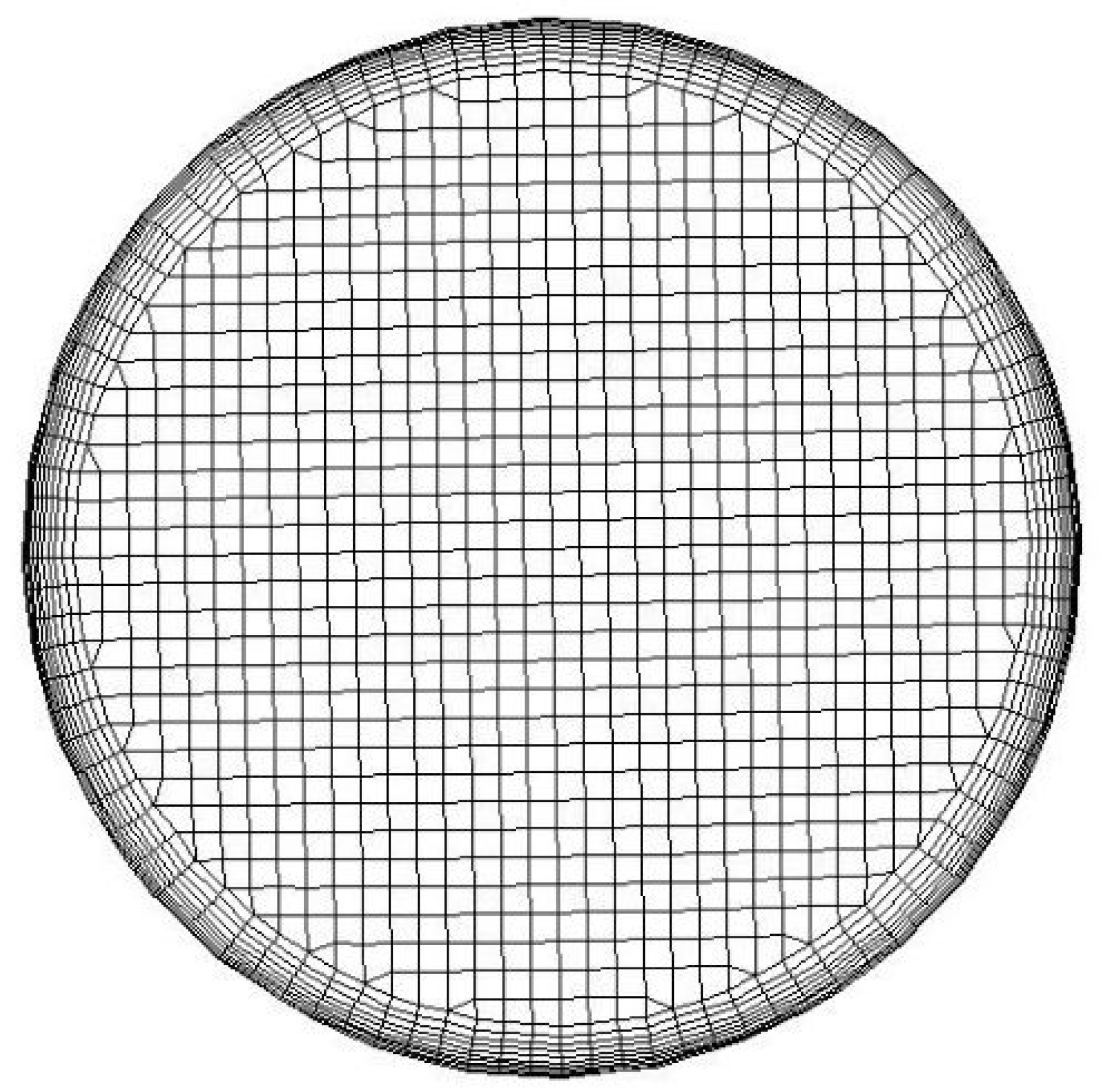
Appendix C. Mesh Characteristics
References
- Bejan, A. Shape and Structure, From Engineering to Nature, 1st ed.; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar]
- Weible, E.R. Morphometry of the Human Lung; Springer: Berlin/Heidelberg, Germany, 1963. [Google Scholar]
- McCulloh, K.A.; Sperry, J.S.; Adler, F.R. Water transport in plants obeys Murray’s law. Nature 2003, 421, 939–942. [Google Scholar] [CrossRef]
- Sarraf, K.; Launay, S.; Tadrist, L. Complex 3D-flow analysis and corrugation angle effect in plate heat exchangers. Int. J. Therm. Sci. 2015, 94, 126–138. [Google Scholar] [CrossRef]
- Mendoza Orbegoso, E.M.; Alcántara, J.A.; Verástegui, L.J.; Bengoa, J.C.; Marcelo-Aldana, D.; La Madrid Olivares, R.; Kyprianidis, K.G. Thermofluidics in Water-in-Glass Evacuated-Tube Solar Collectors Analysis Based on the Symmetry Conditions of Heat Flux and Tilt Angle. Symmetry 2025, 17, 44. [Google Scholar] [CrossRef]
- Bejan, A. Constructal-theory network of conducting paths for cooling a heat generating volume. Int. J. Heat Mass Transf. 1997, 40, 799–816. [Google Scholar] [CrossRef]
- Sauermoser, M.; Kjelstrup, S.; Kizilova, N.; Pollet, B.; Flekkøy, E.G. Seeking minimum entropy production for a tree-like flow-field in a fuel cell. Phys. Chem. 2020, 22, 6993–7003. [Google Scholar] [CrossRef] [PubMed]
- Fan, C.; Wu, C.L.; Wang, Y.; Wang, B.; Wang, J. Thermal metamaterials: From static to dynamic heat manipulation. Phys. Rep. 2024, 1077, 1–111. [Google Scholar] [CrossRef]
- Ehlers, H.; Olivier, T.; Trietsch, S.J.; Vulto, P.; Burton, T.P.; Van Den Broek, L.J. Microfluidic artery-on-a-chip model with unidirectional gravity-driven flow for high-throughput applications. Lab Chip 2025, 25, 2376–2389. [Google Scholar] [CrossRef]
- Emerson, D.R.; Cieslicki, K.; Gu, X.; Barber, R.W. Biomimetic design of microfluidic manifolds based on a generalised Murray’s law. Lab Chip 2006, 3, 447–454. [Google Scholar] [CrossRef]
- Pepe, V.R.; Miguel, A.F.; Zinani, F.S.F.; Rocha, L.A.O. New insights into creeping fluid flow through dendritic networks: A constructal view. Int. Commun. Heat Mass Transf. 2022, 139, 106409. [Google Scholar] [CrossRef]
- Pepe, V.R.; Miguel, A.F.; Zinani, F.S.F.; Rocha, L.A.O. Fluid Flow Through Isomeric Constructal Networks of Tubes. J. Porous Media 2024, 27, 1–18. [Google Scholar] [CrossRef]
- Pepe, V.; Miguel, A.F.; Zinani, F.; Rocha, L. Numerical Study of Carreau Fluid Flow in Symmetrically Branched Tubes. Symmetry 2025, 17, 48. [Google Scholar] [CrossRef]
- Andrade Jr, J.S.; Alencar, A.M.; Almeida, M.P.; Mendes Filho, J.; Buldyrev, S.V.; Zapperi, S.; Stanley, H.E.; Suki, B. Asymmetric flow in symmetric branched structures. Phys. Rev. Let. 1998, 81, 926–929. [Google Scholar] [CrossRef]
- Pradhan, K.; Guha, A.; Halder, P.K. Characteristics of pressure drop, mass flow distribution and flow asymmetry in three-dimensional branching networks based on model human bronchial tree. Z. Angew. Math. Mech. 2020, 100, e201900022. [Google Scholar] [CrossRef]
- Majumdar, A.; Alencar, A.M.; Buldyrev, S.V.; Hantos, Z.; Lutchen, K.R.; Stanley, H.E.; Suki, B. Relating airway diameter distributions to regular branching asymmetry in the lung. Phys. Rev. Lett. 2005, 95, 168101. [Google Scholar] [CrossRef]
- Deng, D.X.; Zeng, L.; Sun, W. A review on flow boiling enhancement and fabrication of enhanced microchannels of microchannel heat sinks. Int. J. Heat Mass Transf. 2021, 175, 121332. [Google Scholar] [CrossRef]
- Wang, W.; Li, Y.J.; Zhang, Y.N.; Li, B.; Sundén, B. Analysis of laminar flow and heat transfer in an interrupted microchannel heat sink with different shaped ribs. J. Therm. Anal. Calorim. 2020, 140, 1259–1266. [Google Scholar] [CrossRef]
- Chai, L.; Xia, G.D.; Wang, H.S. Laminar flow and heat transfer characteristics of interrupted microchannel heat sink with ribs in the transverse microchambers. Int. J. Therm. Sci. 2016, 110, 1–11. [Google Scholar] [CrossRef]
- Hess, W.R. Über die periphere Regulierung der Blutzirkulation. Arch. Ges. Physiol. 1917, 168, 439–490. [Google Scholar] [CrossRef]
- Murray, C.D. The physiological principle of minimum work. I. The vascular system and the cost of blood volume. Proc. Natl. Acad. Sci. USA 1926, 12, 207–214. [Google Scholar] [CrossRef]
- Murray, C.D. The physiological principle of minimum work applied to the angle of branching of arteries. J. Gen. Physiol. 1926, 9, 835–841. [Google Scholar] [CrossRef] [PubMed]
- Bejan, A.; Lorente, S. Design with Constructal Theory, 1st ed.; John Wiley & Sons: Hoboken, NJ, USA, 2008. [Google Scholar]
- Miguel, A.F. Low dissipative configuration in flow networks subject to constraints. Phys. D 2014, 467, 13426. [Google Scholar] [CrossRef]
- Martin, K.; Campos-Celador, A.; Escudero, C.; Gómez, I.; Sala, J.M. Analysis of a thermal bridge in a guarded hot box testing facility. Energy Build. 2012, 50, 139–149. [Google Scholar] [CrossRef]
- Martin, K.; Flores, I.; Escudero, C.; Apaolaza, A.; Sala, J.M. Methodology for the calculation of response factors through experimental tests and validation with simulation. Energy Build. 2010, 42, 461–467. [Google Scholar] [CrossRef]
- Xiang, X.; Zhao, K.; Liu, X.; Jiang, Y. Cooling performance comparison of radiant floor system and all-air system with solar radiation. Energy Procedia 2015, 78, 2322–2327. [Google Scholar] [CrossRef]
- Zaidan, M.J.; Alhamdo, M.H. Comparative Thermal Analysis of Serpentine and Spiral Tube Configurations in Concrete Solar Collectors Using Numerical and Experimental Approaches. Heat Transf. 2025, 4, 3697–3722. [Google Scholar] [CrossRef]
- Ismail, M. Experimental and numerical analysis of heat sink using various patterns of cylindrical pin-fins. Int. J. Thermofluids 2024, 23, 100737. [Google Scholar] [CrossRef]
- Patankar, S.V. Numerical Heat Transfer and Fluid Flow; McGraw-Hill: New York, NY, USA, 1980. [Google Scholar]
- Schlichting, H.; Kestin, J. Boundary Layer Theory; McGraw-Hill: New York, NY, USA, 1961. [Google Scholar]
- Bejan, A. Convection Heat Transfer, 3rd ed.; John Wiley & Sons: Hoboken, NJ, USA, 2013. [Google Scholar]
- Roache, P.J. Quantification of uncertainty in computational fluid dynamics. Annu. Rev. Fluid Mech. 1997, 29, 123–160. [Google Scholar] [CrossRef]
- Celik, I.B.; Ghia, U.; Roache, P.J.; Freitas, C.J.; Coleman, H.; Raad, P.E. Procedure for estimation and reporting of uncertainty due to discretization in CFD applications. J. Fluids Eng. 2008, 130, 078001. [Google Scholar] [CrossRef]
- Zhang, C.H.; Liu, Y.; So, R.M.C.; Phan-Thien, N. The Influence of Inlet Velocity Profile on Three-Dimensional Three-Generation Bifurcating Flows. Comput. Mech. 2002, 29, 422–429. [Google Scholar] [CrossRef]
- Webb, R.L.; Eckert, E.R. Application of rough surfaces to heat exchanger design. Int. J. Heat Mass Transf. 1972, 15, 1647–1658. [Google Scholar] [CrossRef]
- Ahmed, M.; Yusoff, M.; Ng, K.C.; Shuaib, N. The effects of wavy-wall phase shift on thermal-hydraulic performance of Al2O3-water nanofluid flow in sinusoidal-wavy channel. Therm. Eng. 2014, 4, 153–165. [Google Scholar] [CrossRef]
- Kumar, R.; Kumar, A.; Goel, V. Performance improvement and development of correlation for friction factor and heat transfer using computational fluid dynamics for ribbed triangular duct solar air heater. Renew. Energy 2019, 131, 788–799. [Google Scholar] [CrossRef]
- Prabhakara Rao, B.; Sunden, B.; Das, S.K. An experimental and theoretical investigation of the effect of flow maldistribution on the thermal performance of plate heat exchangers. J. Heat Transf. 2005, 127, 332–343. [Google Scholar] [CrossRef]
- Fakheri, A. Heat Exchanger Efficiency. J. Heat Transf. 2007, 129, 1268–1276. [Google Scholar] [CrossRef]



| Geometric Parameters | Boundary Condition | ||
|---|---|---|---|
| Vi | 1.767 m3 | ṁ | 0.000118 to 0.023633 kg/s |
| θi | 750 | Tin | 300 K |
| aDi | 2−1/3 | q″ | 1 to 1000 W/m2 |
| L0 | 0.100 m | uwall | 0 m/s |
| D0 | 0.015 m | Pout | 0 Pa |
| Isomer | |||||
|---|---|---|---|---|---|
| I | II | III | IV | V | |
| EuN1 | 677.64 | 684.78 | 677.33 | 688.12 | 694.36 |
| EuN2 | 675.53 | 683.52 | 674.96 | 686.09 | 692.30 |
| EuN3 | 540.57 | 569.31 | 570.98 | 562.01 | 544.00 |
| N1 | 1,808,908 | 2,186,438 | 1,752,743 | 2,050,358 | 2,037,221 |
| N2 | 240,490 | 291,860 | 235,690 | 275,100 | 273,337 |
| N3 | 35,208 | 40,098 | 32,344 | 38,592 | 38,792 |
| r21 | 1.959 | 1.952 | 1.957 | 1.953 | 1.953 |
| r32 | 1.897 | 1.939 | 1.938 | 1.925 | 1.917 |
| Eu ext 21 | 677.67 | 684.79 | 677.38 | 688.11 | 694.39 |
| Eu ext 32 | 677.67 | 684.79 | 677.38 | 690.07 | 694.39 |
| ε21 | 0.31% | 0.18% | 0.35 | 0.14% | 0.30% |
| ε32 | 19.98% | 16.71% | 15.41 | 18.44% | 21.42% |
| GCI21 | 0.50% | 0.24% | 0.97% | 0.54% | 0.43% |
| GCI32 | 39.59% | 23.21% | 44.57% | 36.99% | 36.56% |
| Flow Structure | Zhang et al. (2002) [35] | Present Numerical Model Adapted with Two Branching Level |
|---|---|---|
 |  | |
| Number of branching levels | 2 | 2 |
| L0 | 0.0107 m | 0.0107 m |
| L1 | 0.0090 m | 0.0090 m |
| L2 | 0.0076 m | 0.0076 m |
| D0 | 0.0035 m | 0.0035 m |
| D1 | 0.0028 m | 0.0028 m |
| D2 | 0.0023 m | 0.0023 m |
| L0/D0 | 3.01 | 3.01 |
| L1/D1 | 3.21 | 3.21 |
| L1/D1 | 3.30 | 3.30 |
| aD | 0.78 | 0.78 |
| θ | 70° | 70° |
| ΔP* = ΔP∙ρ∙u2 | 19.41 | 20.47 |
| ----- | 0.054 |
| Isomer | Level 1 | Level 2 | Level 3 |
|---|---|---|---|
| I | FRP1A = FRP1B | FRP2A < FRP2B FRP2C > FRP2D | FRP3A < FRP3B FRP3C > FRP3D FRP3E < FRP3F FRP3G > FRP3H |
| II | FRP1A = FRP1B | FRP2A = FRP2B FRP2C = FRP2D | FRP3A < FRP3B FRP3C > FRP3D FRP3E < FRP3F FRP3G > FRP3H |
| III | FRP1A = FRP1B | FRP2A < FRP2B FRP2C > FRP2D | FRP3A < FRP3B FRP3C > FRP3D FRP3E < FRP3F FRP3G > FRP3H |
| IV | FRP1A = FRP1B | FRP2A = FRP2B FRP2C = FRP2D | FRP3A > FRP3B FRP3C > FRP3D FRP3E < FRP3F FRP3G > FRP3H |
| V | FRP1A = FRP1B | FRP2A = FRP2B FRP2C = FRP2D | FRP3A > FRP3B FRP3C > FRP3D FRP3E < FRP3F FRP3G < FRP3H |
| q″ | ReD | Isomer | ||||
|---|---|---|---|---|---|---|
| I | II | III | IV | V | ||
| 1000 W/m2 | 10 | 1.1905 | 1.1900 | 1.1903 | 1.1899 | 1.1899 |
| 50 | 1.0535 | 1.0507 | 1.0513 | 1.0509 | 1.0502 | |
| 100 | 1.0370 | 1.0350 | 1.0347 | 1.0352 | 1.0345 | |
| 200 | 1.0216 | 1.0250 | 1.0227 | 1.0250 | 1.0243 | |
| 300 | 1.0193 | 1.0195 | 1.0186 | 1.0195 | 1.0189 | |
| 400 | 1.0171 | 1.0167 | 1.0166 | 1.0167 | 1.0168 | |
| 500 | 1.0160 | 1.0162 | 1.0161 | 1.0161 | 1.0162 | |
| 750 | 1.0150 | 1.0152 | 1.0150 | 1.0152 | 1.0152 | |
| 1000 | 1.0136 | 1.0129 | 1.0137 | 1.0129 | 1.0129 | |
| 1500 | 1.0101 | 1.0093 | 1.0102 | 1.0092 | 1.0092 | |
| 2000 | 1.0033 | 1.0032 | 1.0032 | 1.0032 | 1.0032 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pepe, V.; Miguel, A.F.; Zinani, F.; Rocha, L. Thermo-Fluid Dynamic Performance of Self-Similar Dendritic Networks: CFD Analysis of Structural Isomers. Symmetry 2025, 17, 1715. https://doi.org/10.3390/sym17101715
Pepe V, Miguel AF, Zinani F, Rocha L. Thermo-Fluid Dynamic Performance of Self-Similar Dendritic Networks: CFD Analysis of Structural Isomers. Symmetry. 2025; 17(10):1715. https://doi.org/10.3390/sym17101715
Chicago/Turabian StylePepe, Vinicius, Antonio F. Miguel, Flávia Zinani, and Luiz Rocha. 2025. "Thermo-Fluid Dynamic Performance of Self-Similar Dendritic Networks: CFD Analysis of Structural Isomers" Symmetry 17, no. 10: 1715. https://doi.org/10.3390/sym17101715
APA StylePepe, V., Miguel, A. F., Zinani, F., & Rocha, L. (2025). Thermo-Fluid Dynamic Performance of Self-Similar Dendritic Networks: CFD Analysis of Structural Isomers. Symmetry, 17(10), 1715. https://doi.org/10.3390/sym17101715







