An Enhanced Particle Swarm Optimization Algorithm for the Permutation Flow Shop Scheduling Problem
Abstract
1. Introduction
2. Particle Swarm Optimization Algorithm
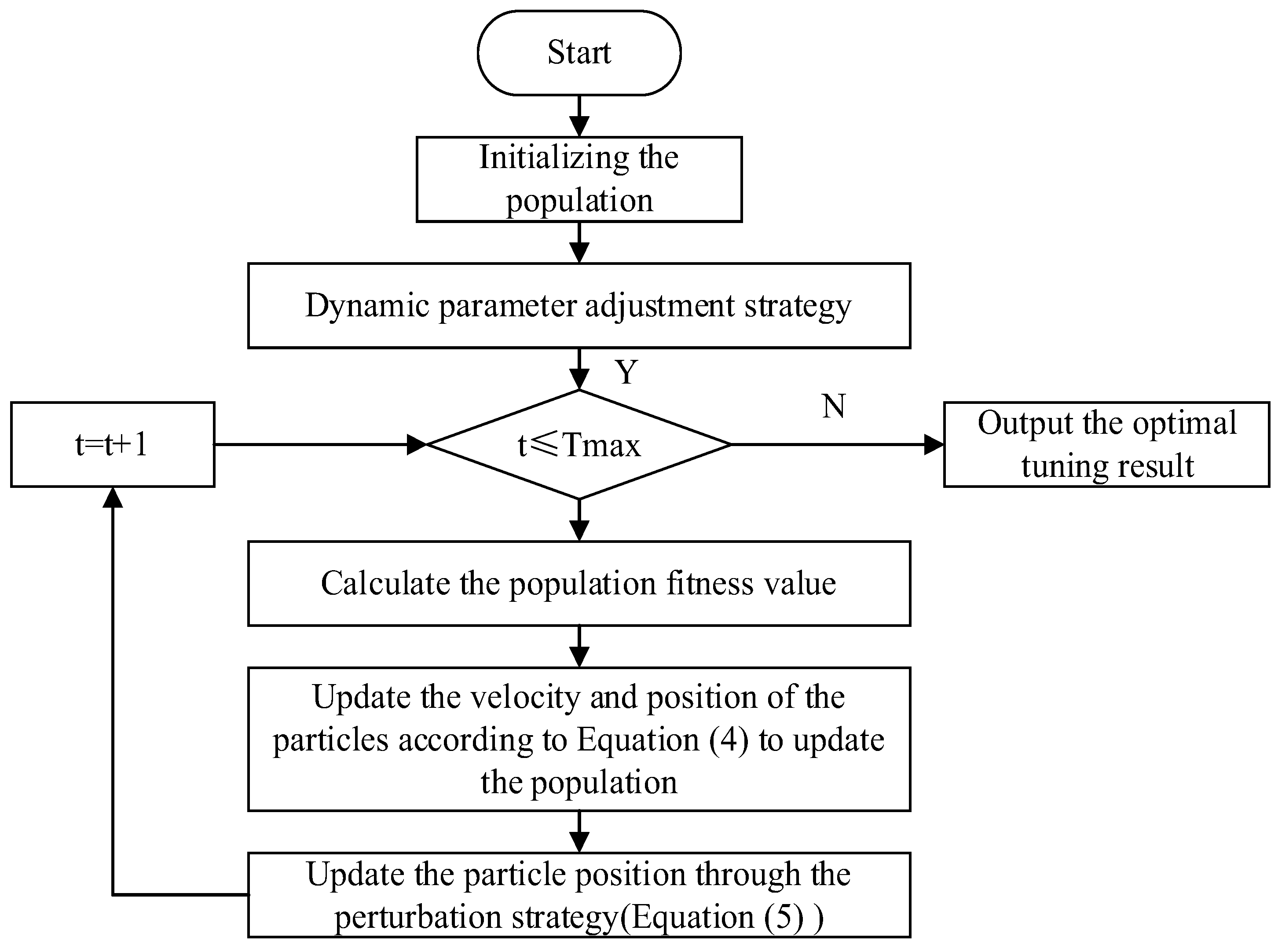
3. Enhanced Particle Swarm Optimization Algorithm
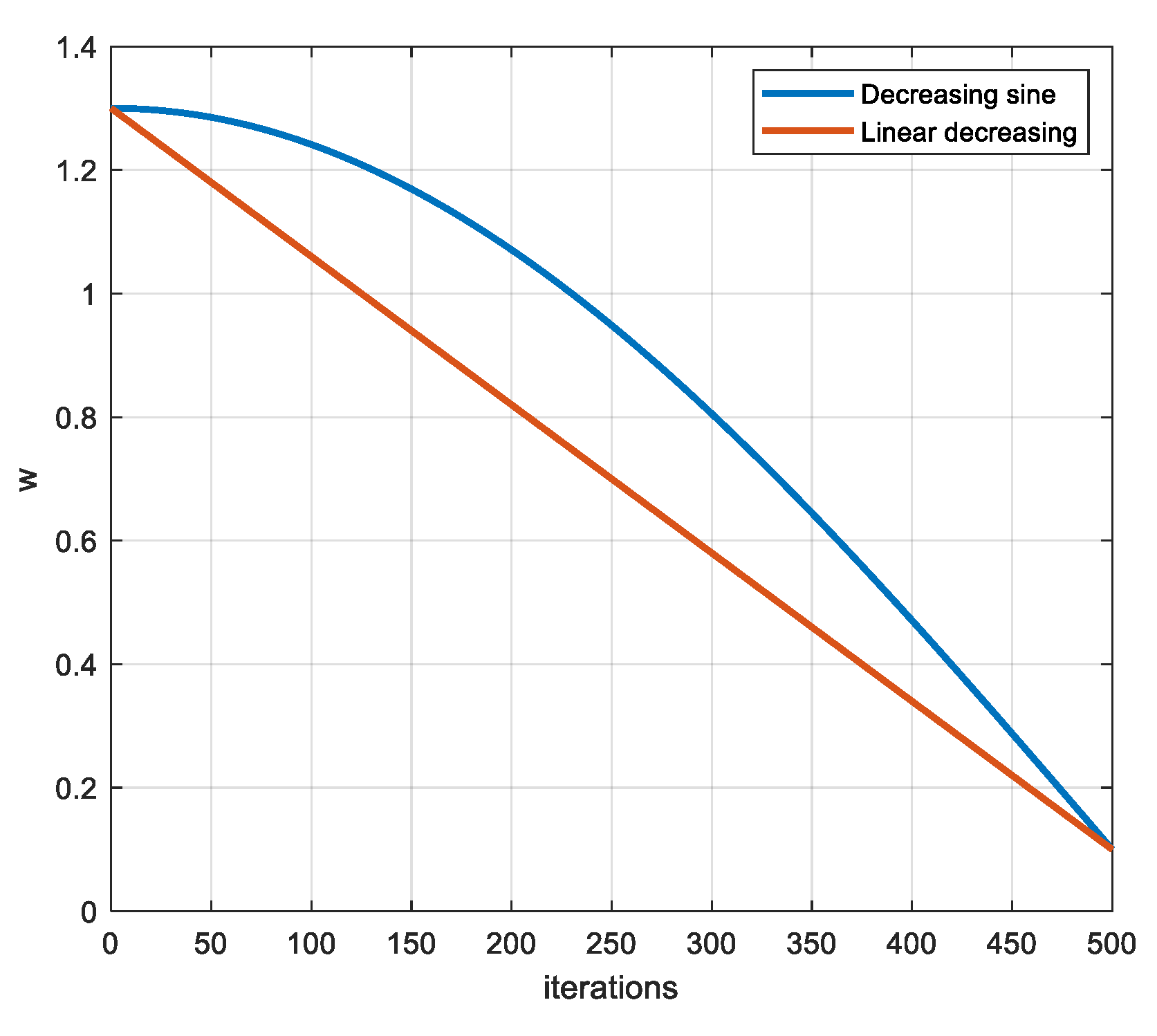
3.1. Dynamic Parameter Adjustment Strategy
3.2. Speed Update Strategy
3.3. Perturbation Strategy
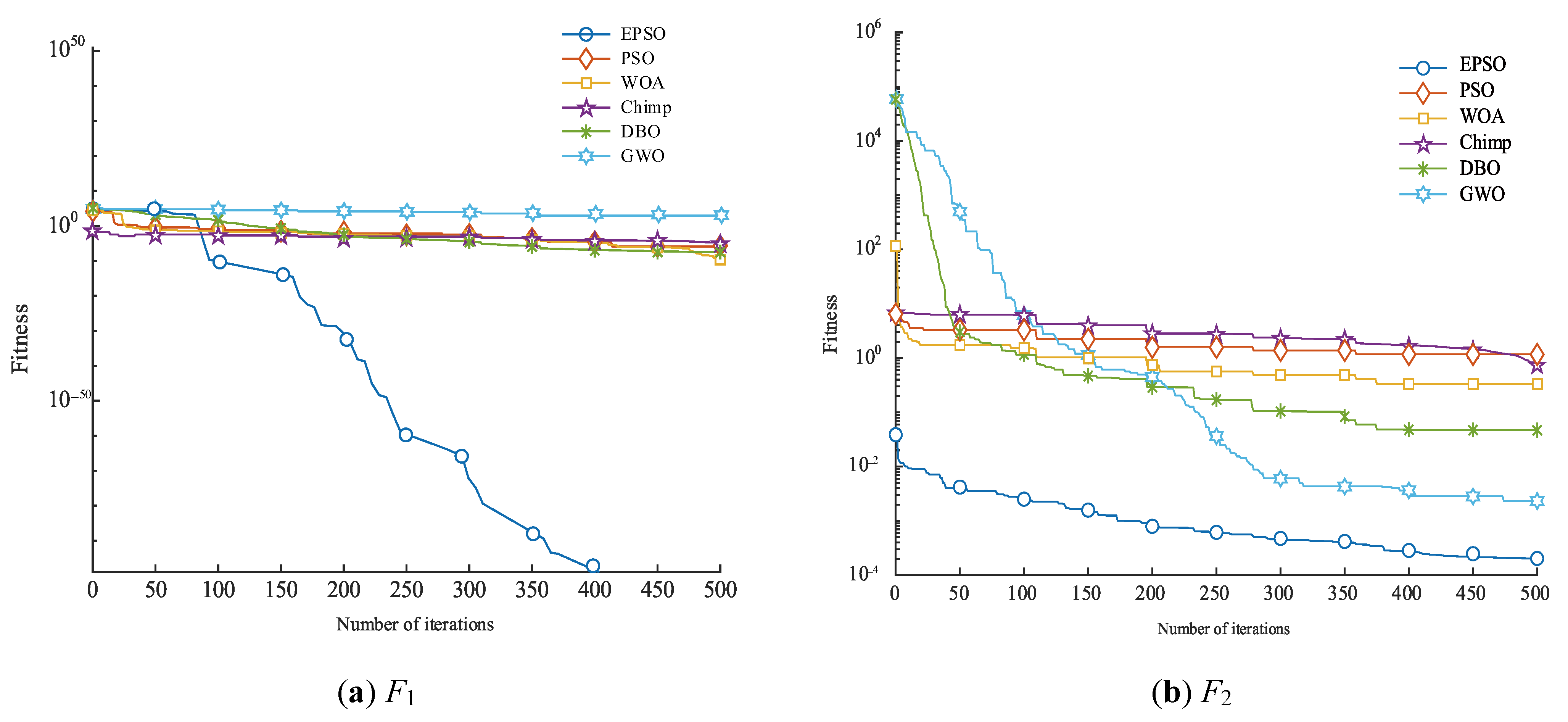
3.4. Algorithm Performance Testing
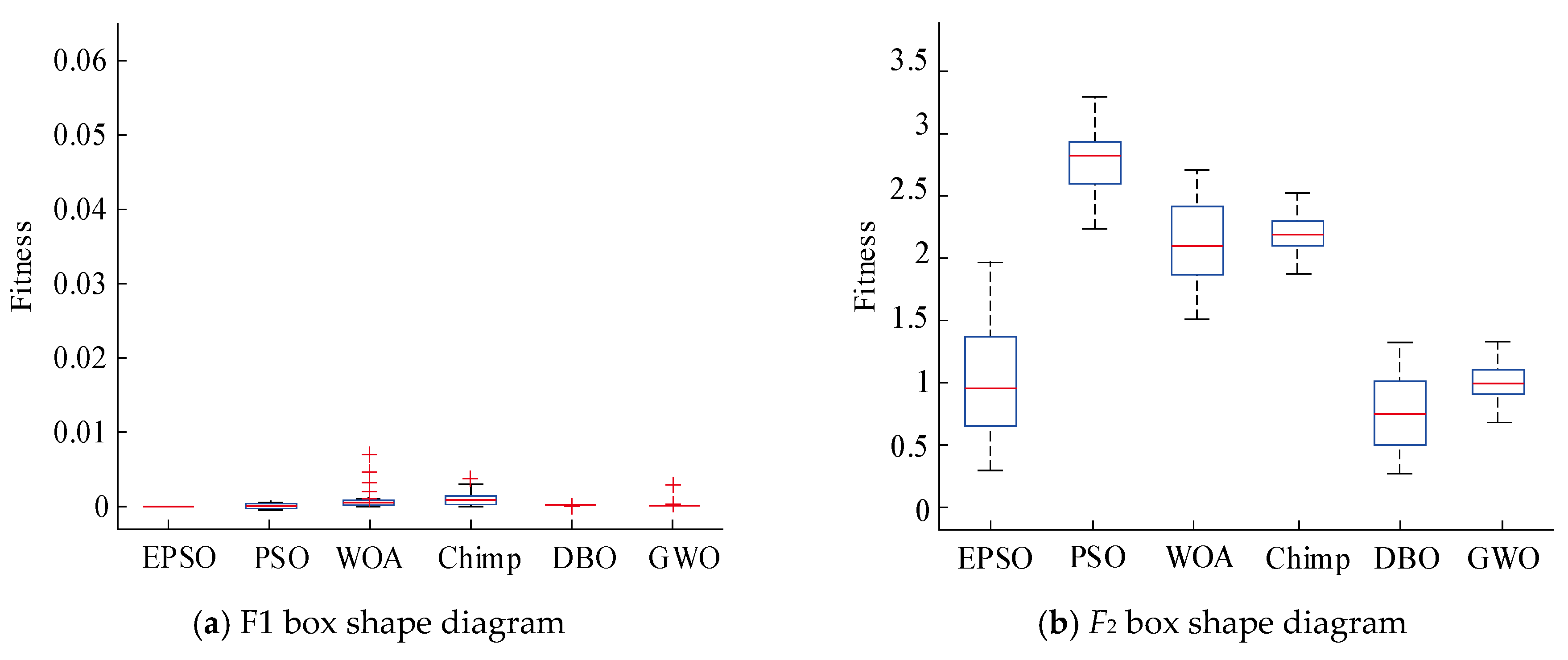
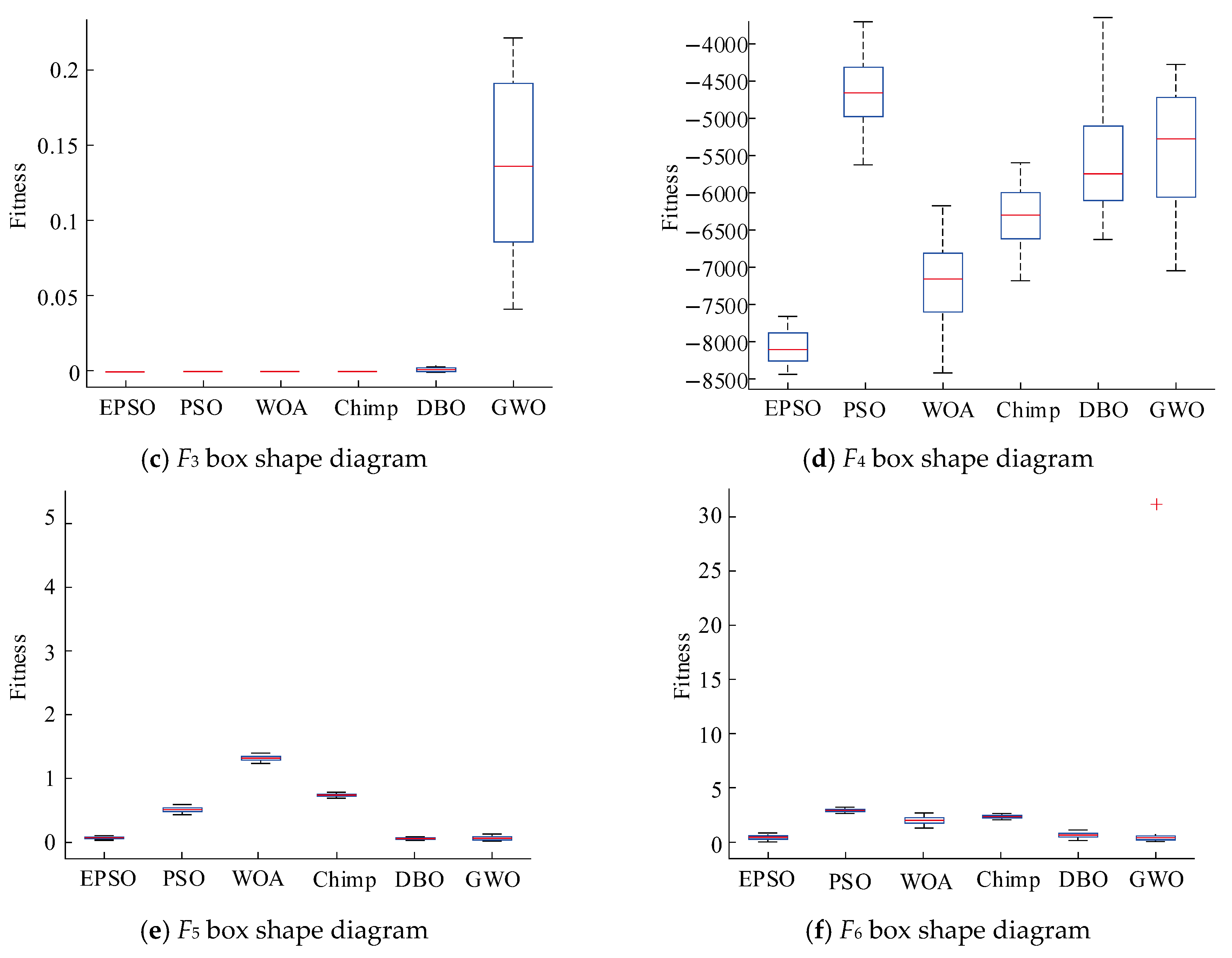
3.5. Strategy Effectiveness Analysis
3.6. EPSO Algorithm
4. Instance Testing
4.1. PFSP Problem Description
4.2. The EPSO Algorithm for Solving the PFSP
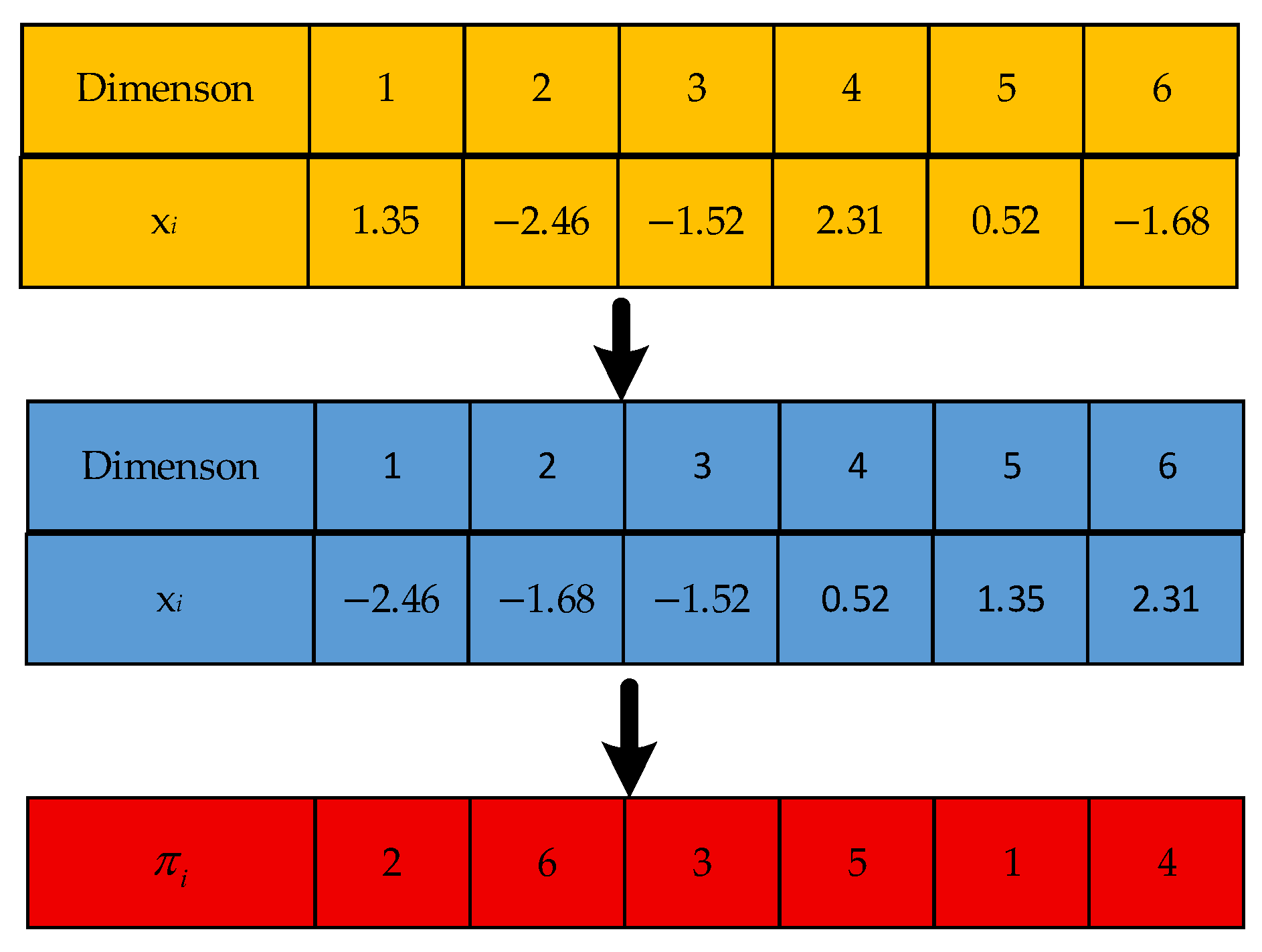
4.2.1. Encoding and Population Initialization
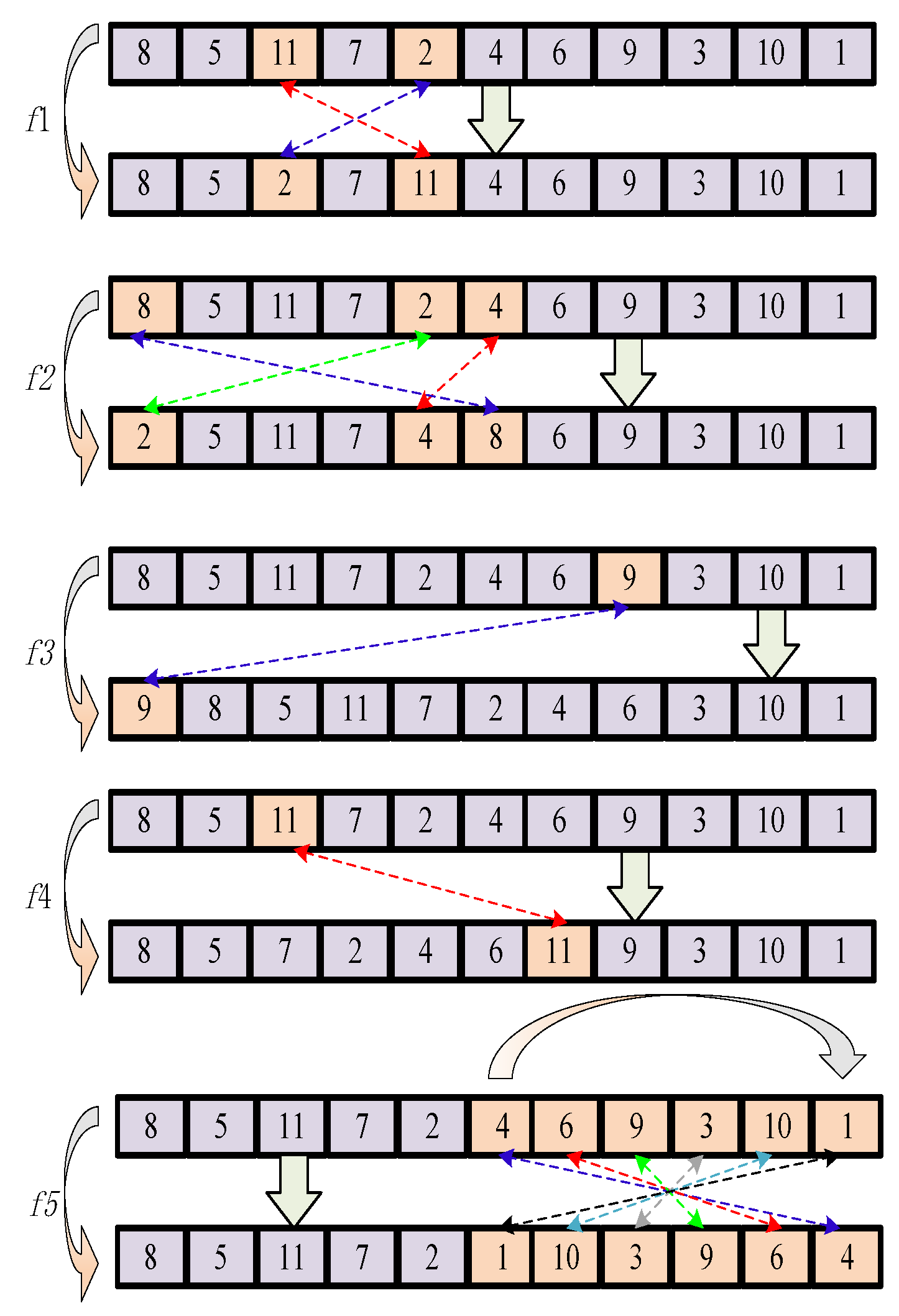
4.2.2. Variable Neighborhood Search Strategy
4.2.3. Complexity Analysis
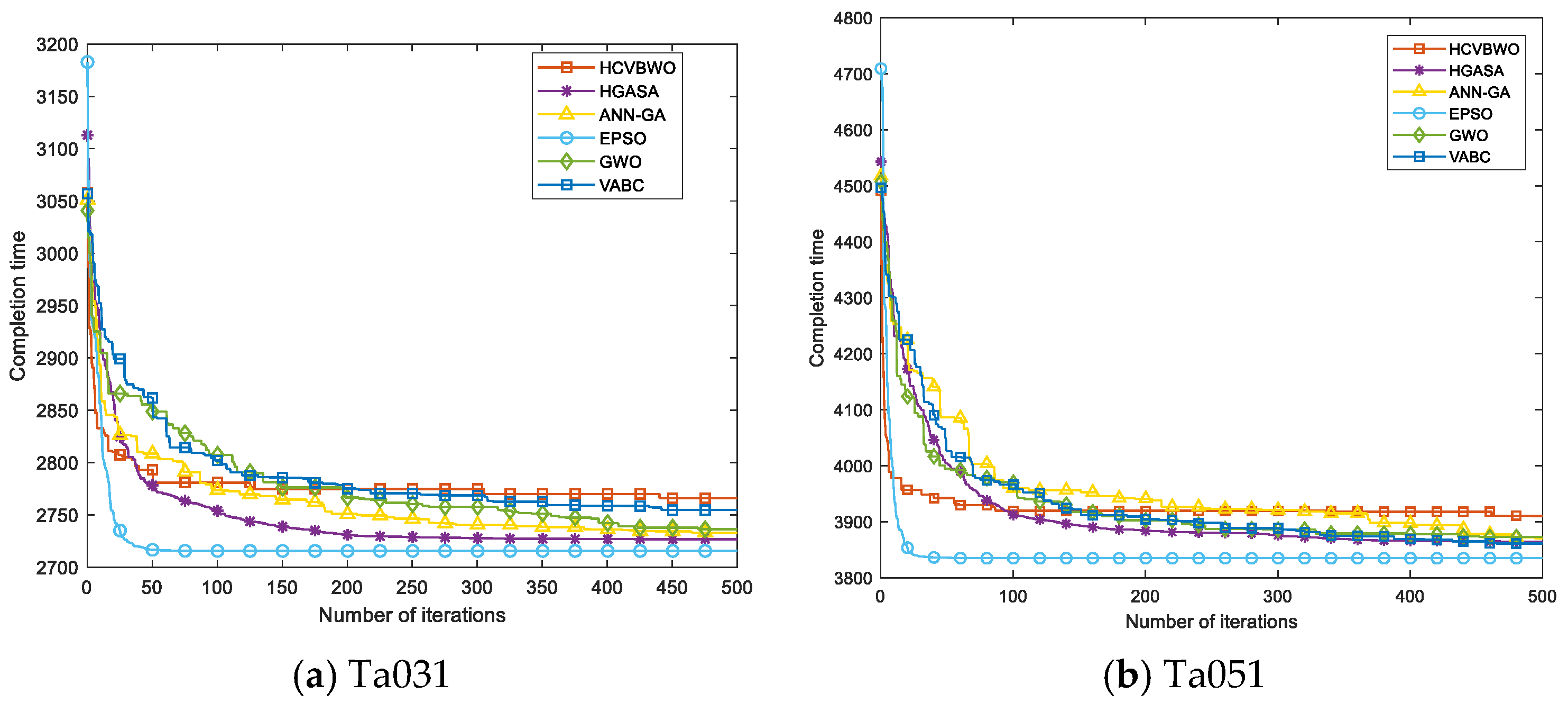
4.3. Analysis of Experimental Results
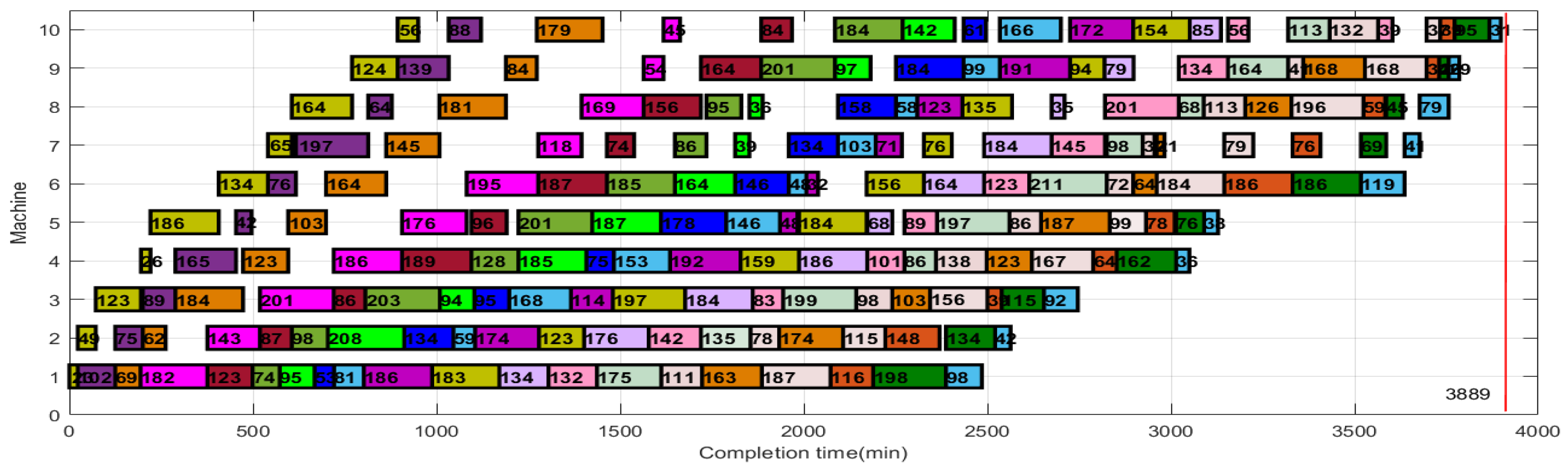
4.4. Engineering Examples
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Xiong, F.; Chen, S.; Xiong, N.; Jing, L. Scheduling distributed heterogeneous non-permutation flowshop to minimize the total weighted tardiness. Expert Syst. Appl. 2025, 272, 126713. [Google Scholar] [CrossRef]
- Qi, X.; Wang, H. Solving Permutation Flowshop Scheduling Problem with Cross-Selection Based Variable Neighborhood Particle Swarm Algorithm. Manuf. Technol. Mach. Tool 2023, 5, 179–187. [Google Scholar] [CrossRef]
- Qi, X.; Zhao, P.; Song, Y.; Wang, R. Hybrid Whale Optimization Algorithm for Solving Engineering Optimization Problems. Manuf. Technol. Mach. Tool 2024, 11, 149–159. [Google Scholar] [CrossRef]
- Robert, J.B.R.; Kumar, R.R. A Hybrid Algorithm for Minimizing Makespan in the Permutation Flow Shop Scheduling Environment. Asian J. Res. Soc. Sci. Humanit. 2016, 6, 1239–1255. [Google Scholar] [CrossRef]
- Han, N.A.; Ramanan, R.T.; Shashikant, S.K.; Sridharan, R. A hybrid neural network–genetic algorithm approach for permutation flow shop scheduling. Int. J. Prod. Res. 2010, 48, 4217–4231. [Google Scholar]
- Yang, Y.Y.; Qian, B.; Li, Z.; Hu, R.; Wang, L. Q-learning based hyper-heuristic with clustering strategy for combinatorial optimization: A case study on permutation flow-shop scheduling problem. Comput. Oper. Res. 2025, 173, 106833. [Google Scholar] [CrossRef]
- Zeng, F.; Cui, J. Improved Fruit Fly Algorithm to Solve No-Idle Permutation Flow Shop Scheduling Problem. Processes 2025, 13, 476. [Google Scholar] [CrossRef]
- Lemtenneche, S.; Bensayah, A.; Cheriet, A. An Estimation of Distribution Algorithm for Permutation Flow-Shop Scheduling Problem. Systems 2023, 11, 389. [Google Scholar] [CrossRef]
- Eberhart, R.; Kennedy, J. Particle swarm optimization. In Proceedings of the IEEE International Conference on Neural Networks, Perth, WA, Australia, 27 November–1 December 1995; Volume 4, pp. 1942–1948. [Google Scholar]
- Zhu, K.; Wang, Q.; Yang, W.; Yu, Q.; Wang, Z.; Wang, X. Research on Ship Collision Avoidance Based on Improved Particle Swarm Optimization Algorithm. Sens. Microsyst. 2025, 44, 40–43+47. [Google Scholar] [CrossRef]
- Mirjalili, S.; Lewis, A. The whale optimization algorithm. Adv. Eng. Softw. 2016, 95, 51–67. [Google Scholar] [CrossRef]
- Khishe, M.; Mosavi, M.R. Chimp optimization algorithm. Expert Syst. Appl. 2020, 149, 113338. [Google Scholar] [CrossRef]
- Xue, J.; Shen, B. Dung beetle optimizer: A new meta-heuristic algorithm for global optimization. J. Supercomput. 2023, 79, 7305–7336. [Google Scholar] [CrossRef]
- Mirjalili, S.; Mirjalili, S.M.; Lewis, A. Grey wolf optimizer. Adv. Eng. Softw. 2014, 69, 46–61. [Google Scholar] [CrossRef]
- Lijun, F. A hybrid adaptive large neighborhood search for time-dependent open electric vehicle routing problem with hybrid energy replenishment strategies. PLoS ONE 2023, 18, e0291473. [Google Scholar]
- Reeves, C.R. A genetic algorithm for flowshop sequencing. Comput. Oper. Res. 1995, 22, 5–13. [Google Scholar] [CrossRef]
- Taillard, E. Benchmarks for basic scheduling problems. Eur. J. Oper. Res. 1993, 64, 278–285. [Google Scholar] [CrossRef]
- Du, S.L.; Zhou, W.J.; Wu, D.K. An effective discrete monarch butterfly optimization algorithm for distributed blocking flow shop scheduling with an assembly machine. Expert Syst. Appl. 2023, 225, 120113. [Google Scholar] [CrossRef]
- Zhao, F.Q.; Zhou, G.; Wang, L. A cooperative scatter search with reinforcement learning mechanism for the distributed permutation flowshop scheduling problem with sequence-dependent setup times. IEEE Trans. Syst. Man Cybern. Syst. 2023, 53, 4899–4911. [Google Scholar] [CrossRef]

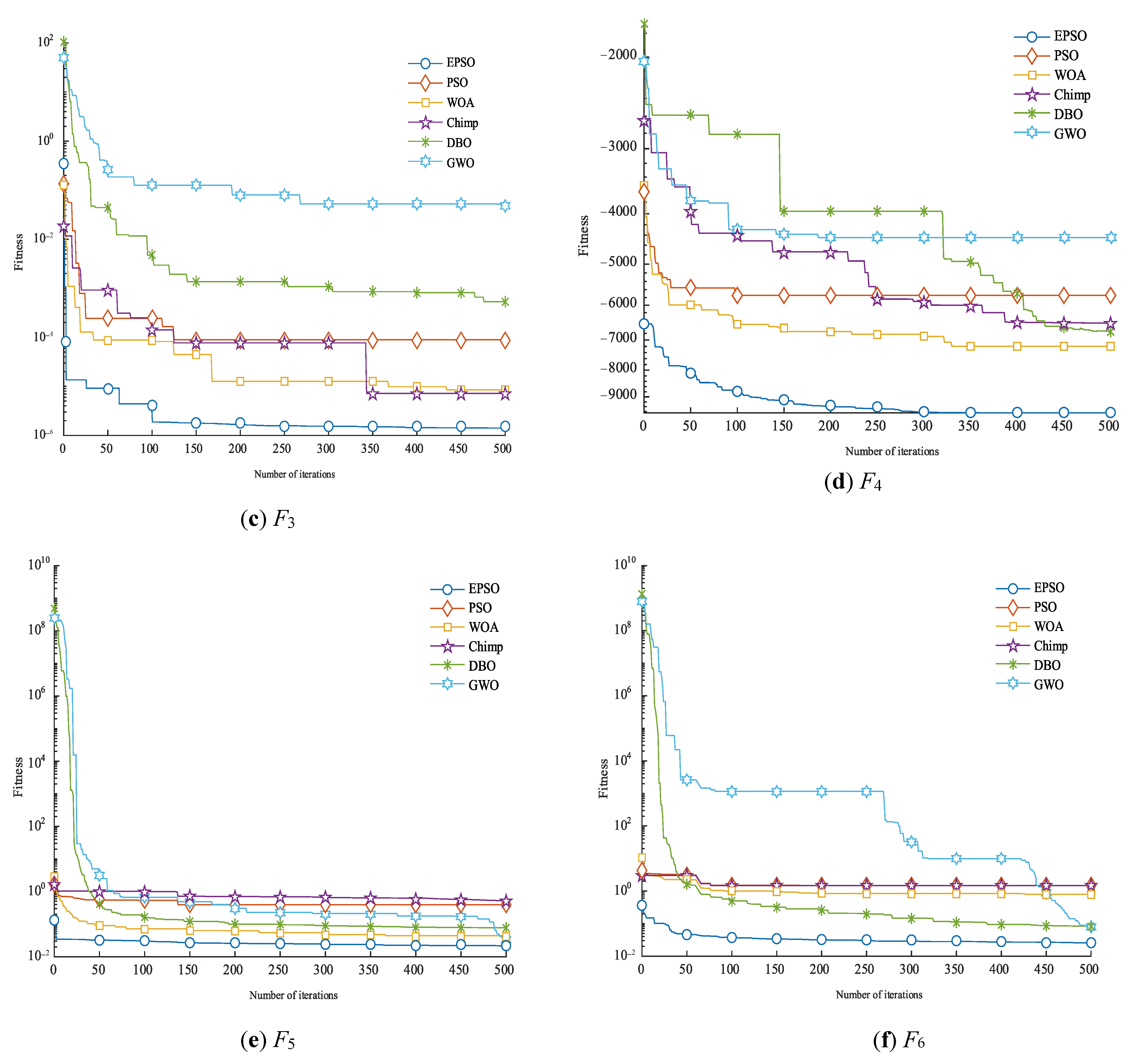



| Functions | Variable Scope | Fmin |
|---|---|---|
| [−100,100] | 0 | |
| [−100,100] | 0 | |
| [−1.28,1.28] | 0 | |
| [−500,500] | −418.98n | |
| [−50,50] | 0 | |
| [−50,50] | 0 |
| Functions | EPSO | PSO | WOA | Chimp | DBO | GWO | |
|---|---|---|---|---|---|---|---|
| F1 | average | 3.12 × 10−98 | 5.12 × 10−3 | 6.12 × 10−3 | 9.21 × 10−3 | 3.22× 10−14 | 6.21× 10−5 |
| standard | 5.12 × 10−92 | 2.23 × 10−3 | 5.12 × 10−3 | 2.62 × 10−1 | 2.15× 10−14 | 3.12× 10−4 | |
| F2 | average | 9.93 × 10−1 | 2.58 × 10−0 | 2.13 × 10−0 | 2.35 × 10−0 | 9.54 × 10−0 | 1.14 × 10−0 |
| standard | 5.68 × 10−1 | 3.51 × 10−1 | 2.56 × 10−1 | 1.76 × 10−1 | 5.84 × 10−1 | 1.73 × 10−1 | |
| F3 | average | 4.26 × 10−13 | 6.21 × 10−6 | 5.12 × 10−6 | 5.12 × 10−6 | 3.12 × 10−6 | 1.42 × 10−1 |
| standard | 5.53 × 10−13 | 6.28 × 10−6 | 3.22 × 10−6 | 4.12 × 10−6 | 4.13 × 10−6 | 1.63 × 10−2 | |
| F4 | average | −8.16 × 10−3 | −4.72 × 10−3 | −7.23 × 10−3 | −6.31 × 10−3 | −5.88 × 10−3 | −5.45 × 10−3 |
| standard | 4.32 × 10+2 | 4.54 × 10+2 | 6.45 × 10+2 | 4.98 × 10+2 | 8.54 × 10+2 | 8.01 × 10+2 | |
| F5 | average | 2.13 × 10−2 | 4.99 × 10−1 | 1.51 × 10−1 | 7.11 × 10−1 | 2.35 × 10−2 | 2.96 × 10−1 |
| standard | 2.11 × 10−2 | 3.02 × 10−2 | 7.31 × 10−2 | 3.28 × 10−2 | 2.68 × 10−2 | 9.99 × 10−1 | |
| F6 | average | 3.17 × 10−1 | 3.94 × 10−0 | 2.56 × 10−0 | 3.12 × 10−0 | 5.21 × 10−1 | 1.32 × 10−0 |
| standard | 1.46 × 10−1 | 2.33 × 10−1 | 3.24 × 10−1 | 4.44 × 10−2 | 1.95 × 10−1 | 5.14 × 10−0 | |
| Functions | EPSO | EPSO1 | EPSO2 | EPSO3 | |
|---|---|---|---|---|---|
| F1 | average | 3.12 × 10−98 | 6.21 × 10−32 | 4.23 × 10−36 | 4.98 × 10−44 |
| standard | 5.12 × 10−92 | 7.23 × 10−23 | 6.45 × 10−92 | 4.23 × 10−43 | |
| F2 | average | 9.93 × 10−1 | 1.01 × 10−0 | 2.23 × 10−0 | 4.23 × 10−0 |
| standard | 5.68 × 10−1 | 6.12 × 10−0 | 3.11 × 10−0 | 4.22 × 10−0 | |
| F3 | average | 4.26 × 10−13 | 7.22 × 10−10 | 5.12 × 10−11 | 5.89 × 10−12 |
| standard | 5.53 × 10−13 | 4.23 × 10−9 | 4.56 × 10−11 | 6.42 × 10−11 | |
| F4 | average | −8.16 × 10−3 | −6.23 × 10−3 | −5.14 × 10−3 | −4.23 × 10−3 |
| standard | 4.32 × 10+2 | 5.31 × 10+2 | 5.23 × 10+2 | 5.23 × 10+2 | |
| F5 | average | 2.13 × 10−2 | 3.23 × 10−2 | 3.14 × 10−2 | 3.11 × 10−2 |
| standard | 2.11 × 10−2 | 2.19 × 10−2 | 3.03 × 10−2 | 4.11 × 10−2 | |
| F6 | average | 3.17 × 10−1 | 1.23 × 10−0 | 2.23 × 10−0 | 3.23 × 10−0 |
| standard | 1.46 × 10−1 | 2.12 × 10−0 | 2.13 × 10−0 | 3.22 × 10−0 | |
| Cases | VABC | HCVBWO | ANN-GA | HGASA | GWO | EPSO | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| BRE | ARE | BRE | ARE | BRE | ARE | BRE | ARE | BRE | ARE | BRE | ARE | |
| Rec01 | 0.000 | 0.526 | 0.000 | 0.563 | 0.000 | 0.325 | 0.000 | 0.160 | 0.522 | 1.369 | 0.000 | 0.000 |
| Rec03 | 0.000 | 0.263 | 0.000 | 0.056 | 0.000 | 0.150 | 0.000 | 0.000 | 0.256 | 1.365 | 0.000 | 0.000 |
| Rec05 | 0.240 | 1.058 | 0.240 | 0.603 | 0.240 | 0.240 | 0.000 | 0.240 | 0.240 | 0.967 | 0.000 | 0.240 |
| Rec07 | 0.160 | 1.326 | 0.000 | 1.652 | 0.053 | 0.768 | 0.000 | 0.539 | 1.213 | 2.352 | 0.000 | 0.635 |
| Rec09 | 0.000 | 2.036 | 0.000 | 1.305 | 0.000 | 0.126 | 0.000 | 0.361 | 1.563 | 2.235 | 0.000 | 0.103 |
| Rec11 | 0.083 | 1.639 | 0.000 | 0.852 | 0.000 | 0.269 | 0.000 | 0.536 | 1.755 | 2.890 | 0.000 | 0.427 |
| Rec13 | 0.632 | 1.721 | 1.026 | 1.852 | 0.661 | 1.263 | 0.711 | 1.032 | 2.065 | 3.127 | 0.522 | 0.756 |
| Rec15 | 0.956 | 2.130 | 0.845 | 1.632 | 0.000 | 1.065 | 0.000 | 1.025 | 1.339 | 2.150 | 0.363 | 0.769 |
| Rec17 | 0.659 | 2.153 | 1.056 | 1.320 | 0.951 | 1.066 | 0.796 | 1.216 | 1.856 | 2.901 | 0.672 | 0.928 |
| Rec19 | 2.698 | 3.452 | 0.000 | 1.143 | 0.000 | 1.606 | 0.356 | 0.812 | 3.326 | 4.338 | 0.986 | 1.592 |
| Rec21 | 1.716 | 1.826 | 1.640 | 2.568 | 1.887 | 2.648 | 1.057 | 1.335 | 4.198 | 5.897 | 0.287 | 0.919 |
| Rec23 | 0.651 | 2.167 | 1.601 | 2.361 | 0.593 | 1.976 | 1.167 | 1.491 | 2.894 | 4.653 | 0.593 | 1.608 |
| Rec25 | 1.332 | 2.987 | 0.349 | 1.501 | 2.509 | 2.795 | 0.493 | 1.185 | 4.327 | 5.354 | 0.346 | 0.790 |
| Rec27 | 0.864 | 2.088 | 1.504 | 1.860 | 1.807 | 2.272 | 0.000 | 2.001 | 4.870 | 6.292 | 0.000 | 2.035 |
| Rec29 | 1.412 | 3.182 | 1.837 | 2.331 | 2.707 | 2.302 | 0.870 | 2.173 | 5.038 | 6.204 | 0.247 | 1.788 |
| Rec31 | 1.222 | 2.387 | 2.074 | 2.618 | 1.551 | 2.914 | 0.860 | 2.341 | 2.944 | 3.151 | 0.820 | 1.937 |
| Rec33 | 0.997 | 1.212 | 2.687 | 2.974 | 1.235 | 3.438 | 0.839 | 2.045 | 7.132 | 8.239 | 0.425 | 1.876 |
| Rec35 | 0.000 | 0.049 | 0.000 | 1.373 | 1.837 | 2.222 | 0.000 | 0.829 | 6.095 | 5.137 | 0.000 | 0.800 |
| Rec37 | 0.765 | 1.778 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 1.630 | 2.864 | 0.000 | 0.000 |
| Rec39 | 2.613 | 2.807 | 4.899 | 5.009 | 2.944 | 3.210 | 2.934 | 4.426 | 11.014 | 11.568 | 2.538 | 3.014 |
| Rec41 | 3.255 | 4.068 | 2.944 | 3.072 | 3.576 | 3.882 | 1.768 | 2.519 | 8.989 | 9.829 | 1.709 | 2.736 |
| AVG | 0.965 | 1.945 | 1.081 | 1.745 | 1.074 | 1.645 | 0.564 | 1.251 | 3.489 | 4.423 | 0.453 | 1.093 |
| Scale | VABC | HCVBWO | ANN-GA | HGASA | GWO | EPSO |
|---|---|---|---|---|---|---|
| 20 × 5 | 1.1466 | 1.8835 | 1.6629 | 1.3650 | 1.4379 | 0.0132 |
| 20 × 10 | 1.1584 | 1.3171 | 1.4562 | 1.3830 | 1.5667 | 0.0125 |
| 20 × 20 | 1.1837 | 1.2256 | 1.5632 | 1.7010 | 1.7337 | 0.0072 |
| 50 × 5 | 1.6494 | 1.7586 | 1.7580 | 1.2580 | 1.7890 | 0.0158 |
| 50 × 10 | 1.9440 | 1.7220 | 1.8696 | 1.5396 | 1.1738 | 0.5362 |
| 50 × 20 | 3.1412 | 1.2956 | 1.7250 | 1.0552 | 1.2461 | 0.9640 |
| 100 × 5 | 1.4844 | 1.7351 | 1.6920 | 2.4910 | 1.6787 | 0.0351 |
| 100 × 10 | 1.8824 | 3.5863 | 1.6364 | 2.1902 | 1.7401 | 0.0802 |
| 100 × 20 | 3.9071 | 4.3747 | 1.5856 | 1.4717 | 1.9607 | 0.9513 |
| 200 × 10 | 1.2446 | 1.0219 | 1.9043 | 1.6670 | 1.6043 | 0.6945 |
| 200 × 20 | 3.7502 | 3.1267 | 2.9388 | 1.5130 | 2.2548 | 1.2757 |
| 500 × 20 | 1.9281 | 2.0417 | 2.9782 | 1.8961 | 3.1266 | 0.5777 |
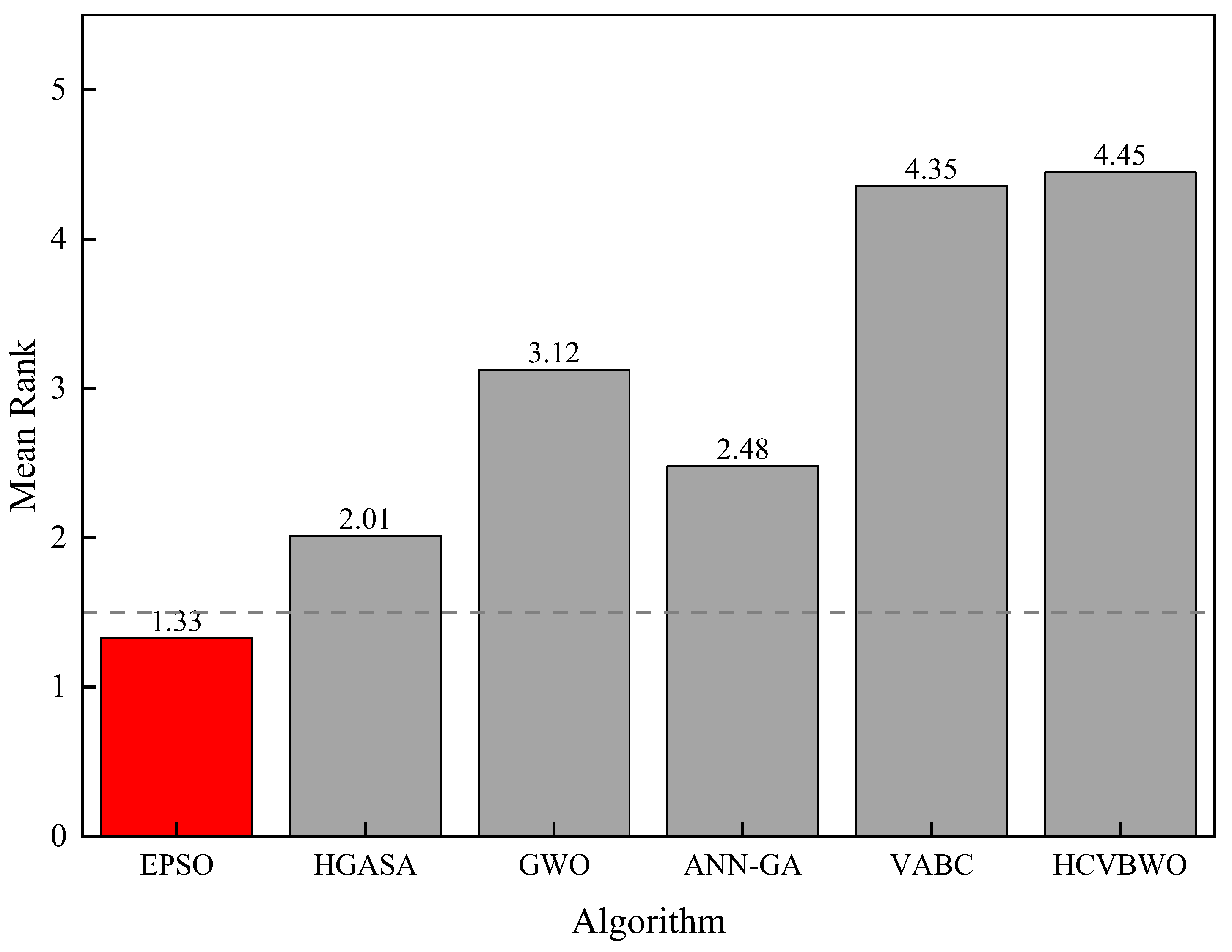
| Algorithm | Mean Ranking | Chi-Square | p-Value | CDa = 0.05 | CDa = 0.1 |
|---|---|---|---|---|---|
| EPSO | 1.326 | 1.235 | 214.213 × 10−18 | 0.623 | 0.687 |
| HGASA | 2.011 | ||||
| GWO | 3.122 | ||||
| ANN-GA | 2.478 | ||||
| VABC | 4.354 | ||||
| HCVBWO | 4.447 |
| E1 | E2 | E3 | E4 | E5 | E6 | E7 | E8 | E9 | E10 | |
|---|---|---|---|---|---|---|---|---|---|---|
| O1 | 186 | 174 | 114 | 192 | 48 | 32 | 71 | 123 | 191 | 172 |
| O2 | 98 | 42 | 92 | 36 | 38 | 119 | 41 | 79 | 29 | 31 |
| O3 | 132 | 142 | 83 | 101 | 89 | 123 | 145 | 201 | 134 | 56 |
| O4 | 69 | 62 | 184 | 123 | 103 | 164 | 145 | 181 | 84 | 179 |
| O5 | 182 | 143 | 201 | 186 | 176 | 195 | 118 | 169 | 54 | 45 |
| O6 | 111 | 78 | 98 | 138 | 86 | 72 | 32 | 113 | 41 | 132 |
| O7 | 81 | 59 | 168 | 153 | 146 | 48 | 103 | 58 | 99 | 166 |
| O8 | 23 | 49 | 123 | 26 | 186 | 134 | 65 | 164 | 124 | 56 |
| O9 | 123 | 87 | 86 | 189 | 96 | 187 | 74 | 156 | 164 | 84 |
| O10 | 134 | 176 | 184 | 186 | 68 | 164 | 184 | 35 | 79 | 85 |
| O11 | 74 | 98 | 203 | 128 | 201 | 185 | 86 | 95 | 201 | 184 |
| O12 | 163 | 174 | 103 | 123 | 187 | 64 | 21 | 126 | 168 | 39 |
| O13 | 95 | 208 | 94 | 185 | 187 | 164 | 39 | 36 | 97 | 142 |
| O14 | 198 | 134 | 115 | 162 | 76 | 186 | 69 | 45 | 26 | 95 |
| O15 | 102 | 75 | 89 | 165 | 42 | 76 | 197 | 64 | 139 | 88 |
| O16 | 175 | 135 | 199 | 86 | 197 | 211 | 98 | 68 | 164 | 113 |
| O17 | 53 | 134 | 95 | 75 | 178 | 146 | 134 | 158 | 184 | 61 |
| O18 | 183 | 123 | 197 | 159 | 184 | 156 | 76 | 135 | 94 | 154 |
| O19 | 116 | 148 | 39 | 64 | 78 | 186 | 76 | 59 | 34 | 39 |
| O20 | 187 | 115 | 156 | 167 | 99 | 184 | 79 | 196 | 168 | 37 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ma, T.; Zhao, C. An Enhanced Particle Swarm Optimization Algorithm for the Permutation Flow Shop Scheduling Problem. Symmetry 2025, 17, 1697. https://doi.org/10.3390/sym17101697
Ma T, Zhao C. An Enhanced Particle Swarm Optimization Algorithm for the Permutation Flow Shop Scheduling Problem. Symmetry. 2025; 17(10):1697. https://doi.org/10.3390/sym17101697
Chicago/Turabian StyleMa, Tao, and Cai Zhao. 2025. "An Enhanced Particle Swarm Optimization Algorithm for the Permutation Flow Shop Scheduling Problem" Symmetry 17, no. 10: 1697. https://doi.org/10.3390/sym17101697
APA StyleMa, T., & Zhao, C. (2025). An Enhanced Particle Swarm Optimization Algorithm for the Permutation Flow Shop Scheduling Problem. Symmetry, 17(10), 1697. https://doi.org/10.3390/sym17101697





