On the Performance of Physics-Based Neural Networks for Symmetric and Asymmetric Domains: A Comparative Study and Hyperparameter Analysis
Abstract
1. Introduction
2. Overview of Physics-Informed Neural Networks
2.1. Structure of the Physics-Informed Neural Networks
2.1.1. Neural Network Architecture
2.1.2. Physics-Informed Loss Function
2.2. Automatic Differentiation
2.3. How PINNs Work
2.4. Theoretical Properties and Analysis
2.4.1. Some Popular Activation Functions
2.4.2. Error and Convergence Analysis
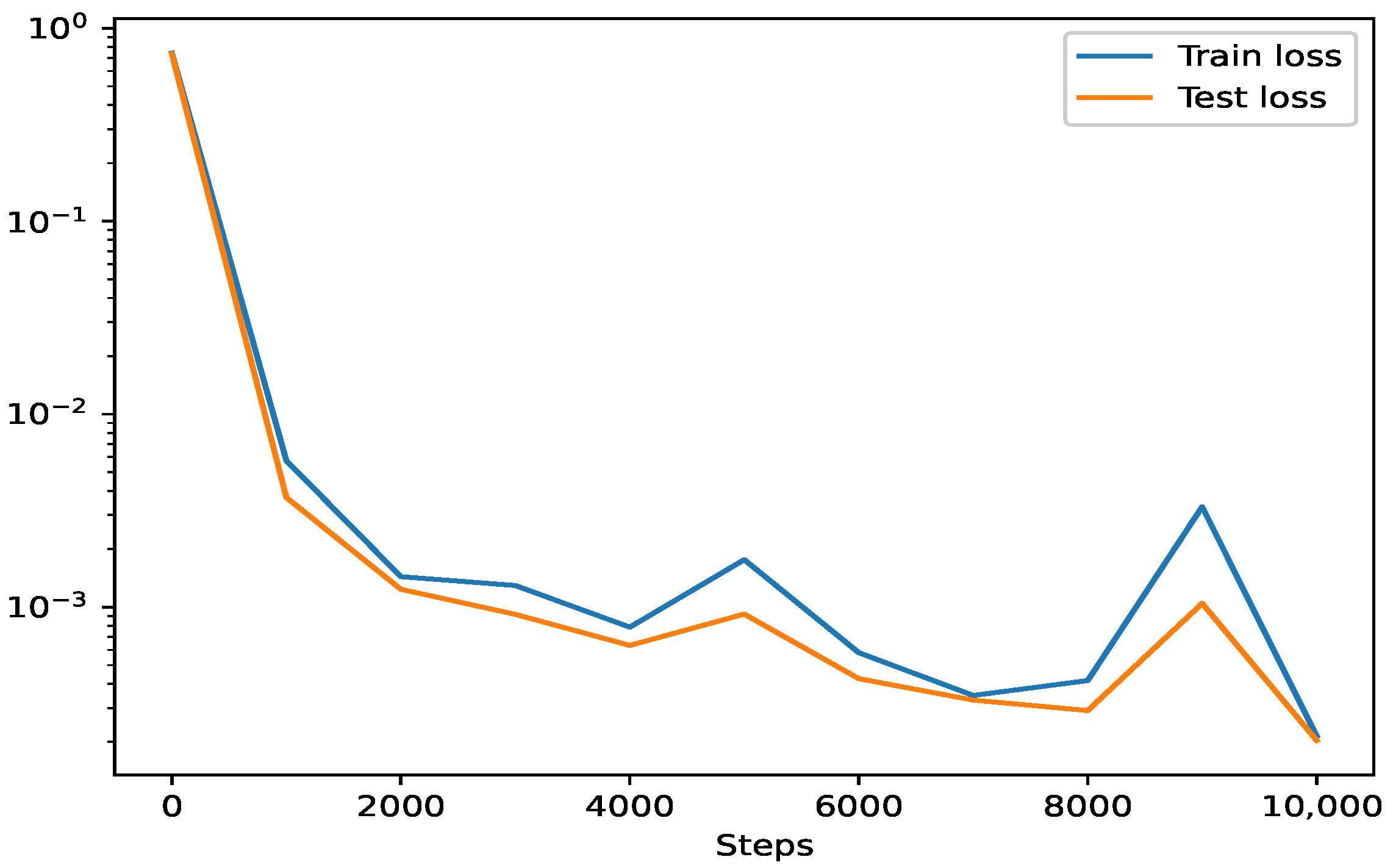
2.5. Training and Optimization in Neural Networks
- (i)
- Forward Pass: Input data is fed into the network and propagates through its layers. Each neuron in a layer receives inputs from the previous layer, applies a weighted sum and an activation function, and passes the output to the next layer. This process continues until an output is generated by the final layer.
- (ii)
- Loss Computation: The network’s output is compared to the true target values using a loss function. This function quantifies the error or discrepancy between the predicted output and the expected output. Common loss functions include measures prediction errors like Mean Squared Error and Cross-Entropy. A higher loss value indicates a greater error.
- (iii)
- Backward Pass: The error calculated by the loss function is propagated backward through the network. It computes the gradient of the loss function with respect to each weight and bias in the network by using chain rule.
- (iv)
- Parameter Update: Using the gradients computed during backpropagation, an optimizer algorithm adjusts the weights and biases of the network. The goal is to update the parameters in a way that reduces the loss function. The size of the steps taken during this adjustment is controlled by the learning rate.
3. Application of PINNs to Selected Equations
3.1. Poisson Equation
3.2. Burgers’ Equation
- u is the solution as a function of space and time, ;
- is the viscosity coefficient which controls the smoothness of the solution;
- and are known functions.
3.2.1. Explicit Finite Difference Method
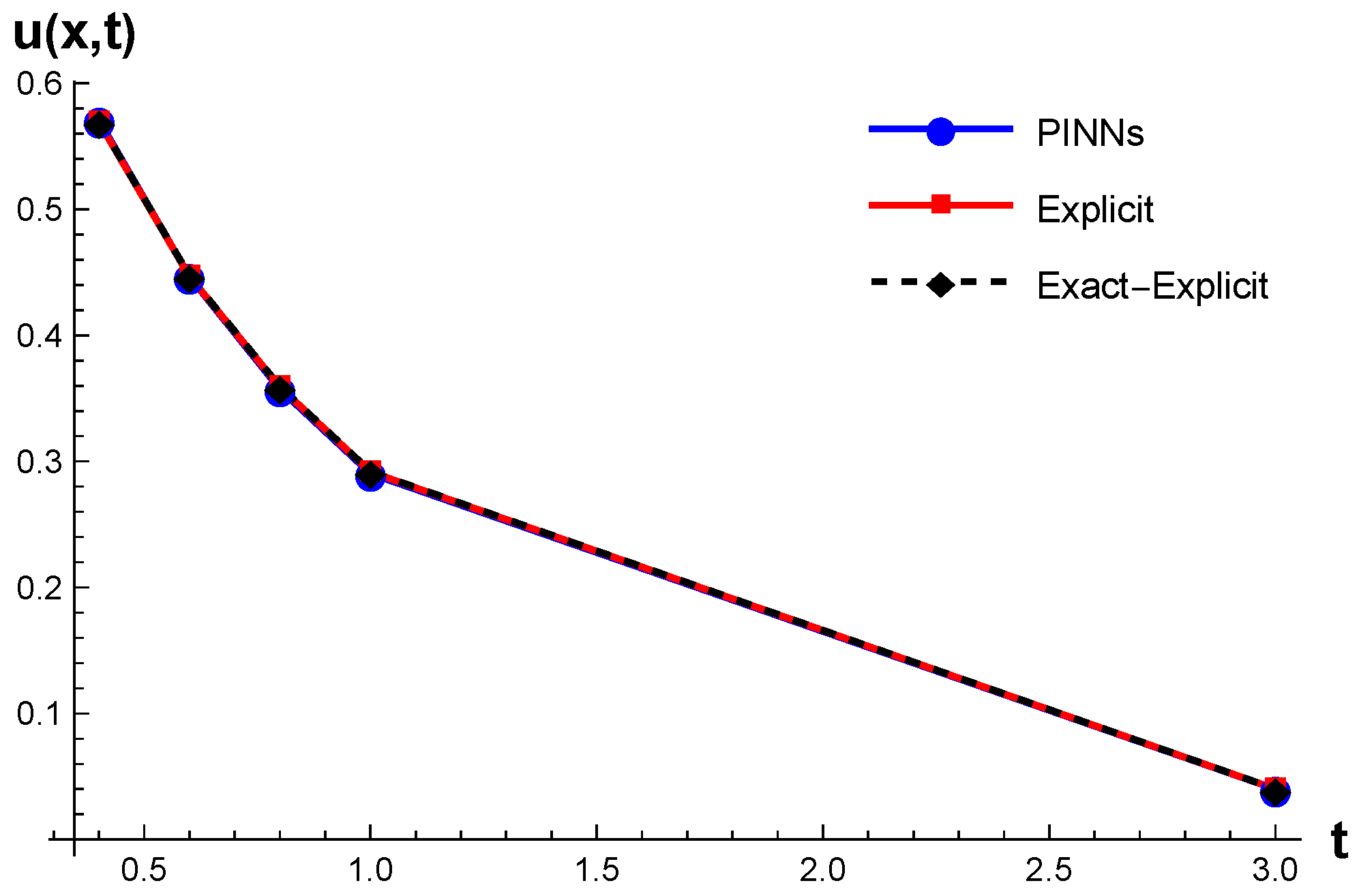
3.2.2. Exact-Explicit Finite Difference Method
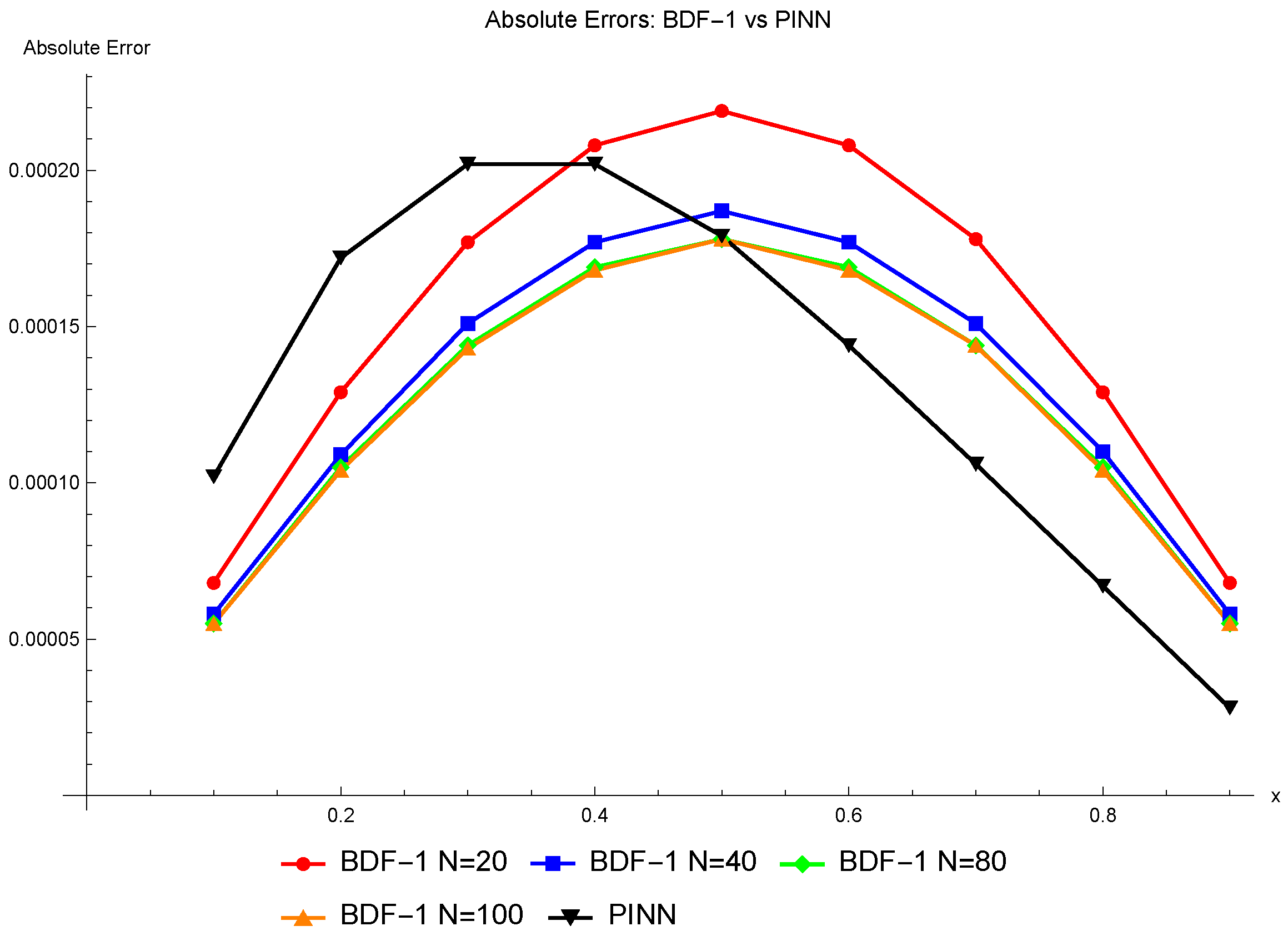
3.2.3. Accuracy Comparison Between Classical Numerical Methods and PINNs
3.3. Volterra Integro-Differential Equation
3.3.1. The Standard Variational Iteration Method Combined with Shifted Chebyshev Polynomials of the Fourth Kind
3.3.2. Convergence of the Method
- 1.
- has a unique fixed point .
- 2.
- The sequence generated by converges to for any initial guess .
3.3.3. Comparison of Results
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Raissi, M.; Perdikaris, P.; Karniadakis, G.E. Physics-informed neural networks: A deep learning framework for solving forward and inverse problems involving nonlinear partial differential equations. J. Comput. Phys. 2019, 378, 686–707. [Google Scholar] [CrossRef]
- Raissi, M.; Perdikaris, P.; Karniadakis, G.E. Physics Informed Deep Learning (Part I): Data-driven Solutions of Nonlinear Partial Differential Equations. arXiv 2017, arXiv:1711.10561. [Google Scholar] [CrossRef]
- Raissi, M.; Perdikaris, P.; Karniadakis, G.E. Physics Informed Deep Learning (Part II): Data-driven Discovery of Nonlinear Partial Differential Equations. arXiv 2017, arXiv:1711.10566. [Google Scholar] [CrossRef]
- Cuomo, S.; Di Cola, V.S.; Giampaolo, F.; Rozza, G.; Raissi, M.; Piccialli, F. Scientific machine learning through physics–informed neural networks: Where we are and what’s next. J. Sci. Comput. 2022, 92, 88. [Google Scholar]
- Brociek, R.; Pleszczyński, M. Differential Transform Method and Neural Network for Solving Variational Calculus Problems. Mathematics 2024, 12, 2182. [Google Scholar] [CrossRef]
- Faroughi, S.A.; Pawar, N.M.; Fernandes, C.; Raissi, M.; Das, S.; Kalantari, N.K.; Kourosh Mahjour, S. Physics-Guided, Physics-Informed, and Physics-Encoded Neural Networks and Operators in Scientific Computing: Fluid and Solid Mechanics. J. Comput. Inf. Sci. Eng. 2024, 24, 040802. [Google Scholar] [CrossRef]
- Usama, M.; Ma, R.; Hart, J.; Wojcik, M. Physics-Informed Neural Networks (PINNs)-Based Traffic State Estimation: An Application to Traffic Network. Algorithms 2022, 15, 447. [Google Scholar] [CrossRef]
- Wang, S.; Wang, H.; Perdikaris, P. On the eigenvector bias of Fourier feature networks: From regression to solving multi-scale PDEs with physics-informed neural networks. Comput. Methods Appl. Mech. Eng. 2021, 384, 113938. [Google Scholar] [CrossRef]
- Yuan, L.; Ni, Y.Q.; Deng, X.Y.; Hao, S. A-PINN: Auxiliary physics informed neural networks for forward and inverse problems of nonlinear integro-differential equations. J. Comput. Phys. 2022, 462, 111260. [Google Scholar] [CrossRef]
- Xiang, Z.; Peng, W.; Liu, X.; Yao, W. Self-adaptive loss balanced Physics-informed neural networks. Neurocomputing 2022, 496, 11–34. [Google Scholar] [CrossRef]
- Dwivedi, V.; Parashar, N.; Srinivasan, B. Distributed learning machines for solving forward and inverse problems in partial differential equations. Neurocomputing 2021, 420, 299–316. [Google Scholar] [CrossRef]
- Lee, J. Anti-derivatives approximator for enhancing physics-informed neural networks. Comput. Methods Appl. Mech. Eng. 2024, 426, 117000. [Google Scholar] [CrossRef]
- McClenny, L.D.; Braga-Neto, U.M. Self-adaptive physics-informed neural networks. J. Comput. Phys. 2023, 474, 111722. [Google Scholar] [CrossRef]
- Brociek, R.; Pleszczyński, M. Differential Transform Method (DTM) and Physics-Informed Neural Networks (PINNs) in Solving Integral–Algebraic Equation Systems. Symmetry 2024, 16, 1619. [Google Scholar] [CrossRef]
- Ren, Z.; Zhou, S.; Liu, D.; Liu, Q. Physics-Informed Neural Networks: A Review of Methodological Evolution, Theoretical Foundations, and Interdisciplinary Frontiers Toward Next-Generation Scientific Computing. Appl. Sci. 2025, 15, 92. [Google Scholar] [CrossRef]
- Lawal, Z.K.; Yassin, H.; Lai, D.T.C.; Che Idris, A. Physics-Informed Neural Network (PINN) Evolution and Beyond: A Systematic Literature Review and Bibliometric Analysis. Big Data Cogn. Comput. 2022, 6, 140. [Google Scholar] [CrossRef]
- Coutinho, E.J.R.; Dall’Aqua, M.; McClenny, L.; Zhong, M.; Braga-Neto, U.; Gildin, E. Physics-informed neural networks with adaptive localized artificial viscosity. J. Comput. Phys. 2023, 489, 112265. [Google Scholar] [CrossRef]
- Diao, Y.; Yang, J.; Zhang, Y.; Zhang, D.; Du, Y. Solving multi-material problems in solid mechanics using physics-informed neural networks based on domain decomposition technology. Comput. Methods Appl. Mech. Eng. 2023, 413, 116120. [Google Scholar] [CrossRef]
- Lazovskaya, T.; Malykhina, G.; Tarkhov, D. Physics-Based Neural Network Methods for Solving Parameterized Singular Perturbation Problem. Computation 2021, 9, 97. [Google Scholar] [CrossRef]
- Jagtap, A.D.; Mao, Z.; Adams, N.; Karniadakis, G.E. Physics-informed neural networks for inverse problems in supersonic flows. J. Comput. Phys. 2022, 466, 111402. [Google Scholar] [CrossRef]
- Hornik, K.; Stinchcombe, M.; White, H. Multilayer feedforward networks are universal approximators. Neural Netw. 1989, 2, 359–366. [Google Scholar] [CrossRef]
- Baydin, A.G.; Pearlmutter, B.A.; Radul, A.A.; Siskind, J.M. Automatic differentiation in machine learning: A survey. J. Mach. Learn. Res. 2018, 18, 1–43. [Google Scholar]
- Uddin, Z.; Ganga, S.; Asthana, R.; Ibrahim, W. Wavelets based physics informed neural networks to solve non-linear differential equations. Sci. Rep. 2023, 13, 2882. [Google Scholar] [CrossRef] [PubMed]
- Shin, Y.; Darbon, J.; Karniadakis, G.E. On the convergence of physics informed neural networks for linear second-order elliptic and parabolic type PDEs. arXiv 2020, arXiv:2004.01806. [Google Scholar] [CrossRef]
- Doumèche, N.; Biau, G.; Boyer, C. Convergence and error analysis of PINNs. arXiv 2023, arXiv:2305.01240. [Google Scholar] [CrossRef]
- Yoo, J.; Lee, H. Robust error estimates of PINN in one-dimensional boundary value problems for linear elliptic equations. arXiv 2024, arXiv:2407.14051. [Google Scholar] [CrossRef]
- De Ryck, T.; Mishra, S. Error analysis for physics-informed neural networks (PINNs) approximating Kolmogorov PDEs. Adv. Comput. Math. 2022, 48, 79. [Google Scholar] [CrossRef]
- Kingma, D.P. Adam: A method for stochastic optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
- Holm, D.D. Applications of Poisson geometry to physical problems. Geom. Topol. Monogr. 2011, 17, 221–384. [Google Scholar]
- Nolasco, C.; Jácome, N.; Hurtado-Lugo, N. Applications of the Poisson and diffusion equations to materials science. J. Phys. Conf. Ser. 2020, 1587, 012014. [Google Scholar]
- Klopfenstein, R.; Wu, C. Computer solution of one-dimensional Poisson’s equation. IEEE Trans. Electron Devices 1975, 22, 329–333. [Google Scholar] [CrossRef]
- Bhardwaj, S.; Gohel, H.; Namuduri, S. A Multiple-Input Deep Neural Network Architecture for Solution of One-Dimensional Poisson Equation. IEEE Antennas Wirel. Propag. Lett. 2019, 18, 2244–2248. [Google Scholar] [CrossRef]
- Kraichnan, R.H. Lagrangian-history statistical theory for Burgers’ equation. Phys. Fluids 1968, 11, 265–277. [Google Scholar] [CrossRef]
- Xie, S.S.; Heo, S.; Kim, S.; Woo, G.; Yi, S. Numerical solution of one-dimensional Burgers’ equation using reproducing kernel function. J. Comput. Appl. Math. 2008, 214, 417–434. [Google Scholar] [CrossRef]
- Inan, B.; Bahadir, A.R. Numerical solution of the one-dimensional Burgers’ equation: Implicit and fully implicit exponential finite difference methods. Pramana 2013, 81, 547–556. [Google Scholar] [CrossRef]
- Bonkile, M.P.; Awasthi, A.; Lakshmi, C.; Mukundan, V.; Aswin, V. A systematic literature review of Burgers’ equation with recent advances. Pramana 2018, 90, 69. [Google Scholar] [CrossRef]
- Kutluay, S.; Bahadir, A.; Özdeş, A. Numerical solution of one-dimensional Burgers equation: Explicit and exact-explicit finite difference methods. J. Comput. Appl. Math. 1999, 103, 251–261. [Google Scholar] [CrossRef]
- Mukundan, V.; Awasthi, A. Efficient numerical techniques for Burgers’ equation. Appl. Math. Comput. 2015, 262, 282–297. [Google Scholar] [CrossRef]
- Brunner, H. Collocation Methods for Volterra Integral and Related Functional Differential Equations; Cambridge University Press: Cambridge, UK, 2004; Volume 15. [Google Scholar]
- Volterra, V. Leçons sur la Théorie Mathématique de la Lutte pour la Vie; Gauthier Villars: Paris, France, 1931. [Google Scholar]
- Joseph, D.D.; Preziosi, L. Heat waves. Rev. Mod. Phys. 1989, 61, 41. [Google Scholar] [CrossRef]
- Otaide, I.J.; Oluwayemi, M.O. Numerical treatment of linear volterra integro differential equations using variational iteration algorithm with collocation. Partial. Differ. Equ. Appl. Math. 2024, 10, 100693. [Google Scholar] [CrossRef]
- Lu, L.; Meng, X.; Mao, Z.; Karniadakis, G.E. DeepXDE: A deep learning library for solving differential equations. SIAM Rev. 2021, 63, 208–228. [Google Scholar] [CrossRef]

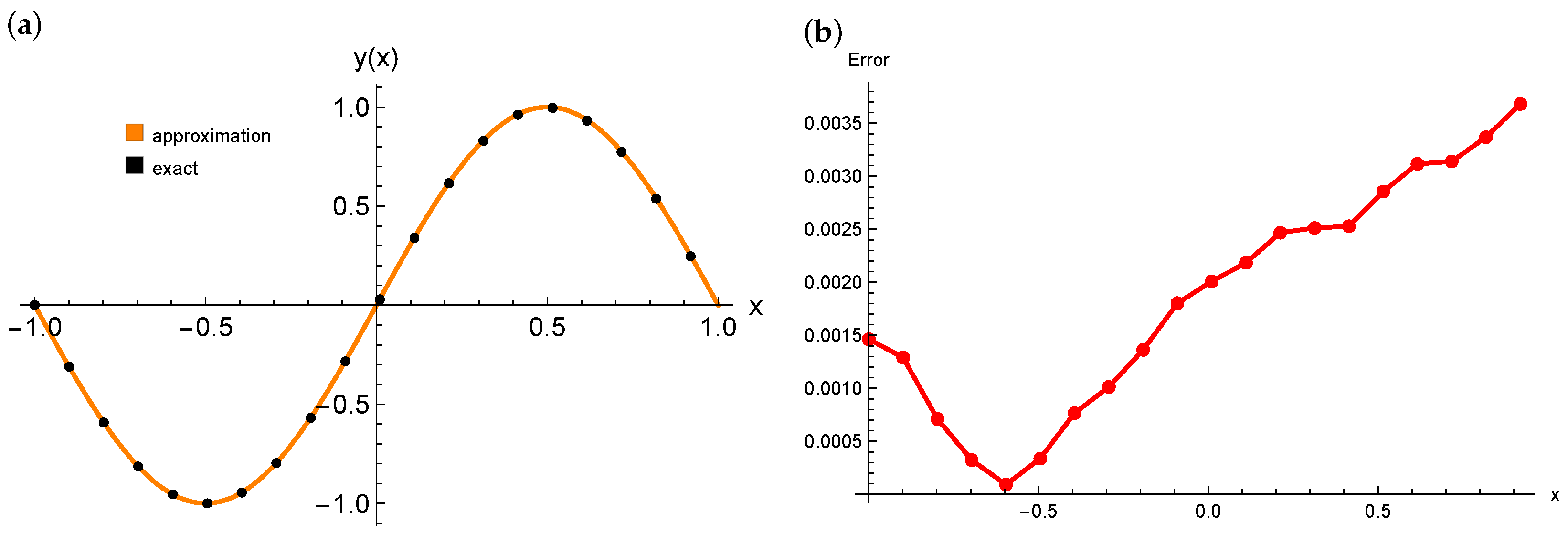
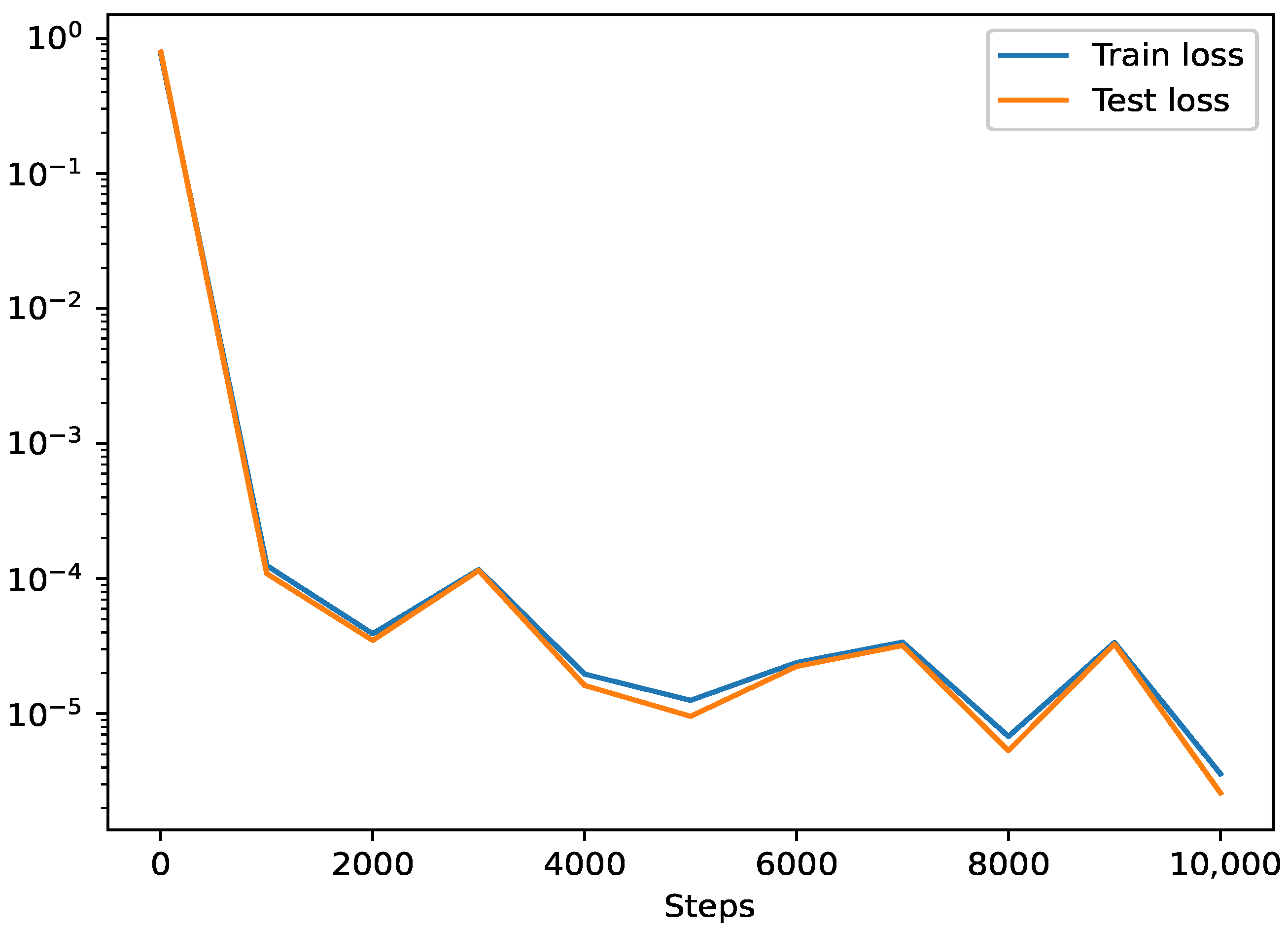

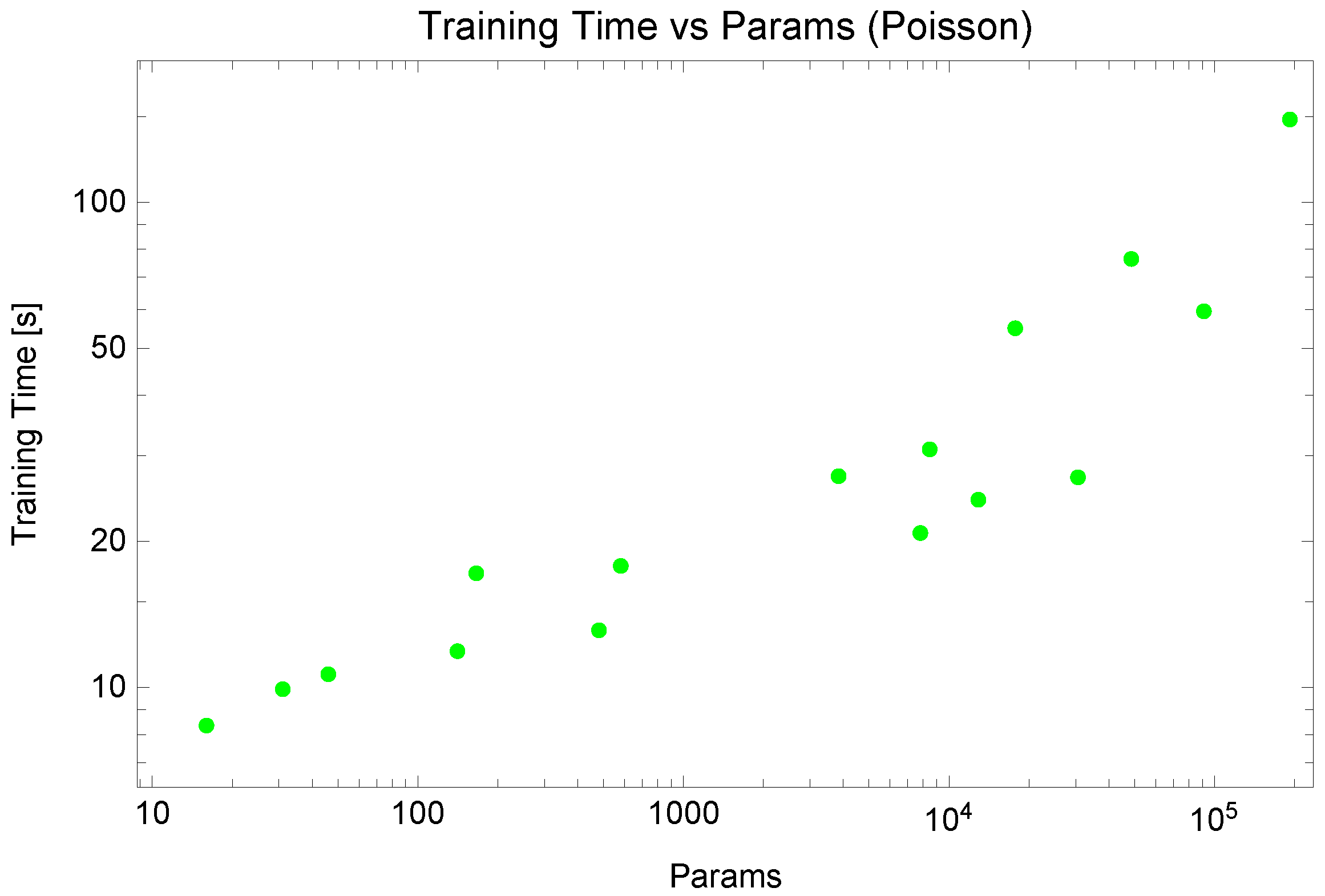

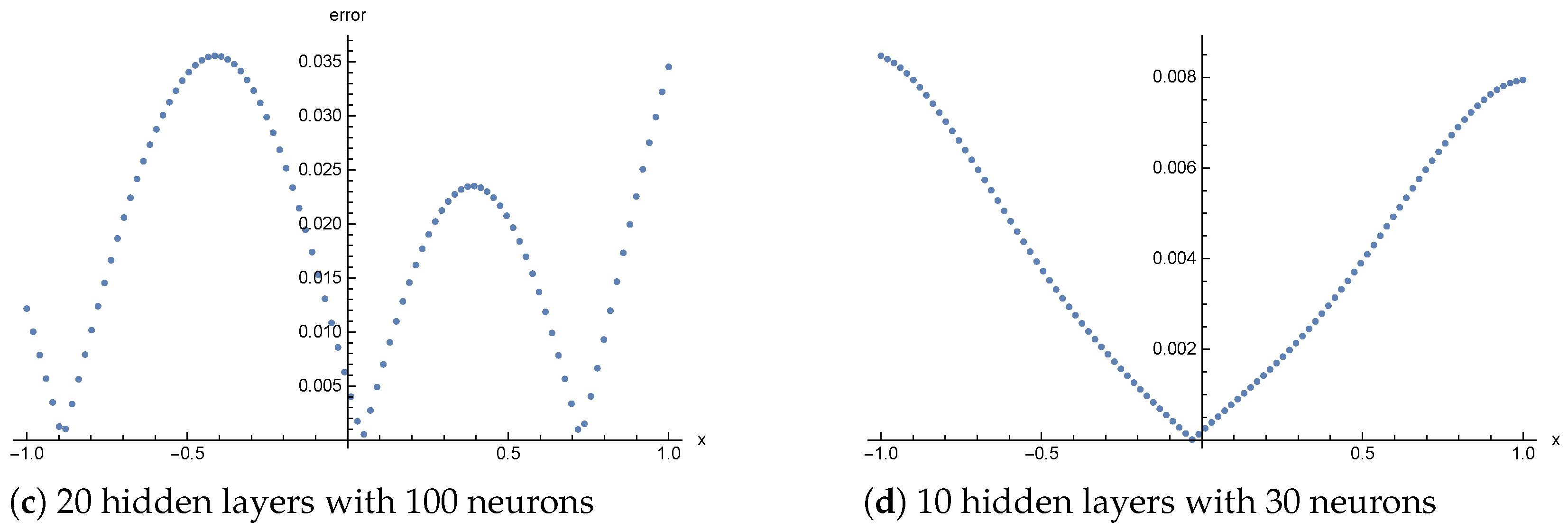


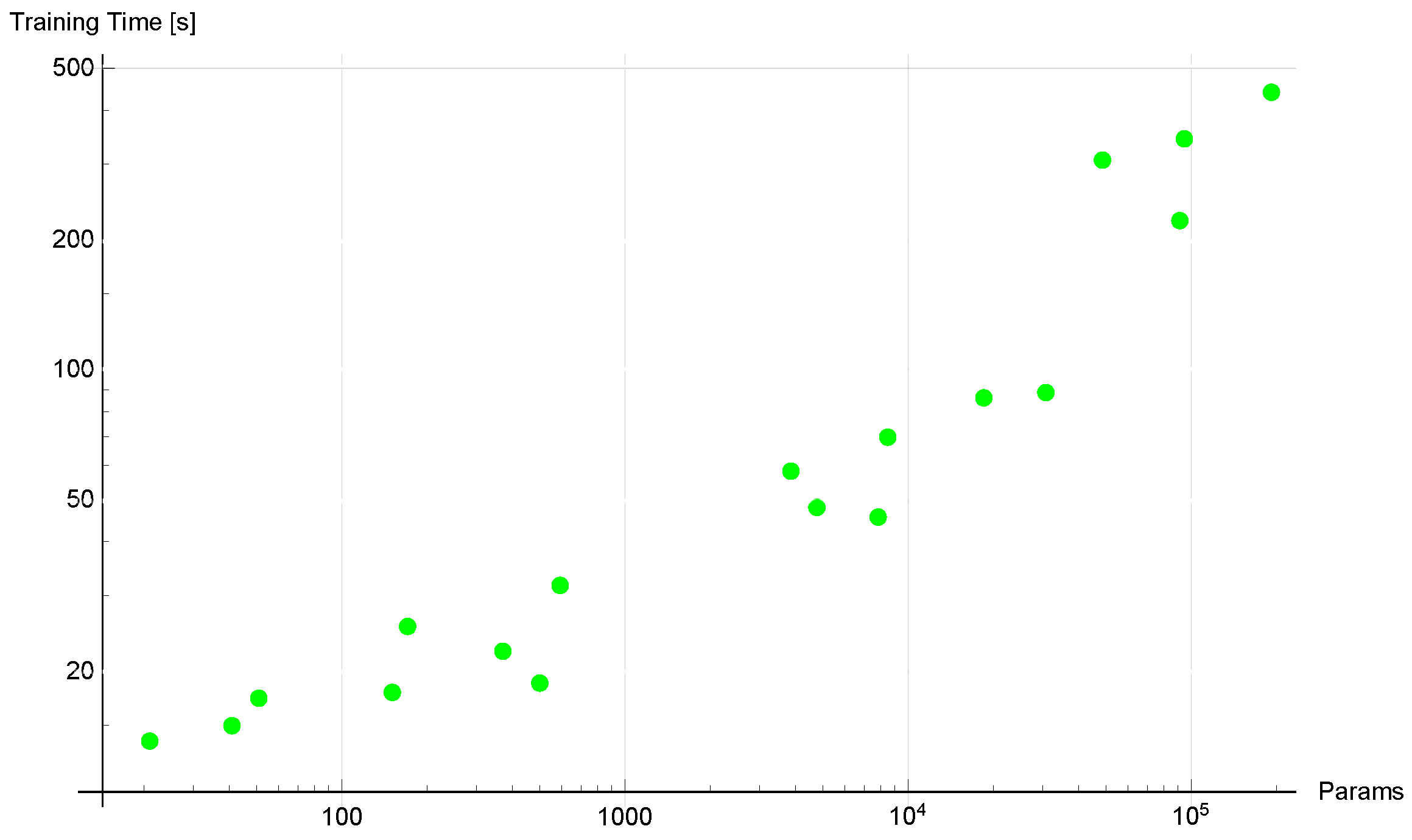

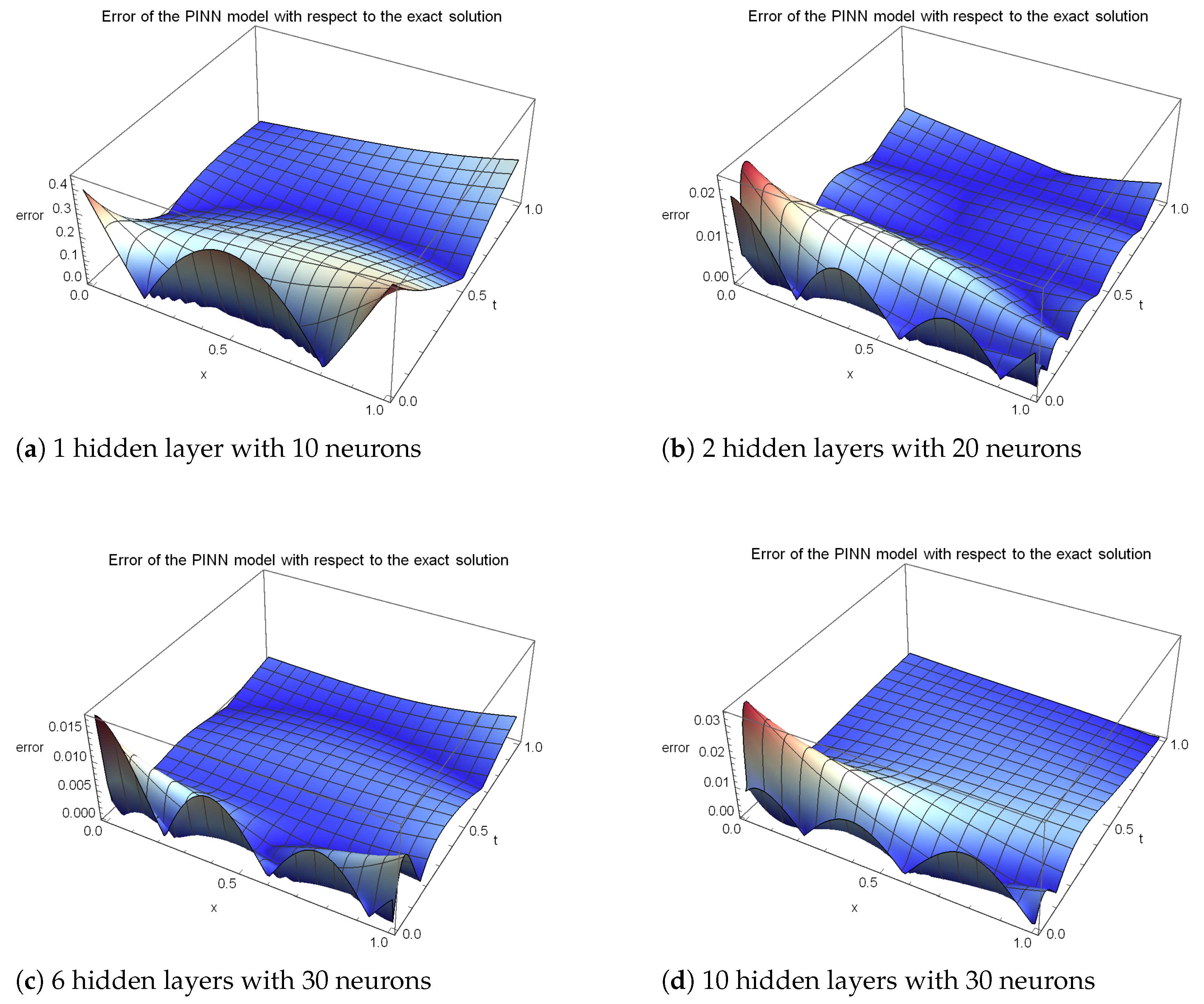
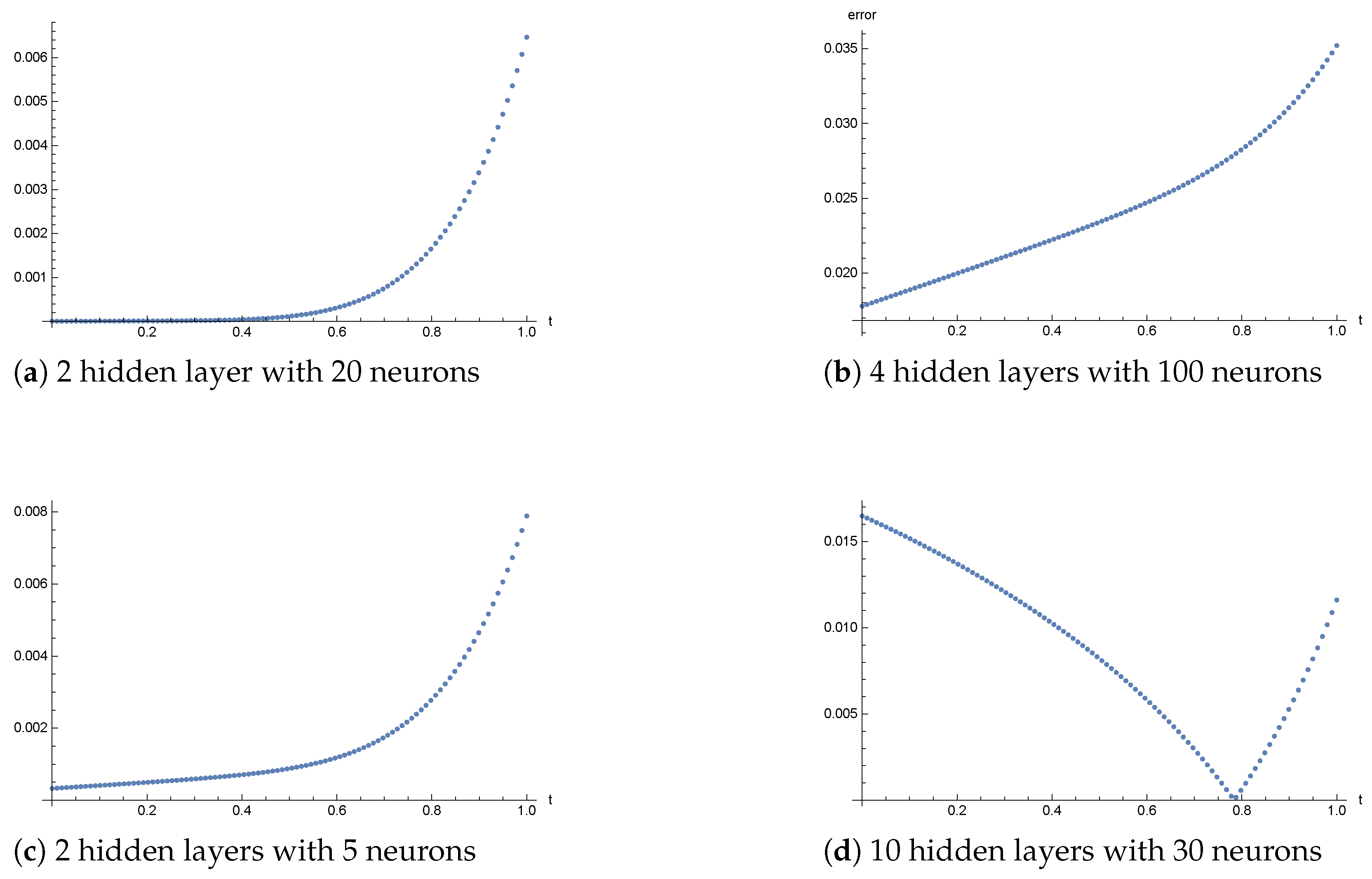
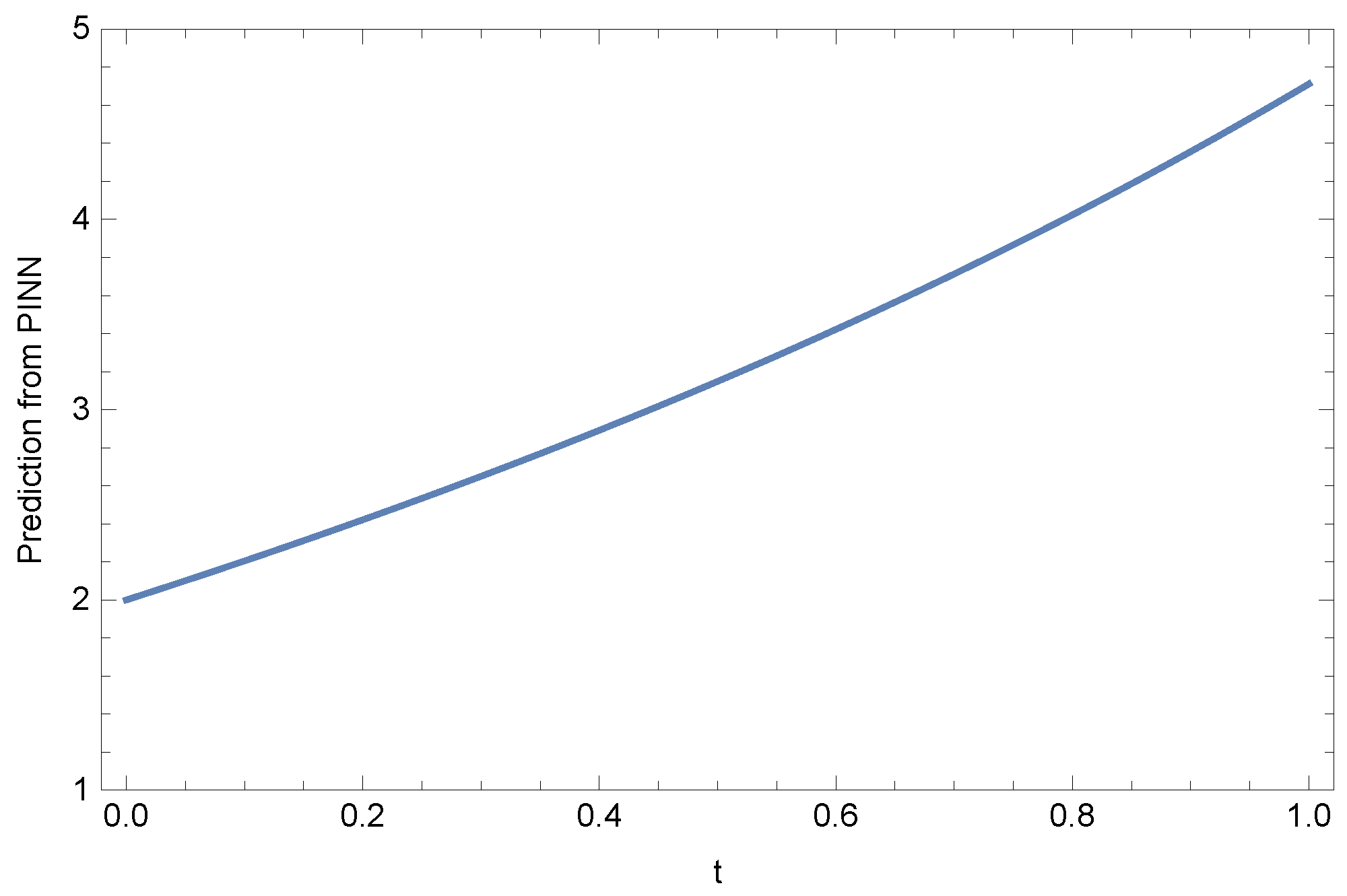
| Training Points | Neurons | Layers | Mean Error | Max Error |
|---|---|---|---|---|
| 32 | 10 | 5 | 0.0001789 | 0.0003578 |
| 64 | 10 | 5 | 0.0042591 | 0.0018514 |
| 64 | 15 | 7 | 0.0012387 | 0.0027478 |
| 128 | 15 | 5 | 0.0001534 | 0.0004693 |
| 128 | 20 | 7 | 0.0001092 | 0.0003296 |
| Neurons | Hidden Layers | Mean Error | Max Error | Training Time [s] | Params |
|---|---|---|---|---|---|
| 5 | 1 | 0.0000962 | 0.0004039 | 8.35 | 16 |
| 10 | 1 | 0.0002057 | 0.0004992 | 9.92 | 31 |
| 5 | 2 | 0.0000971 | 0.0002125 | 10.65 | 46 |
| 10 | 2 | 0.0002535 | 0.0007126 | 11.88 | 141 |
| 20 | 2 | 0.0000545 | 0.0001862 | 13.12 | 481 |
| 50 | 4 | 0.0012889 | 0.0023040 | 20.81 | 7801 |
| 100 | 4 | 0.0033755 | 0.0063511 | 27.10 | 30,601 |
| 5 | 6 | 0.0000933 | 0.0002061 | 17.19 | 166 |
| 10 | 6 | 0.0013967 | 0.0028064 | 17.80 | 581 |
| 50 | 6 | 0.0042395 | 0.0137589 | 24.37 | 12,901 |
| 20 | 10 | 0.0132887 | 0.0235891 | 27.25 | 3841 |
| 30 | 10 | 0.0041084 | 0.0084747 | 30.95 | 8461 |
| 100 | 10 | 0.0120098 | 0.0292455 | 59.57 | 91,201 |
| 30 | 20 | 0.0023960 | 0.0056850 | 54.97 | 17,761 |
| 50 | 20 | 0.0149564 | 0.0352005 | 76.35 | 48,601 |
| 100 | 20 | 0.0183402 | 0.0355639 | 147.95 | 192,201 |
| Training Points | Mean Error | Max Error |
|---|---|---|
| 100 | 0.0000069 | 0.0000126 |
| 500 | 0.0000030 | 0.0000067 |
| 1000 | 0.0000022 | 0.0000053 |
| 5000 | 0.0000013 | 0.0000037 |
| 10,000 | 0.0000011 | 0.0000022 |
| Activation | Mean Error | Max Error |
|---|---|---|
| ReLU | 0.6331564 | 0.9996860 |
| Sigmoid | 0.0000459 | 0.0000838 |
| sin | 0.0000770 | 0.0001597 |
| Swish | 0.0000285 | 0.0000698 |
| tanh | 0.0000158 | 0.0000494 |
| ELU | 0.0045412 | 0.0107337 |
| x | Explicit [37] | Exact-Explicit [37] | PINNs | Exact Solution |
|---|---|---|---|---|
| 0.1 | 0.10863 | 0.11048 | 0.11166 | 0.10954 |
| 0.2 | 0.20805 | 0.21159 | 0.21210 | 0.20979 |
| 0.3 | 0.28946 | 0.29435 | 0.29440 | 0.29190 |
| 0.4 | 0.34501 | 0.35080 | 0.35059 | 0.34792 |
| 0.5 | 0.36845 | 0.37458 | 0.37446 | 0.37158 |
| 0.6 | 0.35601 | 0.36189 | 0.36214 | 0.35905 |
| 0.7 | 0.30728 | 0.31231 | 0.31310 | 0.30991 |
| 0.8 | 0.22588 | 0.22955 | 0.23133 | 0.22782 |
| 0.9 | 0.11966 | 0.12160 | 0.12559 | 0.12069 |
| x | t | Numerical Solution | Exact Solution | ||
|---|---|---|---|---|---|
| Explicit [37] | Exact-Explicit [37] | PINNs | |||
| 0.5 | 0.4 | 0.56911 | 0.56964 | 0.57055 | 0.56963 |
| 0.6 | 0.44676 | 0.44721 | 0.44644 | 0.44721 | |
| 0.8 | 0.35888 | 0.35924 | 0.35721 | 0.35924 | |
| 1.0 | 0.29162 | 0.29192 | 0.29031 | 0.29192 | |
| 3.0 | 0.04017 | 0.04021 | 0.04003 | 0.04021 | |
| x | Exact Solution | PINN | ||||
|---|---|---|---|---|---|---|
| 0.1 | 2.281 × 10−3 | 2.271 × 10−3 | 2.268 × 10−3 | 2.268 × 10−3 | 2.213 × 10−3 | 2.315 × 10−3 |
| 0.2 | 4.339 × 10−3 | 4.319 × 10−3 | 4.315 × 10−3 | 4.314 × 10−3 | 4.210 × 10−3 | 4.382 × 10−3 |
| 0.3 | 5.973 × 10−3 | 5.947 × 10−3 | 5.940 × 10−3 | 5.939 × 10−3 | 5.796 × 10−3 | 5.998 × 10−3 |
| 0.4 | 7.024 × 10−3 | 6.993 × 10−3 | 6.985 × 10−3 | 6.984 × 10−3 | 6.816 × 10−3 | 7.018 × 10−3 |
| 0.5 | 7.388 × 10−3 | 7.356 × 10−3 | 7.347 × 10−3 | 7.347 × 10−3 | 7.169 × 10−3 | 7.348 × 10−3 |
| 0.6 | 7.029 × 10−3 | 6.998 × 10−3 | 6.990 × 10−3 | 6.989 × 10−3 | 6.821 × 10−3 | 6.965 × 10−3 |
| 0.7 | 5.982 × 10−3 | 5.955 × 10−3 | 5.948 × 10−3 | 5.948 × 10−3 | 5.804 × 10−3 | 5.910 × 10−3 |
| 0.8 | 4.347 × 10−3 | 4.328 × 10−3 | 4.323 × 10−3 | 4.322 × 10−3 | 4.218 × 10−3 | 4.285 × 10−3 |
| 0.9 | 2.286 × 10−3 | 2.276 × 10−3 | 2.273 × 10−3 | 2.273 × 10−3 | 2.218 × 10−3 | 2.246 × 10−3 |
| Weights | Mean Error | Max Error |
|---|---|---|
| (5.0, 1.0, 1.0, 1.0) | 0.0126755 | 0.0766495 |
| (1.0, 5.0, 1.0, 1.0) | 0.00730921 | 0.0546295 |
| (1.0, 1.0, 5.0, 5.0) | 0.00579474 | 0.0411806 |
| (10.0, 1.0, 1.0, 1.0) | 0.0111069 | 0.103218 |
| (1.0, 10.0, 10.0, 10.0) | 0.00258062 | 0.0196944 |
| (1.0, 5.0, 5.0, 5.0) | 0.00197403 | 0.0177932 |
| Collocation Point Distribution Type | Mean Error | Max Error |
|---|---|---|
| uniform (equispaced grid) | 0.00511845 | 0.0278437 |
| pseudo (pseudorandom) | 0.00418709 | 0.029266 |
| LHS (Latin hypercube sampling) | 0.00696592 | 0.0361623 |
| Halton (Halton sequence) | 0.00759538 | 0.0478001 |
| Hammersley (Hammersley sequence) | 0.00372326 | 0.0329703 |
| Sobol (Sobol sequence) | 0.00485239 | 0.0341695 |
| Number of Collocation Points | Mean Error | Max Error | Time of Training Model [s] |
|---|---|---|---|
| 50 | 0.00541526 | 0.0308579 | 25.12 |
| 100 | 0.00516718 | 0.0317111 | 28.76 |
| 500 | 0.00630318 | 0.0403584 | 31.06 |
| 1000 | 0.00418513 | 0.0254188 | 34.44 |
| 10,000 | 0.00140849 | 0.0123031 | 120.84 |
| Neurons | Hidden Layers | Mean Error | Max Error | Training Time [s] | Params |
|---|---|---|---|---|---|
| 5 | 1 | 0.0666834 | 0.436997 | 13.79 | 21 |
| 10 | 1 | 0.0969972 | 0.445789 | 14.97 | 41 |
| 5 | 2 | 0.0229704 | 0.147473 | 17.33 | 51 |
| 10 | 2 | 0.0037768 | 0.045616 | 17.88 | 151 |
| 20 | 2 | 0.0030077 | 0.024509 | 18.79 | 501 |
| 10 | 4 | 0.0044155 | 0.035810 | 22.28 | 371 |
| 50 | 4 | 0.0055573 | 0.029546 | 45.59 | 7851 |
| 100 | 4 | 0.0110681 | 0.020511 | 88.62 | 30,701 |
| 5 | 6 | 0.0141401 | 0.084471 | 25.42 | 171 |
| 10 | 6 | 0.0029999 | 0.018322 | 31.66 | 591 |
| 30 | 6 | 0.0018869 | 0.017416 | 48.00 | 4771 |
| 60 | 6 | 0.0119612 | 0.058198 | 86.14 | 18,541 |
| 20 | 10 | 0.0049465 | 0.024834 | 58.23 | 3861 |
| 30 | 10 | 0.0059858 | 0.033673 | 69.82 | 8491 |
| 100 | 10 | 0.0050738 | 0.059602 | 221.90 | 91,301 |
| 50 | 20 | 0.0052591 | 0.034503 | 306.45 | 48,651 |
| 70 | 20 | 0.0343433 | 0.0484721 | 343.27 | 94,711 |
| 100 | 20 | 0.0089822 | 0.0848633 | 440.17 | 192,301 |
| Neurons | Hidden Layers | Mean Error | Max Error | Training Time [s] | Params |
|---|---|---|---|---|---|
| 5 | 1 | 0.00111956 | 0.00684174 | 13.32 | 16 |
| 10 | 1 | 0.00102483 | 0.00675019 | 14.14 | 31 |
| 5 | 2 | 0.00174907 | 0.00788888 | 20.45 | 46 |
| 10 | 2 | 0.000961112 | 0.00644263 | 26.92 | 141 |
| 20 | 2 | 0.000949299 | 0.00646266 | 38.24 | 481 |
| 50 | 4 | 0.000996002 | 0.00644883 | 335.16 | 7801 |
| 100 | 4 | 0.0242298 | 0.0352155 | 706.06 | 30,601 |
| 5 | 6 | 0.00109214 | 0.00678214 | 129.42 | 166 |
| 10 | 6 | 0.00102154 | 0.00660905 | 314.78 | 581 |
| 50 | 6 | 0.000891232 | 0.00629672 | 663.80 | 12,901 |
| 20 | 10 | 0.0424468 | 0.0460251 | 1036.78 | 3841 |
| 30 | 10 | 0.00881867 | 0.016485 | 1168.29 | 8461 |
| 100 | 10 | 0.00157222 | 0.00746592 | 1870.17 | 91,201 |
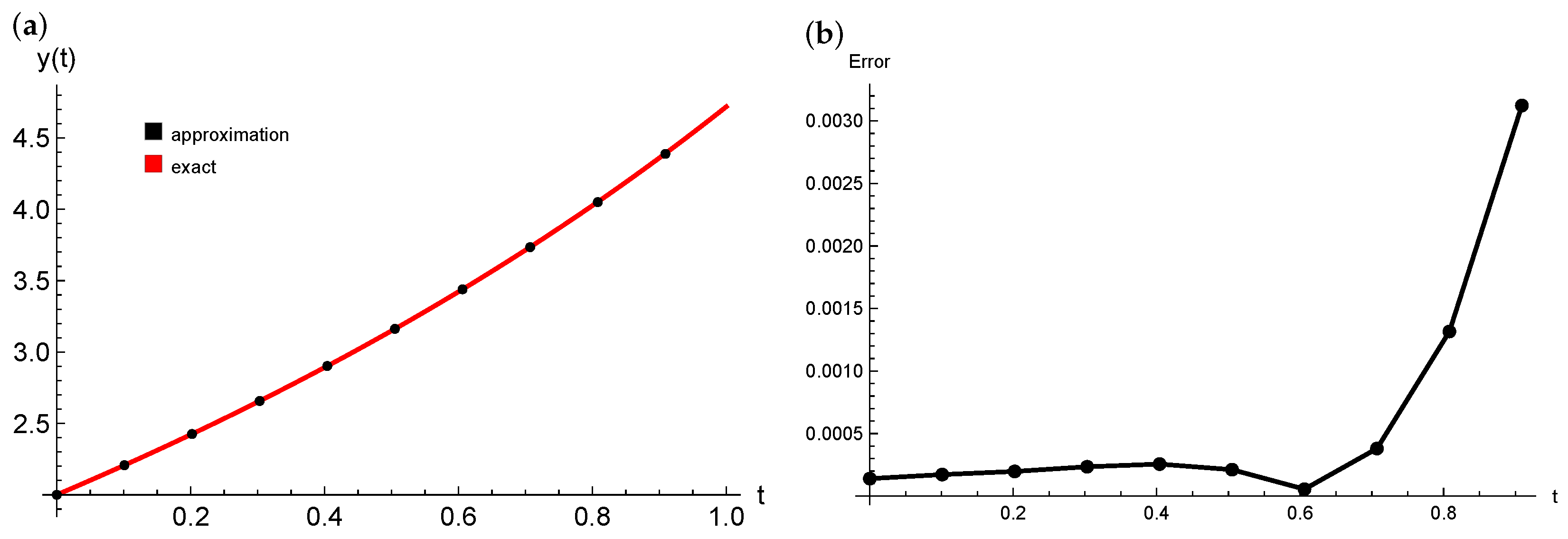
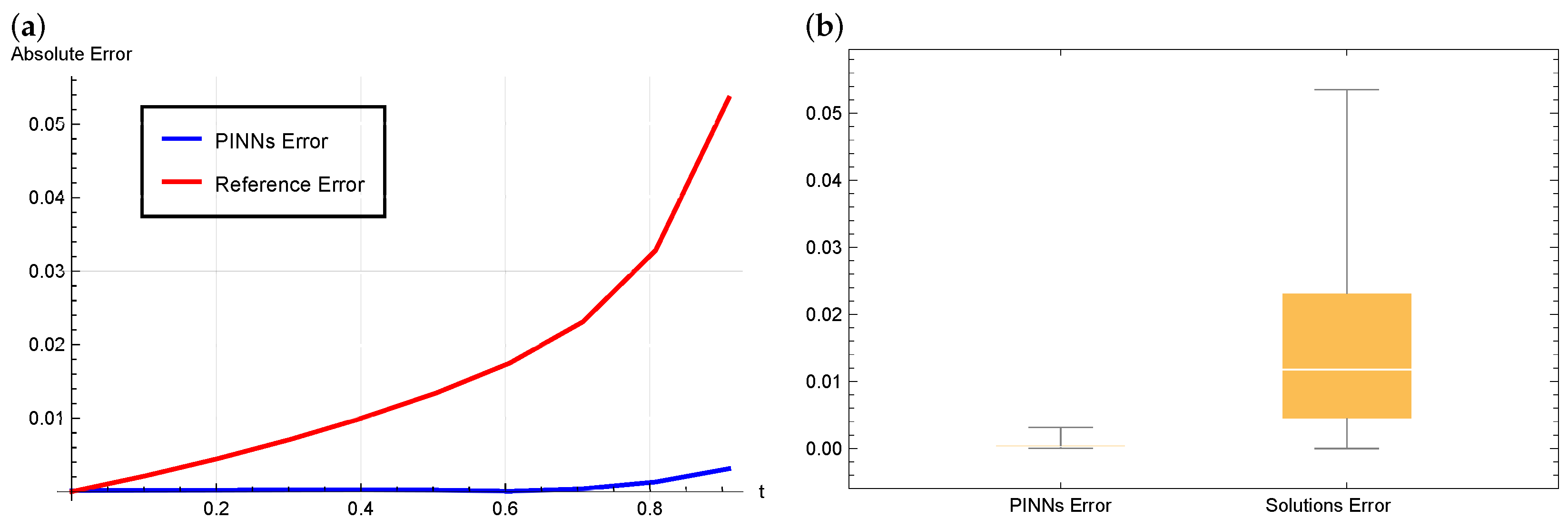
| t | Solutions [42] | PINNs | Exact Solution |
|---|---|---|---|
| 0.0 | 2.00000 | 2.00014 | 2.00000 |
| 0.1 | 2.20517 | 2.20747 | 2.20730 |
| 0.2 | 2.42140 | 2.42609 | 2.42589 |
| 0.3 | 2.64986 | 2.65722 | 2.65699 |
| 0.4 | 2.89182 | 2.90216 | 2.90190 |
| 0.5 | 3.14867 | 3.16233 | 3.16212 |
| 0.6 | 3.42200 | 3.43931 | 3.43925 |
| 0.7 | 3.71440 | 3.73473 | 3.73511 |
| 0.8 | 4.03267 | 4.05036 | 4.05168 |
| 0.9 | 4.39798 | 4.38803 | 4.39115 |
| 1.0 | 4.87221 | 4.71233 | 4.71828 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Brociek, R.; Pleszczyński, M.; Mughal, D.A. On the Performance of Physics-Based Neural Networks for Symmetric and Asymmetric Domains: A Comparative Study and Hyperparameter Analysis. Symmetry 2025, 17, 1698. https://doi.org/10.3390/sym17101698
Brociek R, Pleszczyński M, Mughal DA. On the Performance of Physics-Based Neural Networks for Symmetric and Asymmetric Domains: A Comparative Study and Hyperparameter Analysis. Symmetry. 2025; 17(10):1698. https://doi.org/10.3390/sym17101698
Chicago/Turabian StyleBrociek, Rafał, Mariusz Pleszczyński, and Dawood Asghar Mughal. 2025. "On the Performance of Physics-Based Neural Networks for Symmetric and Asymmetric Domains: A Comparative Study and Hyperparameter Analysis" Symmetry 17, no. 10: 1698. https://doi.org/10.3390/sym17101698
APA StyleBrociek, R., Pleszczyński, M., & Mughal, D. A. (2025). On the Performance of Physics-Based Neural Networks for Symmetric and Asymmetric Domains: A Comparative Study and Hyperparameter Analysis. Symmetry, 17(10), 1698. https://doi.org/10.3390/sym17101698








