Symmetry-Aware EKV-Based Metaheuristic Optimization of CMOS LC-VCOs for Low-Phase-Noise Applications

Abstract

The integration of AI-driven optimization into Electronic Design Automation (EDA) enables smarter and more adaptive circuit design, where symmetry and asymmetry play key roles in balancing performance, robustness, and manufacturability. This work presents a model-driven optimization methodology for sizing low-phase-noise LC voltage-controlled oscillators (VCOs) at 5 GHz, targeting Wi-Fi, 5G, and automotive radar applications. The approach uses the EKV transistor model for analytical CMOS device characterization and applies a diverse set of metaheuristic algorithms for both single-objective (phase noise minimization) and multi-objective (joint phase noise and power) optimization. A central focus is on how symmetry—embedded in the complementary cross-coupled LC-VCO topology—and asymmetry—introduced by parasitics, mismatch, and layout constraints—affect optimization outcomes. The methodology implicitly captures these effects during simulation-based optimization, enabling design-space exploration that is both symmetry-aware and robust to unavoidable asymmetries. Implemented in CMOS 180 nm technology, the approach delivers designs with improved phase noise and power efficiency while ensuring manufacturability. Yield analysis confirms that integrating symmetry considerations into metaheuristic-based optimization enhances performance predictability and resilience to process variations, offering a scalable, AI-aligned solution for high-performance analog circuit design within EDA workflows.

1. Introduction

The continuous scaling of CMOS technology to nanometer sizes has enabled the development of highly integrated systems for wireless communication, offering benefits such as higher speed, lower power consumption, and reduced area. As a result, CMOS technology is widely adopted for RF applications due to its high-density integration and cost effectiveness. However, this comes with challenges, particularly in maintaining low phase noise and power efficiency. One key issue is the degradation of the on-chip LC tank quality factor, which is typically limited in the GHz range due to thin metal layers and substrate losses [1]. While advancements in process technology and additional metal layers have gradually improved the quality factor of passive elements [2], designing high-performance LC voltage-controlled oscillator (VCOs) remains a complex task, especially with the reduced supply voltage that complicates achieving wide linearity and full output swing [3].

The 5 GHz frequency band is widely used in modern RF applications, including Wi-Fi standards such as 802.11a/n/ac/ax [4], mid-band 5G networks [5], and automotive radar systems [6]. These applications demand low-phase-noise oscillators to ensure reliable communication, reduced signal distortion, and enhanced performance. Furthermore, IoT devices operating in this band benefit from reduced interference and higher data throughput compared to the crowded 2.4 GHz spectrum [7]. Designing VCOs optimized for such applications is critical to meet the stringent requirements of high-speed data transfer, low power consumption, and robust performance in the presence of noise and interference. This work aims to address these challenges by proposing an efficient optimization methodology tailored to the needs of these 5 GHz applications.

Numerous methodologies for designing LC VCOs have been proposed in the literature. Most studies rely on analytical models to characterize circuit behavior but often ignore parasitic effects, which are only accounted for through simulations. For instance, the $g_m/I_D$ methodology explored in [8] optimizes LC VCOs across all transistor inversion regions but lacks applicability for varactor characterization. Furthermore, model-based optimization methods combined with genetic algorithms (GAs) have been employed to enhance phase noise and power consumption in RF applications [9,10]. Despite their effectiveness, these approaches might miss certain non-idealities captured by electromagnetic simulations, highlighting the need for further validation through Process, Voltage, and Temperature (PVT) and yield analysis.

Recent work in [11] introduces a wide-tunable, low-voltage LC-VCO using a novel active inductor, achieving impressive performance metrics. However, the absence of optimization algorithms limits further enhancement of phase noise and power consumption, and the use of an active inductor can introduce higher noise and power consumption compared to traditional inductors. Moreover, studies like [12] employ EDA tools and Evolutionary Algorithms (EAs) for optimal VCO sizing, achieving precise performance trade-offs. Still, their focus on only two LC-VCO topologies may overlook alternative designs that could offer better results, and the computational intensity of such simulations may increase design time and complexity. Similarly, ref. [13] presents a simulation-based methodology for multi-objective optimization of LC-VCOs, focusing on key metrics like power consumption and phase noise. While validated using 0.13 µm RF CMOS technology, this approach’s reliance on extensive simulations can make it computationally expensive, demanding significant time and resources, especially for more complex RF circuits. In [14], the authors propose a new multi-objective optimization methodology for designing a complementary cross-coupled LC-VCO, aiming to minimize both phase noise and power consumption. This approach leverages a multi-objective algorithm that enhances exploration and exploitation, theoretically improving oscillator performance. However, the work has several limitations: it lacks validation through circuit simulation, limiting practical applicability, and, despite claiming a multi-objective approach, only a single solution is presented, which undermines the multi-objective framework. Additionally, the VCO modeling uses simplified equations that may not adequately capture the complexities of real-world VCO behavior.

According to recent reviews of metaheuristic optimization in analog circuit design, the vast majority of reported studies rely on population-based approaches, particularly genetic algorithms, evolutionary strategies, and swarm intelligence. Among these, GAs and NSGA-II are by far the most frequently employed for analog and RF circuit sizing, reflecting their maturity and community adoption [15,16]. Nonetheless, the same reviews also document an increasing adoption of hybrid schemes (e.g., PSO–DE combinations), surrogate-assisted optimizers (such as surrogate-augmented DE or ESSAB [17]), and more recent swarm-based innovations (e.g., MSSA, MOBO/D), which offer promising improvements in convergence speed and scalability [18,19,20]. While classical algorithms remain critical as baselines and for comparability across studies, the integration of recent algorithms highlights the research momentum toward more efficient, hybridized, and machine-learning-assisted metaheuristics in analog design [21,22].

Recent surveys of metaheuristic-based analog design confirm that these methods remain the most widely adopted tools for circuit optimization due to their ability to handle nonlinear, non-differentiable, and simulation-driven objectives. Evolutionary and swarm intelligence approaches such as GA, PSO, and DE dominate the literature, while multi-objective variants like NSGA-II and SPEA2 remain the most frequently applied to balance conflicting circuit performance metrics. At the same time, newer trends include hybrid [20] and surrogate-assisted metaheuristics [18,19] that aim to reduce the high computational cost of repeated SPICE simulations, as well as physics-inspired and decomposition-based approaches (e.g., MOEA/D, MSSA) that enhance convergence speed and Pareto diversity. Importantly, the recent taxonomy of methods also highlights the growing role of machine learning integration [17,21,22], such as ANN-assisted differential evolution [16] or surrogate-guided search [17], for handling high-dimensional analog design tasks. These findings emphasize both the maturity of classical algorithms and the momentum of recent innovations, situating our proposed framework at the intersection of reliability and state-of-the-art advancement.

While differential LC-VCOs inherently benefit from symmetric topologies to ensure balanced outputs and effective common-mode rejection, practical implementations often introduce asymmetries due to layout constraints, parasitic mismatches, or non-uniform biasing. These asymmetries can degrade performance, particularly phase noise and power efficiency; however, when properly characterized, they may also offer optimization flexibility. In this context, this paper explores how model-based metaheuristic optimization can implicitly account for such structural and layout asymmetries while enforcing performance-driven symmetry in key signal paths.

In this work, we propose a model-based optimization approach that leverages the EKV model for accurate characterization of circuit elements combined with metaheuristic algorithms. Our methodology, demonstrated through case studies using 180 nm CMOS technology, effectively minimizes phase noise and power consumption. The accuracy of the optimized LC-VCO designs is validated through detailed simulations, and their robustness is confirmed via yield analysis.

It is important to note that the novelty of this work does not lie in introducing a new optimization algorithm. Instead, it resides in the methodological contribution of embedding symmetry and asymmetry considerations directly into EKV-based analytical modeling of LC-VCOs. By enriching the modeling layer, the proposed approach enables existing metaheuristics—whether classical (e.g., GA, PSO, DE, NSGA-II) or modern (e.g., new, hybrid, surrogate-assisted, or machine-learning-based)—to converge toward physically consistent, verifiable, and practically implementable designs. This modeling innovation ensures that optimization outcomes remain both robust and relevant, even without the development of a new algorithm.

The main motivations of this work can be summarized as follows:

• To integrate EKV-based physical models with metaheuristics for verifiable LC-VCO design;
• To assess how symmetry and asymmetry influence optimization outcomes;
• To compare single- and multi-objective optimization in minimizing phase noise and power;
• To validate robustness through yield-oriented Monte Carlo simulations.

The rest of this paper is structured as follows: Section 2 formulates the optimization problem for LC-VCO design. Section 3 presents the LC-VCO topology and modeling, providing the foundational analytical models for the spiral inductor and CMOS varactor as well as performance characterization. Section 4 discusses the LC-VCO optimization results, with detailed analysis and comparisons. Finally, conclusions are drawn in Section 5.

2. LC-VCO Optimization Formulation

The circuit optimization problem focuses on determining the optimal set of design parameters that maximize or minimize specific performance metrics of a circuit, while satisfying a set of constraints. In the context of LC-VCO design, the optimization problem seeks to determine the optimal set of design parameters that improve critical performance metrics. The optimization can be formulated as follows:

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill Find& X\hfill \\ \hfill \underset{X\in S}{Minimize}& F\left(X\right)\hfill \\ \hfill subjectto& g\left(X\right)\le 0\hfill \\ \hfill & h\left(X\right)=0\hfill \end{array}\end{array}$$

(1)

Here, $F\left(X\right)$ represents the set of objective functions, which can be a circuit characteristic or combination of characteristics to be optimized. In the case of LC-VCO design, this typically includes phase noise, power consumption, and other metrics such as the tuning range or oscillation frequency.

The vector $X\in$ ${\mathbf{R}}^d$ consists of the d design parameters, where each parameter $x_i$ corresponds to a specific element of the LC-VCO circuit, such as transistor dimensions, inductor and capacitor sizes, or biasing currents. Each design parameter is constrained by lower bounds $l{b}_i$ and upper bounds $u{b}_i$, ensuring that they remain within feasible ranges based on technology limitations or physical constraints. The set S denotes the design space, encompassing all possible combinations of design parameters within their bounds.

The inequality constraints $g\left(X\right)\le 0$ typically represent physical limitations, such as the maximum allowable power or biasing conditions, while the equality constraints $h\left(X\right)=0$ might correspond to specific circuit conditions, such as ensuring that the oscillation frequency of the LC tank matches the desired target frequency.

Constraint handling is implemented using a static penalty approach. Violations of design constraints—such as deviations in oscillation frequency ($|f_{\mathrm{osc}}-f_{\mathrm{osc},\mathrm{output}}| >5\%$) or exceeding power limits—incur additive penalties proportional to the severity of the violation. This method ensures that infeasible solutions are penalized, guiding the optimization algorithm toward feasible and high-performance LC-VCO designs.

By formulating the problem in this way, the optimization aims to balance multiple objectives, such as reducing phase noise while minimizing power consumption, under the constraints imposed by the LC-VCO design and technology. This problem formulation enables the use of various optimization algorithms to explore the design space and find the best solution and/or trade-off between competing performance goals.

3. LC-VCO Topology and Modeling

3.1. LC-VCO Topology

Designing a VCO is challenging due to the need to balance multiple specifications—such as phase noise, power consumption, tuning range, and voltage swing—even after choosing a topology. With ongoing transistor scaling and lower supply voltages, maintaining a high-quality factor $Q_{\mathrm{tank}}$ in LC-tank designs has become harder, particularly with integrated inductors, which typically have low $Q_{\mathrm{tank}}$. Minimizing power consumption requires lower transistor currents but can degrade phase noise, while improving phase noise demands higher voltage swings, increasing power consumption. As a result, optimizing an LC-VCO involves extensive exploration to balance these trade-offs.

In this paper, we focus on the sizing of the LC-VCO topology shown in Figure 1, a complementary nMOS-pMOS cross-coupled LC-VCO. This topology consists of two main sub-circuits: an LC tank that determines the oscillation frequency $f_{osc}$ and an active sub-circuit that provides the necessary negative conductance to compensate for the LC tank losses. In this topology, the complementary nMOS-pMOS pair compensates for the tank losses.

The chosen LC-VCO topology (Figure 1) is inherently symmetric, utilizing a complementary cross-coupled pair (nMOS and pMOS) to maintain signal balance and reduce even-order harmonics. However, symmetry in layout and device matching can be disrupted by practical design constraints, such as metal routing, unequal parasitics, or technology-specific limitations. These asymmetries must be either compensated during optimization or strategically leveraged to enhance design trade-offs.

3.2. LC-VCO Modeling

The small-signal model of the complementary LC-VCO circuit is shown in Figure 2a, along with its equivalent simplified model in Figure 2b. This model incorporates the equivalent inductor (L) and the varactors ($C_{\mathrm{var}}$), both evaluated at the oscillation frequency ($f_{osc}$) defined by Equation (2). Additionally, it includes the parasitic capacitances of the nMOS and pMOS transistors ($C_{\mathrm{nmos}}$ and $C_{\mathrm{pmos}}$), as well as the load capacitance ($C_{\mathrm{load}}$). In this configuration, the nMOS and pMOS transistors are sized to equalize their transconductances ($g_{mn}$ and $g_{mp}$), ensuring that $g_m=g_{mn}=g_{mp}$.

Defining $g_{\mathrm{active}}$ as the equivalent conductance of the transistors, and $C_{\mathrm{tank}}$ and $g_{\mathrm{tank}}$ as the equivalent capacitance and conductance of the VCO tank, respectively, we derive the well-known expressions for the oscillation frequency and the start-up condition in Equations (2) and (3).

$$f_{osc}={\displaystyle \frac{1}{2\pi \sqrt{\mathrm{L}·C_{\mathrm{tank}}}}}$$

(2)

$$g_{\mathrm{active}}\ge \alpha ·g_{\mathrm{tank}}$$

(3)

where $\alpha$ represents the excess gain, typically ranging between 2 and 3. And

$$C_{\mathrm{tank}}={\displaystyle \frac{1}{2}}\left(C_{\mathrm{var}}+C_{\mathrm{load}}+C_{nmos}+C_{pmos}\right)$$

(4)

$$\begin{array}{c}{g}_{\mathrm{tank}}={\displaystyle \frac{1}{2}}\left(g_{\mathrm{var}}+2g_{\mathrm{L}}+g_{\mathrm{dsn}}+g_{\mathrm{dsp}}\right)\hfill \\ g_{\mathrm{active}}=-{\displaystyle \frac{1}{2}}\left(g_{\mathrm{mn}}+g_{\mathrm{mp}}\right)=-g_m\hfill \end{array}$$

(5)

Here, $g_{\mathrm{L}}$ and $g_{\mathrm{var}}$ represent the effective parallel conductances of the inductor and varactor, respectively, while $g_{\mathrm{dsn}}$ and $g_{\mathrm{dsp}}$ refer to the drain-source conductances of the nMOS and pMOS transistors. Detailed expressions for $g_{\mathrm{L}}$ and $g_{\mathrm{var}}$ are provided in the following subsections, where the inductor and varactor models are discussed.

The equivalent cross-coupled transistor capacitance in CMOS, applicable to both nMOS and pMOS transistors, is

$$C_{mos}=4C_{gd}+\left(C_{gs}+C_{gb}+C_{db}+C_{ds}\right)$$

(6)

where $C_{gd}$ represents the gate-to-drain capacitance, $C_{gs}$ the gate-to-source capacitance, $C_{gb}$ the gate-to-bulk capacitance, $C_{db}$ the drain-to-bulk capacitance, and $C_{ds}$ the drain-to-source capacitance.

The tuning range of oscillations can be expressed as

$${\displaystyle \frac{1}{2\pi \sqrt{\mathrm{L}·C_{\mathrm{tank},\max }}}}⩽f_{osc}⩽{\displaystyle \frac{1}{2\pi \sqrt{\mathrm{L}·C_{\mathrm{tank},\min }}}}$$

(7)

The output voltage is given by

$$V_{\mathrm{out}}=V_{O2}-V_{O1}\simeq {\displaystyle \frac{4}{\pi }}{\displaystyle \frac{2I_{bias}}{g_{\mathrm{tank}}}}$$

(8)

The power consumption is defined as

$$P=I_{\mathrm{bias}}{V}_{DD}.$$

(9)

The spectral purity of the VCO’s output signal near the frequency $f_{osc}$ is a key characteristic that is quantified by phase noise. By specifying a frequency offset $\Delta f$ around $f_{osc}$, phase noise can be measured as outlined in [23,24].

$$\mathcal{L}\left({\Delta }_f\right)=10log\left[{\displaystyle \frac{1}{16{\pi }^2{\Delta }_{\mathrm{f}}^2}}\times {\displaystyle \frac{{\mathrm{L}}_{\mathrm{tank}}^2{\left(2\pi f_{osc}\right)}^4}{V_{\mathrm{tank}}^2}}\times 2K_{B}T\left({\mathrm{g}}_{\mathrm{L}}+{\mathrm{g}}_{\mathrm{var}}+\gamma \left({\mathrm{g}}_{d0,\mathrm{n}}+{\mathrm{g}}_{d0,\mathrm{p}}\right)\right)\right]$$

(10)

Equation (10) is derived from Leeson’s model, under small-signal assumptions, with $\Delta f=1$ MHz across all experiments. Here, $\gamma$ denotes the excess noise factor (typically 1.5–2 for CMOS), $g_{d0,n/p}$ are the output conductances at $V_{ds}=0$, and $V_{\mathrm{tank}}$ is obtained from steady-state oscillation amplitude in transient simulation.

Additionally, ${\Delta }_f$ is the frequency shift around $f_{osc}$, $K_B$ and T are the Boltzmann constant and the temperature, respectively, and $g_{\mathrm{var}}$ and $g_L$ are the conductance of the varactor and the conductance of the inductor, respectively.

The figure of merit (FoM) for the LC-VCO is given by

$$\mathrm{FoM}=\mathrm{L}\left\{{\Delta }_{\mathrm{f}}\right\}-20log\left({\displaystyle \frac{{\mathrm{f}}_0}{{\Delta }_{\mathrm{f}}}}\right)+10log\left({\mathrm{P}}_{dc}\left(\mathrm{mW}\right)\right)$$

(11)

3.3. Modeling of Planar Spiral Inductor

Figure 3 illustrates the hexagonal spiral inductor, showing both its layout and the corresponding $\pi$-model. The $\pi$-model, shown in Figure 3b, includes the effects of parasitic elements, with their expressions provided in [25] as follows:

$$\begin{array}{c}{R}_s={\displaystyle \frac{l}{\sigma \mathrm{w}\delta \left(1-e^{-\frac{t}{\delta }}\right)}}\hfill \\ C_s={\displaystyle \frac{{\epsilon }_{\mathrm{ox}}}{t_{\mathrm{ox},M_1-M_2}}}n{\mathrm{w}}^2\hfill \\ C_{\mathrm{ox}}={\displaystyle \frac{1}{2}}{\displaystyle \frac{{\epsilon }_{\mathrm{ox}}}{t_{\mathrm{ox}}}}l\mathrm{w};C_{\mathrm{si}}={\displaystyle \frac{1}{2}}{C}_{\mathrm{sub}}l\mathrm{w};R_{\mathrm{si}}={\displaystyle \frac{2}{G_{\mathrm{sub}}l\mathrm{w}}}\hfill \end{array}$$

(12)

where $R_s$ denotes the series resistance of the spiral, where l is the total length of the spiral and $\sigma$ is the metal conductivity. The trace has a width w, thickness t, and a skin depth $\delta$. The spiral-to-underpass capacitance, $C_s$, is determined by the oxide permittivity ${\epsilon }_{\mathrm{ox}}$, oxide thickness $t_{\mathrm{ox},M_1-M_2}$, and number of turns n. Oxide capacitance between the spiral and substrate is $C_{\mathrm{ox}}$, with oxide thickness $t_{\mathrm{ox}}$. Additionally, $C_{\mathrm{si}}$ represents capacitance between the spiral and the silicon substrate, $C_{\mathrm{sub}}$ is substrate capacitance per unit area, $R_{\mathrm{si}}$ is the resistance to the silicon substrate, and $G_{\mathrm{sub}}$ is the substrate conductance per unit area.

The quality factor of the inductor ($Q_L$) is generally the characteristic used to compare inductor performance. It is analytically expressed as

$$\begin{array}{cc}\hfill Q_L& ={\displaystyle \frac{\omega L}{R_s}}{\displaystyle \frac{R_p}{R_p+\left({\left(\frac{\omega L}{R_s}\right)}^2+1\right)R_s}}\hfill \\ & \times \left(1-{\displaystyle \frac{R_s^2}{L}}\left(C_s+C_p\right)-{\omega }^{2}L\left(C_s+C_p\right)\right)\hfill \end{array}$$

(13)

where $\omega =2\pi f_{osc}$, and $R_p$ and $C_p$ represent the parallel resistance and capacitance, respectively, with their expressions given by

$$\begin{array}{c}{R}_p={\displaystyle \frac{1}{{\omega }^2{C}_{0\mathrm{x}}^2{R}_{si}}}+{\displaystyle \frac{R_{si}{\left(C_{ox}+C_{si}\right)}^2}{C_{ox}^2}}\hfill \\ C_p=C_{ox}{\displaystyle \frac{1+{\omega }^2\left(C_{ox}+C_{si}\right)C_{si}{R}_{si}^2}{1+{\omega }^2{\left(C_{ox}+C_{si}\right)}^2{R}_{si}^2}}\hfill \end{array}$$

(14)

The inductance L of a planar spiral inductor can be approximated using various empirical formulas. One of the widely used formulas for accurate estimation is the Wheeler formula given by Equation (15), which works well for spiral inductors in integrated circuits [26].

$$L_s={\displaystyle \frac{k_1·{\mu }_0·n^2·d_{\mathrm{avg}}^2}{1+k_2·\rho }}$$

(15)

where $k_1$ and $k_2$ are empirical constants (for a hexagonal spiral, $k_1$ ≈ 2.33, $k_2$ ≈ 3.82, and ${\mu }_0$ ≈ 4$\pi$ × 10⁻⁷ H/m

$$d_{\mathrm{avg}}={\displaystyle \frac{d_{\mathrm{out}}+d_{\mathrm{in}}}{2}}\mathrm{and}\rho ={\displaystyle \frac{d_{\mathrm{out}}-d_{\mathrm{in}}}{d_{\mathrm{out}}+d_{\mathrm{in}}}}$$

The effective parallel conductance $g_L$ of the inductor modeled in Figure 2a can be expressed as

$$g_L={\displaystyle \frac{1}{R_p}}+{\displaystyle \frac{R_s}{{\left(2\pi f_{osc}L\right)}^2}}.$$

(16)

3.4. Varactor Modeling

An inversion-mode MOS varactor is formed by connecting the source and drain terminals of an MOS transistor to create a tunable capacitor. The capacitance is controlled by an adjustable voltage between the gate and bulk terminals. For a consistent capacitance–voltage (C-V) characteristic slope, the varactor must operate across weak, moderate, and strong inversion regions. To achieve this, the bulk terminal is connected to the highest voltage ($V_{DD}$) for pMOS varactors and to ground for nMOS varactors.

The physical modeling of CMOS varactors offers two key advantages:

• It relies on technological and process parameters, avoiding empirical adjustments.
• It employs the EKV MOS transistor model [27,28], which ensures accuracy in low-voltage circuit design.

The EKV model is particularly suited for analytical C-V modeling of inversion-mode varactors due to its continuity across inversion regions and its use of minimal parameters. This makes it highly compatible with symbolic computation tools like Maple [29].

Based on the EKV model [30,31], the intrinsic capacitances of the varactor are given by

$$C_{\mathrm{xy}}=\pm {\displaystyle \frac{\partial Q_x}{\partial V_y}},x,y=\{G,D,S,B\}$$

(17)

where $C_{\mathrm{xy}}$ is the capacitance between terminals x and y, $Q_x$ is the charge at terminal x, and $V_y$ is the voltage at terminal y. $G,D,S,B$ refer to the gate, drain, source, and bulk terminals, respectively.

The total capacitance of the MOS varactor, $C_{\mathrm{var}}$, can be expressed as

$$\begin{array}{c}{C}_{\mathrm{var}}=C_{\mathrm{gb}}+C_{\mathrm{gd}}+C_{\mathrm{gs}}+C_{\mathrm{db}}+C_{\mathrm{sb}}+C_{\mathrm{extrinsic}}\hfill \\ C_{\mathrm{extrinsic}}=C_{GS0}+C_{GD0}+C_{GB0}\hfill \end{array}$$

(18)

where $C_{\mathrm{extrinsic}}$ accounts for extrinsic capacitances; $C_{\mathrm{gb}}$, $C_{\mathrm{gd}}$, $C_{\mathrm{gs}}$, $C_{\mathrm{db}}$, and $C_{\mathrm{sb}}$ are the intrinsic capacitances between the corresponding terminals; and $C_{GS0}$, $C_{GD0}$, and $C_{GB0}$ are the extrinsic capacitances between the gate and source, gate and drain, and gate and bulk, respectively. The expressions of all the intrinsic and extrinsic capacitances are provided in the Appendix A. Detailed MATLAB (version R2024b) scripts and the random seeds used in optimization are available from the corresponding author upon reasonable request.

Two main parameters are used to evaluate the quality of a CMOS varactor design: the quality factor ($Q_{\mathrm{var}}$) and the tuning range (${\beta }_{\mathrm{var}}$).

$$\begin{array}{cc}\hfill & Q_{\mathrm{var}}={\displaystyle \frac{1}{2\pi f_{osc}{R}_{sv}{C}_{\mathrm{var}}}}\hfill \\ \hfill & {\beta }_{\mathrm{var}}={\displaystyle \frac{C_{\mathrm{var},\max }}{C_{\mathrm{var},\min }}}\hfill \end{array}$$

(19)

where $C_{\mathrm{var},\max }$ is the maximum capacitance and $C_{\mathrm{var},\min }$ is the minimum capacitance.

Here, $R_{sv}$ is expressed as

$$R_{sv}=R_{\mathrm{poly}/\mathrm{square}}{\displaystyle \frac{1}{N_f^2}}{\displaystyle \frac{W}{L}}$$

(20)

where $R_{\mathrm{poly}/\mathrm{square}}$ is the sheet resistance of the poly-silicon, $N_f$ is the number of fingers, W is the channel width, and L is the channel length.

The effective conductance of the varactor ($g_{\mathrm{var}}$), shown in Figure 2a, is given by

$$g_{\mathrm{var}}=R_{sv}\times {\left(2\pi f_{osc}{C}_{\mathrm{var}}\right)}^2$$

(21)

4. Optimization Results and Discussions

This section outlines the optimization procedure for the LC-VCO circuit, addressing two experimental setups:

(i) Single-objective optimization, where the goal is to minimize phase noise to enhance signal purity. Here, the outcome is a single optimal solution that achieves the minimum phase noise while satisfying imposed constraints.

(ii) Multi-objective optimization, which simultaneously minimizes both phase noise and power consumption, $F=[f_1\left(\mathbf{x}\right),f_2\left(\mathbf{x}\right)]$, to achieve a balanced trade-off between performance and energy efficiency. In this case, minimizing F in Equation (1) generates a set of Pareto-optimal solutions, forming the Pareto set, representing trade-offs between phase noise and power consumption. The mapping of the Pareto set into the objective space results in the Pareto Front.

In both setups, the circuit optimization is formulated as a constrained optimization task, as described in Equation (1). A key constraint in the VCO design optimization is ensuring that the output signal frequency closely matches the desired target frequency, $f_{osc}$. To achieve this, the constraint $g_1\left(\mathbf{x}\right)\le 0.05$ is imposed, representing the allowable deviation of the actual output frequency from the target frequency $f_{osc}$. This ensures that $|f_{osc}-f_{osc,output}|$ is constrained to be within $5\%$, allowing a small relaxation margin in line with design requirements. Here, the target oscillation frequency of the LC-VCO is $f_{osc}$ = 5 GHz, while $f_{osc,output}$ denotes the actual oscillation frequency of the optimized LC-VCO.

For the single-objective optimization experiments, we used several metaheuristic algorithms, including Particle Swarm Optimization (PSO) [32], Artificial Bee Colony (ABC) [33], Ant Colony Optimization (ACO) [34], Butterfly Optimization Algorithm (BOA) [35], Differential Evolution (DE) [36], Equilibrium Optimizer (EO) [37], Firefly Algorithm (FA) [38], Genetic Algorithm (GA) [39], Simulated Annealing (SA) [40], and Whale Optimization Algorithm (WOA) [41]. For the multi-objective optimization experiments, we employed multi-objective metaheuristics, specifically, Non-dominated Sorting Genetic Algorithm II (NSGA-II) [42], Multi-Objective Particle Swarm Optimization (MOPSO) [43], Strength Pareto Evolutionary Algorithm 2(SPEA2) [44], Multi-Objective Evolutionary Algorithm Based on Decomposition (MOEA/D) [42], Multi-Objective Optimization Based on Decomposition (MOBO/D) [45], and Multi-objective Salp Swarm Algorithm (MSSA) [46]. All experiments and algorithms were implemented in Matlab.

The experiments were conducted on a computer equipped with an Intel Corporation^® Core^TM i7-7820HQ CPU @ 2.90 GHz (8 cores) and 16 GB of RAM. Each algorithm was run 100 times for all experiments to reduce the random effects inherent in non-deterministic algorithms. The performance of the algorithms was evaluated and compared based on the average results across these 50 runs, providing a robust measure of algorithmic effectiveness and consistency.

4.1. Experiment 1: Minimizing Phase Noise

In this first experiment, the sizing process is formulated to ensure that the phase noise is minimized while satisfying the required design constraints given in

Table 1. Design specifications in case of single-objective optimization.

Performance	Specification
Phase Noise @ 1 MHz ($\mathcal{L}\left({\Delta }_f\right)$)	minimize
$f_{osc}$	5 GHz
$|f_{osc}-f_{osc,output}|$	≤5%
$P_{\mathrm{dc}}$	≤1.8 mW
$N_{\mathrm{f}}-W_v.N_{\mathrm{f}}/(4.L_{min})$	≤0
$C_{\min }/C_{\max }$	≤0.1
$5\mathrm{w}-d_{\mathrm{in}}$	≤0
$d_{\mathrm{in}}/d_{\mathrm{out}}$	≥0.2
$d_{\mathrm{out}}$	≤200 µm
$|L-L_{\mathrm{target}}|$	≤5%

Notes: All specifications refer to the constraints used during single-objective optimization.

. This approach emphasizes achieving the best possible phase noise performance without considering the optimization of other factors such as power consumption.

In this single-objective optimization experiment, we consider two optimization scenarios:

• In the first scenario, the varactor and spiral inductor are optimized separately, and their optimal values are then used as fixed parameters in the subsequent LC-VCO optimization.
• In the second scenario, the varactor and spiral inductor are treated as optimization variables directly integrated into the LC-VCO optimization process.

4.1.1. Scenario 1: Size Components First, Then Optimize

As mentioned before, in this scenario, we first optimize the spiral inductor and varactor independently. These optimized values are then used as fixed parameters in the LC-VCO optimization, allowing for targeted improvement of the circuit’s overall performance.

(A)

Spiral inductor sizing

The objective is to maximize the quality factor of the spiral inductor, $Q_L$, as defined in Equation (13). This optimization must be achieved while maintaining a fixed inductance of $L_{\mathrm{spec}}=0.5\mathrm{nH}$ at the operating frequency $f_{osc}=5\mathrm{GHz}$ and satisfying the area constraint imposed by the outer diameter $d_{\mathrm{out}}$.

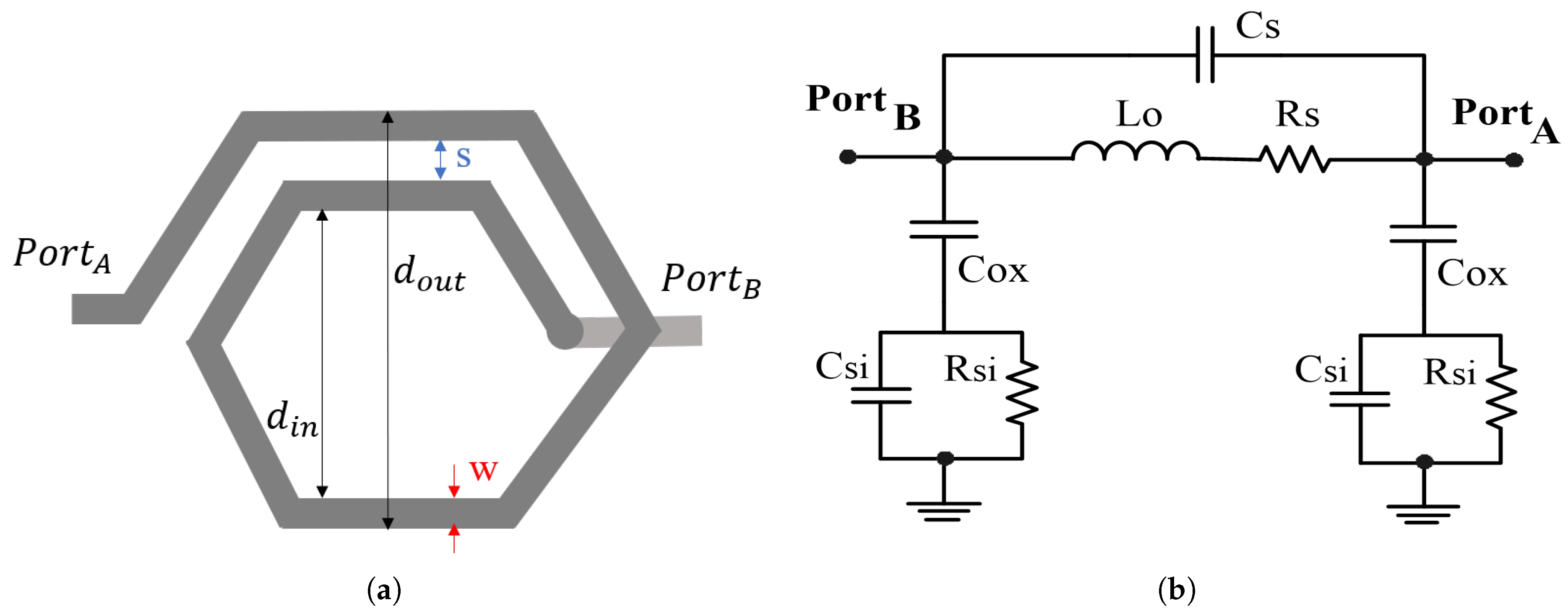
We consider a hexagonal planar spiral inductor topology, as modeled in Section 3.3. The design variables include the track width (w), the number of turns (n), and the internal diameter ($d_{\mathrm{in}}$). These variables are constrained within the following ranges: $2\mathsf{\mu }\mathrm{m}\le w\le 10\mathsf{\mu }\mathrm{m}$, $10\mathsf{\mu }\mathrm{m}\le d_{\mathrm{in}}\le 100\mathsf{\mu }\mathrm{m}$, and $2\le n\le 10$. The spacing between turns is fixed at $2.5$ $\mathsf{\mu }$$\mathrm{m}$, as no improvement is expected from larger spacing.

Table 2. Statistical performance comparison of algorithms for inductor sizing, summarizing key metrics: mean, median, worst, best, standard deviation of the quality factor, and convergence time.

Opt. Algorithm	Success Rate [-]	Mean [-]	Median [-]	Worst [-]	Best [-]	Std. Dev. [-]	Time [s]
PSO	100/100	13.0902	13.0902	13.0902	13.0902	0.00	30.1632
ABC	100/100	13.0448	13.0611	12.7212	13.0902	0.0589	31.6812
ACO	100/100	12.9207	12.9589	12.3099	13.0841	0.1435	144.4630
BOA	100/100	12.8032	12.9708	11.3439	13.0878	0.3591	58.2832
DE	100/100	13.0902	13.0902	13.0902	13.0902	0.0000	37.3419
EO	100/100	13.0902	13.0902	13.0902	13.0902	0.0000	12.0112
FA	100/100	13.0902	13.0902	13.0902	13.0902	0.0000	42.2361
GA	100/100	11.4619	11.9649	3.6837	12.9942	1.5661	261.4662
SA	100/100	13.0902	13.0902	13.0902	13.0902	0.0000	15.7004
WOA	100/100	13.0902	13.0902	13.0902	13.0902	0.0000	10.0529

presents a statistical performance comparison of algorithms for spiral inductor sizing, where all methods successfully produced feasible designs in every run. Among the algorithms, PSO, DE, EO, FA, SA, and WOA consistently achieved the best solution (13.0902) with zero variability, demonstrating exceptional efficiency and reliability. WOA is particularly distinguished for its fastest convergence time (10.05 s), closely followed by EO (12.01 s), both excelling in solution quality and speed. ABC also performed well, achieving a good mean solution (13.0448) with low variability (0.0589); however, its convergence time (31.68 s) was slower, but still faster than DE (37.34 s) and FA (42.24 s).

In contrast, BOA shows high variability and gives one of the worst solutions (11.3439), highlighting its reduced reliability. Finally, GA had the worst performance (3.6837), with the lowest mean solution (11.4619), significant variability, and the slowest convergence time (261.47 s), making it less efficient than all other methods in this experiment.

(B)

CMOS varactor sizing

Here, the objective is to maximize the quality factor of the CMOS varactor, $Q_{\mathrm{var}}$, as defined in Equation (19), leveraging the EKV MOS model equations described in Section 3.4. This optimization is carried out at the operating frequency $f_{osc}=5\mathrm{GHz}$. The design variables for the varactor include the MOS channel width ($W_{\mathrm{v}}$), length ($L_{\mathrm{v}}$), and the number of fingers (${\mathrm{N}}_{\mathrm{v}}$). Their respective ranges are $1\mathsf{\mu }\mathrm{m}\le W_{\mathrm{v}}\le 50\mathsf{\mu }\mathrm{m}$, $0.18\mathsf{\mu }\mathrm{m}\le L_{\mathrm{v}}\le 10\mathsf{\mu }\mathrm{m}$, and $10\le {\mathrm{N}}_{\mathrm{v}}\le 30$.

Table 3. Statistical performance comparison of algorithms for varactor sizing, summarizing key metrics: mean, median, worst, best, standard deviation, and convergence time.

Opt. Algorithm	Success Rate [-]	Mean [-]	Median [-]	Worst [-]	Best [-]	Std. Dev. [-]	Time [s]
PSO	100/100	10.8066	10.8066	10.8066	10.8066	0.0000	32.9298
ABC	100/100	10.6777	10.7507	9.7336	10.8048	0.1989	36.1652
ACO	100/100	10.8066	10.8066	10.8066	10.8066	0.0000	35.2689
BOA	69/100	6.3054	8.5278	4.7841	10.8047	1.6013	132.9768
DE	100/100	10.8066	10.8066	10.8066	10.8066	0.0000	39.0998
EO	100/100	10.8066	10.8066	10.8066	10.8066	0.0000	13.1874
FA	100/100	10.8066	10.8066	10.8066	10.8066	0.0000	45.9708
GA	82/100	6.1972	7.1236	3.6855	10.4463	2.7230	181.6196
SA	100/100	10.8066	10.8066	10.8066	10.8066	0.0000	17.4809
WOA	100/100	10.8066	10.8066	10.8066	10.8066	0.0000	11.5296

compares the statistical performance of algorithms for varactor sizing, showing their success rates, optimization results, and convergence times. All algorithms achieved feasible designs in every run, except for the BOA algorithm, which had a success rate of 69%, and the GA algorithm, which had a success rate of 82%. PSO, ACO, DE, EO, FA, SA, and WOA consistently found the best solution (10.8066) with no variability, highlighting their reliability. Among these, WOA was the fastest (11.53 s), followed by EO (13.19 s) and SA (17.48 s). DE (39.10 s) and FA (45.97 s) were slower but still efficient. The ABC algorithm, while performing well with a slightly lower mean (10.6777) and minor variability (0.1989), did not achieve the best solution. In contrast, BOA had significant variability, with a mean of 6.3054 and a worst-case value of 4.7841, making it less reliable, despite its best-case solution (10.8047). GA, although it had a competitive best solution (10.4463), showed extreme variability (2.7230) and was the slowest (181.62 s), indicating inefficiency. Overall, WOA excelled in speed and reliability, with EO and SA also providing robust and efficient performance, while BOA and GA were less suited for this task.

(C)

LC-VCO sizing based on sized LC tank parameters

The objective in this experiment is to minimize phase noise in the cross-coupled CMOS LC-VCO, optimized in $0.18$ $\mathsf{\mu }$$\mathrm{m}$ CMOS technology, using the previously optimized spiral inductor and varactor, fulfilling the constraints listed in Table 1. Some of these constraints are already met through the prior optimization of the LC tank components. The optimized component sizes for the varactor are $W_{\mathrm{v}}=21.6\mathsf{\mu }\mathrm{m}$, $L_{\mathrm{v}}=0.31\mathsf{\mu }\mathrm{m}$, and ${\mathrm{N}}_{\mathrm{v}}=30$; and for the spiral inductor are $w=62.07\mathsf{\mu }\mathrm{m}$, $d_{\mathrm{in}}=62.07\mathsf{\mu }\mathrm{m}$, and $n=2$.

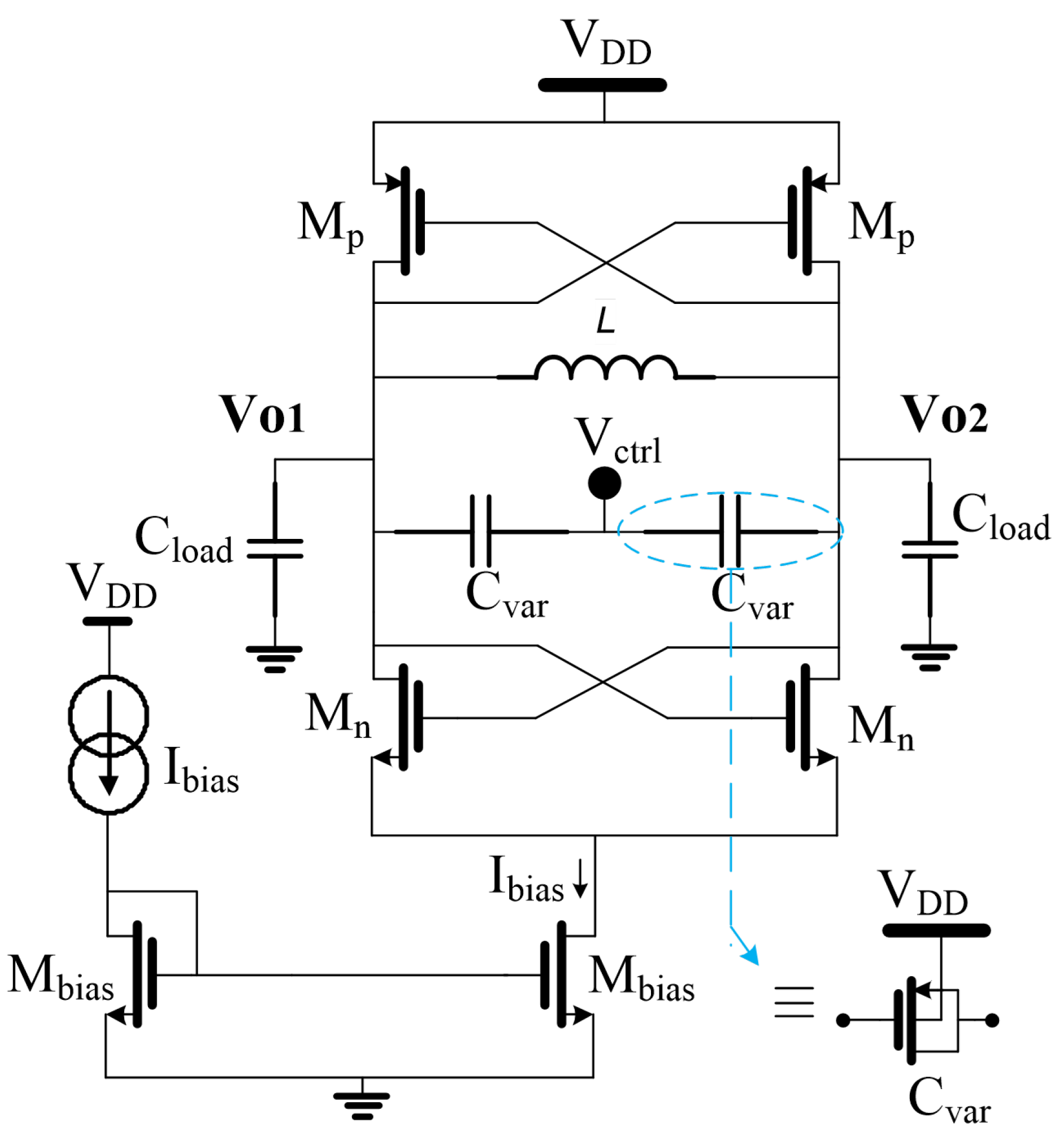
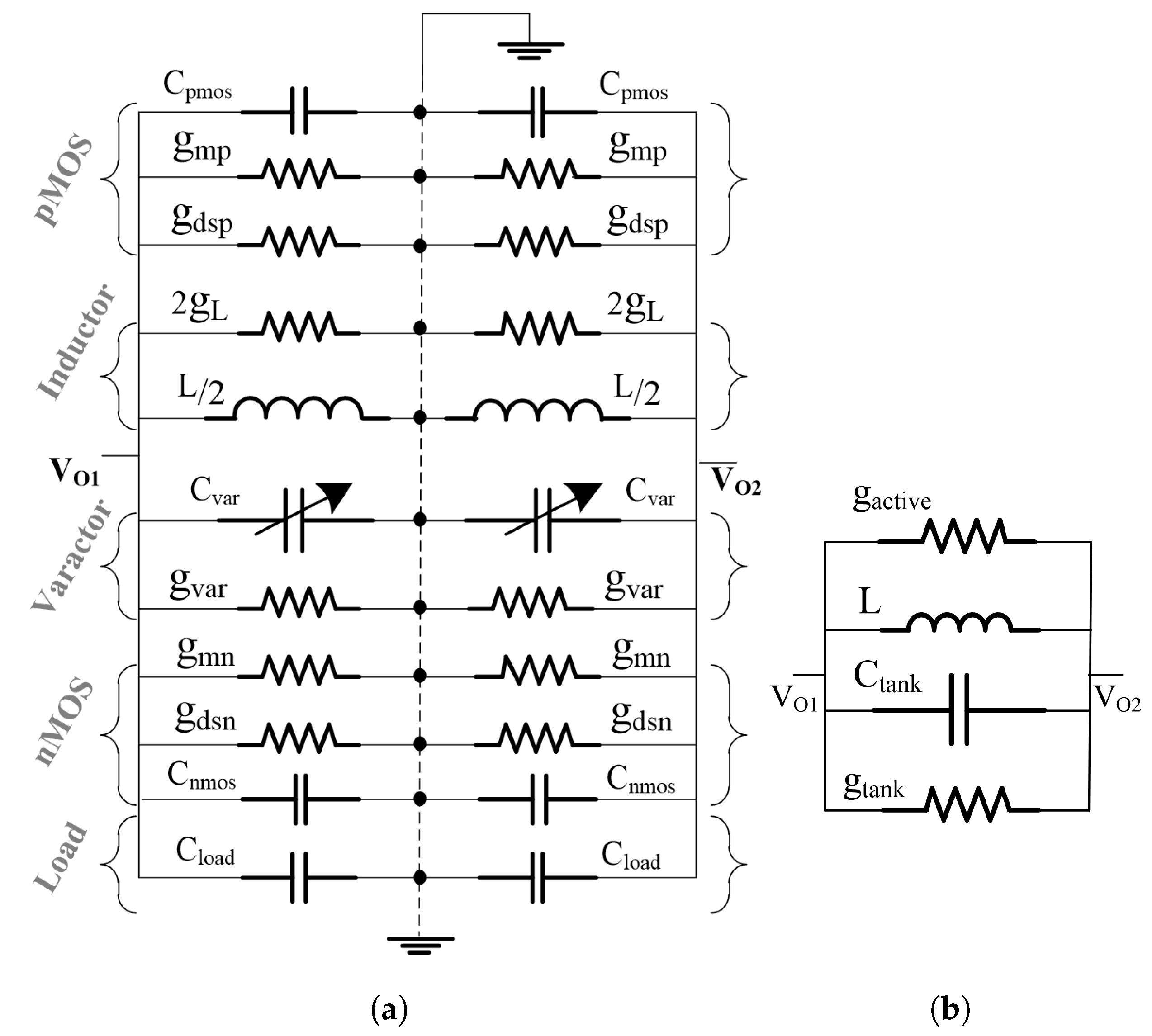
In this setup, the design variables for the LC-VCO are $W_{\mathrm{n}}$, $L_{\mathrm{n}}$, $W_{\mathrm{p}}$, $L_{\mathrm{p}}$, $W_{\mathrm{b}}$, $L_{\mathrm{b}}$, and $I_{\mathrm{bias}}$. To simplify the design, all transistors of the same channel type are assigned the same geometric sizes, with $W_{\mathrm{p}}={\mu }_{\mathrm{n}}/{\mu }_{\mathrm{p}}·W_{\mathrm{n}}$ and $L_{\mathrm{n}}=L_{\mathrm{p}}$. This simplification reduces the set of design variables to three key parameters: $W_{\mathrm{n}}$, $L_{\mathrm{n}}$, and $I_{\mathrm{bias}}$. The ranges for these variables are defined as follows: $1\mathsf{\mu }\mathrm{m}\le W_{\mathrm{n}}\le 50\mathsf{\mu }\mathrm{m}$, $0.54\mathsf{\mu }\mathrm{m}\le L_{\mathrm{n}}\le 1\mathsf{\mu }\mathrm{m}$, and $0.5\mathrm{mA}\le I_{\mathrm{bias}}\le 2\mathrm{mA}$.

Table 4. Statistical performance comparison of algorithms for LC-VCO sizing, using the previously sized LC tank.

Opt. Algorithm	Success Rate (-)	Mean [dBc/Hz]	Median [dBc/Hz]	Worst [dBc/Hz]	Best [dBc/Hz]	Std. Dev. [dBc/Hz]	Time [s]
PSO	100/100	119.9111	119.9111	119.9111	119.9111	0.0000	44.6820
ABC	100/100	119.9111	119.9111	119.9111	119.9111	0.0000	43.7273
ACO	100/100	119.9108	119.9111	119.9000	119.9111	0.0016	105.9735
BOA	100/100	119.9111	119.9111	119.9111	119.9111	0.0000	72.5444
DE	100/100	119.9111	119.9111	119.9111	119.9111	0.0000	52.2225
EO	100/100	119.9111	119.9111	119.9111	119.9111	0.0000	34.1986
FA	100/100	119.9111	119.9111	119.9111	119.9111	0.0000	37.4786
GA	84/100	117.4707	118.1628	108.9229	119.9081	2.4741	698.8525
SA	100/100	119.9111	119.9111	119.9111	119.9111	0.0000	22.6595
WOA	100/100	119.9111	119.9111	119.9111	119.9111	0.0000	17.5676

Notes: Success rate is calculated as number of successful runs over total runs. All times are reported in seconds.

compares the performance of various algorithms for LC-VCO sizing, showing that most algorithms, with the exception of ACO and GA, consistently achieved identical objective function values with a 100% success rate and zero standard deviation, demonstrating high reliability in phase noise minimization. ACO, with a 100% success rate and a standard deviation of 0.0016, performed similarly to the other algorithms, while GA achieved a success rate of 84% but showed a higher variability (standard deviation of 2.47). Notably, PSO, ABC, ACO, BOA, DE, EO, FA, SA, and WOA showed consistent results, with WOA being the fastest (17.57 s), followed by SA (22.66 s). GA, while efficient in some runs, exhibited a lower mean value (117.47) and the highest variability (2.47), along with the longest computational time (698.85 s), making it less stable. GA was the slowest algorithm (698.85 s). These results highlight WOA and SA as the most efficient and reliable algorithms for this task.

Although several algorithms in Table 4 achieved identical best values and 100% success rates, this stems from the convex-like landscape induced by EKV-based constraints in Scenario 1. The challenge persists in Scenario 2, where added design variables increase complexity and convergence speed and variability become key discriminators among algorithms.

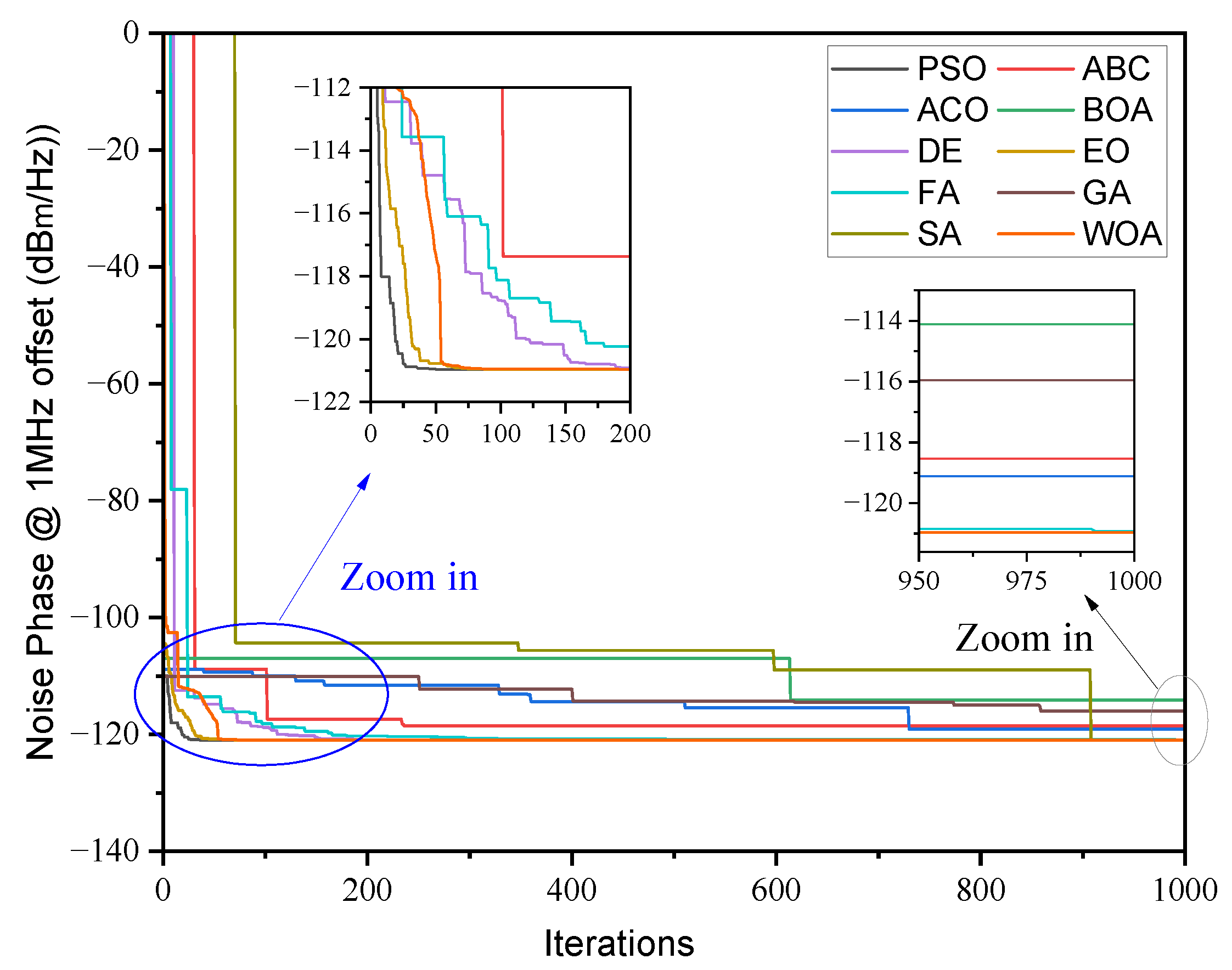
Figure 4 shows the convergence curves for phase noise obtained by the algorithms in the best case, where all algorithms achieved almost the same minimum value. All algorithms demonstrate convergence in fewer than 10 iterations, with DE, ACO, and EO converging after 1, 3, and 4 iterations, respectively.

4.1.2. Scenario 2: Optimize the Entire VCO

The robustness of the results is already reflected in the statistical indicators in Table 2, Table 3, Table 4 and

Table 5. Statistical performance comparison of algorithms for LC-VCO sizing, incorporating varactor and spiral inductor parameters as optimization variables.

Opt. Algorithm	Success Rate (-)	Mean [dBc/Hz]	Median [dBc/Hz]	Worst [dBc/Hz]	Best [dBc/Hz]	Std. Dev. [dBc/Hz]	Time [s]
PSO	100/100	−120.9616	−120.9616	−120.9616	−120.9616	0.0000	40.9912
ABC	100/100	−112.4677	−112.5276	−99.8454	−118.5304	3.5635	46.4739
ACO	100/100	−116.2337	−116.3361	−113.4713	−119.1124	1.0899	300.1278
BOA	38/100	−78.8834	−101.1355	−1.7074	−114.1156	36.8147	68.8545
DE	100/100	−120.9616	−120.9616	−120.9615	−120.9616	0.0000	54.1194
EO	100/100	−120.9616	−120.9616	−120.9616	−120.9616	0.0000	26.8535
FA	100/100	−120.6275	−120.7876	−119.2097	−120.9249	0.5094	53.2783
GA	23/100	−104.4615	−105.5386	−51.3429	−115.9570	12.9699	985.0018
SA	100/100	−120.9346	−120.9529	−120.7555	−120.9609	0.0425	24.2482
WOA	100/100	−120.5234	−120.9426	−116.1826	−120.9615	0.9839	17.6376

(mean, median, best, worst, standard deviation, success rate). These descriptors provide equivalent insights to boxplot visualizations. Moreover, convergence plots (Figure 4 and Figure 5) illustrate the consistency of the algorithms, ensuring statistical soundness without redundant figures.

In this scenario, the varactor and spiral inductor parameters are incorporated as optimization variables integrated into the LC-VCO optimization process. The optimization targets the same oscillation frequency as in Scenario 1, using the same variable ranges for the spiral inductor, varactor, MOS transistors, and current bias.

Table 5 presents a statistical performance comparison of algorithms for the LC-VCO sizing in the second scenario. As in Scenario 1, all algorithms achieved 100% success rates, except for BOA (38%) and GA (23%). PSO, DE, and EO demonstrated exceptional performance, consistently achieving the same optimal value of −120.9616 across all runs, with no variability (standard deviation = 0), indicating perfect consistency. These algorithms also exhibited relatively short convergence times, with EO being the fastest (26.85 s), followed by PSO (40.99 s) and DE (54.12 s). FA, SA, and WOA delivered slightly lower performance values, with FA reaching −120.6275, SA −120.9346, and WOA −120.5234, yet they maintained high consistency, as indicated by their negligible standard deviations, particularly in the case of SA. In contrast, ACO, with a mean of −116.23, was much slower (300.13 s) and showed a small standard deviation (1.09), suggesting that it could be more computationally expensive without a proportional gain in performance. ABC also achieved a competitive mean value (−112.47), but with a higher standard deviation (3.56) and a moderate convergence time (46.47 s). On the other hand, BOA and GA were significantly outperformed, with BOA achieving a mean of −78.88 and GA reaching only −104.46, indicating lower reliability and inferior performance. BOA also exhibited a high variability, shown by a high standard deviation (36.81), suggesting that it may not be a suitable choice for LC-VCO sizing in this scenario. The results suggest that PSO, DE, and EO are the most reliable and efficient algorithms, with DE and EO being particularly fast.

Figure 5 illustrates the convergence curves for phase noise optimization under the best-case scenario, where all algorithms reach their best minimum values. In this scenario, PSO, EO, and WOA demonstrate rapid convergence, completing the process in under 80 iterations. Notably, PSO achieves convergence the fastest, stabilizing before 50 iterations, while EO and WOA follow closely behind, requiring only a few more iterations to converge.

4.1.3. Comparison of Results Between Scenario 1 and Scenario 2

The results of both scenarios highlight key differences in performance and computational time. In Scenario 1, where the inductor and varactor were pre-optimized, all algorithms except GA showed consistent performance with identical phase noise values (−119.91) and zero standard deviation. GA achieved the worst value (−108.92) and had higher variability (2.47). Scenario 2, which involved full optimization of the VCO, resulted in significantly better phase noise performance (−120.96) for PSO, DE, and EO, while ABC, BOA, and GA exhibited greater variability. Computationally, WOA was the fastest algorithm in both scenarios; however, it was not consistent (with 0.98 standard deviation) in Scenario 2. PSO and EO were fast and consistent in both scenarios, while ACO and GA remained the slowest algorithms. Overall, Scenario 2 provided superior phase noise performance due to the inclusion of the varactor and inductor as optimization variables, but at the cost of increased optimization time and complexity, particularly for algorithms like ABC, ACO, BOA, and GA, which struggled with the additional variables.

4.2. Experiment 2: Minimizing Both Phase Noise and Power Consumption

In this experiment, we explore the multi-objective optimization of the complementary cross-coupled LC-VCO circuit, focusing on the trade-off between phase noise and power consumption at a 5 GHz operating frequency. The spiral inductor topology used in previous experiments was maintained. The optimization problem is formulated to simultaneously minimize the two conflicting objectives, resulting in a set of Pareto-optimal solutions. This enables designers to evaluate the trade-offs between phase noise and power consumption, streamlining a more balanced and efficient VCO design that meets the specifications detailed in

Table 6. Design specifications in case of multi-objective optimization.

Performance	Specification
Phase Noise @ 1 MHz ($\mathcal{L}\left({\Delta }_f\right)$)	minimize
Power consumption ($P_{\mathrm{dc}}$)	minimize
$|f_{osc}-f_{osc,output}|$	≤5%
$N_{\mathrm{f}}-W_v.N_{\mathrm{f}}/(4.L_{min})$	≤0
$5\mathrm{w}-d_{\mathrm{in}}$	≤0
$d_{\mathrm{in}}/d_{\mathrm{out}}$	≥0.2
$d_{\mathrm{out}}$	≤200 µm

Notes: All specifications refer to the constraints used during multi-objective optimization.

. It should be noted that some of the multi-objective algorithms employed in this study, such as NSGA-II and SPEA2, are mature methods that remain widely used as community benchmarks in analog/RF optimization. Their inclusion allows meaningful comparison with prior LC-VCO optimization studies. At the same time, we also evaluate more recent approaches, including MOEA/D, MOBO/D, and MSSA, which represent modern decomposition-based and swarm-inspired metaheuristics. By combining both classical and emerging methods within a symmetry-aware EKV-driven modeling framework, the present work provides a balanced and up-to-date evaluation that, to the best of our knowledge, has not been previously reported for GHz-range LC-VCO design.

To explore these trade-offs, we use different multi-objective metaheuristics, including Non-dominated Sorting Genetic Algorithm II (NSGA-II), Multi-Objective Particle Swarm Optimization (MOPSO), Strength Pareto Evolutionary Algorithm 2 (SPEA2), Multi-Objective Evolutionary Algorithm Based on Decomposition (MOEA/D), Multi-Objective Optimization Based on Decomposition (MOBO/D), and Multi-objective Salp Swarm Algorithm (MSSA). Each of these algorithms offers unique advantages in balancing the conflicting objectives, and their application allows for a comprehensive evaluation of the solution space. The same design variables and ranges from previous experiments are used, except for the current bias, which is explored over a wider range due to its significant impact on power consumption: $0.5\mathrm{mA}\le I_{\mathrm{bias}}\le 10\mathrm{mA}$.

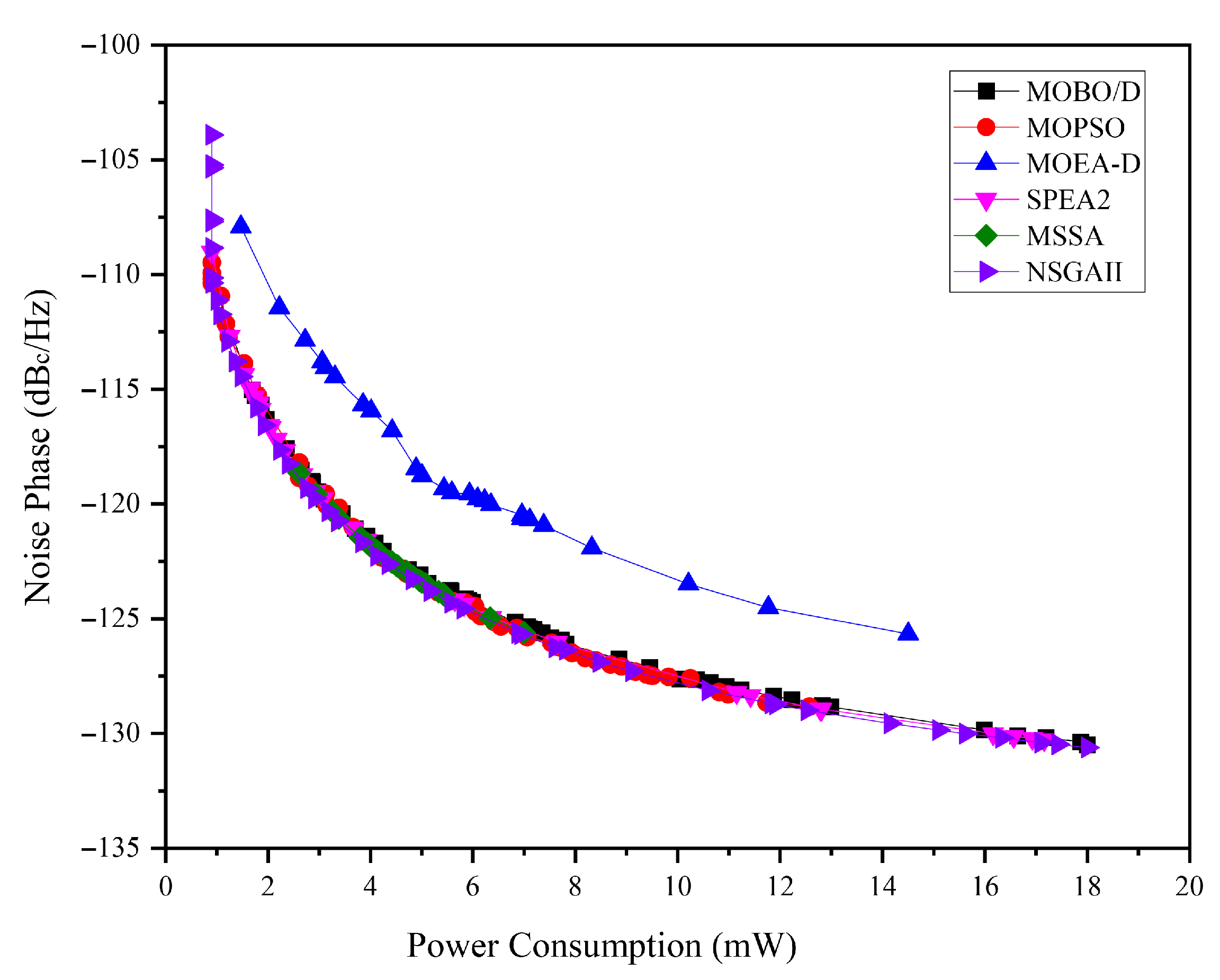
Figure 6 illustrates the combined Pareto fronts generated by the multi-objective metaheuristic algorithms used in this study. The two objectives—minimizing phase noise (dBc/Hz) and power consumption (mW)—represent conflicting trade-offs inherent in the VCO design process. The figure compares the performance of NSGA-II, MOPSO, SPEA2, MOEA/D, MOBO/D, and MSSA. While all algorithms demonstrate well-distributed Pareto fronts, the MOEA/D indicates challenges in achieving both convergence and diversity.

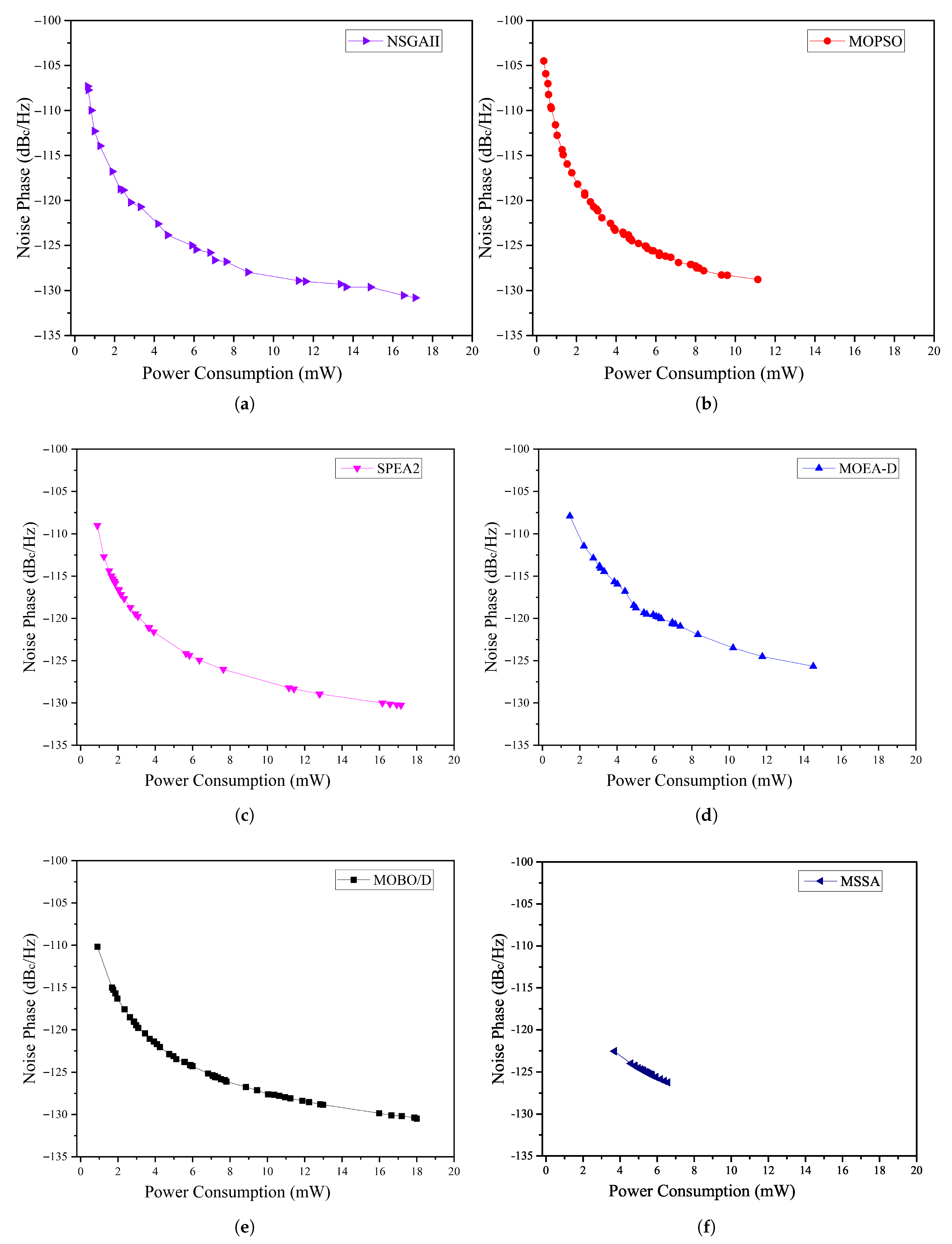
Figure 7 presents the separated Pareto fronts for each algorithm, providing detailed insights into their performance. NSGA-II exhibits a well-distributed front, effectively capturing extreme trade-offs and balancing convergence and diversity. SPEA2 and MOBO/D closely mirror the performance of NSGA-II but provide less smooth fronts with visible gaps, prioritizing convergence over diversity. MOPSO produces a dense front but shows signs of clustering, potentially limiting its ability to maintain a uniform solution spread across the trade-off space. MOEA/D struggles with both convergence and diversity, while MSSA generates a small and but dense front, indicating limited exploration of the objective space and a focus on a specific region.

Overall, the combined and separated Pareto fronts provide valuable insights into the strengths and limitations of each algorithm in handling the conflicting objectives of low phase noise and low power consumption. These results emphasize the importance of selecting algorithms based on the specific requirements of VCO design.

Table 7. Performance comparison of multi-objective metaheuristics based on convergence time, hypervolume, and IGD metrics.

Algorithms	NSGAII	SPEA2	MOPSO	MOEA/D	MOBO/D	MSSA
Conv. time (s)	60.23	35.92	12.18	35.93	15.26	11.19
Hypervolume	0.8343	0.8028	0.7573	0.7341	0.7745	0.6373
IGD	0	0.0176	0.0291	0.0464	0.0203	0.0894

presents a comparison of six multi-objective optimization algorithms using three key metrics: convergence time, hypervolume, and IGD. Higher hypervolume and lower IGD values indicate better Pareto front quality.

MSSA achieves the fastest convergence (11.19 s) but yields the least favorable IGD (0.0894) and hypervolume (0.6373). NSGA-II, though the slowest (60.23 s), provides the best overall performance, with the highest hypervolume (0.8343) and the lowest IGD (0), confirming its strength in producing high-quality, well-distributed Pareto fronts.

SPEA2 offers a strong compromise, with the second-best IGD (0.0176), competitive hypervolume (0.8028), and a relatively low convergence time (35.92 s). It stands out as a practical option when balancing solution quality and efficiency.

While MOPSO and MOBO/D converge faster than SPEA2, they deliver inferior Pareto front quality. NSGA-II produces the highest-quality results in terms of IGD and hypervolume, but at the expense of convergence time. In contrast, SPEA2 provides a balanced trade-off between solution quality and computational cost, making it well-suited for applications where both performance and efficiency are important.

Statistical Analysis of Multi-Objective Results

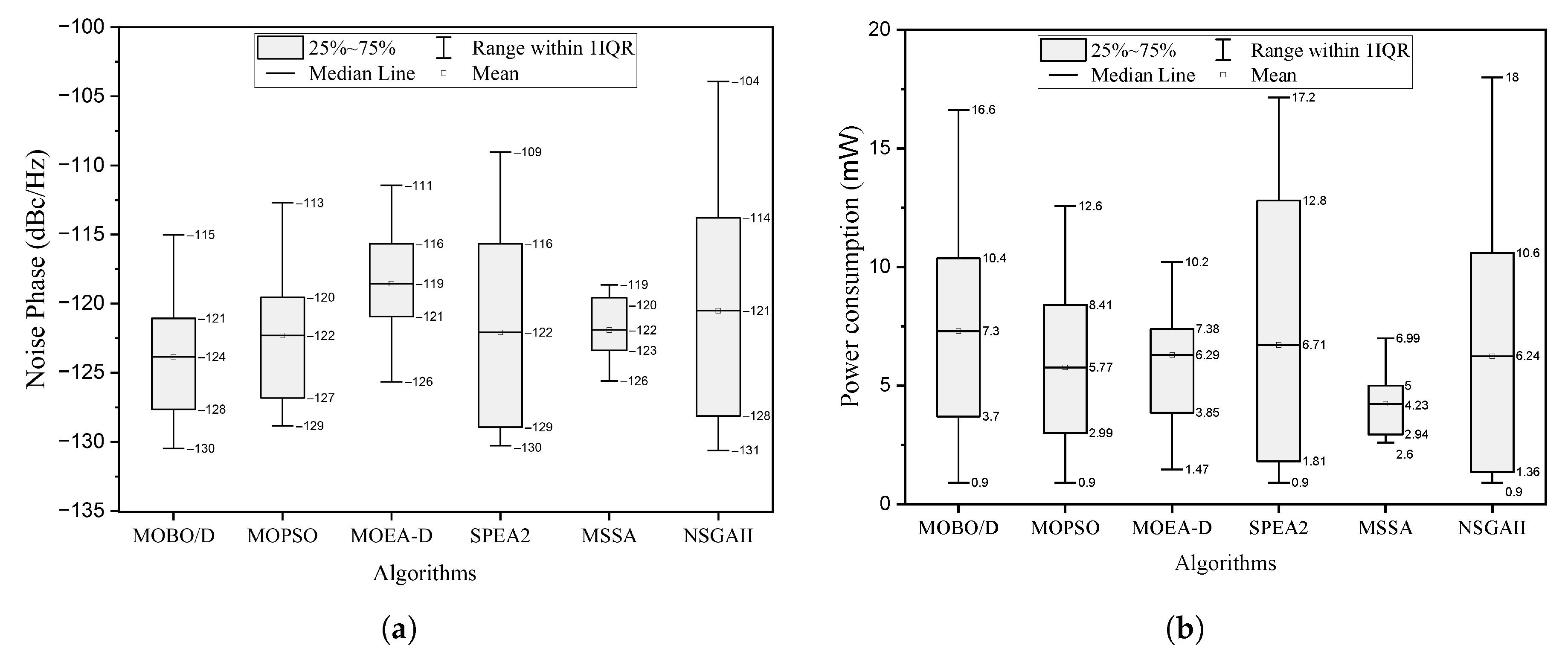
While hypervolume and IGD metrics (Table 7) provide quantitative measures of Pareto front quality, additional statistical analysis is required to evaluate robustness across multiple runs. Figure 8 presents boxplots for phase noise (Figure 8a) and power consumption (Figure 8b) across the six multi-objective metaheuristics. Each boxplot shows the median (horizontal line), interquartile range (25%–75%, box), mean (square marker), and whiskers, with outliers individually marked.

The boxplots reveal several key observations. NSGA-II and SPEA2 exhibit narrow interquartile ranges, indicating stable performance across runs. NSGA-II achieves consistently low phase noise, confirming its high hypervolume and lowest IGD (Table 7), while SPEA2 also demonstrates strong robustness. MOPSO and MOBO/D show broader spreads, reflecting higher sensitivity to initial conditions and greater variability. MSSA maintains competitive phase noise levels but shows less variability in power consumption, consistent with the smaller Pareto fronts observed in Figure 7. MOEA-D presents moderate variability with occasional outliers.

Overall, these boxplots complement the convergence and Pareto front analyses by visually confirming the relative robustness and variability of the tested algorithms, highlighting NSGA-II as the most reliable and SPEA2 as a well-balanced option between performance and efficiency.

4.3. Simulation and Yield Analysis

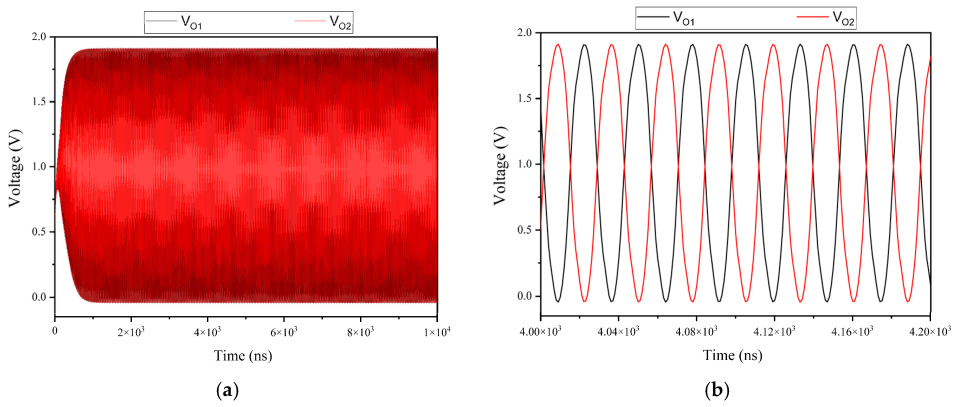
Since we obtained multiple solutions in both scenarios, we only validated the best-performing solution from Table 5. The simulation results, shown in Figure 9, illustrate the output waveforms of the sized CMOS LC-VCO. Figure 9a presents the complete simulation, capturing both the transient and steady-state behaviors of the oscillator. During the transient phase, the oscillation amplitude gradually increases, demonstrating a successful startup mechanism. In the steady-state phase, the oscillations stabilize at approximately 1.8 V peak-to-peak, indicating robust and reliable operation.

Figure 9b provides a zoomed-in view of the steady-state oscillator behavior. The two differential outputs, $V_{\mathrm{O}1}$ and $V_{\mathrm{O}2}$, exhibit a periodic waveform with a consistent 180° phase difference. This symmetry confirms the proper functioning of the differential circuit design.

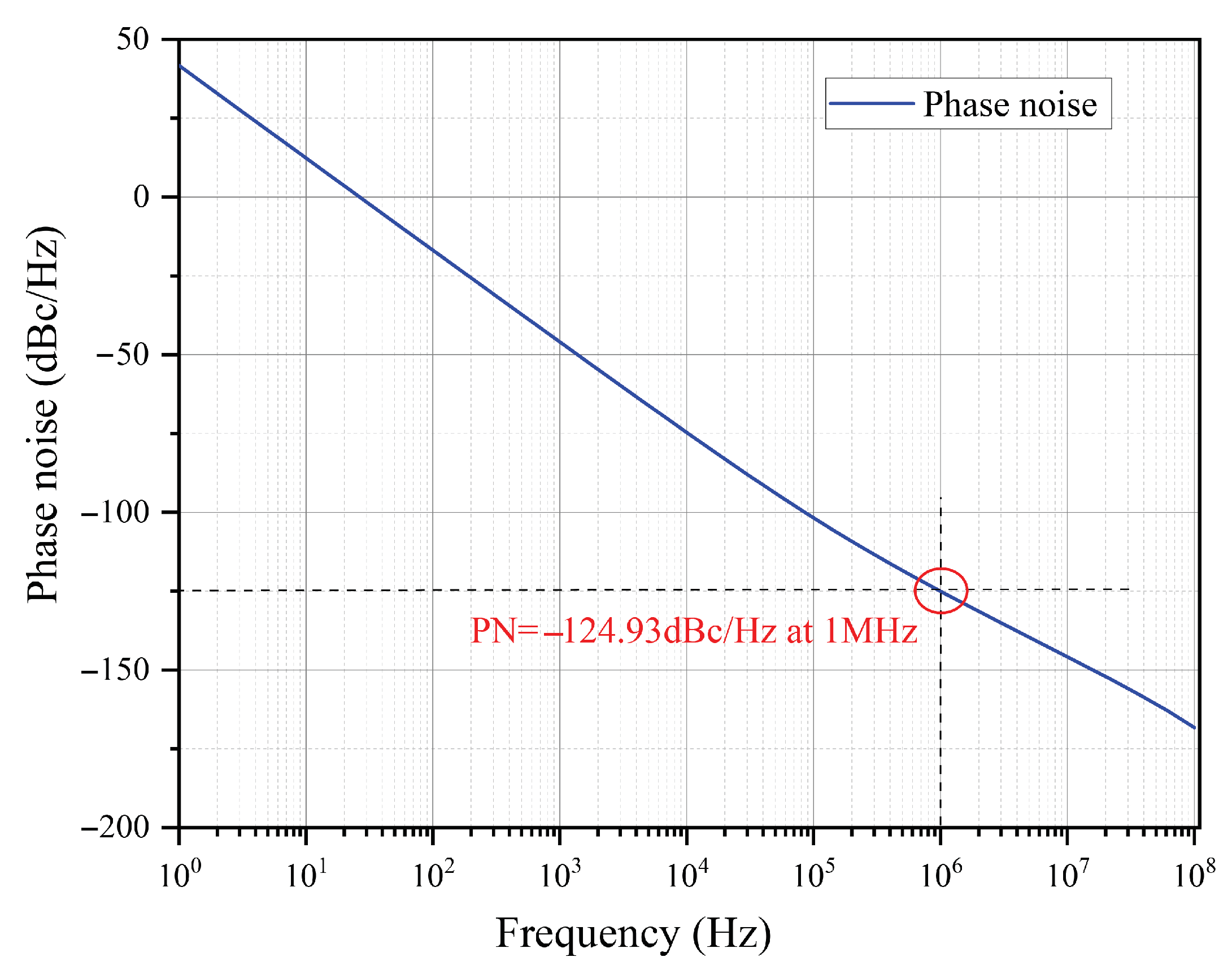
The simulated oscillation frequency of 4.96 GHz and phase noise of $-124.93$ dBc/Hz (see Figure 10) closely match the targeted design specifications, demonstrating the effectiveness of the proposed setup. These results verify that the CMOS LC-VCO delivers stable oscillations with the intended frequency and amplitude, confirming its suitability for RF and communication applications.

The Monte Carlo simulation results for the LC VCO oscillator provide critical insights into its performance variability across 200 samples. The phase noise distribution (Figure 11a) demonstrates a tight clustering around the mean value of −124.93 dBc/Hz, with a standard deviation of 56.37 µ, indicating robust noise characteristics within the acceptable design range. Similarly, the oscillation frequency distribution (Figure 11b) reveals a mean frequency of 4.96113 GHz with minimal deviation (standard deviation of 486.945 MHz), underscoring the stability of the oscillator. Both simulations exhibit 100% pass rates, indicating a high yield that ensures the design consistently meets the performance requirements under process and mismatch variations. These findings validate the effectiveness of the proposed EKV-model-based metaheuristic methodology, reinforcing its potential for high-precision applications and its reliability under diverse operating conditions.

4.4. Symmetry and Asymmetry in EKV-Based VCO Optimization

In high-frequency VCO designs, symmetry is typically sought to ensure phase alignment and minimize common-mode noise. However, the optimization process must address unavoidable asymmetries—such as layout-induced parasitics or finger mismatches—that influence effective capacitance and inductance values.

By embedding physical models (EKV, spiral $\pi$-model, and parasitic-aware varactor models) into the metaheuristic optimization loop, our approach allows the algorithm to implicitly explore both symmetric and asymmetric configurations. This enables the discovery of Pareto-optimal solutions that either preserve symmetry (for noise minimization) or tolerate controlled asymmetry (for enhanced power efficiency or area reduction).

Moreover, the simulation results show that phase noise minima often correspond to symmetric sizing conditions, whereas power minimization occasionally yields asymmetrical transistor biasing or LC tank element dimensions. This interplay reinforces the importance of considering symmetry and asymmetry as part of AI-driven optimization strategies.

5. Conclusions

In this paper, we introduced an automated sizing methodology for a complementary cross-coupled CMOS LC-VCO circuit, using the EKV model and metaheuristic optimization algorithms. The VCO is fully modeled through analytical equations and a technology-specific EKV model, offering a high degree of adaptability to emerging technologies and significantly faster computation than traditional electromagnetic simulation-based methods.

Two distinct scenarios were explored for single-objective optimization: (1) optimizing the LC tank (varactor and spiral inductor) as a preliminary step, followed by LC-VCO optimization using the fixed LC tank parameters; and (2) treating the varactor and spiral inductor as design variables integrated within the LC-VCO optimization. Metaheuristic algorithms proved highly effective in navigating the complex design space, particularly in addressing the sensitivity of on-chip LC tank quality factors to degradation, which directly impacts phase noise.

We further extended the methodology to multi-objective optimization, simultaneously minimizing phase noise and power consumption. Among the various algorithms tested, NSGA-II achieved the most balanced trade-off between Pareto front quality and diversity. These results underscore the suitability of multi-objective metaheuristics in resolving conflicting design goals.

To validate robustness under manufacturing variations, Monte Carlo simulations were conducted on the best-performing solution. The results demonstrated excellent yield, with a 100% pass rate for both phase noise and oscillation frequency specifications across 200 samples, confirming the method’s ability to indicate robustness under evaluated scenarios. The optimized LC-VCO achieved a mean phase noise of −124.93 dBc/Hz and an oscillation frequency centered around 4.96 GHz with minimal deviation, confirming the method’s ability to meet stringent RF performance requirements.

In summary, the proposed methodology effectively minimizes phase noise and power consumption, providing a scalable and accurate solution for analog circuit sizing in advanced CMOS technologies. The novelty of this work lies not in proposing a new optimization algorithm but in embedding symmetry/asymmetry considerations into EKV-based analytical modeling, thereby enabling existing algorithms to achieve physically consistent and verifiable LC-VCO designs.

This distinction is crucial: while many recent works focus on creating new metaheuristic variants, our contribution addresses the equally important gap of providing a physically grounded, symmetry-aware modeling framework that makes optimization results meaningful for real CMOS implementations. In this way, the proposed methodology complements ongoing algorithmic innovations by ensuring that both classical and modern optimizers produce designs that are not only optimal in theory but also valid and verifiable in practice.

Our study complements recent survey findings by demonstrating how a symmetry-aware EKV modeling layer can be combined with both classical and modern metaheuristics (including hybrid, surrogate-assisted, and decomposition-based approaches) to produce physically consistent and efficient LC-VCO designs while keeping simulation cost tractable.

Crucially, beyond its algorithmic effectiveness, this work emphasizes the implicit handling of structural symmetry and asymmetry in RF circuit design. While symmetric topologies ensure balanced performance, asymmetries arising from parasitics or design constraints can be strategically exploited within the optimization framework. By relying on physically grounded models and algorithmic intelligence, the proposed method aligns with the broader goals of symmetry-aware EDA, offering a practical approach to balancing regularity and deviation in high-performance analog systems.