An Explicit Positivity-Preserving Method for Nonlinear Aït-Sahalia Model Driven by Fractional Brownian Motion
Abstract
1. Introduction
2. Preliminaries
3. Numerical Method for Auxiliary Equation (2)
4. Numerical Method for ASIRM (1)
5. Numerical Experiments
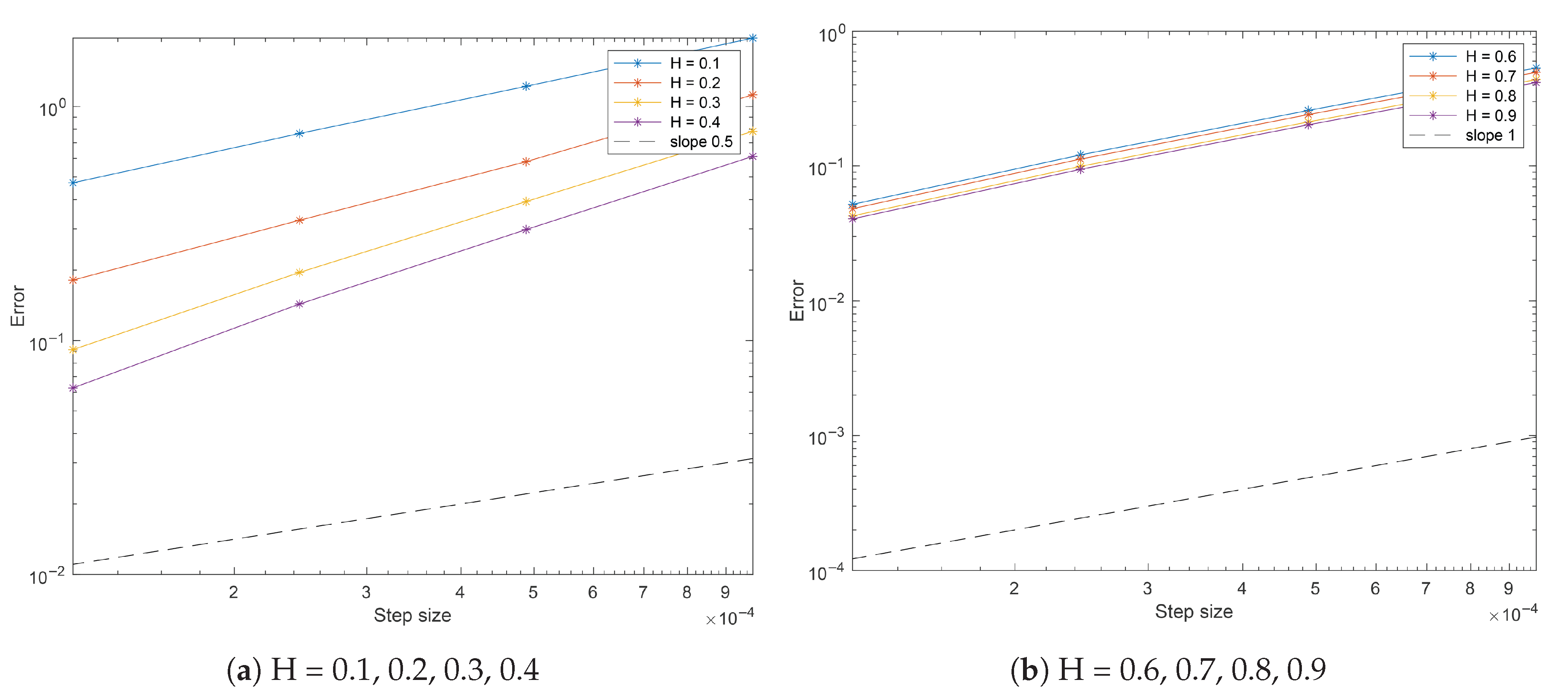
5.1. Example 1
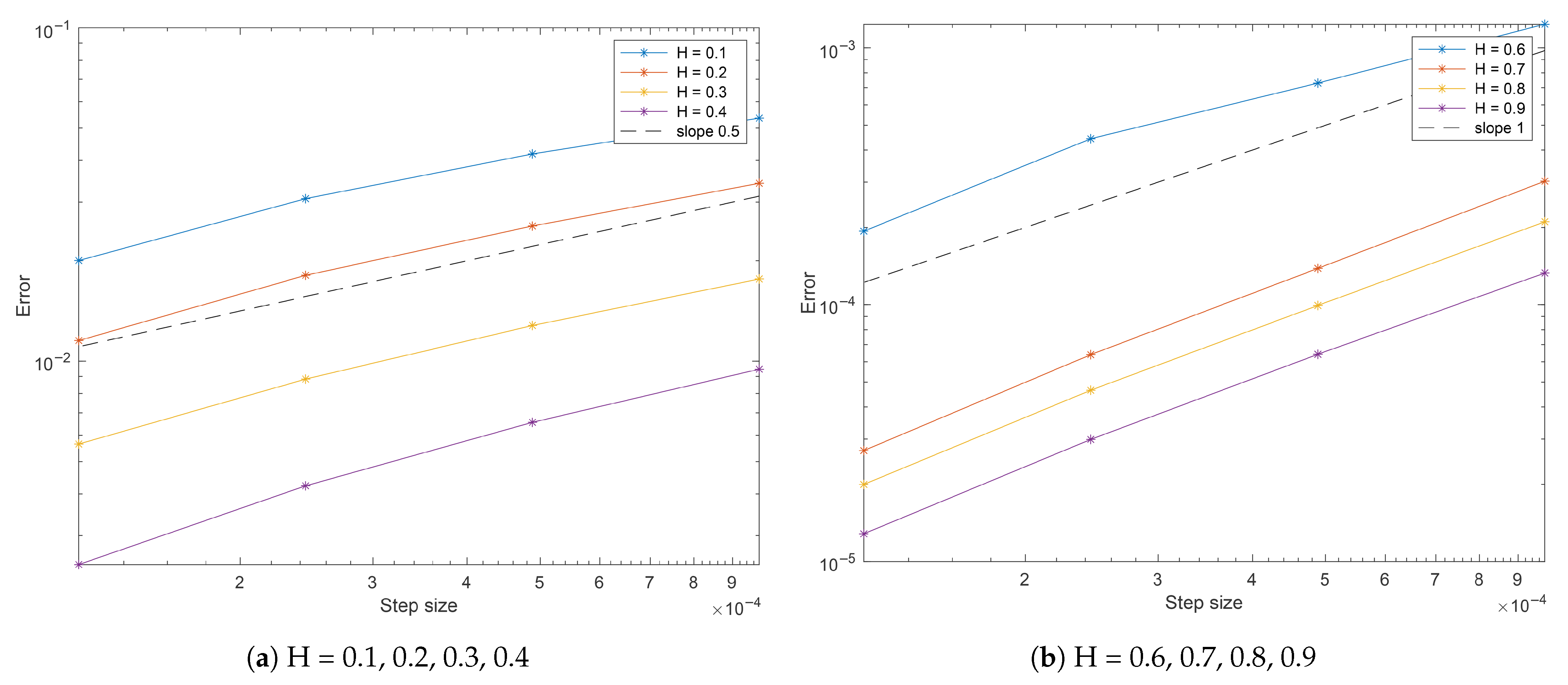
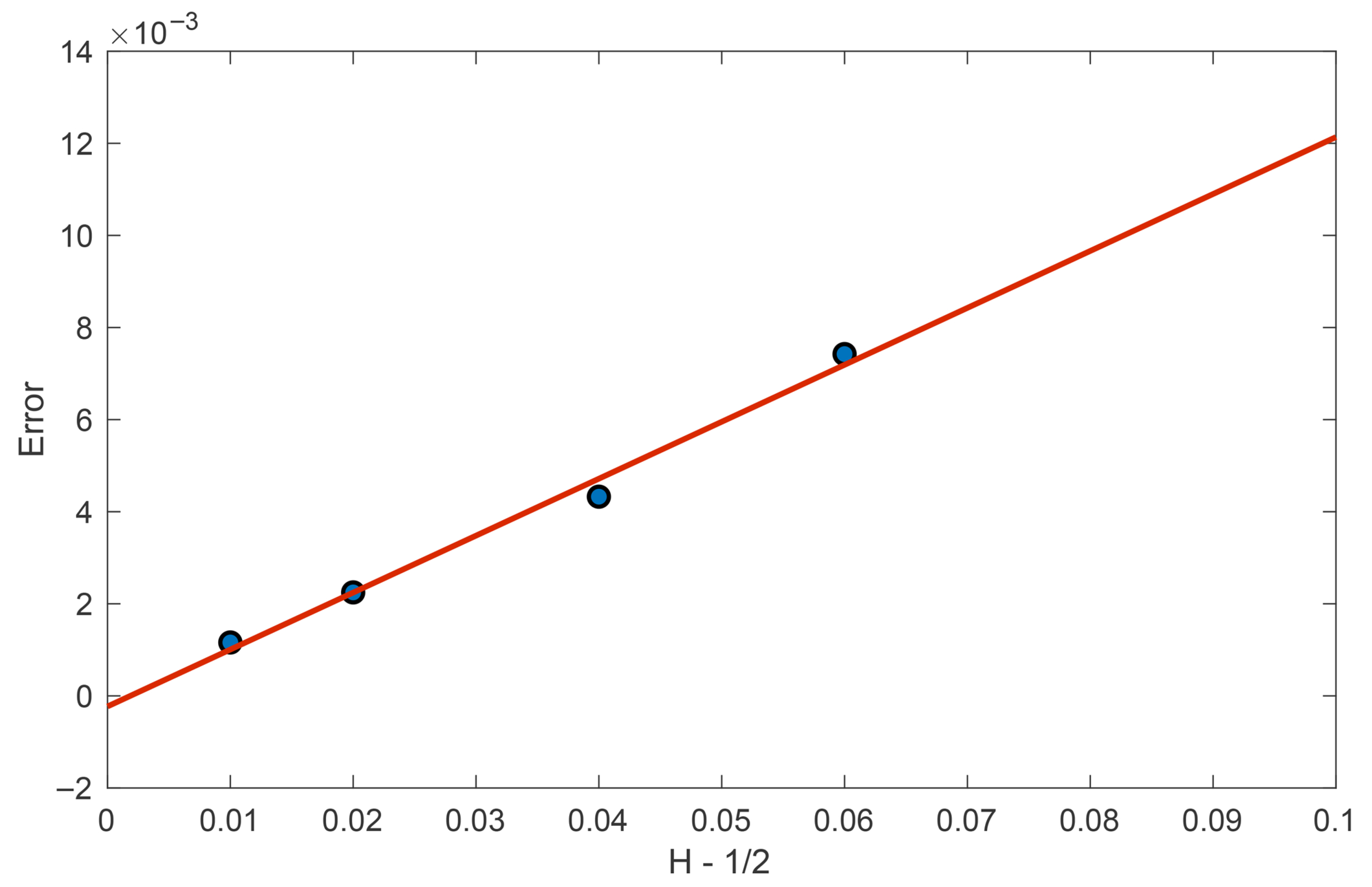
5.1.1. Strong Convergence
5.1.2. Running Times
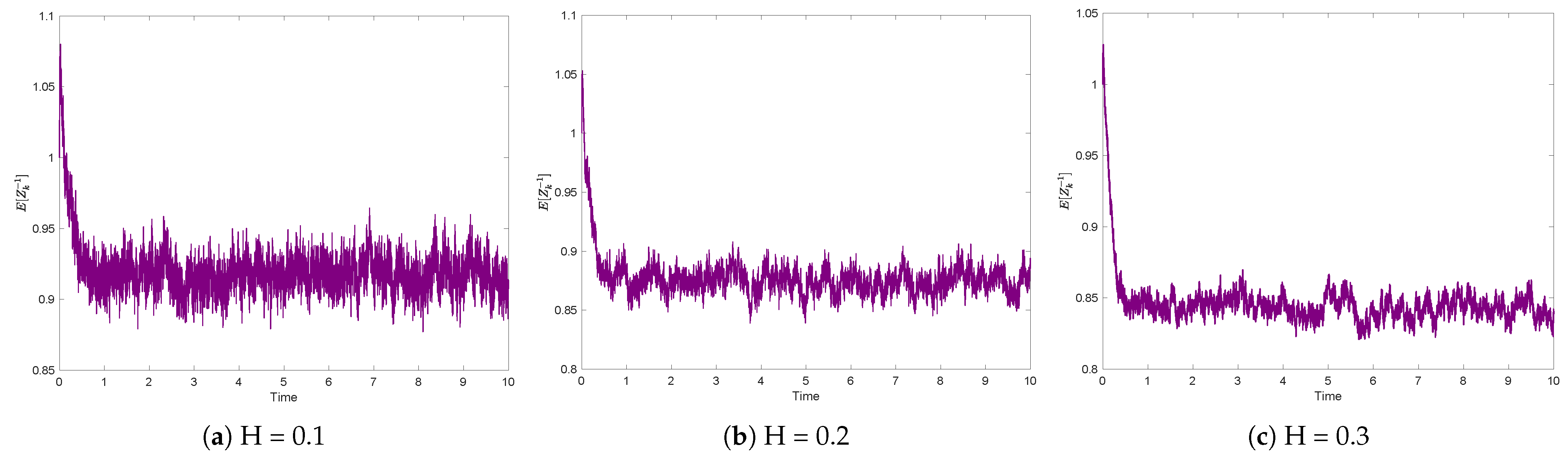
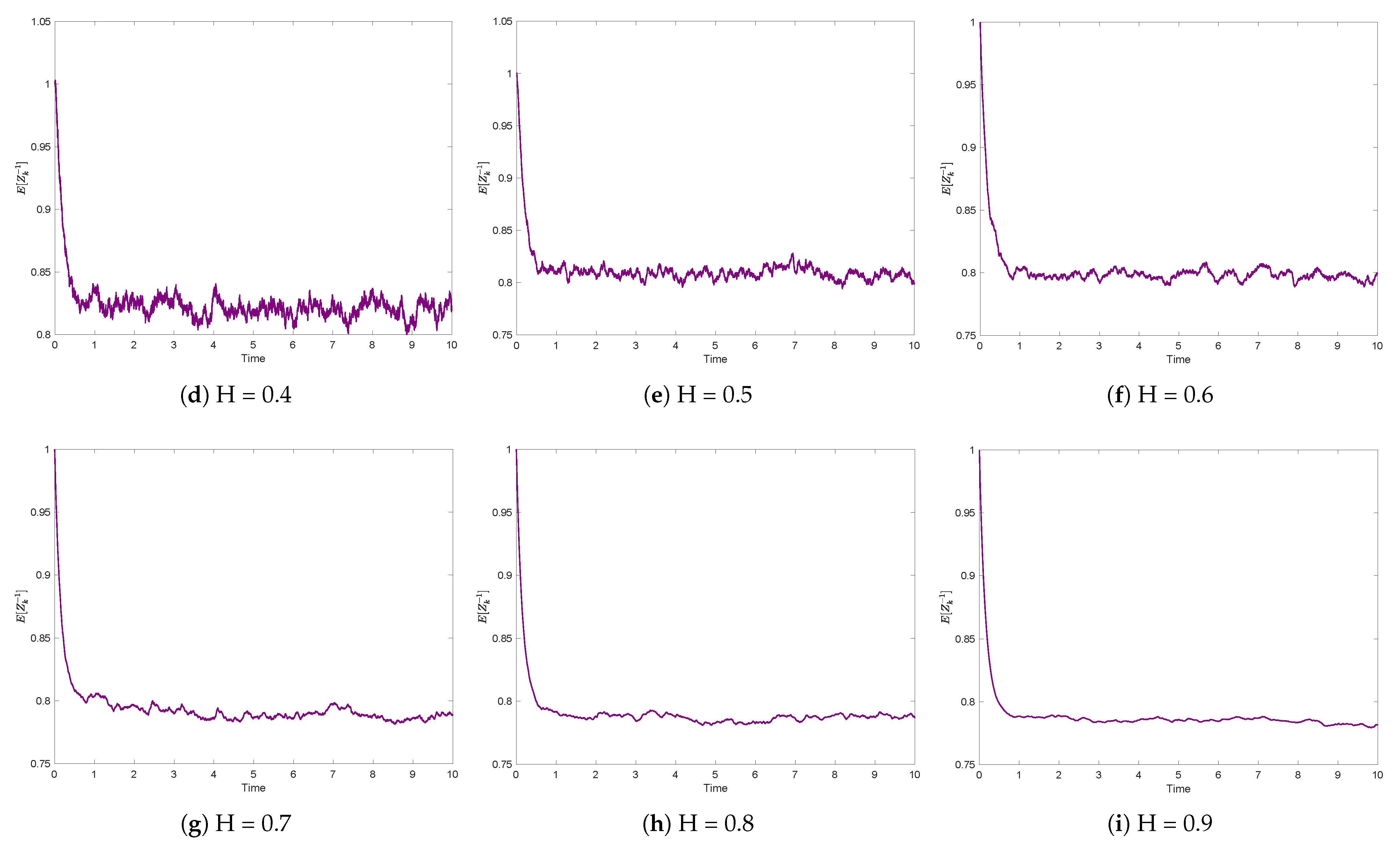
5.1.3. Sensitivity Analysis
5.2. Example 2
Funding
Data Availability Statement
Conflicts of Interest
References
- Aït-Sahalia, Y. Testing continuous-time models of the spot interest rate. Rev. Financ. Stud. 1996, 9, 385–426. [Google Scholar] [CrossRef]
- Hong, Y.; Lin, H.; Wang, S. Modeling the dynamics of Chinese spot interest rates. J. Bank. Financ. 2010, 34, 1047–1061. [Google Scholar] [CrossRef]
- Aït-Sahalia, Y. Transition densities for interest rate and other nonlinear diffusions. J. Financ. 1999, 54, 1361–1395. [Google Scholar] [CrossRef]
- Szpruch, L.; Mao, X.; Higham, D.J.; Pan, J. Numerical simulation of a strongly nonlinear Aït-Sahalia-type interest rate model. BIT Numer. Math. 2011, 51, 405–425. [Google Scholar] [CrossRef]
- Emmanuel, C.; Mao, X. Truncated EM numerical method for generalised Ait-Sahalia-type interest rate model with delay. J. Comput. Appl. Math. 2021, 383, 113137. [Google Scholar] [CrossRef]
- Liu, R.; Cao, Y.; Wang, X. Unconditionally positivity-preserving explicit Euler-type schemes for a generalized Aït-Sahalia model. Numer. Algorithms 2025, 98, 651–675. [Google Scholar] [CrossRef]
- Deng, S.; Fei, C.; Fei, W.; Mao, X. Positivity-preserving truncated Euler–Maruyama method for generalised Ait-Sahalia-type interest model. BIT Numer. Math. 2023, 63, 59. [Google Scholar] [CrossRef]
- Wang, B.; Zhu, Q. The stabilization problem for a class of discrete-time semi-Markov jump singular systems. Automatica 2025, 171, 111960. [Google Scholar] [CrossRef]
- Bao, J.; Huang, X. Approximations of McKean–Vlasov Stochastic Differential Equations with Irregular Coefficients. J. Theor. Probab. 2022, 35, 1187–1215. [Google Scholar] [CrossRef]
- Xie, L.; Zhang, X. Ergodicity of stochastic differential equations with jumps and singular coefficients. Annales de l’Institut Henri Poincaré, Probabilités et Statistiques. Ann. Inst. H. Poincaré Probab. Statist. 2020, 56, 175–229. [Google Scholar] [CrossRef]
- Merton, R.C. Theory of rational option pricing. Bell J. Econ. 1973, 4, 141–183. [Google Scholar] [CrossRef]
- Cox, J.C.; Ingersoll, J.E.; Ross, S.A. A theory of the term structure of interest rates. Econometrica 1985, 53, 385–407. [Google Scholar] [CrossRef]
- Chen, J.; Li, X.; Shao, Y. Numerical analysis of fractional order Black–Scholes option pricing model with band equation method. J. Comput. Appl. Math. 2024, 451, 115998. [Google Scholar] [CrossRef]
- Biagini, F.; Hu, Y.; Øksendal, B.; Zhang, T. Stochastic Calculus for Fractional Brownian Motion and Applications; Springer: London, UK, 2008. [Google Scholar]
- Mishura, Y. Stochastic Calculus for Fractional Brownian Motion and Related Processes; Springer: Berlin/Heidelberg, Germany, 2008. [Google Scholar]
- Rahman, M.; Karaca, Y.; Agarwal, R.P.; David, S.A. Mathematical modelling with computational fractional order for the unfolding dynamics of the communicable diseases. Appl. Math. Sci. Eng. 2024, 32, 2300330. [Google Scholar] [CrossRef]
- Zhang, S.; Yuan, C. Stochastic differential equations driven by fractional Brownian motion with locally Lipschitz drift and their implicit Euler approximation. Proc. R. Soc. Edinburgh Sect. A 2021, 151, 1278–1304. [Google Scholar] [CrossRef]
- Hong, J.; Huang, C.; Kamrani, M.; Wang, X. Optimal strong convergence rate of a backward Euler type scheme for the Cox-Ingersoll-Ross model driven by fractional Brownian motion. Stochastic Process. Appl. 2020, 130, 2675–2692. [Google Scholar] [CrossRef]
- Gao, X.; Wang, J.; Wang, Y.; Yang, H. The truncated Euler-Maruyama method for CIR model driven by fractional Brownian motion. Stat. Probab. Lett. 2022, 189, 109573. [Google Scholar] [CrossRef]
- Gao, S.; Guo, Q.; Liu, Z.; Yuan, C. Euler–Maruyama scheme for delay-type stochastic McKean–Vlasov equations driven by fractional Brownian motion. Commun. Nonlinear Sci. Numer. Simul. 2025, 149, 108927. [Google Scholar] [CrossRef]
- Ma, W.; Liu, W.; Zhu, Q.; Shi, K. Dynamics of the Exponential Population Growth System with Mixed Fractional Brownian Motion. Complexity 2021, 2021, 5079147. [Google Scholar] [CrossRef]
- Zhou, H.; Hu, Y.; Zhao, J. Numerical method for singular drift stochastic differential equation driven by fractional Brownian motion. J. Comput. Appl. Math. 2024, 447, 115902. [Google Scholar] [CrossRef]
- Naserifar, S.; Mirzaee, F. Innovative computational model for variable order fractional Brownian motion and solving stochastic differential equations. Numer. Algorithms 2025, 1–30. [Google Scholar] [CrossRef]
- Arthi, G.; Park, J.H.; Jung, H.Y. Existence and exponential stability for neutral stochastic integrodifferential equations with impulses driven by a fractional Brownian motion. Commun. Nonlinear Sci. Numer. Simul. 2016, 32, 145–157. [Google Scholar] [CrossRef]
- Li, P.; Han, L.; Xu, C.; Peng, X.; Rahman, M.; Shi, S. Dynamical properties of a meminductor chaotic system with fractal–fractional power law operator. Chaos Solitons Fractals 2023, 175, 114040. [Google Scholar] [CrossRef]
- Qu, H.; Rahman, M.; Arfan, M. Fractional model of smoking with relapse and harmonic mean type incidence rate under Caputo operator. Appl. Math. Comput. 2023, 69, 403–420. [Google Scholar]
- Chassagneux, J.-F.; Jacquier, A.; Mihaylov, I. An explicit Euler scheme with strong rate of convergence for financial SDEs with non-Lipschitz coefficients. SIAM J. Financ. Math. 2016, 7, 993–1021. [Google Scholar] [CrossRef]
- Zähle, M. Integration with respect to fractal functions and stochastic calculus I. Probab. Theory Relat. Fields 1998, 111, 333–374. [Google Scholar] [CrossRef]
- Nualart, D. The Malliavin Calculus and Related Topics, 2nd ed.; Springer: Berlin/Heidelberg, Germany, 2006. [Google Scholar]
- Alòs, A.; Nualart, D. Stochastic integration with respect to the fractional Brownian motion. Stoch. Stoch. Rep. 2003, 75, 129–152. [Google Scholar] [CrossRef]
- Zhou, H.; Hu, Y.; Liu, Y. Backward Euler method for stochastic differential equations with non-Lipschitz coefficients driven by fractional Brownian motion. BIT Numer. Math. 2023, 63, 40. [Google Scholar] [CrossRef]
- Haress, E.M.; Richard, A. Long-time Hurst regularity of fractional stochastic differential equations and their ergodic means. J. Theoret. Probab. 2025, 38, 24. [Google Scholar] [CrossRef]
- Richard, A.; Talay, D. Lipschitz continuity in the Hurst parameter of functionals of stochastic differential equations driven by a fractional Brownian motion. Electron. J. Probab. 2024, 29, 1–70. [Google Scholar] [CrossRef]

| M = 50 | M = 100 | M = 500 | M = 1000 | |
|---|---|---|---|---|
| Explicit | 1.2713 | 2.5949 | 9.8056 | 18.4476 |
| Backward | 2.4108 | 4.7618 | 21.0012 | 43.7890 |
| M = 50 | M = 100 | M = 500 | M = 1000 | |
|---|---|---|---|---|
| Explicit | 1.8593 | 3.6351 | 18.1139 | 35.6824 |
| Backward | 4.3168 | 8.4042 | 41.0005 | 80.0627 |
| M = 50 | M = 100 | M = 500 | M = 1000 | |
|---|---|---|---|---|
| Explicit | 1.2908 | 2.1439 | 10.1114 | 18.3588 |
| Backward | 2.4238 | 4.4650 | 20.9171 | 41.4412 |
| M = 50 | M = 100 | M = 500 | M = 1000 | |
|---|---|---|---|---|
| Explicit | 1.9005 | 3.6695 | 17.8736 | 34.7272 |
| Backward | 4.3894 | 8.5113 | 40.3358 | 81.1058 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Z. An Explicit Positivity-Preserving Method for Nonlinear Aït-Sahalia Model Driven by Fractional Brownian Motion. Symmetry 2025, 17, 1649. https://doi.org/10.3390/sym17101649
Liu Z. An Explicit Positivity-Preserving Method for Nonlinear Aït-Sahalia Model Driven by Fractional Brownian Motion. Symmetry. 2025; 17(10):1649. https://doi.org/10.3390/sym17101649
Chicago/Turabian StyleLiu, Zhuoqi. 2025. "An Explicit Positivity-Preserving Method for Nonlinear Aït-Sahalia Model Driven by Fractional Brownian Motion" Symmetry 17, no. 10: 1649. https://doi.org/10.3390/sym17101649
APA StyleLiu, Z. (2025). An Explicit Positivity-Preserving Method for Nonlinear Aït-Sahalia Model Driven by Fractional Brownian Motion. Symmetry, 17(10), 1649. https://doi.org/10.3390/sym17101649





