Research on Broadband Oscillation Mode Identification Based on Improved Symplectic Geometry Algorithm
Abstract
1. Introduction
2. Prony Algorithm
3. Symplectic Geometric Mode Decomposition and Improvement
3.1. Classic SGMD Method
3.2. Local Outlier Factor
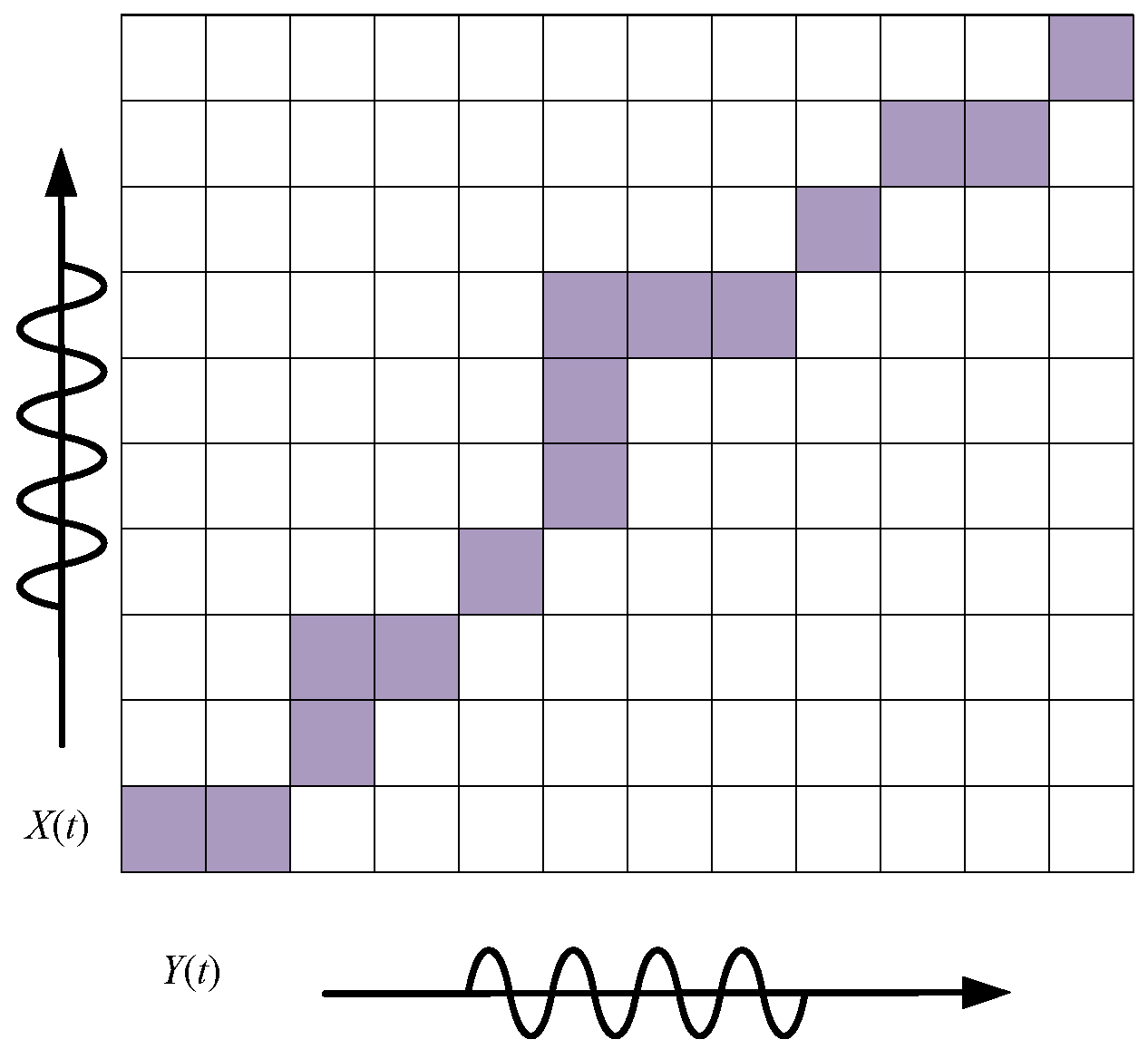
3.3. Normalized Dynamic Warping Time
4. Broadband Oscillation Mode Identification Algorithm Flow
- (1)
- The modal separation of the original signal is carried out by the symplectic geometric mode decomposition method, and the modal quantities are obtained.
- (2)
- Consequently, the frequency domain attributes of each decomposition mode are evaluated utilizing the local outlier factor. If Equation (16) is not satisfied, repeat step (1). Otherwise, it is regarded as complete decomposition.
- (3)
- Using dynamic warping time to compare the similarity of the component obtained from step (2) to obtain the real harmonic component.
- (4)
- The real harmonic component is reconstructed, and the reconstructed signal is identified by the Prony algorithm to obtain the amplitude, frequency, initial phase, and damping factor of the signal.

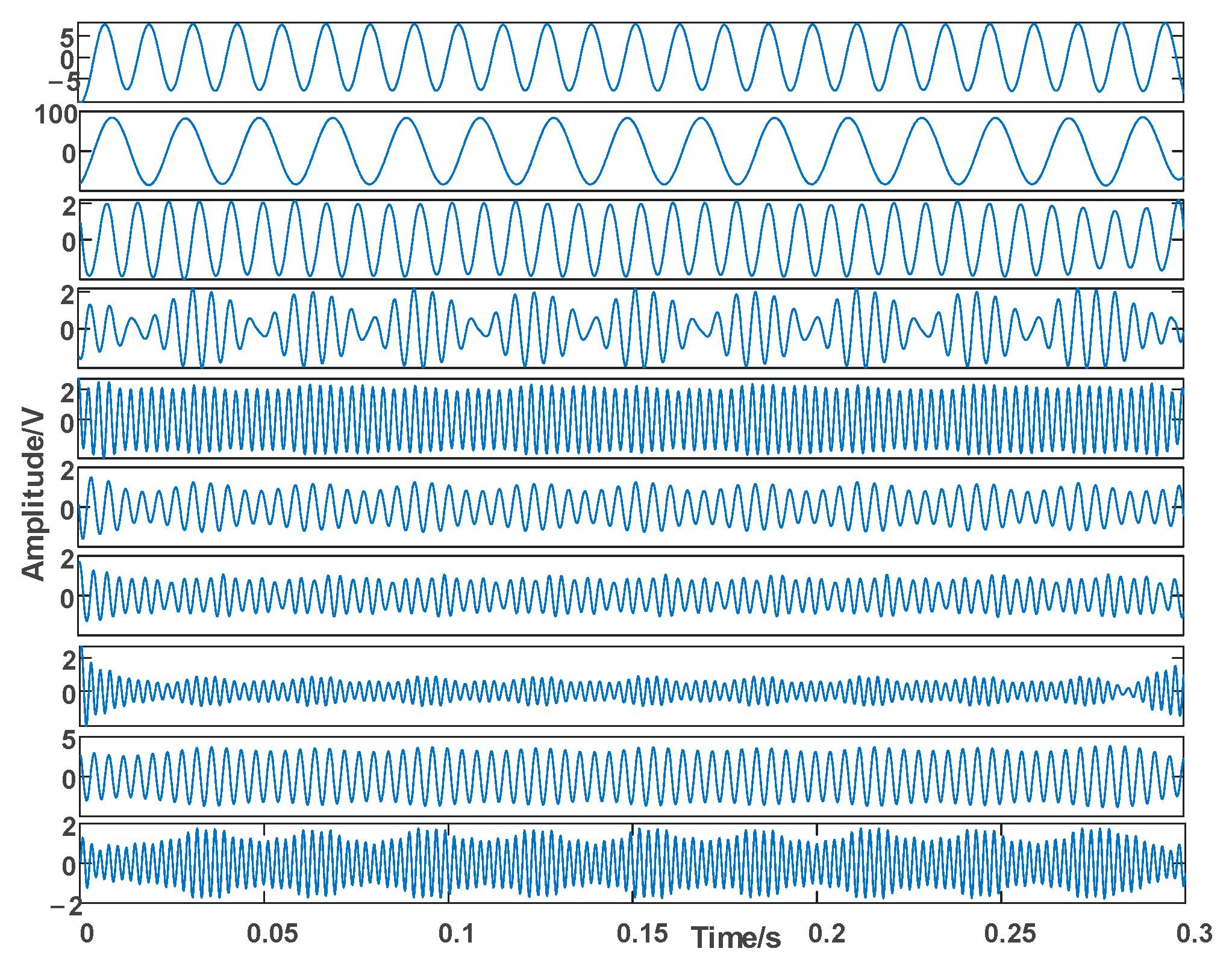
5. Example Analysis
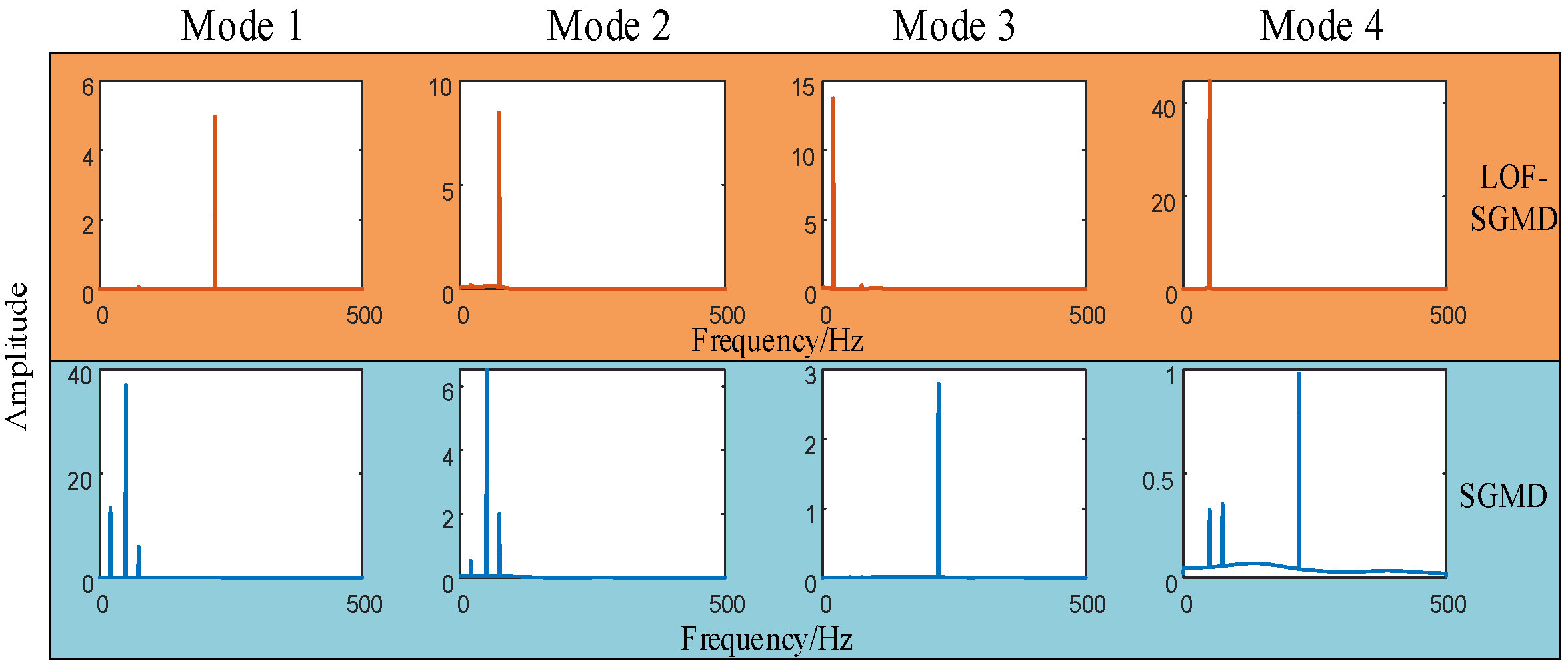
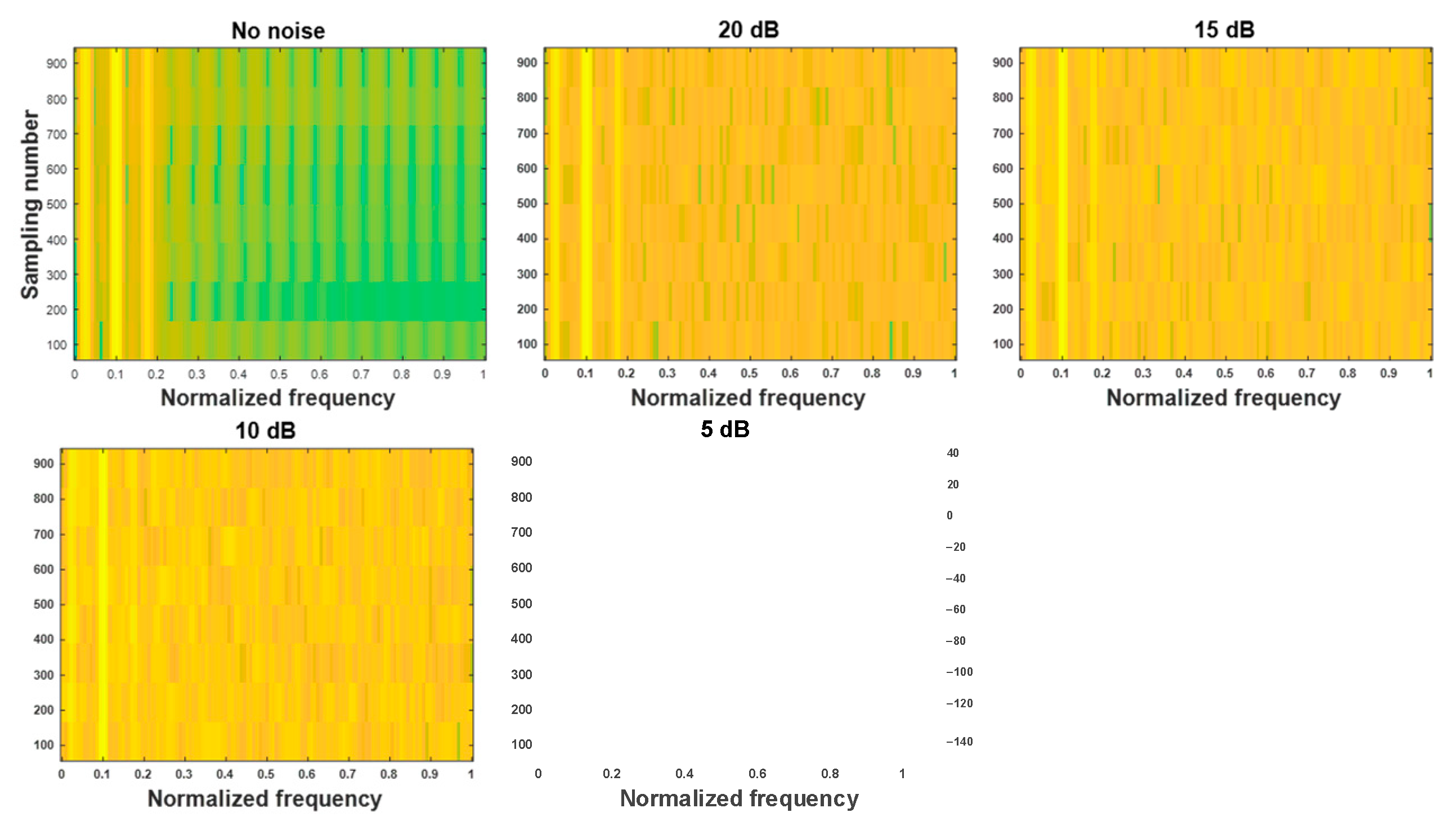
5.1. Denoising Performance Analysis of Example Signal
5.2. Detection Performance Analysis of Example Signal
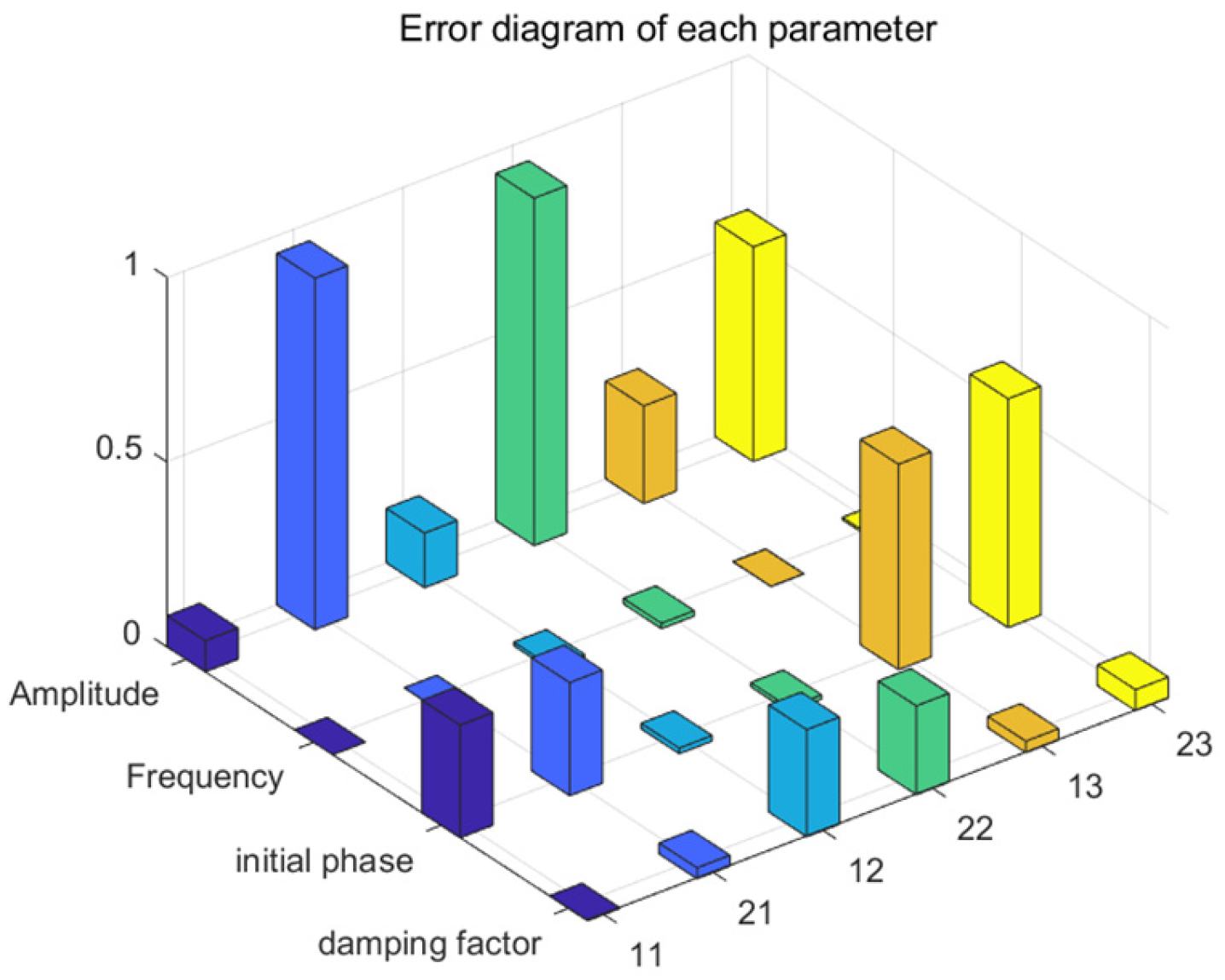
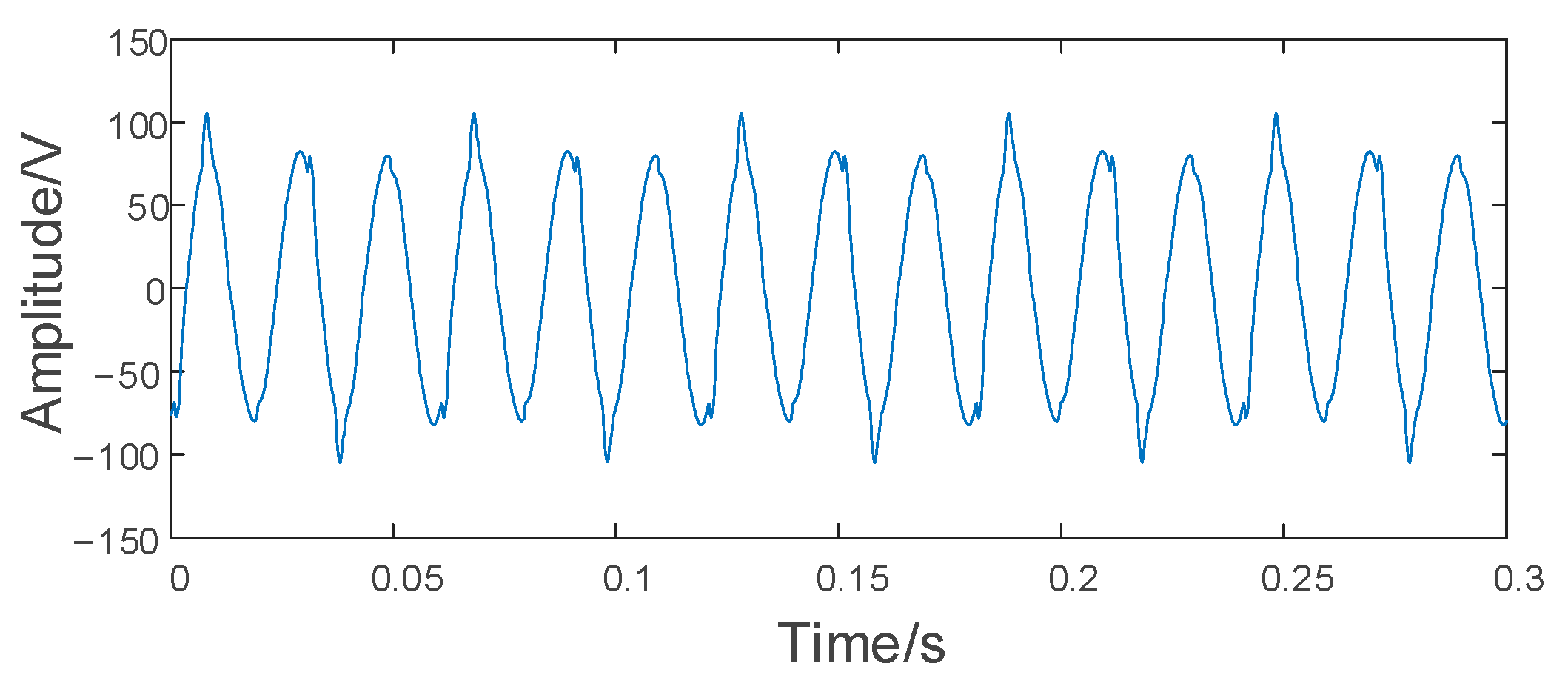
6. Measurement Analysis
6.1. Denoising Performance Analysis of Measurement Signal
6.2. Detection Performance Analysis of Measurement Signal
7. Conclusions
- (1)
- It should be noted that the algorithm design of this study is oriented towards the general analysis of broadband oscillations. Although the measured data sources are from the high-permeability areas of renewable energy, the method itself does not rely on a specific type of oscillation source.
- (2)
- The primary innovation is centered on a paradigm shift within the algorithm. While the traditional iterative loop judgment point of iterated symplectic geometry focuses on the residual component of the decomposition result in ISGMD, this paper proposes a new emphasis on assessing whether each decomposition component is uncoupled.
- (3)
- This paper verifies the effectiveness of the algorithm through simulation data and measured data. The final fitting SNR of the proposed algorithm in the simulation data is much higher than that of the original data, and almost twice that of the SVD method in the measured data.
- (4)
- The algorithm proposed in this paper demonstrates a slow increase in runtime as the data volume grows, while maintaining a relatively high convergence rate with no requirement for multiple iterations. Therefore, the proposed method exhibits practical feasibility in real-world applications.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Li, H.; Qiao, Y.; Lu, Z.; Zhang, B.; Teng, F. Frequency-Constrained Stochastic Planning Towards a High Renewable Target Considering Frequency Response Support From Wind Power. IEEE Trans. Power Syst. 2021, 36, 4632–4644. [Google Scholar] [CrossRef]
- Zong, H.; Lyu, J.; Wang, X.; Zhang, C.; Zhang, R.; Cai, X. Grey box aggregation modeling of wind farm for wideband oscillations analysis. Appl. Energy 2021, 283, 116035. [Google Scholar] [CrossRef]
- Cheng, Y.; Fan, L.; Rose, J. Real-world subsynchronous oscillation events in power grids with high penetrations of inverter-based resources. IEEE Trans. Power Syst. 2023, 38, 316–330. [Google Scholar] [CrossRef]
- Ying, Y.; Yang, X.; Wang, Z.; Gao, X.; Yu, H.; Xu, J.; Bao, W.; Ding, L. Drivetrain torsional vibration analysis and mitigation of grid-forming DFIG-based wind turbine generators. Int. J. Electr. Power Energy Syst. 2025, 170, 110882. [Google Scholar] [CrossRef]
- Chi, Y.; Tang, B.; Hu, J.; Tian, X.; Tang, H.; Li, Y.; Sun, S.; Shi, L.; Shuai, L. Overview of mechanism and mitigation measures on multi-frequency oscillation caused by large-scale integration of wind power. CSEE J. Power Energy Syst. 2019, 5, 433–443. [Google Scholar]
- Zhang, D.; Hu, J.; Ma, S.; He, Q.; Guo, Q. Impacts of PLL on the DFIG-based WTG’s electromechanical response under transient conditions:analysis and modeling. CSEE J. Power Energy Syst. 2016, 2, 30–39. [Google Scholar] [CrossRef]
- Shah, S.; Koralewicz, P.; Gevorgian, V.; Wallen, R.; Jha, K.; Mashtare, D.; Burra, R.; Parsa, L. Large-signal impedance-based modeling and mitigation of resonance of converter-grid systems. IEEE Trans. Sustain. Energy 2019, 10, 1439–1449. [Google Scholar] [CrossRef]
- Wang, C.; Zheng, W.; Wang, Z.; Dan, Y.; Ju, P. Partition-Based Network Equivalent Method for Power System Subsynchronous Oscillation Analysis. J. Mod. Power Syst. Clean. Energy 2024, 12, 313–320. [Google Scholar] [CrossRef]
- Liu, F.; Lin, S.; Ma, J.; Li, Y. Data-Driven Mode Identification Method for Broad-Band Oscillation of Interconnected Power System. IEEE Sens. J. 2022, 22, 15273–15283. [Google Scholar] [CrossRef]
- Zhang, F.; Cheng, L.; Gao, W.; Huang, R. Synchrophasors-based identification for subsynchronous oscillations in power systems. IEEE Trans. Smart Grid 2018, 10, 2224–2233. [Google Scholar] [CrossRef]
- Yang, X.; Zhang, J.; Xie, X.; Xiao, X.; Yang, W. Interpolated DFT-based identification of sub-synchronous oscillation parameters using synchrophasor data. IEEE Trans. Smart Grid 2019, 11, 2662–2675. [Google Scholar] [CrossRef]
- Wu, Q.; Huang, Y.; Li, C.; Gu, Y.; Zhao, H.; Zhan, Y. Small Signal Stability of Synchronous Motor-Generator Pair for Power System With High Penetration of Renewable Energy. IEEE Access 2019, 7, 166964–166974. [Google Scholar] [CrossRef]
- Fang, H.; Zhang, B.; Yu, F.; Zhao, B.; Ma, Z. A Pipelined Algorithm and Area-Efficient Architecture for Serial Real-Valued FFT. IEEE Trans. Circuits Syst. II Express Briefs 2022, 69, 4533–4537. [Google Scholar] [CrossRef]
- Yu, Y.; Zhao, W.; Li, S.; Huang, S. A Two-Stage Wavelet Decomposition Method for Instantaneous Power Quality Indices Estimation Considering Interharmonics and Transient Disturbances. IEEE Trans. Instrum. Meas. 2021, 70, 9001813. [Google Scholar] [CrossRef]
- Lee, W.; Jeong, T.; Lee, D.; Woo, K.; Lee, K.Y.; Yun, C.R.; Seo, C.; Oh, J.; Yun, C.R.; Seo, C.; et al. Fully Digital Phased Array Harmonic Radar for Detecting Concealed Electronic Devices. IEEE J. Microw. 2025, 5, 868–881. [Google Scholar] [CrossRef]
- Raj, V.A.; Nayak, S.G.; Thalengala, A. A hybrid framework for muscle artifact removal in EEG: Combining variational mode decomposition, stationary wavelet transform, and canonical correlation analysis. Cogent Eng. 2025, 12, 2514941. [Google Scholar] [CrossRef]
- Riaz, F.; Hassan, A.; Rehman, S.; Niazi, I.K.; Dremstrup, K. EMD-Based Temporal and Spectral Features for the Classification of EEG Signals Using Supervised Learning. IEEE Trans. Neural Syst. Rehabil. Eng. 2016, 24, 28–35. [Google Scholar] [CrossRef]
- Gao, Z.; Chang, Y.; Ren, F. The micro-shearing mechanism of the rock-concrete interface from acoustic emission using the improved Hilbert-Huang transform. Constr. Build. Mater. 2025, 489, 142301. [Google Scholar] [CrossRef]
- Chen, K.; Jin, T.; Mohamed, M.A.; Wang, M. An Adaptive TLS-ESPRIT Algorithm Based on an S-G Filter for Analysis of Low Frequency Oscillation in Wide Area Measurement Systems. IEEE Access 2019, 7, 47644–47654. [Google Scholar] [CrossRef]
- Shaikh, M.S.; Lin, H.; Xie, S.; Dong, X.; Lin, Y.; Shiva, C.K. An intelligent hybrid grey wolf-particle swarm optimizer for optimization in complex engineering design problem. Sci. Rep. 2025, 15, 18313. [Google Scholar] [CrossRef]
- Shaikh, M.S.; Hua, C.; Jatoi, M.A.; Ansari, M.M.; Qader, A.A. Application of grey wolf optimisation algorithm in parameter calculation of overhead transmission line system. IET Sci. Meas. Technol. 2021, 15, 218–231. [Google Scholar] [CrossRef]
- Cartiel, O.; Sainz, L.; Mesas, J.J.; Monjo, L. A Damping Margin Indicator for Compensator Design by the Positive-Mode-Damping Stability Criterion. IEEE Trans. Power Syst. 2025, 40, 3173–3184. [Google Scholar] [CrossRef]
- Sabo, A.; Wahab, N.I.A.; Othman, M.L.; Jaffar, M.Z.A.B.M.; Acikgoz, H.; Nafisi, H. Artificial Intelligence-Based Power System Stabilizers for Frequency Stability Enhancement in Multi-Machine Power Systems. IEEE Access 2021, 9, 166095–166116. [Google Scholar] [CrossRef]
- Gupta, A.K.; Verma, K. PMU-ANN based real time monitoring of power system electromechanical oscillations. In Proceedings of the 2016 IEEE 1st International Conference on Power Electronics, Intelligent Control and Energy Systems (ICPEICES), Delhi, India, 4–6 July 2016; pp. 1–6. [Google Scholar]
- Miao, Y.H.; Zhang, B.Y.; Li, C.H.; Lin, J.; Zhang, D.Y. Feature mode decomposition: New decomposition theory for rotating machinery fault diagnosis. IEEE Trans. Ind. Electron. 2023, 70, 1949–1960. [Google Scholar] [CrossRef]
- Guo, C.; Yang, L.; Dai, J.; Chen, B.; Yin, K.; Dai, J. A New Method for the Analysis of Broadband Oscillation Mode of New Energy Stations. Symmetry 2024, 16, 278. [Google Scholar] [CrossRef]
- Xiang, M.; Zhang, J.; Sun, Y.; Fan, J. A measurement-based dynamic harmonic model for single-phase diode bridge rectifier-type devices. IEEE Trans. Instrum. Meas. 2024, 73, 1501111. [Google Scholar]
- Huang, Y.; Yan, X.; Hu, Z.; Li, Z.; Zhang, Q. Quantized Exponential Hyperbolic Sine Robust Adaptive Filtering Algorithm. Circuits Syst. Signal Process 2025, 5, 12. [Google Scholar] [CrossRef]
- Ciotirnae, P.; Dumitrescu, C.; Chiva, I.C.; Semenescu, A.; Popovici, E.C.; Dranga, D. Method for noise reduction by averaging the filtering results on circular displacements using wavelet transform and local binary pattern. Electronics 2024, 13, 4119. [Google Scholar] [CrossRef]
- Barroso, R.H.; Zozaya Sahad, A.J. Improving the accuracy of the pencil of function method increasing its matrix polynomial degree. Mathematics 2025, 13, 315. [Google Scholar] [CrossRef]
- Li, Y.; Liang, X.; Yang, Y.; Xu, M.; Huang, W. Early Fault Diagnosis of Rotating Machinery by Combining Differential Rational Spline-Based LMD and K–L Divergence. IEEE Trans. Instrum. Meas. 2017, 66, 3077–3090. [Google Scholar] [CrossRef]
- Pan, H.; Yang, Y.; Li, X.; Zheng, J.; Cheng, J. Symplectic geometry mode decomposition and its application to rotating machinery compound fault diagnosis. Mech. Syst. Signal Process. 2019, 114, 189–211. [Google Scholar] [CrossRef]
- Wang, R.; Huang, W.; Hu, B.; Du, Q.; Guo, X. Harmonic Detection for Active Power Filter Based on Two-Step Improved EEMD. IEEE Trans. Instrum. Meas. 2022, 71, 9001510. [Google Scholar] [CrossRef]
- Biswas, M.; Hossain, M.S.; Ahmed Rupok, T.; Hossain, M.S.; Sukasem, C. The association of CYP2C19 LoF alleles with adverse clinical outcomes in stroke patients taking clopidogrel: An updated meta-analysis. Clin. Transl. Sci. 2024, 17, e13792. [Google Scholar] [CrossRef]
- Gao, J.; Xu, H.; Yang, Y.; Zhang, X.; Mao, X.; Dong, H. A multi-mode recognition method for broadband oscillation based on CS-OMP and adaptive VMD. Energies 2024, 17, 5821. [Google Scholar] [CrossRef]


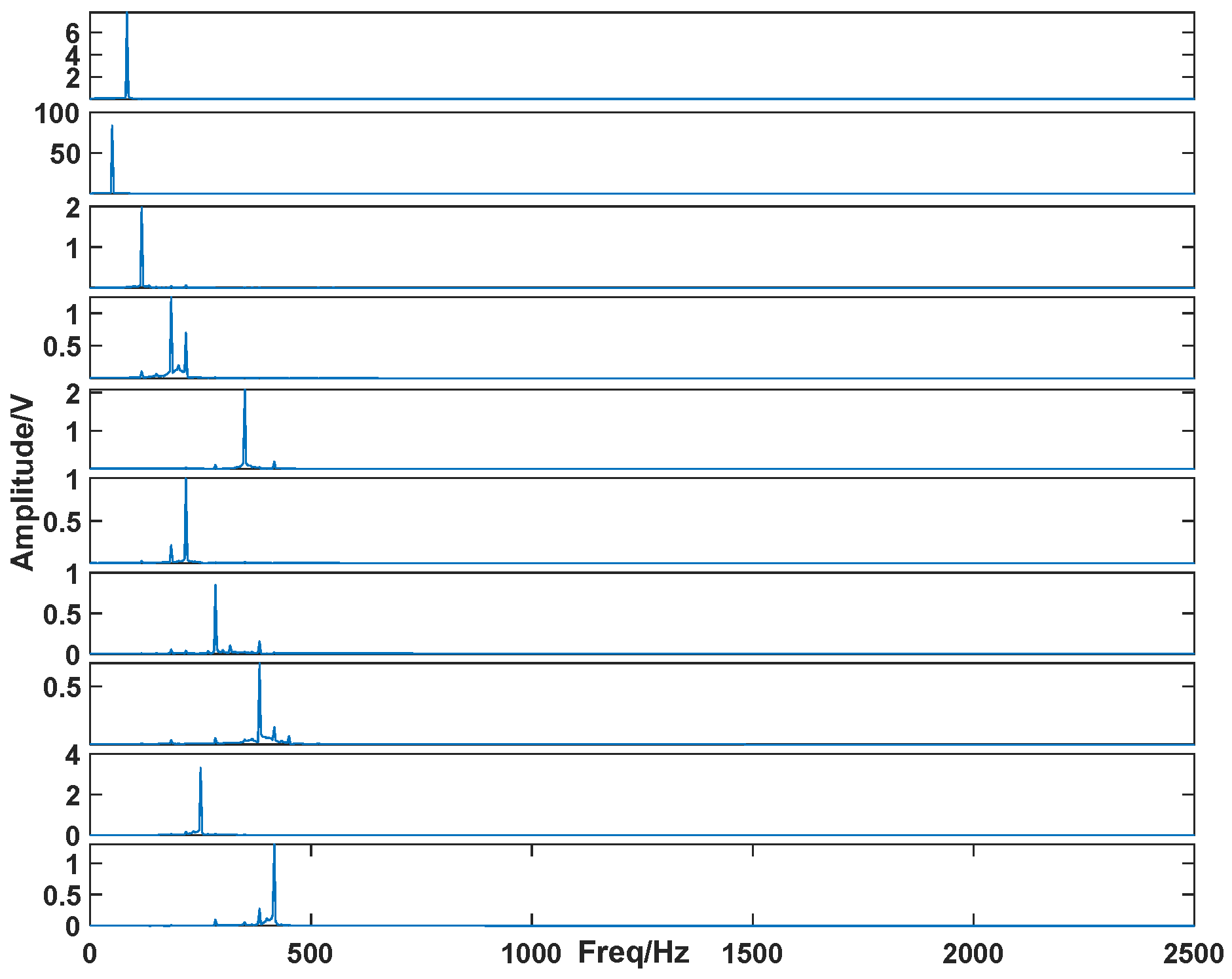
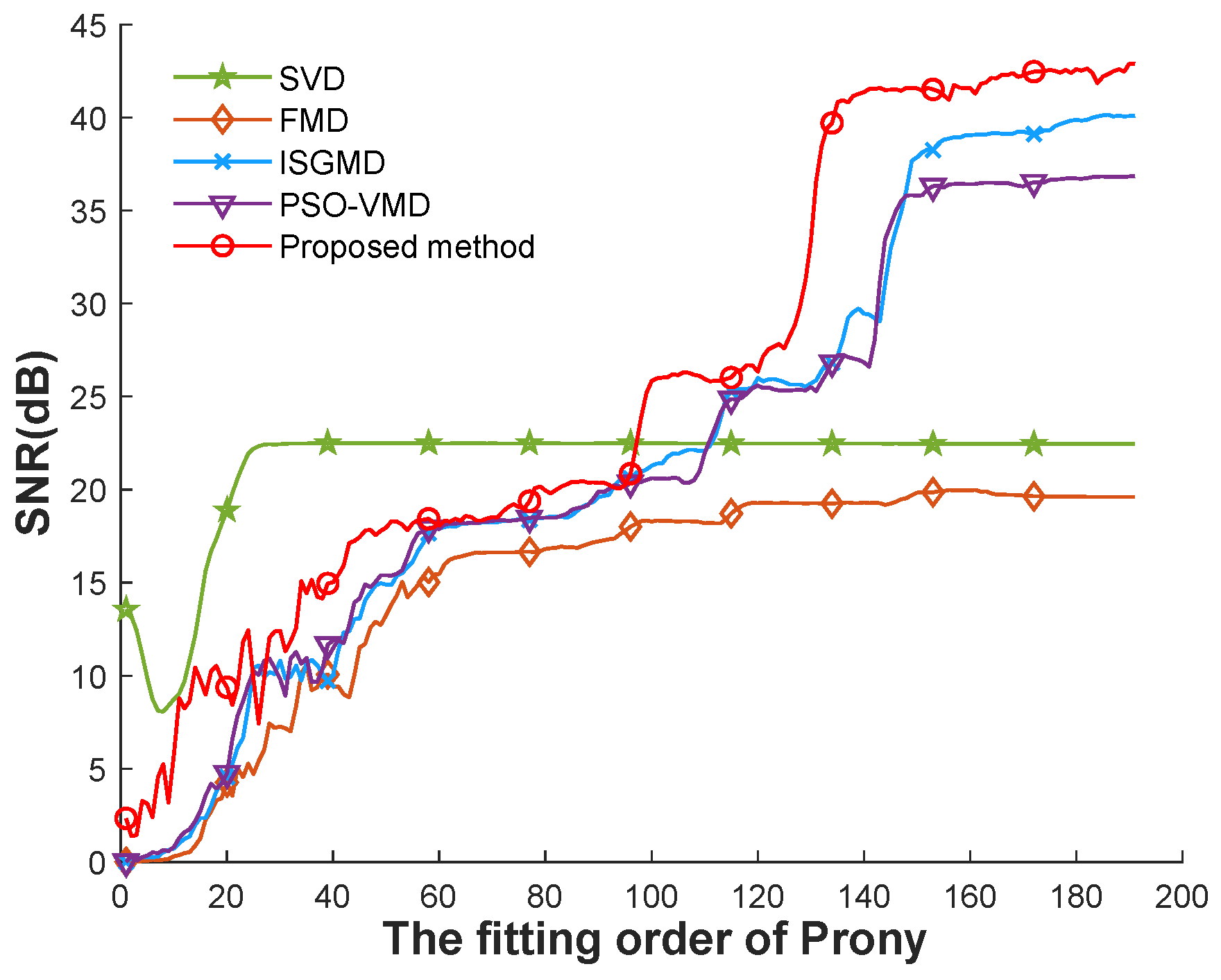
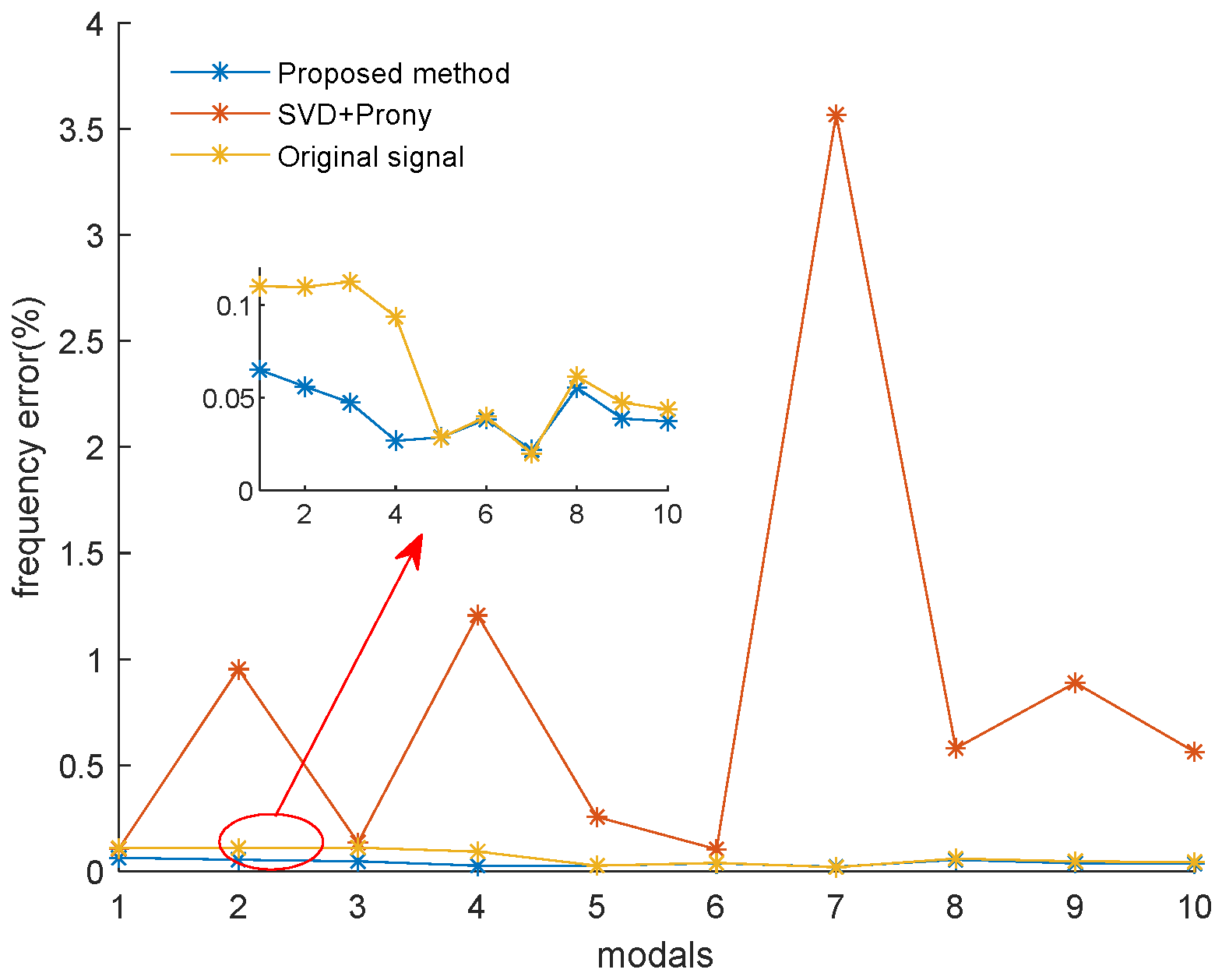

| 0 dB | 5 dB | 15 dB | |||||||
|---|---|---|---|---|---|---|---|---|---|
| SNR | RMSE | NCC | SNR | RMSE | NCC | SNR | RMSE | NCC | |
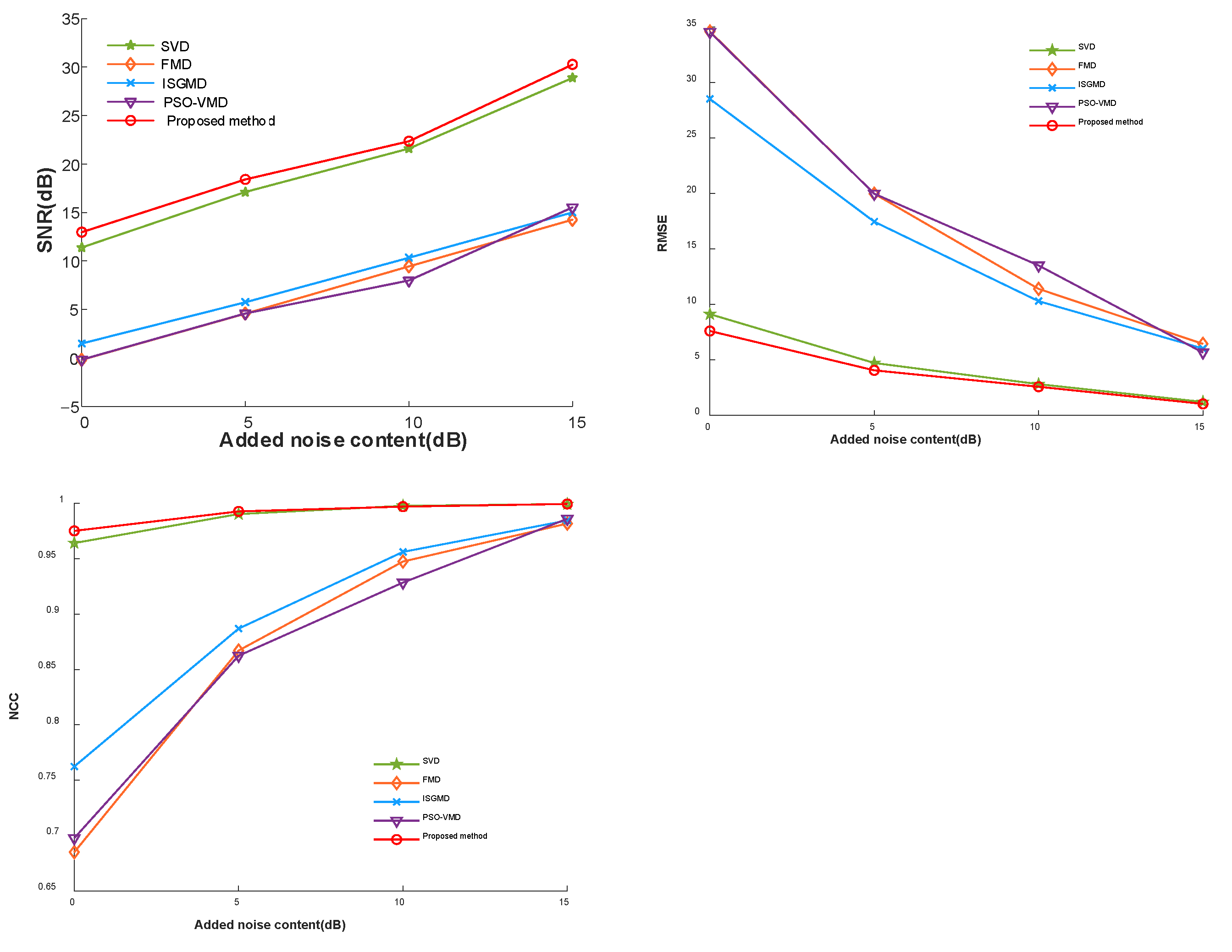
| SVD | 11.3857 | 9.1279 | 0.9642 | 17.1049 | 4.7251 | 0.9904 | 21.5959 | 2.8175 | 0.9978 |
| FMD | −0.1937 | 34.5982 | 0.6849 | 4.5760 | 19.9788 | 0.8671 | 9.4464 | 11.4037 | 0.9475 |
| ISGMD | 1.4891 | 28.5234 | 0.7623 | 5.7527 | 17.4590 | 0.8869 | 10.3397 | 10.2960 | 0.9562 |
| PSO-VMD | −0.1771 | 34.5549 | 0.6976 | 4.5803 | 19.9820 | 0.8624 | 7.9764 | 13.5156 | 0.9285 |
| Proposed method denoising performance | 12.9669 | 7.6087 | 0.9752 | 18.4200 | 4.0612 | 0.9928 | 22.3466 | 2.5842 | 0.9971 |
| Model Order | SNR (dB) | RMSE | NCC | |
|---|---|---|---|---|
| SVD + Prony | 25 | 29.6166 | 1.1190 | 0.9995 |
| Proposed method denoising performance | 25 | 31.3593 | 0.9156 | 0.9996 |
| Mode | A (V) | f (Hz) | (rad) | ||
|---|---|---|---|---|---|
| 1 | Proposed method denoising performance | 45.0841 | 50.0002 | 1.0902 | −0.0197 |
| SVD + Prony | 44.0491 | 49.9997 | 1.0915 | 0.0097 | |
| 2 | Proposed method denoising performance | 14.1476 | 12.0102 | −0.7703 | 0.1597 |
| SVD + Prony | 13.0601 | 12.0146 | −0.7738 | 0.1102 | |
| 3 | Proposed method denoising performance | 8.7359 | 87.9992 | 1.4980 | −0.0010 |
| SVD + Prony | 8.4194 | 87.9932 | 1.5614 | 0.0867 |
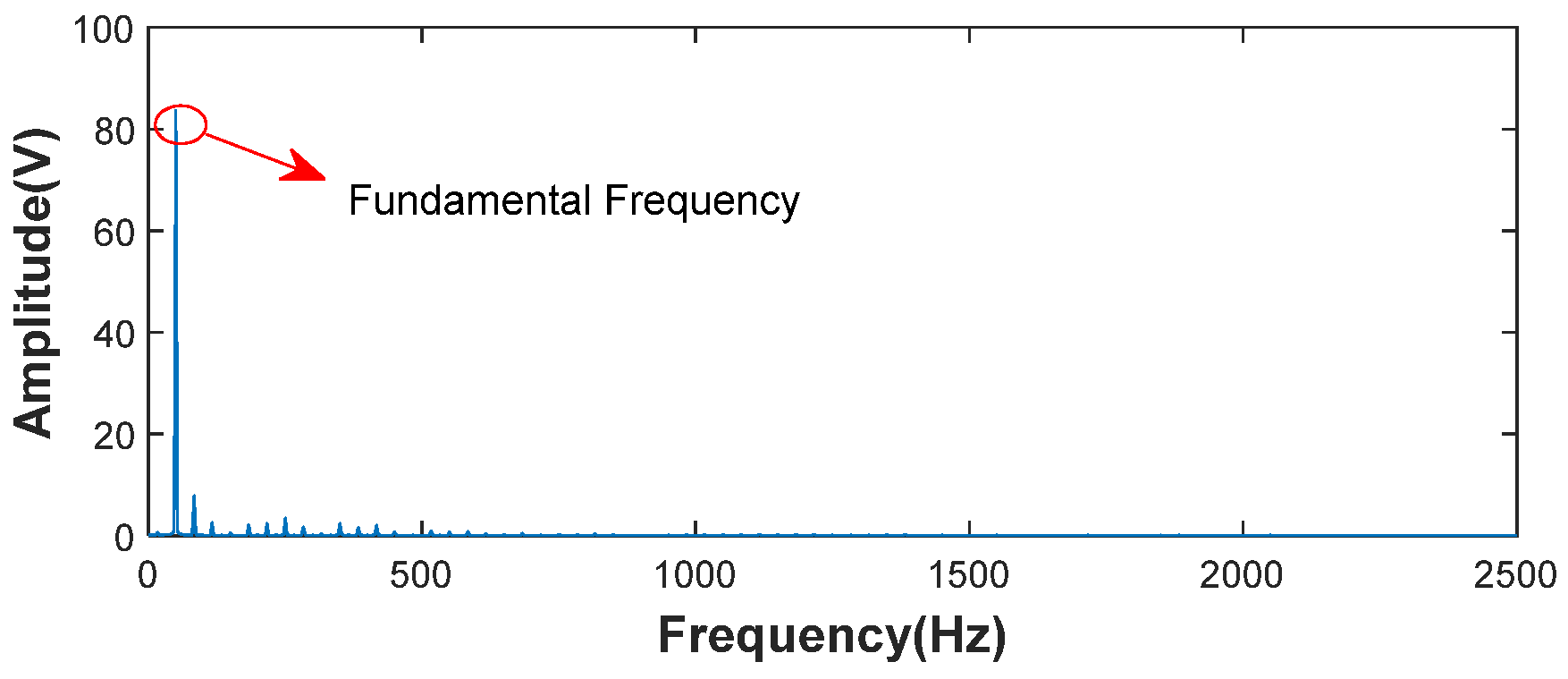
| Frequency (Hz) | Amplitude (V) | Frequency (Hz) | Amplitude (V) |
|---|---|---|---|
| 50 | 83.6529 | 350 | 2.38193 |
| 83.3333 | 7.91129 | 183.333 | 2.17834 |
| 250 | 3.42412 | 416.667 | 2.02222 |
| 116.667 | 2.59863 | 283.333 | 1.71047 |
| 216.667 | 2.44238 | 383.333 | 1.64848 |
| Evaluation Index | Model Order | SNR (dB) |
|---|---|---|
| this work | 150 | 41.5783 |
| SVD | 150 | 22.4703 |
| Modal | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Method | |||||||||||
| Amplitude (V) | 1 | 83.6529 | 7.91129 | 3.42412 | 2.59863 | 2.44238 | 2.38193 | 2.17834 | 2.02222 | 1.71047 | 1.64848 |
| 2 | 83.6976 | 7.9690 | 3.3594 | 2.7028 | 2.4239 | 2.5302 | 2.2587 | 2.0302 | 1.8084 | 1.6891 | |
| 3 | 83.7549 | 7.8937 | 3.5612 | 2.5332 | 2.3904 | 2.6313 | 2.1083 | 2.0431 | 1.8055 | 1.7964 | |
| 4 | 83.9513 | 10.0728 | 3.9778 | 4.9826 | 0.8793 | 2.9856 | 1.4862 | 0.5624 | 0.5699 | 0.7243 | |
| Frequency (Hz) | 1 | 50 | 83.3333 | 250 | 116.667 | 216.667 | 350 | 183.333 | 416.667 | 283.333 | 383.333 |
| 2 | 49.9675 | 83.2867 | 249.8818 | 116.6358 | 216.6052 | 349.8658 | 183.3728 | 416.4367 | 283.2233 | 383.1901 | |
| 3 | 49.9449 | 83.2417 | 249.7186 | 116.5578 | 216.6055 | 349.8611 | 183.3693 | 416.4111 | 283.1988 | 383.1650 | |
| 4 | 49.9471 | 84.1276 | 249.6608 | 115.2586 | 216.1113 | 350.3675 | 189.8726 | 414.2450 | 285.8541 | 381.1682 | |
| Initial phase | 1 | / | |||||||||
| 2 | 0.4762 | −0.5350 | 0.5991 | 1.3313 | −1.5548 | 0.4644 | −0.9315 | −1.1713 | −0.6472 | −0.3681 | |
| 3 | 0.4746 | −0.5368 | 0.6290 | 1.3430 | −1.5559 | 0.4681 | −0.9297 | −1.1501 | −0.6277 | −0.3467 | |
| 4 | 0.4797 | −0.3740 | 0.6990 | −1.5222 | 1.1278 | 0.5688 | 1.5211 | 0.8542 | −0.4415 | 1.2737 | |
| Damping factor | 1 | / | |||||||||
| 2 | −0.0015 | −0.0652 | 0.1518 | −0.1713 | 0.0992 | −0.3952 | −0.2354 | −0.0019 | −0.3811 | −0.1677 | |
| 3 | −0.0038 | −0.0158 | 0.0104 | 0.1591 | 0.1879 | −0.3919 | −0.0837 | −0.0398 | −0.3653 | −0.1950 | |
| 4 | 0.0003 | −3.7667 | −0.3948 | −10.1811 | −4.4486 | 0.7131 | −76.6435 | −21.8343 | −11.3045 | −48.8654 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gan, Z.; Zhang, R.; Ding, H.; Li, J.; Li, C.; Yang, L.; Guo, C. Research on Broadband Oscillation Mode Identification Based on Improved Symplectic Geometry Algorithm. Symmetry 2025, 17, 1650. https://doi.org/10.3390/sym17101650
Gan Z, Zhang R, Ding H, Li J, Li C, Yang L, Guo C. Research on Broadband Oscillation Mode Identification Based on Improved Symplectic Geometry Algorithm. Symmetry. 2025; 17(10):1650. https://doi.org/10.3390/sym17101650
Chicago/Turabian StyleGan, Zhan, Rui Zhang, Hanlin Ding, Jinsong Li, Chao Li, Lingrui Yang, and Cheng Guo. 2025. "Research on Broadband Oscillation Mode Identification Based on Improved Symplectic Geometry Algorithm" Symmetry 17, no. 10: 1650. https://doi.org/10.3390/sym17101650
APA StyleGan, Z., Zhang, R., Ding, H., Li, J., Li, C., Yang, L., & Guo, C. (2025). Research on Broadband Oscillation Mode Identification Based on Improved Symplectic Geometry Algorithm. Symmetry, 17(10), 1650. https://doi.org/10.3390/sym17101650





