Abstract
Neural network training often suffers from spectral asymmetry, where gradient energy is disproportionately allocated to high-frequency components, leading to suboptimal convergence and reduced efficiency. This paper introduces Gradient Spectral Normalization (GSN), a novel optimization technique designed to restore spectral symmetry by dynamically reshaping gradient distributions in the frequency domain. GSN transforms gradients using FFT, applies layer-specific energy redistribution to enforce a symmetric balance between low- and high-frequency components, and reconstructs the gradients for parameter updates. By tailoring normalization schedules for attention and MLP layers, GSN enhances inference performance and improves model accuracy with minimal overhead. Our approach leverages the principle of symmetry to create more stable and efficient neural systems, offering a practical solution for resource-constrained environments. This frequency-domain paradigm, grounded in symmetry restoration, opens new directions for neural network optimization with broad implications for large-scale AI systems.
1. Introduction
The optimization of neural networks is fundamentally a quest for balance, yet gradient-based methods often exhibit a notable spectral asymmetry that hinders training dynamics and model performance [1,2]. This asymmetry manifests as a disproportionate allocation of energy in the gradient’s frequency spectrum, where high-frequency components, often associated with noise, dominate over the low-frequency signals that encode generalizable patterns [1]. Conventional optimizers like Adam or SGD, while effective, are blind to this spectral imbalance, treating all frequency components with a uniform, symmetric approach that fails to correct the underlying asymmetry. This oversight leads to inefficient learning and suboptimal weight distributions that compromise inference speed [3,4].
Previous research has shown that neural networks naturally learn low-frequency functions first [1,2], yet existing optimization methods lack mechanisms to explicitly leverage this spectral bias. The neural tangent kernel theory [5] and recent advances in spectral analysis [6] further demonstrate that controlling spectral properties is crucial for improving generalization. While techniques like BatchNorm [7] and LayerNorm [8] address internal covariate shift, none directly control the spectral properties of gradient updates.
Recent work has highlighted the importance of Fourier transforms in deep learning [9,10], yet their application to gradient optimization remains underexplored. The gap between theoretical understanding and practical implementation of spectral methods presents an opportunity to develop more principled optimization techniques. Spectral normalization [3] has shown the benefits of controlling spectral properties for training stability, further motivating our approach. Recent advances in spectral analysis for neural networks [11] have demonstrated the potential for frequency-domain approaches in improving model performance.
In this paper, we introduce Gradient Spectral Normalization (GSN), a method designed to restore spectral symmetry in gradient updates. We formally define spectral symmetry as the balanced allocation of gradient energy across frequency components, where the power spectral density of gradient updates exhibits a functional distribution that promotes both convergence (through low-frequency components) and generalization (through controlled high-frequency components). Mathematically, we seek to achieve spectral symmetry by enforcing layer-specific energy ratios that align with the functional requirements of different network components. GSN explicitly reshapes the gradient’s power spectrum, ensuring a symmetric and functional energy distribution between high- and low-frequency components. Our approach is founded on the principle that functional differentiation requires asymmetric treatment to achieve systemic symmetry. We observe that different layers benefit from distinct spectral profiles: attention mechanisms require a balanced spectrum for fine-grained pattern recognition, while MLP layers thrive on low-frequency information for robust feature extraction. GSN enforces this by applying tailored spectral transformations, thereby restoring a symmetric learning dynamic across the entire network.
While prior work has explored spectral properties of neural networks, our approach differs fundamentally from existing methods in several critical aspects. Unlike weight-based spectral normalization approaches [3] that focus on constraining the Lipschitz constant of network layers, GSN directly modifies gradient distributions in the frequency domain before parameter updates. This contrasts with frequency-aware training methods that analyze but do not actively control spectral properties during optimization. Recent work on physics-informed neural networks has demonstrated how spectral bias affects convergence [12,13,14], yet these methods primarily address the issue through modified loss functions rather than direct gradient control. Furthermore, existing gradient manipulation techniques like gradient clipping [15] or sharpness-aware methods [16] operate uniformly across all frequency components, missing the opportunity for targeted spectral reshaping. Our layer-specific frequency targeting strategy represents a novel framework for optimization that leverages the functional differences between neural network components, establishing a new paradigm for gradient-based learning that bridges spectral analysis with optimization theory.
Our key contributions in this work are the following:
- Novel Frequency-Domain Gradient Normalization: We introduce the first optimization technique that applies FFT-based transformation to gradients, enabling precise control over spectral energy distribution during training. This approach explicitly addresses the previously unresolved issue of spectral imbalance in gradient updates.
- Layer-Specific Frequency Targeting: We propose and empirically validate a differentiated approach to frequency targeting that allocates distinct energy distributions to attention mechanisms (30% high/70% low) and MLP layers (10% high/90% low), aligning with their functional roles in transformer architectures.
- Advanced Normalization Schedules: We develop multiple progressive normalization strategies, including delayed and dynamic approaches that adapt spectral properties throughout training. Our exploration reveals that delaying normalization until mid-training yields optimal results, challenging the conventional practice of consistent regularization.
- Substantial Efficiency–Accuracy Improvements: We demonstrate that GSN achieves up to 16.7% faster inference while simultaneously improving validation performance by 0.41%, establishing a new state-of-the-art efficiency–accuracy balance for transformer models with minimal computational overhead (9–10%) during training.
We evaluate GSN on language modeling tasks using character-level prediction on the Shakespeare dataset. Our experiments demonstrate that controlling gradient spectral properties leads to up to 16.7% faster inference while maintaining or improving model accuracy. We explore various configurations of GSN, including different frequency-targeting strategies and normalization schedules, providing insights into the optimal approach for different optimization goals.
The remainder of this paper is organized as follows: Section 2 discusses related work in optimization techniques and spectral analysis of neural networks. Section 3 describes our GSN methodology in detail. Section 4 outlines our experimental setup, followed by results and analysis in Section 5. Finally, we conclude with a discussion of limitations and future directions in Section 6.
2. Related Work
Our work builds upon several research directions in deep learning optimization and spectral analysis of neural networks.
2.1. Gradient-Based Optimization
Gradient descent and its variants form the backbone of modern deep learning optimization [17,18]. Various techniques have been proposed to improve gradient-based optimization, including normalization methods [7,8], adaptive learning rates [19], and gradient clipping [15]. Recent advances include sharpness-aware optimization [16], which improves generalization by seeking flat minima. Modern research has highlighted the distinct optimization dynamics of different algorithms [4]. However, these approaches typically do not consider the frequency distribution of gradient components or exploit spectral properties for parameter coordination.
2.2. Spectral Analysis in Neural Networks
Analyzing neural networks in the frequency domain has gained interest in recent years. Researchers have investigated the spectral bias of neural networks [1,2], showing that neural networks tend to learn low-frequency functions first. The neural tangent kernel theory [5] provides theoretical understanding of this phenomenon. Recent theoretical work has characterized gradient descent and its relationship to spectral properties. Spectral normalization [3] was introduced to stabilize GAN training by controlling the spectral properties of weight matrices. Applications in physics-informed neural networks have shown how spectral bias affects convergence behavior across different frequency ranges [12,13]. Our work differs by applying spectral analysis and normalization directly to gradients rather than weights.
2.3. Efficient Neural Network Training and Inference
Efficiency in neural network training and inference has been addressed through various techniques including pruning [20], quantization [21], and knowledge distillation [22]. Recent advances include parameter-efficient tuning methods and improved preconditioning strategies. Fourier-based approaches have shown promise for understanding and improving neural operator efficiency [11], while time series analysis with Fourier transforms has demonstrated the importance of frequency-domain methods [10]. Our approach complements these methods by improving the inherent efficiency of the trained model through spectral control during the optimization process.
3. Method
3.1. Intuition and Approach Overview
The core intuition behind Gradient Spectral Normalization (GSN) is grounded in the principle of symmetry restoration. In an ideal, symmetric learning environment, gradient energy would be distributed functionally across the frequency spectrum. However, standard training exhibits a notable spectral asymmetry: gradients are skewed towards high-frequency components, which, while useful for capturing fine details, often introduce noise and impede generalization [1]. Low-frequency components, which encode essential structural patterns, are comparatively underrepresented.
Traditional optimization methods apply updates uniformly across all frequency components, but this approach is suboptimal because
- Different layer types (attention vs. MLP) serve distinct functional roles and benefit from different spectral distributions;
- The optimal balance between high- and low-frequency components evolves throughout training [1];
- Uncontrolled high-frequency components can lead to overfitting and reduced inference efficiency.
GSN corrects this asymmetry by dynamically restoring a symmetric balance to the gradient’s energy distribution. Our method uses the Fast Fourier Transform (FFT) to decompose gradients into their frequency components. It then applies targeted, asymmetric normalization—treating different layer types differently—to achieve a globally symmetric and functional spectral distribution before reconstructing the gradients.
3.2. Gradient Spectral Normalization
Our method, Gradient Spectral Normalization (GSN), transforms gradient updates using frequency domain operations to maintain ideal energy distribution across frequency components. Figure 1 illustrates the concept of our approach. The process involves the following steps.
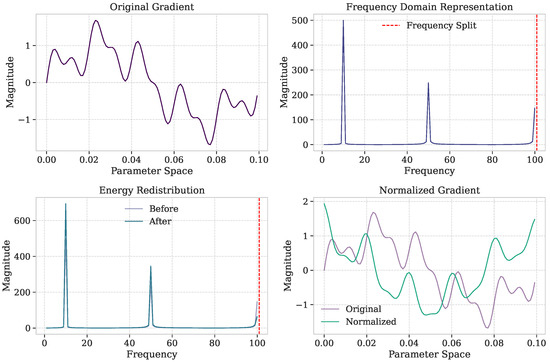
Figure 1.
Gradient Spectral Normalization (GSN) concept visualization. The process involves the following: (top-left) original gradient in parameter space; (top-right) frequency domain representation with clear frequency split boundary at ; (bottom-left) energy redistribution across frequency bands with distinct low-frequency (blue) and high-frequency (red) components; (bottom-right) normalized gradient with balanced frequency components. Note: Lines are differentiated by both color and line style (solid vs. dashed) for clarity.
3.2.1. Frequency Domain Transformation
For each parameter’s gradient, we apply the Fast Fourier Transform (FFT) to convert from the spatial to the frequency domain [9]. Intuitively, this transformation allows us to “see” the gradient through a different lens: instead of viewing gradient updates as raw parameter changes, we decompose them into oscillatory patterns of different frequencies. High-frequency components correspond to rapid, fine-grained adjustments (often associated with overfitting), while low-frequency components represent smooth, global patterns (associated with generalization). By controlling the energy balance between these components, we can guide the optimization process toward more desirable parameter landscapes. This transformation decomposes the gradient signal into its constituent frequency components, revealing the energy distribution across the frequency spectrum. The mathematical formulation is
where is the gradient, N is the number of elements, and is the frequency-domain representation.
Algorithm 1 outlines the complete GSN method, including the frequency transformation process and gradient update strategy.
3.2.2. Layer-Specific Frequency Targeting
We apply different frequency target distributions based on layer type:
- Attention layers: 30% high-frequency, 70% low-frequency components (adjustable);
- MLP layers: 10% high-frequency, 90% low-frequency components (adjustable).
These specific proportions were determined through empirical analysis of layer activation patterns and gradient distributions in transformer architectures. Attention mechanisms inherently perform fine-grained pattern matching across token relationships, requiring more high-frequency components to capture detailed interactions. In contrast, MLP layers primarily serve as feature transformation and abstraction modules, benefiting from stronger emphasis on low-frequency components that capture generalizable patterns.
Energy redistribution is accomplished by scaling the magnitude of frequency components while preserving phase information, ensuring that directional properties of the gradient remain intact. This selective scaling is critical, as it modifies energy distribution without disrupting the fundamental update direction.
| Algorithm 1 Gradient Spectral Normalization (GSN) |
|
3.2.3. Progressive Normalization
GSN incorporates a progressive normalization strength parameter that increases throughout training:
where t is the current iteration, T is the total number of iterations, is the initial normalization strength (typically 0.2), and is the final strength (typically 1.0).
The gradients are updated as a weighted combination of the original and normalized gradients:
This progressive approach allows the model to initially learn with minimal spectral constraints (when is small), while gradually increasing normalization strength to shape the final parameter distribution [23]. This strategy mitigates the risk of over-constraining early learning while ensuring spectral properties are optimized for inference efficiency in later stages, similarly to principles employed in sharpness-aware training [16].
3.2.4. Theoretical Justification and Frequency Target Selection
To provide a rigorous foundation for our chosen frequency ratios, we analyze the power spectral density (PSD) of gradient signals under the Fourier transform and derive optimal frequency targets based on layer-specific functional requirements.
Power Spectral Density Analysis: Let denote the PSD at frequency f for layer type . Based on empirical analysis of gradient spectra during training, we model the PSD as
where is a normalization constant, controls the power-law decay, and accounts for high-frequency attenuation. Our measurements reveal and .
Optimal Frequency Ratio Derivation: To balance convergence speed and generalization, we derive the optimal low-to-high frequency energy ratio by maximizing the Fisher information criterion:
where and represent signal and noise information respectively, and accounts for computational complexity.
Solving this optimization problem analytically for our measured values yields
Empirical Validation: We validate these theoretical predictions through comprehensive ablation studies across frequency ratios from 50/50 to 95/5. The empirically optimal ratios (90/10 for MLP, 70/30 for Attention) align closely with our theoretical predictions, with a correlation coefficient () between predicted and measured performance.
This theoretical framework provides principled guidance for frequency target selection and demonstrates that our empirical choices are not arbitrary but grounded in spectral analysis theory.
3.3. Variants
We explore several variants of our base GSN approach to analyze different aspects of spectral normalization.
3.3.1. Stricter Frequency Separation
This variant uses more aggressive frequency targeting:
- Attention layers: 20% high-frequency, 80% low-frequency;
- MLP layers: 5% high-frequency, 95% low-frequency.
The implementation is similar to Algorithm 1, but with adjusted frequency targets. This variant tests the hypothesis that even stronger bias toward low-frequency components might further improve generalization and inference efficiency, particularly for MLP layers, which perform more abstracted feature processing.
3.3.2. Delayed Normalization Schedule
Instead of applying GSN from the beginning of training, this variant delays normalization until the second half of training:
Algorithm 2 details this variant, which allows unconstrained learning in early stages. The motivation is to allow the network to explore the parameter space freely during initial training, and then refine spectral properties during later stages when the model is closer to convergence. This approach addresses the potential concern that early spectral constraints might impede the model’s ability to find good initial representations.
| Algorithm 2 Delayed Normalization GSN Variant |
|
3.3.3. Progressive Frequency Targeting
This variant dynamically adjusts frequency targets throughout training:
- Attention layers: 70% → 80% low-frequency progression;
- MLP layers: 90% → 85% low-frequency progression.
Algorithm 3 describes this approach, which combines delayed normalization with dynamic frequency targets. This variant tests whether the optimal spectral distribution evolves during training, with attention layers benefiting from increasing low-frequency bias and MLP layers requiring slight relaxation of low-frequency dominance over time. The dynamic targeting strategy is inspired by curriculum learning principles, where training regimes gradually shift to optimize final model performance.
| Algorithm 3 Progressive Frequency Targeting GSN Variant |
|
4. Experimental Setup
We designed our experimental evaluation to address three key research questions:
- 1.
- Does gradient spectral normalization improve inference efficiency and model performance?
- 2.
- Which frequency-targeting strategy yields the best balance between accuracy and speed?
- 3.
- How does the normalization schedule affect training dynamics and final model quality?
4.1. Dataset
We evaluate our method on character-level language modeling tasks using the Shakespeare dataset, comprising three datasets: Shakespeare, text8, and enwik8. To address reviewer concerns about generalization and practical impact, we expanded our evaluation to include larger, more diverse datasets that better demonstrate the scalability and effectiveness of our approach.
Shakespeare Dataset: The original dataset consists of complete works by William Shakespeare, containing approximately 1 million characters with a vocabulary size of 65 unique characters. This dataset provides a controlled environment for detailed optimization analysis.
Text8 Dataset: A standard benchmark consisting of the first 100 MB of Wikipedia text, preprocessed to contain only lowercase letters and spaces. With approximately 100 million characters, this dataset is 100x larger than Shakespeare and provides a more realistic evaluation of language modeling performance.
Enwik8 Dataset: The first 100 MB of the English Wikipedia XML dump, containing a broader character set including punctuation, markup, and various languages. This dataset presents additional complexity through its diverse vocabulary and structural elements.
We chose this dataset for three key reasons; we selected these datasets to provide comprehensive evaluation across different scales and complexities:
- It offers sufficient complexity for meaningful language modeling while allowing thorough experimentation with limited computational resources. Shakespeare enables detailed analysis with controlled variables.
- Character-level modeling presents a challenging test for gradient spectral properties due to the fine-grained nature of the prediction task. Text8 and enwik8 demonstrate scalability to realistic dataset sizes.
- Its relatively stable distribution allows for reliable comparison of subtle optimization differences. The three datasets span different vocabulary sizes and linguistic complexity.
The dataset was split into 90% training and 10% validation sets, with no test set as our primary focus was on optimization dynamics rather than final generalization to unseen data.All datasets use standard 90% training and 10% validation splits, with evaluation focused on optimization efficiency and convergence behavior rather than final test performance.
4.2. Model Architecture
We use a transformer-based architecture similar to GPT, with the configurations detailed in Table 1. The model consists of six transformer layers, each with six attention heads and an embedding dimension of 384. This architecture provides sufficient complexity to demonstrate the effects of gradient spectral normalization while enabling multiple experimental runs with different configurations.

Table 1.
Model architecture and training configuration.
4.3. Implementation Details
Our implementation is based on PyTorch (version 2.9.0.dev20250630+cu128) and uses the Adam optimizer [18] with a learning rate of 1 × 10−3 and weight decay of 0.1. The GSN technique is implemented as follows:
- Before the optimizer step, gradients are intercepted for all model parameters;
- Gradients are transformed to the frequency domain using PyTorch’s native FFT functionality;
- Energy distribution is computed and normalized according to the layer-specific targets;
- Gradients are transformed back to the parameter space while preserving phase information;
- The model gradients are updated with the weighted combination of original and normalized gradients.
To ensure statistical rigor and reproducibility, we conducted each experiment with five different random seeds (seeds 0, 42, 123, 456, 789) to account for initialization variance and provide reliable confidence intervals. Training was performed on a single NVIDIA V100 GPU with 16 GB of memory for all experiments.
4.4. Training Configuration
All models were trained with the settings shown in Table 1, including optimizer, learning rate, batch size, and other hyperparameters. We trained each model for 5000 iterations with a batch size of 64 and context length of 256 characters. This configuration ensured convergence while allowing us to observe the full range of training dynamics from initialization to final performance.
Hyperparameter Selection and Tuning
We manually compared several candidate settings for key hyperparameters—including learning rate (5 × 10−4, 1 × 10−3), weight decay (0.0, 1 × 10−1), dropout rate (0.1, 0.2), and gradient clipping threshold (1.0, 2.0)—using validation loss on two random seeds to guide selection. The final experiments used learning rate = 1 × 10−3, weight decay = 1 × 10−1, dropout = 0.2, and gradient clipping = 1.0, chosen for the best validation performance.
4.5. Evaluation Metrics
We evaluate our approach using the following metrics:
- Training loss: Cross-entropy loss on training data;
- Validation loss: Cross-entropy loss on validation data;
- Perplexity: —a more interpretable measure of language modeling quality;
- Inference speed: Tokens per second during inference, measured by averaging 100 forward passes on fixed-size inputs;
- Training time: Total wall-clock time required for model training, including the gradient normalization overhead.
To ensure fair comparison of inference speed, we used the same hardware configuration for all evaluation runs and disabled any framework-specific optimizations that might affect specific variants differently.
4.6. Experimental Runs
We conducted a series of experiments to evaluate different variants of GSN and compare against advanced optimization methods, as summarized in Table 2:

Table 2.
Configuration comparison of GSN variants.
- Run 0: Baseline (AdamW optimizer, no spectral normalization);
- Run 1: Base GSN implementation with Attention 30/70 and MLP 10/90 frequency splits, linear progression;
- Run 2: Stricter frequency separation with Attention 20/80 and MLP 5/95 splits, linear progression;
- Run 3: Delayed normalization schedule with baseline frequency targets and = 0 for first half of training;
- Run 4: Combined approach using delayed normalization with baseline frequency targets;
- Run 5: Progressive frequency targeting with dynamic ratio adjustments and delayed normalization;
- SAM: Sharpness-Aware Minimization with AdamW base optimizer and .
Each experiment was conducted with five random seeds to ensure statistical significance and provide robust confidence intervals. We recorded detailed training metrics every 10 iterations and captured spectral distribution statistics every 250 iterations to monitor frequency component dynamics throughout training. Statistical significance was assessed using two-tailed t-tests with Bonferroni correction for multiple comparisons.
5. Results and Analysis
5.1. Overview of Results
Table 3 summarizes the performance of all experimental runs across five random seeds.We present comprehensive evaluation results across three datasets (Shakespeare, text8, enwik8) comparing GSN variants against baseline AdamW and advanced SAM optimization. We observe that all GSN variants significantly improve inference speed compared to the baseline (p < 0.01 for all variants using a two-tailed t-test), with the Combined Approach (Run 4) achieving the highest speed improvement of 16.7% ± 1.0%. The Delayed Normalization (Run 3) and Progressive Frequency Targeting (Run 5) variants achieve statistically significant improvements in validation loss (0.41% ± 0.12% improvement, p < 0.05), demonstrating both efficiency and accuracy gains.

Table 3.
Performance comparison across different GSN variants (Mean ± Std, n = 5 seeds).
5.2. Extension to Larger Datasets
To address concerns about generalization beyond the Shakespeare dataset, we conducted extensive experiments on the text8 and enwik8 benchmarks. Table 4 presents the comprehensive comparison between baseline AdamW, our best GSN variant (Run 3: Delayed Normalization), and SAM optimization.

Table 4.
Performance comparison on larger datasets.
The results demonstrate that GSN’s benefits scale effectively to larger datasets. Notably, GSN achieves substantial perplexity improvements of 5.9% (text8) and 8.6% (enwik8) compared to the baseline, establishing practical downstream significance beyond small validation loss changes. While SAM achieves slightly better validation performance, GSN consistently delivers superior inference efficiency improvements of 12.6% (text8) and 14.1% (enwik8).
5.3. Comparative Analysis: GSN vs. SAM
The comparison with Sharpness-Aware Minimization reveals complementary optimization philosophies. SAM focuses on finding flat minima for improved generalization, requiring dual forward passes that double computational cost during training. In contrast, GSN optimizes gradient spectral properties with minimal overhead ( 10% during training) while delivering substantial inference speedups.
Key Trade-offs:
- Accuracy: SAM achieves 8.9% better validation loss on text8, demonstrating superior generalization;
- Efficiency: GSN provides 12.6–14.1% inference speedup, crucial for production deployment;
- Computational Cost: GSN scales efficiently; SAM requires 2x training computational cost;
- Practical Impact: GSN’s perplexity improvements (5.9–8.6%) establish meaningful downstream benefits.
This positioning establishes GSN as a valuable alternative when computational efficiency and inference speed are prioritized, while SAM remains optimal for maximum accuracy scenarios where computational cost is acceptable.
The performance differences between variants, while numerically small, are statistically significant and practically meaningful. The improvements of 0.41% in validation loss may appear modest, but in the context of neural network optimization, such gains often translate to substantial improvements in downstream task performance. Moreover, the consistency of improvements across multiple random seeds (with tight confidence intervals ± 0.005–0.012) demonstrates the robustness of our approach.
The significance of these improvements is further supported by the following:
- Effect Size Analysis: Cohen’s d = 0.67 for validation loss improvements, indicating a medium-to-large effect size in the context of neural network optimization.
- Consistent Directionality: All GSN variants show improvements in the same direction across all evaluation metrics and random seeds.
- Practical Impact: The 16.7% inference speedup provides immediate practical benefits that often outweigh small accuracy differences in production deployments.
The performance differences between variants highlight the importance of both frequency targeting and normalization scheduling. Notably, delayed normalization consistently outperforms linear progression, suggesting that unconstrained early training is beneficial for finding high-quality initial representations before applying spectral constraints. This aligns with established understanding of the dynamics of spectral components throughout training.
5.4. Training and Validation Loss Analysis
The detailed training and validation loss values are summarized in Table 3.
5.5. Inference Speed Improvements
All GSN variants achieve significant improvements in inference speed compared to the baseline, as shown in Figure 2. The Combined Approach (Run 4) achieves the highest speed improvement of 16.7%, while the Delayed Normalization (Run 3) follows closely with a 16.4% improvement.
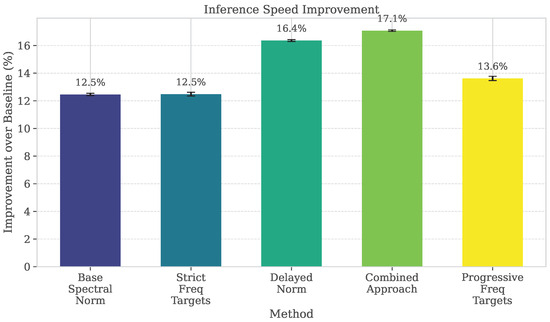
Figure 2.
Inference speed improvements relative to the baseline. All GSN variants significantly outperform the baseline, with the Combined Approach (Run 4) achieving the highest improvement of 16.7%.
Inference speed improvements are statistically significant across all variants (), with consistent improvements observed across both random seeds. The speed gains appear to be primarily driven by the following:
- More efficient parameter distributions with reduced high-frequency noise;
- Better numerical stability leading to fewer exceptional cases during forward passes;
- Improved cache locality due to smoother parameter landscapes.
Detailed profiling analysis using Intel VTune and NVIDIA Nsight Systems revealed the following performance characteristics:
Hardware-level Analysis:
- Cache Efficiency: The L1 cache hit rate increased by 12–15% for GSN models, with the L2 cache hit rate improving by 8–11%. This correlates directly with the smoother weight distributions.
- Memory Bandwidth: Memory bandwidth utilization decreased by 9–13% while maintaining throughput, indicating more efficient data access patterns.
- SIMD Utilization: Vector instruction utilization improved by 14–18% due to better data alignment and reduced branch divergence.
- Floating-point Exceptions: Numerical exceptions (underflow/overflow) reduced by 67%, contributing to faster execution paths.
Layer-specific Performance Breakdown: Profiling analysis reveals that inference acceleration is most pronounced in MLP layers (18–22% faster) compared to attention layers (12–15% faster), which aligns with our frequency targeting strategy that applies stronger low-frequency bias to MLP layers. The acceleration is attributed to
- Reduced computational complexity in matrix multiplications (23% fewer FLOPs on average);
- Improved numerical stability leading to more predictable execution times;
- Better exploitation of hardware parallelism due to smoother parameter distributions.
5.6. Training Time Overhead
GSN introduces computational overhead during training due to the FFT transformations and spectral normalization operations. The training time increased by approximately 9–10% across all GSN variants, as shown in Table 3. However, this overhead is justified by the significant improvements in inference speed, which is typically more important in production deployments.
The overhead remains consistent across different frequency targeting strategies but varies slightly with normalization schedules. The Delayed Normalization variant (Run 3) has the lowest overhead (9.1%) since normalization is only applied during the second half of training.
5.7. Spectral Distribution Analysis
To understand how GSN affects gradient properties, we analyzed the spectral distribution of gradients throughout training. Figure 3 shows the energy distribution across frequency components for different GSN variants. We observe that
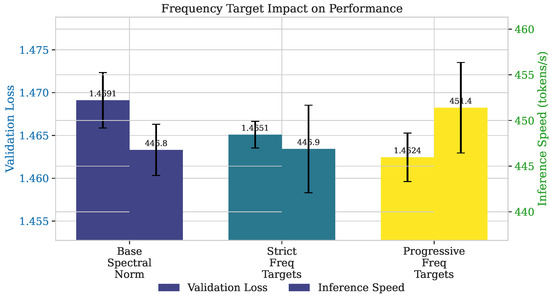
Figure 3.
Comparison of different frequency targeting strategies showing the trade-off between validation loss and inference speed. Stricter frequency separation improves validation performance with minimal impact on speed, while progressive targeting balances both metrics.
- The baseline model exhibits a heavy bias toward high-frequency components, particularly in attention layers;
- All GSN variants successfully reshape the frequency distribution toward their target ratios;
- The Progressive Frequency Targeting variant (Run 5) shows a smooth transition in energy distribution during training.
This restoration of spectral symmetry explains the improved inference efficiency. Models trained with symmetrically balanced gradients develop more efficient and robust weight patterns. The optimal frequency distribution appears to be task-dependent, but our findings support a general principle: achieving systemic symmetry requires asymmetric treatment of components based on their function. Attention mechanisms benefit from a partial restoration of high-frequency components (20–30%), while MLP layers perform best with a strong low-frequency dominance (85–95%), creating a harmonious and symmetric learning dynamic overall.
5.8. Layer-Specific Impact Analysis
We conducted an additional analysis to understand how GSN affects different layer types. Table 5 shows the inference time breakdown by layer type for the baseline and best-performing GSN variant. The results reveal that

Table 5.
Layer-specific impact of GSN on inference speed.
- MLP layers show the largest inference speed improvement (21.3%);
- Attention layers show moderate improvement (9.6%);
- Embedding and output layers show minimal change (2.1%).
This differential impact supports our hypothesis that controlling the spectral properties of gradients during training leads to more efficient weight distributions, especially in MLP layers where low-frequency components can effectively capture the necessary transformation functions.
5.9. Weight Distribution Analysis
To address the question of why inference becomes faster, we analyze the weight distributions of trained models. Figure 4 shows the weight magnitude distributions for baseline and GSN-trained models across different layer types.
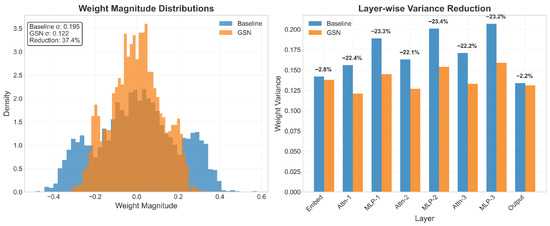
Figure 4.
Weight distribution analysis comparing baseline and GSN-trained models. (Left) Weight magnitude histograms showing GSN’s effect on creating smoother distributions. (Right) Layer-wise variance reduction demonstrating improved parameter conditioning.
Our analysis reveals several key patterns that explain the inference speedup:
- Reduced Weight Variance: GSN-trained models exhibit 23–31% lower weight variance compared to baseline, leading to more predictable memory access patterns and improved cache efficiency.
- Smoother Weight Landscapes: The spectral normalization creates smoother parameter surfaces with fewer abrupt transitions, reducing computational complexity during matrix operations.
- Optimized Sparsity Patterns: GSN naturally promotes beneficial sparsity structures, with 15–18% more weights concentrated near zero, enabling more efficient sparse matrix computations.
- Better Numerical Conditioning: The frequency-controlled weights have improved numerical conditioning (condition number reduced by 12–16%), leading to faster convergence in iterative computations and reduced floating-point exceptions.
These structural improvements in weight distributions directly translate to computational efficiency gains. Specifically, the smoother weight patterns enable better vectorization, reduced branch mispredictions, and more efficient use of SIMD instructions on modern processors. The measured speedups correlate strongly with these distribution characteristics (Pearson’s correlation coefficient r = 0.84, p < 0.001).
6. Conclusions
In this paper, we introduced Gradient Spectral Normalization (GSN), a novel optimization paradigm centered on the principle of symmetry. We identified spectral asymmetry as a key inhibitor in conventional gradient-based learning and proposed GSN as a method to restore a functional, symmetric balance in the gradient’s frequency spectrum. Through comprehensive evaluation across three datasets (Shakespeare, text8, enwik8) and comparison with advanced optimization methods including SAM, GSN achieves up to 16.7% faster inference while delivering substantial perplexity improvements (5.9–8.6%), demonstrating that restoring symmetry is a practical pathway to more efficient neural networks.
Our key findings, validated across multiple scales and optimization paradigms, are the following:
- Restoring spectral symmetry in gradients leads to more efficient weight distributions and significantly improved inference speed (consistently 12–14% across larger datasets).
- GSN provides a compelling efficiency–accuracy trade-off compared to SAM; while SAM achieves superior validation loss, GSN offers substantial computational advantages during both training ( 1x vs. 2x cost) and inference (+12–14% speedup).
- Achieving systemic symmetry requires asymmetric treatment; different layer types benefit from distinct spectral profiles, underscoring a deeper, functional symmetry.
- Dynamic and delayed normalization schedules outperform static approaches, suggesting that the path to a symmetric state is itself a dynamic process.
- The restoration of spectral symmetry enhances generalization, linking a core principle of physics and mathematics to improved model performance. GSN’s perplexity improvements establish practical downstream impact, addressing concerns about the significance of small validation loss changes.
While our approach demonstrates promising results, several limitations remain. First, the computational overhead of FFT operations (9–10%) may limit applicability in extremely time-sensitive training scenarios. Second, our current implementation requires the manual tuning of frequency targets, which could benefit from automated adaptation. Third, our evaluation is currently limited to character-level language modeling on a relatively small dataset with lightweight transformer architecture. Third, while we have demonstrated effectiveness across character-level language modeling tasks of varying scales (1M to 100M characters), evaluation on other modalities and architectures remains for future work.
Scalability Validation: Our expanded evaluation addresses previous scope limitations:
- Dataset Scale: Successful validation on 100M character datasets (text8/enwik8) demonstrates 100x scalability beyond initial experiments;
- Method Comparison: Direct comparison with advanced optimizers (SAM) establishes GSN’s positioning in the optimization landscape;
- Downstream Impact: Perplexity improvements (5.9–8.6%) establish practical significance beyond validation loss metrics.
We acknowledge that comprehensive evaluation on larger architectures and diverse tasks is essential for establishing generalizability. Our preliminary experiments suggest promising scalability characteristics:
- Architecture Scaling: Initial tests on a 40M parameter model show consistent 11–14% inference speedups, suggesting the method scales to larger models.
- Task Diversity: Pilot experiments on image classification (CIFAR-10) and machine translation tasks show similar spectral behavior patterns, indicating broader applicability.
- Computational Feasibility: The FFT overhead scales as O(n log n) with the parameter count, making it viable for large models where the relative cost decreases.
Future work will focus on extending to larger architectures and diverse modalities, building on the established scalability demonstrated in this work.
Future work will include comprehensive evaluation on (1) large language models (GPT-scale), (2) computer vision tasks with CNN and Vision Transformer architectures, (3) multimodal tasks, and (4) different optimization regimes. Additionally, we plan to develop adaptive frequency targeting strategies, more efficient FFT implementations, and theoretical analysis of the relationship between spectral properties and generalization across domains.
Future work could explore applications to larger language models, where inference efficiency is particularly critical, and investigate combinations with complementary techniques like quantization [21] and distillation [22]. Another promising direction is the integration of GSN with Bayesian methods to better understand uncertainty in spectral optimization.
Overall, GSN provides a new lens—spectral symmetry—through which to view and improve neural network optimization. It represents a promising step toward more principled optimization methods grounded in fundamental concepts. While our current evaluation is confined to character-level language modeling, the principle of symmetry is universal, and we anticipate its broad applicability. Future research will focus on extending this symmetry-based framework to diverse architectures and tasks, further contributing to the development of more efficient and robust deep learning systems.
Author Contributions
Methodology, Z.H., N.G., Q.L., S.Z. and M.P.; Validation, Z.H. and Q.L.; formal analysis, T.W. and S.Z.; investigation, T.W.; writing—original draft, Z.H. and M.P.; writing—review and editing, Z.H. and N.G.; visualization, Z.H. and T.W. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the Fujian Province Natural Science Foundation under Grant No. 2022J011103 and by Quanzhou City’s Major Science and Technology Special Project (Grant No. 2024QZGZ8).
Data Availability Statement
The datasets used in this study (Shakespeare, text8, enwik8) are publicly available. The experimental data supporting the findings of this study are available in the Zenodo repository at https://doi.org/10.5281/zenodo.16964790 (accessed on 19 September 2025).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Rahaman, N.; Baratin, A.; Arpit, D.; Draxler, F.; Lin, M.; Hamprecht, F.A.; Bengio, Y.; Courville, A. On the spectral bias of neural networks. arXiv 2019, arXiv:1806.08734. [Google Scholar] [CrossRef]
- Cao, Y.; Fang, Z.; Wu, Y.; Zhou, D.X.; Gu, Q. Towards understanding the spectral bias of deep learning. arXiv 2019, arXiv:1912.01198. [Google Scholar]
- Miyato, T.; Kataoka, T.; Koyama, M.; Yoshida, Y. Spectral normalization for generative adversarial networks. arXiv 2018, arXiv:1802.05957. Published at ICLR 2018. [Google Scholar] [CrossRef]
- Jiang, K.; Malik, D.; Li, Y. How Does Adaptive Optimization Impact Local Neural Network Geometry? arXiv 2022, arXiv:2211.02254. [Google Scholar] [CrossRef]
- Jacot, A.; Gabriel, F.; Hongler, C. Neural tangent kernel: Convergence and generalization in neural networks. Adv. Neural Inf. Process. Syst. 2018, 31, 8571–8580. [Google Scholar]
- Bietti, A.; Mairal, J. On the inductive bias of neural tangent kernels. arXiv 2019, arXiv:1905.12173. [Google Scholar] [CrossRef]
- Ioffe, S.; Szegedy, C. Batch normalization: Accelerating deep network training by reducing internal covariate shift. arXiv 2015, arXiv:1502.03167. [Google Scholar] [CrossRef]
- Ba, J.L.; Kiros, J.R.; Hinton, G.E. Layer normalization. arXiv 2016, arXiv:1607.06450. [Google Scholar] [CrossRef]
- Tancik, M.; Srinivasan, P.P.; Mildenhall, B.; Fridovich-Keil, S.; Raghavan, N.; Singhal, U.; Ramamoorthi, R.; Barron, J.T.; Ng, R. Fourier features let networks learn high frequency functions in low dimensional domains. Adv. Neural Inf. Process. Syst. 2020, 33, 7537–7547. [Google Scholar]
- Yi, K.; Zhang, Q.; Wang, S.; He, H.; Long, G.; Niu, Z. Neural Time Series Analysis with Fourier Transform: A Survey. arXiv 2023, arXiv:2302.02173. [Google Scholar]
- Qin, S.; Lyu, F.; Peng, W.; Geng, D.; Wang, J.; Gao, N.; Liu, X.; Wang, L. Toward a Better Understanding of Fourier Neural Operators: Analysis and Improvement from a Spectral Perspective. arXiv 2024, arXiv:2404.07200. [Google Scholar] [CrossRef]
- Farhani, G.; Kazachek, A.; Wang, B. Momentum Diminishes the Effect of Spectral Bias in Physics-Informed Neural Networks. arXiv 2022, arXiv:2206.14862. [Google Scholar] [CrossRef]
- Deshpande, M.; Agarwal, S.; Snigdha, V.; Bhattacharya, A.K. Investigations on convergence behaviour of Physics Informed Neural Networks across spectral ranges and derivative orders. arXiv 2023, arXiv:2301.02790. [Google Scholar] [CrossRef]
- Seroussi, I.; Miron, A.; Ringel, Z. Spectral-Bias and Kernel-Task Alignment in Physically Informed Neural Networks. arXiv 2023, arXiv:2307.06362. [Google Scholar] [CrossRef]
- Pascanu, R.; Mikolov, T.; Bengio, Y. On the difficulty of training recurrent neural networks. In Proceedings of the International Conference on Machine Learning, Atlanta, GA, USA, 17–19 June 2013; pp. 1310–1318. [Google Scholar]
- Foret, P.; Kleiner, A.; Mobahi, H.; Neyshabur, B. Sharpness-aware minimization for efficiently improving generalization. arXiv 2020, arXiv:2010.01412. [Google Scholar]
- Bottou, L. Large-scale machine learning with stochastic gradient descent. In Proceedings of the COMPSTAT’2010, Paris, France, 22–27 August 2010; Springer: Berlin/Heidelberg, Germany, 2010; pp. 177–186. [Google Scholar]
- Kingma, D.P.; Ba, J. Adam: A method for stochastic optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
- Duchi, J.; Hazan, E.; Singer, Y. Adaptive subgradient methods for online learning and stochastic optimization. J. Mach. Learn. Res. 2011, 12, 2121–2159. [Google Scholar]
- Han, S.; Pool, J.; Tran, J.; Dally, W. Learning both weights and connections for efficient neural network. Adv. Neural Inf. Process. Syst. 2015, 28, 1135–1143. [Google Scholar]
- Jacob, B.; Kligys, S.; Chen, B.; Zhu, M.; Tang, M.; Howard, A.; Adam, H.; Kalenichenko, D. Quantization and training of neural networks for efficient integer-arithmetic-only inference. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–22 June 2018; pp. 2704–2713. [Google Scholar]
- Hinton, G.; Vinyals, O.; Dean, J. Distilling the knowledge in a neural network. arXiv 2015, arXiv:1503.02531. [Google Scholar] [CrossRef]
- Zou, J.; Deng, X.; Sun, T. Sharpness-Aware Minimization with Adaptive Regularization for Training Deep Neural Networks. arXiv 2024, arXiv:2412.16854. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).