Terminal Forensics in Mobile Botnet Command and Control Detection Using a Novel Complex Picture Fuzzy CODAS Algorithm

Abstract

Terminal forensics in large mobile networks is a vital activity for identifying compromised devices and analyzing malicious actions. In contrast, the study described here begins with the domain of terminal forensics as the primary focus, rather than the threat itself. This paper proposes a new multi-criteria decision-making (MCDM) model that integrates complex picture fuzzy sets (CPFS) with the combinative distance-based assessment (CODAS), referred to throughout as complex picture fuzzy CODAS (CPF-CODAS). The aim is to assist in forensic analysis for detecting mobile botnet command and control (C&C) systems. The CPF-CODAS model accounts for the uncertainty, hesitation, and complex numerical values involved in expert decision-making, using degrees of membership as positive, neutral, and negative values. An illustrative forensic case study is constructed where three mobile devices are evaluated by three cybersecurity professionals based on six key parameters related to botnet activity. The results demonstrate that the model can effectively distinguish suspicious devices and support the use of the CPF-CODAS approach in terminal forensics of mobile networks. The robustness, symmetry, and advantages of this model over existing MCDM methods are confirmed through sensitivity and comparison analyses. In conclusion, this paper introduces a novel probabilistic decision-support tool that digital forensic specialists can incorporate into their workflow to proactively identify and prevent actions of mobile botnet C&C servers.

1. Introduction

Terminal forensics is concerned with the detection, analysis, and scrutiny of rogue activities at the terminal transfer stage, that is, the origin station where botnet activities are presumably initiated and where devices are mostly exposed, making it a vital method of mobile botnet C&C detection [1]. The mobile botnet attack has emerged as a significant issue in the current digital world of technology, whereby mobile and IoT devices continue to increase in number. Such attacks may include various networks of hacked gadgets that are managed remotely through C&C servers by organized cybercriminals to conduct distributed denial of service (DDoS) attacks or data theft, or ransomware. In recent years, the increased sophistication of mobile botnets, including the use of dynamic C&C channels and encryption to render them invisible to detection efforts, has been noted [2]. The purpose of this forensic investigation is to trace the illegal orders typically relayed via C&C infrastructures, pursue electronic evidence, and comprehend the attack routes to prevent the invasion from spreading to other logged-on networks. Several researchers have proposed terminal-level forensic models that suit heterogeneous mobile settings, enabling the real-time identification of C&C patterns [3].

It is subject to specific issues, given that mobile terminals are heterogeneous and characterized by limited computing capabilities, which presents a particular challenge to the process of classification and detection of command-and-control patterns at terminal devices. Forensics in terminals ought to employ intelligent decision-making systems to process large amounts of inconclusive, uncertain, and erroneous information. Innovative models comprising fuzzy logic, as mentioned in [4], are necessary in exploiting botnet behavior in low-constrained mobile nodes. The principle of symmetry is applied in digital forensics, particularly in cases where cause and effect are connected, and user or system actions are reflected in the produced digital artifact. Such mirrors allow analysts to recreate the occurrence by pondering the proportional relationship between illicit activities and their computerized recourses, especially in terminal forensics [5]. In the given case, the MCDM approaches align with the principle of symmetry, i.e., the equal correspondence between evaluation outcomes and decision criteria, such that all alternatives are treated equally and in an opposite manner, which can be viewed as an efficient analysis toolbox. Since MCDM is a broader area of analysis compared to terminal forensics, it provides a systematic way of assessing a wide range of detection variables, which theoretically makes it fit into more complex cybersecurity investigations. MCDM enables cybersecurity analysts to focus on multiple factors, including network traffic, CPU anomalies, memory activity, and machine-to-machine communications, across various terminal devices. Consequently, terminal forensics will be able to switch to a refined version characterized by a complex, criteria-based decision support model. It has been demonstrated that MCDM integration with sophisticated forensics enhances the accuracy of detecting botnets within mobile ecosystems [6].

The application of MCDM methods to the field of terminal forensics must, however, contend with uncertainty and ambiguity, which are inherent features of expert judgment and system performance. The traditional theory of fuzzy set (FS) formulated by Zadeh [7] addressed the problem of partial truth by assigning elements a membership degree (MD) within a [0, 1] interval. Still, it was unable to address the issue of indeterminacy. To deal with this, Atanassov [8] introduced intuitionistic fuzzy sets (IFS) that included non-membership degree (NMD) and MD. After that, Yager [9] introduced Pythagorean fuzzy sets (PyFS) that give more expressive capability, as the squared sum of MD and NMD may have a value of $1$. This development was followed by Yager’s [10] q-rung orthopair fuzzy sets (q-ROFS), which aim to be more flexible in complicated situations. To improve the modeling of acceptance, neutrality, and rejection, Cuong [11] proposed picture fuzzy sets (PFS), which implement abstinence degree (AD). However, PFS was also unable to capture phase information or multi-dimensional uncertainties. Recent extensions include risk-based fuzzy sets [12] and q-ROFS [13], which are effective for risk aggregation and flexible membership modeling. However, these models lack the four-way (positive, neutral, negative, refusal) structure and complex phases of CPFS, which provide richer uncertainty representation for adversarial environments. Consequently, a new form, called CPFS [14], later emerged, which is the focus of this paper.

The study will use the CPF-CODAS method because data has become more complex in mobile botnet detection. The CODAS algorithm, as described by Ghorabaee et al. [15], utilizes Euclidean and Taxicab distances to rank alternatives based on their proximity to the negative-ideal solution. This feature makes CODAS very suitable for decision scenarios where the certainty of information and multi-dimensional data are key characteristics in terminal forensics for C&C detection. An even more involving CPFS in this framework significantly enhances this representation by allowing it to be expressed in terms of expert uncertainty, encompassing MD, AD, and NMD, all of which are represented as a complex number consisting of a real and imaginary part. The real part represents the level of certainty or the strength of the expert judgment, whereas the imaginary part indicates the indecisiveness or psychological bias of the given judgment. This two-dimensional basis of the model allows a more detailed representation of undecided or contradicting information, and hence the CPF-CODAS approach is very powerful in terms of requiring less simplification/generalization in complex domains, like mobile botnet terminal forensics. It enables the expressive and realistic modeling of experts’ opinions concerning cyber-forensic investigations. The capacity to deal with complex decision-making environments, and the ability to capture nuanced specialist judgments, which is best suited to our scenario of application, is incorporated into CPFS.

To demonstrate the practicality of the CPF-CODAS method, this study will conduct a thorough comparison and sensitivity testing of other well-known approaches to MCDM, including WASPAS [16], COCOSO [17], TOPSIS [18], and EDAS [19]. More than merely indicating the superiority of CPF-CODAS in handling fuzzy uncertainties, these comparisons also highlight the method’s versatility in addressing variations across a broad range of situations. A comprehensive algorithmic blueprint and trial flow are represented in this paper, including, but not limited to, criteria selection, CPF amalgamation, distance-based ranking, and sensitivity analysis, which comprise an integrated decision-support blueprint in terminal forensics.

To conclude this paper, it is proposed that a new framework utilizing CPF-CODAS for analyzing terminal behavior introduces the capability of detecting command and control in mobile botnets. This study demonstrates the application of an effective MCDM method suitable for cybersecurity, as it combines advanced fuzzy logic to provide a robust and systematic approach to digital forensics. The proposed method enhances detection levels, models uncertainty, and supports sound decision-making by cyber-defense practitioners working in terminal-rich environments.

1.1. Research Gap and Motivations

Although the threat of mobile botnets has been increasing and their presence is currently of high concern for international cybersecurity due to their significant impact on the terminal level, the effectiveness of current detection and forensic tools remains limited in identifying C&C activity at the terminal level [20]. Most existing strategies rely on predefined behavioral rules, signature-based techniques, or simple statistical models and fail to operate effectively against dynamic, evolving, and stealthy botnet infrastructures. Additionally, conventional forensic analysis tools do not provide a framework to integrate various ambiguous, subjective, and intersecting signs necessary for analyzing compromised mobile terminals. Although new research has been conducted on MCDM techniques for security assessments, these tools are generally designed for crisp, fuzzy, and intuitionistic fuzzy environments, which cannot fully capture the cognitive state of humans as observed by expert witnesses who are not restricted to security-related matters.

The gap is met through a new integration of CPFSs and the CODAS method, which has not been previously examined in the domain of cybersecurity forensics. Uncertainty, contradiction, and hesitation can be modeled simultaneously in both the amplitude and phase components by the combination of CPF-CODAS, providing a more expressive and realistic framework for decision-making than conventional models. Such methodological contribution to mobile botnet terminal detection is particularly appropriate, as expert evaluations tend to be vague, complex, and context-dependent. Therefore, it is the power of introducing a new operator and influencing a new sphere of science, which is viewed as new, or rather new in this advanced fuzzy paradigm adjusted to an extremely sensitive and poorly explored field of application, thus closing the gap between theory and practice.

Moreover, the CODAS method, despite its effectiveness in distance-based ranking, has not been explored in the context of CPFS applications. This complex fuzzy model allows representing positive, neutral, and negative evaluations while working with complex-valued logic simultaneously. This creates a significant gap in research; specifically, there is no efficient MCDM model capable of combining high-order fuzzy logic with a ranking mechanism robust enough to support multi-perspective forensic assessments when uncertainty is present. The choice of the CODAS method used in this study was the result of its higher potential to distinguish alternatives concerning both the Euclidean and Taxicab distances, which enables the CODAS method to be more sensitive to minute changes in the complexity indicator than other MCDM techniques, such as either TOPSIS or VIKOR. In contrast to outranking processes, which are based on defining thresholds, CODAS offers a straightforward and transparent ranking process, particularly beneficial when there is uncertainty in the evidence and conflicting pieces of evidence. Also, CODAS does not mandate the normalization of the decision matrices into benefit/cost division; thus, it can be used in cybersecurity cases where the characteristics of the criteria cannot be well-defined. Besides these gaps, based on the strengths of the two concepts, this paper advances an idea to unify the effective elements of the two approaches: CODAS: its superior discrimination ability using dual-distance assessment, resiliency under conflicting evidence, and in-dependence of normalization; CPFS: its ability to jointly model two properties of MD, AD, and NMD (in both amplitude and phase space), which allows even rich description of expert uncertainty and contradiction, in a hybrid decision-assistance framework. Its goal is to help cybersecurity analysts and forensic specialists identify the existence of a mobile botnet C&C server more effectively, through a more transparent and mathematically sound framework for modeling vague, inconsistent, and contradictory evidence. This is anticipated to enhance the robustness of decision-making, forensic awareness at the terminal level, and enable more proactive cyber defense approaches.

1.2. Objectives and Contributions of the Study

To this end, the goal of this study is to develop a robust and intelligent decision-making solution for terminal forensics in detecting mobile botnet C&C servers that incorporates the CODAS approach with CPFS. This hybridization deals with the high degrees of uncertainty, wavering, and inconsistency that tend to occur during expert evaluations in mobile digital forensic investigations. The suggested method is confirmed by a case study based on real-world forensic circumstances that are practical and applicable.

Primarily, these are the objectives of the study:

• Specify relevant forensic guidelines to assess mobile terminals that may be used to perform botnet C&C operations, and the forensic guidelines need to be operationalized and used in the methodology section.
• Advance CPF-CODAS by augmenting the conventional CODAS methodology with the expressive potential of CPFS to work with more sensitivity and precision in decision-making.
• Prove the applicability of the proposed method using a detailed case study that will include several decision-makers, various alternatives, and explicitly stated criteria, which can be considered warranted in the real investigative conditions.
• Demonstrate model reliability and robustness through a sensitivity analysis of different parameter settings, indicative of the stability of the method when run on various settings.
• Compare CPF-CODAS to well-known MCDM methods (e.g., WASPAS, COCOSO, TOPSIS, and EDAS) and validate the relative merits of CPF-CODAS.

Central findings of the research include the following:

• Novel hybrid MCDM framework: First CPFS incorporation into CODAS applied to forensic determination problem allows better characterization of uncertainty in fields of expertise indicators.
• Application to mobile botnet terminal forensics: Builds on methodological development in this underdeveloped field, with the proposed model applicable to frameworks developed elsewhere such as SING, in identifying terminal-level botnet C&C activity.
• Comprehensive evaluation and validation: Entail a case-based application of the model, sensitivity analysis, and comparison of its performance with that of other methods of MCDM to ascertain empirical data about the effectiveness of the model.
• Enhanced decision-support capability: Provides a scalable and decipherable device addressed to the cybersecurity expert and forensics investigator, heightening the resolution and confidence of mobile botnets identification.

1.3. Structure of the Study

The remaining part of the paper will progress as follows: Section 2 will review the literature of the corresponding struggles regarding fuzzy MCDM; Section 3 will address the fundamentals of CPFS; Section 4 will elaborate on the methodology of CPF CODAS; Section 5 will provide a case study together with a discussion of its outcome. Comparative evaluation, sensitivity analysis, and management implications are provided in Section 6. Lastly, Section 7 provides the conclusion and the proposal for future studies.

2. Literature Review

In this section, studies will be discussed on earlier research in terminal forensics, mobile botnet command and control detection, models of decision-making, and the progress of fuzzy set theories.

2.1. Terminal Forensics in Mobile Botnet Command and Control Detection

Terminal forensics is also crucial in detecting and retrieving malicious activities within mobile botnet networks, particularly the C&C mechanisms that coordinate attacks. As the number of IoT devices and mobile terminals increases, these systems have become more effective in creating botnets due to their low security and high connectivity. Recently, Ma et al. [21] emphasized lightweight botnet detection models applied to terminal nodes to analyze IoT-based mobile environments in real-time for forensic purposes. Similarly, Drabent et al. [22] explained how botnet C&C systems operate with Android OS, where terminals typically execute commands via HTTP, allowing ransomware to modify commands sent to remote servers without authorization. Mirai, a common botnet used in many attacks, transmits remote commands to terminals using Telnet, as noted by Gelgi et al. [23]. This makes analyzing communication at the terminal level essential for tracing C&C operations. In more complex networks, the suggestions by Qian et al. [24] on graph partitioning, which enable the monitoring of IoT terminal activity and the generation of automated forensic reports, help reveal hidden control structures. Additionally, Shin et al. [25] demonstrated how analyzing logs and interactions of heterogeneous terminals with digital forensic tools can help detect botnet-controlled attacks and unusual intrusion patterns. Overall, these studies underscore the importance of terminal forensics as a vital layer for identifying and examining the mobile botnet C&C infrastructure, providing detailed insights to counter botnets at their source. Nonetheless, these works manage to address detection mechanisms and forensic logging; however, limited studies integrate decision-making frameworks into the forensic evaluation process. As an example, Priya and Gupta [26] used fuzzy-based models to rank forensics indicators during the identification of mobile botnets, indicating the applicability of subjective expert opinion. In a similar way, Allifah and Zualkernan [27] applied multi-criteria methods to the evaluation of IoT compromised nodes attack paths with a focus on structured assessment as part of C&C detection. Such investigations affirm the necessity of incorporating intelligent models of decision-making, such as MCDM methods, in terminal forensics to facilitate robust and consistent searches in the face of ambiguous or incomplete data.

2.2. CODAS MCDM Method

Ghorabaee et al. [15] were the first to introduce the fuzzy CODAS method formally, and they were combining fuzzy numbers to edit the classical CODAS model to represent the particularities of their application domain; in this case, it handling linguistic and imprecise information. This background research demonstrated that when fuzzy logic is deployed within the CODAS structure, its flexibility and applicability in real-world decision-making problems improve. The CODAS approach has become one of the most popular methods in recent years due to its efficiency as a MCDM technique. It is popular partly because it can combine Euclidean and Taxicab distances to produce more accurate decisions. One notable application involves using the Intuitionistic Fuzzy approach with CODAS to estimate the location of an authorized dismantling center (ADC) in Istanbul [28]. Their research showed that, under uncertainty, CODAS works better when combined with IFS, making it more reliable. Similarly, a broader MCDM analysis of economic datasets examined how normalization parameters and data types influence results, concluding that CODAS is a strong alternative to fuzzy approaches [29]. Another multi-model MCDM solution was suggested by [30], who used CRITIC, EDAS, CODAS, and CoCoSo to select among renewable energy sources in India, highlighting CODAS’s adaptability and stability. It proved effective even in environmental and policy contexts, as demonstrated by Lukic [31], who applied AHP-CODAS to assess climate change performance across G7 countries, showing its potential as a decision-making tool for geopolitical issues.

Additionally, Singh [32] used a fuzzy CODAS method to evaluate industrial performance parameters, emphasizing its strong evaluation capabilities compared to traditional MCDM approaches. Later developments were interval-valued intuitionistic fuzzy CODAS [33], Pythagorean fuzzy CODAS [34], and Fermatean fuzzy CODAS [35] models, which permit more flexible representation of uncertainty in a variety of applications to supply chain management, healthcare evaluation, and cyber-physical system selection. Additionally, Gul and Aydogdu [36] proposed new definitions of entropy measures. They applied them in a revised CODAS procedure within the picture fuzzy setting, marking an important step toward addressing uncertainty and enhancing decision accuracy. Conversely, the current research incorporates the CODAS framework into a cybersecurity complex to facilitate forensic assessment and identification of botnet command and control attacks on mobile devices, an application domain not yet covered in the literature. Additionally, it provides specific forensic evaluation criteria and high-fidelity detection parameters for a large-scale mobile network. Nevertheless, although there is literature covering CODAS applications in IoT-based terminal points (a specialized domain of end-point devices of handlers) that used exclusively the method proposed, they are relatively simple/niche compared to the more complex scenarios of mobile devices (especially smartphones, and tablets) pertinent in the current research [37]. As an example, Nguyen et al. [38] applied a spherical fuzzy CODAS model of sustainability assessment in the green supply chains context, demonstrating its application in a high-ambiguity environment. Overall, these studies confirm the versatility of CODAS across various fields and its usefulness for making decisions involving complex criteria and uncertainty.

3. Preliminaries and Theoretical Background

The FS was introduced by Zadeh [7], and it is a mathematical system for working with uncertainty. However, in an ambiguous context, it functions on an MD and not on an NMD or any ambiguity in an ambiguous situation. To solve this kind of limitation, Atanassov [8] developed a new technology, commonly known as IFS. Cuong [11] designed the PFS in response to more complicated situations of AD and RD. Very recently, [14] suggested a CPFS that has real and imaginary parties of MD, AD, NMD, and refusal degree (RD).

Definition 1

[11]. Consider a fixed universe$X$; then, a PFS is defined by $\mathcal{S}=\{\mathfrak{u}\in X, (\mathfrak{m}\left(\mathfrak{u}\right),\mathcal{a}\left(\mathfrak{u}\right),\mathfrak{n}\left(\mathfrak{u}\right)\left)\right\}$ where $\mathfrak{m}\left(\mathfrak{u}\right)\in [0, 1]$ represents MD, $\mathcal{a}\left(\mathfrak{u}\right)\in [0, 1]$ represents AD, and $\mathfrak{n}\left(\mathfrak{u}\right)\in [0, 1]$ represents NMD.

These degrees satisfy the following Equation (1):

$$0 \le \mathfrak{m}\left(\mathfrak{u}\right)+\mathcal{a}\left(\mathfrak{u}\right)+\mathfrak{n}\left(\mathfrak{u}\right)\le 1$$

(1)

Furthermore, the RD is defined as follows for every PFS $\mathcal{S}$:

$$\pi \left(\mathfrak{u}\right)=1-\mathfrak{m}\left(\mathfrak{u}\right)-\mathcal{a}\left(\mathfrak{u}\right)-\mathfrak{n}\left(\mathfrak{u}\right)$$

Definition 2

[14]. A CPFS is elaborated through:

$$\mathcal{S}=\left\{\mathfrak{u}\in X \left({\mathfrak{m}}^{\mathfrak{r}}\right(\mathfrak{u}),{\mathfrak{m}}^{\mathfrak{i}}(\mathfrak{u}\left)\right),\left({\mathcal{a}}^{\mathfrak{r}}\right(\mathfrak{u}),{\mathcal{a}}^{\mathfrak{i}}(\mathfrak{u}\left)\right),\left({\mathfrak{n}}^{\mathfrak{r}}\right(\mathfrak{u}),{\mathfrak{n}}^{\mathfrak{i}}(\mathfrak{u}\left)\right)\right\}$$

with the rule that is:

$$0 \le {\mathfrak{m}}^{\mathfrak{r}}\left(\mathfrak{u}\right)+{\mathcal{a}}^{\mathfrak{r}}\left(\mathfrak{u}\right)+{\mathfrak{n}}^{\mathfrak{r}}\left(\mathfrak{u}\right)\le 1$$

(2)

$$0 \le {\mathfrak{m}}^{\mathfrak{i}}\left(\mathfrak{u}\right)+{\mathcal{a}}^{\mathfrak{i}}\left(\mathfrak{u}\right)+{\mathfrak{n}}^{\mathfrak{i}}\left(\mathfrak{u}\right)\le 1$$

(3)

where$\left({\mathfrak{m}}^{\mathfrak{r}}\right(\mathfrak{u}),{\mathfrak{m}}^{\mathfrak{i}}(\mathfrak{u}\left)\right)\in [0, 1]$represents MD,$( {\mathcal{a}}^{\mathfrak{r}}(\mathfrak{u}),{\mathcal{a}}^{\mathfrak{i}}(\mathfrak{u}\left)\right)\in [0, 1]$represents AD, and$( {\mathfrak{n}}^{\mathfrak{r}}(\mathfrak{u}),{\mathfrak{n}}^{\mathfrak{i}}(\mathfrak{u}\left)\right)\in [0, 1]$represents NMD. The pair$F=\left(( {\mathfrak{m}}^{\mathfrak{r}}(\mathfrak{u}),{\mathfrak{m}}^{\mathfrak{i}}(\mathfrak{u}\left)\right),\left({\mathcal{a}}^{\mathfrak{r}}\right(\mathfrak{u}),{\mathcal{a}}^{\mathfrak{i}}(\mathfrak{u}\left)\right),\left({\mathfrak{n}}^{\mathfrak{r}}\right(\mathfrak{u}),{\mathfrak{n}}^{\mathfrak{i}}(\mathfrak{u}\left)\right)\right)$express a CPFV. Furthermore, the RD is defined as follows for every CPFS$\mathcal{S}$:

$$\pi \left(\mathfrak{u}\right)=1-{\mathfrak{m}}^{\mathfrak{r}}\left(\mathfrak{u}\right)-{\mathcal{a}}^{\mathfrak{r}}\left(\mathfrak{u}\right)-{\mathfrak{n}}^{\mathfrak{r}}\left(\mathfrak{u}\right)$$

$$\pi \left(\mathfrak{u}\right)=1-{\mathfrak{m}}^{\mathfrak{i}}\left(\mathfrak{u}\right)-{\mathcal{a}}^{\mathfrak{i}}\left(\mathfrak{u}\right)-{\mathfrak{n}}^{\mathfrak{i}}\left(\mathfrak{u}\right).$$

Definition 3

[14]. Let${\mathcal{S}}_i=\left(\left({\mathfrak{m}}_i^{\mathfrak{r}}\right(\mathfrak{u}),{{\mathfrak{m}}_i}^{\mathfrak{i}}(\mathfrak{u}\left)\right),\left({\mathcal{a}}_i^{\mathfrak{r}}\right(\mathfrak{u}),{\mathcal{a}}_i^{\mathfrak{i}}(\mathfrak{u}\left)\right),\left({\mathfrak{n}}_i^{\mathfrak{r}}\right(\mathfrak{u}),{\mathfrak{n}}_i^{\mathfrak{i}}(\mathfrak{u}\left)\right)\right)$ and${\mathcal{S}}_j=\left(\left({\mathfrak{m}}_j^{\mathfrak{r}}\right(\mathfrak{u}),{{\mathfrak{m}}_j}^{\mathfrak{i}}(\mathfrak{u}\left)\right),\left({\mathcal{a}}_j^{\mathfrak{r}}\right(\mathfrak{u}),{\mathcal{a}}_j^{\mathfrak{i}}(\mathfrak{u}\left)\right),\left({\mathfrak{n}}_j^{\mathfrak{r}}\right(\mathfrak{u}),{\mathfrak{n}}_j^{\mathfrak{i}}(\mathfrak{u}\left)\right)\right)$ be two CPFVs where

• The subscript$i$and$j$refer to two different CPFVs,
• The superscript$\mathfrak{r}$denotes the real part,
• The superscript$\mathfrak{i}$denotes the imaginary part,
• $\lambda >0$is a scalar constant,

then the following operations are defined:

$${\mathcal{S}}_i\oplus {\mathcal{S}}_j=\left(\begin{array}{c}\left(\begin{array}{c}({\mathfrak{m}}_i^{\mathfrak{r}}\left(\mathfrak{u}\right),{\mathfrak{m}}_i^{\mathfrak{i}}\left(\mathfrak{u}\right))+({\mathfrak{m}}_j^{\mathfrak{r}}\left(\mathfrak{u}\right),{\mathfrak{m}}_j^{\mathfrak{i}}\left(\mathfrak{u}\right))\\ -({\mathfrak{m}}_i^{\mathfrak{r}}\left(\mathfrak{u}\right),{\mathfrak{m}}_i^{\mathfrak{i}}\left(\mathfrak{u}\right))·({\mathfrak{m}}_j^{\mathfrak{r}}\left(\mathfrak{u}\right),{\mathfrak{m}}_j^{\mathfrak{i}}\left(\mathfrak{u}\right))\end{array}\right),\\ \left(({\mathcal{a}}_i^{\mathfrak{r}}\left(\mathfrak{u}\right),{\mathcal{a}}_i^{\mathfrak{i}}\left(\mathfrak{u}\right))·({\mathcal{a}}_j^{\mathfrak{r}}\left(\mathfrak{u}\right),{\mathcal{a}}_j^{\mathfrak{i}}\left(\mathfrak{u}\right))\right),\\ \left(({\mathfrak{n}}_i^{\mathfrak{r}}\left(\mathfrak{u}\right),{\mathfrak{n}}_i^{\mathfrak{i}}\left(\mathfrak{u}\right))·({\mathfrak{n}}_j^{\mathfrak{r}}\left(\mathfrak{u}\right),{\mathfrak{n}}_j^{\mathfrak{i}}\left(\mathfrak{u}\right))\right)\end{array}\right)$$

(4)

$${\mathcal{S}}_i\otimes {\mathcal{S}}_j=\left(\begin{array}{c}\left(({\mathfrak{m}}_i^{\mathfrak{r}}\left(\mathfrak{u}\right),{\mathfrak{m}}_i^{\mathfrak{i}}\left(\mathfrak{u}\right))·({\mathfrak{m}}_j^{\mathfrak{r}}\left(\mathfrak{u}\right),{\mathfrak{m}}_j^{\mathfrak{i}}\left(\mathfrak{u}\right))\right),\\ \left(\begin{array}{c}({\mathcal{a}}_i^{\mathfrak{r}}\left(\mathfrak{u}\right),{\mathcal{a}}_i^{\mathfrak{i}}\left(\mathfrak{u}\right))+({\mathcal{a}}_j^{\mathfrak{r}}\left(\mathfrak{u}\right),{\mathcal{a}}_j^{\mathfrak{i}}\left(\mathfrak{u}\right))\\ -({\mathcal{a}}_i^{\mathfrak{r}}\left(\mathfrak{u}\right),{\mathcal{a}}_i^{\mathfrak{i}}\left(\mathfrak{u}\right))·({\mathcal{a}}_j^{\mathfrak{r}}\left(\mathfrak{u}\right),{\mathcal{a}}_j^{\mathfrak{i}}\left(\mathfrak{u}\right))\end{array}\right),\\ \left(\begin{array}{c}({\mathfrak{n}}_i^{\mathfrak{r}}\left(\mathfrak{u}\right),{\mathfrak{n}}_i^{\mathfrak{i}}\left(\mathfrak{u}\right))+({\mathfrak{n}}_j^{\mathfrak{r}}\left(\mathfrak{u}\right),{\mathfrak{n}}_j^{\mathfrak{i}}\left(\mathfrak{u}\right))\\ -({\mathfrak{n}}_i^{\mathfrak{r}}\left(\mathfrak{u}\right),{\mathfrak{n}}_i^{\mathfrak{i}}\left(\mathfrak{u}\right))·({\mathfrak{n}}_j^{\mathfrak{r}}\left(\mathfrak{u}\right),{\mathfrak{n}}_j^{\mathfrak{i}}\left(\mathfrak{u}\right))\end{array}\right)\end{array}\right)$$

(5)

$$\lambda ·{\mathcal{S}}_i=\left(\begin{array}{c}1-{\left(1-\left({\mathfrak{m}}_i^{\mathfrak{r}}\left(\mathfrak{u}\right),{\mathfrak{m}}_i^{\mathfrak{i}}\left(\mathfrak{u}\right)\right)\right)}^{\lambda },\\ {\left({\mathcal{a}}_i^{\mathfrak{r}}\left(\mathfrak{u}\right),{\mathcal{a}}_i^{\mathfrak{i}}\left(\mathfrak{u}\right)\right)}^{\lambda },\\ {\left({\mathfrak{n}}_i^{\mathfrak{r}}\left(\mathfrak{u}\right),{\mathfrak{n}}_i^{\mathfrak{i}}\left(\mathfrak{u}\right)\right)}^{\lambda }\end{array}\right)$$

(6)

$${\mathcal{S}}_i^{\lambda }=\left(\begin{array}{c}{\left({\mathfrak{m}}_i^{\mathfrak{r}}\left(\mathfrak{u}\right),{\mathfrak{m}}_i^{\mathfrak{i}}\left(\mathfrak{u}\right)\right)}^{\lambda },\\ 1-{\left(1-({\mathcal{a}}_i^{\mathfrak{r}}\left(\mathfrak{u}\right),{\mathcal{a}}_i^{\mathfrak{i}}\left(\mathfrak{u}\right))\right)}^{\lambda },\\ 1-{\left(1-({\mathfrak{n}}_i^{\mathfrak{r}}\left(\mathfrak{u}\right),{\mathfrak{n}}_i^{\mathfrak{i}}\left(\mathfrak{u}\right))\right)}^{\lambda } \end{array}\right)$$

(7)

$${\mathcal{S}}_i^c=\left(\begin{array}{c}({\mathfrak{n}}_i^{\mathfrak{r}}\left(\mathfrak{u}\right),{\mathfrak{n}}_i^{\mathfrak{i}}\left(\mathfrak{u}\right)),\\ ({\mathcal{a}}_i^{\mathfrak{r}}\left(\mathfrak{u}\right),{\mathcal{a}}_i^{\mathfrak{i}}\left(\mathfrak{u}\right)),({\mathfrak{m}}_i^{\mathfrak{r}}\left(\mathfrak{u}\right),{\mathfrak{m}}_i^{\mathfrak{i}}\left(\mathfrak{u}\right))\end{array}\right)$$

(8)

Definition 4

[39]. Let $A$ and $B$ be two PFSs, then the picture fuzzy Euclidean and Hamming distances between $A$ and $B$ are defined as follows:

$$E_i=\sqrt{{\displaystyle \frac{1}{2}}\sum _{j=1}^n\left({\left({\mathfrak{m}}_A-{\mathfrak{m}}_B\right)}^2+{\left({\mathcal{a}}_A-{\mathcal{a}}_B\right)}^2+{\left({\mathfrak{n}}_A-{\mathfrak{n}}_B\right)}^2\right)}$$

(9)

$$H_i={\displaystyle \frac{1}{2}}\sum _{j=1}^n\left(\left|{\mathfrak{m}}_A-{\mathfrak{m}}_B\right|+\left|{\mathcal{a}}_A-{\mathcal{a}}_B\right|+\left|{\mathfrak{n}}_A-{\mathfrak{n}}_B\right|\right)$$

(10)

The proposed convergence technique, CPF-CODAS, is designed to handle uncertain, inconsistent, and imprecise data, thereby providing a solid theoretical foundation for addressing the challenges of terminal forensics in mobile botnet C&C detection. Under such cyber conditions, decision-makers must evaluate multiple conflicting criteria expressed in ambiguous linguistic terms. The CPF-CODAS framework accommodates MD, AD, and NMD alongside the phase (argument) component embedded within CPFVs. This capability allows for richer modeling of uncertainty. By employing the complex picture fuzzy weighted averaging (CPFWA) operator to aggregate expert evaluations and by ranking alternatives based on the differences between their Euclidean and Taxicab distances from the negative-ideal solution, CPF-CODAS offers robust decision support. This methodological integration ensures a precise and reliable evaluation of suspicious terminals in mobile botnet research, setting the stage for the procedural details discussed in Section 4.

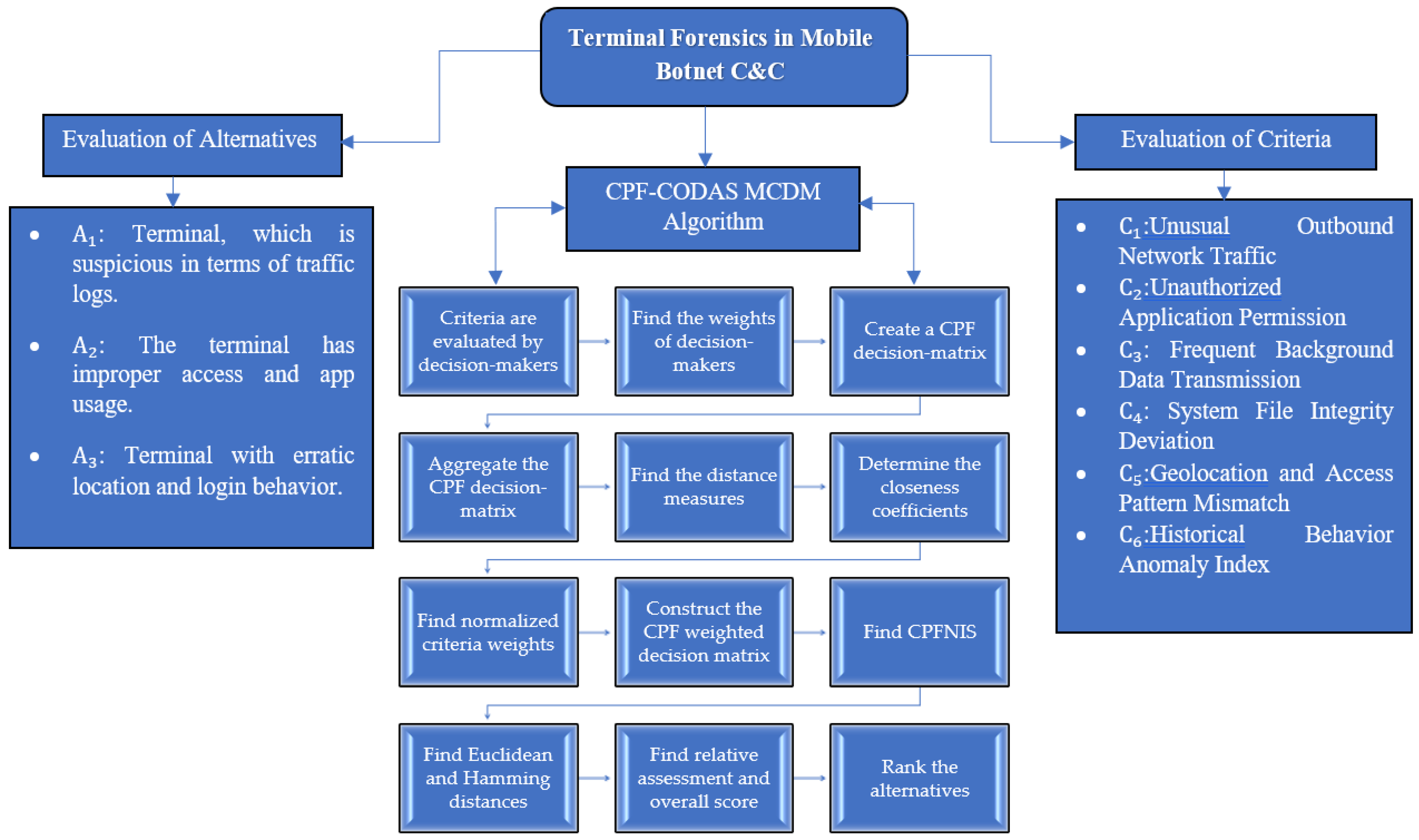
4. Complex Picture Fuzzy CODAS MCDM Framework

In this section, the formal definitions and conceptual foundations developed in Section 3 are extended to introduce the proposed CPF-CODAS framework for decision-making in mobile botnet terminal forensics. The approach aims to combine the representational density of the CPFS with the positive ranking properties of the CODAS method, thereby reducing uncertainty, inconsistency, and imprecision in forensic assessments. The concept of symmetry (used here) allows users to ensure that observed digital artifacts (effects) accurately reflect underlying user or system actions (causes), enabling a balanced analysis process. Incorporating simultaneous actions of magnitude and argument (phase), as well as multi-dimensional distances (Euclidean and Taxicab), provides it with novel functionality capable of offering greater confidence in ranking terminal devices within more complex cyber environments. Figure 1 illustrates the entire CPF-CODAS procedure, and the subsections below explain each methodological step as shown in this flowchart.

Step 1. Decision-makers analyze the criteria.

Table 1. Linguistic terms to evaluate criteria based on DM’s preferences.

Linguistic Terms	$\mathbf{CPFVs} (\mathfrak{m},\mathcal{a},\mathfrak{n})$
Very important (VI)	$0.80$	$0.85$	$0.04$	$0.06$	$0.06$	$0.09$
Important (I)	$0.70$	$0.75$	$0.04$	$0.09$	$0.06$	$0.12$
Medium (M)	$0.50$	$0.55$	$0.14$	$0.26$	$0.10$	$0.15$
Unimportant (UI)	$0.30$	$0.35$	$0.24$	$0.31$	$0.16$	$0.28$
Very unimportant (VU)	$0.10$	$0.05$	$0.04$	$0.06$	$0.80$	$0.85$

illustrates how decision-makers (DMs) utilize linguistic terms related to CPFVs in evaluating the worth of each condition based on their experience, where:

• $\left({\mathfrak{m}}^{\mathfrak{r}}\left(\mathfrak{u}\right),{\mathfrak{m}}^{\mathfrak{i}}\left(\mathfrak{u}\right)\right)$: real and imaginary parts of the MD,
• $\left({\mathcal{a}}^{\mathfrak{r}}\right(\mathfrak{u}),{\mathcal{a}}^{\mathfrak{i}}(\mathfrak{u}\left)\right)$: real and imaginary parts of the AD,
• $\left({\mathfrak{n}}^{\mathfrak{r}}\right(\mathfrak{u}),{\mathfrak{n}}^{\mathfrak{i}}(\mathfrak{u}\left)\right)$: real and imaginary parts of the NMD,
• $ⱸ$: index of the decision-maker, where $ⱸ=1,2,\dots ,l,$
• $l$: total number of decision-makers.

Then, the weights of the DMs are:

$$\left(w_{ⱸ}^{\mathfrak{r}},w_{ⱸ}^{\mathfrak{i}}\right)=\left(\begin{array}{c}{\displaystyle \frac{\left({\mathfrak{m}}_{ⱸ}^{\mathfrak{r}} + {\mathcal{a}}_{ⱸ}^{\mathfrak{r}} . \left(\frac{{\mathfrak{m}}_{ⱸ}^{\mathfrak{r}}}{{\mathfrak{m}}_{ⱸ}^{\mathfrak{r}}+{\mathfrak{n}}_{ⱸ}^{\mathfrak{r}}}\right)\right)}{\sum _{k=1}^l\left({\mathfrak{m}}_{ⱸ}^{\mathfrak{r}} + {\mathcal{a}}_{ⱸ}^{\mathfrak{r}} . \left(\frac{{\mathfrak{m}}_{ⱸ}^{\mathfrak{r}}}{{\mathfrak{m}}_{ⱸ}^{\mathfrak{r}}+{\mathfrak{n}}_{ⱸ}^{\mathfrak{r}}}\right)\right)}},\\ {\displaystyle \frac{\left({\mathfrak{m}}_{ⱸ}^{\mathfrak{i}} + {\mathcal{a}}_{ⱸ}^{\mathfrak{i}} . (\frac{{\mathfrak{m}}_{ⱸ}^{\mathfrak{i}}}{{\mathfrak{m}}_{ⱸ}^{\mathfrak{i}}+{\mathfrak{n}}_{ⱸ}^{\mathfrak{i}}})\right)}{\sum _{k=1}^l\left({\mathfrak{m}}_{ⱸ}^{\mathfrak{i}} + {\mathcal{a}}_{ⱸ}^{\mathfrak{i}} . (\frac{{\mathfrak{m}}_{ⱸ}^{\mathfrak{i}}}{{\mathfrak{m}}_{ⱸ}^{\mathfrak{i}}+{\mathfrak{n}}_{ⱸ}^{\mathfrak{i}}})\right)}}\end{array}\right)$$

(11)

where

$${\sum }_{k=1}^l{w}_k=1.$$

In this research, the following linguistic terms, along with presented CPFVs, were suggested (Table 1). The decision-makers constructed these values in Equations (2) and (3) concerning the subjective analysis of the semantic significance of each term and Definition 2. Therefore, Table 1 is proposed within this study and represents original contributions, not taken from external sources.

Step 2. Generate an aggregated CPF decision matrix.

The CPF decision matrix for a group of decision-makers is $D={\left[{₽}_{\mathfrak{m}\mathfrak{ⱸ}}\right]}_{\mathfrak{n}\ast \mathsf{f}}\left(ⱸ=\mathrm{1,2},\dots ,\mathsf{f};\mathfrak{m}=\mathrm{1,2},\dots ,\mathfrak{n}\right).$ ${₽}_{\mathrm{me}}$ represents the evaluation of $d^{th}$ based on the $j^{th}$ criteria. The CPFV ${₽}_{\mathfrak{m}\mathfrak{ⱸ}}$ is defined as ${₽}_{\mathfrak{m}\mathfrak{ⱸ}}=\left({\mathfrak{m}}_{{₽}_{\mathfrak{m}\mathfrak{ⱸ}}},{\mathcal{a}}_{{₽}_{\mathfrak{m}\mathfrak{ⱸ}}},{\mathfrak{n}}_{{₽}_{\mathfrak{m}\mathfrak{ⱸ}}}\right)$.

The aggregated CPF decision matrix is represented as follows:

$$\begin{array}{ll}{₽}_q& =CPFW{A}_{\mathcal{S}}\left({₽}_{q1},{₽}_{q2},\dots ,{₽}_{qⱸ}\right)\\ & =\left[\begin{array}{c}\left(\begin{array}{c}{(1-\prod _{ⱸ=1}^{\mathsf{f}}{\left(1-{\mathfrak{m}}_{{₽}_{qⱸ}}\right)}^{w_{ⱸ}})}^{\mathfrak{r}},\\ {(1-\prod _{ⱸ=1}^{\mathsf{f}}{\left(1-{\mathfrak{m}}_{{₽}_{qⱸ}}\right)}^{w_{ⱸ}})}^{\mathfrak{i}}\end{array}\right),\\ \left(\begin{array}{c}{\left(\prod _{ⱸ=1}^{\mathsf{f}}{\left({\mathcal{a}}_{{₽}_{qⱸ}}^{\left(k\right)}\right)}^{w_{ⱸ}}\right)}^{\mathfrak{r}},\\ {\left(\prod _{ⱸ=1}^{\mathsf{f}}{\left({\mathcal{a}}_{{₽}_{qⱸ}}^{\left(k\right)}\right)}^{w_{ⱸ}}\right)}^{\mathfrak{i}}\end{array}\right),\\ \left(\begin{array}{c}{\left(\prod _{ⱸ=1}^{\mathsf{f}}{\left({\mathfrak{n}}_{{₽}_{qⱸ}}^{\left(k\right)}\right)}^{w_{ⱸ}}\right)}^{\mathfrak{r}},\\ {\left(\prod _{ⱸ=1}^{\mathsf{f}}{\left({\mathfrak{n}}_{{₽}_{qⱸ}}^{\left(k\right)}\right)}^{w_{ⱸ}}\right)}^{\mathfrak{i}}\end{array}\right)\end{array}\right]\end{array}.$$

(12)

where ${\widehat{₽}}_q=\left(({\mathfrak{m}}_{{\widehat{₽}}_q}^{\mathfrak{r}},{\mathfrak{m}}_{{\widehat{₽}}_q}^{\mathfrak{i}}),({\mathcal{a}}_{{\widehat{₽}}_q}^{\mathfrak{r}},{\mathcal{a}}_{{\widehat{₽}}_q}^{\mathfrak{i}}),({\mathfrak{n}}_{{\widehat{₽}}_q}^{\mathfrak{r}},{\mathfrak{n}}_{{\widehat{₽}}_q}^{\mathfrak{i}})\right)$.

Step 3. Find the best solutions for CPF.

The complex picture fuzzy positive ideal solutions (CPFPIS) and complex picture fuzzy negative ideal solutions (CPFNIS) work out to be the best solution at ${\tau }^{+}=\left(\mathrm{1,1}),(\mathrm{0,0}),(\mathrm{0,0}\right)$, and ${\tau }^{-}=\left(\mathrm{0,0}),(\mathrm{0,0}),(\mathrm{1,1}\right)$ respectively. Although the maximum operator and the minimum operator construct CPFNIS and CPFPIS, a similarity in the results is noted.

Step 4. Measure the distance.

The distance measure is based on the fuzzy normalized Euclidean distance equation. The following equations are used in finding positive and negative values of distance measures using $z_q^{+}$ and $z_q^{-}$, respectively.

$$z_q^{+}=\left(\sqrt{\begin{array}{c}{\left({\mathfrak{m}}_{{\widehat{₽}}_q}^{\mathfrak{r}}-{\tau }^{+}\right)}^2+{\left({\mathcal{a}}_{{\widehat{₽}}_q}^{\mathfrak{r}}-{\tau }^{+}\right)}^2+{\left({\mathfrak{n}}_{{\widehat{₽}}_q}^{\mathfrak{r}}-{\tau }^{+}\right)}^2\\ +{\left({\mathfrak{m}}_{{\widehat{₽}}_{\mathfrak{m}}}^{\mathfrak{i}}-{\tau }^{+}\right)}^2+{\left({\mathcal{a}}_{{\widehat{₽}}_q}^{\mathfrak{i}}-{\tau }^{+}\right)}^2+{\left({\mathfrak{n}}_{{\widehat{₽}}_q}^{\mathfrak{i}}-{\tau }^{+}\right)}^2\end{array}}\right).$$

(13)

$$z_q^{-}=\left(\sqrt{\begin{array}{c}{\left({\mathfrak{m}}_{{\widehat{₽}}_q}^{\mathfrak{r}}-{\tau }^{-}\right)}^2+{\left({\mathcal{a}}_{{\widehat{₽}}_q}^{\mathfrak{r}}-{\tau }^{-}\right)}^2+{\left({\mathfrak{n}}_{{\widehat{₽}}_q}^{\mathfrak{r}}-{\tau }^{-}\right)}^2\\ +{\left({\mathfrak{m}}_{{\widehat{₽}}_{\mathfrak{m}}}^{\mathfrak{i}}-{\tau }^{-}\right)}^2+{\left({\mathcal{a}}_{{\widehat{₽}}_q}^{\mathfrak{i}}-{\tau }^{-}\right)}^2+{\left({\mathfrak{n}}_{{\widehat{₽}}_q}^{\mathfrak{i}}-{\tau }^{-}\right)}^2\end{array}}\right).$$

(14)

Step 5. Determine the values of the closeness coefficients (CCs).

$C{C}_m$ illustrates the CCs of the $m^{th}$ criterion, utilizing CPFPIS $z_q^{+}$ and CPFNIS $z_q^{-}$, as shown below.

$$C{C}_m={\displaystyle \frac{z_q^{-}}{z_q^{-}+z_q^{+}}}$$

(15)

Step 6. Calculate the weight of each criterion and alternative.

The CC values will indicate the relative importance of each of the criteria. It is said that normalization is performed to obtain the finalized weight, where the total of the weights is $1$.

Step 7. Create a CPF decision matrix.

Use

Table 2. Linguistic terms for an alternative ranking system.

Linguistic Terms	$\mathbf{CPFVs} \left(\mathfrak{m},\mathcal{a},\mathfrak{n}\right)$
Extremely good (EG)	$0.90$	$0.10$	$0.00$	$0.00$	$0.00$	$0.00$
Very very good (VVG)	$0.80$	$0.85$	$0.04$	$0.10$	$0.02$	$0.05$
Very good (VG)	$0.70$	$0.80$	$0.04$	$0.10$	$0.05$	$0.09$
Good (G)	$0.65$	$0.75$	$0.05$	$0.01$	$0.07$	$0.12$
Medium good (MG)	$0.55$	$0.70$	$0.07$	$0.14$	$0.08$	$0.13$
Fair (F)	$0.49$	$0.60$	$0.14$	$0.17$	$0.10$	$0.18$
Medium bad (MB)	$0.40$	$0.50$	$0.10$	$0.20$	$0.12$	$0.25$
Bad (B)	$0.35$	$0.40$	$0.15$	$0.30$	$0.26$	$0.30$
Very bad (VB)	$0.10$	$0.25$	$0.24$	$0.35$	$0.26$	$0.40$
Very very bad (VVB)	$0.05$	$0.10$	$0.04$	$0.15$	$0.40$	$0.70$

to create a CPF decision matrix.

$$\mathfrak{r}=\left[\begin{array}{lll}\left({\mathfrak{m}}_{\mathsf{Ɣ}1}\left({\mathfrak{u}}_1\right),{\mathcal{a}}_{\mathsf{Ɣ}1}\left({\mathfrak{u}}_1\right),{\mathfrak{n}}_{\mathsf{Ɣ}1}\left({\mathfrak{u}}_1\right)\right),\left({\mathfrak{m}}_{\mathsf{Ɣ}1}\left({\mathfrak{u}}_2\right),{\mathcal{a}}_{\mathsf{Ɣ}1}\left({\mathfrak{u}}_2\right),{\mathfrak{n}}_{\mathsf{Ɣ}1}\left({\mathfrak{u}}_2\right)\right)& \cdots & \left({\mathfrak{m}}_{\mathsf{Ɣ}1}\left({\mathfrak{u}}_{\mathfrak{n}}\right),{\mathcal{a}}_{\mathsf{Ɣ}1}\left({\mathfrak{u}}_{\mathfrak{n}}\right),{\mathfrak{n}}_{\mathsf{Ɣ}1}\left({\mathfrak{u}}_{\mathfrak{n}}\right)\right)\\ \left({\mathfrak{m}}_{\mathsf{Ɣ}2}\left({\mathfrak{u}}_1\right),{\mathcal{a}}_{\mathsf{Ɣ}2}\left({\mathfrak{u}}_1\right),{\mathfrak{n}}_{\mathsf{Ɣ}2}\left({\mathfrak{u}}_1\right)\right),\left({\mathfrak{m}}_{\mathsf{Ɣ}2}\left({\mathfrak{u}}_2\right),{\mathcal{a}}_{\mathsf{Ɣ}2}\left({\mathfrak{u}}_2\right),{\mathfrak{n}}_{\mathsf{Ɣ}2}\left({\mathfrak{u}}_2\right)\right)& \cdots & \left({\mathfrak{m}}_{\mathsf{Ɣ}2}\left({\mathfrak{u}}_{\mathfrak{n}}\right),{\mathcal{a}}_{\mathsf{Ɣ}2}\left({\mathfrak{u}}_{\mathfrak{n}}\right),{\mathfrak{n}}_{\mathsf{Ɣ}2}\left({\mathfrak{u}}_{\mathfrak{n}}\right)\right)\\ ⋮& \ddots & ⋮\\ \left({\mathfrak{m}}_{\mathfrak{Ɣ}\mathfrak{m}}\left({\mathfrak{u}}_1\right),{\mathcal{a}}_{\mathfrak{Ɣ}\mathfrak{m}}\left({\mathfrak{u}}_1\right),{\mathfrak{n}}_{\mathfrak{Ɣ}\mathfrak{m}}\left({\mathfrak{u}}_1\right)\right),\left({\mathfrak{m}}_{\mathfrak{Ɣ}\mathfrak{m}}\left({\mathfrak{u}}_2\right),{\mathcal{a}}_{\mathfrak{Ɣ}\mathfrak{m}}\left({\mathfrak{u}}_2\right),{\mathfrak{n}}_{\mathfrak{Ɣ}\mathfrak{m}}\left({\mathfrak{u}}_{\mathfrak{m}}\right)\right)& \cdots & \left({\mathfrak{m}}_{\mathfrak{Ɣ}\mathfrak{m}}\left({\mathfrak{u}}_{\mathfrak{m}}\right),{\mathcal{a}}_{\mathfrak{Ɣ}\mathfrak{m}}\left({\mathfrak{u}}_{\mathfrak{m}}\right),{\mathfrak{n}}_{\mathfrak{Ɣ}\mathfrak{m}}\left({\mathfrak{u}}_{\mathfrak{m}}\right)\right)\end{array}\right]$$

(16)

Table 2 presents linguistic terms and the associated CPFVs that were conceived within the frame of this research aimed at ranking alternatives. Table 2 is proposed within this study and represents original contributions, not taken from external sources. These values were identified as a result of expert consultation with the decision-makers and conformed to the form that is noted in Definition 2 and Equations (2) and (3), and granted the possibility to reflect the uncertainty and hesitancy through alternative evaluations.

Step 8. Construct a weighted aggregated CPF decision matrix.

Using Equation (16), compute the weighted aggregated CPF decision matrix as the product of the criteria weights.

$${\widetilde{\mathsf{Ɣ}}}^{\prime }=\left\{{\tilde{\mathfrak{u}}}_{ij}^{\prime }\right\}$$

(17)

where ${\tilde{\mathfrak{u}}}_{ij}^{\prime }={\tilde{w}}_j\otimes {\tilde{\mathfrak{u}}}_{ij}$.

Step 9. Calculate the CPFNIS for each criterion using the weighted aggregated CPF decision matrix Equation (17).

$${\beta }^{+}={{\mathfrak{m}}^{\mathfrak{r}}}_j^{-},{{\mathfrak{m}}^{\mathfrak{i}}}_j^{-},{{\mathcal{a}}^{\mathfrak{r}}}_j^{-},{{\mathcal{a}}^{\mathfrak{i}}}_j^{-},{{\mathfrak{n}}^{\mathfrak{r}}}_j^{-},{{\mathfrak{n}}^{\mathfrak{i}}}_j^{-}$$

(18)

where

• ${{\mathfrak{m}}^{\mathfrak{r}}}_j^{-}=\underset{i}{\mathrm{m}\mathrm{i}\mathrm{n}}\left\{{{\mathfrak{m}}_{ij}^{\mathfrak{r}}}^{\prime }\right\}, {{\mathfrak{m}}^{\mathfrak{i}}}_j^{-}=\underset{i}{\mathrm{m}\mathrm{i}\mathrm{n}}\left\{{{\mathfrak{m}}_{ij}^{\mathfrak{i}}}^{\prime }\right\},$
• ${{\mathcal{a}}^{\mathfrak{r}}}_j^{-}=\underset{i}{\mathrm{m}\mathrm{a}\mathrm{x}}\left\{{{\mathcal{a}}_{ij}^{\mathfrak{r}}}^{\prime }\right\}$, ${{\mathcal{a}}^{\mathfrak{i}}}_j^{-}=\underset{i}{\mathrm{m}\mathrm{a}\mathrm{x}}\left\{{{\mathcal{a}}_{ij}^{\mathfrak{i}}}^{\prime }\right\}$,
• ${{\mathfrak{n}}^{\mathfrak{r}}}_j^{-}=\underset{i}{\mathrm{m}\mathrm{a}\mathrm{x}}\left\{{{\mathfrak{n}}_{ij}^{\mathfrak{r}}}^{\prime }\right\}$, ${{\mathfrak{n}}^{\mathfrak{i}}}_j^{-}=\underset{i}{\mathrm{m}\mathrm{a}\mathrm{x}}\left\{{{\mathfrak{n}}_{ij}^{\mathfrak{i}}}^{\prime }\right\}$.

This choice serves as the point of reference for the worst-case scenario when comparing within the CODAS approach in the setting of the CPFS.

Step 10. We calculate the Euclidean distance ($E_i$) and Hamming distance ($H_i$) between the alternatives and the CPFNIS through the following procedure to rank the alternatives. These distances are generalizations of the classical definition of distances as given in Definition 4 to CPFVs:

$$E_i=\sqrt{{\displaystyle \frac{1}{2}}\sum _{j=1}^{\mathfrak{n}}\left(\begin{array}{c}{\left({{\mathfrak{m}}^{\mathfrak{r}}}_{ij}^{\prime }-{{\mathfrak{m}}^{\mathfrak{r}}}_j^{-}\right)}^2+{\left({{\mathfrak{m}}^{\mathfrak{i}}}_{ij}^{\prime }-{{\mathfrak{m}}^{\mathfrak{i}}}_j^{-}\right)}^2+{\left({{\mathcal{a}}^{\mathfrak{r}}}_{ij}^{\prime }-{{\mathcal{a}}^{\mathfrak{r}}}_j^{-}\right)}^2+{\left({{\mathcal{a}}^{\mathfrak{i}}}_{ij}^{\prime }-{{\mathcal{a}}^{\mathfrak{i}}}_j^{-}\right)}^2+\\ {\left({{\mathfrak{n}}^{\mathfrak{r}}}_{ij}^{\prime }-{{\mathfrak{n}}^{\mathfrak{r}}}_j^{-}\right)}^2+{\left({{\mathfrak{n}}^{\mathfrak{i}}}_{ij}^{\prime }-{{\mathfrak{n}}^{\mathfrak{i}}}_j^{-}\right)}^2\end{array}\right)}$$

(19)

$$H_i={\displaystyle \frac{1}{2}}\sum _{j=1}^{\mathfrak{n}}\left(\begin{array}{c}\left|{{\mathfrak{m}}^{\mathfrak{r}}}_{ij}^{\prime }-{{\mathfrak{m}}^{\mathfrak{r}}}_j^{-}\right|+\left|{{\mathfrak{m}}^{\mathfrak{i}}}_{ij}^{\prime }-{{\mathfrak{m}}^{\mathfrak{i}}}_j^{-}\right|+\left|{{\mathcal{a}}^{\mathfrak{r}}}_{ij}^{\prime }-{{\mathcal{a}}^{\mathfrak{r}}}_j^{-}\right|+\left|{{\mathcal{a}}^{\mathfrak{i}}}_{ij}^{\prime }-{{\mathcal{a}}^{\mathfrak{i}}}_j^{-}\right|+\\ \left|{{\mathfrak{n}}^{\mathfrak{r}}}_{ij}^{\prime }-{{\mathfrak{n}}^{\mathfrak{r}}}_j^{-}\right|+\left|{{\mathfrak{n}}^{\mathfrak{i}}}_{ij}^{\prime }-{{\mathfrak{n}}^{\mathfrak{i}}}_j^{-}\right|\end{array}\right)$$

(20)

These distances are the distance of each alternative to the worst-case CPFNIS in the three complex items (MD, MAD, or NMD): they take into consideration the effect of certainty (real part) and uncertainty/hesitation (imaginary part).

Step 11. This step generates a relative assessment matrix.

$$\mathfrak{r}\mathfrak{Ɣ}={\left\{r_{\mathit{ail}}\right\}}_{\mathfrak{m}\times \mathfrak{m}}$$

(21)

where

$$r_{\mathit{ail}}=\left[E_i-E_l\right]+\left[\phi \left(E_i-E_l\right)\times \left(H_i-H_l\right)\right],(i=\mathrm{1,2},\dots \mathfrak{m})$$

$$\phi \left(E_i-E_l\right)=\left\{\begin{array}{c}1, \mathrm{if} \left|E_i-E_l\right|\ge w\\ 0, \mathrm{otherwise}\end{array}\right.$$

(22)

The quality of Euclidean distances between the two alternatives can be assessed with the help of the threshold function $\phi$, and the parameter of a threshold value $\omega$ is frequently implemented as $0.05$.

Step 12. Determine the global score of the alternatives.

$${\delta }_i=\sum _{j=1}^{\mathfrak{m}}{r}_{ail}$$

(23)

Step 13. Rank the alternatives from the highest to the lowest global scores computed. Any alternative that has the highest magnitude of ${\delta }_i$ is the most preferred.

To conclude, the CPF-CODAS framework offers a science-based and symmetry-informed approach to mobile botnet terminal forensics. The proposed framework effectively supports transparent, reasoned decision-making by incorporating expert opinion aggregation (CPFWA operator) and ranking based on CODAS combined with CPFS modeling. The flowchart of methods (Figure 1), aligns with these steps, ensuring transparency and repeatability. With the operational sequence now established, the next section will demonstrate the framework’s practical application through a real-world case study on terminal forensics, focusing on detecting mobile botnet command and control cases, thereby illustrating its practical relevance and effectiveness.

5. Case Study: Terminal Forensics in Mobile Botnet Command and Control Detection

Mobile botnets have become one of the significant threats in the evolving cybersecurity landscape, partly because of their ability to remotely control infected devices through their C&C infrastructures. Terminal forensics is crucial for detecting these compromised endpoints using behavioral profiling, communication logs, and invisible traces on mobile phones. The dynamics of the botnet, encryption measures, and evasion techniques make detecting C&C very complex. Therefore, combining forensic analysis with intelligent decision-making models can be key to identifying infected devices and disrupting the control chain.

The availability of publicly accessible and non-confidential real-world datasets in the study was impossible, which is why this analysis uses a hypothetical but practically modeled case study to explain the use of the proposed methodology. It is an unconventional yet standard practice in previous bodies of the MCDM literature, enabling the technique to be illustrated without violating data confidentiality in a cybersecurity setting. The synthesized case is realistic in terms of its simulated operational environment in terminal forensics and allows an objective assessment of the offered model.

Signs and symptoms that detectives may examine to present a possible condition of a terminal being a victim of infection include irregular performance, network traffic abnormalities, access privileges, and earlier interaction, among others. This is attributable to the fact that these involve complexity and ambiguity in decision-making. The MCDM concepts could be utilized successfully to examine these indicators and assist with prioritizing investigation responses systematically. The MCDM model is beneficial in terms of integrating expert knowledge, quantification, and yields uniform, tractable, and explainable results of forensic findings, particularly in situations involving mobile botnets.

CPF-CODAS is considered in this paper as one of the numerous methods of MCDM due to its capacity in tackling uncertainty, contradiction, and indeterminacy of expert knowledge. Such ambiguous and uncertain conditions are not something confined to Standard MCDM procedures, such as locating mobile botnets in terminal C&C forensics. In the CPF-CODAS model, CPFVs are employed that may be applied to MD, AD, as well as NMDs of the CPFS in amplitude and phase. This provides a more comprehensive picture of the analysis for decision-makers and is therefore the best form of assessment for them when it comes to high-risk projects in terms of cybersecurity.

To prove the practical applicability of the offered methodology, we created the hypothetical case described above based on the typical MCDM case construction approach applied in previous publications [6,40]. Such a structure involves defining the decision environment, identifying alternatives, and delineating evaluation criteria through model-based expert literature and practice relevant to digital forensics. The structure comprises the definition of a decision environment, identification of alternatives, and determination of evaluation criteria, based on expert modeling as evidenced by relevant literature and practical importance in the field of digital forensics. An imaginary case is built of three decision-makers ($D{M}_1, D{M}_2, D{M}_3$) with all of them being professional cybersecurity analysts who are required to determine which of a number of suspect terminals is the most suspicious. Three other terminals are taken as options:

• ${\mathit{A}}_1$: Terminal suspect, as far as traffic logs are concerned.
  There is a high volume of outgoing encrypted traffic, mainly to non-standard ports and favorable domains on this terminal. By searching through the network logs, it is possible to identify repeated attempts to connect to known malicious IP addresses or repeated connections at unusual times, which could indicate a botnet beaconing pattern [41].
• ${\mathit{A}}_2$: There is misuse of inappropriate access and apps on the terminal.
  The characteristics of this terminal include mismatched permission requests from newly installed applications, many of which exceed what the app claims to do. The device history displays activity related to the use of non-official application stores, which allows downloading applications that can attain root access, thereby raising suspicions of access to backdoors or hijacking of device management [42].
• ${\mathit{A}}_3$: Terminal that exhibits unreliable location and login patterns.
  The terminal displays geo-anomalies, including an abrupt login from a geographically distant location within a short period, which does not coincide with the user’s movements. Additionally, patterns of access suggest possible simultaneous connections using different IP addresses and locations, potentially indicating session hijacking or remote command execution [43].

These options are considered based on the following six criteria that are briefly described:

• ${\mathit{C}}_1$: Unusual Outbound Network Traffic: Such a criterion talks of the quantity, frequency, and type of outbound packets as they are expounded through the terminal. Devices infected with botnets present unusual communication behavior as they frequently contact unfamiliar servers or make data exfiltration attempts, or send concerted DNS queries. Bizarre traffic communication, particularly at the idle times of the devices, could indicate concealed C&C traffic [44].
• ${\mathit{C}}_2$: Unauthorized Application Permission: This determines whether a set of applications installed in the phone request extra permission other than what is intended in the application, which may reflect something malicious. An example is a calculator app that requests access to SMS, contacts, or location; this is suspect. Applications that possess enhanced privileges could be used to gain a backdoor entry for remote control or steal information [45].
• ${\mathit{C}}_3$: Frequent Background Data Transmission: This criterion refers to the presence of ongoing processes during background data transmission or reception. A constant flow of background network data, particularly that which is unrelated to identifiable services, may indicate malware or bot-controlled command fetching [46].
• ${\mathit{C}}_4$: System File Integrity Deviation: This includes the identification of changes in system or configuration files that are unexpectedly altered, potentially indicating the presence of rootkits, injected scripts, or interference. To achieve persistence, or hide processes in detection tools, malware frequently changes files at the OS level. Such unauthorized alteration can be detected by integrity monitoring tools, which typically raise an alarm [47].
• ${\mathit{C}}_5$: Geolocation and Access Pattern Mismatch: This requirement identifies the dislocation between the anticipated geolocation of the user and actual login/access activities. When a device is displayed as having logged into multiple distant locations over short intervals or exhibiting unusual day/time log-in patterns, it represents spoofed access or remote exploitation [48].
• ${\mathit{C}}_6$: Historical Behavior Anomaly Index: This corresponds to the extent to which the activity of the current device does not conform to long-run usage patterns. A terminal that abruptly shows variability in application utilization, communication pattern, or resource utilization in the context of its prior historical pattern is likely to be compromised [49].

Additionally, the values of weight determined per criterion were extracted after three forensic analysts made an expert judgment with knowledge of mobile botnet detection. Individually, the relative consideration of the criteria was determined by each expert based on their pure experience in finding malicious activity on mobile terminals. This was then summarized using the CPFWA operator to obtain a suitable weight vector. This helps to give real-world forensic priority to weight assignment as opposed to random allocation. The literature and expert-tuned threshold values applied in the CODAS method were also used to ensure decision reliability in uncertainty.

Step 1. Using Equation (11), calculate the weights of the three decision-makers that can be seen in

Table 3. DM’s weights.

	$\mathit{D}{\mathit{M}}_1$	$\mathit{D}{\mathit{M}}_2$	$\mathit{D}{\mathit{M}}_3$
LTs	M	VI	M
${\mathit{w}}^{\mathit{r}}$	$0.298$	$0.404$	$0.298$
${\mathit{w}}^{\mathit{i}}$	$0.313$	$0.375$	$0.313$

.

Step 2. Use Table 1 to assign DM scores to the criterion, as illustrated in

Table 4. DMs assigned ratings to the criteria.

	$\mathit{D}{\mathit{M}}_1$	$\mathit{D}{\mathit{M}}_2$	$\mathit{D}{\mathit{M}}_3$
${\mathit{C}}_1$	VI	I	VU
${\mathit{C}}_2$	I	M	U
${\mathit{C}}_3$	VI	I	M
${\mathit{C}}_4$	I	VI	M
${\mathit{C}}_5$	M	M	I
${\mathit{C}}_6$	M	U	VI

. Using Equation (12), aggregate it as shown in

Table 5. Aggregated criteria.

	${\mathfrak{m}}^{\mathfrak{r}}$	${\mathfrak{m}}^{\mathfrak{i}}$	${\mathcal{a}}^{\mathfrak{r}}$	${\mathcal{a}}^{\mathfrak{i}}$	${\mathfrak{y}}^{\mathfrak{r}}$	${\mathfrak{y}}^{\mathfrak{i}}$
${\mathit{C}}_1$	$0.631$	$0.677$	$0.040$	$0.070$	$0.130$	$0.202$
${\mathit{C}}_2$	$0.525$	$0.580$	$0.113$	$0.197$	$0.099$	$0.170$
${\mathit{C}}_3$	$0.690$	$0.744$	$0.058$	$0.110$	$0.070$	$0.118$
${\mathit{C}}_4$	$0.704$	$0.752$	$0.058$	$0.108$	$0.070$	$0.116$
${\mathit{C}}_5$	$0.571$	$0.626$	$0.096$	$0.187$	$0.086$	$0.140$
${\mathit{C}}_6$	$0.564$	$0.634$	$0.120$	$0.176$	$0.104$	$0.162$

.

Step 3. Using Equations (13)–(15), compute normalized criteria weights as given in

Table 6. Normalized criteria weights.

	${\mathit{z}}_{\mathit{q}}^{+}$	${\mathit{z}}_{\mathit{q}}^{-}$	$\mathit{C}\mathit{C}$	Normalized Weights
${\mathit{C}}_1$	$0.466$	$2.862$	$0.860$	$0.169$
${\mathit{C}}_2$	$0.633$	$2.223$	$0.778$	$0.153$
${\mathit{C}}_3$	$0.299$	$2.831$	$0.904$	$0.178$
${\mathit{C}}_4$	$0.285$	$2.864$	$0.910$	$0.179$
${\mathit{C}}_5$	$0.516$	$2.342$	$0.819$	$0.161$
${\mathit{C}}_6$	$0.542$	$2.346$	$0.812$	$0.160$

.

Step 4. Using Table 2, DMs assigned scores to alternatives, as shown in

Table 7. DMs assigned ratings to alternatives.

		${\mathit{C}}_1$	${\mathit{C}}_2$	${\mathit{C}}_3$	${\mathit{C}}_4$	${\mathit{C}}_5$	${\mathit{C}}_6$
DM1	$A_1$	VVG	EG	G	MG	VVG	G
	$A_2$	VVG	VVG	G	MG	VG	MG
	$A_3$	G	VG	F	MB	G	F
DM2	$A_1$	MB	G	F	MB	MG	MB
	$A_2$	MG	MG	B	G	F	B
	$A_3$	VB	F	B	F	MB	VB
DM3	$A_1$	B	MB	MB	G	B	VVB
	$A_2$	F	B	MB	VVG	VB	B
	$A_3$	F	VB	EG	VG	VVB	B

.

Step 5. Multiply the weights of the criteria by Table 7 and apply Definition 3, as stated in

Table 8. Weighted complex picture fuzzy decision matrix.

		${\mathit{C}}_1$						${\mathit{C}}_2$
		${\mathfrak{m}}^{\mathfrak{r}}$	${\mathfrak{m}}^{\mathfrak{i}}$	${\mathcal{a}}^{\mathfrak{r}}$	${\mathcal{a}}^{\mathfrak{i}}$	${\mathfrak{n}}^{\mathfrak{r}}$	${\mathfrak{n}}^{\mathfrak{i}}$	${\mathfrak{m}}^{\mathfrak{r}}$	${\mathfrak{m}}^{\mathfrak{i}}$	${\mathcal{a}}^{\mathfrak{r}}$	${\mathcal{a}}^{\mathfrak{i}}$	${\mathfrak{n}}^{\mathfrak{r}}$	${\mathfrak{n}}^{\mathfrak{i}}$
DM1	$A_1$	$0.135$	$0.144$	$0.202$	$0.252$	$0.186$	$0.211$	$0.152$	$0.017$	$0.169$	$0.169$	$0.169$	$0.169$
	$A_2$	$0.135$	$0.144$	$0.202$	$0.252$	$0.186$	$0.211$	$0.135$	$0.144$	$0.202$	$0.252$	$0.186$	$0.211$
	$A_3$	$0.110$	$0.127$	$0.211$	$0.177$	$0.227$	$0.269$	$0.118$	$0.135$	$0.202$	$0.252$	$0.211$	$0.244$
DM2	$A_1$	$0.068$	$0.085$	$0.252$	$0.335$	$0.269$	$0.377$	$0.110$	$0.127$	$0.211$	$0.177$	$0.227$	$0.269$
	$A_2$	$0.093$	$0.118$	$0.227$	$0.285$	$0.236$	$0.277$	$0.093$	$0.118$	$0.227$	$0.285$	$0.236$	$0.277$
	$A_3$	$0.017$	$0.042$	$0.369$	$0.460$	$0.385$	$0.501$	$0.083$	$0.101$	$0.285$	$0.310$	$0.252$	$0.319$
DM3	$A_1$	$0.059$	$0.068$	$0.294$	$0.418$	$0.385$	$0.418$	$0.068$	$0.085$	$0.252$	$0.335$	$0.269$	$0.377$
	$A_2$	$0.083$	$0.101$	$0.285$	$0.310$	$0.252$	$0.319$	$0.059$	$0.068$	$0.294$	$0.418$	$0.385$	$0.418$
	$A_3$	$0.083$	$0.101$	$0.285$	$0.310$	$0.252$	$0.319$	$0.017$	$0.042$	$0.369$	$0.460$	$0.385$	$0.501$
		${\mathit{C}}_3$						${\mathit{C}}_4$
		${\mathfrak{m}}^{\mathfrak{r}}$	${\mathfrak{m}}^{\mathfrak{i}}$	${\mathcal{a}}^{\mathfrak{r}}$	${\mathcal{a}}^{\mathfrak{i}}$	${\mathfrak{n}}^{\mathfrak{r}}$	${\mathfrak{n}}^{\mathfrak{i}}$	${\mathfrak{m}}^{\mathfrak{r}}$	${\mathfrak{m}}^{\mathfrak{i}}$	${\mathcal{a}}^{\mathfrak{r}}$	${\mathcal{a}}^{\mathfrak{i}}$	${\mathfrak{n}}^{\mathfrak{r}}$	${\mathfrak{n}}^{\mathfrak{i}}$
DM1	$A_1$	$0.110$	$0.127$	$0.211$	$0.177$	$0.227$	$0.269$	$0.093$	$0.118$	$0.227$	$0.285$	$0.236$	$0.277$
	$A_2$	$0.110$	$0.127$	$0.211$	$0.177$	$0.227$	$0.269$	$0.093$	$0.118$	$0.227$	$0.285$	$0.236$	$0.277$
	$A_3$	$0.083$	$0.101$	$0.285$	$0.310$	$0.252$	$0.319$	$0.068$	$0.085$	$0.252$	$0.335$	$0.269$	$0.377$
DM2	$A_1$	$0.083$	$0.101$	$0.285$	$0.310$	$0.252$	$0.319$	$0.068$	$0.085$	$0.252$	$0.335$	$0.269$	$0.377$
	$A_2$	$0.059$	$0.068$	$0.294$	$0.418$	$0.385$	$0.418$	$0.110$	$0.127$	$0.211$	$0.177$	$0.227$	$0.269$
	$A_3$	$0.059$	$0.068$	$0.294$	$0.418$	$0.385$	$0.418$	$0.083$	$0.101$	$0.285$	$0.310$	$0.252$	$0.319$
DM3	$A_1$	$0.068$	$0.085$	$0.252$	$0.335$	$0.269$	$0.377$	$0.110$	$0.127$	$0.211$	$0.177$	$0.227$	$0.269$
	$A_2$	$0.068$	$0.085$	$0.252$	$0.335$	$0.269$	$0.377$	$0.135$	$0.144$	$0.202$	$0.252$	$0.186$	$0.211$
	$A_3$	$0.152$	$0.017$	$0.169$	$0.169$	$0.169$	$0.169$	$0.118$	$0.135$	$0.202$	$0.252$	$0.211$	$0.244$
		${\mathit{C}}_5$						${\mathit{C}}_6$
		${\mathfrak{m}}^{\mathfrak{r}}$	${\mathfrak{m}}^{\mathfrak{i}}$	${\mathcal{a}}^{\mathfrak{r}}$	${\mathcal{a}}^{\mathfrak{i}}$	${\mathfrak{n}}^{\mathfrak{r}}$	${\mathfrak{n}}^{\mathfrak{i}}$	${\mathfrak{m}}^{\mathfrak{r}}$	${\mathfrak{m}}^{\mathfrak{i}}$	${\mathcal{a}}^{\mathfrak{r}}$	${\mathcal{a}}^{\mathfrak{i}}$	${\mathfrak{n}}^{\mathfrak{r}}$	${\mathfrak{n}}^{\mathfrak{i}}$
DM1	$A_1$	$0.135$	$0.144$	$0.202$	$0.252$	$0.186$	$0.211$	$0.110$	$0.127$	$0.211$	$0.177$	$0.227$	$0.269$
	$A_2$	$0.118$	$0.135$	$0.202$	$0.252$	$0.211$	$0.244$	$0.093$	$0.118$	$0.227$	$0.285$	$0.236$	$0.277$
	$A_3$	$0.110$	$0.127$	$0.211$	$0.177$	$0.227$	$0.269$	$0.083$	$0.101$	$0.285$	$0.310$	$0.252$	$0.319$
DM2	$A_1$	$0.093$	$0.118$	$0.227$	$0.285$	$0.236$	$0.277$	$0.068$	$0.085$	$0.252$	$0.335$	$0.269$	$0.377$
	$A_2$	$0.083$	$0.101$	$0.285$	$0.310$	$0.252$	$0.319$	$0.059$	$0.068$	$0.294$	$0.418$	$0.385$	$0.418$
	$A_3$	$0.068$	$0.085$	$0.252$	$0.335$	$0.269$	$0.377$	$0.017$	$0.042$	$0.369$	$0.460$	$0.385$	$0.501$
DM3	$A_1$	$0.059$	$0.068$	$0.294$	$0.418$	$0.385$	$0.418$	$0.008$	$0.017$	$0.202$	$0.294$	$0.501$	$0.751$
	$A_2$	$0.017$	$0.042$	$0.369$	$0.460$	$0.385$	$0.501$	$0.059$	$0.068$	$0.294$	$0.418$	$0.385$	$0.418$
	$A_3$	$0.008$	$0.017$	$0.202$	$0.294$	$0.501$	$0.751$	$0.059$	$0.068$	$0.294$	$0.418$	$0.385$	$0.418$

.

Step 6. Calculate CPFNIS using Equation (8), as given in

Table 9. Complex picture fuzzy negative ideal solution.

	${\mathit{C}}_1$						${\mathit{C}}_2$
	${\mathfrak{m}}^{\mathfrak{r}}$	${\mathfrak{m}}^{\mathfrak{i}}$	${\mathcal{a}}^{\mathfrak{r}}$	${\mathcal{a}}^{\mathfrak{i}}$	${\mathfrak{n}}^{\mathfrak{r}}$	${\mathfrak{n}}^{\mathfrak{i}}$	${\mathfrak{m}}^{\mathfrak{r}}$	${\mathfrak{m}}^{\mathfrak{i}}$	${\mathcal{a}}^{\mathfrak{r}}$	${\mathcal{a}}^{\mathfrak{i}}$	${\mathfrak{n}}^{\mathfrak{r}}$	${\mathfrak{n}}^{\mathfrak{i}}$
$\mathit{D}{\mathit{M}}_1$	$0.110$	$0.127$	$0.211$	$0.252$	$0.227$	$0.269$	$0.118$	$0.017$	$0.202$	$0.252$	$0.211$	$0.244$
$\mathit{D}{\mathit{M}}_2$	$0.068$	$0.085$	$0.252$	$0.335$	$0.269$	$0.377$	$0.110$	$0.127$	$0.211$	$0.252$	$0.227$	$0.269$
$\mathit{D}{\mathit{M}}_3$	$0.068$	$0.085$	$0.252$	$0.335$	$0.269$	$0.377$	$0.093$	$0.118$	$0.227$	$0.285$	$0.236$	$0.277$
	$C_3$						$C_4$
	${\mathfrak{m}}^{\mathfrak{r}}$	${\mathfrak{m}}^{\mathfrak{i}}$	${\mathcal{a}}^{\mathfrak{r}}$	${\mathcal{a}}^{\mathfrak{i}}$	${\mathfrak{n}}^{\mathfrak{r}}$	${\mathfrak{n}}^{\mathfrak{i}}$	${\mathfrak{m}}^{\mathfrak{r}}$	${\mathfrak{m}}^{\mathfrak{i}}$	${\mathcal{a}}^{\mathfrak{r}}$	${\mathcal{a}}^{\mathfrak{i}}$	${\mathfrak{n}}^{\mathfrak{r}}$	${\mathfrak{n}}^{\mathfrak{i}}$
$\mathit{D}{\mathit{M}}_1$	$0.083$	$0.101$	$0.285$	$0.310$	$0.252$	$0.319$	$0.068$	$0.085$	$0.252$	$0.335$	$0.269$	$0.377$
$\mathit{D}{\mathit{M}}_2$	$0.083$	$0.101$	$0.285$	$0.310$	$0.252$	$0.319$	$0.068$	$0.085$	$0.252$	$0.335$	$0.269$	$0.377$
$\mathit{D}{\mathit{M}}_3$	$0.059$	$0.068$	$0.294$	$0.418$	$0.385$	$0.418$	$0.068$	$0.085$	$0.252$	$0.335$	$0.269$	$0.377$
	$C_5$						$C_6$
	${\mathfrak{m}}^{\mathfrak{r}}$	${\mathfrak{m}}^{\mathfrak{i}}$	${\mathcal{a}}^{\mathfrak{r}}$	${\mathcal{a}}^{\mathfrak{i}}$	${\mathfrak{n}}^{\mathfrak{r}}$	${\mathfrak{n}}^{\mathfrak{i}}$	${\mathfrak{m}}^{\mathfrak{r}}$	${\mathfrak{m}}^{\mathfrak{i}}$	${\mathcal{a}}^{\mathfrak{r}}$	${\mathcal{a}}^{\mathfrak{i}}$	${\mathfrak{n}}^{\mathfrak{r}}$	${\mathfrak{n}}^{\mathfrak{i}}$
$\mathit{D}{\mathit{M}}_1$	$0.110$	$0.127$	$0.211$	$0.252$	$0.227$	$0.269$	$0.083$	$0.101$	$0.285$	$0.310$	$0.252$	$0.319$
$\mathit{D}{\mathit{M}}_2$	$0.093$	$0.118$	$0.227$	$0.285$	$0.236$	$0.277$	$0.068$	$0.085$	$0.285$	$0.335$	$0.269$	$0.377$
$\mathit{D}{\mathit{M}}_3$	$0.083$	$0.101$	$0.285$	$0.310$	$0.252$	$0.319$	$0.059$	$0.068$	$0.294$	$0.418$	$0.385$	$0.418$

.

Step 7.

Table 10. Euclidean and Hamming distance.

		Euclidean Distance	Hamming Distance
$\mathit{D}{\mathit{M}}_1$	$A_1$	$0.274$	$1.128$
	$A_2$	$0.222$	$0.846$
	$A_3$	$0.124$	$0.171$
$\mathit{D}{\mathit{M}}_2$	$A_1$	$0.173$	$0.558$
	$A_2$	$0.356$	$1.471$
	$A_3$	$0.484$	$2.056$
$\mathit{D}{\mathit{M}}_3$	$A_1$	$0.683$	$2.677$
	$A_2$	$0.563$	$2.420$
	$A_3$	$0.736$	$2.768$

is obtained by using Equations (19) and (20).

Step 8.

Table 11. Results of the CPF-CODAS method.

		${\mathit{A}}_1$	${\mathit{A}}_2$	${\mathit{A}}_3$	$\mathit{\delta }$	Rank
$\mathit{D}{\mathit{M}}_1$	$A_1$	$0.000$	$0.334$	$1.106$	$1.440$	$1$
	$A_2$	$-0.334$	$0.000$	$0.772$	$0.439$	$2$
	$A_3$	$-1.106$	$-0.772$	$0.000$	$-1.879$	$3$
$\mathit{D}{\mathit{M}}_2$	$A_1$	$0.000$	$-1.096$	$-1.810$	$-2.906$	$3$
	$A_2$	$1.096$	$0.000$	$-0.714$	$0.382$	$2$
	$A_3$	$1.810$	$0.714$	$0.000$	$2.524$	$1$
$\mathit{D}{\mathit{M}}_3$	$A_1$	$0.000$	$0.377$	$-0.144$	$0.233$	$2$
	$A_2$	$-0.377$	$0.000$	$-0.521$	$-0.897$	$3$
	$A_3$	$0.144$	$0.521$	$0.000$	$0.665$	$1$

shows the results of the CPF-CODAS technique, obtained using Equations (21)–(23). The values of $\delta$ are represented as the addition of the difference between the positive relative Euclidean distance of each alternative, rounded off, as shown in the table. The computation is end-to-end traceable in the ranking results and can be referred to just as the values in the Euclidean distance columns.

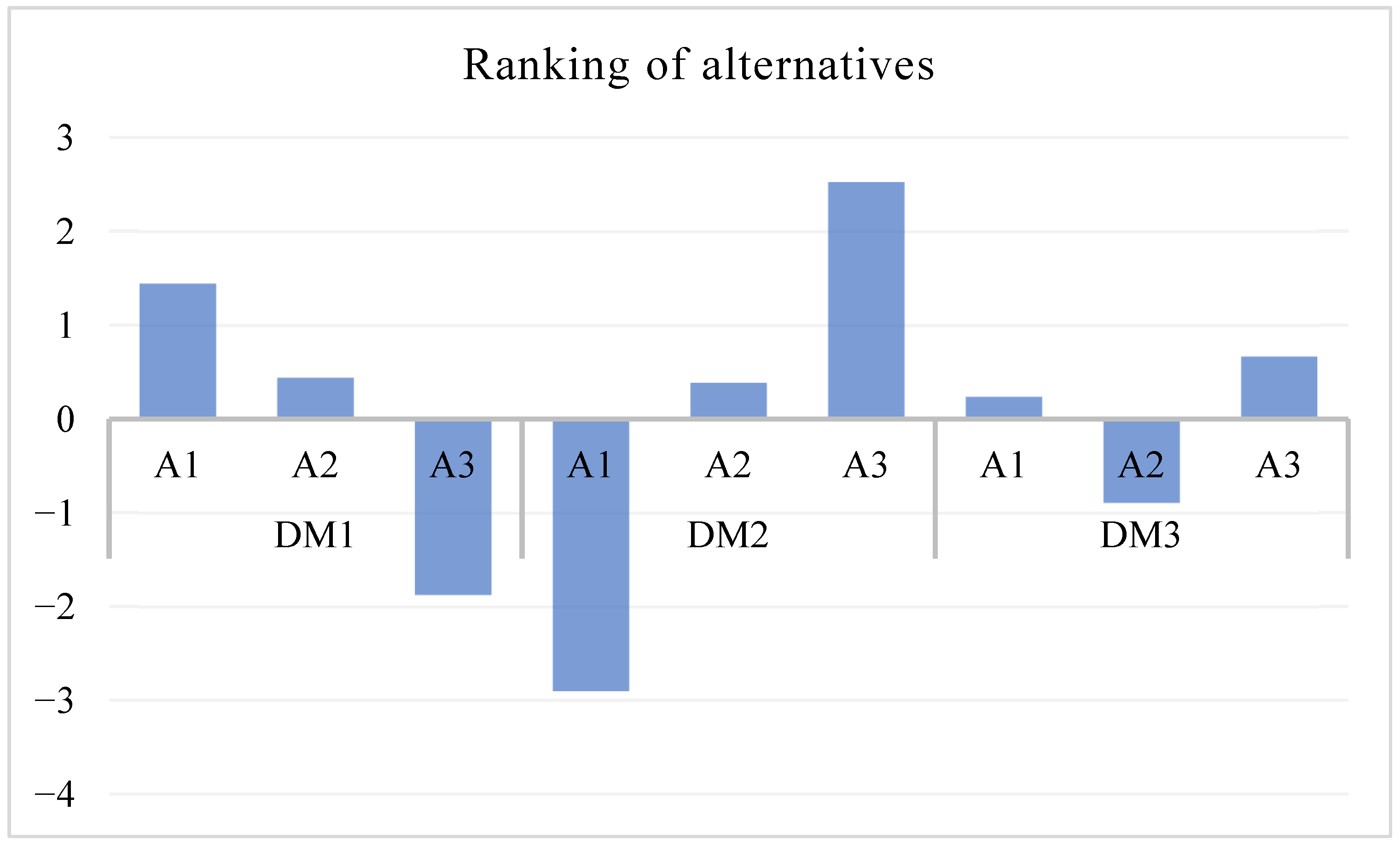
5.1. Result Discussion

The algorithm based on the CPF-CODAS approach yields significant findings that can be used to assess the three mobile devices in terms of their forensic analysis. According to the grading of three professional decision-makers ($D{M}_1$, $D{M}_2$, and $D{M}_3$), all three terminals were graded under different preference ranks toward six forensic outcomes. Using $D{M}_1$, the score of $A_1$ was found to be $1.441$ as the most suspicious, $0.438$ for $A_2$ as the second most suspicious, and $-1.879$ was the score of $A_3$ as the least suspicious terminal. Conversely, $D{M}_2$ ranked $A_3$ as the most probable terminal involved in botnet command and control, giving it the highest score of $2.524$, which is obtained by summing the pairwise Euclidean distance differences ($1.810+0.714$) as shown in Table 11, with $A_2$ and $A_1$ having lower ranks as indicated by its score of $0.383$ and $-2.907$ respectively. In the same manner, $D{M}_3$ also did $A_3$ (0.664) the greatest suspicion, $A_1 \left(0.233\right)$ the second and $A_2$ the least with an index of $-0.898$. This explanation makes the mathematical calculation of all $\delta$ values traceable, hence removing any ambiguity on the score allocation and final ranking. Such a difference in opinions illustrates the complexity and subjectivity that characterizes a lot of forensic decision-making when interpreting multifaceted indicators of mobile bot net activity, see Figure 2. Even though these diverse opinions lead to different evaluations, the CPF-CODAS methodology manages to unify these controversial views by taking into account the magnitude in addition to the directions of the experts’ tastes. When the scores are added, the average of the preference values can be obtained as $-0.411,-0.025$ and $0.436$ of $A_1$, $A_2$ and $A_3$ respectively. These findings leave no doubt that $A_3$ is the most suspect terminal since it reaches the biggest overall score and shows the most significant forensic indications of the possible botnet-related activity, namely regarding access anomalies and inconsistent data transmission patterns. $A_2$ is regarded as moderately dubious, and $A_1$ turns out to be the least probable, although it is rated highly by one of the experts. This result demonstrates how the CPF-CODAS approach is practical in the integration of subjective judgment and the production of a strong and explainable forensic verdict. It strengthens the usefulness of this course of action in aiding cybersecurity analysts throughout the necessary decision-making steps in mobile botnet command and control.

5.2. Theoretical Implications

The present research contributes to the theory of MCDM by integrating the CODAS method with the CPFS framework, offering a robust approach to managing uncertainty in expert assessments. Unlike traditional fuzzy models, CPFS captures a broader range of expert judgments, including contradiction and neutrality, leading to more accurate decision-making. The proposed CPF-CODAS model further advances the theoretical foundation of distance-based MCDM methods and demonstrates their practical use in cybersecurity and terminal forensics, effectively broadening their application to other sensitive areas with greater emphasis.

6. Sensitivity Analysis

The sensitivity of the suggested CPF-CODAS method was established through a sensitivity analysis, where the threshold coefficient was varied from $0$ to $1$. This coefficient is used to offset the emphasis between both Euclidean and Taxicab distances in the CODAS method. The performance score of each of the three alternatives $A_1$, $A_2$ and $A_3$ were analyzed with varying values of omega under each decision-maker, as shown in Figure 3. The outcomes have evident changes in ranking at a particular weight. As an example, in the case of $D{M}_1$, $A_1$ has an initial score of $1.441$ at $\omega = 0$, but greatly decreases to $0.201$ at $\omega =0.20$, signifying a severe reliance on the distance measure setup. A sudden decrease in score between $A_3$ is observed on $D{M}_2$ of $2.524$ (when $\omega = 0$) to 0.440 (when $\omega \ge 0.35$), but the same terminal will nonetheless remain as the highest-ranked one where this expert is concerned. The assessments of $D{M}_3$ have moderate changes, though in the same observation as $A_3$ would be the most suspicious terminal at different values of omega. In general, the sensitivity testing demonstrates the congruency of the alternative $A_3$ as the most serious suspect in every scenario, which proves the quality of the decision and the soundness of the CPF-CODAS model in the terminal forensics of mobile botnets C&C identification.

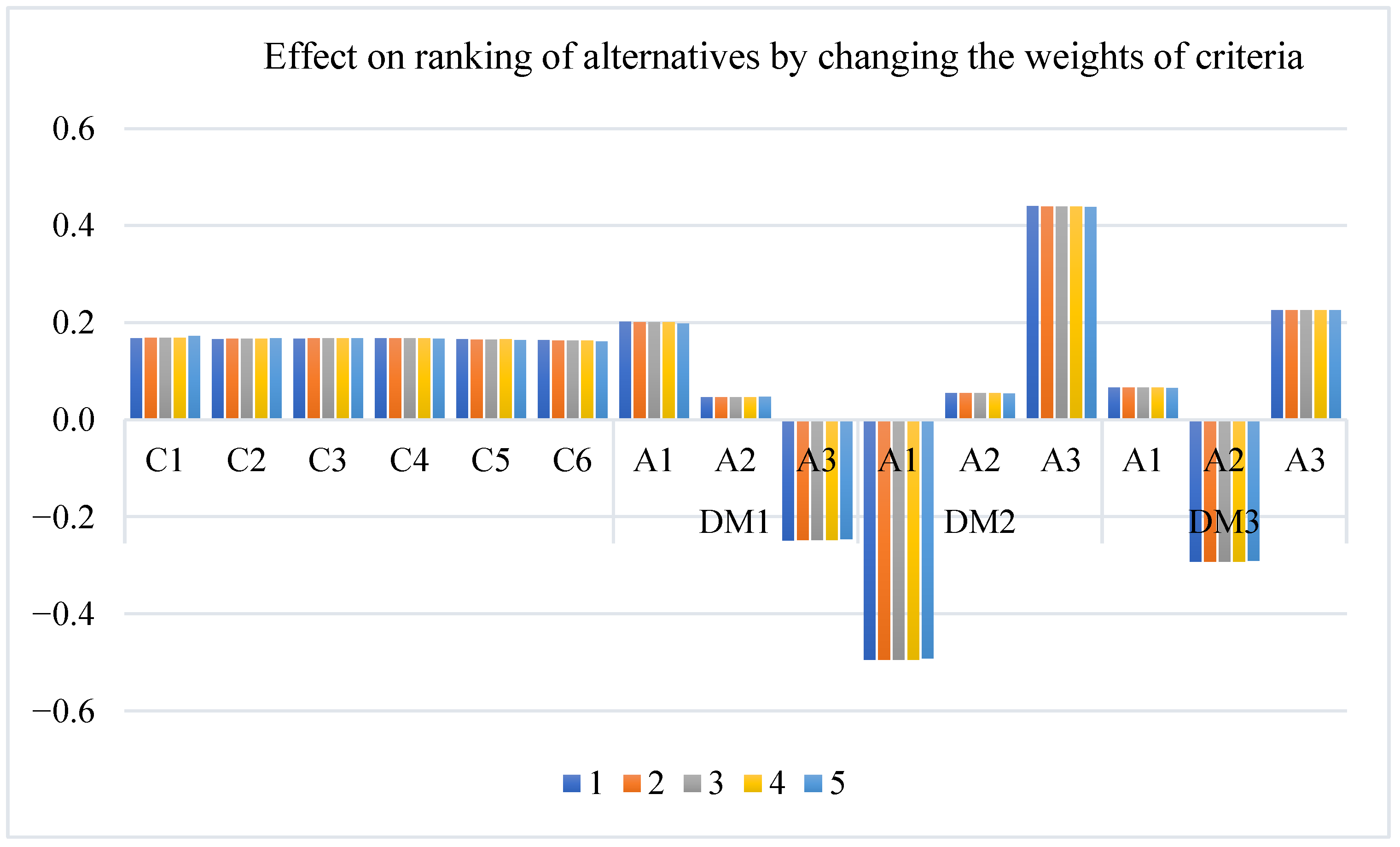
To test the strength and consistency of the CPF-CODAS suggested approach, a sensitivity analysis was conducted by varying the weight of the evaluation criteria within a narrow range. The display in Figure 4 shows the differences in the total results of both alternatives by all the decision-makers ($D{M}_1$, $D{M}_2$, and $D{M}_3$) under the variation in the weighting capacities. The findings indicate that, with a slight change in the criteria weights, there are only moderate changes in alternative rankings and scores, suggesting that the method is adept at handling weight perturbations. This form of stability is crucial in cybersecurity decision-making scenarios, where input data often exhibits variability and randomness. The results confirm that the CPF-CODAS method is capable of generating similar and dependable results even under varying weights, thereby validating its feasibility in forensic assessment and the detection of botnets within mobile networks. In contrast to data-driven deep learning frameworks in the field of cybersecurity, where the method tends to rely on repeated training procedure over numerous epochs and observing other indicators of algorithm performance, such as accuracy and loss [50], fuzzy MCDM techniques, such as CPF-CODAS are robust in the sense that sensitivity analysis of parameters (e.g., weights and thresholds), as well as input variation are monitored as means of establishing robustness. This enables the model to achieve stable and interpretable decision outcomes that can be used with minimal retraining and, in particular, can be applied to forensics to detect fraud in high-stakes applications where reliability and explainability are critical.

6.1. Benchmark Comparison with Existing CPF-MCDM Approaches

To establish the validity of the suggested CPF-CODAS approach, a comparison with four existing methods of MCDM: WASPAS [51], COCOSO [52], TOPSIS [53], and EDAS [54] is carried out. The CPF-CODAS technique addresses these issues better than any other technique, as summarized in

Table 12. Comparison analysis.

Criteria	CPF-CODAS	WASPAS	COCOSO	TOPSIS	EDAS
Handling Complex Uncertainty	High	Medium	Medium	Low	Low
Ability to Model Hesitation & Indeterminacy	High	Medium	Medium	Low	Low
Discrimination Power in Ranking	High	Medium	High	Medium	Medium
Sensitivity to Decision Variations	Low	Medium	High	High	Medium
Computational Complexity	Medium	Low	Medium	Low	Low
Robustness in Forensic Decision-Making	High	Medium	Medium	Low	Medium
Adaptability to a Complex Picture Fuzzy Environment	High	Low	Low	Low	Low

, in areas such as coping with complex uncertainty, modeling hesitation and indeterminacy, and robustness in high-stakes forensic settings, among others. Mobile botnets’ command and control state is a case of terminal forensics, as it involves the ability to represent expert opinions in a nuanced manner based on the capability of its CPFS. Whereas approaches such as TOPSIS and EDAS demonstrate a relatively low level of fuzzy uncertainty management, WASPAS and COCOSO exhibit a medium level of adaptability, yet do not reveal richness in dealing with indeterminate or conflicting information. In addition, CPF-CODAS has been highly discriminating between alternatives and performs stably with changing levels of sensitivity, unlike increased sensitivity expressed by TOPSIS and COCOSO. Although the computational complexity of CPF-CODAS is moderate, it is worth paying this price, as it offers higher accuracy and robustness in decision-making. Indicatively, the comparative review has affirmed that CPF-CODAS presents a more wholesome and trustworthy model of decision-supported structure than the other available alternatives in perceived complex cyber-forensic backgrounds.

To further justify the usefulness of the proposed CPF-CODAS technique, the effectiveness of the proposed method was compared with the other two CPF-based CODM techniques, i.e., CPF-WASPAS and CPF-CoCoSo, and the rank achieved by these two techniques when they are applied to the same set of decision matrices. The rankings obtained using the three different methods of each decision-maker ($D{M}_1$–$D{M}_3$) as seen in Figure 5, a good level of consistency is shown, with the CPF-CODAS method recommended in that it provides a highly stable and discriminating level of rankings regardless of the case. However, it is essential to note that CPF-CODAS continues to provide the most appropriate alternative according to expert expectations, with minimal changes in the rank among the decision-makers. Such comparative evidence solidifies the strength and credibility of CPF-CODAS against the alternative CPF-MCDM methods in acquiring a complex cyber-forensics setting. Although the main emphasis of the current study is to prove the methodological convenience and performance reliability of CPF-CODAS, a more thorough statistical analysis will be conducted in future research where coefficients of Spearman rank correlation will be calculated between the proposed and the benchmark methods. This will give the quantitative dimension of the ranking stability and further confirm the strength of the methodology.

6.2. Practical and Managerial Implications

The proposed CPF-CODAS approach offers practical value to cybersecurity professionals and system administrators as a reliable, structured tool to assess and prioritize terminal devices at risk of mobile botnet attacks. It supports effective and efficient responses and decision-making during forensic investigations by accurately identifying suspicious or non-suspicious nodes. This model allows managers to improve detection systems, assign resources, and strengthen security networks based on prioritized threat levels, according to expert evaluation.

Also, this approach shows the effectiveness of using CPFS and transforming the opinion of experts into linguistic statements and expressing opinions with conversion into the CPFVs with the use of standard fuzzy scales. This creates better interpretability and enables real-life cybersecurity experts to affect the model effectively when used in forensics of terminals. The algorithm also has a regularized computation procedure that makes it possible to guarantee the transparency, traceability, and reality of the work of decision-making in the form of correspondences with the work of a forensic.

6.3. Advantages of the Study

This study has notable strengths. First, it introduces a new combination of the CPFS environment with the CODAS approach, which improves the handling of uncertainty and imprecision in expert assessment results. The integration is also a novel way to model the use of amplitudes and phases related to expert judgments, unlike preexisting methods of MCDM that allow more expressiveness in decision-making involving complex and contradictory cybersecurity conditions. Second, it strengthens the robustness of terminal forensics in mobile botnet detection by effectively capturing hesitation and contradiction in decision-makers’ judgments. This is particularly advantageous in forensic environments where expert evaluations are uncertain, subjective, and often overlapping. Third, the method is adaptable, portable, and performs better than traditional MCDMs such as WASPAS, TOPSIS, EDAS, and COCOSO; therefore, it is likely to be highly useful in real-time cyber forensics settings.

6.4. Limitations of the Study

This study has limitations, but it may still yield valuable results. Although the suggested CPF-CODAS method is quite effective, it relies heavily on expert judgment, which can introduce subjectivity into the decision-making process. Additionally, the existing model has only been tested with a few alternatives and criteria in a narrow setting, specifically a terminal in the forensic field, which may limit its validity. Furthermore, complexity could become more computationally demanding when using larger datasets or a more detailed fuzzy scale, which might require real-time results even on high-speed mobile networks.

The given assessment is based on hypothetical information illustrating the methodological structure in a well-regulated environment. Although this method is practical in terms of demonstrating the applicability and intelligibility of the proposed decision-making process, it fails to substitute for validation using empirical forensic data. A practical evaluation of the model’s performance would require real-life datasets and is a step that should be taken in the future. Such datasets could include CTU-13 and IoT-23 botnet traces. In addition, the proposed design has practical limitations, including reliance on precise and complete input data, the possibility that forensic indicators may change in different network contexts, and the inability to maintain model accuracy when the behavior of botnets is continually altered randomly. Such variables may influence the consistency and soundness of the decision-making results. Additionally, the proposed CPF-CODAS model is based on a non-dynamic tool of forensic assessment. Although this is appropriate in structured tests, it has limitations when applied to the dynamic behaviors of advanced botnets, such as Emotet and Mirai, which maintain dynamic command and control. This is one of the current limitations. Suggesting a direction of future research, it is possible to recommend adding temporal or adaptive extensions to the model to increase the ability to capture changing behavior of threats in the detection of mobile botnets.

7. Conclusions

In this paper, a decision-making framework that combines CPFS with the CODAS approach to enhance terminal forensics in mobile botnet C&C detection is presented. The CPF-CODAS model characterizes degrees of membership, non-membership, and abstention amplitude and phase, effectively representing expert judgment closely and covering a larger area than the use of the traditional single value. This gives more credible results in case of uncertainty. The hypothetical but practically relevant case study involving three different options, six evaluation criteria, and three practitioners in cybersecurity used in the proposed framework demonstrated that the specified framework may be utilized in the evaluation of professional decision-making in terms of different cybersecurity options. The findings indicated that CPF-CODAS was an effective method for the prioritization of the most suspicious terminal node and is superior to the existing MCDM methods in the processing of conflicting and rough forensic evidence like WASPAS, COCOSO, TOPSIS, and EDAS. These results validate its ability to enhance accuracy and discrimination within cybersecurity decision-making.

The suggested CPF-CODAS might be further augmented to work in more infinite-dimensional fuzzy environments, such as spherical fuzzy sets [55], picture fuzzy AHP with interval-valued [56] and Dombi-based aggregation operators [57]. Furthermore, such methods as the interval-valued T-spherical fuzzy information [58], and a series of fuzzy approaches, e.g., EDAS [59], OPARA [60], MEREC [61], can be consulted in order to offer more effective decision-making opportunities in complex and continuous cybersecurity scenarios. In addition, future studies must solve significant constraints to forensic investigations in cybersecurity, like privacy issues with terminal data, the threat of false positives (i.e., identifying benign applications as malicious), and an exhaustive evaluation of computational cost to mobile device forensics to ensure the suggested approach is plausible and can readily scale.