Quantum Behavior of 10D Planck Unit: Stationary Electron, Compton Photon and Gravitational Field
Abstract
1. Introduction
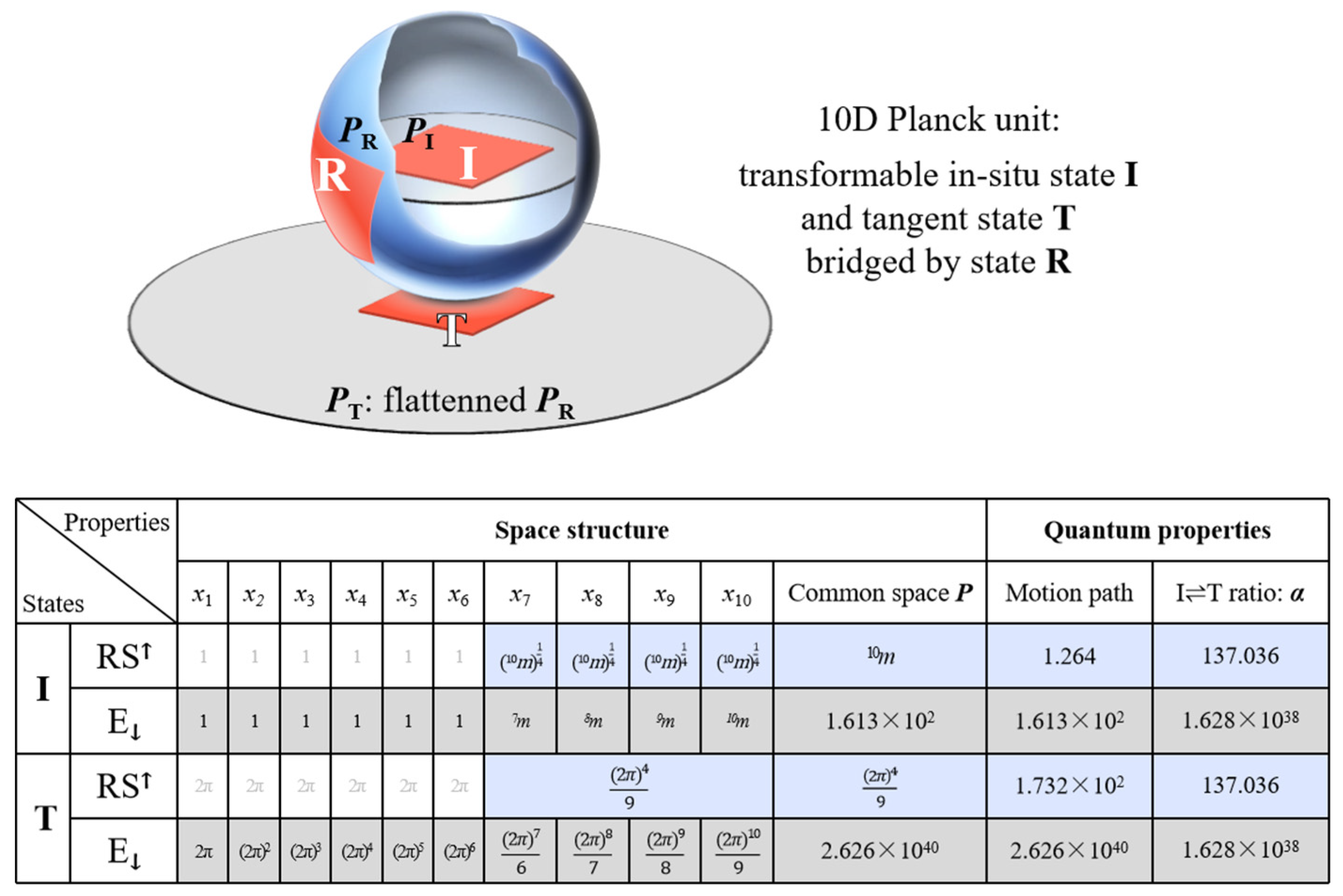
2. Physical Behavior of 10D Planck Unit 10
2.1. 10: Doublet Candidates Due to the Incompatible Principles of RS↑ and E↓
2.2. 10: Singlet States Determined by Conservation of Energy
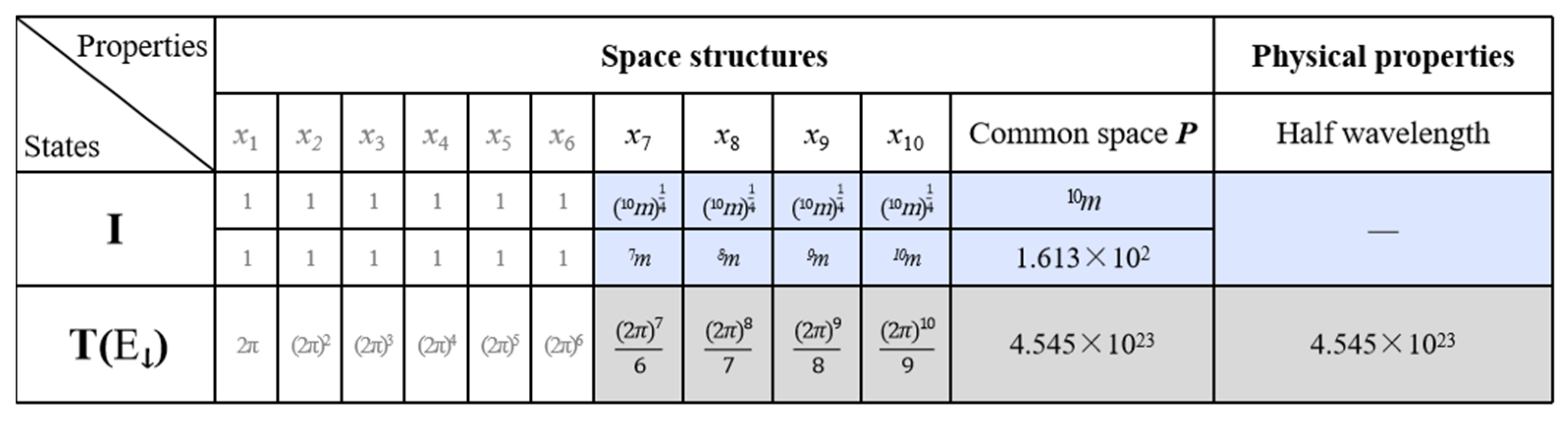
2.3. 10: Physical Behavior of I/T
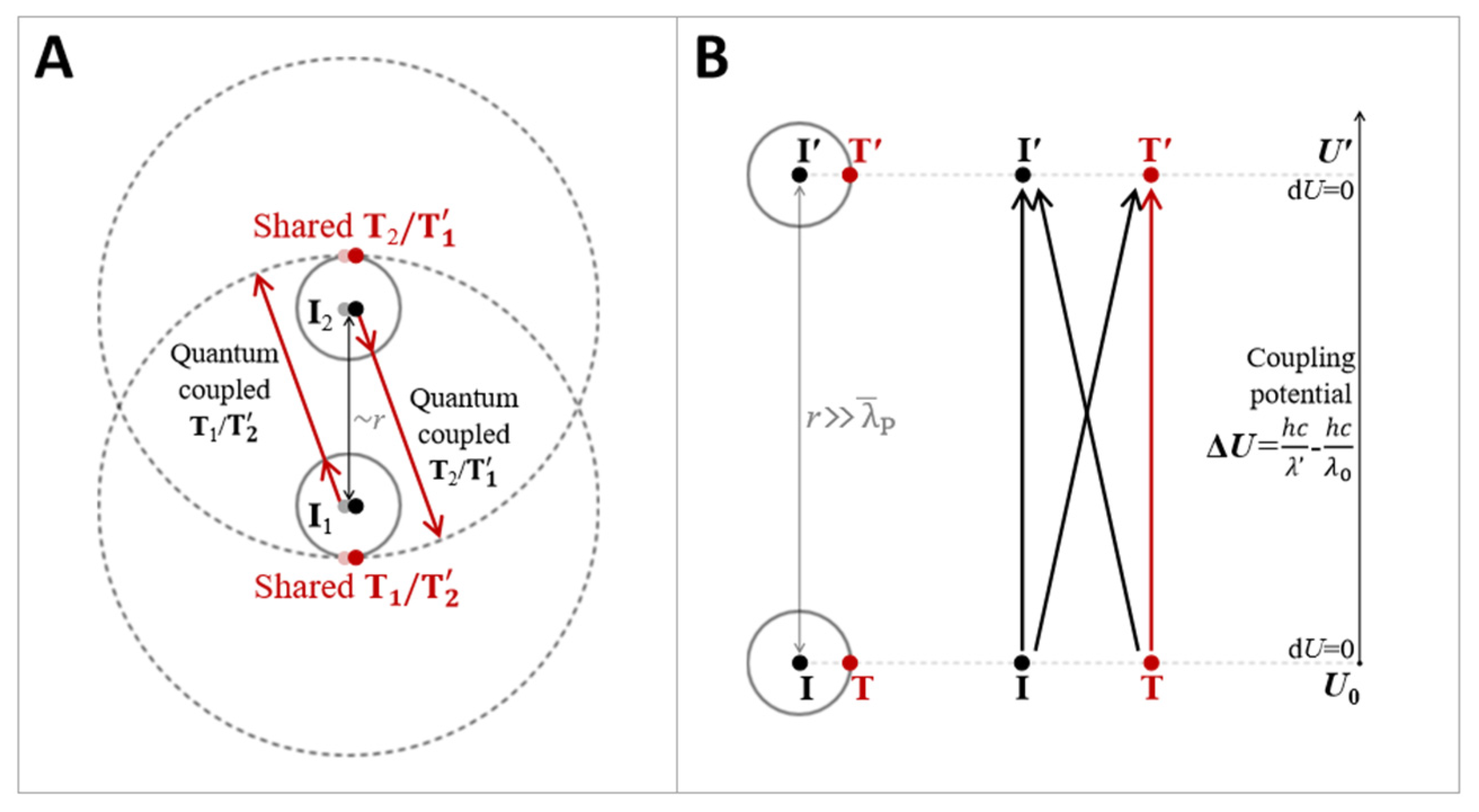
3. I/T and Electron/Compton Photon
3.1. Comparison Between I/T of 10 and e/γof Electron/Compton Photon
3.2. Hidden Properties of e/γ
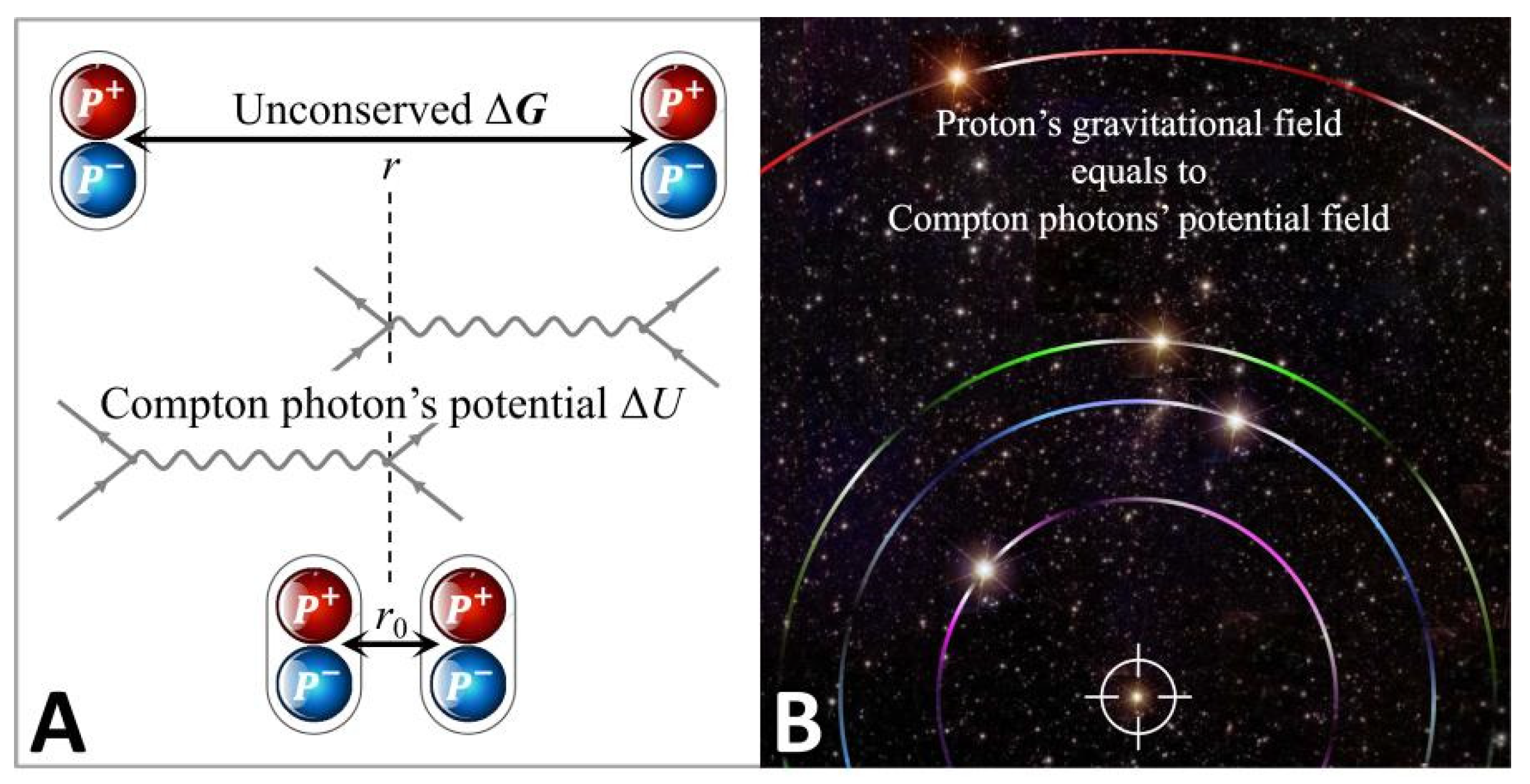
4. Compton Photons’ Field and Gravitational Field of a Proton
4.1. Annihilating Paradox and Its Solution
4.2. General Application of Compton Photons’ Potential
5. Conclusions and Discussion
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Arkani-Hamed, N. The Future of Fundamental Physics. Daedalus 2012, 141, 53–66. [Google Scholar] [CrossRef]
- Kostelecký, V.A. Gravity, Lorentz violation, and the standard model. Phys. Rev. D 2004, 69, 105009. [Google Scholar] [CrossRef]
- Joyce, A.; Jain, B.; Khoury, J.; Trodden, M. Beyond the cosmological standard model. Phys. Rep. 2015, 568, 1–98. [Google Scholar] [CrossRef]
- Ashtekar, A. Gravity and the quantum. New J. Phys. 2005, 7, 198. [Google Scholar] [CrossRef]
- Eichhorn, A.; Lippoldt, S. Quantum gravity and Standard-Model-like fermions. Phys. Lett. B 2017, 767, 142–146. [Google Scholar] [CrossRef]
- Spira, M.; Djouadi, A.; Graudenz, D.; Zerwas, R.M. Higgs boson production at the LHC. Nucl. Phys. B 1995, 453, 17–82. [Google Scholar] [CrossRef]
- Pitkin, M.; Reid, S.; Rowan, S.; Hough, J. Gravitational wave detection by interferometry (ground and space). Living Rev. Relativ. 2011, 14, 5. [Google Scholar] [CrossRef]
- Schwarz, J.H. Superstring theory. Phys. Rep. 1982, 89, 223–322. [Google Scholar] [CrossRef]
- Kiritsis, E. D-branes in standard model building, gravity and cosmology. Phys. Rep. 2005, 52, 200–263. [Google Scholar] [CrossRef]
- Rovelli, C. Loop quantum gravity. Living Rev. Relativ. 2008, 11, 5. [Google Scholar] [CrossRef]
- Castro, C. A Clifford algebra-based grand unification program of gravity and the Standard Model: A review study. Can. J. Phys. 2014, 92, 1501–1527. [Google Scholar] [CrossRef]
- Aprile, F.; Drummond, J.M.; Heslop, P.; Paul, H. Quantum gravity from conformal field theory. J. High Energy 2018, 2018, 35. [Google Scholar] [CrossRef]
- Odintsov, S.D.; Oikonomou, V.K. Aspects of axion F (R) gravity. Euro Phys. Lett. 2020, 129, 40001. [Google Scholar] [CrossRef]
- Antoniadis, I.; Benakli, K. Weak Gravity Conjecture in de Sitter Space-Time. Fortschritte Phys. 2020, 68, 2000054. [Google Scholar] [CrossRef]
- Bianconi, G. Gravity from entropy. Phys. Rev. D 2025, 111, 066001. [Google Scholar] [CrossRef]
- Sonner, J.; Withers, B. Linear gravity from conformal symmetry. Class. Quantum Gravity 2019, 36, 085011. [Google Scholar] [CrossRef]
- Chen, B.Y. Geometry of Submanifolds; Dover Publications: Mineola, NY, USA, 2019. [Google Scholar]
- Modanese, G. Metrics with zero and almost-zero Einstein action in quantum gravity. Symmetry 2019, 11, 1288. [Google Scholar] [CrossRef]
- Santos, F.F.; Boschi-Filho, H. Geometric Josephson junction. J. High Energy Phys. 2025, 2025, 135. [Google Scholar] [CrossRef]
- Bravo-Gaete, M.; Stetsko, M.M. Planar black holes configurations and shear viscosity in arbitrary dimensions with shift and reflection symmetric scalar-tensor theories. Phys. Rev. D 2022, 105, 024038. [Google Scholar] [CrossRef]
- Zhou, Y.; Zhang, J.; Meyer, E.; Zhang, X.; Zhang, J. Quantum Mechanics of a Quasi-Euclidean Space with Planck Length, Rotational Symmetry and Translational Symmetry. J. Appl. Math. Phys. 2025, 13, 302–326. [Google Scholar] [CrossRef]
- Mohr, P.J.; Taylor, B.N.; Newell, D.B. CODATA recommended values of the fundamental physical constants: 2006. J. Phys. Chem. Ref. Data 2008, 37, 1187–1284. [Google Scholar] [CrossRef]
- Macdonald, A. Spooky action at a distance: The puzzle of entanglement in quantum theory. Quantum 2012, 15. Available online: http://home.ustc.edu.cn/~gengb/201014/Spooky-action-in-QMs.pdf (accessed on 27 September 2025).
| I/T | e/γ | Deviation |
|---|---|---|
| I: v = 0 | e: v << c | – |
| m = 0.530 MeV | m = 0.511 MeV | 3.7% |
| interacting constant 1/137.036 082 with unknown ± | interacting constant 1/137.035 999 with certain ± | <10−6 |
| T: 10−12 m | γ 10−12 m | 3.7% |
| m = 0 | m = 0 | 0 |
| constant velocity v = c interacting constant 1038) with unknown ± | constant velocity c Gravitational constant 1038) with certain + | – 3.8% |
| I/T: 2T process with conserved quantum momentum | e/γ: (e++e−)2γ process with conserved momentum, charge, etc. | – |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, Y.; Zhang, J.; Meyer, E.; Zhang, X.; Liang, H. Quantum Behavior of 10D Planck Unit: Stationary Electron, Compton Photon and Gravitational Field. Symmetry 2025, 17, 1636. https://doi.org/10.3390/sym17101636
Zhou Y, Zhang J, Meyer E, Zhang X, Liang H. Quantum Behavior of 10D Planck Unit: Stationary Electron, Compton Photon and Gravitational Field. Symmetry. 2025; 17(10):1636. https://doi.org/10.3390/sym17101636
Chicago/Turabian StyleZhou, Yan, Junyan Zhang, Ernst Meyer, Xingkai Zhang, and Hongyu Liang. 2025. "Quantum Behavior of 10D Planck Unit: Stationary Electron, Compton Photon and Gravitational Field" Symmetry 17, no. 10: 1636. https://doi.org/10.3390/sym17101636
APA StyleZhou, Y., Zhang, J., Meyer, E., Zhang, X., & Liang, H. (2025). Quantum Behavior of 10D Planck Unit: Stationary Electron, Compton Photon and Gravitational Field. Symmetry, 17(10), 1636. https://doi.org/10.3390/sym17101636









