Quantum Coherence and Mixedness in Hydrogen Atoms: Probing Hyperfine Structure Dynamics Under Dephasing Constraints

Abstract

We investigate the quantum dynamics of coherence in the hyperfine structure of hydrogen atoms subjected to dephasing noise, modeled using the Lindblad master equation. The effective Hamiltonian describes the spin–spin interaction between the electron and proton, with dephasing introduced via Lindblad operators. Analytical solutions for the time-dependent density matrix are derived for various initial states, including separable, partially entangled, and maximally entangled configurations. Quantum coherence is quantified through the $l_1$-norm measures, while purity is evaluated to assess mixedness. Results demonstrate that coherence exhibits oscillatory decay modulated by the dephasing rate, with antiparallel spin states showing greater resilience against noise compared to parallel configurations. These findings highlight the interplay between coherent hyperfine dynamics and environmental dephasing, offering insights into preserving quantum resources in atomic systems for applications in quantum information science.

1. Introduction

The hydrogen atom, distinguished by its remarkably simple configuration, has long functioned as a fundamental basis for understanding quantum mechanics, producing significant revelations about the interactions of electrons and nuclei in a broad spectrum of physical, chemical, and biological settings [1,2,3,4,5]. Apart from its central position in quantum theory, the hydrogen atom assumes a critical function in quantum information science, acting as an inherent model for examining quantum correlations. The spins of the electron and nucleus within the hydrogen atom supply a conceptually straightforward setup and a clearly specified Hilbert space for analyzing two-party quantum entanglement. Its degree is assessed via two-qubit concurrence and quantum coherence metrics, which are intimately tied to essential constants such as the Planck constant, Boltzmann constant, electron and proton masses, fine-structure constant, Bohr radius, and Bohr magneton. In low temperature regimes, the hyperfine structure (HFS) levels of the hydrogen atom manifest built-in entanglement that rapidly diminishes with increasing temperature, fully dissipating past a pivotal limit of ${\tau }_c\approx 5.35\mu \mathrm{eV}$. This occurrence arises from the thermal equilibrium properties of the HFS states, in which the entanglement proves to be highly sensitive to the equilibrium between the energy difference and thermal agitation [6,7,8]. Modern explorations have identified nuclear-polarized states of hydrogen atoms integrated into solid H₂ matrices [6,9], exhibiting pronounced anomalies from the Boltzmann distribution under chilled conditions [6,7,8]. This has provoked fascinating inquiries into the contributions of quantum mechanisms in these setups. Furthermore, cutting-edge research has revealed innovative mechanisms that influence entanglement and coherence in hydrogen atomic systems. In particular, cosmic expansion of the universe has been shown to induce the emergence of quantum entanglement within the hyperfine structure of hydrogen atoms, culminating in a “sudden birth” of entanglement over vast cosmological timescales [10]. In parallel, analyses of dissipative processes via the Lindblad master equation have illuminated the temporal decay of quantum coherence and purity in hyperfine states, emphasizing how environmental dissipation affects the sustenance of quantum features in such atoms [11].

Quantum coherence (QC), arising from the principle of superposition, is foundational in quantum mechanics and represents a vital resource for numerous quantum information processing applications, ranging from quantum reference frames [12,13] to quantum transport in biological systems [14,15,16] and quantum thermodynamics [17,18,19]. Quantifying QC remains a pivotal challenge for deepening the theoretical principles of quantum mechanics as well as for advancing practical applications in quantum information science, leading to substantial research attention in recent years [20]. This framework has illuminated the critical role of coherence in enabling quantum advantages, as exemplified in quantum state merging [21], deterministic quantum computation with one qubit (DQC1) [22], the Deutsch–Jozsa algorithm [23], and Grover’s search algorithm [24]. Moreover, coherence resource theory offers a robust framework for understanding the wavelike properties of quantum systems [25] and the nature of quantum correlations, including entanglement [26] and various discord-like measures [27]. Baumgratz et al. [20] introduced a resource-theoretic approach for systematically measuring QC in quantum states, laying the groundwork for diverse coherence measures based on distinct physical principles. Initial measures included the $l_1$-norm of coherence and the relative entropy of coherence, both of which are grounded in distance-based metrics [20], while subsequent developments have incorporated entanglement-based measures [28], operational perspectives [29,30], and convex-roof constructions [31,32]. These tools have enabled detailed studies of QC’s diverse properties, including its interaction with other quantum resources [28,33,34], its behavior in infinite-dimensional Hilbert spaces [35,36], its related complementarity principles [37], and the characterization of macroscopic coherence [38]. This resource-based approach has led to extensive research into the wider implications of QC [13,39,40].

The study of open quantum systems explores the dynamical evolution of quantum systems coupled to their surrounding environment, forming a field of paramount importance since the inception of quantum mechanics [41]. Despite substantial theoretical advancements, fundamental challenges persist, particularly regarding decoherence, i.e., the dissipation of quantum coherence arising from system–environment interactions. This process has garnered extensive investigation in the realms of quantum information processing and quantum computation, where it poses a formidable barrier to the realization of quantum information technologies [42,43,44]. The preservation of quantum coherence is essential for the efficacy of quantum computing architectures, quantum cryptographic protocols, and quantum teleportation schemes. Furthermore, decoherence plays a critical role in elucidating the quantum-to-classical transition, wherein classical properties emerge from quantum systems through environmentally induced decoherence. Recent investigations have enriched our understanding of the dynamics of decoherence in open quantum systems. For example, explorations have established that decoherence manifests itself as a reflection of Anderson localization phenomena in systems governed by locally generated Lindblad dynamics, underscoring the exponential attenuation of coherence [45]. In addition, innovative methodologies for robust and optimal control have been devised to counteract system flaws and environmental noise in open quantum setups, achieving markedly reduced infidelity and improved scalability in experimental platforms such as superconducting circuits [46]. Parallel efforts have probed the coherence–decoherence balance in multilevel quantum arrangements subjected to projective stochastic pulses [47]. Furthermore, comprehensive reviews of non-equilibrium boundary-driven quantum systems have detailed models, methods, and properties that elucidate irreversibility in dissipative environments, providing fresh insights into transport phenomena and phase transitions in Markovian open quantum systems [48].

The aim of the present manuscript is to investigate the quantum dynamics of coherence in the hyperfine structure of hydrogen atoms under the influence of pure dephasing noise by utilizing the Lindblad master equation to model the system’s evolution. By deriving analytical solutions for the time-dependent density matrix across various initial states ranging from separable to partially and maximally entangled configurations, we quantify quantum coherence via the $l_1$ norm measures and evaluate its purity to assess the degree of mixedness induced by environmental interactions.

Studies of coherence and hyperfine dynamics in atomic hydrogen remain central in quantum optics and precision measurement. Notably, extraordinary spin-coherence lifetimes ($T_2\approx 280\mu \mathrm{s}$ at 90 K) have been reported for atomic hydrogen encapsulated in silsesquioxane cages using dynamical decoupling techniques [49], while the intrinsic entanglement and coherence of hyperfine levels as well as their enhancement by magnetic fields have been quantified in terms of fundamental constants [50]. High-resolution two-photon frequency-comb spectroscopy also provides direct experimental access to hyperfine coherence [51], and recent advances in manipulating cold hydrogen beams for probing gravitational quantum states further highlight the precision and control achievable in these systems [52]. Building on this background, our study complements and extends these efforts by analyzing the interplay of coherence and mixedness in the hyperfine structure of hydrogen under controlled dephasing. In particular, we explicitly characterize how noise channels affect these two complementary quantities, which have not previously been investigated together in this context, thereby embedding the coherence–mixedness dynamics within a realistic open-system framework based on the Lindblad formalism. The novelty of our contribution is twofold: (i) we establish a direct connection between the projection of hyperfine states onto the dephasing axis and their robustness, providing a physical explanation for the enhanced resilience of antiparallel over parallel configurations, and (ii) we demonstrate that the coherence–mixedness dynamics of hydrogen hyperfine levels can serve as sensitive probes of environmental noise. This perspective not only complements existing studies on coherence lifetimes and entanglement generation [10], but also advances understanding by situating these phenomena in the concrete physical setting of hydrogen hyperfine dynamics, a system that is of enduring importance in quantum optics and fundamental physics.

The rest of this manuscript is structured as follows: Section 2 describes the Hamiltonian system and introduces the Lindblad formalism used to model the dynamics of dephasing in the hyperfine structure; Section 3 presents closed-form analytical solutions for the time-dependent density matrix elements corresponding to relevant initial states, including separable, partially entangled, and maximally entangled configurations; Section 4 introduces measures of quantum coherence and the degree of mixedness, then analyzes their time-dependent behavior under the considered model with the support of numerical results and illustrative figures; finally, Section 5 summarizes the key findings and conclusions of this study.

2. Hyperfine Interaction in Hydrogen and Lindblad Formalism

In atomic hydrogen, hyperfine interaction originates from the coupling between the magnetic moments of the electron and proton. The ground-state electron occupies the $1s$ orbital, where the orbital angular momentum vanishes ($\ell =0$). As a result, no magnetic field is produced at the nucleus due to orbital motion. As such, the interaction is purely magnetic dipole–dipole in nature, involving only the intrinsic spins of the electron and proton [4].

This spin–spin interaction leads to energy splitting, observable as the 1420 MHz transition—the well-known 21 cm line—which plays a foundational role in astrophysical and spectroscopic observations [53]. Theoretical modeling via first-order perturbation theory captures this effect through a Hamiltonian proportional to the scalar product $\mathbf{I}·\mathbf{S}$, where $\mathbf{I}$ and $\mathbf{S}$ represent the nuclear and electron spin operators. The inclusion of an external magnetic field further extends the Hamiltonian to account for Zeeman splitting [50,53,54].

2.1. Hyperfine Structure of the Hydrogen Atom and Hamiltonian

The effective Hamiltonian for the hydrogen ground-state hyperfine interaction reads:

$$H_{\mathrm{HF}}=J{\widehat{\sigma }}_e·{\widehat{\sigma }}_p=J\left({\sigma }_x^e{\sigma }_x^p+{\sigma }_y^e{\sigma }_y^p+{\sigma }_z^e{\sigma }_z^p\right),$$

(1)

where J is the hyperfine coupling constant and where ${\widehat{\sigma }}_e$ and ${\widehat{\sigma }}_p$ denote the Pauli matrices for the electron and proton, respectively. Here, $H_{\mathrm{HF}}$ represents the effective hyperfine interaction Hamiltonian of the hydrogen ground state, expressed in the isotropic Heisenberg form. Its origin lies in the magnetic dipole–dipole interaction between the electron and proton spins [53]. Recent works have also employed this Hamiltonian in studying entanglement in hydrogen atoms [10].

This constant J can be expressed explicitly as follows [53]:

$$J={\displaystyle \frac{2\pi }{3}}{\displaystyle \frac{1}{4\pi {\epsilon }_0}}{\displaystyle \frac{g_{e}e}{2m_e}}{\displaystyle \frac{g_{p}e}{2m_p}}{\displaystyle \frac{{\hslash }^2}{c\pi a_0^3}},$$

(2)

where ${\epsilon }_0$ is the vacuum permittivity, ℏ is the reduced Planck constant, c is the speed of light, $a_0$ is the Bohr radius, and $g_e$, $g_p$, $m_e$, and $m_p$ are the respective g-factors and masses of the electron and proton. This formulation reflects the magnetic interaction strength derived from the electron’s wavefunction density at the nucleus.

The full spin Hilbert space of the hydrogen atom is the tensor product space spanned by

$$\mathcal{B}=\left\{\right|{\uparrow }_e{\uparrow }_p\rangle ,|{\uparrow }_e{\downarrow }_p\rangle ,|{\downarrow }_e{\uparrow }_p\rangle ,|{\downarrow }_e{\downarrow }_p\rangle \}.$$

In this basis, the Hamiltonian has four eigenstates: the singlet

$$|a_p\rangle ={\displaystyle \frac{1}{\sqrt{2}}}\left(|{\uparrow }_e{\downarrow }_p\rangle -|{\downarrow }_e{\uparrow }_p\rangle \right),$$

with eigenvalue $E_a=-3J$, and a triplet manifold consisting of

$$|b_p\rangle =|{\uparrow }_e{\uparrow }_p\rangle ,|c_p\rangle ={\displaystyle \frac{1}{\sqrt{2}}}\left(|{\uparrow }_e{\downarrow }_p\rangle +|{\downarrow }_e{\uparrow }_p\rangle \right),|d_p\rangle =|{\downarrow }_e{\downarrow }_p\rangle ,$$

all sharing the eigenvalue $E_b=E_c=E_d=J$. Thus, the hyperfine energy splitting is $\Delta E=4J\approx 5.88\mu \mathrm{eV}$.

In the absence of an external magnetic field, the ground state of the system is the entangled singlet state $|a\rangle$. Upon application of a magnetic field [50], the degeneracy is lifted and the energy levels become field-dependent, enabling controllable transitions. This tunability is crucial in quantum information and metrology applications.

2.2. Quantum Dynamics Under Pure Dephasing

Dephasing is a central decoherence mechanism in quantum systems, arising when environmental fluctuations disrupt the relative phase between quantum states while leaving populations unchanged. In hydrogen hyperfine systems, such dephasing naturally occurs due to local magnetic field variations and phase noise from external electromagnetic fields, which act differently on the spin components of the electron and proton. These fluctuations primarily affect the relative phase between spin states, making dephasing the dominant decoherence process in many experimental settings. While other types of noise may also be present, such as bit-flip or damping processes, pure dephasing provides a realistic and analytically tractable model that can capture the essential dynamics of coherence and mixedness. The Lindblad master equation offers a rigorous framework for describing this process, ensuring that the density matrix evolution remains physically consistent and trace-preserving.

To accurately model such decoherence, we employ the Lindblad formalism with local ${\sigma }_z$-type Lindblad operators, which selectively suppress coherences without inducing energy relaxation. This approach provides a clear and tractable framework for analyzing how entanglement and quantum coherence evolve under phase noise in the two-qubit (electron–proton) system.

2.2.1. Lindblad Master Equation for Dephasing

In our model, the dephasing dynamics of hydrogen hyperfine states are described using the Lindblad master equation, which provides an appropriate and analytically tractable framework for Markovian decoherence without memory effects. Dephasing acts independently on the electron and proton spins, as represented by the Lindblad operators $L_e={\sigma }_z^e\otimes I_p$ and $L_p=I_e\otimes {\sigma }_z^p$. This choice is justified because the dominant decoherence mechanism in hydrogen hyperfine systems arises from local magnetic field fluctuations and phase noise, which primarily affect the relative phase of the spins without altering their populations. While additional noise channels such as bit-flip or damping processes could in principle be present, they are typically weaker under the considered experimental conditions and would complicate the analysis without qualitatively changing the essential coherence and mixedness dynamics. By focusing on independent dephasing, the model remains both physically realistic and analytically manageable.

The evolution of the density matrix $\rho \left(t\right)$ is governed by the Lindblad equation:

$${\displaystyle \frac{d\rho }{dt}}=-i[H_{\mathrm{HF}},\rho ]+\mathcal{D}\left(\rho \right)$$

(3)

where $H_{\mathrm{HF}}$ is the hyperfine Hamiltonian and $\mathcal{D}\left(\rho \right)$ is the dissipator encoding the environmental interaction. For pure dephasing, we consider the following local Lindblad operators:

$$L_e={\sigma }_z^e\otimes I_p,L_p=I_e\otimes {\sigma }_z^p$$

(4)

with corresponding dephasing rates ${\gamma }_e$ and ${\gamma }_p$. The dissipator becomes

$$\mathcal{D}\left(\rho \right)={\gamma }_e(L_e\rho L_e-\rho )+{\gamma }_p(L_p\rho L_p-\rho ),$$

(5)

which simplifies due to the property $L_e^2=L_p^2=I$, valid for Pauli operators. The operators $L_e={\sigma }_z^e\otimes I_p$ and $L_p=I_e\otimes {\sigma }_z^p$ correspond to local dephasing channels acting independently on the electron and proton spins. Such phase-damping operators are widely used in the Lindblad description of spin-$1/2$ systems [55,56].

This framework allows us to directly investigate how independent dephasing of the electron and proton spins influences the time evolution of coherence and mixedness in the hydrogen hyperfine system.

2.2.2. Differential Equations for Matrix Elements

Let $A=J/\hslash$ denote the coherent interaction strength. In the standard computational basis $\mathcal{B}={\left\{\right|\uparrow }_e{\uparrow }_p{\rangle ,|\uparrow }_e{\downarrow }_p{\rangle ,|\downarrow }_e{\uparrow }_p{\rangle ,|\downarrow }_e{\downarrow }_p\rangle \}$, the evolution equations for the density matrix elements ${\rho }_{ij}\left(t\right)$ under dephasing are as follows:

• Populations:

$$\begin{array}{cc}\hfill {\displaystyle \frac{d{\rho }_{11}}{dt}}& =0\hfill \end{array}$$

(6)

$$\begin{array}{cc}\hfill {\displaystyle \frac{d{\rho }_{22}}{dt}}& =-2iA({\rho }_{23}-{\rho }_{32})\hfill \end{array}$$

(7)

$$\begin{array}{cc}\hfill {\displaystyle \frac{d{\rho }_{33}}{dt}}& =2iA({\rho }_{23}-{\rho }_{32})\hfill \end{array}$$

(8)

$$\begin{array}{cc}\hfill {\displaystyle \frac{d{\rho }_{44}}{dt}}& =0\hfill \end{array}$$

(9)

• Coherences:

$$\begin{array}{cc}\hfill {\displaystyle \frac{d{\rho }_{12}}{dt}}& =-2iA({\rho }_{12}-{\rho }_{13})-2{\gamma }_p{\rho }_{12}\hfill \end{array}$$

(10)

$$\begin{array}{cc}\hfill {\displaystyle \frac{d{\rho }_{13}}{dt}}& =-2iA({\rho }_{13}-{\rho }_{12})-2{\gamma }_e{\rho }_{13}\hfill \end{array}$$

(11)

$$\begin{array}{cc}\hfill {\displaystyle \frac{d{\rho }_{14}}{dt}}& =-2({\gamma }_e+{\gamma }_p){\rho }_{14}\hfill \end{array}$$

(12)

$$\begin{array}{cc}\hfill {\displaystyle \frac{d{\rho }_{23}}{dt}}& =-2iA({\rho }_{22}-{\rho }_{33}+{\rho }_{23})-2({\gamma }_e+{\gamma }_p){\rho }_{23}\hfill \end{array}$$

(13)

$$\begin{array}{cc}\hfill {\displaystyle \frac{d{\rho }_{24}}{dt}}& =-2iA({\rho }_{24}-{\rho }_{34})-2{\gamma }_e{\rho }_{24}\hfill \end{array}$$

(14)

$$\begin{array}{cc}\hfill {\displaystyle \frac{d{\rho }_{34}}{dt}}& =-2iA({\rho }_{24}-{\rho }_{34})-2{\gamma }_p{\rho }_{34}\hfill \end{array}$$

(15)

with ${\rho }_{ij}^{*}={\rho }_{ji}$. These equations explicitly capture the essential features of pure dephasing, namely, the invariance of populations and the exponential decay of off-diagonal coherences. Importantly, the coupling between ${\rho }_{22}$, ${\rho }_{33}$, and ${\rho }_{23}$ shows how coherence loss directly influences population transfer between entangled spin configurations.

In the next section, we present the complete analytical expressions for the time-dependent density matrix elements, corresponding to several physically relevant and experimentally accessible initial states.

3. Closed-Form Solutions for Relevant Initial States

Elaborating on the formalism developed in the preceding sections, we now provide explicit analytical expressions for the time-dependent density matrix elements. The results are provided for a set of physically relevant and experimentally accessible initial states in the hyperfine structure of the hydrogen atom, enabling a direct examination of their dynamical behavior. In the following section, we analyze the evolution of quantum correlations in this dephasing scenario by solving these equations for relevant initial conditions.

• First Case:

The following time-dependent solutions ${\rho }_{ij}\left(t\right)$ correspond to the initial pure state

$$\begin{array}{c}\hfill |a\rangle ={cos\left(\alpha \right)|\uparrow }_e{\downarrow }_p{\rangle +sin\left(\alpha \right)|\downarrow }_e{\uparrow }_p\rangle ,\end{array}$$

(16)

which represents a coherent superposition of states with opposite spin alignments and lies in the zero total spin subspace. This state is not an eigenstate of the hyperfine Hamiltonian, and as such is subject to nontrivial coherent dynamics.

We first define the relevant parameters:

$$\begin{array}{c}\hfill \Gamma ={\gamma }_e+{\gamma }_p,\Omega =\sqrt{16A^2-{\Gamma }^2}.\end{array}$$

(17)

Using these definitions, the analytical expressions for the density matrix elements can be systematically derived. These elements naturally fall into two categories: those that vanish identically, and those that remain nonzero. The explicit forms of both types are provided below.

Zero Elements:

$$\begin{array}{cc}\hfill {\rho }_{11}\left(t\right)& ={\rho }_{12}\left(t\right)={\rho }_{13}\left(t\right)={\rho }_{14}\left(t\right)=0\hfill \end{array}$$

(18)

$$\begin{array}{cc}\hfill {\rho }_{21}\left(t\right)& ={\rho }_{24}\left(t\right)=0\hfill \end{array}$$

(19)

$$\begin{array}{cc}\hfill {\rho }_{31}\left(t\right)& ={\rho }_{34}\left(t\right)=0\hfill \end{array}$$

(20)

$$\begin{array}{cc}\hfill {\rho }_{41}\left(t\right)& ={\rho }_{42}\left(t\right)={\rho }_{43}\left(t\right)={\rho }_{44}\left(t\right)=0.\hfill \end{array}$$

(21)

Non-Zero Elements:

$$\begin{array}{cc}\hfill {\rho }_{22}\left(t\right)& ={\displaystyle \frac{1}{2}}+{\displaystyle \frac{1}{2}}cos\left(2\alpha \right)e^{-\Gamma t}\left({\displaystyle \frac{\Gamma }{\Omega }}sin(\Omega t)+cos(\Omega t)\right)\hfill \end{array}$$

(22)

$$\begin{array}{cc}\hfill {\rho }_{33}\left(t\right)& ={\displaystyle \frac{1}{2}}-{\displaystyle \frac{1}{2}}cos\left(2\alpha \right)e^{-\Gamma t}\left({\displaystyle \frac{\Gamma }{\Omega }}sin(\Omega t)+cos(\Omega t)\right)\hfill \end{array}$$

(23)

$$\begin{array}{cc}\hfill {\rho }_{23}\left(t\right)& ={\displaystyle \frac{1}{2}}sin2\alpha e^{-2\Gamma t}+2i{\displaystyle \frac{A}{\Omega }}cos\left(2\alpha \right)e^{-\Gamma t}sin(\Omega t).\hfill \end{array}$$

(24)

Before proceeding to the numerical calculations, it is instructive to briefly discuss three key physical aspects of our system: collective decoherence, coherent oscillations, and subspace confinement. Collective decoherence arises when the qubits (hyperfine states) interact with a common environment, leading to correlated decay processes that can either enhance or suppress decoherence effects. Coherent oscillations reflect the unitary exchange of population and phase between the states, governed by the system’s intrinsic couplings. Subspace confinement occurs when the dynamics of the system remains restricted to a reduced Hilbert space, typically due to symmetry constraints or conservation laws, which can have significant implications for preserving quantum correlations. Indeed, the time evolution of the system under local dephasing reveals a rich interplay between coherent and dissipative effects. The collective decoherence is characterized by the total rate $\Gamma ={\gamma }_e+{\gamma }_p$, which combines the individual dephasing effects of the electron and proton, leading to a global damping of both populations and coherences in the entangled state. The coherent oscillations arise with frequency $\Omega =\sqrt{16A^2-{\Gamma }^2}$, capturing the competition between the hyperfine coupling strength A and the total dephasing rate $\Gamma$; when $16A^2>{\Gamma }^2$, spin states undergo sustained oscillations, whereas for $16A^2\le {\Gamma }^2$ the dynamics become overdamped with purely exponential decay. In addition, this expression reveals two distinct contributions: a purely decaying term ($\propto sin2\alpha$), and an oscillatory term with frequency $\Omega$ weighted by $cos2\alpha$. The oscillations originate from coherent hyperfine spin exchange, while the exponential factors $e^{-\Gamma t}$ and $e^{-2\Gamma t}$ account for dephasing-induced damping. Depending on $\alpha$, the balance between decay and oscillation varies; for $\alpha =\pi /4$, only the exponential decay survives, whereas for $\alpha =0$ or $\pi /2$ the oscillations dominate.

Moreover, subspace confinement ensures that the populations of ${|\uparrow }_e{\uparrow }_p\rangle$ and ${|\downarrow }_e{\downarrow }_p\rangle$ remain zero throughout, restricting the dynamics to the ${|\uparrow }_e{\downarrow }_p\rangle$–${|\downarrow }_e{\uparrow }_p\rangle$ manifold in accordance with the initial state and interaction Hamiltonian. Overall, the dynamics are shaped by the interplay between coherent spin-exchange processes (governed by A) and decoherence (governed by $\Gamma$), with oscillatory components gradually suppressed by environmental noise within the entangled subspace.

• Second Case:

We consider the following initial entangled state on the hyperfine spin basis:

$$\begin{array}{c}\hfill |b\rangle ={cos\left(\alpha \right)|\uparrow }_e{\uparrow }_p{\rangle +sin\left(\alpha \right)|\downarrow }_e{\downarrow }_p\rangle ,\end{array}$$

(25)

where $\alpha$ controls the initial degree of entanglement between the electron and proton spins. This is a coherent superposition of the two aligned spin states, and lies in the symmetric subspace of the two-qubit Hilbert space.

Assuming local pure dephasing acting independently on the electron and proton spins, with decay rates ${\gamma }_e$ and ${\gamma }_p$, respectively, the system evolves under the Lindblad master equation with Lindblad operators of dephasing type. The elements of the non-vanishing density matrix at time t are as follows:

$$\begin{array}{cc}\hfill {\rho }_{11}\left(t\right)& ={cos}^2\left(\alpha \right)\hfill \end{array}$$

(26)

$$\begin{array}{cc}\hfill {\rho }_{14}\left(t\right)& ={\rho }_{41}\left(t\right)={\displaystyle \frac{1}{2}}sin\left(2\alpha \right)e^{-2\Gamma t}\hfill \end{array}$$

(27)

$$\begin{array}{cc}\hfill {\rho }_{44}\left(t\right)& ={sin}^2\left(\alpha \right)\hfill \end{array}$$

(28)

and all other elements vanish:

$$\begin{array}{c}\hfill {\rho }_{ij}\left(t\right)=0\mathrm{for}\mathrm{all}\mathrm{other}(i,j)\notin \{(1,1),(1,4),(4,1),(4,4)\}.\end{array}$$

(29)

The evolution of this system exhibits a clear separation between population and coherence dynamics; indeed, populations (${\rho }_{11}$ and ${\rho }_{44}$) remain constant in time. This reflects the nature of pure dephasing, which preserves energy populations while destroying quantum coherence. Further, coherence between the states ${|\uparrow }_e{\uparrow }_p\rangle$ and ${|\downarrow }_e{\downarrow }_p\rangle$, which is encoded in the off-diagonal elements ${\rho }_{14}$ and ${\rho }_{41}$, decays exponentially as follows:

$$\begin{array}{c}\hfill {\rho }_{14}\left(t\right),{\rho }_{41}\left(t\right)\propto e^{-2\Gamma t},\mathrm{with}\Gamma ={\gamma }_e+{\gamma }_p.\end{array}$$

(30)

This exponential decay is governed solely by the collective dephasing rate $\Gamma$, rather than the individual decay rates; the coherence decay depends on the total strength of dephasing noise across the system, and is insensitive to the partitioning of noise between subsystems.

It should be noted that this solution does not depend on the hyperfine coupling parameter A, which governs the coherent part of the Hamiltonian system. This independence comes from the fact that the initial state $|b\rangle$ is an eigenstate of the interaction Hamiltonian H when cross terms are absent, resulting in a trivial unitary evolution. Consequently, the system dynamics arises solely from decoherence effects rather than from coherent evolution driven by A. This characteristic underscores the stability of population probabilities and the vulnerability of quantum coherence under pure dephasing, with the decay of entanglement and off-diagonal correlations entirely determined by the collective decay rate $\Gamma$. The two initial conditions considered here are chosen to capture complementary aspects of the hydrogen hyperfine structure under dephasing. The state $|a\rangle$ represents an entangled superposition within the triplet–singlet subspace, directly reflecting the hyperfine interaction. In contrast, $|b\rangle$ corresponds to parallel-spin entanglement, which is generally more susceptible to dephasing. This choice allows us to contrast the robustness of antiparallel versus parallel spin configurations as well as to quantify how coherence and mixedness evolve in these two distinct scenarios.

4. Quantum Coherence and Results

While previous works have demonstrated extended hyperfine coherence lifetimes in trapped hydrogen, intrinsic entanglement of hyperfine states, and high-precision spectroscopy of coherence, our focus on how dephasing affects the interplay between coherence and mixedness in the hydrogen hyperfine system provides fresh insight. This perspective complements prior quantum optics-based control studies and opens avenues for understanding decoherence mechanisms within fundamental atomic systems.

To capture this interplay faithfully, it is essential to track not only the loss of coherence but also the accompanying increase in state mixedness, since coherence alone does not provide a complete picture of the degradation of quantum properties under noise. To make this analysis concrete, we quantify coherence and mixedness through two complementary measures applied to the hyperfine dynamics of hydrogen: the $l_1$-norm of coherence, rooted in the resource-theoretic framework, and the purity, which captures the degree of mixedness of the quantum state. The $l_1$-norm satisfies the standard criteria for a valid coherence measure, including non-negativity, vanishing for incoherent states, monotonicity under incoherent operations, and convexity. Purity, although not a coherence monotone in the strict sense, provides valuable insight into the interplay between coherence and decoherence by quantifying the extent of state mixing induced by environmental noise. For completeness, we note that the entanglement dynamics quantified by the concurrence reduce in this case to simple functions of the coherence elements already discussed above. Specifically, for the state $|a\rangle$, the concurrence is $C=2|{\rho }_{23}\left(t\right)|$, while for the state $|b\rangle$ it is $C=2|{\rho }_{14}\left(t\right)|$. Because the density matrix retains an X-state structure throughout the evolution, the concurrence depends only on these off-diagonal elements, which also define the system’s coherence. Therefore, the concurrence follows the same qualitative behavior as coherence and purity under dephasing, and no additional independent features arise in this setting.

4.1. $l_1$-Norm of Coherence

The quantum coherence in our system is quantified using the $l_1$-norm of coherence, defined as

$$C_{l_1}\left(\widehat{\rho }\right)=\sum _{i\ne j}\left|{\rho }_{ij}\right|,$$

(31)

which is obtained by summing the absolute values of all off-diagonal elements of the density matrix. This measure directly captures the extent of quantum superpositions in the chosen basis and provides an operationally transparent way of assessing how coherences decay under dephasing noise.

The $l_1$-norm is particularly advantageous for finite-dimensional systems, such as the two-qubit Hilbert space describing the hyperfine interaction in the hydrogen atom, since it can be evaluated analytically once the density matrix is known. A larger value of $C_{l_1}$ indicates stronger coherence, and consequently a greater ability of the system to exhibit quantum interference effects; conversely, a monotonic decay of $C_{l_1}$ reflects the progressive loss of quantum superposition due to environmental dephasing.

In the present model, the $l_1$-norm reveals distinct dynamical behaviors depending on the initial state. For states with non-vanishing off-diagonal elements, $C_{l_1}$ exhibits oscillatory features driven by the hyperfine coupling, which are progressively damped as the dephasing rate $\Gamma$ increases. For states with no initial coherence (such as $\alpha =0$ in $|b\rangle$), the $l_1$-norm remains identically zero at all times, indicating the absence of any quantum superposition throughout the evolution. This clear distinction underscores the sensitivity of the $l_1$-norm in diagnosing both the presence and robustness of quantum coherence under noise.

In the following, we present the time evolution of this quantity under different dephasing rates and initial conditions, thereby illustrating how coherence jointly characterizes the degradation of quantum properties in the hydrogen hyperfine system.

The parameters employed in our analysis are chosen within experimentally realistic regimes. The hyperfine coupling constant J corresponds to the well-established hydrogen ground state transition 21 cm (frequency $\sim 1420$ MHz) [57,58], while the dephasing rates are taken in ranges consistent with previous studies of atomic coherence and decoherence in hydrogen-like systems [10,59]. These values ensure that the presented results are relevant for potential laboratory investigations.

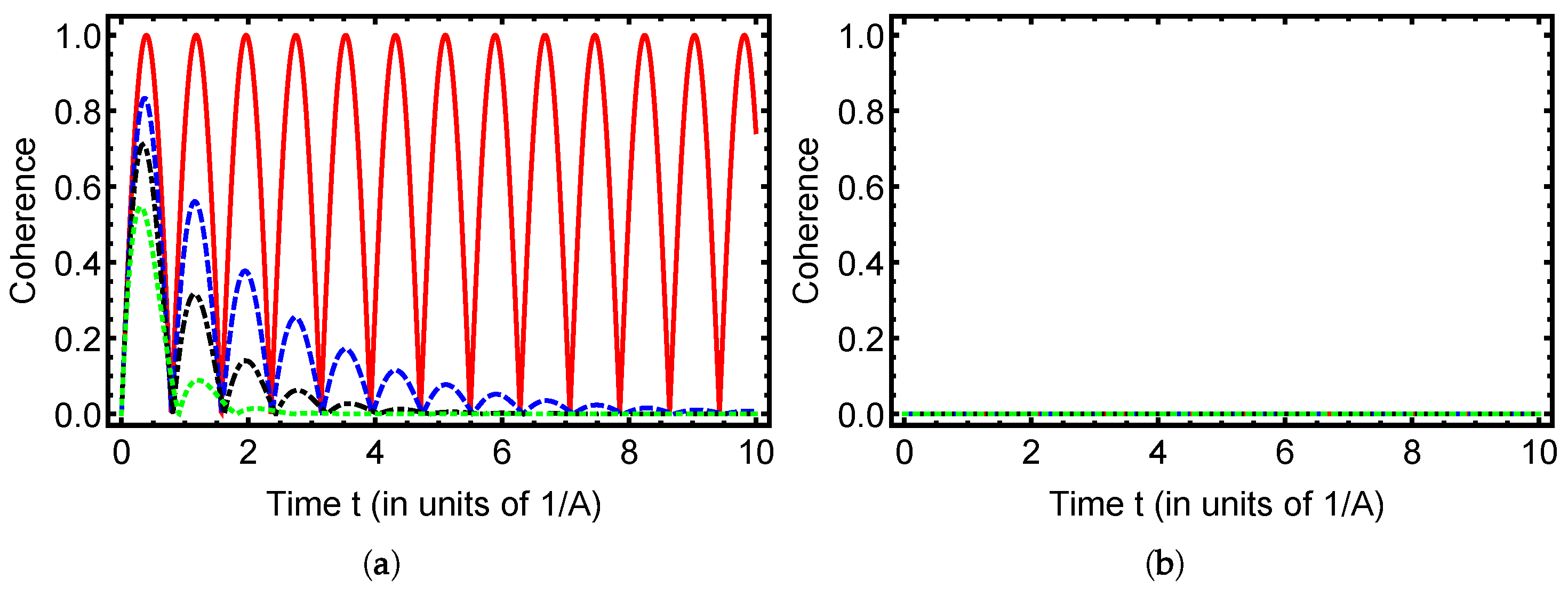
Figure 1a,b depicts the time evolution of quantum coherence for the initial separable state ($\alpha =0$) under different pure dephasing rates $\Gamma$. The curves correspond to the cases $\Gamma =0$ (solid red), $\Gamma =0.5A$ (blue dashed), $\Gamma =A$ (dotted black dashed), and $\Gamma =2A$ (dotted green). Panel (a) corresponds to the initial state $|a\rangle ,$ while panel (b) corresponds to $|b\rangle .$ For $\Gamma =0$, the coherence in Figure 1a exhibits persistent oscillations driven solely by the coherent hyperfine coupling A, reflecting undamped unitary dynamics. As the dephasing rate $\Gamma$ increases, these oscillations are progressively suppressed and the coherence decays more rapidly. This behavior illustrates the detrimental effect of pure dephasing on maintaining quantum superpositions: the larger the value of $\Gamma$, the faster the off-diagonal density matrix elements vanish. For the initial state $|a\rangle$ (Figure 1a), coherence oscillations are clearly visible at low $\Gamma$ and display a gradual amplitude reduction with increasing $\Gamma$. In contrast, for the state $|b\rangle$ (Figure 1b), the coherence remains identically zero for $\alpha =0$ at all times and is independent of $\Gamma$, which is due to the fact that this state is an eigenstate of the noiseless Hamiltonian and contains no initial superposition between the relevant basis states. In summary, while $|a\rangle$ supports coherent exchange dynamics that are gradually suppressed by dephasing, $|b\rangle$ shows no coherence dynamics for $\alpha =0$. In both cases, the long-time limit corresponds to a complete loss of coherence for any $\Gamma >0$, leaving the system in an incoherent statistical mixture.

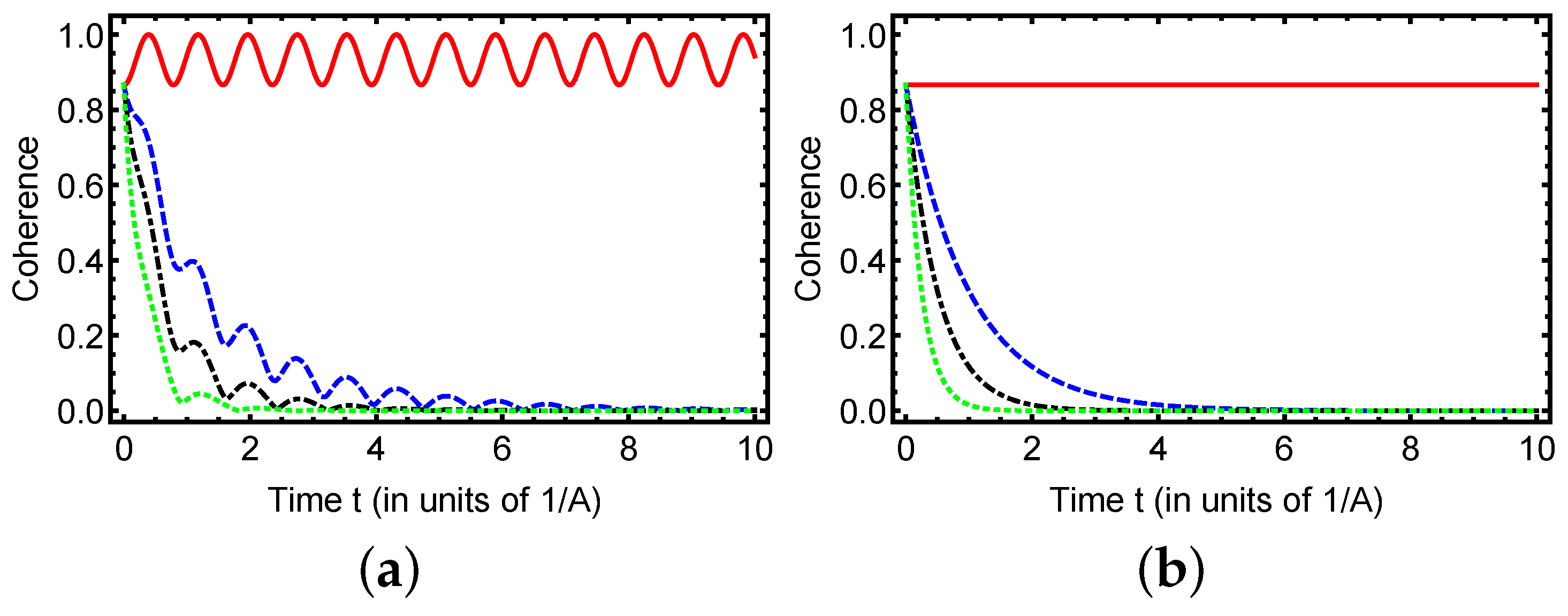
The time evolution of quantum coherence for the initial partially entangled state ($\alpha =\pi /3$) under different dephasing rates $\Gamma$ is shown in Figure 2. Panel (a) corresponds to the initial state $|a\rangle$. For $\Gamma =0$ (red solid curve), the coherence exhibits sustained oscillations driven solely by the coherent hyperfine interaction A, reflecting undamped unitary dynamics. As $\Gamma$ increases, these oscillations are progressively suppressed and the overall coherence decays more rapidly. For moderate values of $\Gamma$ (blue dashed and black dash-dotted curves), oscillations persist for a finite time before vanishing, while for large $\Gamma$ (green dotted curve) the decay is predominantly monotonic with negligible oscillatory behavior. This trend clearly demonstrates the detrimental effect of pure dephasing on maintaining quantum superpositions: the larger the value of $\Gamma$, the faster the off-diagonal elements of the density matrix vanish. Panel (b) corresponds to the initial state b. For the partially entangled case $\alpha =\pi /3$ shown here, the coherence remains time-independent at its initial value when $\Gamma =0$, since b is an eigenstate of the coherent part of the Hamiltonian and the unitary dynamics do not generate phase mixing; accordingly, no oscillations are observed. When dephasing is introduced ($\Gamma >0$), the coherence decays monotonically toward zero, with the decay becoming faster as $\Gamma$ increases. For completeness, note that the initial coherence is zero for $\alpha =0$, and remains so for all t independent of $\Gamma$. Unlike in panel (a), no oscillations are observed even at low dephasing rates, highlighting the strong sensitivity of this state to phase noise. In both cases, the long-time limit corresponds to a complete loss of coherence for any $\Gamma >0$, leaving the system in a fully incoherent statistical mixture.

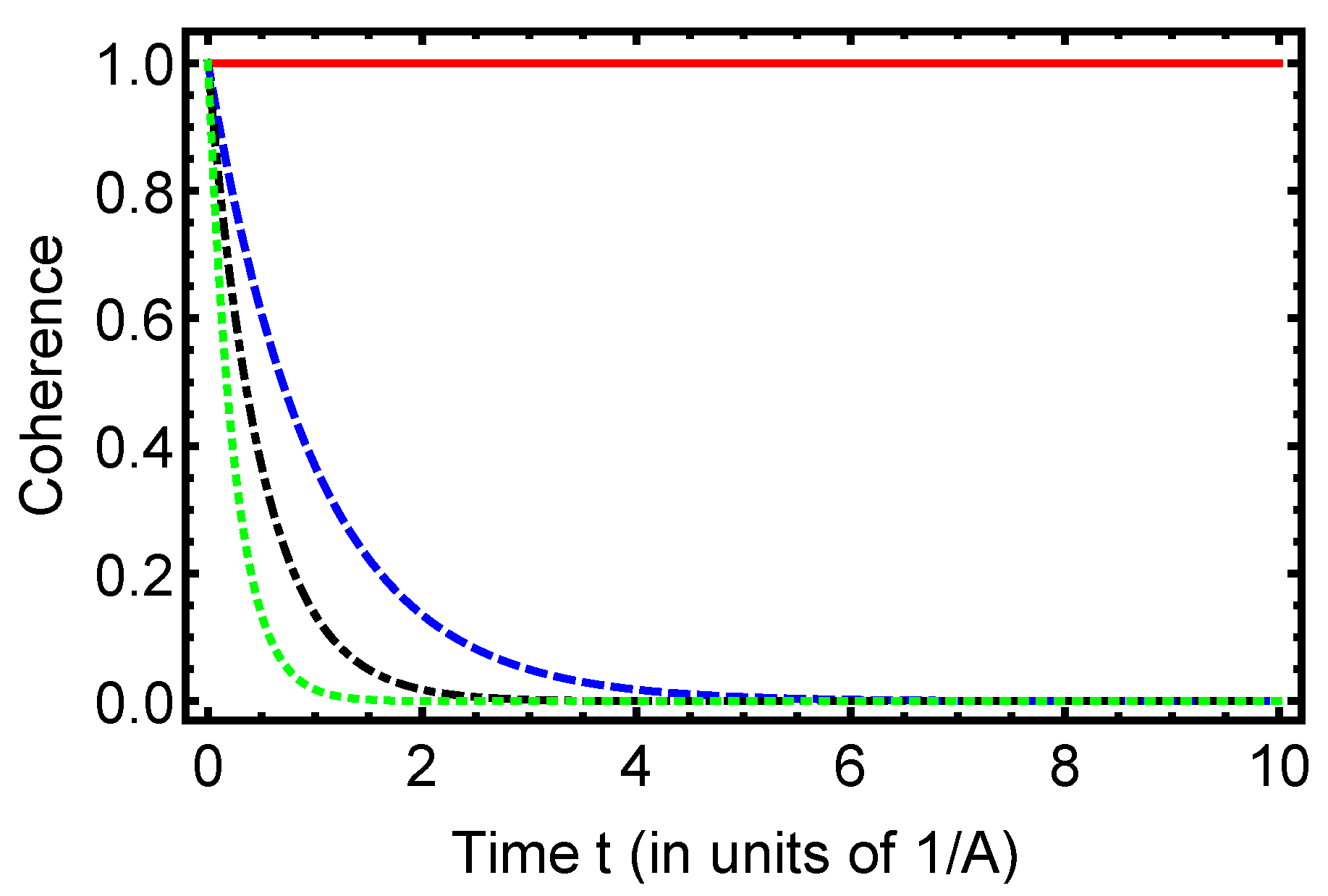
Figure 3 shows the time evolution of quantum coherence for the maximally entangled initial state $|a\rangle$ under varying dephasing rates $\Gamma$. For $\Gamma =0$ (red solid line), coherence remains constant at its maximum value of 1, indicating perfect preservation of quantum correlations in the absence of dephasing. As $\Gamma$ increases (blue dashed: $\Gamma =0.5A$, black dash-dotted: $\Gamma =A$, green dotted: $\Gamma =2A$), coherence decays more rapidly, reflecting the effect of dephasing noise. We note that the dynamics for the second maximally entangled state $|b\rangle$ are identical to those shown for $|a\rangle$, as expected from the equivalence of Equations (24) and (28). Therefore, only one representative figure is presented, while the second state exhibits the same coherence evolution.

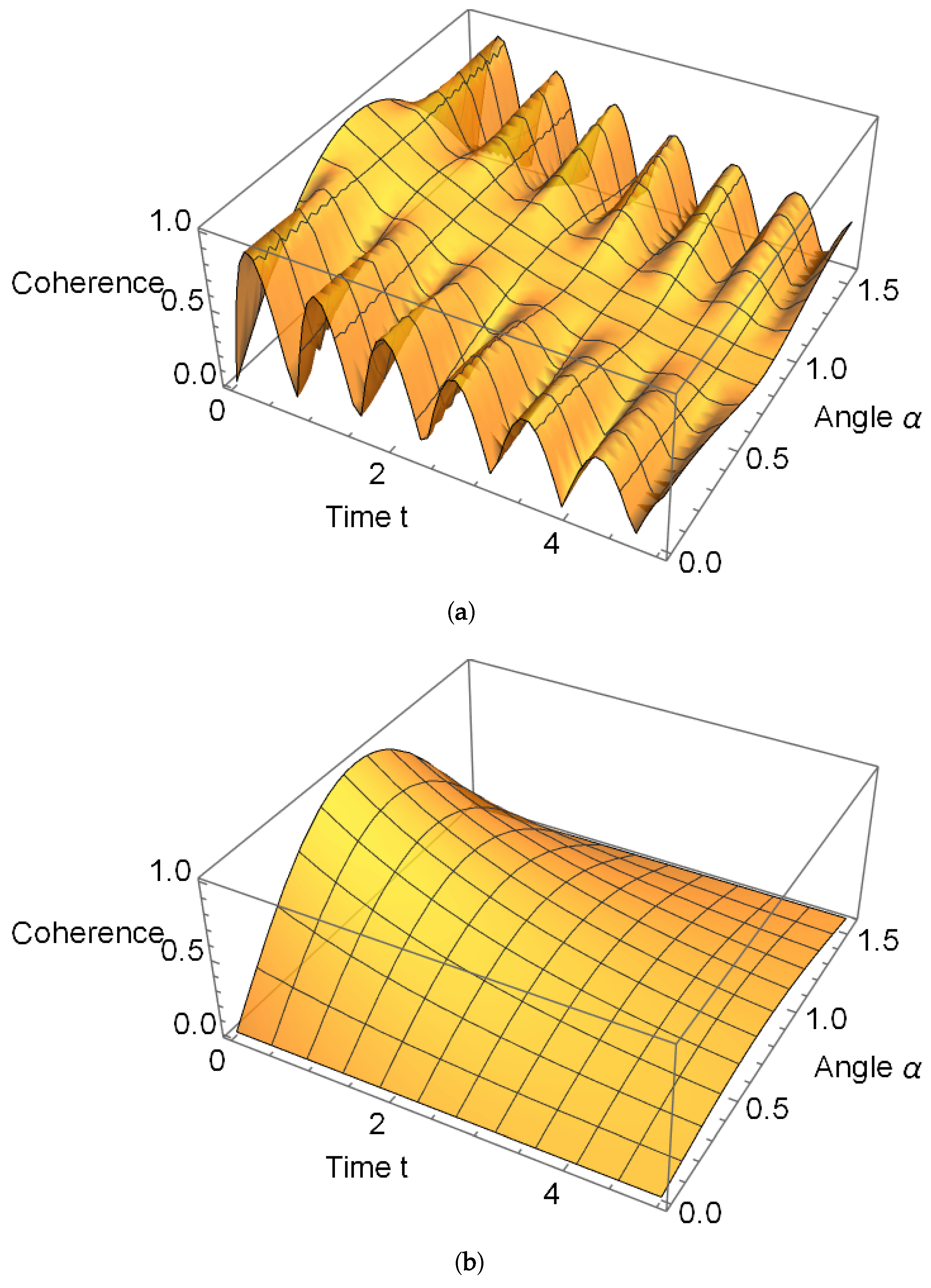
To complement the representative cases discussed above, we extend our analysis by exploring the full dependence of the dynamics on the initial state parameter $\alpha$. Figure 4a,b presents three-dimensional plots showing the joint evolution of coherence as functions of both time and $\alpha$. This representation provides a comprehensive view of how the initial superposition weight influences the robustness of hyperfine states under dephasing, thereby generalizing the results beyond selected examples.

4.2. Purity

In addition to coherence, the purity of a quantum state serves as an essential indicator of how mixed or coherent a system is. Purity is defined as

$$\mathcal{P}\left(\widehat{\rho }\right)=\mathrm{Tr}\left({\widehat{\rho }}^2\right),$$

(32)

where $\mathcal{P}\in \left[{\displaystyle \frac{1}{d}},1\right]$ for a d-dimensional system. A purity of 1 indicates a pure quantum state (i.e., $\widehat{\rho }=|\psi \rangle \langle \psi |$), whereas lower values reflect mixedness due to decoherence or statistical mixing. For a maximally mixed state, the purity reaches its minimum value of $1/d$.

Purity does not directly quantify coherence, but is useful in conjunction with coherence measures to assess the overall integrity of quantum states during evolution. In particular, observing how purity evolves under Lindblad dynamics provides insights into whether coherence loss stems from pure dephasing or is accompanied by entropy increase.

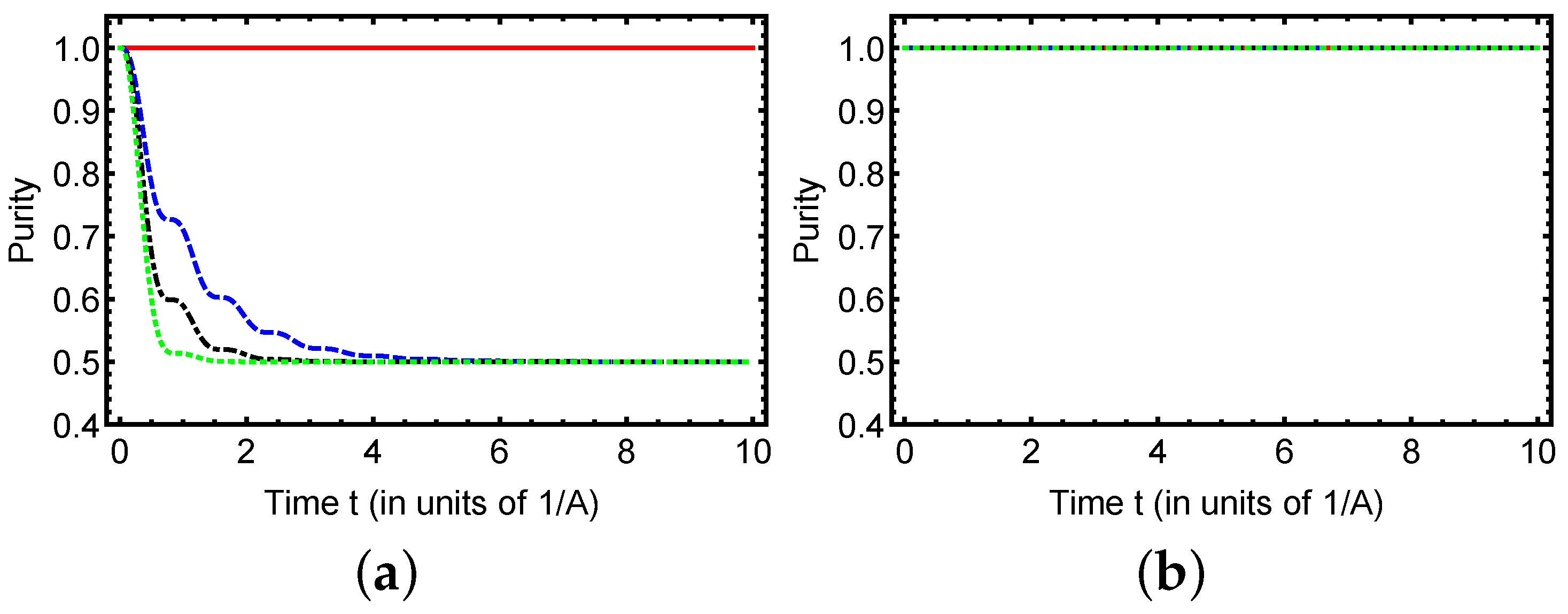
The time evolution of purity for the two initial states is shown in Figure 5. In panel (a), corresponding to the initial state $|a\rangle$ with $\alpha =0$, the purity exhibits a rapid decay from its maximum value of unity as soon as dephasing is introduced. For $\Gamma =0$, the system remains pure throughout the evolution, while for finite $\Gamma$ the purity decreases monotonically and saturates at $1/2$, indicating the onset of a maximally mixed state. The decay becomes faster with increasing $\Gamma$, reflecting the detrimental impact of dephasing noise on maintaining quantum coherence. In contrast, in panel (b), corresponding to the initial state $|b\rangle$ with $\alpha =0$, it can be seen that the purity remains constant at unity for all values of $\Gamma$. This behavior arises from the fact that $|b\rangle$ is already an eigenstate of the noise channel; as such, its evolution is unaffected by dephasing. The comparison between the two panels highlights a striking state-dependent robustness: while $|a\rangle$ is highly sensitive to decoherence, $|b\rangle$ with $\alpha =0$ remains perfectly stable, preserving its purity regardless of the noise strength.

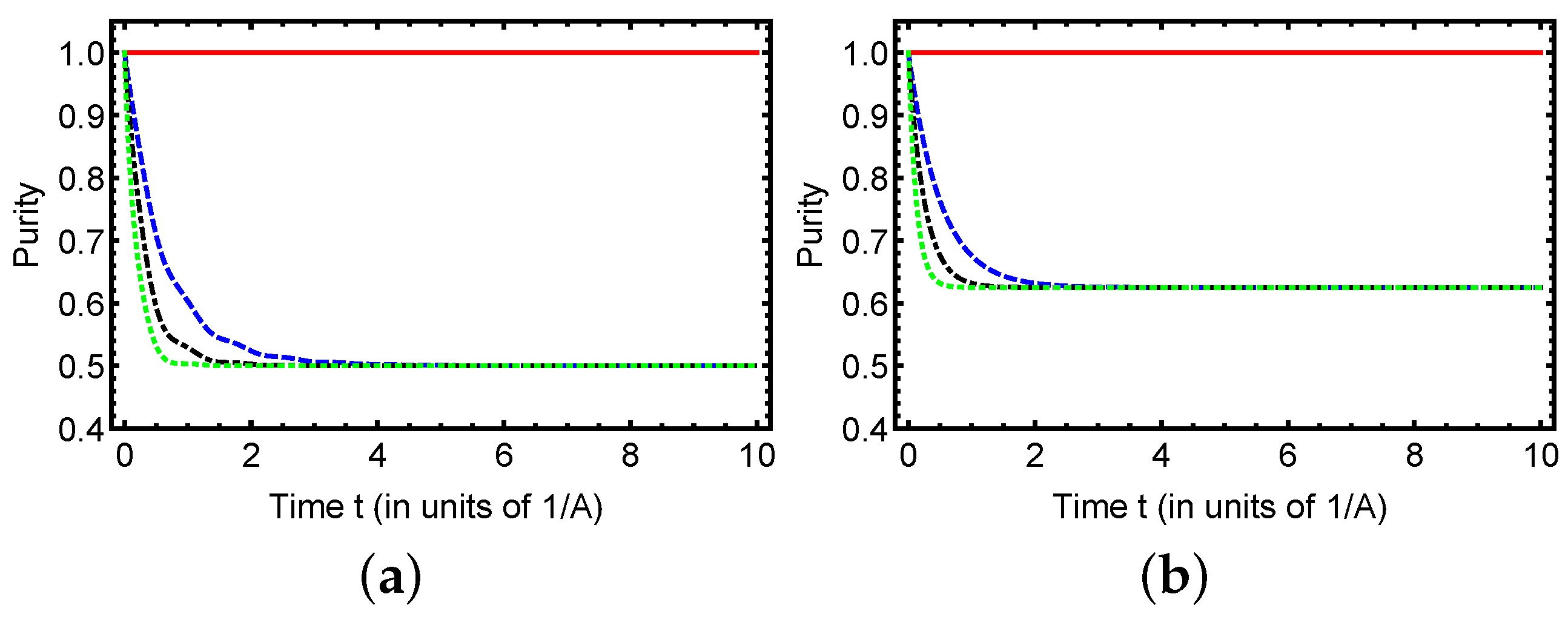
Figure 6 shows the time evolution of purity for partially entangled initial states ($\alpha =\pi /3$) under different dephasing rates $\Gamma$. For the $\Gamma =0$ case (solid red line), both states $|a\rangle ={cos(\pi /3)|\uparrow }_e{\downarrow }_p{\rangle +sin(\pi /3)|\downarrow }_e{\uparrow }_p\rangle$ (panel a) and $|b\rangle ={cos(\pi /3)|\uparrow }_e{\uparrow }_p{\rangle +sin(\pi /3)|\downarrow }_e{\downarrow }_p\rangle$ (panel b) maintain constant purity, demonstrating that unitary evolution preserves quantum coherence. When $\Gamma >0$, the purity decays monotonically, with faster decay rates corresponding to stronger dephasing (blue dashed $\Gamma =0.5A$, black dash-dotted $\Gamma =A$, green dotted $\Gamma =2A$). Notably, state $|b\rangle$ exhibits more rapid purity loss compared to $|a\rangle$ for equivalent values of $\Gamma$, revealing that parallel spin configurations (${|\uparrow }_e{\uparrow }_p\rangle$ and ${|\downarrow }_e{\downarrow }_p\rangle$) are more vulnerable to dephasing than antiparallel ones. This difference in decoherence rates highlights the significant role of initial state selection in quantum systems subject to environmental noise.

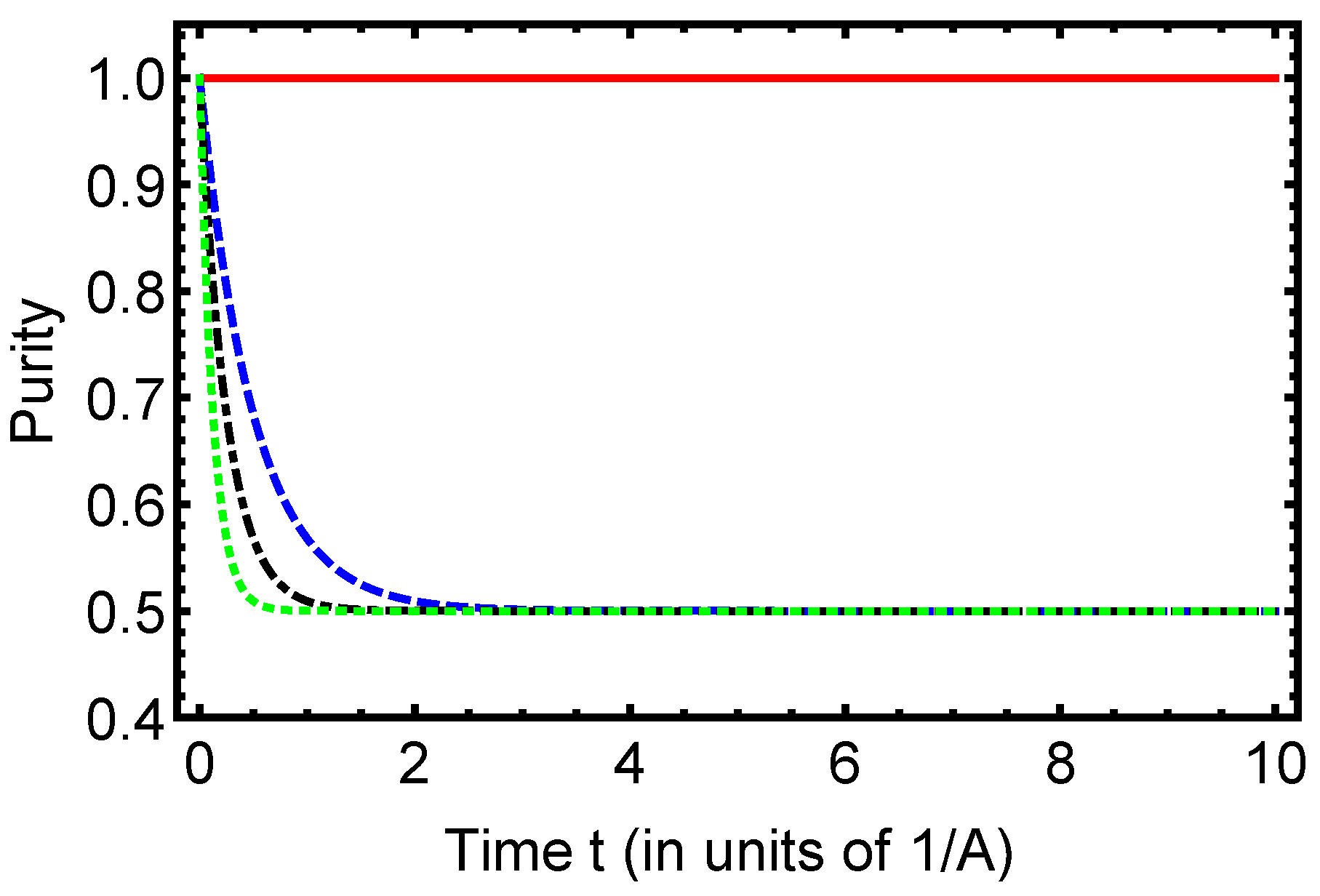
Figure 7 demonstrates the time evolution of purity for maximally entangled initial states ($\alpha =\pi /4$) under varying dephasing strengths $\Gamma$. For the coherent case ($\Gamma =0$, red solid line) the purity remains constant at unity, reflecting the perfect preservation of quantum correlations. When dephasing is introduced ($\Gamma >0$), the purity decays monotonically, with faster decay observed for stronger dephasing rates (blue dashed $\Gamma =0.5A$, black dash-dotted $\Gamma =A$, green dotted $\Gamma =2A$). In this case, the initial states $|a\rangle =\frac{1}{\sqrt{2}}{\left(\right|\uparrow }_e{\downarrow }_p{\rangle +|\downarrow }_e{\uparrow }_p\rangle )$ and $|b\rangle =\frac{1}{\sqrt{2}}{\left(\right|\uparrow }_e{\uparrow }_p{\rangle +|\downarrow }_e{\downarrow }_p\rangle )$ both exhibit identical dynamical behavior, since the analytic solutions yield ${\rho }_{23}\left(t\right)={\rho }_{14}\left(t\right)$. This result highlights that under the considered Hamiltonian and dephasing model, the two Bell states experience the same purity process despite their different spin configurations. This equivalence originates from the rotational invariance of the hyperfine interaction, which ensures that the parallel and antiparallel Bell states are dynamically indistinguishable when subject to pure dephasing noise.

It is worth noting that the robustness of the antiparallel configuration is directly related to its projection onto the dephasing axis (z-axis). Because the dephasing operators are proportional to ${\sigma }_z^e$ and ${\sigma }_z^p$, states with smaller overlap with the ${\sigma }_z$ basis experience weaker decoherence. In particular, the antiparallel state $|a\rangle$ has reduced projection along the z-axis compared to the parallel state $|b\rangle$, which explains its slower loss of coherence and purity. This observation quantitatively links the decay rates of coherence and mixedness to the degree of overlap of the initial state with the dephasing basis. These representative examples effectively capture the contrasting coherence and mixedness dynamics; additional initial states are expected to follow qualitatively similar behavior, as dictated by the dephasing rates and the structure of the hyperfine interaction.

5. Conclusions

In this work, we have systematically examined the impact of dephasing noise on quantum dynamics within the hyperfine structure of the hydrogen atom, employing the Lindblad master equation to model the evolution of the open system. Through our derivation of exact analytical expressions for the time-dependent density matrix across a range of initial states, from fully separable to partially and maximally entangled configurations, we have elucidated the intricate evolution of quantum coherence and purity under environmental effects. Our results reveal that coherence exhibits an oscillatory decay pattern modulated by the dephasing rate relative to the hyperfine coupling constant, with antiparallel spin states demonstrating markedly superior robustness against noise compared to their parallel counterparts. This differential resilience underscores the pivotal role of initial state preparation in preserving quantum features. In complement, our analysis of purity quantifies the progressive transition from pure to mixed states as dephasing intensifies, highlighting the irreversible loss of quantum information and the challenges posed by dissipative interactions. These insights not only enhance our foundational understanding of decoherence mechanisms in atomic systems but also offer practical implications for quantum information technologies, where hyperfine interactions serve as promising platforms for qubits and quantum sensing. By identifying configurations that mitigate decoherence, such as favoring antiparallel spin alignments, our findings pave the way for optimized protocols in noise-resilient quantum control and error correction. Future research could extend this framework to incorporate additional noise channels such as amplitude damping or correlated environments or explore experimental validations in trapped hydrogen-like systems, potentially integrating advanced control techniques to further suppress dephasing effects and harness quantum resources more effectively.