Abstract
In recent years, inverse reinforcement learning algorithms have garnered substantial attention and demonstrated remarkable success across various control domains, including autonomous driving, intelligent gaming, robotic manipulation, and automated industrial systems. Nevertheless, existing methodologies face two persistent challenges: (1) finite or non-optimal expert demonstration and (2) ambiguity in which different reward functions lead to same expert strategies. To improve and enhance the expert demonstration data and to eliminate the ambiguity caused by the symmetry of rewards, there has been a growing interest in research on developing inverse reinforcement learning based on the maximum entropy method. The unique advantage of these algorithms lies in learning rewards from expert presentations by maximizing policy entropy, matching expert expectations, and then optimizing the policy. This paper first provides a comprehensive review of the historical development of maximum entropy-based inverse reinforcement learning (ME-IRL) methodologies. Subsequently, it systematically presents the benchmark experiments and recent application breakthroughs achieved through ME-IRL. The concluding section analyzes the persistent technical challenges, proposes promising solutions, and outlines the emerging research frontiers in this rapidly evolving field.
1. Introduction
Rapid advancement of reinforcement learning (RL) has catalyzed its widespread adoption in various [1,2], including autonomous vehicles, strategic gaming systems, robot control, industrial automation, financial engineering, and trading [3,4]. At its core, RL algorithms seek to optimize decision policies through dynamic agent–environment interactions. Nevertheless, the design of precise reward functions remains a critical bottleneck in complex dynamic environments, where multivariate interference factors significantly impede theoretical advancements and practical implementations of RL frameworks. To bridge this gap, researchers have pioneered inverse reinforcement learning (IRL), which first infers reward structures from expert demonstrations, and then leverages the acquired reward models for strategic optimization [5,6,7]. The IRL algorithm is derived from imitation learning, originally formulated as behavioral cloning (BC), in which a human expert’s demonstration is recorded and then reinstated in the next execution [8]. Significantly advancing beyond this limitation, modern IRL frameworks possess dual capabilities: (1) extracting latent reward functions from human expertise demonstrations and (2) demonstrating superior domain adaptation capabilities through generalizable policy derivation, thereby achieving enhanced performance and broader operational applicability compared with BC methods [9,10,11,12,13].
The conceptual foundations of IRL algorithm were first established in 1998 by Russell and colleagues at the University of California, Berkeley, who pioneered a framework to infer reward functions from observed optimal behaviors and subsequently employ these learned rewards for policy optimization [14]. However, IRL algorithm suffers from the problem of finite or non-optimal expert demonstration, and the ambiguity problem that multiple different reward functions lead to the same expert strategy, complicating strategy optimization [15,16,17]. In response, researchers first developed margin-based IRL algorithms, mainly including the apprenticeship learning-based inverse reinforcement learning [18] and maximum margin planning inverse reinforcement learning [19]. However, these approaches still exhibited persistent ambiguity issues caused by symmetry in reward functions, that is, there are many distinct reward functions that can all perfectly explain the same group of expert behaviors. This makes it impossible to uniquely determine the true reward function of the experts based on the observed behaviors. Subsequently, a paradigm shift occurred in 2008 when Ziebart et al. from Carnegie Mellon University introduced a maximum entropy IRL framework leveraging trajectory probability distributions, which systematically resolved the ambiguity problem through entropy maximization principles, and broke the symmetry [20]. This breakthrough has propelled the widespread application of the algorithm in autonomous navigation systems, robotic manipulation, strategic game AI, industrial process automation, and other fields. Therefore, as a pivotal methodology in contemporary IRL research, maximum entropy inverse reinforcement learning continues to attract sustained research attention.
For real-world applications, conventional RL approaches have achieved linear feature-to-reward mapping through additional theoretical refinements. However, maximum entropy-based IRL (ME-IRL) algorithms are only applicable to low-dimensional state spaces and require action space and state transition probabilities. Considering environmental complexity, Ziebart et al. proposed a causal conditional probability-based framework in 2010 that extends maximum entropy principles to side-information enriched scenarios, enabling temporal modeling of sequentially revealed side information for nonlinear reward modeling [21]. Building upon this foundation, for high-dimensional and complex state environments, Wulfmeier’s team at the University of Oxford proposed the maximum entropy-based deep inverse reinforcement learning in 2016. This end-to-end architecture harnesses deep neural networks to approximate arbitrary nonlinear reward functions [22]. Concurrently, Finn et al. from University of California tackled the persistent challenge of partition function estimation in ME-IRL through sampling-based maximum entropy inverse optimal control (ME-IOC) [23]. This innovative approach simultaneously co-evolves policy learning with cost function adaptation, employing importance sampling techniques to estimate intractable normalizing constants and learn complex nonlinear cost structures, thereby enhancing algorithmic stability and empirical performance.
Furthermore, because expert demonstrations may be finite and non-optimal, Fu’s research group [24] at the University of Strathclyde proposed adversarial inverse reinforcement (AIRL) learning in 2018 to derive reward functions that are robust to dynamic changes. In addition, parallel advances have the extended maximum entropy IRL (ME-IRL) capabilities to recover rewards and policy optimization in more complex environments with multitask, multi-objective, or multi-agent scenarios [25,26,27,28]. IRL algorithms based on the maximum entropy method make no assumptions about any other unknown information except the constraints. Despite its theoretical elegance, the scaling of MaxEnt IRL to complex, real-world problems has exposed profound and interconnected challenges that this review seeks to address, such as the ambiguity of rewards, locally optimal expert demonstration problem, learning inefficiency, multi-agent environments, etc. In light of these challenges, IRL algorithms based on maximum entropy encompass a large body of outstanding research. This survey provides a comprehensive and systematic synthesis of the substantial progress made in advancing the ME-IRL, subsequently presents benchmark experiments and domain-specific applications, culminating in an analysis of persistent challenges, innovative solutions, and emerging research vectors in this transformative field.
The main contributions of this study are as follows:
- (1)
- We offer a critical analysis of ME-IRL and systematically examine the evolutionary trajectory of ME-IRL methodologies, comparing the strengths and weaknesses of different approaches.
- (2)
- The benchmark experiments and domain-specific applications in ME-IRL are summarized, laying the foundation for the development of ME-IRL algorithms in various fields.
- (3)
- We provide an identification of future research frontiers, move beyond a summary of existing work, and critically evaluate the current state of the field and pinpoint promising yet underexplored directions.
An overview of this survey is illustrated in Figure 1. Section 2 reviews the background of the Markov decision process (MDP), IRL, and ME-IRL algorithms. Section 3 demonstrates the research process of maximum entropy-based IRL algorithms. Section 4 provides benchmark experiments for the application of entropy-based IRL algorithms. Section 5 presents the application progress of the entropy-based IRL algorithms. Section 6 discusses the problems and the existing corresponding feasible solution ideas. And finally, Section 7 concludes this paper and presents future research directions.
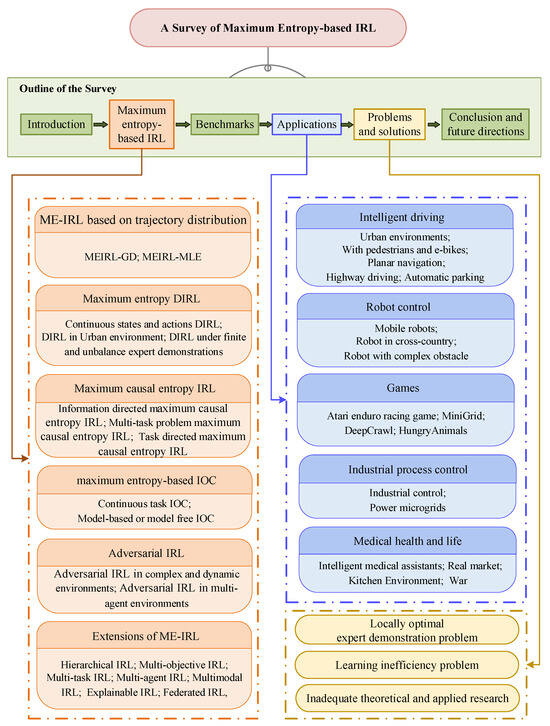
Figure 1.
Overview of the survey. This survey provides a general introduction to IRL algorithms based on maximum entropy method, then categories maximum entropy-based IRL into six domains, which will be discussed detailedly in later sections. Each category is demonstrated with a part of representative works in the figure. The relevant benchmarks are then summarized. Finally, the conclusions and future research directions are presented.
2. Problem Description of Maximum Entropy-Based IRL
RL algorithms are defined as learning to maximize cumulative rewards and make a series of optimal decisions in a given environment through the interaction between an agent and the environment [29,30]. The problem to be solved in the RL algorithm is described as an MDP. An MDP is defined as , where represents the state space, represents the action space, is the state transition probability matrix, represents the reward functions, is a discount factor, . The RL algorithm consists of three elements: states, actions, and rewards. The policy is a function of the agent’s behavior, .
Based on the above definitions, the IRL problem is modeled as an MDP with an unknown reward function MDP\. Given some expert demonstrations that may be optimal or non-optimal, the IRL algorithm reversely derives the reward function of MDPs and then allows agents to learn how to make decisions for complex problems [31,32]. Since IRL algorithms suffer from the ambiguity problem that multiple different reward functions lead to the same expert strategy, based on the concept that entropy is an indicator for measuring uncertainty or randomness, researchers have proposed the maximum entropy-based IRL algorithms. These algorithms use a probabilistic model to solve the symmetry issue in inverse reinforcement learning, aiming to find a reward function such that the trajectory distribution generated by the optimal policy based on this reward function, under the constraint of matching with expert data, has the maximum entropy. The model with the highest entropy is considered the best among all possible probability models. Therefore, it is easier to determine the optimal solution using maximum entropy-based IRL algorithms, which can learn rewards and obtain optimal policies. Traditional maximum entropy-based IRL algorithms are utilized to fit reward functions of the real environments:
where is the weight coefficient, and the constraint is used to limit the size of the reward. is the feature vector with length k, , where each element corresponds to a state.
Given an initial state , the policy of the maximum entropy-based IRL algorithm has a state-action value function :
where the policy is a mapping of the probability distribution of executing an action a in a state s, and is the discount factor.
Thus, satisfying the Bellman optimal in Definition 1, the optimal policy can be obtained.
Definition 1. (Bellman optimal).
Given an MDP, the interaction between the agent and the environment is modeled. For any state and action , the chosen action π for solving state value functions of the MDP must satisfy: , the chosen action π for solving state action value function of the MDP must satisfy: .
Repeated application of the optimal Bellman equation will eventually derive the unique optimal value function for maximum entropy-based IRL algorithms; then, the optimal policy can be obtained with the value function.
3. Foundational Methods of IRL Based on Maximum Entropy
The main objective of the IRL algorithm is to learn rewards and optimize policies with recovered rewards, which faces challenges of finite or non-optimal expert demonstrations, as well as the ambiguity of rewards. The principle of maximum entropy that can best represent the probability distribution of current knowledge is the one with the greatest entropy among the probability distributions that accurately describe prior knowledge, incorporating the fewest additional assumptions about the true distribution of the data. Therefore, the probability distribution corresponding to the IRL based on maximum entropy (ME) theory is the most likely to yield the optimal solution among the many distributions that meet the constraints. The maximum entropy-based IRL algorithm overcomes the problems of finite or non-optimal expert demonstration and learning efficiency. Over the past decade, IRL algorithms have garnered considerable attention and have been significantly developed. In particular, in the last decade, IRL algorithms have received wide attention and gained large development. As illustrated in Figure 1, maximum entropy-based IRL algorithms include maximum entropy IRL based on trajectory distribution (ME-IRL based on trajectory distribution), maximum entropy deep IRL (maximum entropy DIRL), maximum causal entropy IRL, maximum entropy-based inverse optimal control (maximum entropy-based IOC), adversarial IRL, and extensions of ME-IRL. A comparison of the challenges, problems solved, advantages, computational complexity, generalization performance, and application areas of maximum entropy-based IRL methods is shown in Table 1. In addition, we specifically compared the applicable environment, data requirements, reward recovery accuracy, success rate of these maximum entropy-based IRL methods in Table 2.

Table 1.
Research history of maximum entropy-based IRL algorithms.

Table 2.
Comparison of maximum entropy-based IRL algorithms.
3.1. Maximum Entropy IRL Based on Trajectory Distribution
Maximum entropy-based IRL algorithms address the ambiguity problem by maximizing the entropy of the trajectory distribution under the constraints of feature matching. That is, when multiple policies meet matching conditions, any one of these policies might suggest that some trajectories are more probable than others, yet the expert demonstration lacks this inherent bias. The core idea of the maximum entropy-based IRL is to eliminate this bias by making the probabilities of these trajectories as uniform as possible. Ziebart et al. pioneered this approach by modeling the maximum entropy-based IRL problem as a constrained optimization problem [20],
where indicates the probability of the expert demonstration trajectory , is the count of state features along the trajectory , and is the empirical feature count of the expectation of states under the trajectory .
Using Lagrange multipliers, the dual form of the optimization problem in Equation (3) is formulated as follows:
Taking the derivative of Equation (4) with respect to , the model of ME-IRL algorithms can be derived. For the deterministic and stochastic MDPs, the probability distributions of the trajectory are as follows:
where indicates the partition function, represents the reward weight, and represents the state transition distribution. For the deterministic MDPs, the probability distributions of the trajectory is ; for the stochastic MDPs, the probability distributions of the trajectory is . Under these probability distributions, trajectories with high rewards have a higher probability of occurrence. In deterministic MDPs, the dynamics of the system are completely predictable. The outcome of performing an action is unique and certain. In stochastic MDPs, the dynamics of the system are probabilistic. Performing an action may lead to multiple different outcomes, each with a certain probability of occurrence.
Maximizing entropy under feature constraints is equivalent to maximizing the probability of occurrence of an expert demonstration trajectory under maximum entropy conditions, and the weights of the rewards for ME-IRL algorithms are , where represents the single trajectory. The final rewards are derived using a linear combination of weights and features.
The maximum entropy-based IRL algorithm aims to solve the following problems: (1) noise interference in the demonstration data and (2) incorporation of the hidden variable technique, allowing inference of the destination and subsequent trajectories from partial trajectories. In recent years, focusing on these problems, the theory of maximum entropy-based IRL has been continuously improved and developed, which is mainly classified into maximum entropy IRL based on gradient (MEIRL-GD) and maximum entropy IRL based on maximum likelihood estimation (MEIRL-MLE). Current works on MEIRL-GD mainly include the followings: a probabilistic approach based on the principle of maximum entropy was proposed to solve the ambiguity problem caused by the symmetry of rewards in the IRL algorithm [20]; to solve a constrained Markov decision process, the task of inferring the reward function and constraints was transformed into an alternating constrained optimization problem with convex subproblems, which was solved using an exponential gradient descent algorithm [61]. Current works on MEIRL-MLE mainly include a parametric system constructed to learn rewards and optimal policies by adding constraints to the inputs for temporal stochastic systems with continuous state and action space [62].
Additionally, to solve the maximum entropy model in IRL algorithms, problems may exist, such as finite and non-optimal expert demonstration, computational complexity, and slow convergence. In response, researchers have proposed many new algorithms. For example, to achieve a natural interaction between humans and intelligent agents without manually specifying rewards, a sampling-based maximum entropy IRL algorithm was proposed to learn the reward function directly by introducing a continuous-domain trajectory sampler [33]. To address computational complexity, overfitting, and slow convergence, a new maximum entropy IRL based on proximal optimization solved the maximum entropy model using the FTPRL method [63]. In addition, an expert sample preprocessing framework based on the behavioral cloning method was constructed to solve the inaccuracy of maximum entropy IRL algorithms owing to the noise of expert samples [64].
Furthermore, in complex task environments, introducing new theories into maximum entropy-based IRL not only provides maximum entropy-based IRL but also improves the performance of the algorithms. To model the driving behavior, a driving model based on the internal reward function was constructed, which transformed the continuous behavioral modeling problem into a discrete problem and allowed maximum entropy-based IRL to easily learn the reward function [34]. To eliminate errors caused by trajectory projection and path tracking in the automatic parking process, maximum entropy IRL was applied to learn rewards for obtaining the optimal parking strategy [35]. Furthermore, an IRL-based conditional predictive behavioral planning framework based on IRL was proposed to use the behavior generation module, conditional motion prediction network, and scoring module to learn rewards from human driving data [36]. To gain a deeper understanding of the traversal mechanism of e-bikes, a neural network-based nonlinear reward function with five dimensions was constructed [65]. Finally, a generalized maximum entropy idea constructed the maximum entropy IRL and relative entropy IRL for model-free learning by minimizing the KL divergence [66]. All experiments showed that the algorithm improved the accuracy of learning rewards.
Confronted with the inherent methodological limitations of inverse reinforcement learning (IRL) frameworks, researchers have undertaken a series of theoretical innovations, rigorously validated through diverse experimental protocols including benchmark simulations, controlled environments, and real-world applications. The classical maximum entropy IRL algorithm, which relies on estimating state and action visitation frequencies for gradient-based optimization, remains constrained to linear reward representations in discrete, small-scale state and action spaces with known transition dynamics. Despite these notable advancements, extending the applicability of maximum entropy IRL to more complex and uncertain domains remains a critical research direction. This underscores the significant untapped potential for further theoretical development, particularly in areas such as continuous and high-dimensional spaces, partial observability, and nonlinear reward modeling, pointing toward a robust and expanding frontier for future work in IRL.
3.2. Maximum Entropy-Based Deep IRL
To enhance the ability of learning rewards for IRL in complex nonlinear environments, the powerful function approximation ability of neural network is incorporated into the IRL algorithm based on maximum entropy to achieve end-to-end mapping from input features to outputs. Wulfmeier et al. [67] proposed a classical maximum entropy-based nonlinear IRL framework utilizing a fully convolutional neural network to represent a cost model of expert’s driving behaviors. In this framework, rewards are estimated by forward propagation and back-propagated through the gradient of the maximum entropy between the learner’s state visitation frequencies and the expected state visitation frequencies.
Maximum entropy-based deep IRL solves various types of linear and complex nonlinear reward functions by modeling demonstration behavior as probability distributions over demonstration trajectories and then adding a maximum entropy constraint. In a complex environment, the reward function is formulated as a nonlinear function of the feature vector . A deep neural network (DNN) is used to compute the reward function :
where is the weight of the DNN, and is the nonlinear function. DNN can represent arbitrary nonlinear functions and is considered as universal approximators with feature vectors as inputs and reward values as outputs. Using Bayesian inference, the training problem for DNNs is formulated as a graph, maximizing the joint posterior distribution of the expert demonstration and the parameters :
where D represents the expert demonstration. In Equation (7), the gradient descent method is used to optimize the parameters of neural network, the joint log-likelihood function consists of a data term and a model term :
where is the expected state visitation frequency generated by the policy, is the state visitation frequency, is the difference between the state visitation frequency of the expert demonstration and the expected state visitation frequency of the learner’s trajectory distribution. In Equation (8), the derivative of the data term can be expressed as the derivative of the expert demonstration with respect to the reward function multiplied by the derivative of the reward function with respect to .
Maximum entropy-based deep IRL computes rewards using input features and parameters by a end-to-end way. The cost maps learned using the maximum entropy deep IRL algorithm are constructed directly from raw sensor measurements, bypassing the need to manually design the cost map.
Aiming at the continuous state and action space, a continuous maximum entropy deep IRL algorithm was proposed to reconstruct the reward function based on expert demonstrations and employ a hot-start mechanism to acquire deep knowledge of the environment model. Furthermore, a parametric and continuously differentiable DNN was used to approximate the unknown rewards of the maximum entropy IRL problem and to optimize the driving policy based on the expert demonstration data [38,68].
To solve driving problems in complex urban environments, various theories have been introduced for deep maximum entropy-based IRL. First, the maximum entropy-based nonlinear IRL framework used a full convolutional neural network (FCN) to learn cost maps from extensive human driving behaviors, as shown in Figure 2 [67]. For a complex urban road driving task, a multi-task decision-making framework used IRL to learn a reward function and expert drivers’ driving behaviors in urban scenarios containing traffic lights and other vehicles [69]. To achieve the fundamental problem of off-road autonomy for robots, the maximum entropy DIRL used RL ConvNet and Svf ConvNet to solve the exponential growth of state space complexity in path planning, and then encoded kinematic properties into convolution kernels for efficient forward reinforcement learning [41]. Moreover, to develop robot navigation algorithms, the maximum entropy deep IRL was used to learn human navigation behavior through approximating the nonlinear reward function with DNNs [42], as shown in Figure 3. To address path planning with multiple moving pedestrians in a driverless environment, the RNN-based IRL method incorporated pedestrian dynamics into the deep IRL learning environment and mapped features to rewards using a maximum entropy-based nonlinear IRL framework [70].
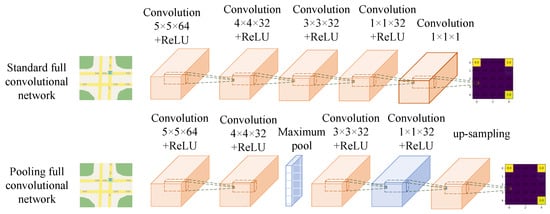
Figure 2.
Proposed FCN architectures.
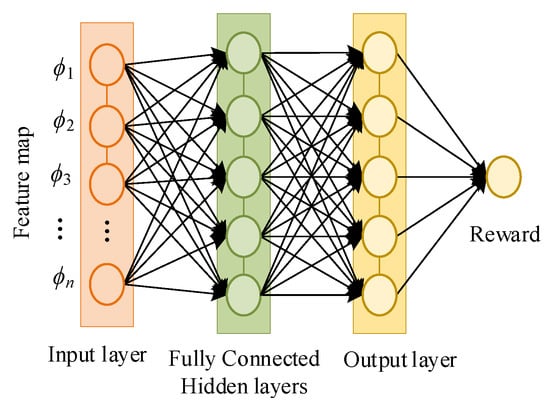
Figure 3.
Reward function approximation with feature space.
Additionally, the finite and unbalanced expert demonstration data, computational complexity, and overfitting in learning nonlinear rewards seriously restrict the development of reinforcement learning. To solve this problem, path integral IRL was first proposed to use a strategy-focused mechanism and a time-focused mechanism to predict rewards and recognize context switches over extended time horizons [71]. And then, a general-purpose planner that combines behavioral planning with local motion planning was introduced into deep maximum entropy-based IRL, which can rely on human driving demonstrations for automatic tuning of the reward function and provide an important guideline for the optimization of the maximum entropy IRL general-purpose planner [39]. For learning rewards in temporally extended tasks, task-driven deep IRL improved the accuracy of the learned rewards through the interactive iteration between the task inference module and the reward learning module [72]. Likewise, the maximum entropy deep IRL used the Adaboost method to integrate multiple ME-DIRL processes into a robust learner, as illustrated in Figure 4 [73]. Subsequently, a motion planning framework was constructed to explore the optimal paths and derive solutions for inverse kinematics in motion planning in robotic environments with obstacles [43].
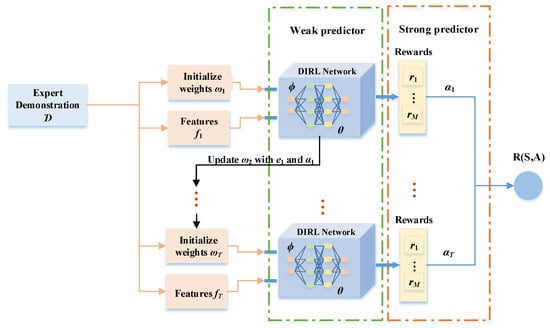
Figure 4.
Model of AME-DIRL.
For further learning precise rewards, the data-driven framework, accurate behavioral prediction, and target-conditional framework have been considered in deep maximum entropy-based IRL. Specifically, a data-driven framework employed a deep IRL approach based on maximum entropy to learn rewards [46]. Then, a maximum entropy deep IRL was trained using both fully connected neural networks and recurrent neural networks to capture the characteristics of various driving styles and better mimic human driving behavior [40]. In addition, the deep maximum entropy-based IRL based on accurate behavioral prediction highlighted the potential of deep IRL to overcome technological limitations in various application domains [74]. Finally, an IRL framework for learning target-conditional spatio-temporal rewards developed a model prediction controller MPC that uses generated cost maps to execute tasks without the need to manually design cost functions [75].
The maximum entropy deep IRL effectively combines the decision-making capabilities of IRL with the perceptual abilities of neural networks, providing robust solutions to IRL challenges. The algorithm has gained extensive attention and has been developed for both theoretical and practical applications. However, significant opportunities for the theoretical advancement of maximum entropy deep IRL still exist in addressing the complexities of actual task environments. Furthermore, networks such as graph neural networks and transformers may be introduced into IRL for learning rewards by an end-to-end manner and embodying the powerful learning ability of IRL.
3.3. Maximum Causal Entropy-Based IRL
Under given policies, maximum entropy-based IRLs are used to calculate the probability distribution of its expert demonstration trajectory . By satisfying the maximum feature matching, the corresponding maximum entropy , and corresponding rewards are derived. Considering the causal strategy model of environmental complexity, the principle of maximum entropy is extended to scenarios involving side information. Ziebart et al. [20] subsequently pioneered an IRL algorithm based on maximum causal entropy grounded in temporal dependency modeling. This advanced framework crucially investigates the entropy of the conditional probability distribution for another sequence of random variables at each time step t with a known sequence [76]. Therefore, this algorithm extends the maximum entropy framework of statistical modeling to processes characterized by information revelation, feedback, and interactions, focusing on “sequences”, “conditional probabilities” triggered by other information, or interactions between two types of information [77]. The core idea of the maximum causal entropy-based IRL algorithm involves addressing the following two optimization issues [21]:
Optimization issue 1: Given expert demonstration , a stochastic strategy is optimized to maximize causal entropy subject to matching feature expectations:
where A indicates the action set, S represents the state set, indicates the discounted factor, represents a set of characteristic functions for rewards. The implied constraints on the optimization variables are: . The Lagrangian function of the optimization problem in Equation (9) is formulated as follows:
where the dual variable represents the weight of feature matching constraint. Then, the dual gradient ascent or dual gradient descent methods are utilized to solve the Lagrangian function.
Optimization issue 2: (1) Ignoring the constraints of the policy function , the Lagrangian dual function of Optimization issue 1 is found; (2) the dual function is minimized.
Finally, the optimal values and are obtained to satisfy . Furthermore, for the case where the reward is a nonlinear function, the maximum causal entropy IRL based on maximum likelihood estimation is used to optimize the parameters of rewards [78].
In addition, researchers have introduced new ideas for maximum causal entropy-based IRL algorithms to address existing problems in complex tasks. In the following, the maximum causal entropy method used a directed information theory-based approach to estimate unknown processes through their interaction with known processes [20]. In scenarios with an infinite time horizon, the maximum discounted causal entropy and maximum average causal entropy were proposed to solve the optimal solution [79]. Based on this, to extend multi-task IRL to complex environments, a multi-task problem in the computationally more efficient maximum causal entropy IRL framework was constructed, which added regularization terms to the losses [48]. To address the challenge of identifying implicit constraints, CMDCE IRL adhered to constraints using the principle of maximum causal entropy for learning optimal policies [80]. Some experiments were conducted to verify the effectiveness of these algorithms.
In complex environments, the maximum causal entropy IRL combined with a specific task context has been proposed to improve the performance of algorithms. First, to study the modeling of human driving behavior in specific situations, a new maximum causal entropy IRL framework was established to predict the car lane-changing behavior [49]. In a virtual 3D space of the real environment, the IRL framework used soft Q-learning and the principle of maximum causal entropy to learn how to navigate [50]). Furthermore, for a transition dynamics mismatch between an expert and a learner, a strict upper bound on the degradation of the learner’s performance was introduced into the maximum causal entropy IRL model [81]. Moreover, some researchers have applied IRL to the field of economics. A previously unknown link between the maximum causal entropy IRL and economic development was proposed to model the relationship as an optimization problem [51].
Maximum causal entropy IRL is one of the most popular inverse reinforcement learning algorithms, extending the principle of maximum entropy to scenarios containing side information and thereby significantly enhancing the robustness and generalizability of learned policies. By explicitly accounting for temporal dependencies and external constraints, the method improves both reward inference accuracy and behavioral prediction in sequential decision-making processes. Recent advancements have integrated state-of-the-art machine learning techniques—such as deep representation learning, attention mechanisms, and meta-learning—into the maximum causal entropy IRL framework. These integrations further elevate its performance, enabling more efficient feature extraction, better handling of high-dimensional state spaces, and improved adaptation to non-stationary environments. Research on maximum causal entropy IRL remains a highly promising and valuable direction within artificial intelligence. Future work may focus on scaling these methods to multi-agent settings, enhancing computational efficiency, and improving interpretability, thereby opening new pathways for intelligent system designs.
3.4. Maximum Entropy-Based Inverse Optimal Control
The inverse optimal control (IOC) method requires the selected features that represent information about the system, avoiding overly complex cost functions through regularization. Each of its inner loops needs to solve the forward RL problem, thereby reducing the algorithmic complexity in environments characterized by unknown dynamics, high dimensionality, and continuity. Sampling-based maximum entropy IOC, which couples the learning of the policy and the updating of the cost function, can address problems in the unknown dynamics, high-dimensional continuous case [23,54]. The derivative of the guide cost learning (GCL) algorithm based on maximum entropy IRL with respect to weight is
where is the weight parameter of the reward, is the log-likelihood function of the GCL model, and is the discount factor.
The ME-IRL algorithm needs to learn the strategy and sample from it at each iteration when calculating item (b) in Equation (11), which leads to a computationally intensive problem. Therefore, importance sampling is proposed to calculate the partition function . Assuming that the expected value of the easily sampled distribution of trajectories is formulated as in Equation (12),
where is the importance weight function. If the sample trajectories are generated from multiple distributions , then the importance weighting function is . After each update of the weight parameters , the RL algorithm is used to maximize Equation (13) for updating :
Let be as close as possible to the true distribution by the learning iterations of the importance sampling, and the optimal solution for is obtained.
Some new ideas have been introduced into IOC algorithms for high-dimensional complex and continuous task environments. Specifically, in a high-dimensional system environment with unknown dynamics, an IOC algorithm used a sample-based approximation of the maximum entropy IOC to learn a complex nonlinear cost [23]. Then, for modeling human interaction based on visual activity, kernel-based RL and IOC of the mean-shift process were used to address the high dimensionality and continuity of human poses [54]. To address the problem of locally optimal examples, an IOC algorithm abandoned the assumption that the demonstration was globally optimal by using a local approximation of the reward function [52].
Model-based and model-free inverse optimal control algorithms have been proposed for solving the game problem. In the following, for the multiplayer apprentice game problem, the model-based IOC and model-free IRL algorithms were designed for homogeneous and heterogeneous control inputs in nonlinear continuous systems [53]. To solve the problem of adversarial apprentice game with nonlinear learners and expert systems, a model-based IRL algorithm and a model-free integral IRL algorithm were used to reconstruct the unknown expert’s cost function [82]. For IRL in a multi-agent system (MAS), a model-based IRL algorithm used the inner-loop optimal control updating and outer-loop inverse optimal control updating loops to learn rewards under the online behavior of the expert and learner [25].
Maximum entropy-based IOC may encounter limitations when applied to highly non-linear problems or systems with complex dynamics. Its performance can be hindered by high-dimensional state-action spaces, intricate reward structures, and challenges related to computational tractability. These constraints highlight the need for further investigation and refinement. Future research could focus on enhancing its scalability, improving its handling of non-linearities through advanced function approximation, and integrating it with modern deep learning or Monte Carlo methods to address both theoretical and practical gaps. There remains significant potential to expand the applicability and robustness of this approach in real-world applications.
3.5. Adversarial IRL and Multi-Agent Adversarial IRL
In recent years, generative adversarial networks (GANs) have been one of the most promising approaches for handling complex data distributions. GANs are used to optimize rewards and policies for IRL and to continuously refine expert demonstrations, solving the problem of finite or non-optimal expert demonstrations in complex dynamic environments. This enhances the accuracy of reward learning. Finn et al. introduced generative adversarial networks into GCL [23,83]. In the adversarial IRL algorithm, the distribution of state–action pairs is utilized to find a discriminator:
where represents the mapping function. Make the reward function be , and the expected rewards of trajectory is
Equation (15) is the RL form of entropy regularization, which yields the optimal policy . The minimization of the original GAN’s optimization objective is transformed into maximization. Thus, the optimization objective of adversarial IRL is obtained:
The optimal solution in GAN is , and can be obtained. The gradient of is computed using the sampling method in the adversarial IRL algorithm and trained based on trajectory distributions. However, in practice, this trajectory distribution-based estimate exhibits high variance. Therefore, researchers conducted a series of studies in related directions to improve the existing problems.
In complex and dynamic environments, GANs assist IRL in enhancing the robustness and stability of algorithm while the reducing learning variance. First, to address the challenge of automatically obtaining rewards in large-scale high-dimensional environments with unknown dynamics, a practical and scalable IRL algorithm based on adversarial learning was developed to learn a reward function that is robust to dynamic changes, and to learn policies under significant changes [23]. To tackle the problem that recovered rewards may be less portable or robust to changing environments, the adversarial IRL algorithm was proposed to learn hierarchical disentanglement rewards through strategies [84]. Furthermore, semantic rewards were added to the learning framework of adversarial IRL to improve and stabilize the performance of adversarial IRL [85]. To make the computational graph end-to-end microscopic, the model-based adversarial IRL employed a self-concerned dynamic model to optimize policies with low variance [55]. Based on that, in procedurally generated environments, adversarial IRL was proposed to successfully identify effective reward functions with minimal expert demonstrations [56].
To address the challenges of inferring reward functions with expert trajectories in multi-agent environments, the multi-agent generative adversarial IRL focuses on setting up agents with numerous variable quantities to learn shared reward functions [86]. In response to the different preferences in manually obtained expert sample trajectories under complex tasks, an adversarial IRL-based behavioral fusion method decomposed complex tasks into subtasks with different preferences and generated network-fitting strategies by fitting reward functions using a discriminator network [57]. Considering the multi-agent nature of interactions between road users, a new multi-agent adversarial IRL approach modeled and simulated interactions in shared-space facilities [87].
Furthermore, to improve the adaptability of the adversarial IRL and multi-agent adversarial IRL, the meta learning is considered. The meta-adversarial inverse reinforcement learning integrated meta-learning and adversarial inverse reinforcement learning to learn adaptive strategies by using different update frequencies and meta-learning rates for discriminators and generators [88,89].
Although the theory of multi-agent maximum entropy inverse reinforcement learning has developed, its security and anti-attack capabilities remain the weak points in current research. The traditional ME-IRL methods usually assume that the environment is friendly and free from interference. However, in practical applications (such as autonomous driving, multi-agent systems), the systems often face security threats such as sensor attacks and false data injection. For example, in multi-agent systems, the attack may target some sensors or communication links, but ME-IRL does not address how to recover the safety constraints from the partially contaminated expert trajectories. The existing MaxEnt IRL lacks a robust mechanism for inferring the reward function under FDI attacks. To improve the stability of multi-agent systems, multi-agent reinforcement learning with the research theme of safety and fault-tolerant control is a worthy topic for study. Additionally, generative adversarial networks may face problems such as instability, mode collapse that generated samples lack diversity. Advanced theoretical concepts like deep convolutional GANs, Wasserstein GANs, and boundary seeking GANs [88,90,91] can be introduced into adversarial maximum entropy IRL to continually enhance its performance based on generative adversarial networks.
3.6. Extension of Maximum Entropy-Based IRL
For specific practical environments, researchers have improved the maximum entropy-based IRL algorithm. In addition to the above analysis of maximum entropy-based IRL algorithm, it also includes hierarchical maximum entropy IRL, multi-objective maximum entropy IRL, multi-agent maximum entropy IRL, multi-modal IRL, federated IRL, interpretable IRL and others.
To solve data inefficiency and the poor performance of multi-task imitation learning algorithms in dealing with complex multi-tasks or multi-objectives, some new methods have been introduced. For one, a multi-task hierarchical adversarial IRL was developed to learn multi-tasking strategies with the hierarchical structure, which synthesizes context-based multi-tasking learning, adversarial IRL, and hierarchical strategy learning by identifying and transferring reusable between tasks [92]. The hierarchical HIRL framework split the task into subtasks with incremental rewards, and learned the local reward function of the subtasks using an inferred structure under expert demonstrations [27]. Moreover, to mitigate the limitations of global learning rewards due to redundant noise and error propagation, a new IRL framework based on curriculum sub-objectives guided the agents to obtain local reward functions at each stage [60], as shown in Figure 5. A multi-intent deep IRL framework used the conditional maximum entropy principle to model an expert’s multi-intentional behavior as a mixture of latent intent distributions, and learned an unknown number of nonlinear reward functions from unlabeled expert presentations [26]. For the problem of multiple experts performing tasks in MDP environments, trajectory clusters were used as latent variables in an adaptive maximum entropy IRL, and utilized the mathematical frameworks of probabilistic assignments and utility functions to jointly estimate the discount factor and reward function [93]. In addition, for robots with sequential tasks, rewards were learned based on subtasks defined by the human–computer interaction framework [94]. The Wasserstein IRL for multi-objective optimization used the shadowing gradient method to construct the inverse optimization problem for multi-objective optimization [95].
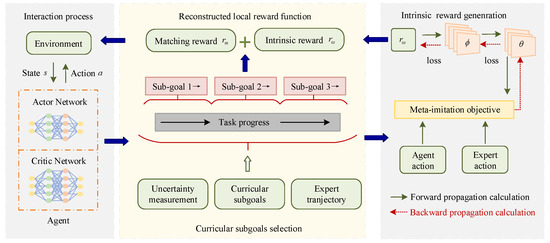
Figure 5.
Curricular Subgoal-based Inverse Reinforcement Learning (CSIRL) method.
For solving the optimization problem between multiple agents in complex experimental environments, multi-agent maximum entropy-based IRLs have been proposed. To address the difficulty of discovering individual goals in collective behaviors of complex dynamical systems, the non-strategy inverse multi-agent RL algorithm combined the ReF-ER technique and guided-cost learning to automatically discover reward functions from expert demonstrations and learn effective strategies [96], as shown in Figure 6. In a multi-agent setting, maximum entropy IRL defined the entropic cost equilibrium to capture interactions between noisy agents, approximated the solution of a general nonlinear countermeasure ECE strategy, and iteratively learned the cost function using interactive demonstrations [59]. Considering that existing diversity-aware predictors may ignore interaction results predicted by multiple agents, game-theoretic IRL was proposed to improve the coverage of multimodal trajectory prediction and used training-time game-theoretic numerical analyzes as an auxiliary loss for improving coverage and accuracy [97]. For the sparse reward problem, the multi-agent IRL for professional ice hockey game analysis introduced a regularization method based on transfer learning [98]. Additionally, to improve the learning efficiency of multi-agent maximum entropy-based IRL, the mean field was introduced. Meta-inverse reinforcement learning for mean field games extended the MFG model to deal with heterogeneous agents by introducing probabilistic context variables [99].
Figure 6.
The model of the IMARL algorithm.
Addressing the challenges of scaling IRL to large datasets and highly parameterized models, the graph compression, parallelization, and problem initialization based on dominant feature vectors were focused on, and the receding horizon inverse planning was introduced to control key performance tradeoffs through its planning horizon [100], as shown in Figure 7.
Figure 7.
Architecture overview.
In practical applications, the demonstration data often contains a mixture of trajectories from various expert agents that follow different constraints, making it challenging to explain the behavior of experts using a unified constraint function. To capture complex human preferences, multimodal IRL infers the implicit, possibly multimodal, reward function from the multimodal expert demonstrations. The expert demonstrations are no longer limited to a single form. The multimodal inverse reinforcement learning (MMICRL) algorithm simultaneously estimates multiple constraint conditions corresponding to different types of experts [101]. A framework based on meta-inverse reinforcement learning, Meta-IRLSoT++, introduces an inverse reinforcement learning framework to explore the association between trajectories and scenarios to achieve task-level scene understanding, enhance the correlation between trajectories and scenes, and utilize meta-learning to implement collaborative training based on IRLSOT++ [102]. Additionally, to achieve data security and privacy protection, distributed federated inverse reinforcement learning collaboratively learns a global reward function through local storage of expert demonstration data on multiple clients without uploading any original local data to a central server [103]. To alleviate the computational burden of nested loops, a novel single-loop algorithm based on inverse reinforcement learning follows a random gradient step for likelihood maximization after each policy improvement step to maintain the accuracy of reward estimation and predict the optimal policy under different dynamic environments or new tasks [104]. However, IRL often operates as a “black box”, outputting a complex mathematical formula for the reward function. In high-risk domains, doctors and engineers cannot trust it. Explainable IRL focuses on making the learned reward function and the resulting strategies interpretable, with the goal of converting the learned weights into human-understandable concepts. An adaptive interpretive feedback system achieves interpretive feedback by studying the application of explainable artificial intelligence in IRL and presenting selected learned trajectories to users [105]. A dynamic network link prediction method based on inverse reinforcement learning designs a reward function to maximize the cumulative expected reward obtained from the expert behavior in the original data and optimize it for social strategies [106].
The research on advanced IRL algorithms, including multi-objective IRL, multimodal IRL, federated IRL, and interpretable IRL, is still in its early stages; consequently, considerable potential remains for theoretical development in these areas. Due to the existing limitations and practical implementation challenges of maximum entropy-based inverse reinforcement learning, there is a pressing need to develop enhanced variants of this approach in real-world applications, with the aim of improving its adaptability and effectiveness. Because of its inherent strengths in handling ambiguous reward scenarios and demonstrating robust probabilistic reasoning capabilities, this technique holds significant research potential, particularly in AI-driven systems.
4. Benchmark Test Platform
Common benchmark experiments used for the validation of the maximum entropy-based IRL algorithm mainly consist of four classic control experiments and the Mujoco experiments, which are the most common.
4.1. Four Classic Control
Four classic control environment includes Acrobot, Cart pole, Mountain car, and Pendulum, as shown in Figure 8. In Gym environments, these are the ones that are easier to address. All environments can be configured with parameters and the initial state is randomized for a given range.
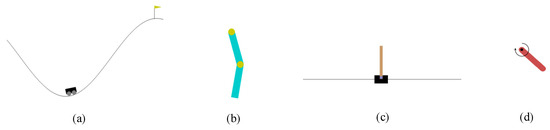
Figure 8.
Classic control environments: (a) is the Mountain car experiment, (b) is the Acrobot experiment, (c) is the Cart pole experiment, (d) is the Pendulum environment.
Benchmark experiments are used to validate the IRL algorithms. The continuous maximum entropy deep IRL achieves comprehensive knowledge of the model for experiment environment comprehensive demonstration-based reward reconstruction. Mountain car experiments show that the deep neural network in this algorithm combines representational power and computational efficiency, thereby better approximating the structure of the reward function [68]. For solving complex computational and overfitting problems, the maximum entropy IRL based on the FTPRL method updates the reward weights in the direction of optimization and uses the truncated gradient method to limit the learned rewards for decision-making, and Mountain car experiments show that the algorithm has good sparsity, generalization [63]. The benchmark experiments in Figure 8 provide a good experimental platform for the validation of the theoretical performance of the IRL algorithms. The main experimental environment settings and objectives are as follows:
- (1)
- Mountain car environment: The Mountain car environment is comprised of a car that is randomly located at the bottom of a sinusoidally curved valley, and the ultimate goal is to climb to the small yellow flag located on the right-hand peak, as shown in Figure 8a.
- (2)
- Acrobot environment: As shown in Figure 8b, the Acrobot environment proposed in [107] is composed of two linearly connected chains, one of which is fixed at one end. The aim is to achieve the target height by applying a torque to the drive joints that causes the free end of the outer linkage to oscillate.
- (3)
- Cart pole environment: In this setting, a pole gets linked to a cart traveling along a frictionless rail by means of a non-driven joint. Aim of the cart is to help hold the pole in an upright position by moving itself from side to side.
- (4)
- Pendulum environment: An inverted pendulum system contains a pendulum with one end fixed and the other end free to swing. By applying a torque to the free end, a pendulum aims to swing itself to an upright position.
4.2. MuJoCo
Mujoco is a commonly used benchmark experiment except for the above four classical control benchmark experiments and is designed for contributing to studies in robotics, mechanics, graphics, and other areas. And it is also often used as a benchmarking environment for RL and IRL algorithms. Mujoco is a collection of environments (20 sub-environments in total), and commonly used sub-environments include: the Ant experiment, the HalfCheetah experiment, the Hopper experiment, the Humanoid environment, the Inverted pendulum environment, the Reacher environment, the Swimmer environment, the Walker2D environment, as shown in Figure 9.
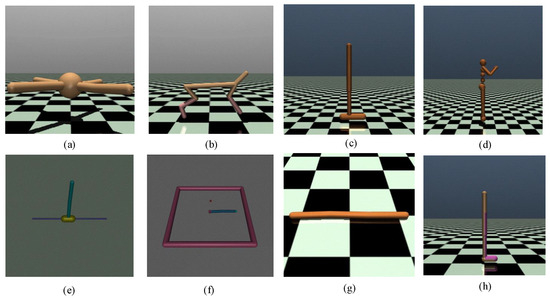
Figure 9.
Mujoco environments: (a) is the Ant experiment, (b) is the HalfCheetah experiment, (c) is the Hopper experiment, (d) is the Humanoid environment, (e) is the Inverted pendulum environment, (f) is the Reacher environment, (g) is the Swimmer environment, (h) is the Walker2D environment.
Mujoco can provide an excellent testbed for the validation of IRL algorithms. The IRL based on adversarial learning can learn rewards and value function simultaneously, using effective adversarial ideas to recover generalizable and portable reward functions. And Ant environment illustrates that this algorithm largely outperforms previous IRL methods on continuous high-dimensional tasks with unknown dynamics [24]. The transfer learning environment in Mojoco is used to illustrate the ability of adversarial IRL to solve transfer learning tasks [84]. To quantify collective behavior in complex systems and multi-agent systems, multi-agent IRL can automatically discover local incentives based only on observed trajectories by exploiting a new combination of multiple agent RL and guide cost learning, and Mujoco experiments demonstrate that the method can approximate suitable rewards through neural networks [96]. Mujoco environment settings and goals are as follows:
- (1)
- Ant experiment: The ant proposed in the [108] is a 3D robot composed of a torso and four legs. By applying torque to the connecting part of the robot, it aims to move forward.
- (2)
- HalfCheetah experiment: A HalfCheetah proposed in [109] is a 2D made of nine links and eight connected joints. By putting torque on the joints, the cheetah is enabled to run forward as quickly as possible.
- (3)
- Hopper experiment: A hopper proposed in [110] contains a torso, a thigh and a calve, a single foot, and three links connecting these four parts. The aim is to achieve a forward-moving jump by applying torque on the hinges.
- (4)
- Humanoid experiment: A humanoid 3D robot proposed in [111] has a torso, two legs, and two arms. In Humanoid experiments include the Humanoid standup experiment and Humanoid experiment. The Humanoid standup environment is designed to allow a lying humanoid to stand up and remain standing through the application of torque on the links. In the Humanoid environment, the robot moves forward as fast as possible without falling.
- (5)
- Inverted pendulum experiment: The Inverted pendulum experiments proposed in [112] conclude two sub-experiments: Inverted double pendulum experiment and Inverted pendulum experiment. The Inverted double pendulum environment comprises a cart, a long pole connected together with two short poles. One end of the long pole is fixed to the cart and the other end is free to move. The long pole is balanced on top of the cart through placing a constant side-to-side shifting force on the cart. The inverted pendulum environment contains a cart and a pole with one end attached to the cart. The pole is kept upright by moving the trolley from side to side.
- (6)
- Reacher environment: A Reacher includes a robotic arm with two joints. By moving the end effector of the arm, it aims to reach the designed goal position.
- (7)
- Swimmer environment: A Swimmer environment proposed in [112] consists of three segments and two articulation joints. The goal is achieved through exerting torque and exploiting friction to make the swimmer move to the right as fast as possible.
- (8)
- Walker2D environment: A walker proposed in [110] is made up of a torso, two thighs, two calves two feet. The feet, calves, and thighs are coordinated to walk forward through applying torque to the hinges linking six parts of the walker.
4.3. Other Benchmark Environments
As shown in Figure 10, the Maze environment consists of a robot, hells, and an exist, aiming to reach the exit with the fewest possible steps and avoid falling into the traps. In the Grid world environment, the agent starts at any grid square and moves through up, down, left, and right to reach the target grid square as fast as possible. As shown in Figure 11, the object world environment includes color 1 objects, color 2 objects, and distractor objects. These objects are randomly placed to populate the object world and learn expert’s rewards through five actions: up, down, left, right, and stay. Figure 12 is the multi-router data transmission task. Many environments involve multiple routers in a network. Effective management of multiple routers is very important for network stability. Figure 13 represents the urban traffic complex driving environment, which consists of a three-lane highway, a red host vehicle v0, and the environmental vehicles v1, v2, v3, v4, and v5. It is assumed that the red car is going faster than the other cars, and there is no communication between the drivers of different vehicles and no sharing of data between the different vehicles. The most important thing for the red host vehicle is to avoid collisions with other vehicles and they are more likely to drive in the right lane than in the left lane and middle lane.
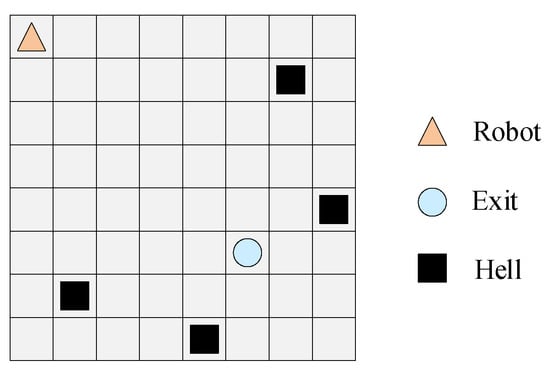
Figure 10.
Maze environment.
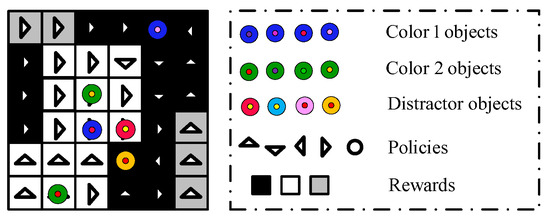
Figure 11.
Object world environment.
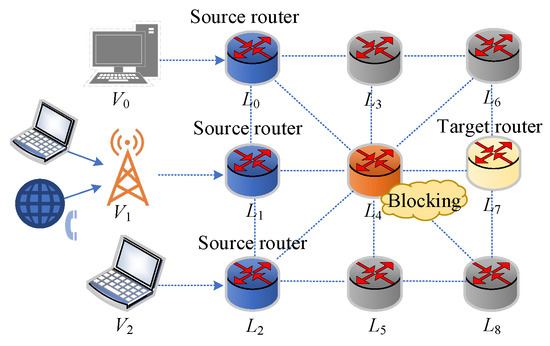
Figure 12.
Multi-router task.
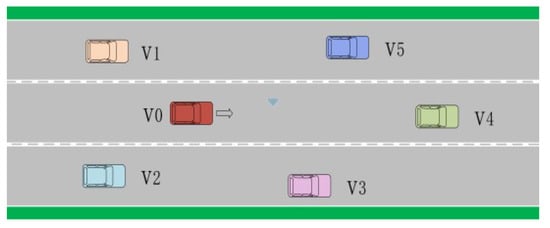
Figure 13.
Urban traffic driving environment. The arrow indicates the direction the vehicle is moving.
These benchmark experiments are used to evaluate the performance of maximum entropy IRL algorithms. To deal with the difficulty of accurately extracting real rewards in high-dimensional environments, the Maze environment demonstrates that adversarial IRL can learn disentangled rewards that are capable of accommodating significant domain shifts [24]. Both the Maze environment and Grid world are used to verify the good transfer performance of robust adversarial IRL with time-scaled actions [84]. The IRL framework recovers complex reward functions by observing the behavior of experts with unknown intentions and validates the algorithm’s merits through a series of Grid world experiments [26]. Maximum entropy IRL based on online proximal optimization uses FTPRL and truncated gradient (TG) methods to solve the complex computational and overfitting problems. Grid world and object world experiments show that the algorithm has better generalization and sparsity [63]. To enhance reward learning under MDP/R, maximum entropy deep IRL based on the Adaboost and TG methods forms multiple ME-DIRL networks into a strong learner, and experiments in grid world and object world environments illustrate the effectiveness of this algorithm in learning rewards [73]. Maximum causal entropy IRL formulates the multitasking problem within the IRL framework, and grid world experiments demonstrate that the algorithm learns rewards and policies more efficiently [48]. Maximum causal entropy IRL learning is able to learn constraints in a stochastic dynamic environment, transferring the cost function of learning to other types of agents with different reward functions, and grid world experimental evaluations have shown that this method outperforms other algorithms [80]. IRL based on the marginal Log-likelihood approach utilizes the probabilistic assignment and a mathematical framework of utility functions to jointly estimate discount factors and rewards, and the grid world experiments demonstrate the great potential of learning rewards for this algorithm [93]. Considering the QoS fluctuations caused by different service call routes, a framework based on collaborative reinforcement training and inverse reinforcement learning is proposed by combining dynamic QoS prediction with intelligent route estimation [113]. Additionally, an interactive perception decision and planning method of humanoid automatic driving under the fusion scene is proposed, which uses deep inverse reinforcement learning to learn the reward function from the natural driving data, and the traffic driving environment shows the superiority of the algorithm [114].
5. Application Study of Maximum Entropy-Based IRL
Maximum entropy-based IRL algorithms have shown strong potential for applications across various fields, including intelligent driving, robot control, games, industrial process control, power system optimization, and healthcare.
5.1. Intelligent Driving
With accelerated advancements in artificial intelligence, autonomous vehicle technology has achieved remarkable breakthroughs in intelligent transportation systems. Emerging as a transformative frontier in smart mobility, self-driving systems have the potential to enhance road safety metrics, optimize energy consumption patterns, and alleviate urban traffic bottlenecks. IRL algorithms have been widely used to solve intelligent driving traffic planning problems. However, complex traffic conditions pose challenges to the path planning. To mitigate these challenges, researchers have proposed an IRL algorithm based on the maximum entropy method, which models the interaction between self-driving cars and the environment as a stochastic MDP, using the driving style of an expert driver as a learning objective to optimize strategies based on learned rewards.
Automatic navigation in complex urban environments is challenging. Specifically, a maximum entropy deep IRL framework is applied to large-scale urban navigation scenarios to learn potential reward mappings and driving behavior using demonstration samples collected from multiple drivers [22]. The learning-based predictive behavioral planning framework, which consists of a behavior generation module, a conditional motion prediction module, and a scoring module, can predict the future trajectories of other agents and the cost function in a large-scale real urban driving [36]. Furthermore, in the area of route recommendation, Ziebart et al. proposed the new IRL and imitation learning methods to address the ambiguity problem of margin-based IRL algorithms, which provides computationally efficient optimization processes [20]. The goal conditional spatio-temporal zeroing maximum entropy deep IRL framework and the model predictive controller MPC are proposed and applied to tasks of automated driving in challenging dense traffic highway scenarios [75], as shown in Figure 14.
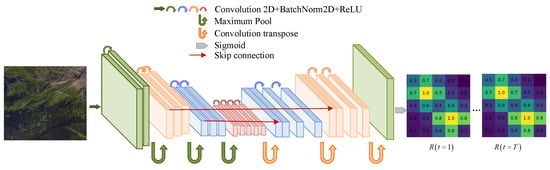
Figure 14.
Model framework of the spatio-temporal cost map learning and NN cost map.
Considering the impact of pedestrians and e-bikes on autonomous driving, deep IRL encodes the motion information of pedestrians and their neighbors using an attention framework and LSTM and maps the dynamics of these encodings into features [70]. An intelligent agent-based microsimulation model is used to simulate the crossing behavior of e-bikes, and a neural network-based nonlinear reward function is constructed with five dimensions of e-bikes, which all help self-driving cars to understand the behavior of e-bikes and make efficient decisions in complex traffic scenarios [65].
In planar navigation and simulated driving, inverse optimal control methods learn rewards as linear combinations of features or use Gaussian processes to learn non-linear reward functions, enabling the learning of more complex policies from locally optimal human demonstrations [52]. For achieving interaction between humans and agents without having to manually design a reward function, a sampling-based continuous-domain maximum entropy IRL algorithm has been proposed to learn rewards and policies with exploiting prior knowledge [33]. Adversarial IRL enhances the learning performance by incorporating state-dependent semantic reward terms into the discriminator network to recover policies and reward functions that can be adapted to different environments [85]. In automated driving planning, IRL uses path integral maximum entropy IRL to learn rewards that can be automatically adjusted to encode the driving rewards [39]. Furthermore, to predict the reward function of a sample-based planning algorithm for automated driving, a maximum entropy deep IRL based on a temporal attention mechanism is used to predict rewards by generating low-dimensional context vectors of the driving situation from the features and actions of the sampled driving strategies [71]. In real-world driving scenarios, a DNN is used to approximate the rewards of the maximum entropy IRL and the entropy of the joint distribution is introduced to obtain the optimal driving strategies [38].
In a highway driving environment, IRL based on driving behavior uses a polynomial trajectory sampler to generate candidate trajectories covering high-level decisions and desired speeds, which can simulate the driving behavior of natural human driving using the NGSIM dataset [34].
To solve the problem that the output of an automatic parking network is difficult to converge and easily falls into local optimal, IRL based on the principle of maximum entropy is adopted to solve the reward function. The car park point information is used as the input of the neural network, and the steering wheel angle command is outputted, achieving end-to-end control in the experimental results of automatic parking [35]. Considering an intelligent driving environment with multiple agents, a multi-agent maximum entropy IRL algorithm is proposed to solve the multi-agent strategy and cost functions [59].
In a task-oriented navigation environment, a new deep IRL algorithm based on active task-orientation is proposed to learn the task structure using a convolutional neural network [72]. The maximum entropy deep IRL model uses a neural network to approximate the driver’s reward during vehicle following and adopts value iteration for solving strategies in real-world driving data [40]. Inspired by human visual attention, a new IRL model uses maximum entropy deep IRL to predict driver’s visual attention in accident-prone scenarios [115].
5.2. Robot Control
The development, manufacture, and application of robots signify a country’s level of scientific and technological innovation and high-end manufacturing capabilities. Currently, the robotics industry is booming, providing significant momentum for economic and social development in various fields. With the development of machine learning technology, controlling robots using IRL algorithms has become a critical research direction.
The sampling-based inverse optimal control algorithm exploits the absence of artificially designed cost function features and intertwines cost optimization with policy learning to learn the optimal policy [23]. In the simulated robot arm control, rewards are learned from locally optimal expert demonstrations using inverse optimal control based on linear combinations and Gaussian processes [52].
As mobile robots increasingly appear in everyday life, the study of human–robot interaction has gained importance. A new maximum entropy deep IRL method uses open pedestrian trajectory data collected in shopping malls as an expert dataset to learn a reward function and pedestrians’ navigational behaviors [42]. IRL based on human–robot interaction utilizes human’s high-level perception of a task in the form of sub-goals [94].
To achieve robot autonomy in cross-country, a maximum entropy deep IRL method based on RL ConvNet and Svf ConvNet encodes kinematic properties into a convolutional kernel to achieve efficient forward reinforcement learning [41]. For tasks of the legged robot terrain traversability, a deep IRL approach is used to learn robot inertial features from extrasensory and proprioceptive data collected by the MIT mini-cheetah robot and mini-cheetah simulator [44].
In complex obstacle environments for robots, a planning framework integrating deep RL is proposed to explore optimal paths in Cartesian space [43]. An end-to-end microscopic model-based adversarial IRL framework uses a self-concerned dynamic model and an exact gradient to learn the strategy on the UR5 Robot Platform [55]. To address the problem of delayed rewards, the hierarchical IRL divides the parallel parking task into sub-tasks with short-term rewards and uses the learned sub-tasks to construct additional features [27]. To alleviate the computational burden of nested loops, a novel single-loop algorithm based on federated learning for inverse reinforcement learning maximizes the likelihood function of the random gradient to enhance the reward and policy learning performance of the robot in MuJoCo [104]. To improve the interpretability of learning rewards from expert demonstrations, an adaptive interpretive feedback system based on IRL achieves feedback by showing selected learned trajectories to the user, thereby enhancing the robot’s performance, teaching efficiency, and the user’s ability to predict the robot’s goals and actions [105].
5.3. Games
RL and IRL algorithms have garnered significant attention for their applications in gaming. The maximum entropy-based IRL algorithm can solve the difficult problem of manually designing rewards in RL algorithm. And with the continuous improvement of the IRL theory, how to better use IRL to enhance the intelligence of the game is an important research direction. Similarly, in an Atari enduro racing game, the IRL-based behavioral fusion approach decomposes a complex task into several simple tasks to learn rewards and strategies using discriminators and generators [57]. In expert demonstrations of professional games, the combination of Q-learning and IRL alternately uses single-agent IRL to learn multi-agent reward function, and analyzes professional ice hockey matches based on recovered rewards and Q-values [37]. In the MiniGrid and DeepCrawl, the proposed adversarial IRL significantly reduces the need for expert demonstrations by using environments with limited initial seed levels [56], as shown in Figure 15.
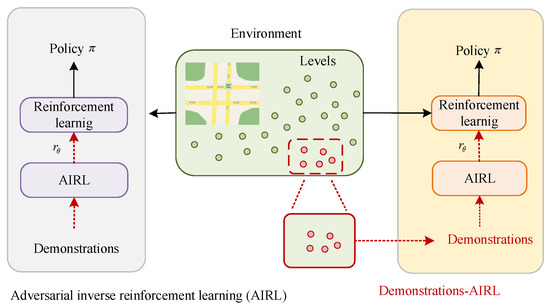
Figure 15.
Demonstration-efficient AIRL.
Game testing is a necessary but challenging task for gaming platforms. An automated game testing framework combines adversarial IRL algorithms and evolutionary multi-objective optimization, aiming to help gaming platforms ensure the quality of market-wide games [37].
5.4. Industrial Process Control
The maximum entropy-inverse reinforcement learning (ME-IRL) framework, endowed with self-evolving learning architectures and inherent nonlinear mapping capabilities, can effectively address various challenging problems in the fault diagnosis of chemical processes and wastewater treatment.
Complex industrial processes are characterized by multivariate, strong coupling, nonlinearity, large time lag, and other characteristics. The maximum entropy-based IRL algorithm demonstrates superior optimization performance in such complex scenarios, driving the development of efficient and intelligent industrial processes. Additionally, this algorithm can solve intelligent control problems in the industry, enabling systems to achieve one or more optimization goals and significantly benefiting industrial operations. In the Industrial Internet of Things (IIoT), maximum entropy IRL is used to approximate the reward function by observing the system trajectory under the control of a trained deep RL-based controller [45]. In nonlinear continuous systems described by multiple differential equations, a model-free IRL algorithm uses homogeneous and heterogeneous control inputs to learn rewards [82]. Moreover, for solving the game problem, new IRL control methods use model-based and model-free IRL algorithms to solve linear and nonlinear expert learning system problems and allow the learner to perform the behavior of the expert [83]. For the optimal synchronization problem of MAS, a model-based IRL algorithm and a model-free IRL algorithm are proposed to solve a graphical apprenticeship game [25].
However, the IRL algorithm has not yet been widely applied in industrial sectors. With continuous theoretical advancements, its potential applications in these fields are extensive.
5.5. Medical Health and Life
Maximum entropy-based IRL algorithm can solve sequential decision-making problems with sampling, evaluation, and delayed feedback, which makes it an effective solution for constructing effective policies in various healthcare and life domains. In pose-based anomaly detection tasks, a novel human interaction modeling approach based on visual activity analysis utilizes kernel-based RL and inverse optimal control of the mean-shift process to simulate the interactive dynamics of human interactions [54]. Additionally, the intelligent medical assistants aim to improve patient comfort. For patients with atresia syndrome, a new efficient IRL algorithm is proposed to process new time-recorded state and patient’s environmental data for suggesting the right action at the right time [47].
To identify the bidding preferences of power producers in the electricity market, a data-driven reward function identification framework employs maximum entropy deep IRL to identify reward functions and simulate bidding behavior [46], as shown in Figure 16. In the Kitchen Env, multi-task hierarchical adversarial IRL can be used to obtain hierarchical policies for solving hybrid execution tasks based on multi-task unannotated expert data [60]. Addressing how pro-Russian propaganda groups for the war in Ukraine strategically shape cyberspeak, an IRL approach analyzes the strategies of the Twitter community for inferring potential rewards when interacting with pro- or anti-invasion users [37]. To advance intelligent research on genetic materials, a new physically-aware IRL algorithm investigates the isomorphism of stocks between time-discrete FPs and MDPs, and uses a variational partitioning system to infer latent functions and strategies in FPs [36]. To ensure data security during the integration of data from multiple hospitals, the federated IRL algorithm based on differential privacy trains a private treatment strategy on the local data that contains the trajectories of clinical doctors [103]. In real dynamic social networks, random social behaviors and unstable spatio-temporal distributions often lead to link predictions that are uninterpretable and inaccurate. The dynamic network link prediction method based on inverse reinforcement learning maximizes the cumulative expected reward obtained from the expert behaviors in the original data and uses it to learn the social strategies of the agents [106].
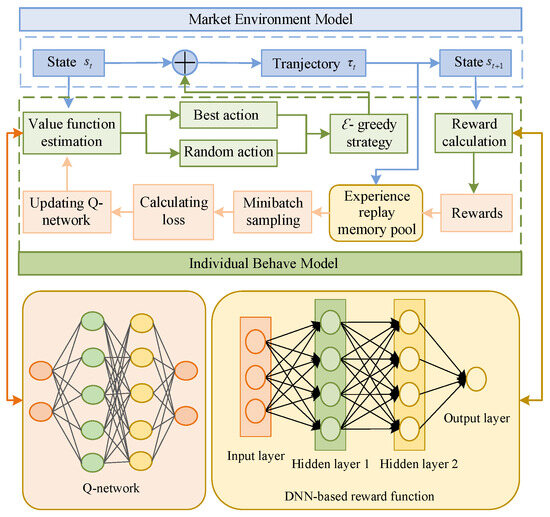
Figure 16.
DQN-based bidding behavior simulation model.
6. Faced Problems by Maximum Entropy-Based IRL and Solution Ideas
The ongoing methodological refinements in maximum entropy-based IRL algorithms have propelled their deployment across intelligent driving, robot control, industrial process control, and other fields. Current research trajectories focus on critical challenges that are actively being investigated. Notwithstanding these developments, there are still unresolved or partially resolved issues that prompt ongoing efforts by researchers to address them. How to better solve these existing problems and promote the development of theoretical and application research on maximum entropy-based IRL are promising research directions. We describe the problems and solutions in detail in the following subsections.
6.1. Locally Optimal Expert Demonstration Problem and Solution Ideas
Maximum entropy-based IRL algorithm learns rewards under expert demonstrations and uses the learned rewards to optimize policies. However, in practical environments, expert demonstrations may be locally optimal, making it difficult to obtain optimal expert demonstrations. This leads to expert demonstrations that may be finite, non-optimal, and data unbalanced. To circumvent these bottlenecks, researchers have pioneered hybrid architectures such as deep maximum entropy-based IRL and maximum entropy-based inverse optimal control, aiming to learn and optimize rewards and policies even with locally optimal expert presentations. Concurrently, the introduction of generative adversarial networks helps the maximum entropy-based IRL generate new samples, which are combined with expert samples to form hybrid samples. These algorithms can solve the local optimal problem of expert demonstrations to some extent and can improve the learning accuracy of rewards [116].
6.2. Learning Inefficiency and Solutions
In complex learning environments, the maximum entropy-based IRL algorithm may have some problems, such as multi-task problem and game problem, leading to learning inefficiency. How to improve learning efficiency and accuracy of maximum entropy-based IRL algorithms is a worthy research topic. For complex and variable environments, maximum entropy-based IRL algorithm combines the advantages of inverse optimal control theory, generative adversarial networks, and deep learning methods to improve the learning performance of the algorithm [22]. Additionally, researchers have considered decomposing complex tasks into multiple subtasks or subgoals for learning, which solves the dimensional disaster and improves the algorithm’s performance by sharing information and complementing each other, aiming to accelerate learning efficiency [27,60]. Considering that there are usually multiple decision-making individuals in real-life scenarios, some researchers have gradually extended their vision from single-agent to multi-agents. Therefore, for the game problem of multiple agents, researchers have proposed a maximum entropy-based multi-agent IRL to enhance the perception and learning ability of the algorithm, which can improve the algorithm’s learning efficiency [86,117].
6.3. Inadequate Theoretical and Applied Research
To better solve the MDP problem without reward function, researchers have successively proposed a maximum entropy-based IRL algorithms, such as maximum entropy IRL based on trajectory distribution, maximum entropy-based deep IRL, maximum entropy-based inverse optimal control, adversarial maximum entropy IRL, and maximum entropy IRL based on multi-task and multi-agent. However, the theoretical research on the maximum entropy-based IRL algorithm is neither deep nor extensive enough, which restricts the application of the algorithm in various fields. Practical and complex environments also place higher demands on the algorithmic performance, and an in-depth exploration of the theory is required. Therefore, it is essential to fully integrate existing IRL research results with the latest machine learning ideas to enhance algorithm performance. The meta-learning method has been introduced into the adversarial IRL for fast adaptation to new tasks [118]. Additionally, introducing the idea of graph convolutional neural networks, transformers, and ensemble methods into maximum entropy-based IRL can improve the learning accuracy of nonlinear rewards is also a promising research direction [119,120,121]. Maximum entropy-based IRL algorithms are mainly used in intelligent driving, robot control, and gaming. Furthermore, due to the complexity and interference of the environment, maximum entropy-based IRL algorithms are less utilized in the finance and trade and complex industrial process control. In addition, maximum entropy-based IRL algorithms have been applied in intelligent driving, robot control, gaming, finance and trade, and complex industrial process control. However, maximum entropy-based IRL algorithm tends to require higher accuracy and stability guarantees in real scenarios, and exploration, trial, and error imply extremely high costs that cannot be afforded in real scenarios where such mistakes are made. Consequently, the practical applications of maximum entropy-based IRL algorithms remain limited in some fields. With theoretical advancements and deeper application research, the development of IRL algorithms and artificial intelligence technologies will progress further.
7. Conclusions
In recent years, IRL algorithms based on the maximum entropy method have emerged with numerous innovative ideas and methods, achieving impressive results. As a key technology in artificial intelligence, the maximum entropy-based IRL algorithm can solve the problem of finite or non-optimal expert demonstration and the ambiguity problem in learning rewards and optimizing policies. Significant theoretical and practical advancements have been made, with new algorithms continually being proposed to address existing issues in IRL, allowing the algorithm to adapt to new environments. This paper highlights the existing theoretical research and application research progress of maximum entropy-based IRL and summarizes its problems, solutions, and future development directions.
Furthermore, maximum entropy-based IRL algorithm holds substantial research potential in both the theoretical research and applied research. Due to the problems of non-optimality, computational complexity, and overfitting faced by the maximum entropy-based IRL algorithm, the algorithm’s theoretical development still has significant room for growth. Introducing the latest ideas into maximum entropy-based IRL is a vital research area. With the advantages of good reasoning and strong interpretability, graph networks can be added into maximum entropy-based IRL for studying novel graph-based multi-agent IRL, which improves the performance of the algorithm. Moreover, using the deformation of GAN networks, such as deep convolutional GANs, Wasserstein GANs, boundary seeking GANs, can address the issues of maximum entropy-based IRL, including non-optimal expert demonstrations, model collapse and instability during training. Additionally, to solve the limitations of the maximum entropy-based IRL algorithm in some practical applications, there are two directions that can be investigated to land maximum entropy-based IRL techniques in real task environments. One is to develop a high-precision simulation environment, allowing intelligent decisions trained in the simulation to be directly transferred to real-world scenarios. The other approach involves using real data to create a virtual environment, applying model-based IRL techniques to optimize intelligent decisions in the virtual setting before deploying them in real scenarios. We anticipate that maximum entropy-based IRL algorithms will be effectively implemented in real-world applications. In addition, the algorithm has promising applications in fields such as material chemical molecule prediction, fund trading prediction, sewage treatment control, and defense military control. Therefore, it is crucial to continue advancing theoretical research on maximum entropy-based IRL algorithms and exploring their application across a broader range of fields. This will promote the maturity of RL and IRL algorithms, significantly contributing to the advancement of artificial intelligence technology.
Author Contributions
Conceptualization, L.S. and I.A.C.; methodology, Q.G. and L.S.; validation, Z.W. and I.A.C.; formal analysis, Q.G. and I.A.C.; investigation, Z.W. and L.S.; resources, L.S.; writing original draft preparation, L.S. and Q.G.; writing—review and editing, Q.G. and I.A.C.; visualization, L.S. and Z.W.; supervision, Q.G. and I.A.C.; project administration, L.S. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by Postdoctoral Research Startup Fund of the Big Picture Center of Hangzhou City University (No.201000-584105/002).
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding author.
Acknowledgments
Thanks to “the Research Center for High-Performance Computing of Ultra-Large-Scale Graph Data at Hangzhou City University”, “the Zhejiang Provincial Engineering Research Center for Real-Time Digital and Intelligent Technology in Urban Safety Governance”, and “the Supercomputing Center of Hangzhou City University” for providing the research start-up funds and some experimental hardware conditions for the research.
Conflicts of Interest
Author Zeyu Wang was employed by the Tongzhou Operation Area of the Beijing Oil and Gas Branch of Beijing Pipeline Limited Company, Beijing 100101, China. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as potential conflicts of interest.
References
- Wang, X.; Wang, S.; Liang, X.X.; Zhao, D.W.; Huang, J.C.; Xu, X.; Dai, B.; Miao, Q.G. Deep reinforcement learning: A survey. IEEE Trans. Neural Netw. Learn. Syst. 2024, 35, 5064–5078. [Google Scholar] [CrossRef] [PubMed]
- Rafailov, R.; Hatch, K.B.; Singh, A.; Kumar, A.; Smith, L.; Kostrikov, I.; Hansen-Estruch, P.; Kolev, V.; Ball, P.J.; Wu, J.J.; et al. D5RL: Diverse datasets for data-driven deep reinforcement learning. In Proceedings of the first Reinforcement Learning Conference, Vienna, Austria, 7–11 May 2024; pp. 1–20. [Google Scholar]
- Zhang, X.L.; Jiang, Y.; Lu, Y.; Xu, X. Receding-horizon reinforcement learning approach for kinodynamic motion planning of autonomous vehicles. IEEE Trans. Intell. Veh. 2022, 7, 556–568. [Google Scholar] [CrossRef]
- Pateria, S.; Subagdja, B.; Tan, A.; Quek, C. End-to-end hierarchical reinforcement learning with integrated subgoal discovery. IEEE Trans. Neural Networks Learn. Syst. 2022, 33, 7778–7790. [Google Scholar] [CrossRef]
- Lian, B.; Kartal, Y.; Lewis, F.L.; Mikulski, D.G.; Hudas, G.R.; Wan, Y.; Davoudi, A. Anomaly detection and correction of optimizing autonomous systems with inverse reinforcement learning. IEEE Trans. Cybern. 2023, 53, 4555–4566. [Google Scholar] [CrossRef]
- Gao, Z.H.; Yan, X.T.; Gao, F. A decision-making method for longitudinal autonomous driving based on inverse reinforcement learning. Aut. Eng. 2022, 44, 969–975. [Google Scholar]
- Zhang, T.; Liu, Y.; Hwang, M.; Hwang, K.; Ma, C.Y.; Cheng, J. An end-to-end inverse reinforcement learning by a boosting approach with relative entropy. Inform. Sci. 2020, 520, 1–14. [Google Scholar] [CrossRef]
- Samak, T.V.; Samak, C.V.; Kandhasamy, S. Robust behavioral cloning for autonomous vehicles using end-to-end imitation learning. SAE Int. J. Connect. Autom. Veh. 2021, 4, 279–295. [Google Scholar] [CrossRef]
- Liu, S.; Jiang, H.; Chen, S.P.; Ye, J.; He, R.Q.; Sun, Z.Z. Integrating dijkstra’s algorithm into deep inverse reinforcement learning for food delivery route planning. Transp. Res. E Logist. Transp. Rev. 2020, 142, 102070. [Google Scholar] [CrossRef]
- Adams, S.; Cody, T.; Beling, P.A. A survey of inverse reinforcement learning. Artif. Intell. Rev. 2022, 55, 4307–4346. [Google Scholar] [CrossRef]
- Chen, X.; Abdelkader, E.K. Neural inverse reinforcement learning in autonomous navigation. Robot. Auton. Syst. 2016, 84, 1–14. [Google Scholar] [CrossRef]
- Li, D.C.; He, Y.Q.; Fu, F. Nonlinear inverse reinforcement learning with mutual information and gaussian process. In Proceedings of the 2014 IEEE International Conference on Robotics and Biomimetics, Bali, Indonesia, 5–10 December 2014; pp. 1445–1450. [Google Scholar]
- Yao, J.Y.; Pan, W.W.; Doshi-Velez, F.; Engelhardt, B.E. Inverse reinforcement learning with multiple planning horizons. In Proceedings of the First Reinforcement Conference, Amherst, MA, USA, 9–12 August 2024; pp. 1–30. [Google Scholar]
- Russel, S. Learning agents for uncertain environments. In Proceedings of the Eleventh Annual Conference on Computational Learning Theory, Madison, WI, USA, 24–26 July 1998; pp. 101–103. [Google Scholar]
- Choi, D.; Min, K.; Choi, J. Regularising neural networks for future trajectory prediction via inverse reinforcement learning framework. IET Comput. Vis. 2020, 14, 192–200. [Google Scholar] [CrossRef]
- Huang, W.H.; Braghin, F.; Wang, Z. Learning to drive via apprenticeship learning and deep reinforcement learning. In Proceedings of the 2019 IEEE 31st International Conference on Tools with Artificial Intelligence, Portland, OR, USA, 4–6 November 2019; pp. 1536–1540. [Google Scholar]
- Lee, D.J.; Srinivasan, S.; Doshi-Velez, F. Truly batch apprenticeship learning with deep successor features. In Proceedings of the 28th International Joint Conference on Artificial Intelligence, Macao, China, 10–16 August 2019; pp. 5909–5915. [Google Scholar]
- Abbeel, P.; Ng, A.Y. Apprenticeship learning via inverse reinforcement learning. In Proceedings of the Twenty-First International Conference on Machine Learning, New York, NY, USA, 4–8 July 2004; pp. 1–8. [Google Scholar]
- Ratliff, N.D.; Bagnell, J.A.; Zinkevich, M.A. Maximum margin planning. In Proceedings of the 23rd International Conference on Machine Learning, New York, NY, USA, 25–29 June 2006; pp. 729–736. [Google Scholar]
- Ziebart, B.D.; Maas, A.; Bagnell, J.A.; Dey, A.K. Maximum entropy inverse reinforcement learning. In Proceedings of the Twenty-Third AAAI Conference on Artificial Intelligence, Chicago, IL, USA, 13–17 July 2008; pp. 1433–1438. [Google Scholar]
- Ziebart, B.D. Modeling Purposeful Adaptive Behavior with the Principle of Maximum Causal Entropy. Ph.D. Thesis, Carnegie Mellon University, Pittsburgh, PA, USA, 2010. [Google Scholar]
- Wulfmeier, M.; Wang, D.Z.; Posner, I. Watch this: Scalable cost-function learning for path planning in urban environments. In Proceedings of the 2016 IEEE/RSJ International Conference on Intelligent Robots and Systems, Daejeon, Republic of Korea, 9–14 October 2016; pp. 2089–2095. [Google Scholar]
- Finn, C.; Levine, S.; Abbeel, P. Guided cost learning: Deep inverse optimal control via policy optimization. In Proceedings of the 33rd International Conference on International Conference on Machine Learning, New York, NY, USA, 19–24 June 2016; pp. 49–58. [Google Scholar]
- Fu, J.; Luo, K.; Levine, S. Learning robust rewards with adversarial inverse reinforcement learning. In Proceedings of the 6th International Conference on Learning Representations, Vancouver, BC, Canada, 30 April–3 May 2018; pp. 1–15. [Google Scholar]
- Donge, V.S.; Lian, B.; Lewis, F.L.; Davoudi, A. Multiagent graphical games with inverse reinforcement learning. IEEE Trans. Control Netw. Syst. 2023, 10, 841–852. [Google Scholar] [CrossRef]
- Bighashdel, A.; Meletis, P.; Jancura, P.; Dubbelman, G. Deep adaptive multi-intention inverse reinforcement learning. In Proceedings of the Joint European Conference on Machine Learning and Knowledge Discovery in Databases, Bilbao, Spain, 13–17 September 2021; pp. 206–221. [Google Scholar]
- Krishnan, S.; Garg, A.; Liaw, R.; Miller, L.; Pokorny, F.T.; Goldberg, K. Hirl: Hierarchical inverse reinforcement learning for long-horizon tasks with delayed rewards. arXiv 2016, arXiv:1604.06508. [Google Scholar] [CrossRef]
- Sun, L.T.; Zhan, W.; Tomizuka, M. Probabilistic prediction of interactive driving behavior via hierarchical inverse reinforcement learning. In Proceedings of the 2018 21st International Conference on Intelligent Transportation Systems, Maui, HI, USA, 4–7 November 2018; pp. 2111–2117. [Google Scholar]
- Kiran, R.; Sobh, I.; Talpaert, V.; Mannion, P.; Sallab, A.A.; Yogamani, S.; Pérez, P. Deep reinforcement learning for autonomous driving: A survey. IEEE Trans. Intell. Transp. 2022, 23, 4909–4926. [Google Scholar] [CrossRef]
- García, J.; Fernández, F. A comprehensive survey on safe reinforcement learning. J. Mach. Learn. Res. 2015, 16, 1437–1480. [Google Scholar]
- Fischer, J.; Eyberg, C.; Werling, M.; Lauer, M. Sampling-based inverse reinforcement learning algorithms with safety constraints. In Proceedings of the 2021 IEEE/RSJ International Conference on Intelligent Robots and Systems, Prague, Czech Republic, 27 September–1 October 2021; pp. 791–798. [Google Scholar]
- Shiarlis, K.; Messias, J.; Whiteson, S. Inverse reinforcement learning from failure. In Proceedings of the 2016 International Conference on Autonomous Agents and Multiagent Systems, Singapore, 9–13 May 2016; pp. 1060–1068. [Google Scholar]
- Wu, Z.; Sun, L.T.; Zhan, W.; Yang, C.Y.; Tomizuka, M. Efficient sampling-based maximum entropy inverse reinforcement learning with application to autonomous driving. IEEE Rob. Autom. Lett. 2020, 5, 5355–5362. [Google Scholar] [CrossRef]
- Huang, Z.Y.; Wu, J.D.; Lv, C. Driving behavior modeling using naturalistic human driving data with inverse reinforcement learning. IEEE Trans. Intell. Transp. 2022, 23, 10239–10251. [Google Scholar] [CrossRef]
- Fang, P.Y.; Yu, Z.P.; Xiong, L.; Fu, Z.Q.; Li, Z.R.; Zeng, D.Q. A maximum entropy inverse reinforcement learning algorithm for automatic parking. In Proceedings of the 2021 5th CAA International Conference on Vehicular Control and Intelligence, Tianjin, China, 29–31 October 2021; pp. 1–6. [Google Scholar]
- Huang, C.Y.; Srivastava, S.; Garikipati, K. Fp-irl: Fokker-planck-based inverse reinforcement learning-a physics-constrained approach to markov decision processes. arXiv 2023, arXiv:2306.10407. [Google Scholar]
- Geissler, D.; Feuerriegel, S. Analyzing the strategy of propaganda using inverse reinforcement learning: Evidence from the 2022 russian invasion of ukraine. arXiv 2023, arXiv:2307.12788. [Google Scholar] [CrossRef]
- You, C.X.; Lu, J.B.; Filev, D.; Tsiotras, P. Advanced planning for autonomous vehicles using reinforcement learning and deep inverse reinforcement learning. Robot. Auton. Syst. 2019, 114, 1–18. [Google Scholar] [CrossRef]
- Rosbach, S.; James, V.; Großjohann, S.; Homoceanu, S.; Roth, S. Driving with style: Inverse reinforcement learning in general-purpose planning for automated driving. In Proceedings of the 2019 IEEE/RSJ International Conference on Intelligent Robots and Systems, Macau, China, 3–8 November 2019; pp. 2658–2665. [Google Scholar]
- Zhou, Y.; Fu, R.; Wang, C. Learning the car-following behavior of drivers using maximum entropy deep inverse reinforcement learning. J. Adv. Transport. 2020, 2020, 4752651. [Google Scholar] [CrossRef]
- Zhu, Z.Y.; Li, N.; Sun, R.Y.; Xu, D.H.; Zhao, H.J. Off-road autonomous vehicles traversability analysis and trajectory planning based on deep inverse reinforcement learning. In Proceedings of the 2020 IEEE Intelligent Vehicles Symposium, Las Vegas, NV, USA, 19 October–13 November 2020; pp. 971–977. [Google Scholar]
- Fahad, M.; Chen, Z.; Guo, Y. Learning how pedestrians navigate: A deep inverse reinforcement learning approach. In Proceedings of the 2018 IEEE/RSJ International Conference on Intelligent Robots and Systems, Madrid, Spain, 1–5 October 2018; pp. 819–826. [Google Scholar]
- Li, X.J.; Liu, H.S.; Dong, M.H. A general framework of motion planning for redundant robot manipulator based on deep reinforcement learning. IEEE Trans. Ind. Inform. 2022, 18, 5253–5263. [Google Scholar] [CrossRef]
- Gan, L.; Grizzle, J.W.; Eustice, R.M.; Ghaffari, M. Energy-based legged robots terrain traversability modeling via deep inverse reinforcement learning. IEEE Rob. Autom. Lett. 2022, 7, 8807–8814. [Google Scholar] [CrossRef]
- Liu, X.; Yu, W.; Liang, F.; Griffith, D.; Golmie, N. On deep reinforcement learning security for industrial internet of things. Comput. Commun. 2022, 168, 20–32. [Google Scholar] [CrossRef]
- Guo, H.Y.; Chen, Q.X.; Xia, Q.; Kang, C.Q. Deep inverse reinforcement learning for objective function identification in bidding models. IEEE Trans. Power. Syst. 2021, 36, 5684–5696. [Google Scholar] [CrossRef]
- Hantous, K.; Rejeb, L.; Hellali, R. Detecting physiological needs using deep inverse reinforcement learning. Appl. Artif. Intell. 2022, 36, 2022340. [Google Scholar] [CrossRef]
- Adam, G.; Oliver, H. Multi-task maximum causal entropy inverse reinforcement learning. arXiv 2018, arXiv:1805.08882. [Google Scholar]
- Zouzou, A.; Bouhoute, A.; Boubouh, K.; Kamili, M.E.; Berrada, I. Predicting lane change maneuvers using inverse reinforcement learning. In Proceedings of the 2017 International Conference on Wireless Networks and Mobile Communications, Rabat, Morocco, 1–4 November 2017; pp. 1–7. [Google Scholar]
- Martinez-Gil, F.; Lozano, M.; García-Fernández, I.; Romero, P.; Serra, D.; Sebastián, R. Using inverse reinforcement learning with real trajectories to get more trustworthy pedestrian simulations. Mathematics 2020, 8, 1479. [Google Scholar] [CrossRef]
- Navyata, S.; Shinnosuke, U.; Mohit, S.; Joachim, G. Inverse reinforcement learning with explicit policy estimates. In Proceedings of the AAAI Conference on Artificial Intelligence, Philadelphia, PA, USA, 25 February–4 March 2025; pp. 9472–9480. [Google Scholar]
- Levine, S.; Koltun, V. Continuous inverse optimal control with locally optimal examples. In Proceedings of the 29th International Conference on International Conference on Machine Learning, Edinburgh, UK, 26 June 2012–1 July 2012; pp. 475–482. [Google Scholar]
- Lian, B.; Xue, W.Q.; Lewis, F.L.; Chai, T.Y. Inverse reinforcement learning for adversarial apprentice games. IEEE Trans. Neural Networks Learn. Syst. 2023, 34, 4596–4609. [Google Scholar] [CrossRef]
- Huang, D.; Kitani, K.M. Action-reaction: Forecasting the dynamics of human interaction. In Proceedings of the European Conference on Computer Vision, Zurich, Switzerland, 6–12 September 2014; pp. 489–504. [Google Scholar]
- Sun, J.K.; Yu, L.T.; Dong, P.Q.; Lu, B.; Zhou, B.L. Adversarial inverse reinforcement learning with self-attention dynamics model. IEEE Rob. Autom. Lett. 2021, 6, 1880–1886. [Google Scholar] [CrossRef]
- Bagdanov, A.D.; Sestini, A.; Kuhnle, A. Demonstration-efficient inverse reinforcement learning in procedurally generated environments. arXiv 2020, arXiv:2012.02527. [Google Scholar] [CrossRef]
- Shi, H.B.; Li, J.C.; Chen, S.C.; Hwang, K.A. A behavior fusion method based on inverse reinforcement learning. Inform. Sci. 2022, 609, 429–444. [Google Scholar] [CrossRef]
- Song, Z.H. An automated framework for gaming platform to test multiple games. In Proceedings of the 2020 IEEE/ACM 42nd International Conference on Software Engineering: Companion Proceedings, Seoul, Republic of Korea, 27 June–19 July 2020; pp. 134–136. [Google Scholar]
- Mehr, N.; Wang, M.Y.; Bhatt, M.; Schwager, M. Maximum-entropy multi-agent dynamic games: Forward and inverse solutions. IEEE Trans. Rob. 2023, 39, 1801–1815. [Google Scholar] [CrossRef]
- Xu, S.Q.; Wu, H.Y.; Zhang, J.T.; Cong, J.Y.; Chen, T.H.; Liu, Y.F.; Liu, S.Y.; Qing, Y.P.; Song, M.L. Curricular subgoals for inverse reinforcement learning. arXiv 2023, arXiv:2306.08232. [Google Scholar] [CrossRef]
- Das, N.; Chattopadhyay, A. Inverse reinforcement learning with constraint recovery. arXiv 2023, arXiv:2305.08130. [Google Scholar] [CrossRef]
- Aghasadeghi, N.; Bretl, T. Maximum entropy inverse reinforcement learning in continuous state spaces with path integrals. Proceedings of 2011 IEEE/RSJ International Conference on Intelligent Robots and Systems, San Francisco, CA, USA, 25–30 September 2011; pp. 1561–1566. [Google Scholar]
- Song, L.; Li, D.Z.; Xu, X. Sparse online maximum entropy inverse reinforcement learning via proximal optimization and truncated gradient. Knowl.-Based Syst. 2022, 252, 1–15. [Google Scholar] [CrossRef]
- Li, D.Z.; Du, J.H. Maximum entropy inverse reinforcement learning based on behavior cloning of expert examples. In Proceedings of the 2021 IEEE 10th Data Driven Control and Learning Systems Conference, Suzhou, China, 14–16 May 2021; pp. 996–1000. [Google Scholar]
- Wang, Y.J.; Wan, S.W.; Li, Q.; Niu, Y.C.; Ma, F. Modeling crossing behaviors of e-bikes at intersection with deep maximum entropy inverse reinforcement learning using drone-based video data. IEEE Trans. Intell. Transp. 2023, 24, 6350–6361. [Google Scholar] [CrossRef]
- Snoswell, A.J.; Singh, S.P.N.; Ye, N. Revisiting maximum entropy inverse reinforcement learning: New perspectives and algorithms. In Proceedings of the 2020 IEEE Symposium Series on Computational Intelligence, Canberra, Australia, 1–4 December 2020; pp. 241–249. [Google Scholar]
- Wulfmeier, M.; Rao, D.; Wang, D.Z.; Ondruska, P.; Posner, I. Large-scale cost function learning for path planning using deep inverse reinforcement learning. Int. J. Robot Res. 2017, 36, 1073–1087. [Google Scholar] [CrossRef]
- Chen, X.L.; Cao, L.; Xu, Z.X.; Lai, J.; Li, C.X. A study of continuous maximum entropy deep inverse reinforcement learning. Math. Probl. Eng. 2019, 2019, 4834516. [Google Scholar] [CrossRef]
- Silva, J.A.R.; Grassi, V.; Wolf, D.F. Continuous deep maximum entropy inverse reinforcement learning using online pomdp. In Proceedings of the 2019 19th International Conference on Advanced Robotics, Belo Horizonte, Brazil, 2–6 December 2019; pp. 382–387. [Google Scholar]
- Fernando, T.; Denman, S.; Sridharan, S.; Fookes, C. Neighbourhood context embeddings in deep inverse reinforcement learning for predicting pedestrian motion over long time horizons. In Proceedings of the 2019 IEEE/CVF International Conference on Computer Vision Workshop, Seoul, Republic of Korea, 27 October–2 November 2019; pp. 1179–1187. [Google Scholar]
- Rosbach, S.; Li, X.; Großjohann, S.; Homoceanu, S.; Roth, S. Planning on the fast lane: Learning to interact using attention mechanisms in path integral inverse reinforcement learning. In Proceedings of the 2020 IEEE/RSJ International Conference on Intelligent Robots and Systems, Las Vegas, NV, USA, 25–29 October 2020; pp. 5187–5193. [Google Scholar]
- Memarian, F.; Xu, Z.; Wu, B.; Wen, M.; Topcu, U. Active task-inference-guided deep inverse reinforcement learning. In Proceedings of the 2020 59th IEEE Conference on Decision and Control, Jeju Island, Republic of Korea, 14–18 December 2020; pp. 1932–1938. [Google Scholar]
- Song, L.; Li, D.Z.; Wang, X.; Xu, X. Adaboost maximum entropy deep inverse reinforcement learning with truncated gradient. Inform. Sci. 2022, 602, 328–350. [Google Scholar] [CrossRef]
- Fernando, T.; Denman, S.; Sridharan, S.; Fookes, C. Deep inverse reinforcement learning for behavior prediction in autonomous driving: Accurate forecasts of vehicle motion. IEEE Signal Process. Mag. 2021, 38, 87–96. [Google Scholar] [CrossRef]
- Lee, K.; Isele, D.; Theodorou, E.A.; Bae, S. Spatiotemporal costmap inference for mpc via deep inverse reinforcement learning. IEEE Rob. Autom. Lett. 2022, 7, 3194–3201. [Google Scholar] [CrossRef]
- Ziebart, B.D.; Bagnell, J.A.; Dey, A.K. Modeling interaction via the principle of maximum causal entropy. In Proceedings of the 27th International Conference on International Conference on Machine Learning, Haifa, Israel, 21–24 June 2010; pp. 1255–1262. [Google Scholar]
- Ziebart, B.D.; Bagnell, J.A.; Dey, A.K. The principle of maximum causal entropy for estimating interacting processes. IEEE Trans. Inf. Theory 2013, 59, 1966–1980. [Google Scholar] [CrossRef]
- Gleave, A.; Toyer, S. A primer on maximum causal entropy inverse reinforcement learning. arXiv 2022, arXiv:2203.11409. [Google Scholar] [CrossRef]
- Zhou, Z.Y.; Bloem, M.; Bambos, N. Infinite time horizon maximum causal entropy inverse reinforcement learning. IEEE Trans. Autom. Control 2018, 63, 2787–2802. [Google Scholar] [CrossRef]
- Mattijs, B.; Pietro, M.; Sam, L.; Pieter, S. Maximum causal entropy inverse constrained reinforcement learning. arXiv 2023, arXiv:2305.02857. [Google Scholar] [CrossRef]
- Viano, L.; Huang, Y.T.; Kamalaruban, P.; Weller, A.; Cevher, V. Robust inverse reinforcement learning under transition dynamics mismatch. In Proceedings of the 35th Conference on Neural Information Processing Systems, Online, 6–14 December 2021; pp. 1–5. [Google Scholar]
- Lian, B.; Xue, W.Q.; Lewis, F.L.; Chai, T.Y.; Davoudi, A. Inverse reinforcement learning for multi-player apprentice games in continuous-time nonlinear systems. In Proceedings of the 2021 60th IEEE Conference on Decision and Control, Austin, TX, USA, 14–17 December 2021; pp. 803–808. [Google Scholar]
- Lian, B.; Xue, W.Q.; Lewis, F.L.; Chai, T.Y. Inverse reinforcement learning for multi-player noncooperative apprentice game. Automatica 2022, 145, 110524. [Google Scholar] [CrossRef]
- Boussioux, L.; Wang, J.H.; Doina, G.M.; Venuto, P.D.; Chakravorty, J. oirl: Robust adversarial inverse reinforcement learning with temporally extended actions. arXiv 2002, arXiv:2002.09043. [Google Scholar]
- Wang, P.; Liu, D.P.; Chen, J.Y.; Li, H.H.; Chan, C. Decision making for autonomous driving via augmented adversarial inverse reinforcement learning. In Proceedings of the 2021 IEEE International Conference on Robotics and Automation, Xi’an, China, 30 May–5 June 2021; pp. 1036–1042. [Google Scholar]
- Gruver, N.; Song, J.M.; Kochenderfer, M.J.; Ermon, S. Multi-agent adversarial inverse reinforcement learning with latent variables. In Proceedings of the 19th International Conference on Autonomous Agents and MultiAgent Systems, Auckland, New Zealand, 9–13 May 2020; pp. 1855–1857. [Google Scholar]
- Alsaleh, R.; Sayed, T. Markov-game modeling of cyclist-pedestrian interactions in shared spaces: A multi-agent adversarial inverse reinforcement learning approach. Transp. Res. Part C Emerg. Technol. 2021, 128, 103191. [Google Scholar] [CrossRef]
- So, S.; Rho, J. Designing nanophotonic structures using conditional deep convolutional generative adversarial networks. Nanophotonics 2019, 8, 1255–1261. [Google Scholar] [CrossRef]
- Ghasemipour, S.K.; Gu, S.X.; Zemel, R. SMILe: Scalable meta inverse reinforcement learning through context-conditional policies. In Proceedings of the 33rd Conference on Neural Information Processing Systems, Vancouver, BC, Canada, 8–14 December 2019; pp. 7879–7889. [Google Scholar]
- Peng, P.; Wang, Y.; Zhang, W.J.; Zhang, Y.; Zhang, H.M. Imbalanced process fault diagnosis using enhanced auxiliary classifier gan. In Proceedings of the 2020 Chinese Automation Congress, Shanghai, China, 6–8 November 2020; pp. 313–316. [Google Scholar]
- Yan, K.; Su, J.Y.; Huang, J.; Mo, Y.C. Chiller fault diagnosis based on vae-enabled generative adversarial networks. IEEE Trans. Autom. Sci. Eng. 2022, 19, 387–395. [Google Scholar] [CrossRef]
- Lan, T.; Chen, J.Y.; Tamboli, D.; Aggarwal, V. Multi-task hierarchical adversarial inverse reinforcement learning. arXiv 2023, arXiv:2305.12633. [Google Scholar] [CrossRef]
- Giwa, B.H.; Lee, C. A marginal log-likelihood approach for the estimation of discount factors of multiple experts in inverse reinforcement learning. In Proceedings of the 2021 IEEE/RSJ International Conference on Intelligent Robots and Systems, Prague, Czech Republic, 27 September–1 October 2021; pp. 7786–7791. [Google Scholar]
- Pan, X.L.; Shen, Y.L. Human-interactive subgoal supervision for efficient inverse reinforcement learning. In Proceedings of the 17th International Conference on Autonomous Agents and MultiAgent Systems, Stockholm, Sweden, 10–15 July 2018; pp. 1380–1387. [Google Scholar]
- Kitaoka, A.; Eto, R. A proof of convergence of inverse reinforcement learning for multi-objective optimization. arXiv 2023, arXiv:2305.06137. [Google Scholar] [CrossRef]
- Waelchli, P.W.D.; Koumoutsakos, P. Discovering individual rewards in collective behavior through inverse multi-agent reinforcement learning. arXiv 2023, arXiv:2305.10548. [Google Scholar] [CrossRef]
- Zhang, Y.X.; DeCastro, J.; Cui, X.Y.; Huang, X.; Kuo, Y.; Leonard, J.; Balachandran, A.; Leonard, N.; Lidard, J.; So, O.; et al. Game-up: Game-aware mode enumeration and understanding for trajectory prediction. arXiv 2023, arXiv:2305.17600. [Google Scholar]
- Luo, Y.D.; Schulte, O.; Poupart, P. Inverse reinforcement learning for team sports: Valuing actions and players. In Proceedings of the Twenty-Ninth International Joint Conference on Artificial Intelligence Main Track, Yokohama Yokohama, Japan, 7–15 January 2020; pp. 3356–3363. [Google Scholar]
- Chen, Y.; Lin, X.; Yan, B.; Zhang, L.; Liu, J.; Özkan, T.N.; Witbrock, M. Meta-inverse reinforcement learning for mean field games via probabilistic context variables. In Proceedings of the AAAI Conference on Artificial Intelligence, Vancouver, BC, Canada, 20–27 February 2024; pp. 11407–11415. [Google Scholar]
- Barnes, M.; Abueg, M.; Lange, O.F.; Deeds, M.; Trader, J.; Molitor, D.; Wulfmeier, M.; O’Banion, S. Massively scalable inverse reinforcement learning in google maps. arXiv 2023, arXiv:2305.11290. [Google Scholar]
- Qiao, G.R.; Liu, G.L.; Poupart, P.; Xu, Z.Q. Multi-Modal Inverse Constrained Reinforcement Learning from a Mixture of Demonstrations. In Proceedings of the 36th International Conference on Neural Information Processing Systems, New Orleans, LA, USA, 10–16 December 2023; pp. 1–13. [Google Scholar]
- Yang, B.; Lu, Y.A.; Yan, B.; Wan, R.; Hu, H.Y.; Yang, C.C.; Ni, R.R. Meta-IRLSOT plus plus: A meta-inverse reinforcement learning method for fast adaptation of trajectory prediction networks. Expert Syst. Appl. 2024, 240, 122499. [Google Scholar] [CrossRef]
- Gong, W.; Cao, L.; Zhu, Y.; Zuo, F.; He, X.; Zhou, H. Federated inverse reinforcement learning for smart ICUs with differential privacy. IEEE Internet Things J. 2023, 10, 19117–19124. [Google Scholar] [CrossRef]
- Zeng, S.L.; Li, C.L.; Garcia, A.; Garcia, A. Maximum-likelihood inverse reinforcement learning with finite-time guarantees. In Proceedings of the 36th Conference on Neural Information Processing Systems, New Orleans, LA, USA, 28 November–9 December 2022; pp. 1–14. [Google Scholar]
- Gu, M.R.; Croft, E.; Kulic, D. Demonstration based explainable AI for learning from demonstration methods. IEEE Rob. Autom. Lett. 2025, 10, 6552–6559. [Google Scholar] [CrossRef]
- Jiang, X.; Liu, H.B.; Yang, L.P.; Zhang, B.; Ward, T.E.; Snásel, V. Unraveling human social behavior motivations via inverse reinforcement learning-based link prediction. Computing 2024, 106, 1963–1986. [Google Scholar] [CrossRef]
- Sutton, R.S. Generalization in reinforcement learning: Successful examples using sparse coarse coding. In Proceedings of the 8th International Conference on Neural Information Processing Systems, Denver, CO, USA, 27–30 November 1995; pp. 1038–1044. [Google Scholar]
- Levine, S.; Jordan, M.; Schulman, J.; Moritz, P.; Abbeel, P. High-dimensional continuous control using generalized advantage estimation. In Proceedings of the 4th International Conference on Learning Representations, San Juan, Puerto Rico, 2–4 May 2016; pp. 1–14. [Google Scholar]
- Wawrzyński, P. A cat-like robot real-time learning to run. In Proceedings of the 9th International Conference on Adaptive and Natural Computing Algorithms, Kuopio, Finland, 23–25 April 2009; pp. 380–390. [Google Scholar]
- Durrant-Whyte, H.; Roy, N.; Abbeel, P. Infinite-horizon model predictive control for periodic tasks with contacts. In Robotics: Science and Systems VII; MIT Press: Cambridge, MA, USA, 2012; pp. 73–80. [Google Scholar]
- Tassa, Y.; Erez, T.; Todorov, E. Synthesis and stabilization of complex behaviors through online trajectory optimization. In Proceedings of the 2012 IEEE/RSJ International Conference on Intelligent Robots and Systems, Vilamoura, Algarve, Portugal, 7–12 October 2012; pp. 4906–4913. [Google Scholar]
- Coulom, R. Reinforcement Learning Using Neural Networks, with Applications to Motor Control. Ph.D. Thesis, Laboratoire IMAG, Institute National Polytechnique de Grenoble, Grenoble, Rhone-Alpes region, France, 2002. [Google Scholar]
- Li, J.; Wu, H.; He, Q.; Zhao, Y.; Wang, X. Dynamic QoS prediction with intelligent route estimation via inverse reinforcement learning. IEEE Trans. Serv. Comput. 2024, 17, 509–523. [Google Scholar] [CrossRef]
- Nan, J.; Deng, W.; Zhang, R.; Wang, Y.; Zhao, R.; Ding, J. Interaction-aware planning with deep inverse reinforcement learning for human-like autonomous driving in merge scenarios. IEEE Trans. Intell. Veh. 2024, 9, 2714–2726. [Google Scholar] [CrossRef]
- Baee, S.; Pakdamanian, E.; Kim, I.; Feng, L.; Ordonez, V.; Barnes, L. Medirl: Predicting the visual attention of drivers via maximum entropy deep inverse reinforcement learning. In Proceedings of the 2021 IEEE/CVF International Conference on Computer Vision, Virtual Conference, 11–17 October 2021; pp. 13158–13168. [Google Scholar]
- Fu, Q.M.; Gao, Z.; Wu, H.J.; Chen, J.P.; Chen, Q.Q.; Lu, Y. Maximum entropy inverse reinforcement learning based on generative adversarial networks. Comput. Eng. Appl. 2019, 55, 119–126. [Google Scholar]
- Wooldridge, M. An Introduction to Multiagent Systems, 2nd ed.; Wiley Publishing: New York, NY, USA, 2009; pp. 1–27. [Google Scholar]
- Wang, P.; Li, H.H.; Chan, C. Meta-adversarial inverse reinforcement learning for decision-making tasks. In Proceedings of the 2021 IEEE International Conference on Robotics and Automation, Xi’an, China, 30 May–5 June 2021; pp. 12632–12638. [Google Scholar]
- Lin, J.-L.; Hwang, K.-S.; Shi, H.B.; Pan, W. An ensemble method for inverse reinforcement learning. Inform. Sci. 2020, 512, 518–532. [Google Scholar] [CrossRef]
- Munikoti, S.; Agarwal, D.; Das, L.; Halappanavar, M.; Natarajan, B. Challenges and opportunities in deep reinforcement learning with graph neural networks: A comprehensive review of algorithms and applications. IEEE Trans. Neural Netw. Learn. Syst. 2023, 15051–15071. [Google Scholar] [CrossRef]
- Pan, W.; Qu, R.P.; Hwang, K.-S.; Lin, H.-S. An ensemble fuzzy approach for inverse reinforcement learning. Int. J. Fuzzy Syst. 2018, 21, 95–103. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).