Zak-Phase Dislocations in Trimer Lattices
Abstract
1. Introduction
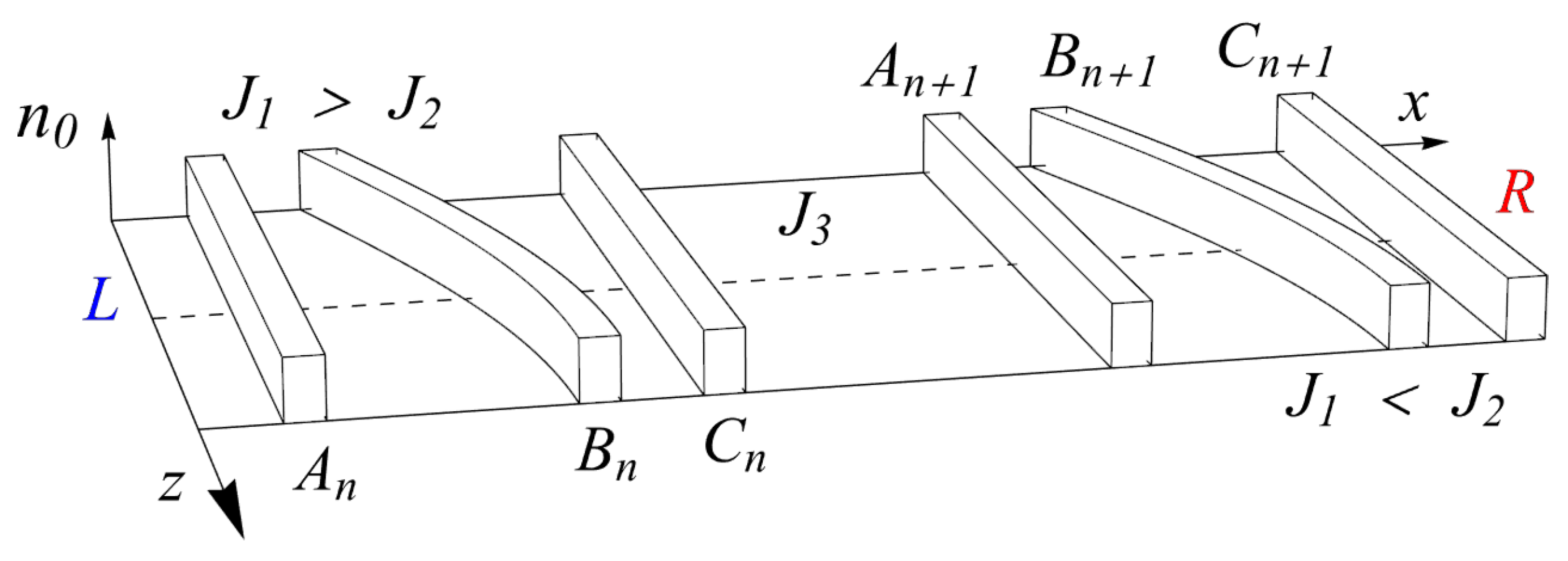
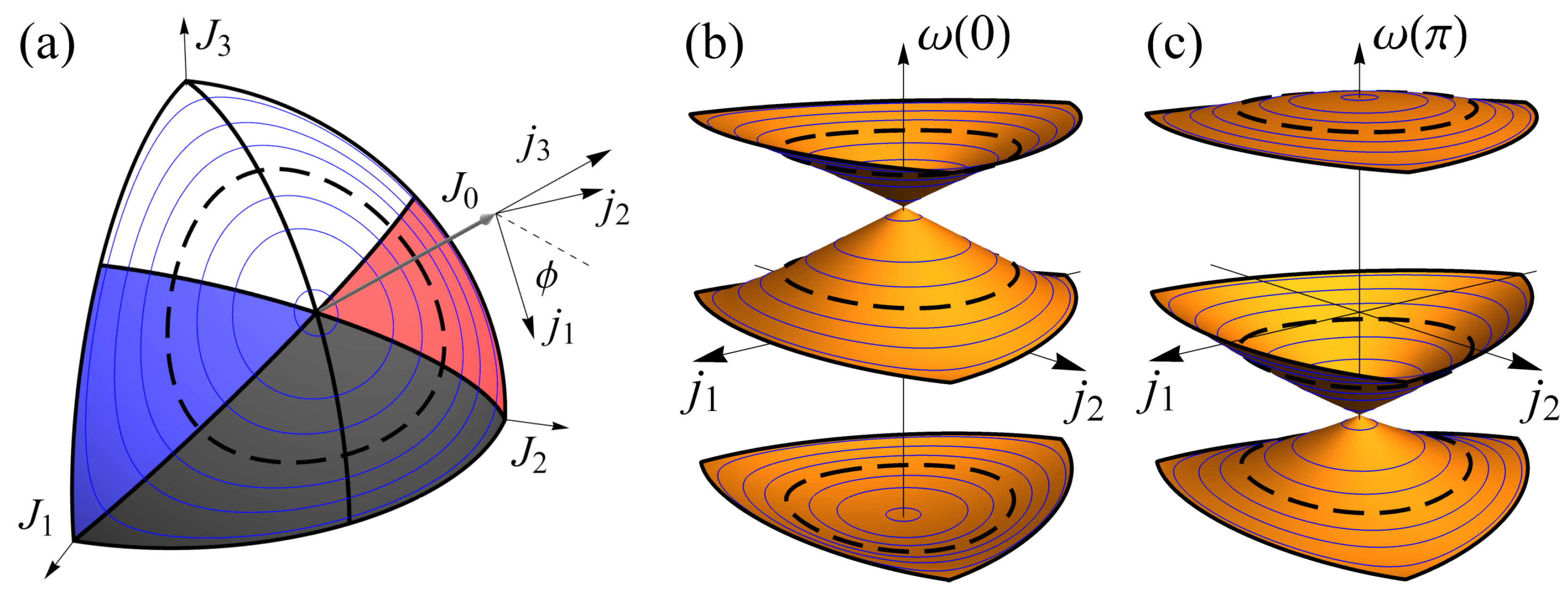
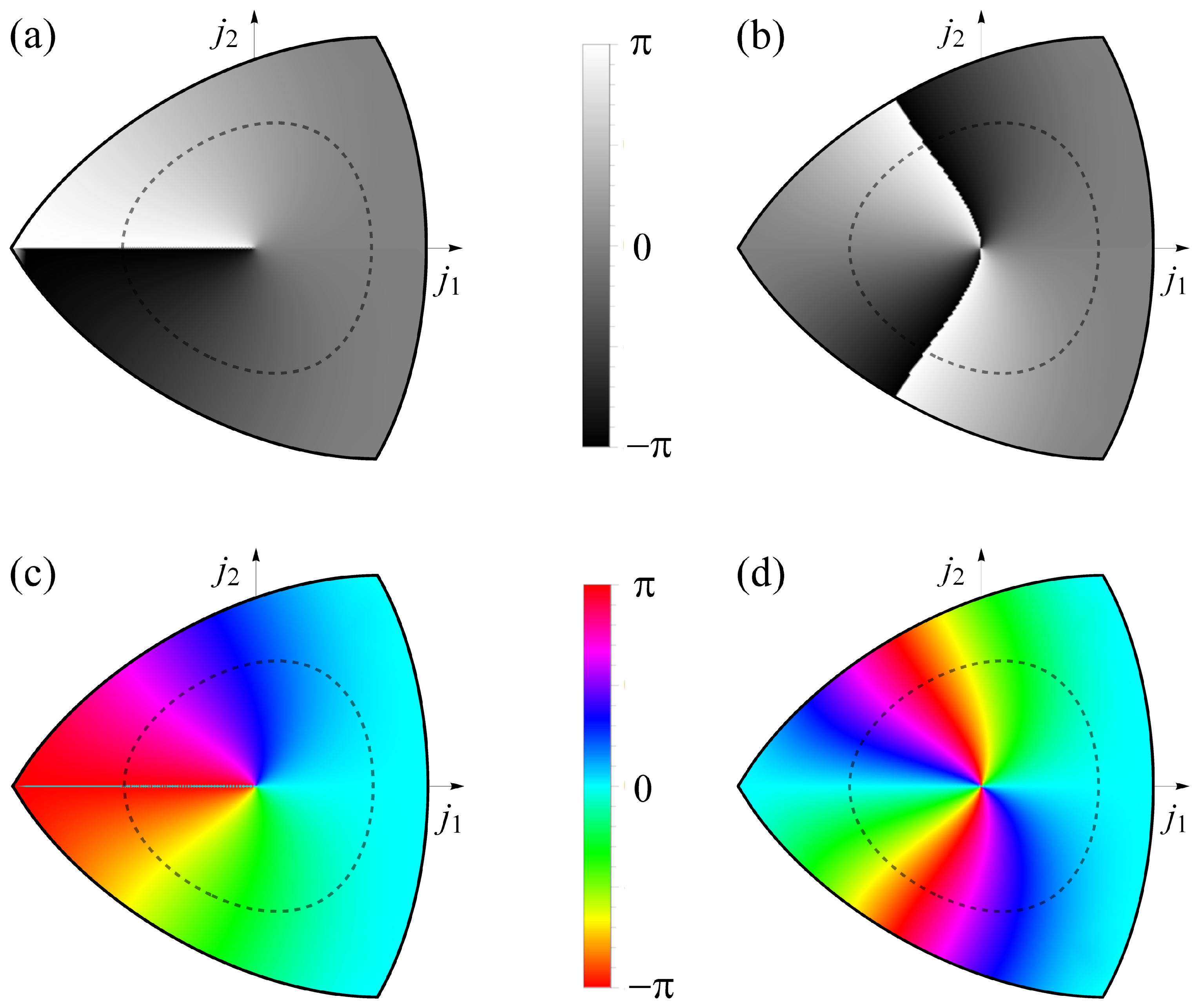
2. Trimer Lattice and Zak Phase
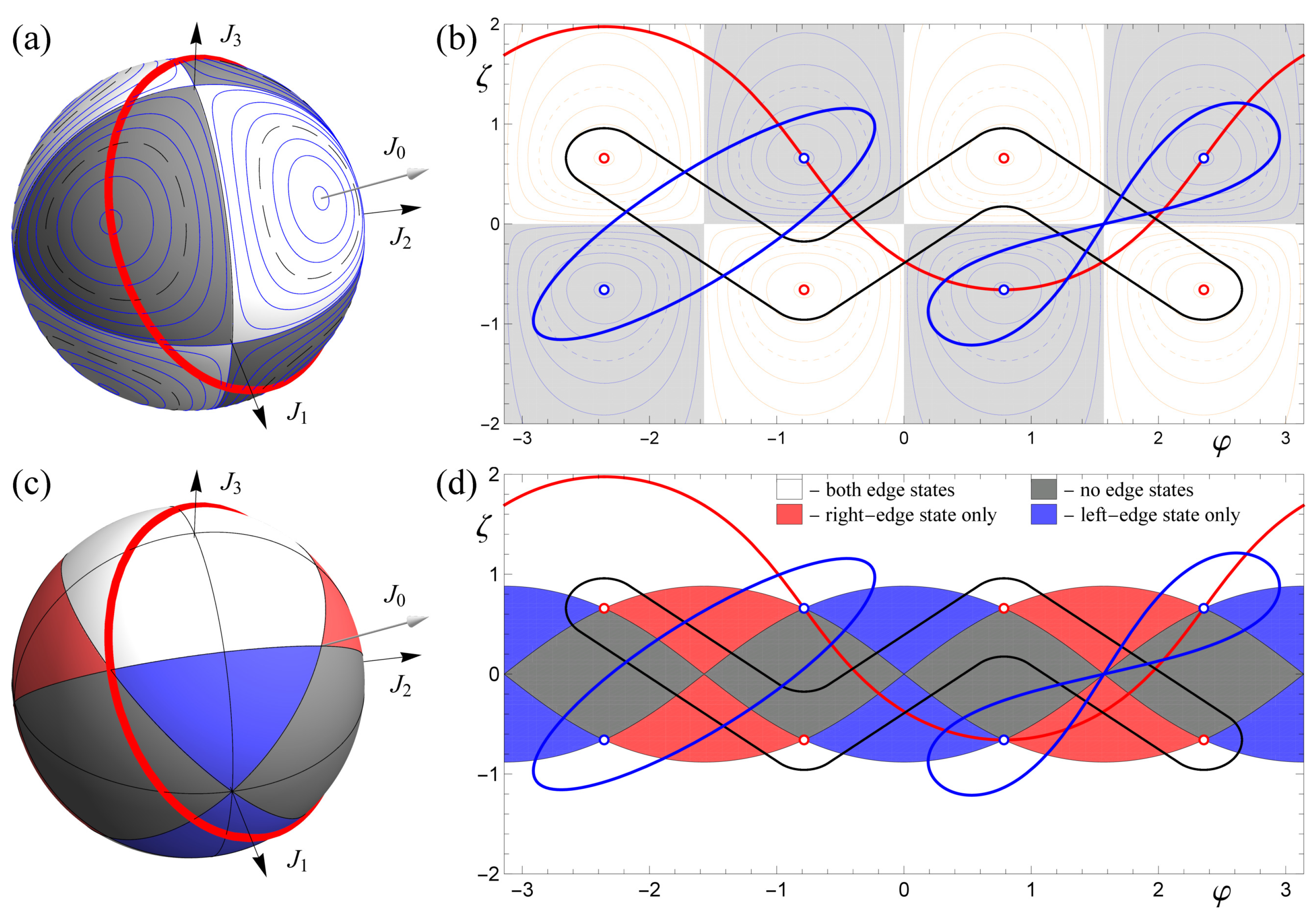
3. Thouless Pump and Chern Numbers
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| SSH | Su–Schrieffer–Heeger model |
| AAH | Aubry–André–Harper model |
Appendix A. Parameter Domain
Appendix B. Calculation of the Zak Phase
Appendix B.1. Zak-Phase Vanishes in the Inversion-Symmetric Lattice
| For | , | , | |
| For | , | , |
Appendix B.2. Band Collapse and Zak Phase in the Anti-Continuum Limit
| Right edge: | , | , | |
| Left edge: | , | , | |
| Bottom edge: | , | , |
References
- Berry, M.V. Quantal Phase Factors Accompanying Adiabatic Changes. Proc. R. Soc. A 1984, 392, 45–57. [Google Scholar] [CrossRef]
- Xiao, D.; Chang, M.C.; Niu, Q. Berry phase effects on electronic properties. Rev. Mod. Phys. 2010, 82, 1959. [Google Scholar] [CrossRef]
- Hasan, M.Z.; Kane, C.L. Colloquium: Topological Insulators. Rev. Mod. Phys. 2010, 82, 3045. [Google Scholar] [CrossRef]
- Qi, X.-L.; Zhang, S.-C. Topological insulators and superconductors. Rev. Mod. Phys. 2011, 83, 1057. [Google Scholar] [CrossRef]
- Lu, L.; Joannopoulos, J.D.; Soljačić, M. Topological photonics. Nat. Photonic 2014, 8, 821–829. [Google Scholar] [CrossRef]
- Ozawa, T.; Price, H.M.; Amo, A.; Goldman, N.; Hafezi, M.; Lu, L.; Rechtsman, M.C.; Schuster, D.; Simon, J.; Zilberberg, O.; et al. Topological photonics. Rev. Mod. Phys. 2019, 91, 015006. [Google Scholar] [CrossRef]
- Segev, M.; Bandres, M.A. Topological photonics: Where do we go from here? Nanophotonics 2021, 10, 425–434. [Google Scholar] [CrossRef]
- Zak, J. Berry’s Phase for Energy Bands in Solids. Phys. Rev. Lett. 1989, 62, 2747–2750. [Google Scholar] [CrossRef]
- Atala, M.; Aidelsburger, M.; Barreiro, J.T.; Abanin, D.; Kitagawa, T.; Demler, E.; Bloch, I. Direct measurement of the Zak phase in topological Bloch bands. Nat. Phys. 2013, 9, 795–800. [Google Scholar] [CrossRef]
- Su, W.P.; Schrieffer, J.R.; Heeger, A.J. Solitons in Polyacetylene. Phys. Rev. Lett. 1979, 42, 1698. [Google Scholar] [CrossRef]
- Rice, M.J.; Mele, E.J. Elementary excitations of a linearly conjugated diatomic polymer. Phys. Rev. Lett. 1982, 49, 1455. [Google Scholar] [CrossRef]
- Delplace, P.; Ullmo, D.; Montambaux, G. Zak phase and the existence of edge states in graphene. Phys. Rev. B 2011, 84, 195452. [Google Scholar] [CrossRef]
- Lang, L.-J.; Cai, X.; Chen, S. Edge States and Topological Phases in One-Dimensional Optical Superlattices. Phys. Rev. Lett. 2012, 108, 220401. [Google Scholar] [CrossRef]
- Ke, Y.; Qin, X.; Mei, F.; Zhong, H.; Kivshar, Y.S.; Lee, C. Topological phase transitions and Thouless pumping of light in photonic waveguide arrays. Laser Phot. Rev. 2016, 10, 995. [Google Scholar] [CrossRef]
- Jin, L. Topological phases and edge states in a non-Hermitian trimerized optical lattice. Phys. Rev. A 2017, 96, 032103. [Google Scholar] [CrossRef]
- Liu, X.; Agarwal, G.S. The New Phases due to Symmetry Protected Piecewise Berry Phases; Enhanced Pumping and Nonreciprocity in Trimer Lattices. Sci. Rep. 2017, 7, 45015. [Google Scholar] [CrossRef]
- Martinez Alvarez, V.M.; Coutinho-Filho, M.D. Edge states in trimer lattices. Phys. Rev. A 2019, 99, 013833. [Google Scholar] [CrossRef]
- Nye, J.F.; Berry, M.V. Dislocations in wave trains. Proc. R. Soc. A 1974, 336, 165. [Google Scholar] [CrossRef]
- Soskin, M.S.; Vasnetsov, M.V. Chapter 4—Singular optics. In Progress in Optics, 1st ed.; Wolf, E., Ed.; Elsevier: Amsterdam, The Netherlands, 2001; Volume 42, pp. 219–276. ISBN 0-444-50908-9. [Google Scholar]
- Desyatnikov, A.S.; Kivshar, Y.S.; Torner, L. Optical Vortices and Vortex Solitons. In Progress in Optics, 1st ed.; Wolf, E., Ed.; Elsevier: Amsterdam, The Netherlands, 2005; Volume 47, pp. 291–391. ISBN 0444515984. [Google Scholar]
- Dennis, M.R.; O’Holleran, K.; Padgett, M.J. Singular Optics: Optical Vortices and Polarization Singularities. In Progress in Optics, 1st ed.; Wolf, E., Ed.; Elsevier: Amsterdam, The Netherlands, 2009; Volume 53, pp. 293–363. ISBN 978-0-444-53360-9. [Google Scholar]
- Allen, L.; Barnett, S.M.; Padgett, M.J. Optical Angular Momentum, 1st ed.; Institute of Physics Publishing: Bristol, UK, 2003; ISBN 9780750309011. [Google Scholar]
- Thouless, D.J. Quantization of particle transport. Phys. Rev. B 1983, 27, 6083. [Google Scholar] [CrossRef]
- Lohse, M.; Schweizer, C.; Zilberberg, O.; Aidelsburger, M.; Bloch, I. A Thouless quantum pump with ultracold bosonic atoms in an optical superlattice. Nat. Phys. 2016, 12, 350–354. [Google Scholar] [CrossRef]
- Nakajima, S.; Tomita, T.; Taie, S.; Ichinose, T.; Ozawa, H.; Wang, L.; Troyer, M.; Takahashi, Y. Topological Thouless pumping of ultracold fermions. Nat. Phys. 2016, 12, 296–300. [Google Scholar] [CrossRef]
- Kraus, Y.E.; Lahini, Y.; Ringel, Z.; Verbin, M.; Zilberberg, O. Topological States and Adiabatic Pumping in Quasicrystals. Phys. Rev. Lett. 2012, 109, 106402. [Google Scholar] [CrossRef]
- Longhi, S. Quantum-optical analogies using photonic structures. Laser Photonics Rev. 2009, 3, 243–261. [Google Scholar] [CrossRef]
- Garanovich, I.L.; Longhi, S.; Sukhorukov, A.A.; Kivshar, Y.S. Light propagation and localization in modulated photonic lattices and waveguides. Phys. Rep. 2012, 518, 1–79. [Google Scholar] [CrossRef]
- Rechtsman, M.C.; Zeuner, J.M.; Plotnik, Y.; Lumer, Y.; Podolsky, D.; Dreisow, F.; Nolte, S.; Segev, M.; Szameit, A. Photonic Floquet topological insulators. Nature 2013, 496, 196–200. [Google Scholar] [CrossRef]
- Smirnova, D.; Leykam, D.; Chong, Y.; Kivshar, Y.S. Nonlinear topological photonics. Appl. Phys. Rev. 2020, 7, 021306. [Google Scholar] [CrossRef]
- Ota, Y.; Takata, K.; Ozawa, T.; Amo, A.; Jia, Z.; Kante, B.; Notomi, M.; Arakawa, Y.; Iwamoto, S. Active topological photonics. Nanophotonics 2020, 9, 547. [Google Scholar] [CrossRef]
- Lohse, M.; Schweizer, C.; Price, H.; Zilberberg, O.; Bloch, I. Exploring 4D quantum Hall physics with a 2D topological charge pump. Nature 2018, 553, 55. [Google Scholar] [CrossRef]
- Zilberberg, O.; Huang, S.; Guglielmon, J.; Wang, M.; Chen, K.P.; Kraus, Y.E.; Rechtsman, M.C. Photonic topological boundary pumping as a probe of 4D quantum Hall physics. Nature 2018, 553, 59. [Google Scholar] [CrossRef]
- Yuan, L.; Lin, Q.; Xiao, M.; Fan, S. Synthetic dimension in photonics. Optica 2018, 5, 1396–1405. [Google Scholar] [CrossRef]
- Lustig, E.; Weimann, S.; Plotnik, Y.; Lumer, Y.; Bandres, M.A.; Szameit, A.; Segev, M. Photonic topological insulator in synthetic dimensions. Nature 2019, 567, 356. [Google Scholar] [CrossRef] [PubMed]
- Dutt, A.; Lin, Q.; Yuan, L.; Minkov, M.; Xiao, M.; Fan, S. A single photonic cavity with two independent physical synthetic dimensions. Science 2020, 367, 59. [Google Scholar] [CrossRef]
- Maczewsky, L.J.; Wang, K.; Dovgiy, A.A.; Miroshnichenko, A.E.; Moroz, A.; Ehrhardt, M.; Heinrich, M.; Christodoulides, D.N.; Szameit, A.; Sukhorukov, A.A. Synthesizing multi-dimensional excitation dynamics and localization transition in one-dimensional lattices. Nat. Photonics 2020, 14, 76–81. [Google Scholar] [CrossRef]
- Aubry, S.; André, G. Analyticity breaking and Anderson localization in incommensurate lattices. Ann. Isr. Phys. Soc. 1980, 3, 18. [Google Scholar]
- Harper, P.G. Single Band Motion of Conduction Electrons in a Uniform Magnetic Field. Proc. Phys. Soc. A 1955, 68, 874. [Google Scholar] [CrossRef]
- Szameit, A.; Nolte, S. Discrete Optics in Femtosecond-Laser-Written Photonic Structures. J. Phys. B At. Mol. Opt. Phys. 2010, 43, 163001. [Google Scholar] [CrossRef]
- Leykam, D.; Desyatnikov, A.S. Conical intersections for light and matter waves. Adv. Phys. X 2016, 1, 101. [Google Scholar] [CrossRef]
- Diebel, F.; Leykam, D.; Kroesen, S.; Denz, C.; Desyatnikov, A.S. Conical Diffraction and Composite Lieb Bosons in Photonic Lattices. Phys. Rev. Lett. 2016, 116, 183902. [Google Scholar] [CrossRef] [PubMed]
- Leykam, D.; Andreanov, A.; Flach, S. Artificial flat band systems: From lattice models to experiments. Adv. Phys. X 2018, 3, 1473052. [Google Scholar] [CrossRef]
- Leykam, D.; Flach, S. Perspective: Photonic flatbands. APL Photonics 2018, 3, 070901. [Google Scholar] [CrossRef]
- Hu, S.; Ke, Y.; Deng, Y.; Lee, C. Dispersion-suppressed topological Thouless pumping. Phys. Rev. B 2019, 100, 064302. [Google Scholar] [CrossRef]
- Marques, A.M.; Dias, R.G. One-dimensional topological insulators with noncentered inversion symmetry axis. Phys. Rev. B 2019, 100, 041104(R). [Google Scholar] [CrossRef]
- Anastasiadis, A.; Styliaris, G.; Chaunsali, R.; Theocharis, G.; Diakonos, F.K. Bulk-edge correspondence in the trimer Su-Schrieffer-Heeger model. Phys. Rev. B 2022, 106, 085109. [Google Scholar] [CrossRef]
- Verma, S.; Ghosh, T.K. Bulk-boundary correspondence in extended trimer Su-Schrieffer-Heeger model. Phys. Rev. B 2024, 110, 125424. [Google Scholar] [CrossRef]
- Guo, Q.-H.; Zhang, Y.; Wan, X.-H.; Zheng, L.-Y. Isospectral reduction of the trimer Su-Schrieffer-Heeger lattice and its bulk-edge correspondence. Phys. Rev. Appl. 2025, 23, L031001. [Google Scholar] [CrossRef]
- Zhang, R.; Chen, T. Symmetry-Related Topological Phases and Applications: From Classical to Quantum Regimes. Symmetry 2024, 16, 1673. [Google Scholar] [CrossRef]
- Haldane, F.D.M. Berry Curvature on the Fermi Surface: Anomalous Hall Effect as a Topological Fermi-Liquid Property. Phys. Rev. Appl. 2004, 93, 206602. [Google Scholar] [CrossRef]
- Fang, K.; Yu, Z.; Fan, S. Realizing effective magnetic field for photons by controlling the phase of dynamic modulation. Nat. Photonics 2012, 6, 782–787. [Google Scholar] [CrossRef]
- Poddubny, A.; Miroshnichenko, A.; Slobozhanyuk, A.; Kivshar, Y. Topological Majorana States in Zigzag Chains of Plasmonic Nanoparticles. ACS Photonics 2014, 1, 101–105. [Google Scholar] [CrossRef]
- Hafezi, M.; Mittal, S.; Fan, J.; Migdall, A.; Taylor, J.M. Imaging topological edge states in silicon photonics. Nat. Photonic 2013, 7, 1001–1005. [Google Scholar] [CrossRef]
- Skirlo, S.A.; Lu, L.; Soljačić, M. Multimode One-Way Waveguides of Large Chern Numbers. Phys. Rev. Lett. 2014, 113, 113904. [Google Scholar] [CrossRef] [PubMed]
- Skirlo, S.A.; Lu, L.; Igarashi, Y.; Yan, Q.; Joannopoulos, J.; Soljačić, M. Experimental Observation of Large Chern Numbers in Photonic Crystals. Phys. Rev. Lett. 2015, 115, 253901. [Google Scholar] [CrossRef] [PubMed]
- Schröter, N.B.M.; Stolz, S.; Manna, K.; de Juan, F.; Vergniory, M.G.; Krieger, J.A.; Pei, D.; Schmitt, T.; Dudin, P.; Kim, T.K.; et al. Observation and control of maximal Chern numbers in a chiral topological semimetal. Science 2020, 369, 179–183. [Google Scholar] [CrossRef]
- Nathan, F.; Rudner, M.S. Topological singularities and the general classification of Floquet–Bloch systems. New J. Phys. 2015, 17, 125014. [Google Scholar] [CrossRef]
- Liu, D.; Peng, P.; Lu, X.; Shi, A.; Peng, Y.; Wei, Y.; Liu, L. Multiple topological states within a common bandgap of two non-trivial photonic crystals. Opt. Lett. 2024, 49, 2393. [Google Scholar] [CrossRef]
- Li, Z.; Li, S.; Yan, B.; Chan, H.-C.; Li, J.; Guan, J.; Bi, W.; Xiang, Y.; Gao, Z.; Zhang, S.; et al. Symmetry-Related Large-Area Corner Mode with a Tunable Mode Area and Stable Frequency. Phys. Rev. Lett. 2025, 134, 116607. [Google Scholar] [CrossRef]
- Yan, B.; Liao, B.; Shi, F.; Xi, X.; Cao, Y.; Xiang, K.; Meng, Y.; Yang, L.; Zhu, Z.; Chen, J.; et al. Realization of Topology-Controlled Photonic Cavities in a Valley Photonic Crystal. Phys. Rev. Lett. 2025, 134, 033803. [Google Scholar] [CrossRef]
- Cao, S.-J.; Zheng, L.-N.; Cheng, L.-Y.; Wang, H.-F. Controllable entangled-state transmission in a non-Hermitian trimer Su-Schrieffer-Heeger chain. Phys. Rev. A 2024, 110, 062409. [Google Scholar] [CrossRef]
- Chen, J.; Shi, A.; Peng, Y.; Peng, P.; Liu, J. Hybrid Skin-Topological Effect Induced by Eight-Site Cells and Arbitrary Adjustment of the Localization of Topological Edge States. Chin. Phys. Lett. 2024, 41, 037103. [Google Scholar] [CrossRef]
- Shi, A.; Bao, L.; Peng, P.; Ning, J.; Wang, Z.; Liu, J. Non-Hermitian Floquet Higher-Order Topological States in Two-Dimensional Quasicrystals. Phys. Rev. B 2025, 111, 094109. [Google Scholar] [CrossRef]
- Xie, X.; Ma, F.; Rui, W.B.; Dong, Z.; Du, Y.; Xie, W.; Zhao, Y.X.; Chen, H.; Gao, F.; Xue, H. Non-Hermitian Dirac Cones with Valley-Dependent Lifetimes. Nat. Commun. 2025, 16, 1627. [Google Scholar] [CrossRef] [PubMed]
- Buendía, Á.; Sánchez-Gil, J.A.; Giannini, V. Exploiting Oriented Field Projectors to Open Topological Gaps in Plasmonic Nanoparticle Arrays. ACS Photonics 2023, 10, 464–474. [Google Scholar] [CrossRef] [PubMed]
- Guo, Z.; Wu, X.; Ke, S.; Dong, L.; Deng, F.; Jiang, H.; Chen, H. Rotation controlled topological edge states in a trimer chain composed of meta-atoms. New J. Phys. 2022, 24, 063001. [Google Scholar] [CrossRef]
- Ioannou Sougleridis, I.; Anastasiadis, A.; Richoux, O.; Achilleos, V.; Theocharis, G.; Pagneux, V.; Diakonos, F.K. Existence and characterization of edge states in an acoustic trimer Su-Schrieffer-Heeger model. Phys. Rev. B 2024, 110, 174311. [Google Scholar] [CrossRef]
- Guo, Q.-H.; Zhang, Y.; Wan, X.-H.; Zheng, L.-Y. Observation of chiral edge state pairs in an acoustic trimer waveguide. Appl. Phys. Lett. 2025, 126, 133102. [Google Scholar] [CrossRef]
- Liu, X.; Xia, S.; Jajtić, E.; Song, D.; Li, D.; Tang, L.; Leykam, D.; Xu, J.; Buljan, H.; Chen, Z. Universal momentum-to-real-space mapping of topological singularities. Nat. Commun. 2020, 11, 1586. [Google Scholar] [CrossRef] [PubMed]
- Poshakinskiy, A.V.; Poddubny, A.N.; Hafezi, M. Phase spectroscopy of topological invariants in photonic crystals. Phys. Rev. A 2015, 91, 043830. [Google Scholar] [CrossRef]
- Li, Q.; Jiang, X. Singularity induced topological transition of different dimensions in one synthetic photonic system. Opt. Commun. 2019, 440, 32–40. [Google Scholar] [CrossRef]
- González-Cuadra, D.; Bermudez, A.; Grzybowski, P.R.; Lewenstein, M.; Dauphin, A. Intertwined topological phases induced by emergent symmetry protection. Nat. Commun. 2019, 10, 2694. [Google Scholar] [CrossRef]
- Maczewsky, L.J.; Heinrich, M.; Kremer, M.; Ivanov, S.K.; Ehrhardt, M.; Martinez, F.; Kartashov, Y.V.; Konotop, V.V.; Torner, L.; Bauer, D.; et al. Nonlinearity-induced photonic topological insulator. Science 2020, 370, 701–704. [Google Scholar] [CrossRef]
- Kartashov, Y.V.; Arkhipova, A.A.; Zhuravitskii, S.A.; Skryabin, N.N.; Dyakonov, I.V.; Kalinkin, A.A.; Kulik, S.P.; Kompanets, V.O.; Chekalin, S.V.; Torner, L.; et al. Observation of Edge Solitons in Topological Trimer Arrays. Phys. Rev. Lett. 2022, 128, 093901. [Google Scholar] [CrossRef] [PubMed]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Uakhitov, T.; Urmanov, A.; Kumekov, S.E.; Desyatnikov, A.S. Zak-Phase Dislocations in Trimer Lattices. Symmetry 2025, 17, 1631. https://doi.org/10.3390/sym17101631
Uakhitov T, Urmanov A, Kumekov SE, Desyatnikov AS. Zak-Phase Dislocations in Trimer Lattices. Symmetry. 2025; 17(10):1631. https://doi.org/10.3390/sym17101631
Chicago/Turabian StyleUakhitov, Tileubek, Abdybek Urmanov, Serik E. Kumekov, and Anton S. Desyatnikov. 2025. "Zak-Phase Dislocations in Trimer Lattices" Symmetry 17, no. 10: 1631. https://doi.org/10.3390/sym17101631
APA StyleUakhitov, T., Urmanov, A., Kumekov, S. E., & Desyatnikov, A. S. (2025). Zak-Phase Dislocations in Trimer Lattices. Symmetry, 17(10), 1631. https://doi.org/10.3390/sym17101631






