Abstract
Seismic metamaterials have gained significant attention for their ability to reduce seismic wave energy. However, numerical simulations have dominated the majority of research on seismic metamaterials, with relatively few field experiments validating their effectiveness. Additionally, the focus has primarily been on attenuating Rayleigh waves, with less attention given to Love waves. In this study, we first designed a seismic metamaterial featuring a periodic and symmetric array of square holes using numerical simulations as our research platform. We then explored its attenuation effects on Rayleigh waves, particularly Love waves, through field experiments. The results revealed not only differences in energy attenuation between these wave types but, more importantly, uncovered a phenomenon that we termed Bandgap-Induced Attenuation Mode Inversion within the ultra-broadband gap that was generated by the seismic metamaterials, where Love waves exhibited greater attenuation than Rayleigh waves below 50 Hz, while Rayleigh waves exhibited greater attenuation above 50 Hz. These findings highlight the necessity of considering both wave types when designing cost-effective seismic metamaterials, providing valuable insights for the development and application of metamaterials that can effectively mitigate the energy of different seismic wave modes.
1. Introduction
The prevention of damage to human society caused by surface waves from earthquakes, traffic, construction, explosions, and other factors has always been a serious challenge [1]. Since 2012, seismic metamaterials (SMs) have attracted significant attention as an artificial material. In that year, Brülé and colleagues conducted large-scale experiments demonstrating that a two-dimensional periodic and symmetric array of vertical cylindrical holes in the ground could effectively shield seismic waves around 50 Hz [2]. This groundbreaking work marked a milestone in the field of seismic resistance and protection. Subsequently, Miniaci and Roux confirmed similar results through numerical simulations and experiments, respectively [3,4]. However, due to the large structural dimensions of these SMs, which are based on the Bragg scattering mechanism, controlling low-frequency seismic waves proved challenging. Inspired by Liu et al.’s work on the generation of bandgaps in locally resonant phononic crystals [5], researchers have begun to focus on the development of locally resonant seismic metamaterials (RSMs) [4,6]. RSMs utilize small-sized resonator units to manage long-wavelength seismic vibrations. When the frequency of seismic waves resonates with that of the resonator units, the seismic wave energy is effectively dissipated [7]. Typically, the resonant units in RSMs are arranged in periodic arrays, forming configurations known as Buried RSMs or Above-Surface RSMs. The periodic arrangement of these resonators leads to the formation of a bandgap, while their interaction with surface waves causes both self-oscillation and scattering of the surface waves. These factors thereby collectively suppress the propagation of the surface waves.
To date, various structures of RSMs have been developed for attenuating surface waves. However, it is worth noting that most of the published literature primarily emphasizes the performance evaluation of RSMs in terms of Rayleigh wave attenuation [8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39], while the impact of SMs on Love waves has received comparatively less attention [40,41,42,43]. In fact, Love waves primarily cause horizontal shear motion, which can be particularly damaging to structures that are not designed to withstand lateral forces. They include cracking or collapse of walls due to excessive horizontal displacement and shear failure in columns and beams, especially in buildings with weak lateral reinforcement. They travel faster than Rayleigh waves and can carry considerable energy over long distances, causing substantial damage. Consequently, Love waves play a notable role in seismic events. Therefore, understanding the attenuation of Love waves by seismic metamaterials is crucial for advancing seismic protection strategies.
In addition, most of the SMs that were mentioned above are studied through simulations [9,10,11,12,13,14,15,16,17,18,19,27,28,29,30,31,32,33,34,35,40,41,42,43] and laboratory experiments [20,21,22,23,24,36,37,38,39], with very few being investigated through field experiments [2,8,25,26]. The advantage of simulation technology is that it can rapidly test SMs with a variety of complex geometric shapes and material properties, which facilitates the optimization of SMs for specific earthquake applications and significantly reduces the time and cost of SMs design. However, the accuracy of simulations largely depends on the assumptions that are made in the models. The complexity of the physical interactions between SMs and actual seismic environments makes it challenging for simulation results to accurately reflect real-world conditions. For instance, due to soil heterogeneity, “its theoretical and numerical analysis requires some simplified assumptions that can lead to inaccurate wave simulations. This means experimental validation is absolutely necessary” [4]. Therefore, while simulation technology is a powerful tool for predicting the performance of SMs, field experimental validation is crucial to ensure its reliability and effectiveness.
In this study, we aimed to harness a structurally simple SM and conduct field experiments to observe and compare its attenuation effects on Rayleigh and Love waves. This included examining the bandgap width, energy variation, and frequency dependence. The research is motivated by the limited attention that has been given to Love waves in existing studies. We first designed an SM consisting of a periodic and symmetric array of holes based on elastic wave propagation theory and numerical simulation techniques as the subject of investigation. Five sensors were strategically and symmetrically positioned behind the metamaterials to measure vibration velocity signals in the x, y, and z directions. Their performance was assessed by comparing scenarios with and without SMs. The experimental results revealed that an ultra-wide bandgap exists for Rayleigh waves within the range of 40 Hz to 60 Hz and for Love waves within 43 Hz to 56 Hz. Moreover, a wave attenuation reversal point occurs at 50 Hz: below this frequency, the attenuation of Love waves surpasses that of Rayleigh waves, whereas above 50 Hz, Rayleigh waves experience greater attenuation. These findings demonstrate that even a simple-structured hole-type SM exhibits differing attenuation effects on Rayleigh and Love waves and underscore the importance of considering the attenuation capacity for Love waves when designing and evaluating SMs for surface wave mitigation. Our work not only deepens the understanding of surface wave mechanics from an experimental perspective but also provides valuable insights for design strategies and applications of metamaterials that are aimed at attenuating surface waves.
2. Theoretical Background
2.1. Elastic Wave Propagation Equation
Considering that the depth of a hole is relatively shallow compared to the thickness of the soil layer, the displacement that is caused by the propagation of elastic waves is a small deformation. We used thin plate theory to describe the propagation of elastic waves. The inspiration for this method came from Brûlé’s pioneering work [2], where the depth of the circular hole is 5 m, and where thin plate theory is also used to simulate bandgap structures. The propagation equation of elastic waves is as follows:
where ω is the angular frequency, ρ is the soil density, u is the displacement field in a vector form, h is the thickness of elastic plate, and D is the plate rigidity, expressed by
where E is Young’s modulus and ν is Poisson’s ratio. The solution of an elastic wave propagating in a periodic potential field can be written as follows:
where r is the space coordinate vector, k is the Bloch wave vector, and uk(r) is a periodic function as follows:
where a is the lattice vector. Accordingly, the Bloch periodic boundary conditions can be expressed as follows:
Substituting Equation (5) into Equation (1), we can obtain the eigenvalue equation:
where Ω(k) is the lattice stiffness matrix, M is the lattice mass matrix, and k is the Bloch wave vector. By calculating the wave vectors under different structures along the first Brillouin region M-Γ-X-M, the dispersion relationship between k and ω can be obtained.
2.2. Numerical Simulation
The design of seismic metamaterials is typically based on periodic structures and symmetry. Periodic structures possess translational symmetry, which allows for effective control over the propagation of seismic waves. Figure 1 illustrates the schematic of the SM structure and the experiment. The structure consists of a 6 × 7 periodic and symmetric square hole array with a lattice constant, denoted as a. The unit cell of the structure features a square hole with a side length of L1 and a depth of H0. The vibration source and five sets of sensors are symmetrically placed at the front and back of the periodic structure.
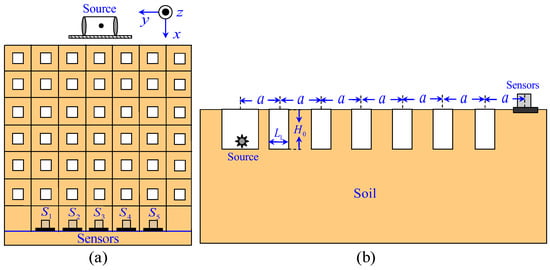
Figure 1.
Schematic of (a) top view and (b) section view of the SM structure.
During the two-dimensional simulation process, we utilized the finite element software COMSOL (version 6.2) Multiphysics, along with Bloch periodic boundary conditions, to calculate the band gaps of the periodic array that is shown in Figure 1. The physical parameters used were a density of ρ = 1500 kg/m3, Young’s modulus E = 100 MPa, and Poisson’s ratio ν = 0.3. The optimized geometric parameters for the SMs, obtained through iterative refinement, were a = 1 m, L1 = 0.27 m, and H0 = 0.35 m. The simulated band structure is shown in Figure 2, where a local band gap can be observed in the MΓ direction, ranging from 34 Hz to 50 Hz, and another local band gap can be seen in the XM direction, ranging from 70 Hz to 82 Hz.
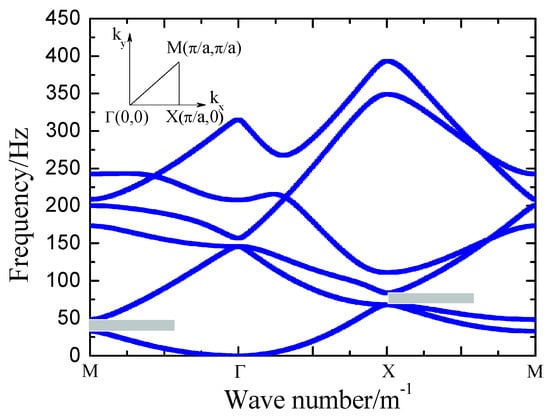
Figure 2.
Simulated dispersion curves in which the gray bands mean the band structure of the SMs.
Figure 3 illustrates the schematic distribution of the displacement field when a surface wave with a frequency of 50 Hz propagates in an SM structure, where (a) represents the scenario without an SM structure, and (b) describes the scenario with an SM structure. In the figures, deeper red indicates larger displacement deformation, while deeper blue indicates smaller displacement deformation. The comparison between (a) and (b) clearly shows that most of the energy is concentrated in the region of the SM, indicating that the designed SM has a significant attenuation effect on the surface waves, thereby generating a band gap.
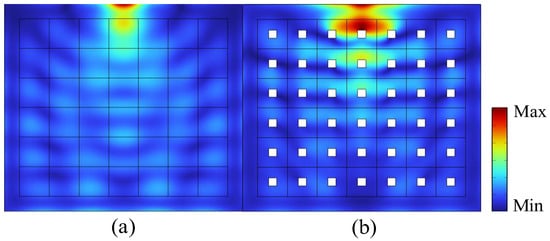
Figure 3.
Schematic of the displacement field distribution without the SM structure (a) and with the SM structure (b).
3. Experimental Procedure
3.1. Set-Up
The experimental site, as shown in Figure 4a, where the 6 × 7 periodic and symmetric square hole array was arranged based on the simulation, is located in the North Campus of the Institute of Disaster Prevention. From the perspective of the SM’s structure, the square holes here are somewhat innovative, as they differ from the circular holes that have been designed by other researchers [2,25]. The soil type is stiff clay, with a relative humidity of 60–70%. The Love wave velocity in the soil is 105 m/s. The vibration source is an eccentric wheel vibrator (XDP-80DC-24, Figure 4b), powered by a 24 V DC power supply, with an adjustable frequency range of 20 Hz to 70 Hz, which is placed 0.5 m underground. Since signals below 40 Hz are weak and do not show significant differences from background noise, the frequency range for the vibration source was set to 40 Hz to 60 Hz during the experiment, with an interval of 2 Hz. A 24-bit data acquisition system was used to record the signals; a signal was considered valid if its energy exceeded five times that of the background noise and its main frequency matched the vibration machine’s frequency. Five sets of sensors (velocity range: low-frequency cutoff at −3 dB and bandwidth of 0.5 Hz to 150 Hz) were symmetrically positioned on the ground at the rear end of the SM structure, spaced 1 m apart and labeled S1 to S5 (Figure 1a). Compared to measuring wave attenuation only at the position that directly faces the wave source [8,26], observing at five different locations provides insights into the attenuation information of SMs for waves propagating in different directions.

Figure 4.
Photos of experimental site (a), eccentric vibrator (b), and sensors (c).
In addition, each set consists of three unidirectional sensors (x, y, z) that are used to measure three signal components along the horizontal inline (x-component), horizontal crossline (y-component), and vertical directions (z-component), as shown in Figure 4a. In contrast to the existing literature, which typically focuses only on the attenuation of the z direction vibration component [8], measuring the attenuation of the x, y, and z vibration components can provide a comprehensive understanding of how SMs impact wave propagation in all spatial directions.
3.2. Data Processing
First, we started the data acquisition instrument and waited for 5–10 s; we then started the vibrator. During the experiment, we recorded data for 120 s and calculated the average energy per unit time from the data collected between 40 s and 80 s, i.e.,
Here, represents the components of energy in the x, y, and z directions, E is the total energy, t2 and t1 are the upper and lower limits of time, vi represents the corresponding velocity components, and m means the mass of the sensor.
During the experimental process, the background noise signal was measured first, and then, the energy was measured with and without SMs separately. To analyze the energy attenuation, we defined the total energy of the structure without SMs as and that of the structure with SMs as , along with their respective components and (i = x, y, z), and the corresponding attenuation coefficients as kH and ki, respectively. We have the following:
3.3. Energy Attenuation of Surface Waves
Figure 5 provides an example of the attenuation of three vibration components of surface waves at the position directly opposite S3. The black square dots represent the x-component (P wave), the red circular dots represent the y-component (SH wave), and the blue triangular dots represent the z-component (SV wave). It can be seen that the SMs generated ultra-wide bandgaps for all three components of the surface waves, with the narrowest ultra-wide bandgap ranging from 43 Hz to 56 Hz. Additionally, the SM exhibited a more pronounced attenuation effect on SH waves and P waves within the bandgap range, while the attenuation of SV waves was relatively weaker. This may be attributed to the localized resonance mechanism of the hole structure. Obviously, observing the attenuation of various vibration components of surface waves helps in designing SMs that selectively attenuate specific vibration components.
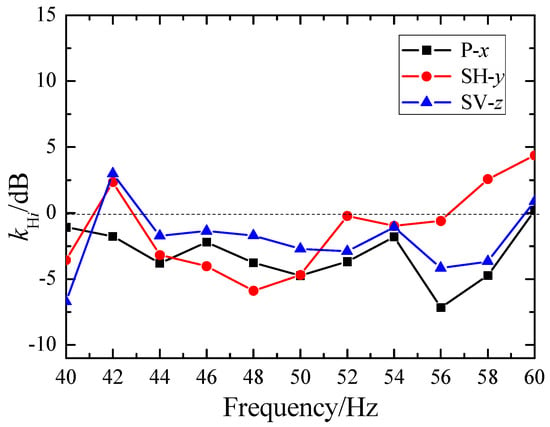
Figure 5.
Energy attenuation of the vibration components of surface waves at different frequencies.
If we consider the vector sum of the energies of the x-, y-, and z-components of vibration as the total energy of the vibration, we can obtain the attenuation of the total energy of surface waves that were measured at different frequencies by five sensor (S1–S5) sets located at different positions, as shown in Figure 6. It is evident that there is a significant ultra-wide bandgap between 43 Hz and 58 Hz, indicating that the SM structure can effectively attenuate surface waves within this frequency range.
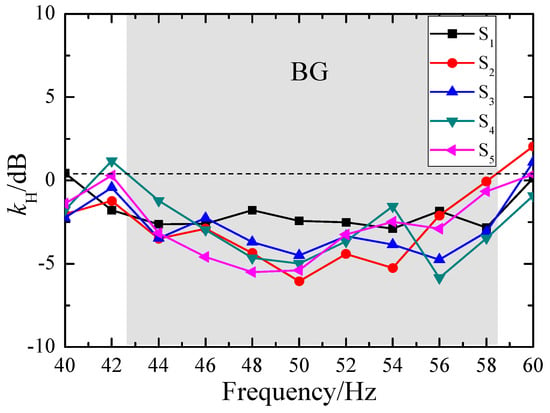
Figure 6.
Attenuation of the total energy of surface waves at different positions.
3.4. Attenuation of Rayleigh and Love Waves
Following this, we used the recorded results from the S3 sensor to further examine the attenuation effects of the RMs on Rayleigh and Love waves. Considering that both Rayleigh and Love waves result from the interaction between the incident waves and the RMS, Rayleigh waves are the superposition of horizontal inline waves (P waves) and vertical waves (SV waves) after passing through the SM structure, they should be included in the sum of the measurement results in the x and z directions. In contrast, Love waves are the superposition of horizontal crossline waves (SH waves) that undergo multiple reflections after encountering the SM structure, and they should be included in the measurement results in the y direction. Therefore, we can define the attenuation coefficients of Rayleigh and Love waves as kR and kL, respectively. That is,
Figure 7 illustrates the attenuation effects of surface waves at the position directly opposite S3. The red square dots represent the attenuation of Love waves, while the blue circular dots represent the attenuation of Rayleigh waves. From the figure, it can be observed that the bandgap for Rayleigh waves is approximately 40 Hz to 60 Hz, while the bandgap for Love waves is around 43 Hz to 56 Hz. Additionally, there is a point of reversal in wave attenuation at 50 Hz: below this frequency, the attenuation of Love waves exceeds that of Rayleigh waves, whereas above 50 Hz, Rayleigh waves experience greater attenuation. We may refer to this result as Bandgap-Induced Attenuation Mode Inversion. This phenomenon can be qualitatively explained from the perspective of SH wave attenuation.
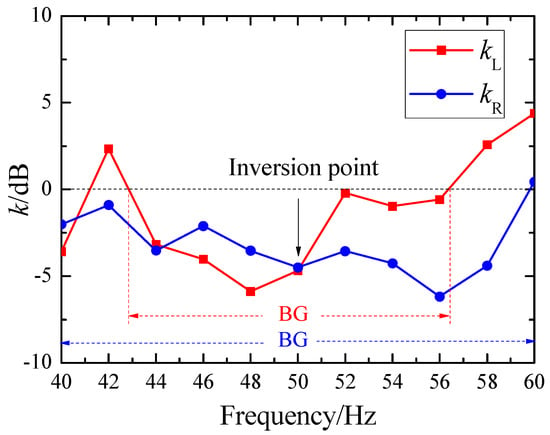
Figure 7.
Attenuation of Love waves and Rayleigh waves.
According to the experimental results presented in Figure 5, SH waves play a dominant role in the phenomenon of Bandgap-Induced Attenuation Mode Inversion. Within the bandgap range (below 50 Hz), the attenuation of SH waves is more effective than that of P waves and SV waves. This is primarily due to Bragg scattering occurring between different holes, where the periodic arrangement of holes more effectively interferes with the shear motion of SH waves in the low-frequency range. Regarding the reversal phenomenon of SH wave energy attenuation at 50 Hz, we believe that in the high-frequency range (above 50 Hz), the vibration absorption of wave energy by the hole array is enhanced. This leads to a weakening of the Bragg scattering effect and results in the reversal of SH wave energy attenuation.
4. Conclusions
We designed a periodic and symmetric square-hole-array seismic metamaterial and conducted field experiments to observe its attenuation effects on Rayleigh waves and Love waves. The experimental results not only revealed the differences in energy attenuation of these two wave types within the bandgap but also uncovered an interesting phenomenon of Bandgap-Induced Attenuation Mode Inversion. The experimental methods and data processing used in this study provide a professional reference for experimental research on seismic metamaterials. For instance, by observing the attenuation effects in the x, y, and z directions using multiple sets of sensors that are placed at different locations, we can more comprehensively and accurately assess the seismic performance of the metamaterial and deepen our understanding of the overall control of complex wave fields. Furthermore, compared to numerical simulations, our field experiments closely resemble real-world scenarios, providing greater reliability for our conclusions.
The mechanism of Bandgap-Induced Attenuation Mode Inversion is a phenomenon worth investigating further in the future; however, elucidating the physical mechanisms driving this phenomenon poses a significant challenge. We must acknowledge that the propagation characteristics of seismic surface waves through periodic arrays are influenced by various complex factors, such as the density; elastic modulus; damping properties; nonlinearity of the wave propagation medium (such as soil); symmetry of the geometric structure; and interactions between wave types, frequencies, and the engineering characteristics of the metamaterial.
In summary, our work emphasizes the necessity of considering the differences in energy attenuation between Rayleigh waves and Love waves when designing and evaluating cost-effective seismic metamaterials, providing valuable insights for the development and application of metamaterials that can effectively mitigate the energy of different seismic wave modes.
Author Contributions
Conceptualization, X.Z. and Q.S.; methodology, Q.S.; software, W.L.; validation, X.Z. and Q.S.; formal analysis, X.Z.; investigation, W.L.; resources, W.L.; data curation, X.Z.; writing—original draft preparation, X.Z.; writing—review and editing, Q.S.; visualization, W.L.; supervision, Q.S.; project administration, W.L.; funding acquisition, Q.S. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by National Natural Science Foundation of China, grant number 11974044.
Data Availability Statement
Data are contained within the article.
Acknowledgments
We would like to express our gratitude to the National Natural Science Foundation for their support (No: 11974044). We also thank Yulin Lu from the School of Civil Engineering at the Institute of Disaster Prevention for his valuable discussions, as well as Changyin Ji from the School of Physics at the Beijing Institute of Technology for his valuable assistance with the simulation program.
Conflicts of Interest
The authors declare no conflicts of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.
References
- di Marzo, M.; Tomassi, A.; Placidi, L. A Methodology for Structural Damage Detection Adding Masses. Res. Nondestruct. Eval. 2024, 35, 172. [Google Scholar] [CrossRef]
- Brûlé, S.; Javelaud, E.H.; Enoch, S.; Guenneau, S. Experiments on Seismic Metamaterials: Molding Surface Waves. Phys. Rev. Lett. 2014, 112, 113901. [Google Scholar] [CrossRef] [PubMed]
- Miniaci, M.; Krushynska, A.; Bosia, F.; Pugno, N.M. Large scale mechanical metamaterials as seismic shields. N. J. Phys. 2016, 18, 083041. [Google Scholar] [CrossRef]
- Brûlé, S.; Enoch, S.; Guenneau, S. Emergence of seismic metamaterials: Current state and future perspectives. Phys. Lett. A 2020, 384, 126034. [Google Scholar] [CrossRef]
- Liu, Z.; Zhang, X.; Mao, Y.; Zhu, Y.Y.; Yang, Z.; Chan, C.T.; Sheng, P. Locally Resonant Sonic Materials. Science 2000, 289, 1734. [Google Scholar] [CrossRef] [PubMed]
- Mu, D.; Shu, H.; Zhao, L.; An, S. A Review of Research on Seismic Metamaterials. Adv. Eng. Mater. 2020, 22, 1901148. [Google Scholar] [CrossRef]
- Zhang, X.; Zheng, N.; Ji, C.; Lu, Y.; Shi, Q. Attenuation of seismic waves using resonant metasurfaces: A field study on an array of rubber oscillators. Mater. Today Commun. 2024, 41, 110659. [Google Scholar] [CrossRef]
- Zeng, Y.; Zhang, S.-Y.; Zhou, H.-T.; Wang, Y.-F.; Cao, L.; Zhu, Y.; Du, Q.-J.; Assouar, B.; Wang, Y.-S. Broadband inverted T-shaped seismic metamaterial. Mater. Des. 2021, 208, 109906. [Google Scholar] [CrossRef]
- Pu, X.; Palermo, A.; Cheng, Z.; Shi, Z.; Marzani, A. Seismic metasurfaces on porous layered media: Surface resonators and fluid-solid interaction effects on the propagation of Rayleigh waves. Int. J. Eng. Sci. 2020, 154, 103347. [Google Scholar] [CrossRef]
- Zeighami, F.; Sandoval, L.; Guadagnini, A.; Di Federico, V. Uncertainty quantification and global sensitivity analysis of seismic Metabarriers. Eng. Struct. 2023, 277, 115415. [Google Scholar] [CrossRef]
- Colombi, A.; Craster, R.V.; Colquitt, D.; Achaoui, Y.; Guenneau, S.; Roux, P.; Rupin, M. Elastic Wave Control Beyond Band Gaps: Shaping the Flow of Waves in Plates and Half-Spaces with Subwavelength Resonant Rods. Front. Mech. Eng. 2017, 3, 1. [Google Scholar] [CrossRef]
- Lou, J.; Fang, X.; Du, J.; Wu, H. Propagation of fundamental and third harmonics along a nonlinear seismic metasurface. Int. J. Mech. Sci. 2022, 221, 107189. [Google Scholar] [CrossRef]
- Colombi, A.; Colquitt, D.; Roux, P.; Guenneau, S.; Craster, R.V. A seismic metamaterial: The resonant metawedge. Sci. Rep. 2016, 6, 27717. [Google Scholar] [CrossRef] [PubMed]
- Colquitt, D.; Colombi, A.; Craster, R.; Roux, P.; Guenneau, S. Seismic metasurfaces: Sub-wavelength resonators and Rayleigh wave interaction. J. Mech. Phys. Solids 2017, 99, 379. [Google Scholar] [CrossRef]
- Zeng, Y.; Xu, Y.; Yang, H.; Muzamil, M.; Xu, R.; Deng, K.; Peng, P.; Du, Q. A Matryoshka-like seismic metamaterial with wide band-gap Characteristics. Int. J. Solids Struct. 2020, 185–186, 334. [Google Scholar] [CrossRef]
- Zeng, C.; Zhao, C.; Zeighami, F. Seismic surface wave attenuation by resonant metasurfaces on stratified soil. Earthq. Eng. Struct. Dyn. 2022, 51, 1201. [Google Scholar] [CrossRef]
- Lou, J.; Fang, X.; Fan, H.; Du, J. A nonlinear seismic metamaterial lying on layered soils. Eng. Struct. 2022, 272, 115032. [Google Scholar] [CrossRef]
- Fang, X.; Lou, J.; Chen, Y.M.; Wang, J.; Xu, M.; Chuang, K.-C. Broadband Rayleigh wave attenuation utilizing an inertant seismic metamaterial. Int. J. Mech. Sci. 2023, 247, 108182. [Google Scholar] [CrossRef]
- Cai, R.; Jin, Y.; Rabczuk, T.; Zhuang, X.; Djafari-Rouhani, B. Propagation and attenuation of Rayleigh and pseudo surface waves in viscoelastic metamaterials. J. Appl. Phys. 2021, 129, 124903. [Google Scholar] [CrossRef]
- Palermo, A.; Krödel, S.; Marzani, A.; Daraio, C. Engineered metabarrier as shield from seismic surface waves. Sci. Rep. 2016, 6, 39356. [Google Scholar] [CrossRef] [PubMed]
- Zaccherini, R.; Palermo, A.; Marzani, A.; Colombi, A.; Dertimanis, V.; Chatzi, E. Mitigation of Rayleigh-like waves in granular media via multi-layer resonant metabarriers. Appl. Phys. Lett. 2020, 117, 254103. [Google Scholar] [CrossRef]
- Zaccherini, R.; Colombi, A.; Palermo, A.; Dertimanis, V.K.; Marzani, A.; Thomsen, H.R.; Stojadinovic, B.; Chatzi, E.N. Locally Resonant Metasurfaces for Shear Waves in Granular Media. Phys. Rev. Appl. 2020, 13, 034055. [Google Scholar] [CrossRef]
- Palermo, A.; Krödel, S.; Matlack, K.H.; Zaccherini, R.; Dertimanis, V.K.; Chatzi, E.N.; Marzani, A.; Daraio, C. Hybridization of Guided Surface Acoustic Modes in Unconsolidated Granular Media by a Resonant Metasurface. Phys. Rev. Appl. 2018, 9, 054026. [Google Scholar] [CrossRef]
- Ma, M.; Jiang, B.; Gao, J.; Liu, W. Experimental study on attenuation zone of soil-periodic piles system. Soil Dyn. Earthq. Eng. 2019, 126, 105738. [Google Scholar] [CrossRef]
- Kacin, S.; Ozturk, M.; Sevim, U.K.; Mert, B.A.; Ozer, Z.; Akgol, O.; Unal, E.; Karaaslan, M. Seismic metamaterials for low-frequency mechanical wave Attenuation. Nat. Hazards 2021, 107, 213. [Google Scholar] [CrossRef]
- Cai, C.; Gao, L.; He, X.; Zou, Y.; Yu, K.; Wu, D. The surface wave attenuation zone of periodic composite in-filled trenches and its isolation performance in train-induced ground vibration isolation. Comput. Geotech. 2021, 139, 104421. [Google Scholar] [CrossRef]
- Achaoui, Y.; Antonakakis, T.; Brûlé, S.; Craster, R.V.; Enoch, S.; Guenneau, S. Clamped seismic metamaterials: Ultra-low frequency stop bands. N. J. Phys. 2017, 19, 063022. [Google Scholar] [CrossRef]
- Pu, X.; Shi, Z. A novel method for identifying surface waves in periodic structures. Soil Dyn. Earthq. Eng. 2017, 98, 67. [Google Scholar] [CrossRef]
- Palermo, A.; Vitali, M.; Marzani, A. Metabarriers with multi-mass locally resonating units for broad band Rayleigh waves attenuation. Soil Dyn. Earthq. Eng. 2018, 113, 265. [Google Scholar] [CrossRef]
- Achaoui, Y.; Ungureanu, B.; Enoch, S.; Brûlé, S.; Guenneau, S. Seismic waves damping with arrays of inertial resonators. Extrem. Mech. Lett. 2016, 8, 30. [Google Scholar] [CrossRef]
- Wang, X.; Wan, S.; Nian, Y.; Zhou, P.; Zhu, Y. Periodic in-filled pipes embedded in semi-infinite space as seismic metamaterials for filtering ultra-low-frequency surface waves. Constr. Build. Mater. 2021, 313, 125498. [Google Scholar] [CrossRef]
- Zhao, C.; Zeng, C.; Wang, Y.; Bai, W.; Dai, J. Theoretical and Numerical Study on the Pile Barrier in Attenuating Seismic Surface Waves. Buildings 2022, 12, 1488. [Google Scholar] [CrossRef]
- Chen, H.-Y.; Qin, Z.-H.; Liang, S.-N.; Li, X.; Yu, S.-Y.; Chen, Y.-F. Gradient-index surface acoustic metamaterial for steering omnidirectional ultra-broadband seismic waves. Extrem. Mech. Lett. 2023, 58, 101949. [Google Scholar] [CrossRef]
- Li, T.; Su, Q.; Kaewunruen, S. Seismic metamaterial barriers for ground vibration mitigation in railways considering the train-track-soil dynamic interactions. Constr. Build. Mater. 2020, 260, 119936. [Google Scholar] [CrossRef]
- Muhammad; Lim, C.; Żur, K.K. Wide Rayleigh waves bandgap engineered metabarriers for ground born vibration attenuation. Eng. Struct. 2021, 246, 113019. [Google Scholar] [CrossRef]
- Zeng, Y.; Peng, P.; Du, Q.-J.; Wang, Y.-S.; Assouar, B. Subwavelength seismic metamaterial with an ultra-low frequency bandgap. J. Appl. Phys. 2020, 128, 014901. [Google Scholar] [CrossRef]
- Zeng, Y.; Xu, Y.; Deng, K.; Peng, P.; Yang, H.; Muzamil, M.; Du, Q. A broadband seismic metamaterial plate with simple structure and easy realization. J. Appl. Phys. 2019, 125, 224901. [Google Scholar] [CrossRef]
- Maheshwari, H.K.; Rajagopal, P. Novel locally resonant and widely scalable seismic metamaterials for broadband mitigation of disturbances in the very low frequency range of 0–33 Hz. Soil Dyn. Earthq. Eng. 2022, 161, 107409. [Google Scholar] [CrossRef]
- Yu, W.; Zhou, L. Seismic metamaterial surface for broadband Rayleigh waves attenuation. Mater. Des. 2023, 225, 111509. [Google Scholar] [CrossRef]
- Pu, X.; Palermo, A.; Marzani, A. Lamb’s problem for a half-space coupled to a generic distribution of oscillators at the surface. Int. J. Eng. Sci. 2021, 168, 103547. [Google Scholar] [CrossRef]
- Du, Q.; Zeng, Y.; Huang, G.; Yang, H. Elastic metamaterial-based seismic shield for both Lamb and surface waves. AIP Adv. 2017, 7, 075015. [Google Scholar] [CrossRef]
- Guo, D.-K.; Chen, T. Seismic metamaterials for energy attenuation of shear horizontal waves in transversely isotropic media. Mater. Today Commun. 2021, 28, 102526. [Google Scholar] [CrossRef]
- Zhang, K.; Luo, J.; Hong, F.; Deng, Z. Seismic metamaterials with cross-like and square steel sections for low-frequency wide band gaps. Eng. Struct. 2021, 232, 111870. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).