Chiral Effective Model of Cold and Dense Two-Color QCD: The Linear Sigma Model Approach
Abstract
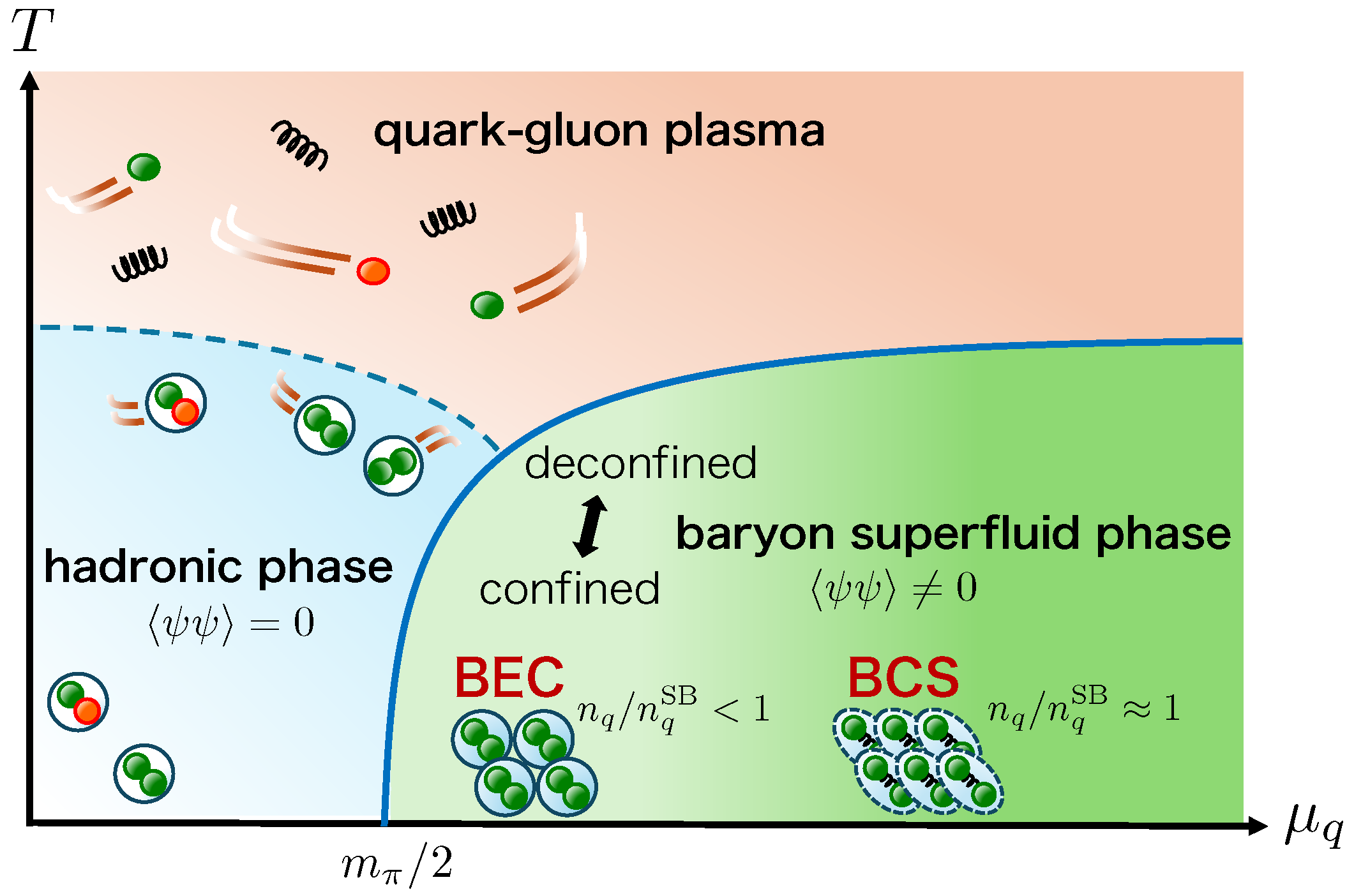
1. Introduction
2. QC2D Lagrangian for Quarks
2.1. Pauli–Gürsey Symmetry
2.2. Algebra of and
2.3. Spurion Fields
2.4. Ward–Takahashi Identities
2.5. Gell–Mann–Oakes–Renner Relationships with the Diquark Source
2.6. Comment on the Decay Constant
3. Chiral Perturbation Theory
3.1. Model Construction Based on the Maurer–Cartan 1-Form
3.2. ChPT in the Hadronic Phase
3.3. ChPT in the Baryon Superfluid Phase
3.4. ChPT with a Diquark Source j
3.5. Thermodynamic Properties
3.6. Hidden Local Symmetry
4. Linear Sigma Model
4.1. Model Construction
4.2. Phase Structure from the LSM
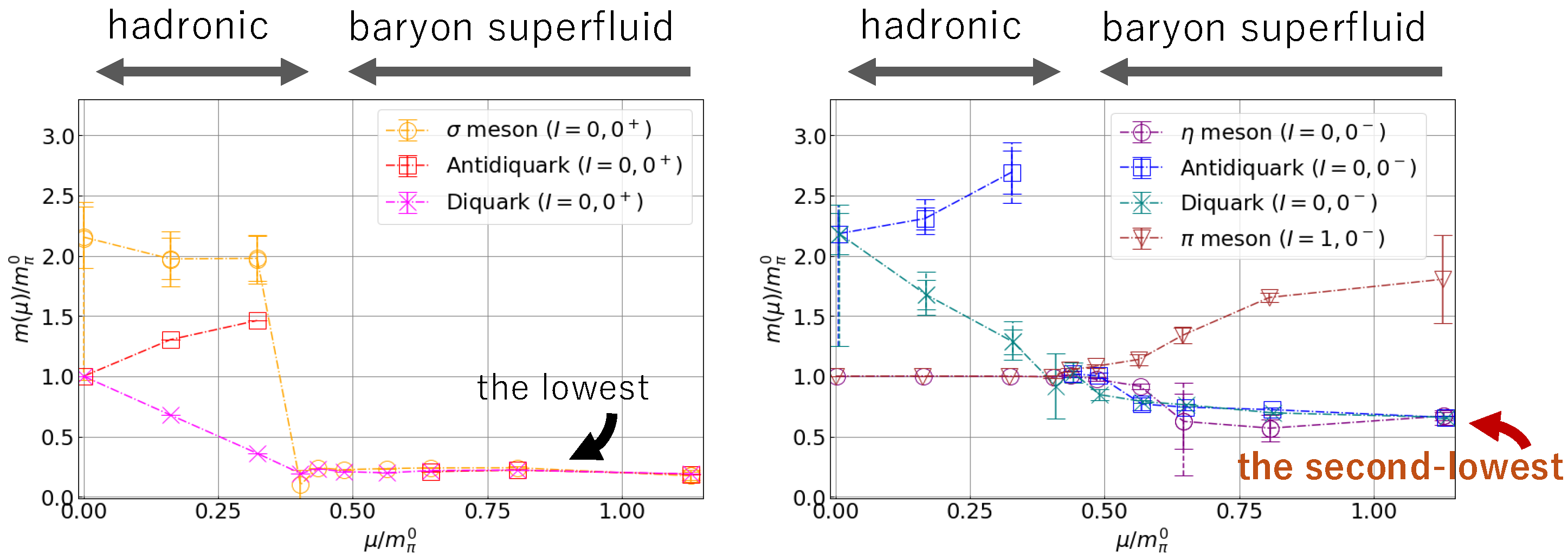
4.3. Hadron Mass Spectrum at Finite
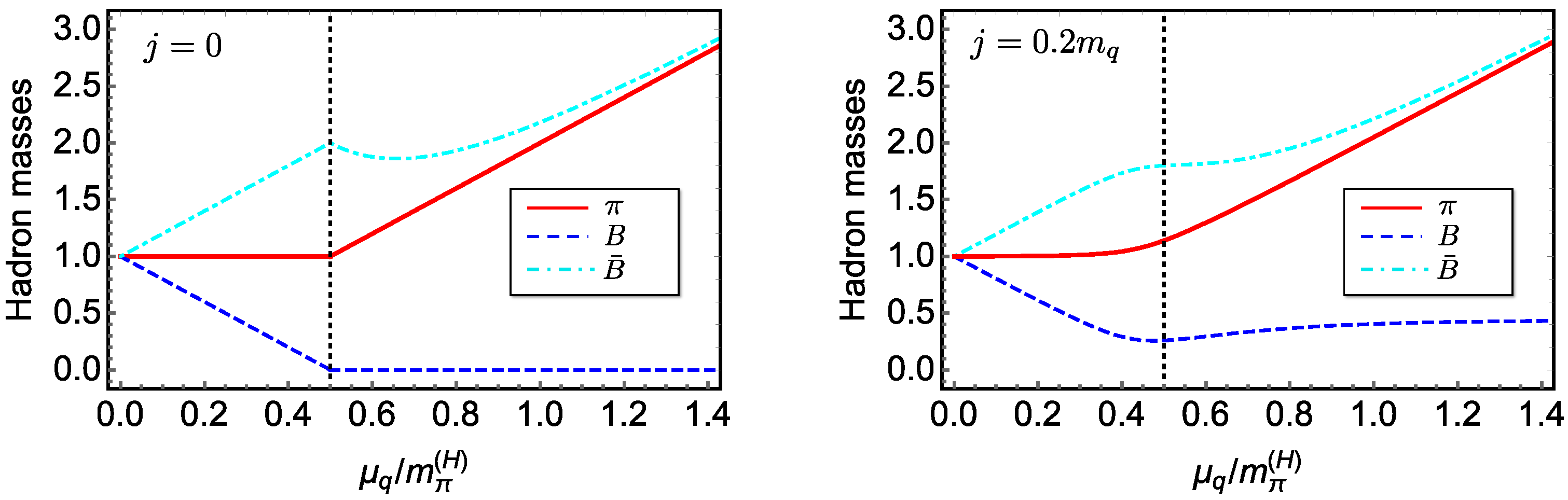
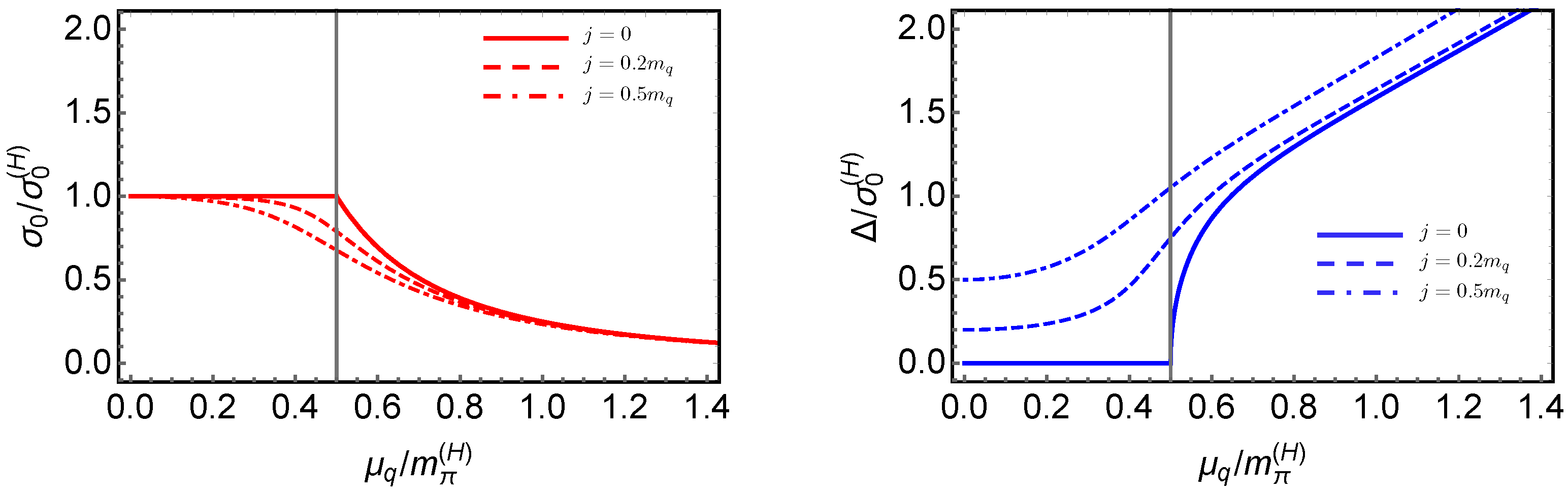
4.4. LSM with a Diquark Source j
4.5. Topological Susceptibility
4.6. Sound Velocity
5. Extended Linear Sigma Model (eLSM)
5.1. Model Construction
5.2. Hadron Mass Spectrum
6. Conclusions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| BCS | Bardeen–Cooper–Schrieffer |
| BEC | Bose–Einstein condensation |
| ChPT | Chiral perturbation theory |
| ELSM | Extended linear sigma model |
| GOR | Gell–Mann–Oakes–Renner |
| LHS | Left-hand side |
| LSM | Linear sigma model |
| NG | Nambu–Goldstone |
| QCD | Quantum chromodynamics |
| QC2D | Two-color QCD |
| QCDI | Isospin QCD |
| RHS | Right-hand side |
| SHB | Singly heavy baryon |
| VEV | Vacuum expectation value |
| WTI | Ward–Takahashi identity |
References
- Baym, G.; Hatsuda, T.; Kojo, T.; Powell, P.D.; Song, Y.; Takatsuka, T. From hadrons to quarks in neutron stars: A review. Rept. Prog. Phys. 2018, 81, 056902. [Google Scholar] [CrossRef] [PubMed]
- Aarts, G. Introductory lectures on lattice QCD at nonzero baryon number. J. Phys. Conf. Ser. 2016, 706, 022004. [Google Scholar] [CrossRef]
- Nagata, K. Finite-density lattice QCD and sign problem: Current status and open problems. Prog. Part. Nucl. Phys. 2022, 127, 103991. [Google Scholar] [CrossRef]
- Hands, S.; Kogut, J.B.; Lombardo, M.P.; Morrison, S.E. Symmetries and spectrum of SU(2) lattice gauge theory at finite chemical potential. Nucl. Phys. B 1999, 558, 327–346. [Google Scholar] [CrossRef]
- Kogut, J.B.; Sinclair, D.K.; Hands, S.J.; Morrison, S.E. Two color QCD at nonzero quark number density. Phys. Rev. D 2001, 64, 094505. [Google Scholar] [CrossRef]
- Hands, S.; Montvay, I.; Scorzato, L.; Skullerud, J. Diquark condensation in dense adjoint matter. Eur. Phys. J. C 2001, 22, 451–461. [Google Scholar] [CrossRef]
- Muroya, S.; Nakamura, A.; Nonaka, C. Behavior of hadrons at finite density: Lattice study of color SU(2) QCD. Phys. Lett. B 2003, 551, 305–310. [Google Scholar] [CrossRef]
- Muroya, S.; Nakamura, A.; Nonaka, C.; Takaishi, T. Lattice QCD at finite density: An Introductory review. Prog. Theor. Phys. 2003, 110, 615–668. [Google Scholar] [CrossRef]
- Chandrasekharan, S.; Jiang, F.J. Phase-diagram of two-color lattice QCD in the chiral limit. Phys. Rev. D 2006, 74, 014506. [Google Scholar] [CrossRef]
- Hands, S.; Kim, S.; Skullerud, J.I. Deconfinement in dense 2-color QCD. Eur. Phys. J. C 2006, 48, 193. [Google Scholar] [CrossRef]
- Hands, S.; Sitch, P.; Skullerud, J.I. Hadron Spectrum in a Two-Colour Baryon-Rich Medium. Phys. Lett. B 2008, 662, 405–412. [Google Scholar] [CrossRef]
- Hands, S.; Kim, S.; Skullerud, J.I. A Quarkyonic Phase in Dense Two Color Matter? Phys. Rev. D 2010, 81, 091502. [Google Scholar] [CrossRef]
- Cotter, S.; Giudice, P.; Hands, S.; Skullerud, J.I. Towards the phase diagram of dense two-color matter. Phys. Rev. D 2013, 87, 034507. [Google Scholar] [CrossRef]
- Hands, S.; Kim, S.; Skullerud, J.I. Non-relativistic spectrum of two-color QCD at non-zero baryon density. Phys. Lett. B 2012, 711, 199–204. [Google Scholar] [CrossRef]
- Boz, T.; Cotter, S.; Fister, L.; Mehta, D.; Skullerud, J.I. Phase transitions and gluodynamics in 2-colour matter at high density. Eur. Phys. J. A 2013, 49, 87. [Google Scholar] [CrossRef]
- Braguta, V.V.; Ilgenfritz, E.M.; Kotov, A.Y.; Molochkov, A.V.; Nikolaev, A.A. Study of the phase diagram of dense two-color QCD within lattice simulation. Phys. Rev. D 2016, 94, 114510. [Google Scholar] [CrossRef]
- Puhr, M.; Buividovich, P.V. Numerical Study of Nonperturbative Corrections to the Chiral Separation Effect in Quenched Finite-Density QCD. Phys. Rev. Lett. 2017, 118, 192003. [Google Scholar] [CrossRef] [PubMed]
- Boz, T.; Hajizadeh, O.; Maas, A.; Skullerud, J.I. Finite-density gauge correlation functions in QC2D. Phys. Rev. D 2019, 99, 074514. [Google Scholar] [CrossRef]
- Astrakhantsev, N.Y.; Bornyakov, V.G.; Braguta, V.V.; Ilgenfritz, E.M.; Kotov, A.Y.; Nikolaev, A.A.; Rothkopf, A. Lattice study of static quark-antiquark interactions in dense quark matter. J. High Energy Phys. 2019, 05, 171. [Google Scholar] [CrossRef]
- Iida, K.; Itou, E.; Lee, T.G. Two-colour QCD phases and the topology at low temperature and high density. J. High Energy Phys. 2020, 1, 181. [Google Scholar] [CrossRef]
- Wilhelm, J.; Holicki, L.; Smith, D.; Wellegehausen, B.; von Smekal, L. Continuum Goldstone spectrum of two-color QCD at finite density with staggered quarks. Phys. Rev. D 2019, 100, 114507. [Google Scholar] [CrossRef]
- Boz, T.; Giudice, P.; Hands, S.; Skullerud, J.I. Dense two-color QCD towards continuum and chiral limits. Phys. Rev. D 2020, 101, 074506. [Google Scholar] [CrossRef]
- Buividovich, P.V.; Smith, D.; von Smekal, L. Numerical study of the chiral separation effect in two-color QCD at finite density. Phys. Rev. D 2021, 104, 014511. [Google Scholar] [CrossRef]
- Iida, K.; Itou, E.; Lee, T.G. Relative scale setting for two-color QCD with Nf = 2 Wilson fermions. Prog. Theor. Exp. Phys. 2021, 2021, 013B05. [Google Scholar] [CrossRef]
- Astrakhantsev, N.; Braguta, V.V.; Ilgenfritz, E.M.; Kotov, A.Y.; Nikolaev, A.A. Lattice study of thermodynamic properties of dense QC2D. Phys. Rev. D 2020, 102, 074507. [Google Scholar] [CrossRef]
- Bornyakov, V.G.; Braguta, V.V.; Nikolaev, A.A.; Rogalyov, R.N. Effects of Dense Quark Matter on Gluon Propagators in Lattice QC2D. Phys. Rev. D 2020, 102, 114511. [Google Scholar] [CrossRef]
- Buividovich, P.V.; Smith, D.; von Smekal, L. Electric conductivity in finite-density SU(2) lattice gauge theory with dynamical fermions. Phys. Rev. D 2020, 102, 094510. [Google Scholar] [CrossRef]
- Buividovich, P.V.; Smith, D.; von Smekal, L. Static magnetic susceptibility in finite-density SU(2) lattice gauge theory. Eur. Phys. J. A 2021, 57, 293. [Google Scholar] [CrossRef]
- Begun, A.; Bornyakov, V.G.; Gerasimeniuk, N.V.; Goy, V.A.; Nakamura, A.; Rogalyov, R.N.; Vovchenko, V. Quark Density in Lattice QC2D at Imaginary and Real Chemical Potential. arXiv 2021, arXiv:2103.07442. [Google Scholar]
- Iida, K.; Itou, E. Velocity of Sound beyond the High-Density Relativistic Limit from Lattice Simulation of Dense Two-Color QCD. arXiv 2022, arXiv:2207.01253. [Google Scholar] [CrossRef]
- Begun, A.; Bornyakov, V.G.; Goy, V.A.; Nakamura, A.; Rogalyov, R.N. Study of two color QCD on large lattices. Phys. Rev. D 2022, 105, 114505. [Google Scholar] [CrossRef]
- Murakami, K.; Itou, E.; Iida, K. Chemical potential (in)dependence of hadron scatterings in the hadronic phase of QCD-like theories and its applications. arXiv 2023, arXiv:2309.08143. [Google Scholar] [CrossRef]
- Braguta, V.V. Phase Diagram of Dense Two-Color QCD at Low Temperatures. Symmetry 2023, 15, 1466. [Google Scholar] [CrossRef]
- Iida, K.; Itou, E.; Murakami, K.; Suenaga, D. Lattice study on finite density QC2D towards zero temperature. J. High Energy Phys. 2024, 10, 022. [Google Scholar] [CrossRef]
- Pauli, W. On the conservation of the Lepton charge. Nuovo Cim. 1957, 6, 204–215. [Google Scholar] [CrossRef]
- Gürsey, F. Relation of charge independence and baryon conservation to Pauli’s transformation. Nuovo Cim. 1958, 7, 411–415. [Google Scholar] [CrossRef]
- Gasser, J.; Leutwyler, H. Chiral Perturbation Theory to One Loop. Ann. Phys. 1984, 158, 142. [Google Scholar] [CrossRef]
- Gasser, J.; Leutwyler, H. Chiral Perturbation Theory: Expansions in the Mass of the Strange Quark. Nucl. Phys. B 1985, 250, 465–516. [Google Scholar] [CrossRef]
- Kogut, J.B.; Stephanov, M.A.; Toublan, D. On two color QCD with baryon chemical potential. Phys. Lett. B 1999, 464, 183–191. [Google Scholar] [CrossRef]
- Kogut, J.B.; Stephanov, M.A.; Toublan, D.; Verbaarschot, J.J.M.; Zhitnitsky, A. QCD—Like theories at finite baryon density. Nucl. Phys. B 2000, 582, 477–513. [Google Scholar] [CrossRef]
- Murakami, K.; Suenaga, D.; Iida, K.; Itou, E. Measurement of hadron masses in 2-color finite density QCD. PoS 2023, LATTICE2022, 154. [Google Scholar] [CrossRef]
- Coleman, S.R.; Wess, J.; Zumino, B. Structure of phenomenological Lagrangians. 1. Phys. Rev. 1969, 177, 2239–2247. [Google Scholar] [CrossRef]
- Callan, C.G., Jr.; Coleman, S.R.; Wess, J.; Zumino, B. Structure of phenomenological Lagrangians. 2. Phys. Rev. 1969, 177, 2247–2250. [Google Scholar] [CrossRef]
- Suenaga, D.; Murakami, K.; Itou, E.; Iida, K. Probing the hadron mass spectrum in dense two-color QCD with the linear sigma model. Phys. Rev. D 2023, 107, 054001. [Google Scholar] [CrossRef]
- Lenaghan, J.T.; Sannino, F.; Splittorff, K. The Superfluid and conformal phase transitions of two color QCD. Phys. Rev. D 2002, 65, 054002. [Google Scholar] [CrossRef]
- Splittorff, K.; Toublan, D.; Verbaarschot, J.J.M. Diquark condensate in QCD with two colors at next-to-leading order. Nucl. Phys. B 2002, 620, 290–314. [Google Scholar] [CrossRef]
- Ratti, C.; Weise, W. Thermodynamics of two-colour QCD and the Nambu Jona-Lasinio model. Phys. Rev. D 2004, 70, 054013. [Google Scholar] [CrossRef]
- Sun, G.f.; He, L.; Zhuang, P. BEC-BCS crossover in the Nambu-Jona-Lasinio model of QCD. Phys. Rev. D 2007, 75, 096004. [Google Scholar] [CrossRef]
- Fukushima, K.; Iida, K. Larkin-Ovchinnikov-Fulde-Ferrell state in two-color quark matter. Phys. Rev. D 2007, 76, 054004. [Google Scholar] [CrossRef]
- Brauner, T.; Fukushima, K.; Hidaka, Y. Two-color quark matter: U(1)(A) restoration, superfluidity, and quarkyonic phase. Phys. Rev. D 2009, 80, 074035, Erratum in Phys. Rev. D 2010, 81, 119904. [Google Scholar] [CrossRef]
- Kanazawa, T.; Wettig, T.; Yamamoto, N. Chiral Lagrangian and spectral sum rules for dense two-color QCD. J. High Energy Phys. 2009, 8, 3. [Google Scholar] [CrossRef]
- Harada, M.; Nonaka, C.; Yamaoka, T. Masses of vector bosons in two-color dense QCD based on the hidden local symmetry. Phys. Rev. D 2010, 81, 096003. [Google Scholar] [CrossRef]
- Andersen, J.O.; Brauner, T. Phase diagram of two-color quark matter at nonzero baryon and isospin density. Phys. Rev. D 2010, 81, 096004. [Google Scholar] [CrossRef]
- Zhang, T.; Brauner, T.; Rischke, D.H. QCD-like theories at nonzero temperature and density. J. High Energy Phys. 2010, 6, 64. [Google Scholar] [CrossRef]
- He, L. Nambu-Jona-Lasinio model description of weakly interacting Bose condensate and BEC-BCS crossover in dense QCD-like theories. Phys. Rev. D 2010, 82, 096003. [Google Scholar] [CrossRef]
- Strodthoff, N.; Schaefer, B.J.; von Smekal, L. Quark-meson-diquark model for two-color QCD. Phys. Rev. D 2012, 85, 074007. [Google Scholar] [CrossRef]
- Imai, S.; Toki, H.; Weise, W. Quark-Hadron Matter at Finite Temperature and Density in a Two-Color PNJL model. Nucl. Phys. A 2013, 913, 71–102. [Google Scholar] [CrossRef]
- Strodthoff, N.; von Smekal, L. Polyakov-Quark-Meson-Diquark Model for two-color QCD. Phys. Lett. B 2014, 731, 350–357. [Google Scholar] [CrossRef]
- Khan, N.; Pawlowski, J.M.; Rennecke, F.; Scherer, M.M. The Phase Diagram of QC2D from Functional Methods. arxiv 2015, arXiv:1512.03673. [Google Scholar]
- Duarte, D.C.; Allen, P.G.; Farias, R.L.S.; Manso, P.H.A.; Ramos, R.O.; Scoccola, N.N. BEC-BCS crossover in a cold and magnetized two color NJL model. Phys. Rev. D 2016, 93, 025017. [Google Scholar] [CrossRef]
- Chao, J. Phase diagram of two-color QCD matter at finite baryon and axial isospin densities. Chin. Phys. C 2020, 44, 034108. [Google Scholar] [CrossRef]
- Adhikari, P.; Beleznay, S.B.; Mannarelli, M. Finite Density Two Color Chiral Perturbation Theory Revisited. Eur. Phys. J. C 2018, 78, 441. [Google Scholar] [CrossRef]
- Contant, R.; Huber, M.Q. Dense two-color QCD from Dyson-Schwinger equations. Phys. Rev. D 2020, 101, 014016. [Google Scholar] [CrossRef]
- Suenaga, D.; Kojo, T. Gluon propagator in two-color dense QCD: Massive Yang-Mills approach at one-loop. Phys. Rev. D 2019, 100, 076017. [Google Scholar] [CrossRef]
- Khunjua, T.G.; Klimenko, K.G.; Zhokhov, R.N. The dual properties of chiral and isospin asymmetric dense quark matter formed of two-color quarks. J. High Energy Phys. 2020, 6, 148. [Google Scholar] [CrossRef]
- Kojo, T.; Suenaga, D. Thermal quarks and gluon propagators in two-color dense QCD. Phys. Rev. D 2021, 103, 094008. [Google Scholar] [CrossRef]
- Suenaga, D.; Kojo, T. Delineating chiral separation effect in two-color dense QCD. Phys. Rev. D 2021, 104, 034038. [Google Scholar] [CrossRef]
- Kojo, T.; Suenaga, D. Peaks of sound velocity in two color dense QCD: Quark saturation effects and semishort range correlations. Phys. Rev. D 2022, 105, 076001. [Google Scholar] [CrossRef]
- Khunjua, T.G.; Klimenko, K.G.; Zhokhov, R.N. Influence of chiral chemical potential μ5 on phase structure of the two-color quark matter. Phys. Rev. D 2022, 106, 045008. [Google Scholar] [CrossRef]
- Kawaguchi, M.; Suenaga, D. Fate of the topological susceptibility in two-color dense QCD. J. High Energy Phys. 2023, 08, 189. [Google Scholar] [CrossRef]
- Suenaga, D.; Murakami, K.; Itou, E.; Iida, K. Mass spectrum of spin-one hadrons in dense two-color QCD: Novel predictions by extended linear sigma model. Phys. Rev. D 2024, 109, 074031. [Google Scholar] [CrossRef]
- Kawaguchi, M.; Suenaga, D. Sound velocity peak induced by the chiral partner in dense two-color QCD. Phys. Rev. D 2024, 109, 096034. [Google Scholar] [CrossRef]
- Acharyya, N.; Aich, P.; Bandyopadhyay, A.; Vaidya, S. Matrix model of two-color one-flavor QCD: The ultrastrong coupling regime. Phys. Rev. D 2024, 110, 054016. [Google Scholar] [CrossRef]
- Khunjua, T.G.; Klimenko, K.G.; Zhokhov, R.N. Dual symmetries of dense three and two-color QCD and some QCD-like NJL models. arXiv 2024, arXiv:2403.00444. [Google Scholar]
- Cheng, T.; Li, L. Gauge Theory of Elementary Particle Physics; Oxford University Press: Oxford, UK, 1995. [Google Scholar]
- Bando, M.; Kugo, T.; Yamawaki, K. Nonlinear Realization and Hidden Local Symmetries. Phys. Rept. 1988, 164, 217–314. [Google Scholar] [CrossRef]
- Son, D.T.; Stephanov, M.A. QCD at finite isospin density: From pion to quark - anti-quark condensation. Phys. Atom. Nucl. 2001, 64, 834–842. [Google Scholar] [CrossRef]
- Harada, M.; Yamawaki, K. Hidden local symmetry at loop: A New perspective of composite gauge boson and chiral phase transition. Phys. Rept. 2003, 381, 1–233. [Google Scholar] [CrossRef]
- Murakami, K.; Suenaga, D.; Itou, E.; Iida, K. in preparation.
- Witten, E. Baryons in the 1/n Expansion. Nucl. Phys. B 1979, 160, 57–115. [Google Scholar] [CrossRef]
- Fejos, G.; Hosaka, A. Thermal properties and evolution of the UA(1) factor for 2+1 flavors. Phys. Rev. D 2016, 94, 036005. [Google Scholar] [CrossRef]
- Fejos, G.; Hosaka, A. Mesonic and nucleon fluctuation effects at finite baryon density. Phys. Rev. D 2017, 95, 116011. [Google Scholar] [CrossRef]
- Lombardo, M.P. Topological Aspects of Dense Matter: Lattice Studies. Universe 2021, 7, 336. [Google Scholar] [CrossRef]
- Fujikawa, K. Path Integral Measure for Gauge Invariant Fermion Theories. Phys. Rev. Lett. 1979, 42, 1195–1198. [Google Scholar] [CrossRef]
- Parganlija, D.; Giacosa, F.; Rischke, D.H. Vacuum Properties of Mesons in a Linear Sigma Model with Vector Mesons and Global Chiral Invariance. Phys. Rev. D 2010, 82, 054024. [Google Scholar] [CrossRef]
- Parganlija, D.; Kovacs, P.; Wolf, G.; Giacosa, F.; Rischke, D.H. Meson vacuum phenomenology in a three-flavor linear sigma model with (axial-)vector mesons. Phys. Rev. D 2013, 87, 014011. [Google Scholar] [CrossRef]
- Son, D.T.; Stephanov, M.A. QCD at finite isospin density. Phys. Rev. Lett. 2001, 86, 592–595. [Google Scholar] [CrossRef] [PubMed]
- Splittorff, K.; Son, D.T.; Stephanov, M.A. QCD—Like theories at finite baryon and isospin density. Phys. Rev. D 2001, 64, 016003. [Google Scholar] [CrossRef]
- Lu, Z.Y.; Xia, C.J.; Ruggieri, M. Thermodynamics and susceptibilities of isospin imbalanced QCD matter. Eur. Phys. J. C 2020, 80, 46. [Google Scholar] [CrossRef]
- Gómez Nicola, A.; Vioque-Rodríguez, A. Effective Lagrangian at nonzero isospin chemical potential. Phys. Rev. D 2022, 106, 114017. [Google Scholar] [CrossRef]
- Brandt, B.B.; Cuteri, F.; Endrodi, G. Equation of state and speed of sound of isospin-asymmetric QCD on the lattice. J. High Energy Phys. 2023, 7, 55. [Google Scholar] [CrossRef]
- Abbott, R.; Detmold, W.; Romero-López, F.; Davoudi, Z.; Illa, M.; Parreño, A.; Perry, R.J.; Shanahan, P.E.; Wagman, M.L. Lattice quantum chromodynamics at large isospin density. Phys. Rev. D 2023, 108, 114506. [Google Scholar] [CrossRef]
- Abbott, R.; Detmold, W.; Illa, M.; Parreño, A.; Perry, R.J.; Romero-López, F.; Shanahan, P.E.; Wagman, M.L. QCD constraints on isospin-dense matter and the nuclear equation of state. arXiv 2024, arXiv:2406.09273. [Google Scholar] [CrossRef]
- Komoltsev, O.; Kurkela, A. How Perturbative QCD Constrains the Equation of State at Neutron-Star Densities. Phys. Rev. Lett. 2022, 128, 202701. [Google Scholar] [CrossRef] [PubMed]
- Koehn, H.; Rose, H.; Pang, P.T.H.; Somasundaram, R.; Reed, B.T. From existing and new nuclear and astrophysical constraints to stringent limits on the equation of state of neutron-rich dense matter. arXiv 2024, arXiv:2402.04172. [Google Scholar]
- Hochberg, Y.; Kuflik, E.; Murayama, H.; Volansky, T.; Wacker, J.G. Model for Thermal Relic Dark Matter of Strongly Interacting Massive Particles. Phys. Rev. Lett. 2015, 115, 021301. [Google Scholar] [CrossRef]
- Detmold, W.; McCullough, M.; Pochinsky, A. Dark nuclei. II. Nuclear spectroscopy in two-color QCD. Phys. Rev. D 2014, 90, 114506. [Google Scholar] [CrossRef]
- Hochberg, Y.; Kuflik, E.; Murayama, H. SIMP Spectroscopy. J. High Energy Phys. 2016, 5, 90. [Google Scholar] [CrossRef]
- Kamada, A.; Kobayashi, S.; Kuwahara, T. Perturbative unitarity of strongly interacting massive particle models. J. High Energy Phys. 2023, 2, 217. [Google Scholar] [CrossRef]
- Kulkarni, S.; Maas, A.; Mee, S.; Nikolic, M.; Pradler, J.; Zierler, F. Low-energy effective description of dark Sp(4) theories. SciPost Phys. 2023, 14, 44. [Google Scholar] [CrossRef]
- Chu, X.; Nikolic, M.; Pradler, J. Even SIMP miracles are possible. Phys. Rev. Lett. 2024, 133, 2. [Google Scholar] [CrossRef]
- Dengler, Y.; Maas, A.; Zierler, F. Scattering of dark pions in Sp(4) gauge theory. Phys. Rev. D 2024, 110, 054513. [Google Scholar] [CrossRef]
- Manohar, A.; Wise, M.; Ericson, T.; Landshoff, P. Heavy Quark Physics; Cambridge Monographs on Particle Physics, Nuclear Physics and Cosmology, Cambridge University Press: Cambridge, UK, 2000. [Google Scholar]
- Harada, M.; Liu, Y.R.; Oka, M.; Suzuki, K. Chiral effective theory of diquarks and the UA(1) anomaly. Phys. Rev. D 2020, 101, 054038. [Google Scholar] [CrossRef]
- Suenaga, D.; Oka, M. Axial anomaly effect on the chiral-partner structure of diquarks at high temperature. Phys. Rev. D 2023, 108, 014030. [Google Scholar] [CrossRef]
- Suenaga, D.; Oka, M. Fate of Σc, Ξc′ and Ωc baryons at high temperature with chiral restoration. arXiv 2024, arXiv:2411.12172. [Google Scholar]
- Hess, M.; Karsch, F.; Laermann, E.; Wetzorke, I. Diquark masses from lattice QCD. Phys. Rev. D 1998, 58, 111502. [Google Scholar] [CrossRef]
- Alexandrou, C.; de Forcrand, P.; Lucini, B. Evidence for diquarks in lattice QCD. Phys. Rev. Lett. 2006, 97, 222002. [Google Scholar] [CrossRef] [PubMed]
- Babich, R.; Garron, N.; Hoelbling, C.; Howard, J.; Lellouch, L.; Rebbi, C. Diquark correlations in baryons on the lattice with overlap quarks. Phys. Rev. D 2007, 76, 074021. [Google Scholar] [CrossRef]
- Bi, Y.; Cai, H.; Chen, Y.; Gong, M.; Liu, Z.; Qiao, H.X.; Yang, Y.B. Diquark mass differences from unquenched lattice QCD. Chin. Phys. C 2016, 40, 073106. [Google Scholar] [CrossRef][Green Version]
- Francis, A.; de Forcrand, P.; Lewis, R.; Maltman, K. Diquark properties from full QCD lattice simulations. J. High Energy Phys. 2022, 5, 62. [Google Scholar] [CrossRef]
- Watanabe, K. Quark-diquark potential and diquark mass from lattice QCD. Phys. Rev. D 2022, 105, 074510. [Google Scholar] [CrossRef]

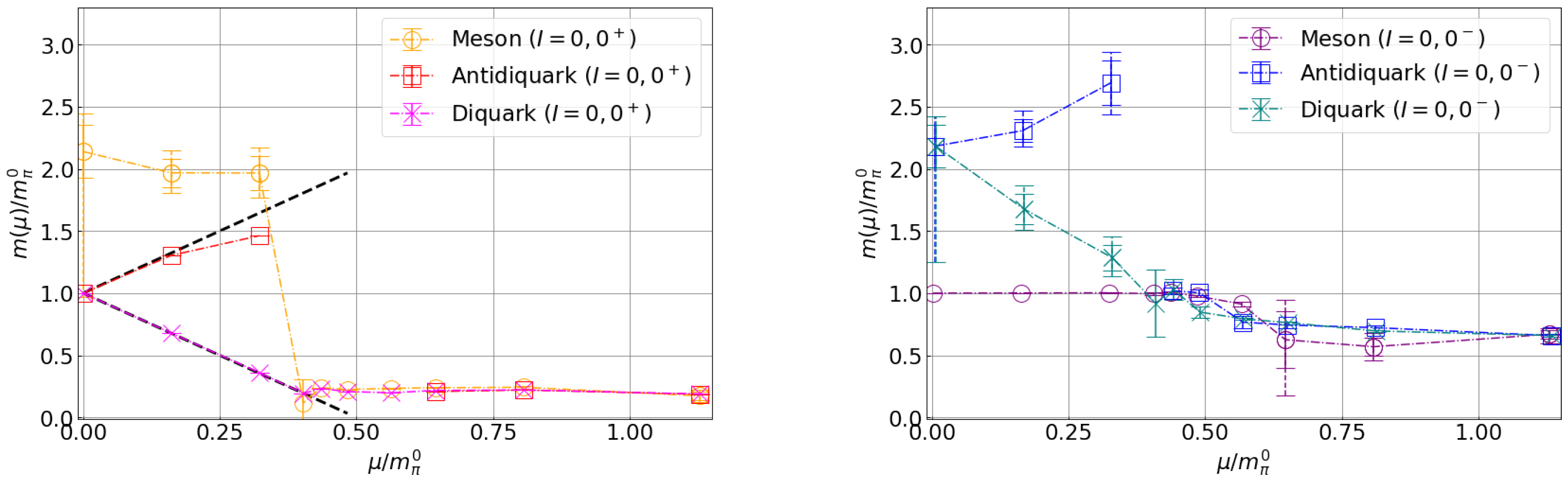
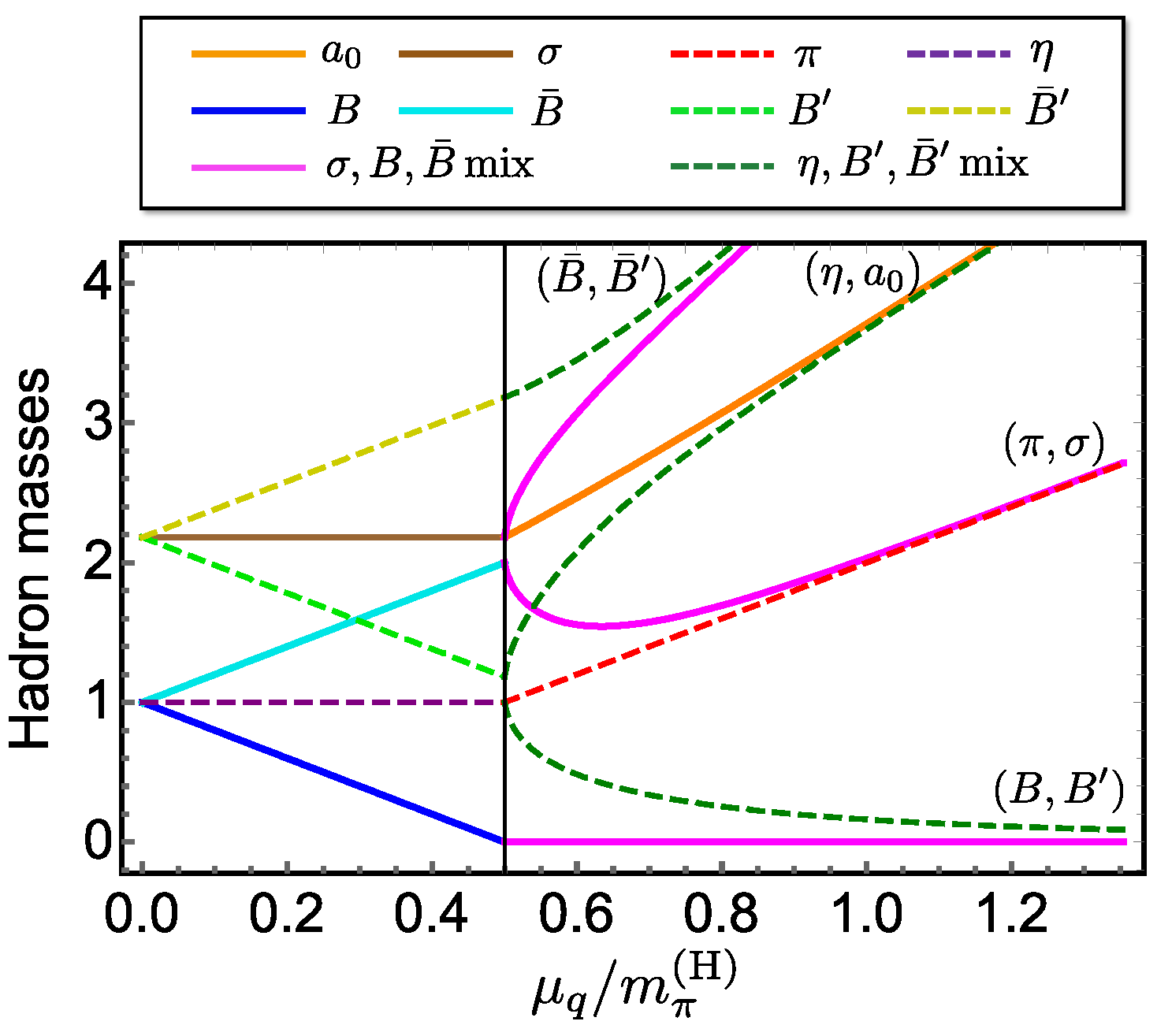
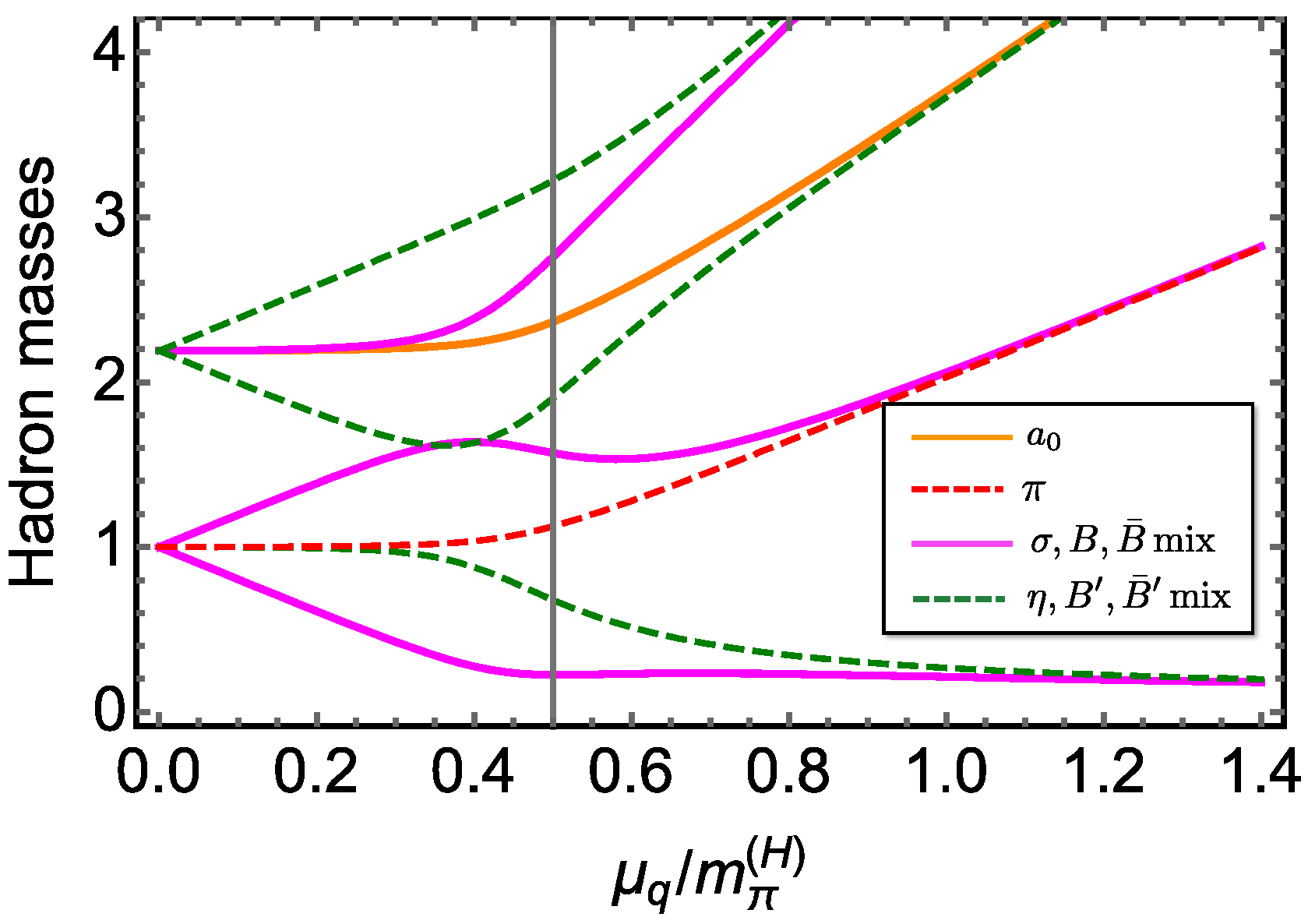
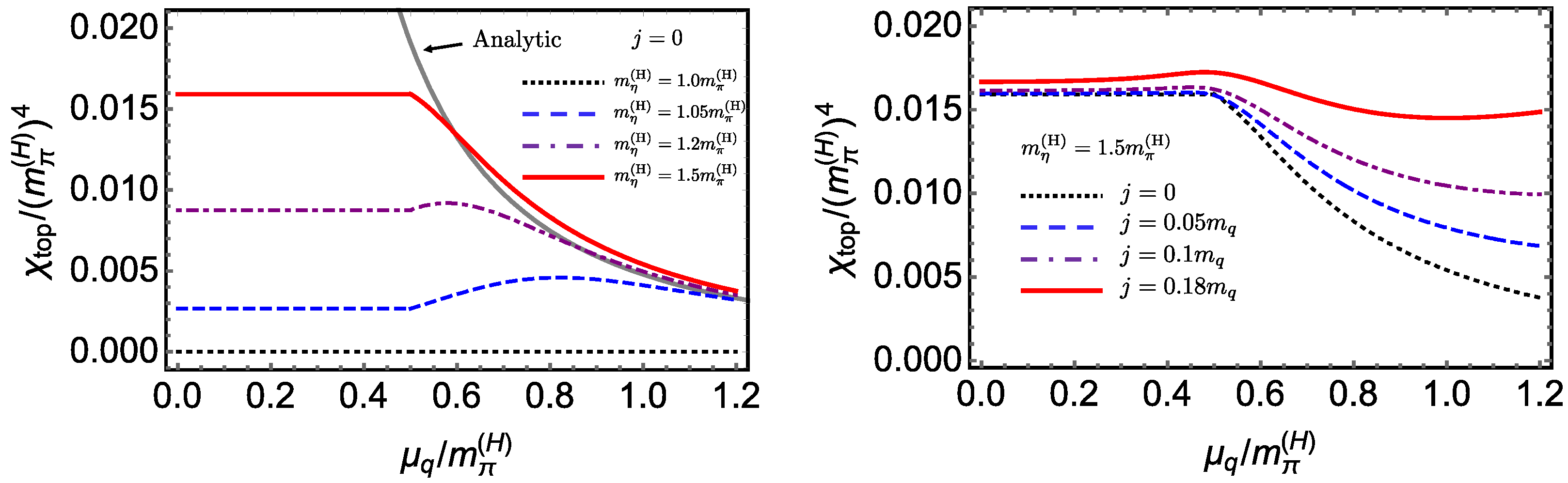



| Hadron | Spin and Parity () | Quark Number | Isospin |
|---|---|---|---|
| 0 | 0 | ||
| 0 | 1 | ||
| 0 | 0 | ||
| 0 | 1 | ||
| B () | () | 0 | |
| () | () | 0 |
| Hadron | Spin and Parity () | Quark Number | Isospin |
|---|---|---|---|
| 0 | 0 | ||
| 0 | 1 | ||
| 0 | 0 | ||
| 0 | 1 | ||
| () | () | 1 | |
| () | () | 0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Suenaga, D. Chiral Effective Model of Cold and Dense Two-Color QCD: The Linear Sigma Model Approach. Symmetry 2025, 17, 124. https://doi.org/10.3390/sym17010124
Suenaga D. Chiral Effective Model of Cold and Dense Two-Color QCD: The Linear Sigma Model Approach. Symmetry. 2025; 17(1):124. https://doi.org/10.3390/sym17010124
Chicago/Turabian StyleSuenaga, Daiki. 2025. "Chiral Effective Model of Cold and Dense Two-Color QCD: The Linear Sigma Model Approach" Symmetry 17, no. 1: 124. https://doi.org/10.3390/sym17010124
APA StyleSuenaga, D. (2025). Chiral Effective Model of Cold and Dense Two-Color QCD: The Linear Sigma Model Approach. Symmetry, 17(1), 124. https://doi.org/10.3390/sym17010124






