Abstract
The gauge covariance of the quark gap equation is compared for the case of three different quark–gluon vertices: the bare vertex, a Ball–Chiu-like vertex constrained by the corresponding Slavnov–Taylor identity, and a full vertex including the transverse components derived from transverse Slavnov–Taylor identities. The covariance properties are verified with the chiral quark condensate and the pion decay constant in the chiral limit.
1. Symmetries: When to Break, When to Preserve
One of the great achievements of hadron physics in the past decades has been the demonstration that dynamical chiral symmetry breaking is overwhelmingly responsible for the masses of nucleons and atoms [1,2]. Indeed, while the Brout-Englert-Higgs mechanism is the source of explicit chiral symmetry breaking, expressed by current-quark mass terms in the Standard Model Lagrangian, the symmetry breaking due to gluon dynamics is incomparably more efficient in generating the mass scales we observe in nuclear physics. This is possible because in describing strong interactions with a relativistic quantum field theory, namely Quantum Chromodynamics (QCD), we also deal with the implicit Einstein formula . In other words, most of the visible mass we observe is due to radiation energy. It seems as though Nature is telling us in a twisted manner that perfect symmetry is not always what she aims at.
On the other hand, gauge symmetry and its preservation have been the leitmotif in developing relativistic quantum field theories during the past century and are still guiding physicists in the pursuit of Standard Model extensions. This is a natural demand for any theory, as one can redefine the fields and particles by a gauge transformation in such a way that the physical laws remain the same. Simply put, gauge symmetries are nothing else but redundant degrees of freedom or an over-complete description of a physical system. One may do whatever one wishes with the superfluous degrees of freedom, as the physics of a given system remains the same and any measurable quantities cannot depend on how we choose them. This is commonly called gauge invariance and is also intimately related to the renormalizability of a quantum field theory. For instance, the Ward-Green-Takahashi identity (WGTI) [3,4,5] that describes current conservation in Quantum Electrodynamics (QED) implies that the wave function renormalization of the electron and its vertex renormalization constant are equal. This identity is crucial to the cancellation of the ultraviolet divergences that occur in loop calculations to all orders in perturbation theory.
Now, while we insist on gauge symmetry to be preserved at all times, we still have to deal with the freedom to redefine fermion and gauge fields. The consequence is that their equations of motion, or their Green functions, are altered. This brings gauge covariance into play, which means that the Green functions are not gauge invariant though they obey well-defined transformations with respect to the local gauge group. How these Green functions specifically transform under gauge variation is described by the Landau-Khalatnikov-Fradkin transformations (LKFT) [6,7] within the class of linear covariant gauges. If these transformations are correctly applied, physical observables derived from Green functions in any given gauge should be identical. This is exactly what we call gauge invariance. We recall that the Nielsen identities also provide a means to relate variations of Green functions under a gauge parameter change [8,9].
In practice, the application of the LFKT is rather cumbersome, as they are written in coordinate space. One must first obtain a nonperturbative solution for a Green function in a given gauge, for instance the quark propagator in Landau gauge, and then Fourier transform this solution to coordinate space. After this one applies the LFKT and Fourier transforms this gauge-transformed propagator back to the momentum space for any arbitrary covariant gauge. This is an arduous and nontrivial task and the procedure was shown to be feasible with analytical expressions in leading truncation schemes in QED [10]. In an SU(N) gauge field theory and for covariant gauges, the transformation law for the quark propagator was derived with a perturbative expansion of the SU(N) gauge transformation of the quark field to in the corresponding two-point Green function [11]. Another derivation of the LFKT in non-Abelian theories was given in Ref. [12].
On the other hand, since the LFKT are nonperturbative in nature, the initial propagator should also be the solution of the nonperturbative gap equation. The latter is described by a Dyson-Schwinger equation (DSE) which involves, besides the boson and fermion propagators, the fully-dressed fermion-boson vertex. The LFKT themselves do not tell us anything about the general form of this vertex, but we can make use of the WGTI identity in QED or of the Slavnov-Taylor identity (STI) in QCD [13,14] to constrain at least its non-transverse parts, and also of transverse WGTIs [15,16,17,18,19] and STIs [20] to deduce the transverse vertices [21,22].
Recently, an alternative path to the LFKT was taken comparing the solutions of the quark DSE in different covariant gauges [23]. The gauge dependence in this gap equation is twofold, for the dependence on enters directly via the gluon dressing function in gauges, obtained in lattice QCD simulations [24] up to , and the strong coupling . Indirectly, the dressed quark-gluon vertex also contributes to this dependence and this feature will be exploited in the present study. The numerical data of the -dependent gluon propagators was fitted with a Padé approximant which revealed that the fit parameters exhibit a nearly linear dependence on the gauge parameter. This feature was taken advantage of and the gluon propagator was then extrapolated to Feynman gauge. Employing the full quark-gluon vertex derived from Slavnov-Taylor identities and gauge covariance in Ref. [22], the quark’s mass and wave renormalization functions were computed in the range . The quark condensate derived therefrom exhibits a modest dependence on the gauge parameter within the error estimates of the lattice predictions for the gluon, in agreement with a prediction of the LKFT in QCD [11].
We here take the opportunity to extend the study of Ref. [23] by including simpler truncations of the DSE for comparison and to highlight their effect on the gauge covariance of the gap equation. As we shall see, the functional -dependence of the quark-mass function is diametrically opposed when the DSE is solved in either the rainbow truncation or with the full vertex structure. Moreover, the quark condensate and pion decay constant, the gauge-parameter dependence of the latter presented here for the first time, decrease as functions of in this leading truncation scheme in disagreement with the gauge-invariance predictions of the LFKT. To a certain extent this is expected, as the rainbow-ladder truncation badly violates the WGTI and STI and is therefore commonly employed in Landau gauge to “minimize” the error. Nonetheless, we here explicitly demonstrate the failure of a simpler truncation to satisfy gauge covariance.
2. Quark Gap Equation: Truncation Schemes
In QCD, two-point Green functions, in particular the nonperturbative dressing of a current quark, are described by DSEs which are the relativistic equations of motion in that theory [1]. For arbitrary gauge and written in Euclidean space, the DSE of the quark propagator is given by:
In this DSE, , and are the vertex, wave function and mass renormalization constants, respectively, and is the renormalized current-quark mass. In the self-energy integral, is a Poincaré-invariant cut-off, whereas is the renormalization point chosen such that .
The quark-gluon interaction is described by the dressed vertex , where are the SU(3) color-group generators in the fundamental representation, p is the incoming and k the outgoing quark momentum, respectively, while is the gluon momentum. The gluon propagator in gauge,
is characterized by a transverse dressing function, renormalized as . The gauge-parameter dependence of this dressing function has been studied with lattice-QCD and functional approaches [24,25,26].
The covariant decomposition of the DSE solutions is generally written in terms of two amplitudes, namely and ,
where the flavor- and gauge-dependent mass and wave renormalization functions can be expressed by the two momentum dependent amplitudes:
The renormalization scale we employ is low, GeV, as it is the scale at which the transverse dressing function in gauge is renormalized [24] and allows for comparison of and with lattice QCD at this scale [27]. We therefore also impose the following conditions: and MeV [28,29].
Coming back to the quark-gluon vertex introduced in Equation (1), its most general covariant decomposition is not unique. For all that, one can express this vertex most generally as [30],
where we stress the gauge dependence of the so-called longitudinal and transverse form factors, and , respectively. The transverse vertex is naturally defined by . The 12 vector structures and are build upon the three available vectors, namely , and and variations thereof, with the constraint that should exhibit the same transformation properties as the bare vertex under charge conjugation C, parity transformation P and time reversal T.
In Section 3 we will observe the impact of a given truncation of Equation (1) on gauge covariance. To this end, we consider three cases, namely the leading rainbow truncation, a ghost-corrected Ball-Chiu vertex that satisfies the “longitudinal” STI [28,31,32], and the full longitudinal and transverse vertex structure derived with an additional transverse STI [22]. In the following, we present the form factors and considered in each case, while the common basis elements and are listed in the Appendix A.
- Rainbow truncation
: the bare vertex, successfully employed with phenomenological interaction models to describe light hadrons carries neither dynamical nor gauge information: , . This truncation is commonly employed with an interaction model or an artificially scaled-up strong coupling to compensate for the lack of support in the DSE kernel [29]. Simple extensions include a flavor dependent coupling in the treatment of heavy-light mesons and heavy quarkonia [33,34,35,36,37].
- STI Ball-Chiu vertex
: this vertex is constructed to satisfy the STI, however the quark-ghost scattering amplitude that enters this identity is modeled in a dressed-propagator approach and only the leading form factor is kept; see Refs. [28,31,32,38] for details.
The dressing function we use [39] is defined by the ghost propagator and renormalized as . Moreover, .
- Full STI vertex
: the transverse STI constrains the vertex structures that are transverse to the gluon momentum and in addition to Equations (6) to (9) one finds, with the same approximation for the quark-ghost kernel [22], the following transverse form factors:
where and the Gram determinant is defined by: . In Equations (10) to (17), the functions are the form factors of the most general decomposition of a Fourier transformed four-point function in coordinate space. The latter involves a non-local vector vertex along with a Wilson line to preserve gauge invariance and contributes to the transverse STI. Since we deal with a rather complex object for which no calculations exist yet, we refer to the discussion in Ref. [20] and note that the were constrained [21] with a vertex ansatz guided by pQCD and multiplicative renormalizability [40]. We do stress the fact, however, that the functions , and are massive, i.e., they are proportional to the mass function . The contribution to DCSB of the vertex form factors in Equations (6) to (17) that depend directly on or indirectly via these functions is therefore crucial and we observe that no mass-function solutions are found if all are zero, regardless of the value of the strong coupling . The same occurs if one chooses . Indeed, these two transverse form factors are responsible for the overwhelming contribution to DCSB in the gap equation [22].
The gauge dependence of the strong coupling has been studied with the Schwinger mechanism in the three-gluon vertex, which is crucial to the generation of an effective gluon mass in the infrared domain [41]:
The coupling is used for the ghost-corrected Ball-Chiu and the full STI vertices at GeV. On the other hand, solving the DSE with this coupling in the rainbow truncation generates a very modest mass: MeV. In analogy with effective interaction models we therefore inflate the coupling strength to and obtain a constituent mass similar to that found with the full STI vertex.
3. Gauge Dependence of the Mass and Wave Renormalization
We now discuss the solutions, and , of Equation (1) for the three cases considered in Section 2. Henceforth, we make use of the gluon and ghost dressing functions from lattice QCD, [24] and [39] respectively, renormalized at GeV and parametrized with a Padé approximant [42],
where , GeV and is the 1-loop anomalous gluon dimension. This parametrization is tantamount to a renormalization-group improved Padé approximation and is motivated by the refined Gribov-Zwanziger tree-level gluon propagator in the infrared region. The parameters Z, , , and were determined in a least- fit in Ref. [23] and exhibit a nearly linear dependence on the gauge parameter when fitted to the lattice data for the six values, . This feature was used to extrapolate the gluon propagator up to Feynman gauge [23].
The ghost propagator [39] is parametrized with a similar expression,
and is assumed to be independent of [43]. The anomalous ghost dimension is given by while , and are as in Equation (19). The fit parameters are also found in Ref. [23].
In Figure 1 we plot the mass and wave-renormalization functions and their gauge-parameter dependence for the bare vertex. As mentioned earlier, with the dynamical mass generation is insufficient to produce a true constituent-quark mass for any gauge parameter. Hence, we inflate the constant to , as this will allow us to compare quark condensates and weak decay constants obtained with the full STI vertex later on. The gauge dependence of is pronounced and the mass steadily decreases as a function of the gauge parameter. This behavior was also observed in mass and wave-renormalization functions solving the DSE in quenched QED3 with [10]. Likewise, also decreases with in the range considered here.
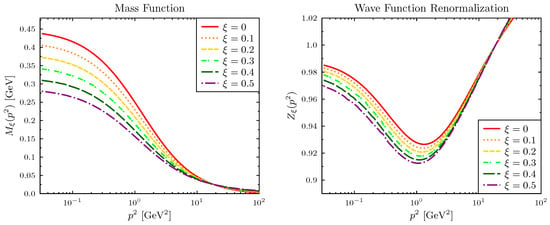
Figure 1.
Gauge-parameter dependence of the and functions of light quarks () in the rainbow truncation of the DSE. Note that the strong coupling is large: .
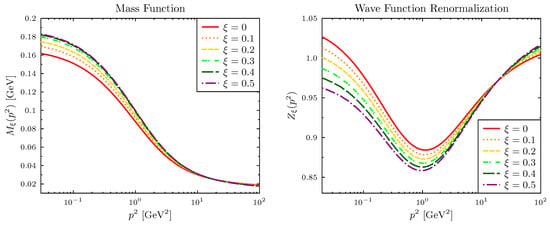
Solving the DSE (1) with the non-transverse vertex defined by Equations (6) to (9), we obtain the mass and wave-renormalization functions of Figure 2. We observe that the gauge dependence of the gap equation leads to a behavior of opposed to that in Figure 1: the effect of the additional gauge dependence in the vertex is an increase of up to , at which point the function seemingly freezes. The functional behavior of exhibits the characteristic behavior of the Ball-Chiu vertex, with a local minimum at GeV and a sudden rise in the infrared, though the gauge dependence is more pronounced than in the rainbow truncation of Figure 1. We remark that the solutions of the mass and wave-renormalization functions with the STI Ball-Chiu vertex are increasingly unstable for . We therefore do not include the Feynman-gauge solutions in Figure 2 and for comparison’s sake we also refrain from doing so in Figure 1 and Figure 3.
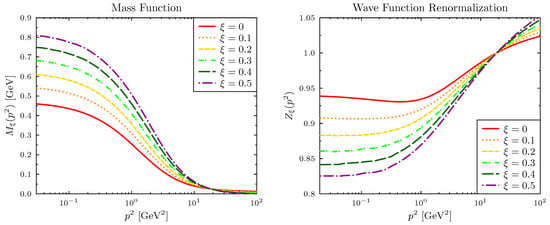
In Figure 3 we present our solutions for and with the full gauge-dependent STI vertex defined by Equations (6) to (17). Clearly, the trend of a rising mass function and a dropping wave renormalization in the low-momentum region, observed with the ghost-corrected Ball-Chiu vertex, is corroborated when the transverse vertex is included. The contrast with the functional behavior in Figure 1 is evident, in particular that of which now decreases steadily with and saturates in the infrared domain. Moreover, the quark-ghost scattering form factor, , is calculated in a dressed approximation [28,31,32] and dynamically generated in consistency with and . We abstain from discussing the gauge-dependent solutions here and refer to Ref. [23] for details.
To conclude our comparison of gauge dependent quark propagators, we ought to ask which is the correct one. This question can only be answered by computing a gauge-invariant quantity with the given quark propagators. A simple quantity that does not require the solutions of a Bethe-Salpeter equation is the quark condensate in the chiral limit ( GeV),
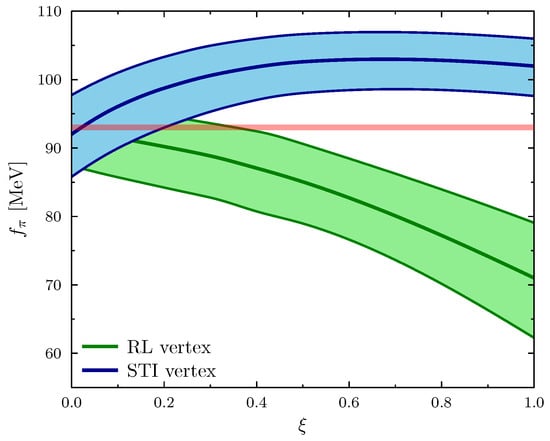
which we can express as a function of . As can be inferred from Figure 4, the condensate calculated with the full STI vertex is the central line in the blue-shaded, fairly horizontal band. The latter depicts our error estimate due to the statistical error of the gluon propagator [24]. A systematic error is not included, but we allow for uncertainties of the ghost dressing function and of (18) by varying by %. In this light, one can argue that the QCD condensate exhibits a moderate dependence on of the order of 7–8%, rising initially from Landau gauge to where the condensate seems to level off. This is in accordance with an invariance proof for any SU(N) theory derived in Ref. [11] and based on the LKFT. The same figure also demonstrates that this is not the case for a quark condensate computed in the rainbow truncation of the DSE. In fact, while an extrapolation beyond of the gluon propagator must be taken with a grain of salt, we verified that the condensate in this simplest truncation keeps falling off with the gauge parameter. This functional behavior expresses the lack of gauge covariance in this leading truncation not constrained by the STI and multiplicative renormalizability.
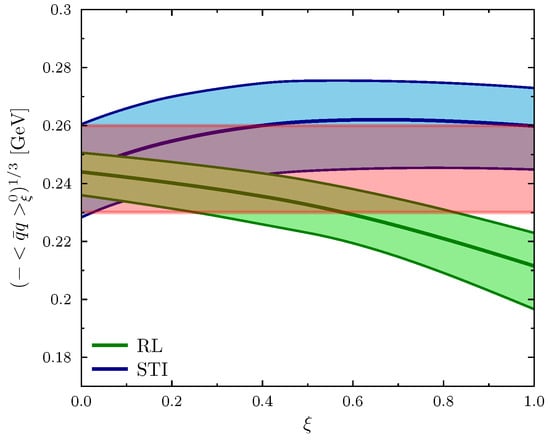
Figure 4.
Gauge dependence of the chiral quark condensate obtained with two different quark–gluon vertices in the DSE. The pink-, green-, and blue-shaded error bands stem from the statistical errors of the lattice QCD predictions for the gluon and ghost propagators [24] on which the gauge-dependent solutions of and depend via Equations (1) and (2). The pink horizontal band indicates the region of a gauge-independent quark condensate as implied by the LKFTs in QCD, where the uncertainty is due to the statistical error of the gauge propagators in Landau gauge.
We can also calculate the weak decay constant of the pion in the chiral limit following Ref. [44], as does not vanish in this limit whereas the pion’s mass does in truncations that preserve the axialvector WGTI. The weak decay constant in the chiral limit can be expressed by the integral,
with and where we dropped the gauge-dependence label. As we are constrained by a low renormalization point due to the quenched lattice-QCD input for the gluon and ghost propagators we employ, we set MeV at GeV, which allows for a sensible approximation for and in Equation (22).
In analogy with the condensates presented in Figure 4, the rainbow truncation of the DSE yields a weak decay constant that decreases relatively fast, as can be appreciated in Figure 5. If we solve the DSE with the full STI vertex, we observe an initial increase of from to after which the decay constant appears to saturate. The variation between Landau and Feynman gauge is about 10%, larger than the 7% increase of the quark condensate as function of . However, this moderate effect is not yet conclusive, as we ought to compute with the complete Bethe-Salpeter amplitude of the pion in this much more challenging truncation.
4. Final Remarks
We have shown that within a functional approach to QCD the transverse quark-gluon vertex plays an eminent role in the dynamics of mass generation and the emergence of a constituent quark mass scale. Regarding the gauge parameter dependence of the gap equation, we find a running mass function that increases with and a quark wave function which is mostly sensible to the gauge parameter in the infrared domain. More precisely, drops from about 0.94 in Landau gauge to 0.83 for , a effect. As far as gauge invariance is concerned, despite the limitations of the setup used herein, a variation of about 6% is observed in the quark condensate when the full vertex is taken into account in the gap equation. This contrasts with the outcome of the rainbow approximation which yields a condensate that decreases with . Likewise, rapidly falls off as a function of the gauge parameter. These results illustrate, once more, the important role of the transverse vertex in the nonperturbative dynamics of the gap equation.
Funding
This research was funded by the São Paulo Research Foundation (FAPESP), grant no. 2023/00195-8 and by the National Council for Scientific and Technological Development (CNPq), grant no. 409032/2023-9. B. E. is a member of the Brazilian nuclear physics network project INCT-Física Nuclear e Aplicações, grant no. 464898/2014-5.
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding author.
Acknowledgments
Much of what I presented in this contribution has only been possible with the precious input and contributions by Luis Albino, Adnan Bashir, Roberto Correa da Silveira, José Lessa, Orlando Oliveira and Fernando Serna over the past years.
Conflicts of Interest
The author declares no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| QCD | Quantum chromodynamics |
| QED | Quantum electrodynamics |
| DSE | Dyson–Schwinger equation |
| LFKT | Landau–Khalatnikov–Fradkin transformations |
| WGTI | Ward–Green–Takahashi identity |
| STI | Slavnov–Taylor identity |
Appendix A
For the longitudinal vertex we employ the common Ball-Chiu decomposition,
where and in Euclidean space. The transverse vertex can generally be decomposed into eight independent vector basis elements. For the kinematical configuration discussed below Equation (1), they are given by,
We use a slightly modified basis [45] with respect to the Ball-Chiu vertex [30] with the effect that all transverse form factors are independent of kinematic singularities in one-loop perturbation theory and arbitrary covariant gauge.
References
- Bashir, A.; Chang, L.; Cloët, I.C.; El-Bennich, B.; Liu, Y.X.; Roberts, C.D.; Tandy, P.C. Collective perspective on advances in Dyson-Schwinger Equation QCD. Commun. Theor. Phys. 2012, 58, 79–134. [Google Scholar] [CrossRef]
- Yang, Y.B.; Liang, J.; Bi, Y.J.; Chen, Y.; Draper, T.; Liu, K.F.; Liu, Z. Proton Mass Decomposition from the QCD Energy Momentum Tensor. Phys. Rev. Lett. 2018, 121, 212001. [Google Scholar] [CrossRef] [PubMed]
- Ward, J.C. An Identity in Quantum Electrodynamics. Phys. Rev. 1950, 78, 182. [Google Scholar] [CrossRef]
- Green, H.S. A Pre-renormalized quantum electrodynamics. Proc. Phys. Soc. A 1953, 66, 873–880. [Google Scholar] [CrossRef]
- Takahashi, Y. On the generalized Ward identity. Nuovo Cim. 1957, 6, 371. [Google Scholar] [CrossRef]
- Landau, L.D.; Khalatnikov, I.M. The gauge transformation of the Green function for charged particles. Zh. Eksp. Teor. Fiz. 1955, 29, 89. [Google Scholar]
- Fradkin, E.S. Concerning some general relations of quantum electrodynamics. Zh. Eksp. Teor. Fiz. 1955, 29, 258–261. [Google Scholar]
- Nielsen, N.K. On the Gauge Dependence of Spontaneous Symmetry Breaking in Gauge Theories. Nucl. Phys. B 1975, 101, 173–188. [Google Scholar] [CrossRef]
- Meerleer, T.D.; Dudal, D.; Sorella, S.P.; Dall’Olio, P.; Bashir, A. Landau-Khalatnikov-Fradkin Transformations, Nielsen Identities, Their Equivalence and Implications for QCD. Phys. Rev. D 2020, 101, 085005. [Google Scholar] [CrossRef]
- Bashir, A.; Raya, A. Dynamical fermion masses and constraints of gauge invariance in quenched QED(3). Nucl. Phys. B 2005, 709, 307–328. [Google Scholar] [CrossRef][Green Version]
- Aslam, M.J.; Bashir, A.; Gutiérrez-Guerrero, L.X. Local Gauge Transformation for the Quark Propagator in an SU(N) Gauge Theory. Phys. Rev. D 2016, 93, 076001. [Google Scholar] [CrossRef]
- Meerleer, T.D.; Dudal, D.; Sorella, S.P.; Dall’Olio, P.; Bashir, A. Fresh look at the Abelian and non-Abelian Landau-Khalatnikov-Fradkin transformations. Phys. Rev. D 2018, 97, 074017. [Google Scholar] [CrossRef]
- Slavnov, A.A. Ward Identities in Gauge Theories. Theor. Math. Phys. 1972, 10, 99–107. [Google Scholar] [CrossRef]
- Taylor, J.C. Ward Identities and Charge Renormalization of the Yang-Mills Field. Nucl. Phys. B 1971, 33, 436–444. [Google Scholar] [CrossRef]
- Kondo, K.I. Transverse Ward-Takahashi identity, anomaly and Schwinger-Dyson equation. Int. J. Mod. Phys. A 1997, 12, 5651–5686. [Google Scholar] [CrossRef]
- He, H.X.; Khanna, F.C.; Takahashi, Y. Transverse Ward-Takahashi identity for the fermion boson vertex in gauge theories. Phys. Lett. B 2000, 480, 222–228. [Google Scholar] [CrossRef]
- He, H.X. Transverse vector vertex function and transverse Ward-Takahashi relations in QED. Commun. Theor. Phys. 2006, 46, 109–112. [Google Scholar] [CrossRef]
- He, H.X. Transverse Ward-Takahashi relation for the fermion-boson vertex function in four-dimensional Abelian gauge theory. Int. J. Mod. Phys. A 2007, 22, 2119–2132. [Google Scholar] [CrossRef]
- Pennington, M.R.; Williams, R. Checking the transverse Ward-Takahashi relation at one loop order in 4-dimensions. J. Phys. G 2006, 32, 2219–2234. [Google Scholar] [CrossRef][Green Version]
- He, H.X. Transverse Symmetry Transformations and the Quark-Gluon Vertex Function in QCD. Phys. Rev. D 2009, 80, 016004. [Google Scholar] [CrossRef]
- Albino, L.; Bashir, A.; Guerrero, L.X.G.; Bennich, B.E.; Rojas, E. Transverse Takahashi Identities and Their Implications for Gauge Independent Dynamical Chiral Symmetry Breaking. Phys. Rev. D 2019, 100, 054028. [Google Scholar] [CrossRef]
- Albino, L.; Bashir, A.; El-Bennich, B.; Rojas, E.; Serna, F.E.; da Silveira, R.C. The impact of transverse Slavnov-Taylor identities on dynamical chiral symmetry breaking. JHEP 2021, 11, 196. [Google Scholar] [CrossRef]
- Lessa, J.R.; Serna, F.E.; El-Bennich, B.; Bashir, A.; Oliveira, O. Gauge dependence of the quark gap equation: An exploratory study. Phys. Rev. D 2023, 107, 074017. [Google Scholar] [CrossRef]
- Bicudo, P.; Binosi, D.; Cardoso, N.; Oliveira, O.; Silva, P.J. Lattice gluon propagator in renormalizable ξ gauges. Phys. Rev. D 2015, 92, 114514. [Google Scholar] [CrossRef]
- Huber, M.Q. Gluon and ghost propagators in linear covariant gauges. Phys. Rev. D 2015, 91, 085018. [Google Scholar] [CrossRef]
- Napetschnig, M.; Alkofer, R.; Huber, M.Q.; Pawlowski, J.M. Yang-Mills propagators in linear covariant gauges from Nielsen identities. Phys. Rev. D 2021, 104, 054003. [Google Scholar] [CrossRef]
- Oliveira, O.; Silva, P.J.; Skullerud, J.I.; Sternbeck, A. Quark propagator with two flavors of O(a)-improved Wilson fermions. Phys. Rev. D 2019, 99, 094506. [Google Scholar] [CrossRef]
- Rojas, E.; de Melo, J.P.B.C.; El-Bennich, B.; Oliveira, O.; Frederico, T. On the Quark-Gluon Vertex and Quark-Ghost Kernel: Combining Lattice Simulations with Dyson-Schwinger equations. JHEP 2013, 10, 193. [Google Scholar] [CrossRef]
- Serna, F.E.; Chen, C.; El-Bennich, B. Interplay of dynamical and explicit chiral symmetry breaking effects on a quark. Phys. Rev. D 2019, 99, 094027. [Google Scholar] [CrossRef]
- Ball, J.S.; Chiu, T.W. Analytic Properties of the Vertex Function in Gauge Theories. 1. Phys. Rev. D 1980, 22, 2542. [Google Scholar] [CrossRef]
- Aguilar, A.C.; Papavassiliou, J. Chiral symmetry breaking with lattice propagators. Phys. Rev. D 2011, 83, 014013. [Google Scholar] [CrossRef]
- Aguilar, A.C.; Cardona, J.C.; Ferreira, M.N.; Papavassiliou, J. Non-Abelian Ball-Chiu vertex for arbitrary Euclidean momenta. Phys. Rev. D 2017, 96, 014029. [Google Scholar] [CrossRef]
- Serna, F.E.; El-Bennich, B.; Krein, G. Charmed mesons with a symmetry-preserving contact interaction. Phys. Rev. D 2017, 96, 014013. [Google Scholar] [CrossRef]
- Serna, F.E.; da Silveira, R.C.; Cobos-Martínez, J.J.; El-Bennich, B.; Rojas, E. Distribution amplitudes of heavy mesons and quarkonia on the light front. Eur. Phys. J. C 2020, 80, 955. [Google Scholar] [CrossRef]
- Serna, F.E.; da Silveira, R.C.; El-Bennich, B. D* and Ds* distribution amplitudes from Bethe-Salpeter wave functions. Phys. Rev. D 2022, 106, L091504. [Google Scholar] [CrossRef]
- da Silveira, R.C.; Serna, F.E.; El-Bennich, B. Strong two-meson decays of light and charmed vector mesons. Phys. Rev. D 2023, 107, 034021. [Google Scholar] [CrossRef]
- Serna, F.E.; El-Bennich, B.; Krein, G. Parton distribution functions and transverse momentum dependence of heavy mesons. Phys. Rev. D 2024, 110, 114033. [Google Scholar] [CrossRef]
- Davydychev, A.I.; Osland, P.; Saks, L. Quark gluon vertex in arbitrary gauge and dimension. Phys. Rev. D 2001, 63, 014022. [Google Scholar] [CrossRef]
- Duarte, A.G.; Oliveira, O.; Silva, P.J. Lattice Gluon and Ghost Propagators, and the Strong Coupling in Pure SU(3) Yang-Mills Theory: Finite Lattice Spacing and Volume Effects. Phys. Rev. D 2016, 94, 014502. [Google Scholar] [CrossRef]
- Bashir, A.; Bermúdez, R.; Chang, L.; Roberts, C.D. Dynamical chiral symmetry breaking and the fermion–gauge-boson vertex. Phys. Rev. C 2012, 85, 045205. [Google Scholar] [CrossRef]
- Aguilar, A.C.; Binosi, D.; Papavassiliou, J. Schwinger mechanism in linear covariant gauges. Phys. Rev. D 2017, 95, 034017. [Google Scholar] [CrossRef]
- Dudal, D.; Oliveira, O.; Silva, P.J. High precision statistical Landau gauge lattice gluon propagator computation vs. the Gribov–Zwanziger approach. Ann. Phys. 2018, 397, 351–364. [Google Scholar] [CrossRef]
- Cucchieri, A.; Dudal, D.; Mendes, T.; Oliveira, O.; Roelfs, M.; Silva, P.J. Lattice Computation of the Ghost Propagator in Linear Covariant Gauges. In Proceedings of the 36th International Symposium on Lattice Field Theory, East Lansing, MI, USA, 22–28 July 2018; p. 252. [Google Scholar] [CrossRef]
- Roberts, C.D. Electromagnetic pion form-factor and neutral pion decay width. Nucl. Phys. A 1996, 605, 475–495. [Google Scholar] [CrossRef]
- Kızılersü, A.; Reenders, M.; Pennington, M.R. One loop QED vertex in any covariant gauge: Its complete analytic form. Phys. Rev. D 1995, 52, 1242–1259. [Google Scholar] [CrossRef] [PubMed]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).