Numerical Simulation Study Considering Discontinuous Longitudinal Joints in Soft Soil under Symmetric Loading
Abstract
1. Introduction
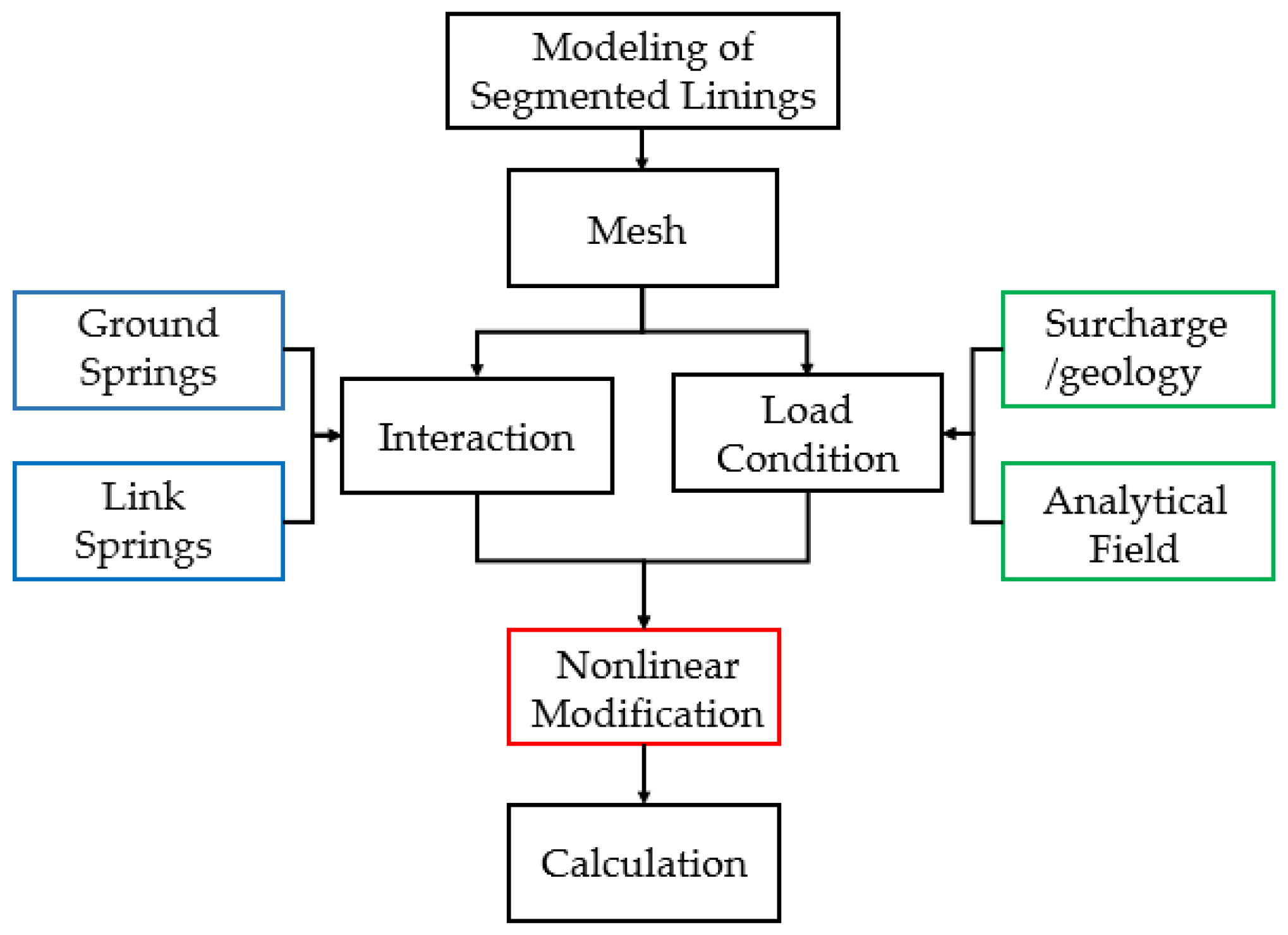
2. Modelling Strategy
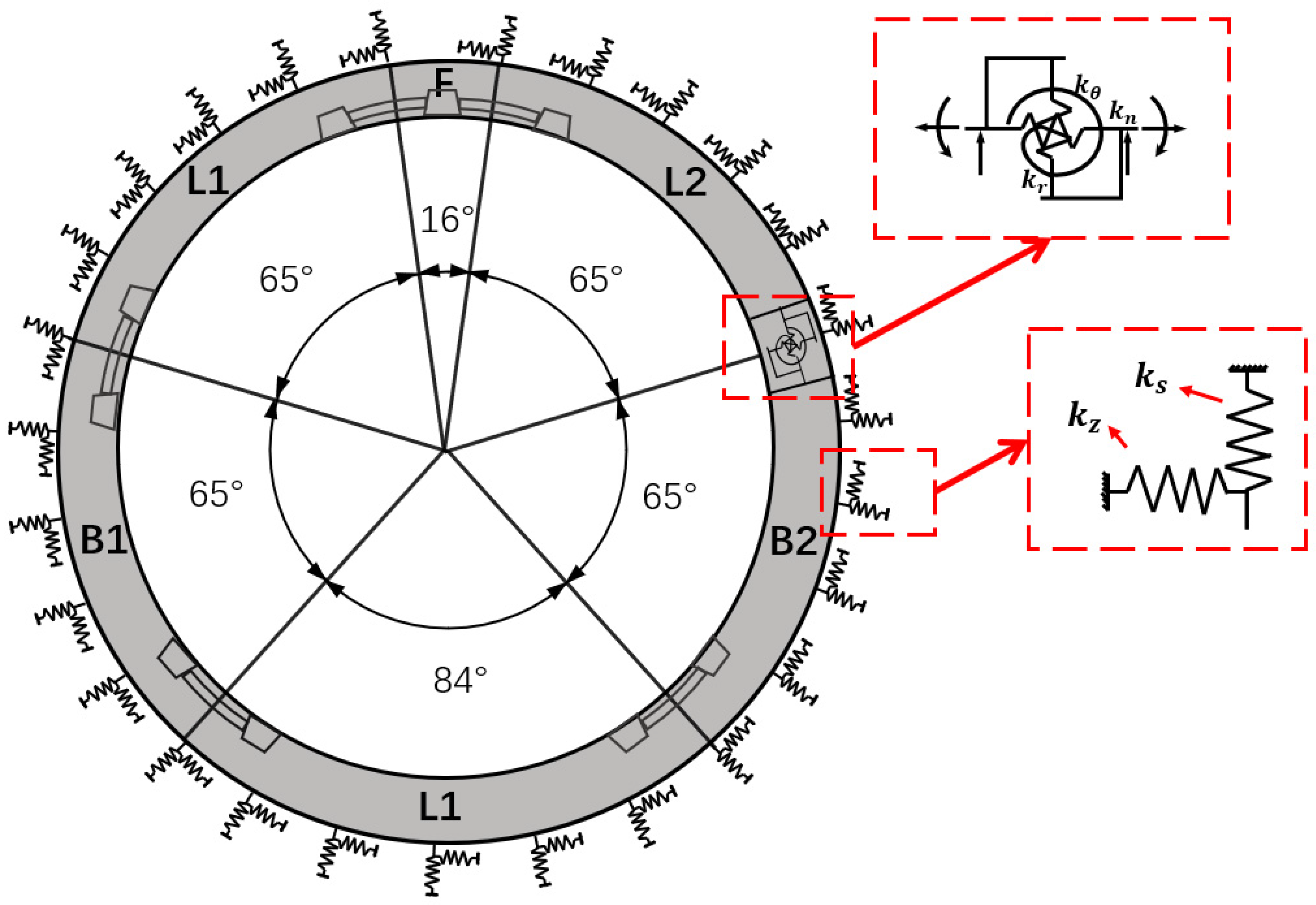
- Based on the Winkler method, radial ground contact springs and tangential ground contact springs are introduced to simulate the contact between the segment structure and the strata (see Figure 2);
- According to the mechanical properties of the soil, the tensile-compressive springs can only withstand compression but not tension, i.e., ;
- At the joints of the segments, three sets of mechanical springs with discontinuous deformations are used to simulate tensile-compressive springs (), shear springs (), and rotational springs (); it is assumed that the node displacements at the joint positions of adjacent segments are different in the calculation (see Figure 2); among them, the influence of tensile-compressive springs and shear springs on the internal forces and deformations of the structure is relatively small [23]; this paper only considers the influence of rotational springs on the structure, and sets the tensile-compressive springs and shear springs to relatively large values;
- In the calculation of the segment structure, we focus more on the bending behavior of the structure, ignoring shear deformations, and use the Euler–Bernoulli beam model to simulate the segment structure.
3. Subgrade Reaction Coefficient and Lateral Pressure Coefficient
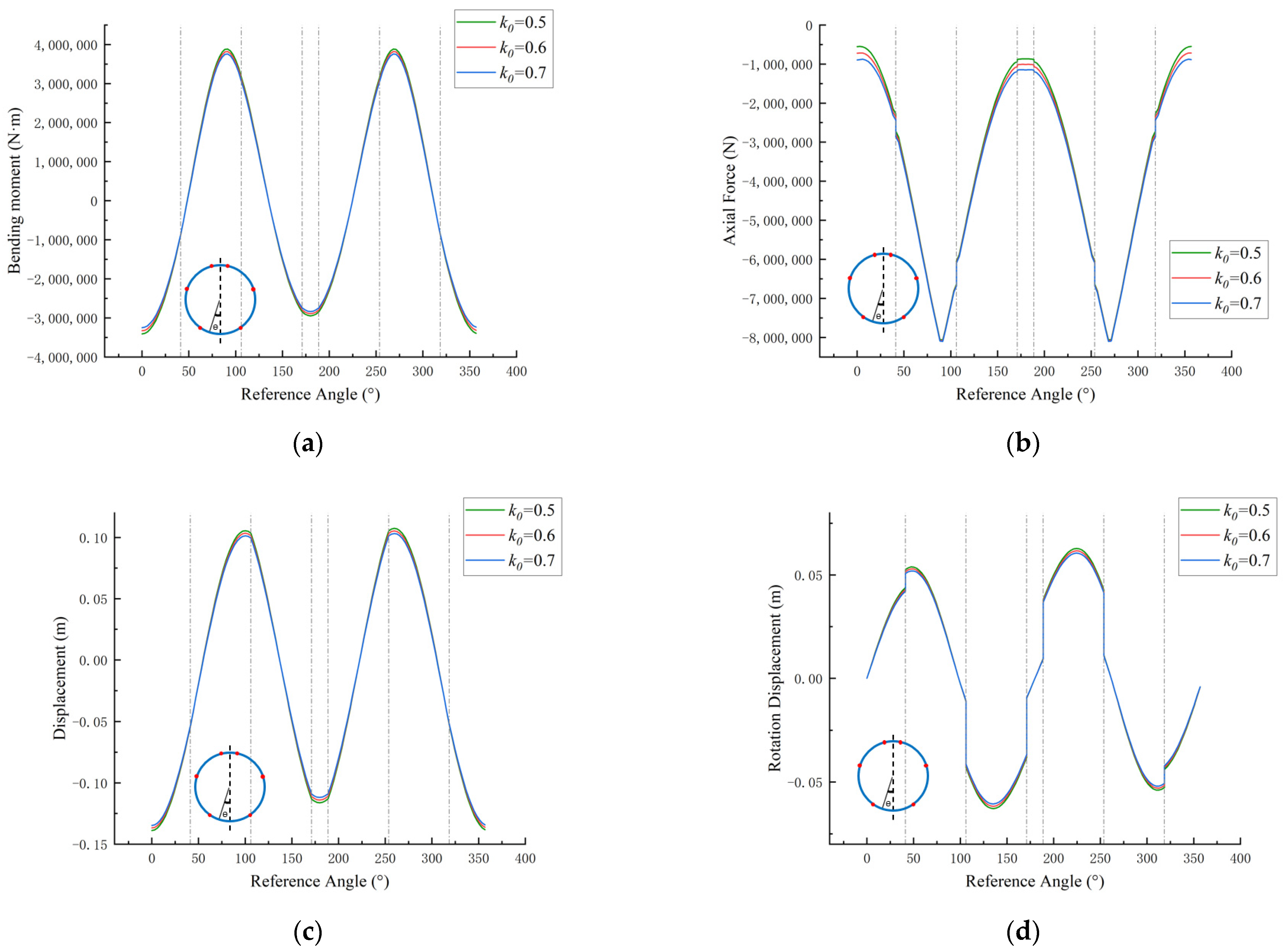
3.1. Subgrade Reaction Coefficient
3.2. Lateral Pressure Coefficient
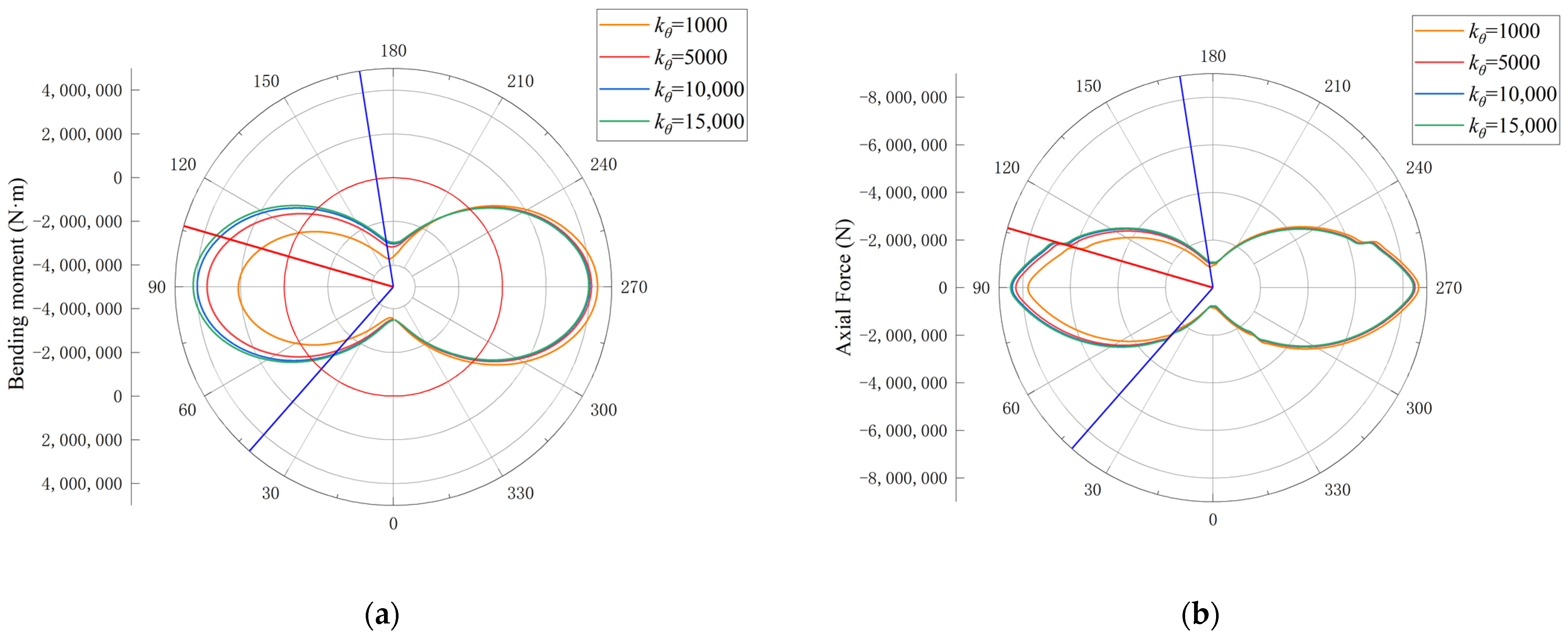
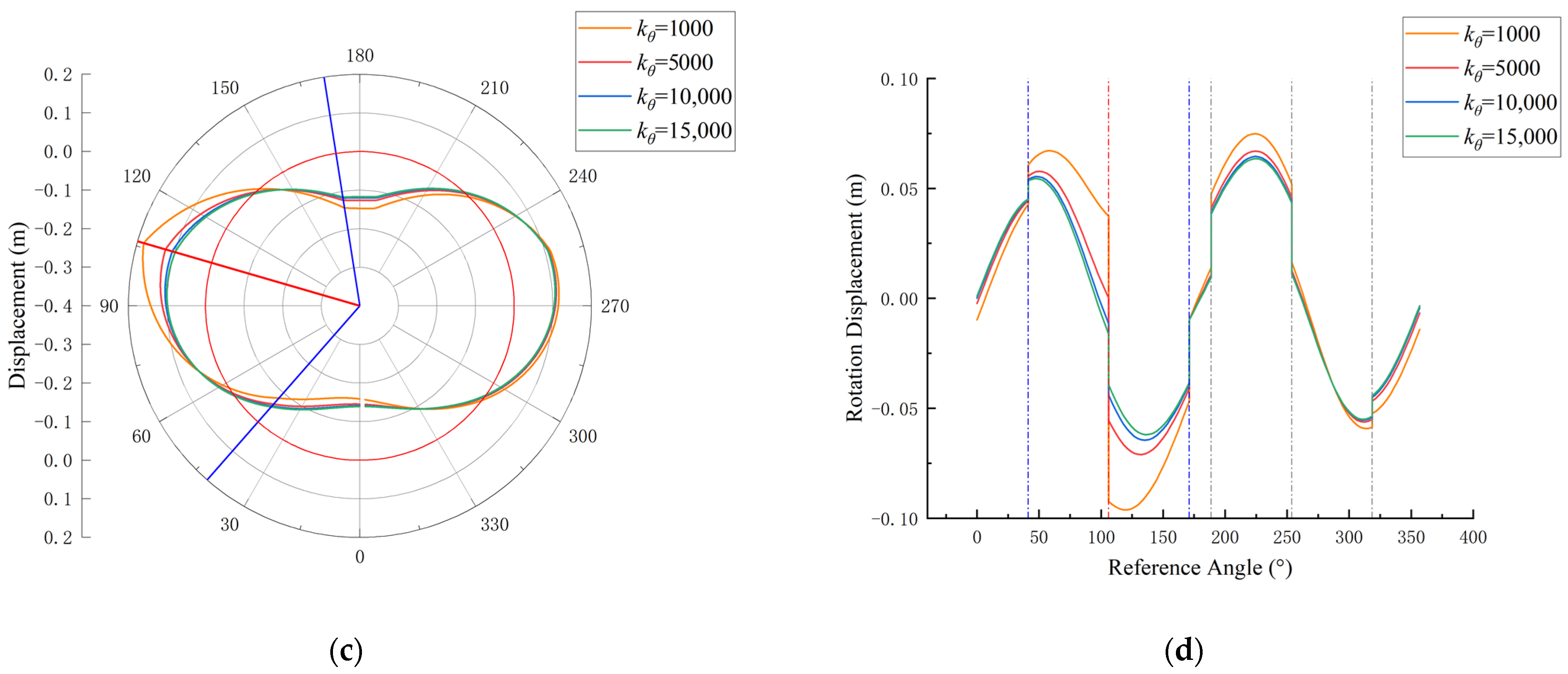
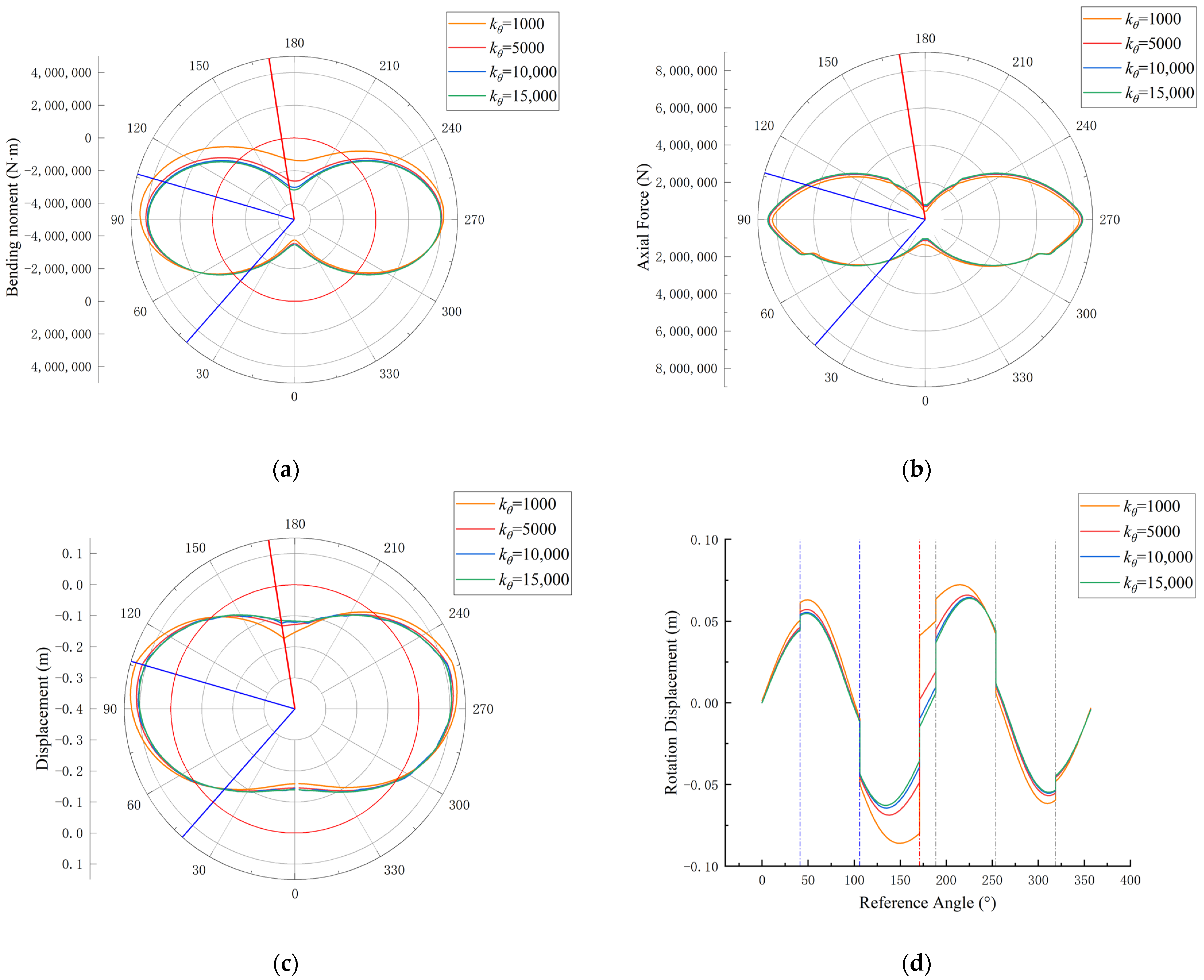
4. Analysis of Individual Joint Bending Stiffness
5. Conclusions
- (1)
- Based on the conditions of the soft soil layers in Shanghai, numerical simulation results show that the tunnel experiences negative bending moments at the crown and bottom, while positive bending moments occur along the sides. The axial force is negative, peaking at the tunnel sidewalls. Tunnel deformation takes on an elliptical shape. Additionally, under the influence of bending moments, joints exhibit angular distortion.
- (2)
- When the subgrade reaction coefficient decreases, the absolute values of bending moments, axial forces, and deformations at the tunnel crown and bottom generally increase. A discontinuity in axial forces occurs at the joints. The effectiveness of the model was verified by comparing the deformation of 3D laser scanning point cloud sections. When the foundation resistance coefficient is 5000 , the deformation is closer to the actual values, with the maximum error occurring at the left sidewall of the tunnel (6.5 mm), followed by the tunnel crown (3.1 mm). When the lateral pressure coefficient decreases, the absolute values of bending moments and deformations at the tunnel crown, bottom, and sidewalls generally increase, while the absolute values of axial forces at the top and bottom decrease.
- (3)
- The bending stiffness of individual joints of single-ring segments in soft soil layers was reduced. When the bending moment at the joint is negative, a decrease in joint bending stiffness leads to an increase in nearby bending moments, while a decrease in joint bending stiffness leads to a decrease in nearby bending moments when the bending moment at the joint is positive. As the bending stiffness decreases, the joint opening angle increases, affecting the entire ring through beam transfer. The extent and magnitude of this effect depend on the bending moment at the joint and the joint’s position, providing reference for the calculation of bending moments in traditional indirect methods for ring segments and joints.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Wang, F.; Shi, J.; Huang, H.; Zhang, D. Modified analytical solution of shield tunnel lining considering nonlinear bending stiffness of longitudinal joint. Tunn. Undergr. Space Technol. 2020, 106, 103625. [Google Scholar] [CrossRef]
- Moreno-Martinez, J.Y.; Galvan, A.; Pena, F.; Carpio, F. Practical Model Proposed for the Structural Analysis of Segmental Tunnels. Appl. Sci. 2020, 10, 8514. [Google Scholar] [CrossRef]
- Ngoc-Anh, D.; Dias, D.; Oreste, P.; Djeran-Maigre, I. Three-dimensional numerical simulation for mechanized tunnelling in soft ground: The influence of the joint pattern. Acta Geotech. 2014, 9, 673–694. [Google Scholar] [CrossRef]
- Wu, Y.; Ding, W.; Li, S.; Qiao, Y. Effect of oblique bolt arrangement on flexural behavior of segmental joint for shield tunnel. Tunn. Undergr. Space Technol. 2023, 135, 105043. [Google Scholar] [CrossRef]
- Zhong, X.; Zhu, W.; Huang, Z.; Han, Y. Effect of joint structure on joint stiffness for shield tunnel lining. Tunn. Undergr. Space Technol. 2006, 21, 407–408. [Google Scholar]
- Gong, C.; Ding, W.; Mosalam, K.M.; Gunay, S.; Soga, K. Comparison of the structural behavior of reinforced concrete and steel fiber reinforced concrete tunnel segmental joints. Tunn. Undergr. Space Technol. 2017, 68, 38–57. [Google Scholar] [CrossRef]
- Zhang, D.-M.; Zhang, B.-L.; Luo, T.-L.; Zhang, D.-M.; Li, B.-J. Full-scale testing and numerical modelling of segmental-joint performance with corroded bolt. Tunn. Undergr. Space Technol. 2022, 119, 104260. [Google Scholar] [CrossRef]
- Guo, W.; Feng, K.; Zhou, Y.; Yang, W.; Lu, X.; Xiao, M.; He, C. Full-scale test and numerical modeling on deformation and damage behavior of segmental joints under ultimate compression-bending load. Eng. Struct. 2023, 279, 115648. [Google Scholar] [CrossRef]
- Li, Z.; Yue, X.; Wu, G. Calculation and Analysis of Pipe Joint Settlement Control in Large Back Silting Immersed Tube Tunnel. Sustainability 2023, 15, 7446. [Google Scholar] [CrossRef]
- Oreste, P.P. A numerical approach to the hyperstatic reaction method for the dimensioning of tunnel supports. Tunn. Undergr. Space Technol. 2007, 22, 185–205. [Google Scholar] [CrossRef]
- Do, N.A.; Dias, D.; Oreste, P.; Djeran-Maigre, I. A new numerical approach to the hyperstatic reaction method for segmental tunnel linings. Int. J. Numer. Anal. Methods Geomech. 2014, 38, 1617–1632. [Google Scholar] [CrossRef]
- Do, N.A.; Dias, D.; Oreste, P.; Djeran-Maigre, I. 2D numerical investigation of segmental tunnel lining behavior. Tunn. Undergr. Space Technol. 2013, 37, 115–127. [Google Scholar] [CrossRef]
- Chen, Q.J.; Wang, J.C.; Huang, W.M.; Yang, Z.X.; Xu, R.Q. Analytical solution for a jointed shield tunnel lining reinforced by secondary linings. Int. J. Mech. Sci. 2020, 185, 105813. [Google Scholar] [CrossRef]
- Wang, J.; Huang, W.; Xu, R.; Yang, Z.; Xu, R. Analytical approach for circular-jointed shield tunnel lining based on the state space method. Int. J. Numer. Anal. Methods Geomech. 2020, 44, 575–595. [Google Scholar] [CrossRef]
- Chen, Z.P.; Wang, J.C.; Xu, R.Q.; Yang, Z.X.; Gong, X.N. Dynamic analysis of segmental linings of shield tunnels using a state space method and its application in physical test interpretation. Tunn. Undergr. Space Technol. 2023, 137, 105103. [Google Scholar] [CrossRef]
- Zhou, L.; Zhu, H.; Yan, Z.; Shen, Y.; Guan, L.; Wen, Z.; Li, Y. Experimental study on mechanical behaviors of segmental joints with ductile-iron joint panels for deep-buried shield tunnels bearing high inner water pressure. Tunn. Undergr. Space Technol. 2022, 127, 104590. [Google Scholar] [CrossRef]
- Huang, W.M.; Wang, J.C.; Yang, Z.X.; Xu, R.Q. Analytical model for segmental tunnel lining with nonlinear joints. Tunn. Undergr. Space Technol. 2021, 114, 103994. [Google Scholar] [CrossRef]
- Liu, X.; Liu, Y.; Jiang, Z.; Wang, J.; Mang, H.A. Numerical investigation of the mechanical behavior of segmental tunnel linings reinforced by a steel plate—Concrete composite structure. Eng. Struct. 2023, 276, 115350. [Google Scholar] [CrossRef]
- Zhang, D.M.; Phoon, K.K.; Hu, Q.F.; Huang, H.W. Nonlinear subgrade reaction solution for circular tunnel lining design based on mobilized strength of undrained clay. Can. Geotech. J. 2018, 55, 155–170. [Google Scholar] [CrossRef]
- Yuan, Q.; Liang, F.; Wang, R. Analytical approach for segmental tunnels considering nonlinear longitudinal joints in soft soils. Transp. Geotech. 2022, 36, 100807. [Google Scholar] [CrossRef]
- Sugimoto, M.; Chen, J.; Sramoon, A. Frame structure analysis model of tunnel lining using nonlinear ground reaction curve. Tunn. Undergr. Space Technol. 2019, 94, 103135. [Google Scholar] [CrossRef]
- Anh The, P.; Sugimoto, M. The Effects of Tangential Ground-Lining Interaction on Segmental Lining Behavior Using the Beam-Spring Model. Appl. Sci. 2020, 10, 1084. [Google Scholar] [CrossRef]
- Lee, K.M.; Hou, X.Y.; Ge, X.W.; Tang, Y. An analytical solution for a jointed shield-driven tunnel lining. Int. J. Numer. Anal. Methods Geomech. 2001, 25, 365–390. [Google Scholar] [CrossRef]
- Li, X.; Yan, Z.; Wang, Z.; Zhu, H. A progressive model to simulate the full mechanical behavior of concrete segmental lining longitudinal joints. Eng. Struct. 2015, 93, 97–113. [Google Scholar] [CrossRef]
- Zhai, W.; Zhang, D.; Huang, H.; Chapman, D. Numerical investigation into the composite behaviour of over-deformed segmental tunnel linings strengthened by bonding steel plates. Soils Found. 2023, 63, 101335. [Google Scholar] [CrossRef]
- Yuan, Q.; Liang, F.; Fang, Y. Numerical simulation and simplified analytical model for the longitudinal joint bending stiffness of a tunnel considering axial force. Struct. Concr. 2021, 22, 3368–3384. [Google Scholar] [CrossRef]
- Xu, X.; Wang, Z.; Shi, P.; Liu, W.; Tang, Q.; Bao, X.; Chen, X.; Yang, H. Intelligent monitoring and residual analysis of tunnel point cloud data based on free-form approximation. Mech. Adv. Mater. Struct. 2023, 30, 1703–1712. [Google Scholar] [CrossRef]
- Wang, Z.; Xu, X.; He, X.; Wei, X.; Yang, H. A Method for Convergent Deformation Analysis of a Shield Tunnel Incorporating B-Spline Fitting and ICP Alignment. Remote Sens. 2023, 15, 5112. [Google Scholar] [CrossRef]
- Wang, Z.; Shi, P.; Xu, X.; Xu, X.; Xie, F.; Yang, H. Automatic Identification and Intelligent Optimization of Tunnel-Free Curve Reconfiguration. Symmetry 2022, 14, 2505. [Google Scholar] [CrossRef]
- Arnau, O.; Molins, C. Experimental and analytical study of the structural response of segmental tunnel linings based on an in situ loading test. Part 2: Numerical simulation. Tunn. Undergr. Space Technol. 2011, 26, 778–788. [Google Scholar] [CrossRef]
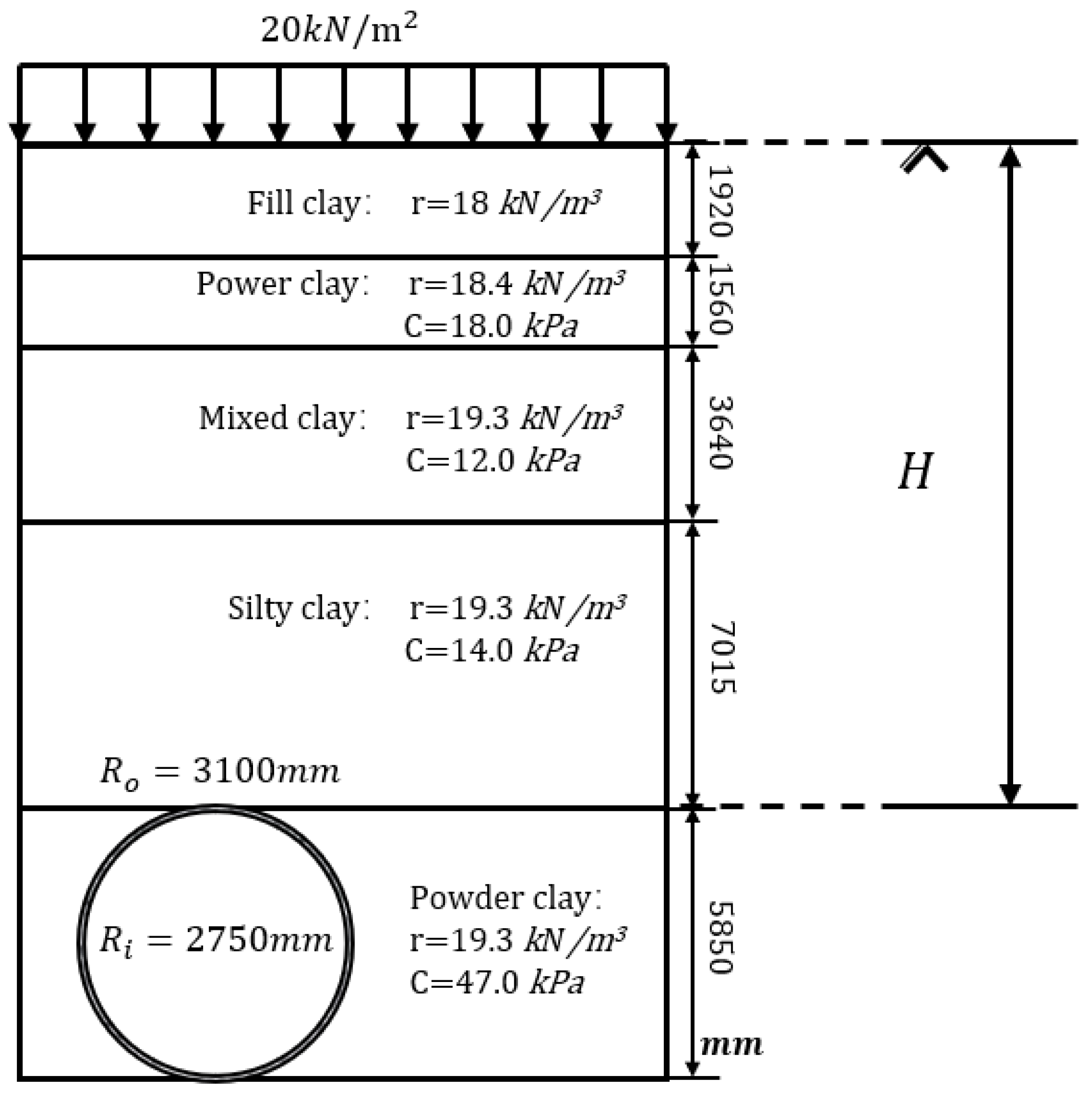


| Symbol | Properties | Unit | Value | |
|---|---|---|---|---|
| Material parameters of soil | Density of soil | 18 | ||
| Subgrade reaction coefficient(compression) | 3000~15,000 | |||
| Subgrade reaction coefficient(tension) | 0 | |||
| Coefficient of lateral pressure | 0.5~0.7 | |||
| of soil | 0.35 | |||
| Young’s modulus of soil | 1.68 × 104 | |||
| Embedded depth | 14 |
| Parameter Classification | Symbol | Properties | Unit | Value |
|---|---|---|---|---|
| Geometrical parameters of tunnel lining | Radius | 2.925 | ||
| Width | 1 | |||
| Thickness | 0.35 | |||
| Material parameters of tunnel lining | Density of segment | 2.5 | ||
| Young’s modulus of segment | 3.45 × 107 | |||
| Poisson’s ratio of segment | / | 0.2 | ||
| Stiffness parameters of soil spring | Radial | 450 | ||
| Tangential | 150 | |||
| Stiffness parameters of joints | Compress spring | 1 × 107 | ||
| Shear spring | 1 × 1010 | |||
| Moment spring | 1.54 × 105 | |||
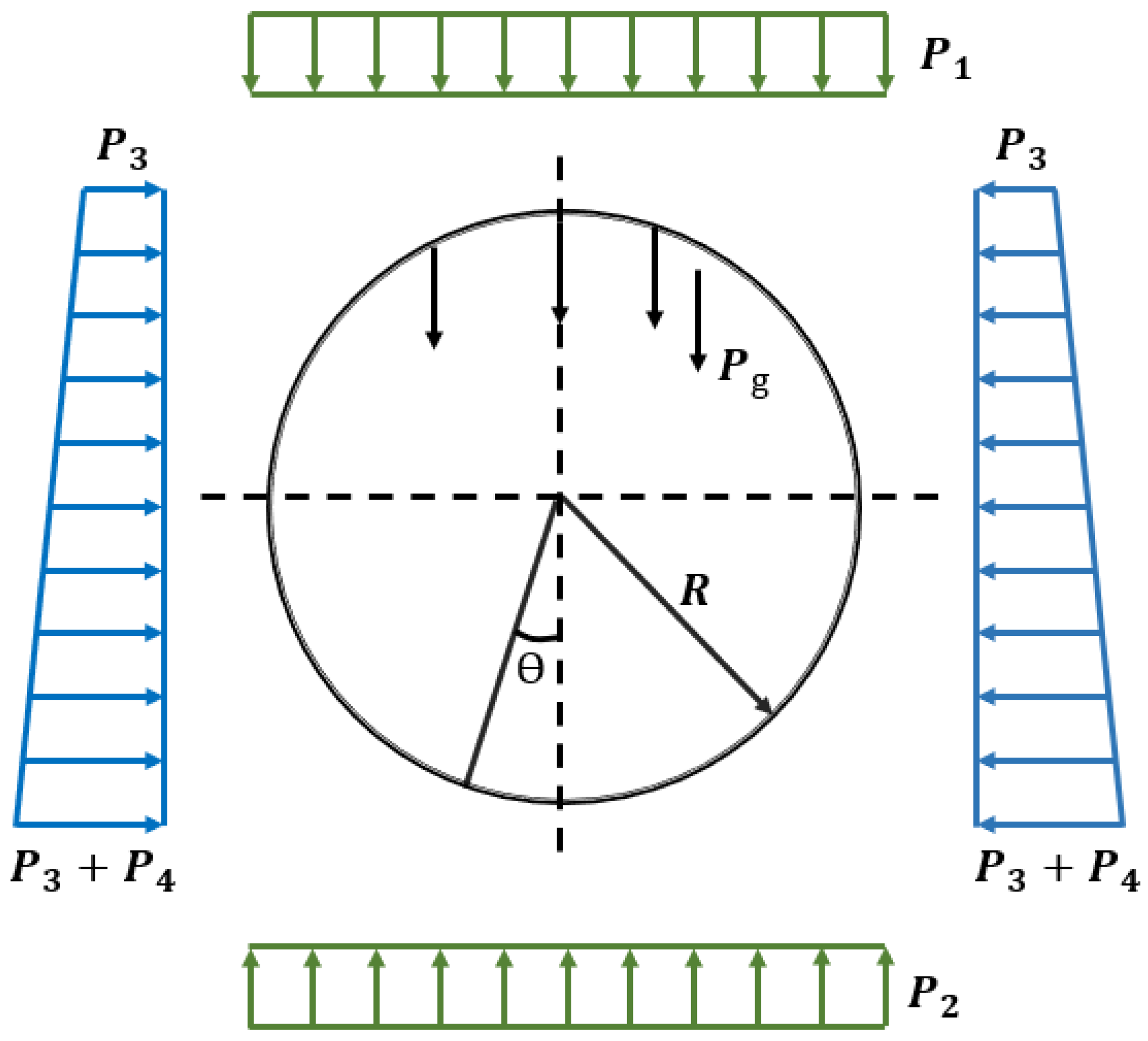
| Load | ground overload | 20 | ||
| Self weight of the tunnel lining | 317 | |||
| Vertical overburden earth pressure at the tunnel crown | 270 | |||
| Vertical overburden earth pressure at the tunnel invert | 317 | |||
| Lateral earth pressure at the tunnel crown | 175 | |||
| Additional earth pressure at the tunnel invert | 245 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
He, X.; Xu, X.; Yang, H. Numerical Simulation Study Considering Discontinuous Longitudinal Joints in Soft Soil under Symmetric Loading. Symmetry 2024, 16, 650. https://doi.org/10.3390/sym16060650
He X, Xu X, Yang H. Numerical Simulation Study Considering Discontinuous Longitudinal Joints in Soft Soil under Symmetric Loading. Symmetry. 2024; 16(6):650. https://doi.org/10.3390/sym16060650
Chicago/Turabian StyleHe, Xianwei, Xiangyang Xu, and Hao Yang. 2024. "Numerical Simulation Study Considering Discontinuous Longitudinal Joints in Soft Soil under Symmetric Loading" Symmetry 16, no. 6: 650. https://doi.org/10.3390/sym16060650
APA StyleHe, X., Xu, X., & Yang, H. (2024). Numerical Simulation Study Considering Discontinuous Longitudinal Joints in Soft Soil under Symmetric Loading. Symmetry, 16(6), 650. https://doi.org/10.3390/sym16060650






