Abstract
This paper introduces the concept of proper 2-dominating sets in graphs, providing a comprehensive characterisation of graphs that possess such sets. We give the necessary and sufficient conditions for a graph to have a proper 2-dominating set. Graphs with proper dominating sets can have a symmetric structure. Moreover, we estimate the bounds of the proper 2-domination number in the graphs with respect to the 2-domination and 3-domination numbers. We show that the cardinality of -set is greater by one at most than the cardinality of -set.
1. Introduction and Preliminary Results
In general, we use the standard notation of graph theory; see [1]. We consider simple, undirected, connected graphs , where denotes the set of vertices and the set of edges of the graph. The order of a graph refers to the number of its vertices, and its size corresponds to the number of its edges. We say that a vertex is a neighbour of a vertex in a graph G if there is an edge . The set of all neighbours of is called a neighbourhood of the vertex x and is denoted by . We also denote . Generally for , the vertices of that are adjacent to the vertices of U are called neighbours of U and their set is denoted by . By we mean the degree of the vertex x in G. A vertex of degree one is called a leaf, every neighbour of a leaf is called a support vertex. If a support vertex is adjacent to at least two leaves, it is said to be a strong support vertex and a weak support vertex otherwise. For a graph G, by we mean the set of support vertices of G and by the set of leaves of G.
We use , , , , and to denote a path, a cycle, a complete graph, a bipartite graph, and an edgeless graph, respectively.
A subset is called a dominating set of graph G if every vertex outside this set has at least one neighbour in the set B. The parameter denotes the cardinality of the smallest dominating set in graph G. Similarly, a subset is an independent set of graph G if any two vertices in the set I are not adjacent to each other. An empty set and a set containing only one vertex are also independent. An independent set that is not a proper subset of any other independent set is called a maximal independent set. The independence number of a graph G, denoted by , is the maximal size of an independent set in G.
1.1. Background
The idea of domination appears in chessboard problems described in 1862 by De Jaenisch [2] and it was formalised by C. Berge [3] and then by O. Ore [4] in 1962 who was the first who used the terms dominating set and dominating number. In 1977, the survey of E.J. Cockayne and S.T. Hedetniemi [5] collected results related to domination and also used the notation as the domination number. Since then, much has been written about dominating sets and dominating numbers. Over the following decades, the theory of domination was extended, and a huge development of this theory is still being observed. Dominating sets are studied not only from a purely theoretical point of view, but also interesting applications are considered. A review of the literature shows that dominating sets and domination parameters can be found in different fields, ranging from health care technology, through peer-to-peer messaging, location problems, and robotics, to crisis management and air/land/naval defence; see [6]. For these reasons, the concept of dominating sets and their variants is relevant in modern graph theory. Dominating sets combined with the property of independence as an additional restriction can be used to model some mathematical objects, winning strategies in certain games played on graphs, or optimal sets of decisions. In the literature, we can find a number of variants and generalisations of dominating sets in graphs. In [7], more than 70 types of dominating sets and domination parameters were described and new types of dominating sets still appear.
The study of dominating sets has also led to various specialised types of dominating sets, either by introducing additional restrictions or by generalising the classical domination concept. Some of these types are described in [7,8,9]. F. Harary and T.W. Haynes in [10,11] introduced double domination, which generalises domination in graphs, and more generally, the concept of k-tuple domination, which has been studied in [12,13] too. Let k be a positive integer. The subset is said to be a k-tuple dominating set if for every vertex . The parameter is equal to the minimum cardinality of a k-tuple dominating in the graph G. For , the k-tuple domination coincides with the double domination, which was also studied by M. Blidia, M. Chellali, and T.W. Haynes [14,15,16]. A set is a double dominating set of G if each vertex is dominated by at least two vertices in S. D.W. Bange, A.E. Barkauskas, and P.J. Slater [17], and F. Harary and T.W. Haynes [10] defined and studied the concept of an efficient doubly dominating set. M. Chellali, A. Khelladi, and F. Maffray also considered these sets in [18], but they referred to them as exact doubly dominating sets. A set is an exact dominating set of G if each vertex is dominated by exactly two vertices of S.
1.2. Definitions of Multiply Domination and Proper 2-Domination
Another of the extensively researched types of dominating sets is the concept of multiple dominating sets, which was introduced by J.M. Fink and M.S. Jacobson in [19]. For any integer , a subset is referred to as a p-dominating set if every vertex outside of S has at least p neighbours within S. For , the p-dominating set coincides with the classical dominating set. When , we obtain the concept of 2-dominating sets, which has been studied in [20,21]. The parameter represents the cardinality of the smallest p-dominating set in the graph G. We say that vertex is called exactly p-dominated if .
As we mentioned, 2-dominating sets are intensively studied. However, for the literature survey shows that p-dominating sets are not a very popular topic. This follows from the fact that large p vertices not belonging to p-dominating sets must have large degrees, and this restriction limits classes of graphs with nontrivial (i.e., different from ) p-dominating sets. Furthermore, a set is termed a kernel if it is both independent and dominating. The concept of kernels in graph theory originated in the field of digraphs and was introduced by J. von Neumann and O. Morgerstern in the context of game theory [22]. Over the years, this topic has been extensively studied for various purposes, including list coloring, perfectness, and location problems. C. Berge, a renowned mathematician, made significant contributions to the study of kernels in digraphs and applied them to solve various mathematical problems [23,24]. Numerous variants and generalisations of kernels have been proposed in the literature, with works such as [23,24,25,26,27] exploring different aspects of this concept. For example, if we consider a set that is both independent and 2-dominating, we obtain a 2-dominating kernel. The concept of a 2-dominating kernel ((2-d)-kernel in short) was introduced by A. Włoch (see [28]) and was intensively studied over the following years; see [29,30,31,32,33]. In 2020, T. Haynes, S.T. Hedetniemi, and M.A. Henning in [8] included a section written by A. Hansberg and L. Volkman that collected and classified results related to multiply domination. Contributing to this research, in this paper, we study a special subclass of 2-dominating sets.
From the definition of a p-dominating set, it follows that for any graph G, . By definition, any p-dominating set is also a k-dominating set for . Thus, any 3-dominating set is also a 2-dominating set. Therefore, it is interesting to study 2-dominating sets that are not 3-dominating. This motivates the introduction of proper 2-dominating sets. The idea of defining proper dominating sets of some types appeared, for example, in [34,35], in relation to secondary domination.
Definition 1.
A subset is called a proper 2-dominating set if it is a 2-dominating set but not a 3-dominating set.
In other words, is a proper 2-dominating set if there exists a vertex outside the set D that has exactly two neighbours within the set D. Since the set is 3-dominating, it is not a proper 2-dominating set. To simplify the notation, we will write -dset to denote a proper 2-dominating set and by the cardinality of the smallest -dset.
For any graph G, we have the inequality:
Directly from the Definition 1, we obtain the following lemma:
Lemma 1.
Let be an integer. Every vertex of degree belongs to a -dominating set for .
The -dsets can be applied to a wide range of practical problems, such as crisis management. Let us consider a particular inhabited area where a plan should be developed to provide the inhabitants in the event of a critical situation, for example related to damage to critical infrastructure. It is important that each resident has access to help and that this access is further secured in the event of further damage. From the point of view of optimising the problem, it is preferable to plan location points so that the number of distribution points is minimal and that each resident has direct access to at least two of these points in the event of problems at one of the points. By modelling the situation with a graph, the solution to this problem of the location of such points is to find the minimum 2-dominating set of graphs. In turn, the minimum -dsets determine the weakest places where direct access to only two points is possible.
2. Main Results
As mentioned above, a graph does not always have a -dset; as an example, we can consider a path or the star (see Figure 1). In this section, we give a complete characterisation of graphs that have a -dset.

Figure 1.
Graphs and do not have a -dset.
Theorem 1.
A connected graph G of order has a -dset D if and only if there exists a vertex v such that:
- 1.
- , or
- 2.
- and .
Proof.
Let G be a graph with a -dset D. Let us assume, by contradiction, that every vertex and or .
If , then according to Lemma 1, it belongs to set D. Now, if , it must have at least three neighbours in D. Since D is a -dset, there exists a vertex in the set that has at most two neighbours in D, which is a contradiction.
In contrast, let us consider the following cases.
- 1.
- Let us assume that v is a strong support vertex with exactly two leaves in its neighbourhood, and . Let , and , where:
- (i)
- such that ;
- (ii)
- such that ;
- (iii)
- such that .
Let us consider the following cases:- (a)
- .Let be the vertex with the smallest degree in the graph . Note that each vertex of has a degree of at least two, otherwise contains a leaf, which contradicts the assumption that v has exactly two leaves in its neighbourhood. Then, the set where is a -dset and the vertex is exactly 2-dominated.
- (b)
- and .Then, the set is a -dset and each vertex of is exactly 2-dominated.
- (c)
- , , and .Then, the set is a -dset and the vertex v is exactly 2-dominated.
- (d)
- , , and .Then, , the set is a -dset, and the vertex v is exactly 2-dominated by .
- 2.
- Let us assume that v is a weak support vertex with one leaf in its neighbourhood. Let and , where sets , are the same as in case 1. Let us consider the cases:
- (a)
- .Similarly as in case 1(a), let be a vertex with the smallest degree in the graph . Note that every vertex in the set has a degree of at least two. Otherwise, we obtain a contradiction to the assumption that the vertex v has exactly one leaf in its neighbourhood. Then the set , where , is a -dset and the vertex is exactly 2-dominated.
- (b)
- and .Then, the set is a -dset and each vertex of is exactly 2-dominated.
- (c)
- , , and .Let . Then, the set is a -dset and the vertex v is exactly 2-dominated.
- (d)
- , , and .Then, the graph has an order two and does not have a -dset.
- 3.
- Let us assume that . Let and , where sets , are the same as in case 1. Let us consider the cases:
- (a)
- .Similarly as in case 1(a), let be a vertex with the smallest degree in the graph . Note that every vertex in the set has a degree of at least two in G. Otherwise, we obtain a contradiction with the assumption that v is neither a leaf nor a support vertex. Then the set , where , is a -dset and the vertex is exactly 2-dominated.
- (b)
- and .Then, the set is a -dset and each vertex of is exactly 2-dominated.
- (c)
- , , and .Then, the set is a -dset, where the vertices . The existence of at least two such vertices is guaranteed by the assumption that v is neither a leaf nor a support vertex. Furthermore, the vertex v is exactly 2-dominated.
- (d)
- , , and .Then, the graph has an order one and does not have a -dset. □
Now, we give another complete characterisation of graphs that have a -dset using a generalised corona of graphs.
Definition 2.
The generalised corona of a graph G and the sequence is the graph such that and
If in the above definition, for , then we obtain the definition of a corona of two graphs G and H introduced by R. Frucht and F. Harary in [36].
Theorem 2.
Let H be a graph. The graph G has a -dset if and only if , , .
Proof.
The proof is analogous to the proof of Theorem 1. □
Figure 2 shows the corona . By Lemma 1, every leaf belongs to a 2-dominating set. The set is not the -dset because every vertex that is not a leaf is at least 3-dominated. Moreover, since is not -dset, then this graph does not have a -dset.
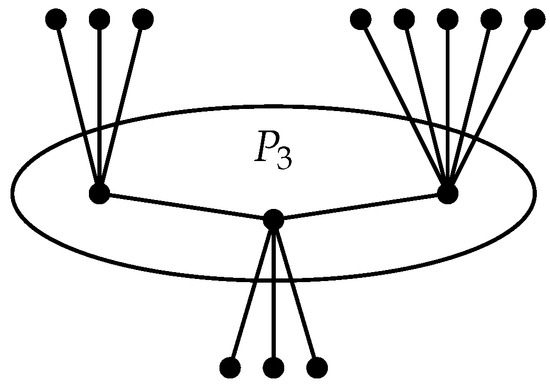
Figure 2.
The graph .
Moreover, from the above theorems we see that the graph G does not have a -dset if and only if every vertex is a support vertex and has at least three leaves in its neighbourhood or x is a leaf itself. Therefore, we immediately obtain the following corollaries.
Corollary 1.
If , then G has a -dset.
Corollary 2.
If a graph G has a vertex v such that , then G has a -dset.
From the above corollaries, we can obtain characterisations of well-known graph products with -dset, such as the Cartesian product, the tensor product, and the strong product. These graph products can be found in the literature under various names. To avoid confusion, we recall necessary definitions.
Let us recall the definitions of some graph products. Let G and H be two disjoint graphs.
Definition 3.
The Cartesian product of two graphs G and H is the graph such that and .
Definition 4.
The tensor product of the graphs G and H is the graph such that and . The tensor product is also called a direct product or a categorical product.
Definition 5.
The strong product of the graphs G and H is the graph such that and .
Some other properties of these products are studied in [37,38,39]. Note that these graph products have a symmetric structure.
Moreover, graph products play an important role in studying different properties and invariants in graphs. To describe classes of graphs with a given property it is easier to study graphs whose structure can be characterised in terms of smaller and simpler graphs, so many existing results come from the study of products of graphs. Operations on graphs also allow us to build families of graphs with a -dset.
The following results specify when the Cartesian product, the tensor product, and the strong product have a -dset.
Theorem 3.
If G and H are nontrivial connected graphs, then the graph has a -dset.
Proof.
In the Cartesian product of two graphs , we have . Since the graphs G and H are nontrivial by Corollary 1, the graph has a -dset. □
Theorem 4.
If G and H are connected graphs of order and , then the graph has a -dset.
Proof.
Since in the tensor product of two graphs , we have and and by Corollary 1, the graph has a -dset. □
Theorem 5.
If G and H are nontrivial connected graphs, then the graph has a -dset.
Proof.
Since for two nontrivial connected graphs, the graph has a -dset. □
Now we will show relations between and . The relationships between parameters of domination are one of the main directions of research in the theory of domination. Bounds for domination parameters can often be expressed in terms of other graph invariants. This means that they can be easily computed.
Theorem 6.
Let G be a connected graph with a -dset. If , then .
Proof.
If , it means that every -set of G is not a -set. In other words, there is a vertex of the -set that is not 3-dominated. Thus, every -set is also a -set. Therefore, , which completes the proof. □
The converse implication is not true. That is, the equality does not necessarily imply that . Consider the tree T from Figure 3. Then, and these parameters are realised by the set . Moreover, the smallest 3-dominating set is the set , so .
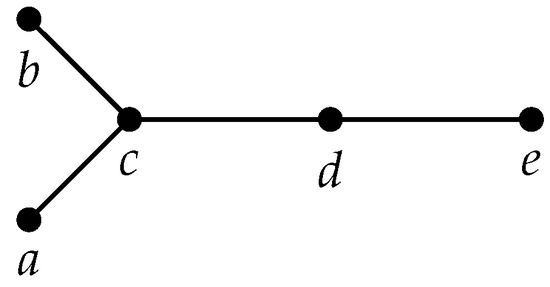
Figure 3.
Graph T.
Theorem 7.
Let G be a connected graph of order , which has a -dset and let . If there exists a -set in the graph G that is not independent, then .
Proof.
Assume that G is a graph such that . Let D be a -set that is not independent. If there exists a vertex that is exactly 2-dominated, then D is a -set. Otherwise, every vertex is 3-dominated. Since D is not independent, there exist two adjacent vertices . Let . The existence of this vertex is guaranteed because G has at least three vertices. Then, or or . Without loss of generality, assume that . We will show that z does not belong to the set D. If , then the set is also a 2-dominating set, contradicting the assumption that D is a -set. This means that . As D is a 3-dominating set, every vertex is 3-dominated. Now, consider the set . Then, the vertex x has exactly two neighbours in the set , and every vertex is dominated by at least two vertices of . This implies that is a -set, which completes the proof. □
From the above theorem, we obtain the following corollary.
Corollary 3.
Let G be a connected graph of order , which has a -dset and let . If then every -set in the graph G is independent.
Theorem 8.
If G is a connected graph of order , which has a -dset, then
Proof.
The left inequality follows directly from the definition of a -dset. We will demonstrate that adding one vertex to the -set is sufficient to obtain a -dset. Therefore, we have the case where and all -sets are independent, and we let D be an arbitrary -set. Thus, there exists a vertex that is not a leaf. Otherwise, we would have a graph without a -dset, which is a contradiction. Every -set is independent. Otherwise, if there is a -set that is not independent, then it is also a -set. This is a contradiction to the assumption that every -set is independent. Since the -set is independent, . Furthermore, each neighbour of x is dominated by at least 3 vertices. As x is not a leaf, it has at least two neighbours, denoted as y and z. We form the set . Thus, every neighbour of x is dominated by at least two vertices of . Hence x is exactly 2-dominated by y and z. The set is a -dset, and , which concludes the proof. □
The following corollary presents the proper 2-domination number in standard classes of graphs. In each of these classes, the equality holds.
Corollary 4.
Let be integers. Then,
- (i)
- ;
- (ii)
- ;
- (iii)
- ;
- (iv)
To illustrate the example of graph where the equality is met, let us consider the tree T such that and . Then, and these parameters are realised by the set . Moreover, the set is -dset and .
Now, we will show that in trees the value of the 2-proper domination number is related to the existence of a (2-d)-kernel. In [20,40], the following theorems have been proved.
Theorem 9.
([20]). For a tree T the following are equivalent:
- 1.
- .
- 2.
- T has a unique -set that also is a unique -set.
Theorem 10.
([40]). A tree T has a --kernel if and only if .
From the two aforementioned theorems it follows that a tree T has a (2-d)-kernel if and only if it possesses exactly one minimal 2-dominating set. This leads to the final result.
Theorem 11.
Let T be a tree of order n, , which has a -dset. Then,
Proof.
Let T be a tree, which has a -dset. By Theorem 2 we obtain , , , where is an arbitrary tree of order n, . By Theorems 9 and 10 it follows that a tree T has (2-d)-kernel if and only if there exists a unique smallest 2-dominating set, which is also a maximum independent set. Let us consider the following cases:
- 1.
- A tree T has (2-d)-kernel J. Let us consider the following subcases.
- (a)
- If the set J is also 3-dominating, then there exists a vertex x that is not a leaf. This means that x has at least two neighbours identified as and . We create the set . Consequently, each neighbour of x is dominated by a minimum of two vertices of . Moreover, x is exactly 2-dominated by and . The set is a -dset, and . Hence .
- (b)
- If the set J is not 3-dominating, then there exists a vertex , which is exactly 2-dominated. Thus, J is also a -dset. Therefore, .
- 2.
- A tree T does not have (2-d)-kernel. Let us consider the following subcases:
- (a)
- If , then by Theorem 6 it follows that .
- (b)
- If , then by Theorem 9 every -set of a tree T is not independent. By Theorem 7 we obtain .
This completes the proof. □
3. Conclusions
In this paper, we introduced and thoroughly investigated the concept of proper 2-dominating sets in graphs, providing a comprehensive characterisation of graphs that possess such sets. Our main focus was to establish necessary and sufficient conditions for the existence of proper 2-dominating sets and to estimate bounds for the proper 2-domination number concerning 2-dominating and 3-dominating numbers.
Our main results, obtained in Theorems 1 and 2, provide a clear understanding of the structural properties of graphs with proper 2-dominating sets. The corollaries derived from these theorems further extend our insight into specific graph classes, such as paths, cycles, complete graphs, and various graph products. Note that Theorems 3–5 show the application of our findings in well-known graph products, showing the existence of proper 2-dominating sets in these products.
In the last part of the article presented in Theorem 8, we showed relations between numbers and . We have proved that the cardinality of -set is greater by one at most than the cardinality of -set. However, the classes of graphs such that are still unknown. In the above, we indicated only one example of such a graph.
Moreover, since we have not found any counterexamples to the statements below, we finish the paper with the following conjectures.
Conjecture 1.
If the graph G has no leaves, then .
Conjecture 2.
If , then the graph has a unique independent -set.
Author Contributions
Both authors contributed equally to this work. Conceptualization, P.B. and M.P.; methodology, P.B. and M.P.; validation, P.B. and M.P.; formal analysis, P.B. and M.P.; writing—original draft preparation, P.B. and M.P.; writing—review and editing, P.B. and M.P. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
No new data were created or analyzed in this study. Data sharing is not applicable to this article.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Diestel, R. Graph Theory; Springer: New York, NY, USA, 2005. [Google Scholar]
- De Jaenish, C.F. Traite des Applications de l’Analyse Mathematique au jeu des Echecs; Academie Imperialedes Sciences: St. Petersburg, Russia, 1862. [Google Scholar]
- Berge, C. Theory of Graphs and Its Applications; Methuen: London, UK, 1962. [Google Scholar]
- Ore, O. Theory of Graphs. Am. Math. Soc. Transl. 1962, 38, 206–212. [Google Scholar]
- Cockayne, E.J.; Hedetniemi, S.T. Towards a theory of domination in graphs. Networks 1977, 7, 247–261. [Google Scholar] [CrossRef]
- Raczek, J. Complexity Issues on of Secondary Domination Number. Algorithmica 2023. [Google Scholar] [CrossRef]
- Haynes, T.W.; Hedetniemi, S.; Slater, P. Fundamentals of Domination in Graphs; CRC Press: Boca Raton, FL, USA, 1998. [Google Scholar]
- Haynes, T.W.; Hedetniemi, S.T.; Henning, M.A. Topics in Domination in Graphs; Springer: Cham, Switzerland, 2020. [Google Scholar]
- Haynes, T.W.; Hedetniemi, S.T.; Slater, P.J. Domination in Graphs; Advanced Topics; Marcel Dekker: New York, NY, USA, 1998. [Google Scholar]
- Harary, F.; Haynes, T.W. Double domination in graphs. Ars Combin. 2000, 55, 201–213. [Google Scholar]
- Harary, F.; Haynes, T.W. Nordhaus-Gaddum inequalities for domination in graphs. Discret. Math. 1996, 155, 99–105. [Google Scholar] [CrossRef]
- Martínez, A.C. A note on the k-tuple domination number of graphs. Ars Math. Contemp. 2022, 22, 1–5. [Google Scholar]
- Martínez, A.C. Some new results on the k-tuple domination number of graphs. RAIRO-Oper. Res. 2022, 56, 3491–3497. [Google Scholar] [CrossRef]
- Blidia, M.; Chellali, M.; Haynes, T.W. Characterizations of trees with equal paired and double domination numbers. Discret. Math. 2006, 306, 1840–1845. [Google Scholar] [CrossRef]
- Blidia, M.; Chellali, M.; Haynes, T.W.; Henning, M. Independent and double domination in trees. Util. Math. 2006, 70, 159–173. [Google Scholar]
- Chellali, M.; Haynes, T.W. On paired and double domination in graphs. Util. Math. 2005, 67, 161–171. [Google Scholar]
- Bange, D.W.; Barkauskas, A.E.; Slater, P.J. Efficient dominating sets in graphs. In Applications of Discrete Mathematics; Ringeisen, R.D., Roberts, F.S., Eds.; SIA: Philadelphia, PA, USA, 1988; pp. 189–199. [Google Scholar]
- Chellali, M.; Khelladi, A.; Maffray, F. Exact double domination in graphs. Discuss. Math. Graph Theory 2005, 25, 291–302. [Google Scholar] [CrossRef][Green Version]
- Fink, J.F.; Jacobson, M.S. n-domination in graphs. In Graph Theory with Applications to Algorithms and Computer Science; John Wiley & Sons, Inc.: New York, NY, USA, 1985; pp. 283–300. [Google Scholar]
- Blidia, M.; Chellali, M.; Favaron, O. Independence and 2-domination in trees. Australas. J. Combin. 2005, 33, 317–327. [Google Scholar]
- Chellali, M. Bounds on the 2-domination number in cactus graphs. Opusc. Math. 2006, 26, 5–12. [Google Scholar]
- Morgenstern, O.; Von Neumann, J. Theory of Games and Economic Behavior; Princeton University Press: Princeton, NJ, USA, 1944. [Google Scholar]
- Berge, C. Graphs and Hypergraphs; North-Holland Pub. Co.: Amsterdam, The Netherland, 1973. [Google Scholar]
- Berge, C.; Duchet, P. Perfect graphs and kernels. Bull. Inst. Math. Acad. Sin. 1988, 16, 263–274. [Google Scholar]
- Bai, Y.; Fujita, S.; Zhang, S. Kernels by properly colored paths in arc-colored digraphs. Discret. Math. 2018, 341, 1523–1533. [Google Scholar] [CrossRef]
- de la Maza, S.G.H.; Hernández-Cruz, C. On the complexity of the k-kernel problem on cyclically k-partite digraphs. Theoret. Comput. Sci. 2019, 795, 9–19. [Google Scholar] [CrossRef]
- Włoch, I. On kernels by monochromatic paths in the corona of digraphs. Open Math. 2008, 6, 537–542. [Google Scholar] [CrossRef]
- Włoch, A. On 2-dominating kernels in graphs. Australas. J. Combin. 2012, 53, 273–284. [Google Scholar]
- Bednarz, P. On (2-d)-kernels in the tensor product of graphs. Symmetry 2021, 13, 230. [Google Scholar] [CrossRef]
- Bednarz, P.; Hernández-Cruz, C.; Włoch, I. On the existence and the number of (2-d)-kernels in graphs. Ars Combin. 2015, 121, 341–351. [Google Scholar]
- Bednarz, P.; Paja, N. On (2-d)-kernels in two generalizations of the Petersen graph. Symmetry 2021, 13, 1948. [Google Scholar] [CrossRef]
- Bednarz, P.; Włoch, I. An algorithm determining (2-d)-kernels in trees. Util. Math. 2017, 102, 215–222. [Google Scholar]
- Bednarz, P.; Włoch, I. On (2-d)-kernels in the cartesian product of graphs. Ann. Univ. Mariae-Curie-Skłodowska Sect. A–Math. 2016, 70, 1–8. [Google Scholar] [CrossRef]
- Kosiorowska, A.; Michalski, A.; Włoch, I. On minimum intersections of certain secondary dominating sets in graphs. Opusc. Math. 2023, 43, 813–827. [Google Scholar] [CrossRef]
- Michalski, A.; Włoch, I.; Dettlaff, M.; Lemańska, M. On proper (1,2)-dominating sets in graphs. Math. Methods Appl. Sci. 2022, 45, 7050–7057. [Google Scholar] [CrossRef]
- Frucht, R.; Harary, F. On the corona of two graphs. Aequationes Math. 1970, 4, 322–325. [Google Scholar] [CrossRef]
- Imrich, W.; Klavzar, S.; Rall, D.F. Topics in Graph Theory: Graphs and Their Cartesian Product; A.K. Peters Ltd.: Wellesley, MA, USA, 2008. [Google Scholar]
- Weichsel, P.M. The Kronecker product of graphs. Proc. Am. Math. Soc. 1962, 13, 47–52. [Google Scholar] [CrossRef]
- Hammack, R.; Imrich, W.; Klavzar, S. Handbook of Product Graphs, 2nd ed.; CRC Press, Inc.: Boca Raton, FL, USA, 2011. [Google Scholar]
- Bednarz, P. Relations between the existence of a (2-d)-kernel and parameters γ2(G), α(G). Indian J. Math. 2022, 64, 93–107. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).