g.ridge: An R Package for Generalized Ridge Regression for Sparse and High-Dimensional Linear Models
Abstract
1. Introduction
2. Ridge Regression and Generalized Ridge Regression
2.1. Linear Regression
2.2. Ridge Regression
2.3. Generalized Ridge Regression
2.4. Significance Test
3. R Package: g.ridge
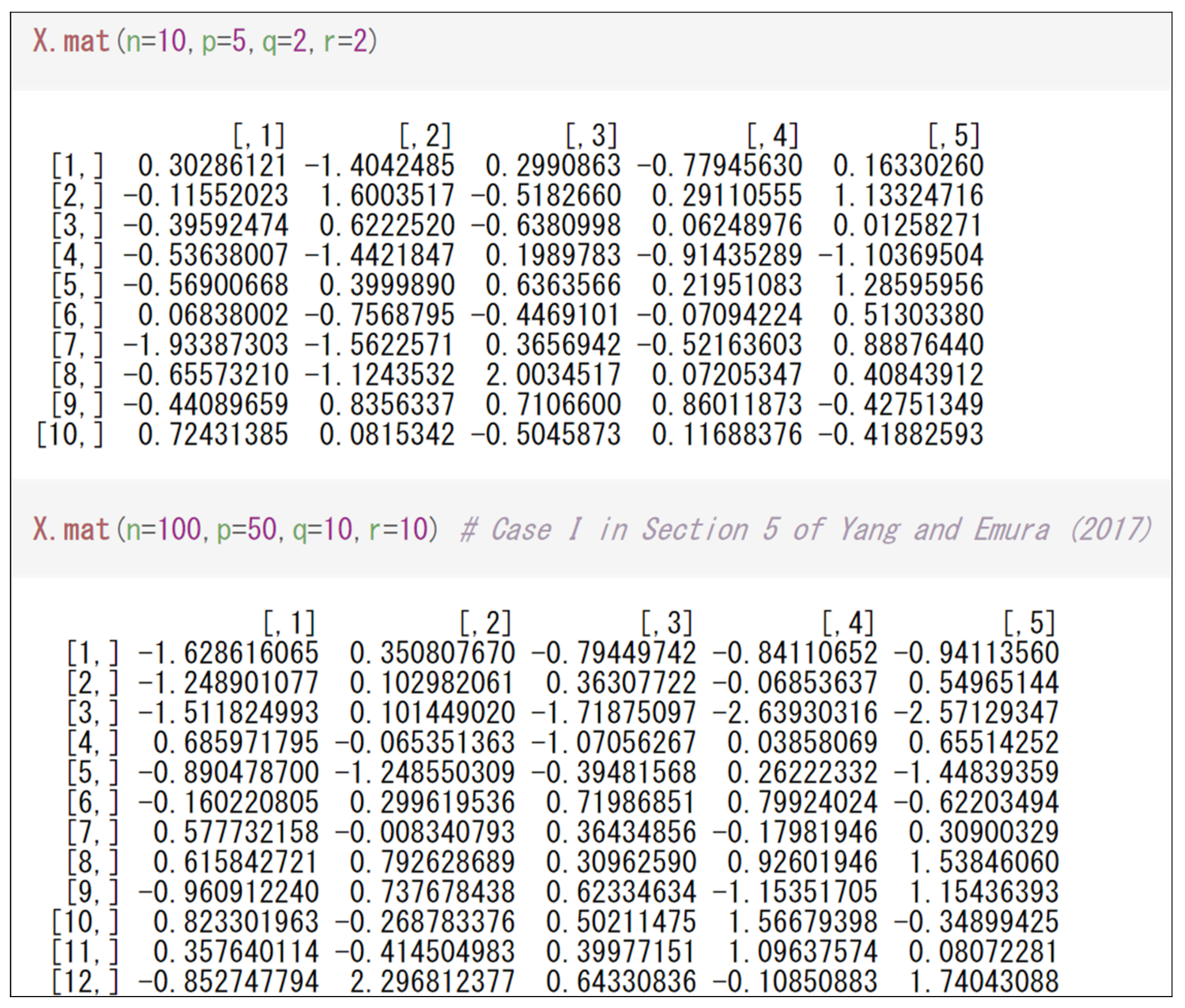
3.1. Generating Data
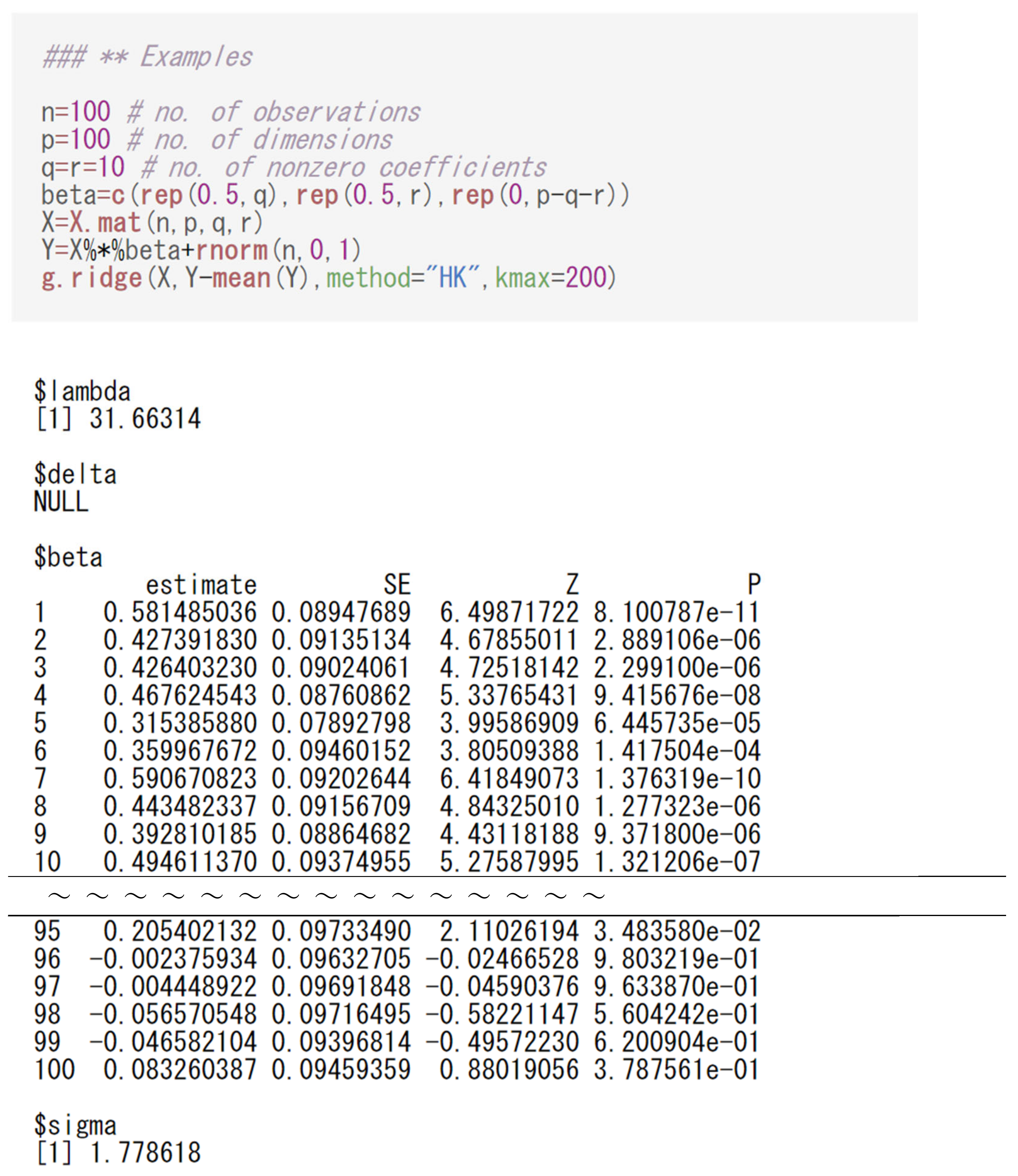
3.2. Performing Regression
3.3. Technical Remarks on Centering and Standardization
4. Simulations
4.1. Simulation Settings
4.2. Simulation Results
5. Data Analysis
6. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
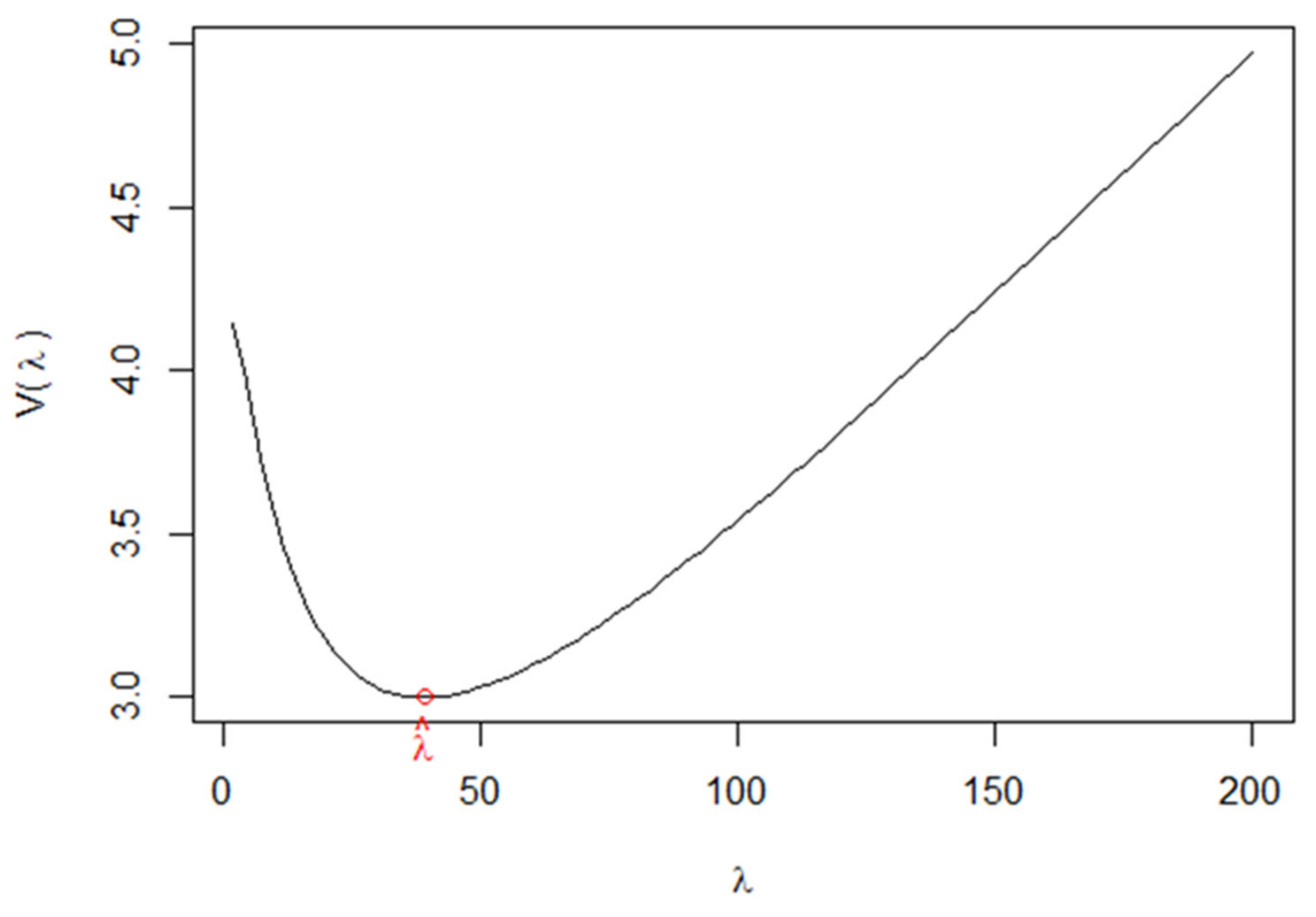
Appendix A. GCV Function
References
- Hoerl, A.E.; Kennard, R.W. Ridge regression: Biased estimation for nonorthogonal problems. Technometrics 1970, 12, 55–67. [Google Scholar] [CrossRef]
- Montgomery, D.C.; Peck, E.A.; Vining, G.G. Introduction to Linear Regression Analysis; John Wiley & Sons: Hoboken, NJ, USA, 2021. [Google Scholar]
- Arashi, M.; Roozbeh, M.; Hamzah, N.A.; Gasparini, M. Ridge regression and its applications in genetic studies. PLoS ONE 2021, 16, e0245376. [Google Scholar] [CrossRef] [PubMed]
- Veerman, J.R.; Leday, G.G.R.; van de Wiel, M.A. Estimation of variance components, heritability and the ridge penalty in high-dimensional generalized linear models. Commun. Stat. Simul. Comput. 2019, 51, 116–134. [Google Scholar] [CrossRef]
- Friedrich, S.; Groll, A.; Ickstadt, K.; Kneib, T.; Pauly, M.; Rahnenführer, J.; Friede, T. Regularization approaches in clinical biostatistics: A review of methods and their applications. Stat. Methods Med. Res. 2023, 32, 425–440. [Google Scholar] [CrossRef]
- Gao, S.; Zhu, G.; Bialkowski, A.; Zhou, X. Stroke Localization Using Multiple Ridge Regression Predictors Based on Electromagnetic Signals. Mathematics 2023, 11, 464. [Google Scholar] [CrossRef]
- Hernandez, J.; Lobos, G.A.; Matus, I.; Del Pozo, A.; Silva, P.; Galleguillos, M. Using Ridge Regression Models to Estimate Grain Yield from Field Spectral Data in Bread Wheat (Triticum Aestivum L.) Grown under Three Water Regimes. Remote Sens. 2015, 7, 2109–2126. [Google Scholar] [CrossRef]
- Golub, G.H.; Heath, M.; Wahba, G. Generalized cross-validation as a method for choosing a good ridge parameter. Technometrics 1979, 21, 215–223. [Google Scholar] [CrossRef]
- Hastie, T.; Tibshirani, R.; Friedman, J. The Elements of Statistical Learning; Springer: New York, NY, USA, 2009. [Google Scholar]
- Van Wieringen, W.N. Lecture notes on ridge regression. arXiv 2015, arXiv:1509.09169. [Google Scholar]
- Saleh, A.M.E.; Arashi, M.; Kibria, B.G. Theory of Ridge Regression Estimation with Applications; John Wiley & Sons: Hoboken, NJ, USA, 2019. [Google Scholar]
- Cule, E.; Vineis, P.; De Iorio, M. Significance testing in ridge regression for genetic data. BMC Bioinform. 2011, 12, 372. [Google Scholar] [CrossRef]
- Whittaker, J.C.; Thompson, R.; Denham, M.C. Marker-assisted selection using ridge regression. Genet. Res. 2000, 75, 249–252. [Google Scholar] [CrossRef]
- Cule, E.; De Iorio, M. Ridge regression in prediction problems: Automatic choice of the ridge parameter. Genet. Epidemiol. 2013, 37, 704–714. [Google Scholar] [CrossRef]
- Yang, S.-P.; Emura, T. A Bayesian approach with generalized ridge estimation for high-dimensional regression and testing. Commun. Stat. Simul. Comput. 2016, 46, 6083–6105. [Google Scholar] [CrossRef]
- Hoerl, A.E.; Kennard, R.W. Ridge regression: Applications to nonorthogonal problems. Technometrics 1970, 12, 69–82. [Google Scholar] [CrossRef]
- Allen, D.M. The relationship between variable selection and data augmentation and a method for prediction. Technometrics 1974, 16, 125–127. [Google Scholar] [CrossRef]
- Loesgen, K.H. A generalization and Bayesian interpretation of ridge-type estimators with good prior means. Stat. Pap. 1990, 31, 147–154. [Google Scholar] [CrossRef]
- Shen, X.; Alam, M.; Fikse, F.; Rönnegård, L. A novel generalized ridge regression method for quantitative genetics. Genetics 2013, 193, 1255–1268. [Google Scholar] [CrossRef] [PubMed]
- Hofheinz, N.; Frisch, M. Heteroscedastic ridge regression approaches for genome-wide prediction with a focus on computational efficiency and accurate effect estimation. G3 Genes Genomes Genet. 2014, 4, 539–546. [Google Scholar] [CrossRef] [PubMed]
- Yüzbaşı, B.; Arashi, M.; Ahmed, S.E. Shrinkage Estimation Strategies in Generalised Ridge Regression Models: Low/High-Dimension Regime. Int. Stat. Rev. 2020, 88, 229–251. [Google Scholar] [CrossRef]
- Saleh, E.A.M.; Kibria, G.B.M. Performance of some new preliminary test ridge regression estimators and their properties. Commun. Stat. Theory Methods 1993, 22, 2747–2764. [Google Scholar] [CrossRef]
- Norouzirad, M.; Arashi, M. Preliminary test and Stein-type shrinkage ridge estimators in robust regression. Stat. Pap. 2017, 60, 1849–1882. [Google Scholar] [CrossRef]
- Shih, J.-H.; Lin, T.-Y.; Jimichi, M.; Emura, T. Robust ridge M-estimators with pretest and Stein-rule shrinkage for an intercept term. Jpn. J. Stat. Data Sci. 2020, 4, 107–150. [Google Scholar] [CrossRef]
- Shih, J.-H.; Konno, Y.; Chang, Y.-T.; Emura, T. A class of general pretest estimators for the univariate normal mean. Commun. Stat. Theory Methods 2023, 52, 2538–2561. [Google Scholar] [CrossRef]
- Taketomi, N.; Chang, Y.-T.; Konno, Y.; Mori, M.; Emura, T. Confidence interval for normal means in meta-analysis based on a pretest estimator. Jpn. J. Stat. Data Sci. 2023, 1–32. [Google Scholar] [CrossRef]
- Wong, K.Y.; Chiu, S.N. An iterative approach to minimize the mean squared error in ridge regression. Comput. Stat. 2015, 30, 625–639. [Google Scholar] [CrossRef]
- Kibria, B.M.G.; Banik, S. Some ridge regression estimators and their performances. J. Mod. Appl. Stat. Methods 2016, 15, 206–238. [Google Scholar] [CrossRef]
- Algamal, Z.Y. Shrinkage parameter selection via modified cross-validation approach for ridge regression model. Commun. Stat. Simul. Comput. 2020, 49, 1922–1930. [Google Scholar] [CrossRef]
- Assaf, A.G.; Tsionas, M.; Tasiopoulos, A. Diagnosing and correcting the effects of multicollinearity: Bayesian implications of ridge regression. Tour. Manag. 2018, 71, 1–8. [Google Scholar] [CrossRef]
- Michimae, H.; Emura, T. Bayesian ridge estimators based on copula-based joint prior distributions for regression coefficients. Comput. Stat. 2022, 37, 2741–2769. [Google Scholar] [CrossRef]
- Chen, A.-C.; Emura, T. A modified Liu-type estimator with an intercept term under mixture experiments. Commun. Stat. Theory Methods 2016, 46, 6645–6667. [Google Scholar] [CrossRef]
- Binder, H.; Allignol, A.; Schumacher, M.; Beyersmann, J. Boosting for high-dimensional time-to-event data with competing risks. Bioinformatics 2009, 25, 890–896. [Google Scholar] [CrossRef]
- Emura, T.; Chen, Y.-H.; Chen, H.-Y. Survival prediction based on compound covariate under cox proportional hazard models. PLoS ONE 2012, 7, e47627. [Google Scholar] [CrossRef]
- Emura, T.; Chen, Y.-H. Gene selection for survival data under dependent censoring: A copula-based approach. Stat. Methods Med. Res. 2016, 25, 2840–2857. [Google Scholar] [CrossRef] [PubMed]
- Emura, T.; Hsu, W.-C.; Chou, W.-C. A survival tree based on stabilized score tests for high-dimensional covariates. J. Appl. Stat. 2023, 50, 264–290. [Google Scholar] [CrossRef] [PubMed]
- Azzalini, A.; Capitanio, A. The Skew-Normal and Related Families; Cambridge University Press (CUP): Cambridge, UK, 2013; ISBN 9781107029279. [Google Scholar]
- Wang, D.; Wang, J.; Li, Z.; Gu, H.; Yang, K.; Zhao, X.; Wang, Y. C-reaction protein and the severity of intracerebral hemorrhage: A study from chinese stroke center alliance. Neurol. Res. 2021, 44, 285–290. [Google Scholar] [CrossRef] [PubMed]
- Chu, H.; Huang, C.; Dong, J.; Yang, X.; Xiang, J.; Dong, Q.; Tang, Y. Lactate dehydrogenase predicts early hematoma expansion and poor outcomes in intracerebral hemorrhage patients. Transl. Stroke Res. 2019, 10, 620–629. [Google Scholar] [CrossRef] [PubMed]
- Kim, S.Y.; Lee, J.W. Ensemble clustering method based on the resampling similarity measure for gene expression data. Stat. Methods Med. Res. 2007, 16, 539–564. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Q.; Ma, S.; Huang, Y. Promote sign consistency in the joint estimation of precision matrices. Comput. Stat. Data Anal. 2021, 159, 107210. [Google Scholar] [CrossRef]
- Bhattacharjee, A. Big Data Analytics in Oncology with R; Taylor & Francis: London, UK, 2022. [Google Scholar]
- Bhatnagar, S.R.; Lu, T.; Lovato, A.; Olds, D.L.; Kobor, M.S.; Meaney, M.J.; O’Donnell, K.; Yang, A.Y.; Greenwood, C.M. A sparse additive model for high-dimensional interactions with an exposure variable. Comput. Stat. Data Anal. 2023, 179, 107624. [Google Scholar] [CrossRef]
- Vishwakarma, G.K.; Thomas, A.; Bhattacharjee, A. A weight function method for selection of proteins to predict an outcome using protein expression data. J. Comput. Appl. Math. 2021, 391, 113465. [Google Scholar] [CrossRef]
- Abe, T.; Shimizu, K.; Kuuluvainen, T.; Aakala, T. Sine-skewed axial distributions with an application for fallen tree data. Environ. Ecol. Stat. 2012, 19, 295–307. [Google Scholar] [CrossRef]
- Huynh, U.; Pal, N.; Nguyen, M. Regression model under skew-normal error with applications in predicting groundwater arsenic level in the Mekong Delta Region. Environ. Ecol. Stat. 2021, 28, 323–353. [Google Scholar] [CrossRef]
- Yoshiba, T.; Koike, T.; Kato, S. On a Measure of Tail Asymmetry for the Bivariate Skew-Normal Copula. Symmetry 2023, 15, 1410. [Google Scholar] [CrossRef]
- Jimichi, M.; Kawasaki, Y.; Miyamoto, D.; Saka, C.; Nagata, S. Statistical Modeling of Financial Data with Skew-Symmetric Error Distributions. Symmetry 2023, 15, 1772. [Google Scholar] [CrossRef]
- Muhammad, I.U.; Aslam, M.; Altaf, S. lmridge: A Comprehensive R Package for Ridge Regression. R J. 2019, 10, 326. [Google Scholar] [CrossRef]
- Meijer, R.J.; Goeman, J.J. Efficient approximate k-fold and leave-one-out cross-validation for ridge regression. Biom. J. 2013, 55, 141–155. [Google Scholar] [CrossRef]



| Error Distribution | Regression Coefficients | (i) ridge | (ii) g-ridge | (iii) glmnet | |
|---|---|---|---|---|---|
| Normal | (I) | 50 | 0.463 | 0.385 | 0.306 |
| 100 | 0.950 | 0.682 | 2.182 | ||
| 150 | 1.146 | 0.658 | 1.996 | ||
| 200 | 1.520 | 0.920 | 2.199 | ||
| (II) | 50 | 0.855 | 0.681 | 0.545 | |
| 100 | 2.151 | 1.562 | 8.688 | ||
| 150 | 3.008 | 1.482 | 7.904 | ||
| 200 | 4.929 | 2.687 | 8.691 | ||
| (III) and | 50 | 0.602 | 0.539 | 0.388 | |
| 100 | 0.990 | 0.628 | 2.025 | ||
| 150 | 1.219 | 0.703 | 2.132 | ||
| 200 | 1.589 | 0.953 | 2.226 | ||
| (IV) and | 50 | 1.541 | 1.290 | 0.737 | |
| 100 | 2.398 | 1.580 | 8.046 | ||
| 150 | 3.231 | 1.614 | 8.434 | ||
| 200 | 4.651 | 2.770 | 8.804 | ||
| Skew-normal | (I) | 50 | 0.440 | 0.361 | 0.294 |
| 100 | 0.957 | 0.670 | 2.182 | ||
| 150 | 1.162 | 0.678 | 2.000 | ||
| 200 | 1.500 | 0.910 | 2.197 | ||
| (II) | 50 | 0.821 | 0.655 | 0.527 | |
| 100 | 2.285 | 1.705 | 8.691 | ||
| 150 | 3.021 | 1.509 | 7.905 | ||
| 200 | 4.883 | 2.673 | 8.686 | ||
| (III) and | 50 | 0.576 | 0.519 | 0.376 | |
| 100 | 0.974 | 0.622 | 2.029 | ||
| 150 | 1.233 | 0.721 | 2.137 | ||
| 200 | 1.582 | 0.949 | 2.243 | ||
| (IV) and | 50 | 1.504 | 1.273 | 0.720 | |
| 100 | 2.449 | 1.508 | 8.054 | ||
| 150 | 3.224 | 1.616 | 8.453 | ||
| 200 | 4.618 | 2.731 | 8.860 |
| Ridge | Generalized Ridge | |||||
|---|---|---|---|---|---|---|
| SE | p-Value | SE | p-Value | |||
| Lactate dehydrogenase | 0.122 | 0.047 | 0.008 | 0.145 | 0.055 | 0.008 |
| Gamma-GT | 0.116 | 0.048 | 0.016 | 0.143 | 0.056 | 0.010 |
| Respiratory rate | −0.120 | 0.052 | 0.020 | −0.140 | 0.059 | 0.018 |
| Prothrombin time | 0.077 | 0.036 | 0.031 | 0.083 | 0.040 | 0.038 |
| Blood platelet count | −0.100 | 0.049 | 0.040 | −0.114 | 0.056 | 0.044 |
| C-reactive protein | None | None | >0.05 | 0.112 | 0.057 | 0.049 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Emura, T.; Matsumoto, K.; Uozumi, R.; Michimae, H. g.ridge: An R Package for Generalized Ridge Regression for Sparse and High-Dimensional Linear Models. Symmetry 2024, 16, 223. https://doi.org/10.3390/sym16020223
Emura T, Matsumoto K, Uozumi R, Michimae H. g.ridge: An R Package for Generalized Ridge Regression for Sparse and High-Dimensional Linear Models. Symmetry. 2024; 16(2):223. https://doi.org/10.3390/sym16020223
Chicago/Turabian StyleEmura, Takeshi, Koutarou Matsumoto, Ryuji Uozumi, and Hirofumi Michimae. 2024. "g.ridge: An R Package for Generalized Ridge Regression for Sparse and High-Dimensional Linear Models" Symmetry 16, no. 2: 223. https://doi.org/10.3390/sym16020223
APA StyleEmura, T., Matsumoto, K., Uozumi, R., & Michimae, H. (2024). g.ridge: An R Package for Generalized Ridge Regression for Sparse and High-Dimensional Linear Models. Symmetry, 16(2), 223. https://doi.org/10.3390/sym16020223







