Abstract
The saturation properties of symmetric and asymmetric nuclear matter have been computed using the finite range simple effective interaction with Yukawa form factor. The results of higher-order derivatives of the energy per particle and the symmetry energy computed at saturation, namely, , , , , are compared with the corresponding values extracted from studies involving theory, experiment and astrophysical observations. The overall uncertainty in the values of these quantities, which results from a wide spectrum of studies described in earlier literature, lies in the ranges MeV, MeV, MeV and MeV, respectively. The ability of the equations of state computed with this simple effective interaction in predicting the threshold mass for prompt collapse in binary neutron star merger and gravitational redshift has been examined in terms of the compactness of the neutron star and the incompressibility at the central density of the maximum mass star. The correlations existing between neutron star properties and the nuclear matter saturation properties have been analyzed and compared with the predictions of other model calculations.
1. Introduction
The empirical properties of infinite nuclear matter (NM) at saturation are key features in the study of any phenomenon resulting from the nucleon–nucleon (NN) interactions in a many-body system. Ideally, the solution to the many-body problem with the NN interaction would be the way to determine the NM properties. But in the absence of comprehensive knowledge of NN interaction, microscopic many-body models, such as Dirac-Brueckner-Hartree-Fock (DBHF) and its non relativistic counterpart BHF [1,2,3,4,5,6,7,8,9], variational methods [10,11], chiral effective field theory [12,13], etc., use realistic potentials whose parameters are fitted to phase shift data in different partial wave channels and properties of few-body systems (deuteron and triton). The inadequacy of our understanding of the in-medium NN interaction is reflected by the fact that in the aforementioned many-body calculations, the saturation density of symmetric nuclear matter (SNM) is over-predicted. This could be brought within the empirical range by incorporating the three-body and higher-order many-body effects in an ad hoc phenomenological manner. The consensus range for the value of saturation density has been estimated from studies of various kinds, which include different variants of the liquid drop model, optical model of NN scattering, muonic atoms, and Hartree–Fock (HF) calculations of nuclear density distributions [14]. The values of energy per nucleon at saturation density have been extracted to be ∼−16 MeV from the mass analysis over the periodic table.
An alternate method, adopted in contrast to the microscopic realistic calculations to handle the many-body problem, is to use phenomenological effective interactions. Though less fundamental compared to the microscopic calculations, its ability in the analytical calculations of nuclear properties makes it highly popular. Skyrme [15], Gogny [16], and M3Y effective forces [17] are some of those successful forces. The basic idea to build up these interactions is to parameterize the effects of the microscopic NN interaction upon averaging over the spin, parity and isospin of the interacting nucleons and constrain the parameters from the ground state properties of finite nuclei and nuclear matter. A drawback of this approach is that the parameter set is not unique, and higher-order nuclear matter properties at saturation cannot be unambiguously predicted. Moreover, many parameters of the effective force become strongly correlated in the course of their fixation. Of late, another effective force, the so-called finite range simple effective interaction (SEI) [18], which has a similar predicting ability as that of Skyrme and Gogny in the NM and finite nuclei domain, has been established. The parameter fitting protocol adopted in the case of SEI makes it different from other effective forces, minimizing the correlation effects. The SEI parameters are systematically fitted in SNM and pure neutron matter (PNM), which allows the study of both SNM and asymmetric nuclear matter (ANM). Moreover, the parameters responsible for the momentum dependence of the mean-field are fixed from the experimental/empirical constraints exclusively so that each of the two aspects of the mean-field, the density dependence and the momentum dependence, could be studied independently without altering the predictions of the other one [19]. Further, in the determination of nine parameter combinations of the eleven SEI parameters required for the study of ANM, one is required to assume only three standard values of saturation properties, namely, , and symmetry energy . Within this parameter fixation protocol, we shall use the SEI to compute higher-order derivatives of the energy per particle and the symmetry energy at saturation density and compare these values with the results extracted from various different studies. The stability conditions, in terms of Landau parameters of the interacting Fermi liquid model, serve as an acid test for the reliability of an effective force for its applicability in the different channels of spin and isospin. We shall check to which extent the observance of the Landau stability conditions is fulfilled by our SEI.
In Section 2, we have given a brief account of SEI and its parameter-fitting protocol. In Section 3, we have obtained different properties of SNM at saturation, which are re-evaluated in the framework of the interacting Fermi liquid model by computing the Landau parameters using SEI. In the same section, the high-order derivatives of the energy per particle and the symmetry energy are calculated and compared with the empirical range of values extracted from theory, experiment and astrophysical observations. In Section 4, we explore the predictive power of the SEI EoSs in the domain of high-density neutron-rich matter pertaining to the recent NS phenomenology associated with the binary neutron star merger (BNSM) and gravitational redshift. Finally, Section 5 contains the summary and outlook.
2. Formalism
The SEI in this work was initially proposed by Behera et al. [18] and has the following explicit expression if a form-factor of Yukawa type is used.
We denote this force as SEI-Y thereafter.
The SEI-Y in Equation (1) has 12 parameters in total, namely, and M plus the spin-orbit strength parameter , which enters in the description of finite nuclei. The energy density in isospin asymmetric nuclear matter for the SEI-Y interaction in Equation (1) is given by,
where , are neutron (n) and proton (p) densities, = + is the total NM density, (=) is the inverse of the range of the Yukawa form-factor, and (i = n, p) is the respective Fermi momentum. The study of ANM involves altogether nine parameters, , b, , , , , , , . The connection of these new parameters to the interaction parameters of Equation (1), which was derived in Ref. [20], is also reported in Appendix A. Here, the indexes l and denote the interaction between like and unlike pairs of nucleons, respectively.
The Fitting Procedure of SEI
The formulation of NM and PNM using SEI and the parameter fixation protocol has been discussed at length in Refs. [20,21]. We briefly outline it in the following. The SNM only requires the following three combinations of the strength parameters,
which, together with , b and , are the six parameters needed to determine the SNM completely. For a given value of the exponent , which characterizes the stiffness parameter and determines the incompressibility K in SNM, the remaining five parameters , , , b and of SNM are determined as follows assuming the standard values of the nucleon mass ( = 939 MeV), the saturation density and the energy per particle at saturation . The range and the exchange strength are determined simultaneously by adopting an optimization procedure [18], using the condition that the nuclear mean-field in SNM at saturation density vanishes for the kinetic energy of the nucleon of 300 MeV, a result extracted from the optical model analysis of nucleon–nucleus scattering data [22,23,24,25]. The parameter b is determined to avoid supra-luminous behavior [26]. The two remaining parameters, namely and , are obtained from the saturation conditions, = = 37 MeV, which allow us to obtain and, therefore, the saturation density , and e = −16 MeV. The stiffness parameter , kept as a free parameter, is chosen from the range of values for which the pressure–density relation in SNM lies within the region extracted from the analysis of flow data in heavy-ion collision experiments at intermediate energies [27]. It is verified that = 1 is the upper limit for which the pressure-density relation is obeyed, which corresponds to the nuclear matter incompressibility = 269 MeV for the SEI-Y model. Therefore, we can study the nuclear matter properties by assuming different values of up to a limiting value = 1. In this work, we will use three EoS corresponding to . In order to study ANM, we need to know how the strength parameters , and of Equation (3) split into the like and unlike components. The splitting of into and is decided to be [28] using the condition that the entropy in PNM does not exceed that of the SNM [28]. The splittings of the remaining two strength parameters, and , are decided from the values of the symmetry energy parameter and its derivative = at saturation density . For a given within its empirical range [29], we can produce different density dependence of symmetry energy by assigning arbitrary values to . The slope parameter in each case will be . In the study where the variation in is not an explicit requirement, the value of is fixed from the condition that the asymmetric contribution of the nucleonic part of the energy density in charge-neutral -equilibrated neutron star matter (NSM), i.e., = is maximum, where is the equilibrium proton fraction. The characteristic value thus obtained predicts a density dependence of the symmetry energy, which is neither stiff nor very soft [30]. With the parameters determined in this way, the SEI is able to reproduce the trends of the EoS and the properties of the momentum dependence of the mean-field with similar quality as predicted by microscopic calculations [10,28,31,32,33]. As a consequence of this fitting procedure, one can also vary the n and p effective mass splitting, which only depend on the and parameters, while the density dependence of , i.e., the slope parameter L, which depends on the splitting of and , remains invariant and the vice-versa [28,33].
We now have three open parameters that we have chosen as , and . However, to describe ANM, the explicit value of the and parameters is not necessary because they enter as specific combinations that can be determined from the and [21]. In our work [20], we further constrained by using the DBHF predictions on the effective mass splitting between spin-up and spin-down neutrons in spin-polarized neutron matter. It was found that the SEI predictions agree well with the DBHF ones [34] for = , where the superscript (“l,l”) (and its counterpart (“l,ul”)) symbolizes the exchange strength for parallel (and anti-parallel) spin orientations in polarized neutron matter. This consideration allows us to determine in a unique way as [20], if is known. The two remaining free parameters, and , have to be fitted to finite nuclei data, as explained in detail in Refs. [21,35], in the case of a SEI with a Gaussian form factor. For the sake of completeness, the twelve numbers of parameters of the SEI-Y EoSs corresponding to = 1/3, 1/2 and 2/3 are given in Table 1. The inputs corresponding to the saturation density, energy per particle in SNM, and symmetry energy needed to obtain these parameters are given in Table 2.

Table 1.
The twelve parameters for the SEI-Y EoSs corresponding to = 1/3, 1/2 and 2/3.

Table 2.
Nuclear matter properties at saturation density for three EoSs—SEI-Y (), SEI-Y () and SEI-Y ().
3. Symmetric and Asymmetric Nuclear Matter Properties
The equation of state of ANM can be expressed as a power series in the isospin asymmetry = , as given by
where is the energy per nucleon in SNM, while is the symmetry energy. The energy per nucleon in SNM can also be Taylor expanded around the saturation density as:
where and and are the incompressibility and skewness parameter, respectively, in SNM. Notice that the first derivative does not appear in this expansion due to the saturation condition.
The symmetry energy is the energy cost to convert SNM in PNM [6,36,37]. It is defined as
The odd-order terms in will not appear in Equation (4) due to the isospin invariance of nuclear force in nuclear matter when one neglects the Coulomb interaction. The nuclear symmetry energy corresponds to the lowest-order coefficient in the expansion of the energy per particle in ANM in terms of the isospin asymmetry. The contribution from higher-order terms , n ≥ 4 is very small and has been estimated to be less than 1 MeV in microscopic many-body, as well as effective model calculations [37]. Keeping up to the -term in Equation (4) refers to the parabolic approximation (PA) of the EoS of ANM. The density dependence of is much better understood than that of , which is still elusive, even more so in the supra saturation regime that makes the study of ANM an important area of contemporary nuclear research. The analysis of the density dependence of is performed in terms of the various coefficients in its Taylor expansion about normal NM density , given by,
where has been defined before. The coefficients
are the slope parameter, curvature parameter and skew symmetry parameter, respectively, and they characterize the density dependence of the nuclear symmetry energy around the normal nuclear density , and thus carry important information about the properties of nuclear symmetry energy at both high and low density regions.
The incompressibility of ANM, which depends on both the density and isospin asymmetry, is given by
where is the pressure in ANM, and is given in Equation (4). At saturation density of ANM, the pressure = 0 and the incompressibility in Equation (9) becomes a function of only, , and is referred to as the isobaric incompressibility coefficient. The saturation density in ANM, , is a function of isospin asymmetry and differs from normal NM density . The corrections to on account of the isospin asymmetry have been worked out in Ref. [37] in terms of expansion in even powers of . For the lowest-order correction . Under the PA of EoS of ANM, the isobaric incompressibility coefficient reads , where is the incompressibility of SNM at saturation density and is the isospin part of [37,38]. The value of the nuclear matter saturation properties, such as isoscalar effective mass (), isovector effective mass (), energy per particle in PNM (), neutron matter incompressibility (), neutron matter skewness (), etc., for the SEI-Y ( = 1/3, 1/2, and 2/3) EoSs at saturation density are given in Table 2.
The incompressibility of SNM at saturation density is mainly obtained from the analysis of experimental data of the giant monopole resonance (GMR) in open- and closed-shell nuclei. Theoretical studies using non-relativistic and relativistic mean-field models and the analysis of PREX-II and CREX data also provide useful information about . Relevant works using these techniques, which predict different values of ), are collected in Table 3. The ) values predicted by the SEI-Y models, which are given in Table 2, lie in the range 220–253 MeV within the limiting values extracted from the analysis of the experimental GMR [39,40] and PREX-II and CREX [41] data as well from the compilation of the predictions of a large set of relativistic and non-relativistic mean-field models [29,42].

Table 3.
Symmetric nuclear matter incompressibility.
3.1. Landau Parameters
In the framework of the Landau theory of normal Fermi liquids [47,48,49,50], the bulk properties of nuclear matter can be written in terms of a two-body interaction expressed as a functional of the second derivative of the energy per particle with respect to the occupation numbers at the Fermi surface. The interaction energy has the following form [51,52],
where is the inverse of the level density at the Fermi surface. The quantity is the effective mass associated with the interaction, and and are the Pauli matrices in spin and isospin space, respectively. Since both particles are on the Fermi surface, F, , G, and are functions of , the angle between and , which are expanded in terms of Legendre polynomials [53] as,
and likewise for , G, and . For a spherical Fermi surface to be stable against any deformation, the parameters must satisfy the relations
We have calculated the Landau parameters for the SEI-Y interaction. The corresponding analytical expressions for , , , and with l = 0, 1 and 2 are given in Appendix B. Landau parameters at predicted by the SEI-Y () EoSs together with the results of different Skyrme, Gogny, and chiral effective interactions are shown in Figure 1. The density dependence of different Landau parameters is shown for the SEI-Y () parameter set in Figure 2. All the Landau parameters satisfy the condition given in Equations (13)–(15) at all densities, except , which violates the condition Equation (13) for densities less than 0.09 . The violation of the stability condition of in the density range 0.09 , as shown in Figure 2, has no significance, as the physical quantity associated with it, the incompressibility , has no physical meaning in this range of density.
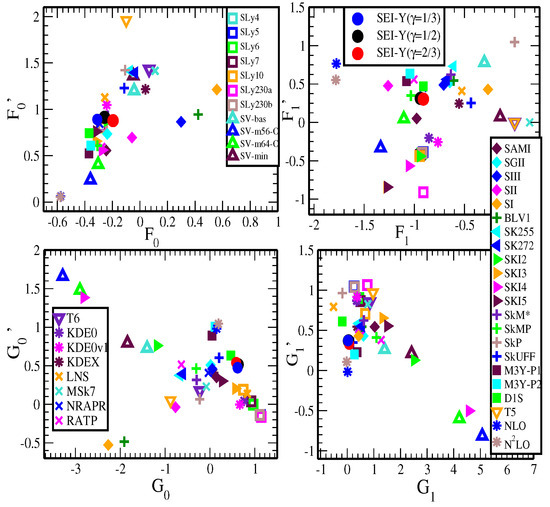
Figure 1.
Landau parameters for SEI-Y () parameter sets compared with different Skyrme sets (SLy4, SLy5, SLy6, SLy7, SLy10, SLy230a, SLy230b, SI, SII, SIII, BLV1, SGII, , RATP, SkP, T6, KDE0, KDE0v1, SK255, SKI2, SKI3, SKI4, SKI5, SkMP, LNS, SV-bas, SV-m56-O, SV-m64-O, SV-min, MSk7, T5, KDEX, NRAPR, SAMi, SK272, SkUFF [54,55,56,57,58,59,60,61,62,63]), Gogny interaction (M3Y-P1, M3Y-P2, D1S [64]), and chiral effective interactions [65].
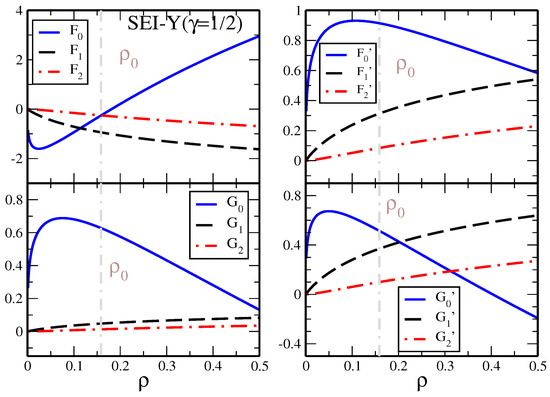
Figure 2.
Landau parameters as a function of density using the SEI-Y () set. Saturation density = 0.158 is denoted by a grey dashed vertical line.
The values of the Landau parameters at saturation for the three SEI-Y sets for () are given in Table 4.

Table 4.
Landau parameters at the saturation density for SEI-Y (), SEI-Y (), and SEI-Y () EoS.
These dimensionless parameters , , , and are directly related to quantities describing SNM and ANM properties, such as effective mass, incompressibility, symmetry energy, the speed of sound, etc., through relationships [66,67],
The sound velocity is directly related to the compression modulus , which can be expressed in terms of the Landau parameters and :
The values of these NM properties at saturation are listed in Table 5 for the three EoSs of SEI-Y, corresponding to . These results are in agreement with the saturation properties predicted under the parameter fitting protocol given in Table 2.

Table 5.
Nuclear matter properties predicted using Landau parameters at saturation density for SEI-Y (), SEI-Y (), and SEI-Y () sets.
3.2. High-Order Derivatives of the Energy per Particle in Asymmetric Nuclear Matter
The symmetry energy is an important quantity in nuclear physics, which rules many properties in the isovector sector of the energy density and has a relevant impact in nuclear astrophysics. The symmetry energy parameter, , is constrained somewhat less rigorously as compared to the energy per particle, , of SNM. It is determined from the analysis of the predictions of a large set of mean-field models [29] and from data of astrophysical observations [68,69,70] but also using experimental nuclear data, such as charged pion spectra at high transverse momenta [71] or charge exchange and elastic nuclear reactions [72]. The values of extracted from these works are reported in the upper panel of Table 6. The symmetry energy values used in the SEI-Y models lie between 34.5 and 35.5 MeV (see Table 2), which are within the ranges predicted by almost all the analyses displayed in Table 6. Heavy-ion collision (HIC) studies have provided relevant constraints on the EoS of SNM at supra-saturation densities, which allow us to predict up to about 4.6 times the normal nuclear matter density [27]. In the recent work of Ref. [73], the value for is constrained in the range at a 68% confidence level. However, the EoS of the high-density neutron-rich matter is still highly uncertain due to the limited progress in the analysis of isospin-sensitive observables of HIC experiments. It also remains an open question whether the symmetry energy is stiffer or super-soft at supra-saturation densities.
In Table 6, the available data found in the literature on nuclear symmetry energy at two times the saturation density, , together with the corresponding predictions provided by the SEI-Y () EoSs, are given. These results are based on theoretical analysis of data from laboratory experiments, such as the ASY-EoS experiment at GSI [74] and HIC [75,76], astrophysical data of different types, as outlined in Refs. [73,77,78,79,80,81,82,83], theoretical calculations within chiral EFT [84,85] and effective mean-field models [86]. From this table, we see that the SEI-Y predictions are in good agreement with the available data reported in Table 6, in particular with the predictions of Refs. [75,77,78,79,80,81,82] obtained using different techniques. The symmetry pressure at twice saturation density predicted by the SEI-Y () EoSs are 10.659, 10.572, and, 10.488 MeV , respectively, which lies within the range MeV extracted from the experimentally derived density functional [87]. The nuclear symmetry energy at three times the saturation density, , for SEI-Y () EoS are 69.64, 69.38, and 69 MeV, respectively. These SEI-Y values are consistent with the results extracted from the GW170817 data ( MeV) [79] but are slightly higher than the predictions of Dutra et al., 2012, which range from 33.65 to 60.92 MeV [29].

Table 6.
Symmetry energy at several densities.
Table 6.
Symmetry energy at several densities.
| Expt./Observation/Theory | [MeV] |
|---|---|
| Mean-field calculations and Astrophysical Observations | |
| Dutra et al., 2012 [29] | 27–36 |
| B A Li and Han, 2013 [68] | 31.6 ± 0.92 |
| Oertel et al., 2017 [69] | 31.7 ± 3.2 |
| PREX II Experiment Reed et al., 2021 [70] | 38.1 ± 4.7 |
| Charged Pion Spectra at high momenta Estee et al., 2021 [71] | 32.5–38.1 |
| Charge exchange and elastic scattering data Danielewicz et al., 2017 [72] | 33.5–36.4 |
| Expt./Observation/Theory | [MeV] |
| SEI-Y () | 55.74 |
| SEI-Y () | 55.38 |
| SEI-Y () | 54.93 |
| HIC and Transport Calculations | |
| ASY-EoS experiment at GSI [74] | 46–54 |
| UrQMD transport calculation [75] | 55 ± 5 |
| Zhang et al., 2020 [76] | 35–55 |
| Gravitational Waves Zhang and Li, 2019 [77] | |
| Xie and Li, 2019 [73] | |
| Tong et al., 2020 [78] | 60.7 ± 10.9 |
| Chiral Effective Field Theory | |
| Drischler et al., 2020 [84] | 45 ± 3 |
| Lonardoni et al., 2020 [85] | 45 ± 5 |
| Neutron Star Observables B A Li et al., 2021 [79] | 51 ± 13 |
| Nakazato and Suzuki, 2019 [80] | 40–60 |
| Yue et al., 2022 [81] | 62.8 ± 15.9 |
| Xie and Li, 2020 [82] | |
| Zhou et al., 2019 [83] | [] |
| Mean-Field Calculations Chen et al., 2015 [86] | 40.2 ± 12.8 |
The parameters associated with higher-order derivatives of the energy per particle and symmetry energy at saturation, specifically , L, , and , remain poorly constrained and present challenges for experimental measurements. Among these parameters, the slope of the symmetry energy L is of particular relevance, as this quantity is nicely correlated with some finite nuclei properties; for example, the neutron skin thickness in heavy neutron-rich nuclei is 208Pb. This parameter has been estimated using information extracted from the analysis of terrestrial nuclear experiments and astrophysical observations [68,69,73,82,88], the analysis of the PREX-II data [70], from results of charge exchange and elastic scattering involving isobaric analog states [72], charged pion spectra [71] and isospin diffusion [89], and, very recently, from the charge radii difference in mirror nuclei [90]. The range of the values of the slope parameter L is relatively large and covers from about 40 MeV to 120 MeV depending on the inputs used in the different analyses carried out, as can be seen in the upper panel of Table 7. The L value predicted by the SEI-Y models is about 75 MeV, which lies approximately in the middle of the range of the various estimates considered.

Table 7.
L, and at saturation density from different experimental and theoretical analyses along with the results of SEI-Y (, 1/2, and 2/3) EoS.
The incompressibility parameter in ANM, , has been estimated from astrophysical inputs provided by astrophysical observations [91,92,93,94], from nuclear and neutron matter calculations using chiral effective field theory [95,96,97], from terrestrial experiments [98] and from the analysis of mean-field predictions [99,100,101]. This parameter is, in general, negative and of the order of a few hundred MeV. The SEI-Y predictions, given in Table 2, are in line with the estimates obtained from terrestrial experiments and astrophysical observations reported in the middle panel of Table 7.
In Ref. [101], a correlation between the and parameters is obtained from the analysis of 500 Skyrme and RMF models. However, in the case of SEI-Y, is also strongly correlated with L in addition to the correlation. In particular, in the case of SEI-Y , we find the linear relation MeV. The isovector incompressibility parameter is mainly extracted from experimental data of the isoscalar giant monopole resonance [43,102,103,104] from theoretical mean-field model calculations for different MDI interactions [37,105] and from information extracted from measurements of neutron skins across the mass table [106]. These estimates have an average value of approximately −500 MeV but with large error bars, as can be seen in the lower panel of Table 7. The values predicted by the SEI-Y models, given in Table 2, are in agreement with the values extracted using different techniques given in the lower panel of Table 7.
Experimental constraints on the skewness parameter in both symmetric and asymmetric nuclear matter, and , respectively, are currently lacking in precision. Based on the analysis of different experimental and observational data [99,107,108,109,110], it is found that the skewness in SNM is negative, and its range is approximately between ≃−1200 and 400 MeV. The situation is similar for the skewness parameter of the symmetry energy, where different estimates constrain its value within the range between −200 and 800 MeV [77,99,100,101]. The values of in SNM predicted by SEI-Y () EoSs are listed in Table 2 and lie consistent with the values extracted from other different analyses. In the same table, we display the skewness parameter of the symmetry energy computed with the SEI-Y models, which are in the range 234–273 MeV, which is in good agreement with the value of MeV suggested in Ref. [101]. With the SEY-Y model, we also find a strong anti-correlation between the and L parameters, which in the case of SEI-Y () EoS reads MeV.
4. Neutron Star Phenomenology
4.1. The Radius of Neutron Stars and the Slope of the Isoscalar Incompressibility
The density derivative of the isoscalar incompressibility of symmetric nuclear matter, which is defined as , can be written at saturation density as a combination of the skewness and the incompressibility of SNM as [111]. The value of this parameter, estimated from a large set of non-relativistic and relativistic mean-field models, lies in the range MeV [112]. A relatively wider range, MeV, is extracted from the analysis of the tidal deformability measurement in the BNSM event GW170817 [93]. In Ref. [112], the correlation of the radius of the NS with the linear combinations of the slopes of the nuclear matter incompressibility and the symmetry energy coefficients at saturation, which is almost independent of the NS mass in the range 0.6 –1.8 , is shown. Here, we explore, using the SEI-Y EoSs with (, 1/2, and 2/3), the possible correlations between the NS radius and the slope of the incompressibility at saturation for NS of 1.4 and 1.6 . To obtain the radii predicted by these EoSs, we solve the Tolman–Oppenheimer–Volkoff (TOV) equation, where the BPS-BBP EoS [113,114] is used up to 0.07468 (the crust-core transition density for SEI) and our EoS thereafter.
The values of the radii of these 1.4 and 1.6 NSs, and are shown as a function of the slope of the incompressibility parameter in Figure 3 and Figure 4, respectively, for the three aforementioned SEI EoSs. The vertical shaded region in brown in the Figures correspond to the values predicted in Refs. [112,115]. The data for NS radii, obtained from various recent studies, are taken from Refs. [70,92,116,117,118,119,120,121] (for ) and [122,123] (for ) and displayed by different color areas in Figure 3 and Figure 4, respectively. The LIGO-Virgo measurement leads to an upper limit of at 13.6 km [124], and that from the BNSM ascertained to be km [125]. The minimum limit for an radius of non-rotating NS, constrained from GW170817 data by Bauswein et al., is km [126]. This value is shown as an orange band in Figure 4. , and values predicted by 44-EoSs of Skyrme, RMF and microscopic interactions, which are taken from Table I of the Supplemental Material given in Alam et al., 2016 [112], are also shown in the two figures by green squares.
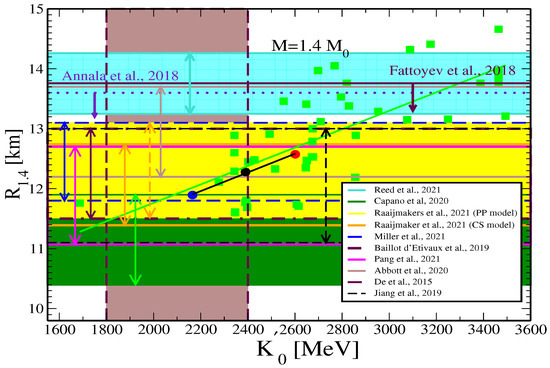
Figure 3.
of 1.4 neutron stars versus the slope of the incompressibility obtained using different EoS of SEI-Y of = 1/3, 1/2, and 2/3. The green square are the results taken from supplementary material given in Alam et al., 2016 [112]. The horizontal shaded region data of are taken from: cyan [Reed et al., 2021 [70]], dark green [Capano et al., 2020 [116]], yellow and orange [Raaijmakers et al., 2021 (PP model and CS model), respectively [117]], blue [Miller et al., 2021 [118]], maroon [Baillot d’ Etivaux et al., 2019 [92]], magenta [Pang et al., 2021 [119]], black dashed [Jiang et al., 2019 [120]], brown [Abbott et al., 2020 [121]], indigo dotted line [Annala et al., 2018 [124]] and Maroon line [Fattoyev et al., 2018 [125]]. The vertical shaded region in brown [De et al., 2015 [115]].
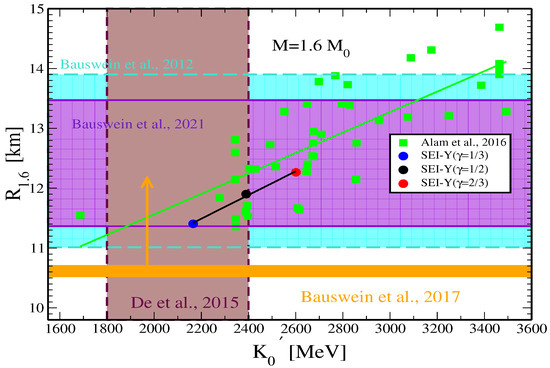
Figure 4.
of 1.6 neutron stars versus the slope of the incompressibility obtained using different EoS of SEI-Y of = 1/3, 1/2, and 2/3. The green square are the results taken from supplementary material given in Alam et al., 2016 [112]. The violet and cyan horizontal shaded region data of are calculated from Table IX of [122] and Table I of [123]. The orange band refers to the minimum limit of in the work of Bauswein et al., 2017 [126]. The vertical shaded region in brown [De et al., 2015 [115]].
Using these 44-EoSs data, a moderate linear correlation between the NS radii and is obtained, as was also pointed out by Alam et al. in Ref. [112], whereas a rather strong correlation over the mass range 0.8 –1.8 was obtained with a linear combination of and , as we mentioned before. However, our three SEI-Y EoSs, with the parameter equal to 1/3, 1/2 and 2/3, show a strong correlation between the radii and the slope of the incompressibility alone for both NS masses, namely, 1.4 and 1.6 . We have also verified that another strong linear correlation exists between and and the linear combination of and , which is in agreement with the previous findings in [112].
4.2. Neutron Star Merger and Incompressibility of Asymmetric Nuclear Matter
The incompressibility of ANM in Equation (9) depends on both density and isospin asymmetry, and it is found to have important implications in BNSM studies [127,128]. The threshold mass for prompt collapse (PC) to form a black hole (BH) in BNSM is scaled in terms of maximum mass of the non-rotating NS as , where the scaling parameter is EoS dependent [129,130]. Bauswein et al. [127], from a simulation study of the BNSM for symmetric binary NS, found that using temperature-dependent nuclear EoSs, there was a strong correlation of with the compactness of the TOV configuration (, ) of the NS, where c and G are the speed of light and the gravitational constant, respectively. A universal ansatz proposed by Bauswein et al. (2013) is
which is independent of the EoS. Such a linear ansatz represents a reasonable first approximation to the data, but it is not the most general one [131]. By using weighted averaged values of the linear-fit constants a and b of different works, given in Table II of Ref. [132], we computed the threshold mass predicted by the three EoSs of SEI-Y ( = 1/3, 1/2, and 2/3), which are reported in Table 8. In the case of delayed/no collapse, the estimated total binary mass of GW170817 provides a lower bound on the threshold mass for direct BH formation, [126]. SEI-Y predictions of for the three sets of values of a and b in Table 8 closely conform to this limiting value.

Table 8.
Threshold mass for the three EoSs of SEI-Y ( = 1/3, 1/2, and 2/3) using the values of constants a and b from the literature, given in Table II of Ref. [132].
In recent work, Perego et al. [128] performed a BNSM simulation study taking asymmetric masses in the NS binary. These authors have shown that the nuclear incompressibility at the central density of , , contains information on for PC in the BNS merger. Consequently, if is known, then can potentially be predicted, which is not possible nowadays in any laboratory experiment. In Ref. [128], the authors examined the correlation between and compactness of maximum mass NS considering a large sample of EoSs comprising the nucleonic part, as well as containing hyperons and the transition to the quark phase.
A strong power law correlation has been obtained among these data. We have computed the density dependence of for the three SEI-Y EoSs, where for each is obtained by solving the charge neutral -equilibrated NSM, and the results are shown as a function of the density in panel (a) of Figure 5. The values of the computed at the central density of predicted by the SEI-Y EoSs are shown as a function of the compactness in panel (b) together with the data of the 66-EoSs taken from the supplementary material of Ref. [128]. The values of the , shown in panel (b) of Figure 5 for different EoSs, lie below the empirical limit of compactness allowed by general relativity, C = 4/9 [133], and the Tolman VII analytical solution of the TOV equation, C = 0.3428. These limiting values are the universal upper bounds for compactness, as corroborated by the incorporation of realistic EoS [134,135]. The three SEI data points lie in the tighter threshold region of 12 GeV of Perego et al., 2022 (Figure 4 of [128]). They have also suggested that the information of at different mass asymmetries q of the two NSs in the binary can provide constraints on the velocity of sound close to the central density of .
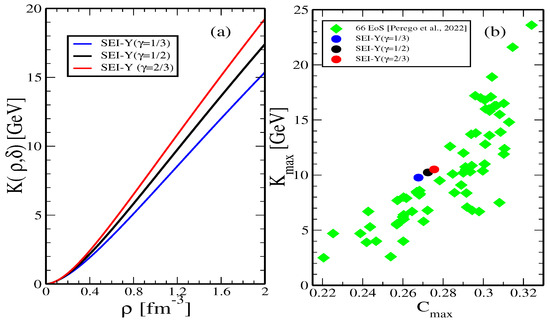
Figure 5.
(a) K () as a function of density in NSM for the SEI-Y (), SEI-Y (), and SEI-Y () EoS, (b) as a function of the compactness of the heaviest NS for the three EoSs of SEI-Y. The green diamonds are the 66 EoS results taken from [128].
4.3. Sound Speed in Neutron Star Matter
The adiabatic speed of sound in ANM evaluated at constant entropy is given by [97,136,137].
where H is the energy density given by Equation (2), and m is the average nucleon mass.
The square of the speed of the sound in NSM, where for each in Equation (24) is the equilibrium value obtained from the -stability condition, predicted by the three SEI-Y EoSs , is displayed as a function of density in panel (a) of Figure 6. From this figure, we can see that the square of the speed of sound increases with the density without exceeding the causality limit, and it also increases linearly with the incompressibility of nuclear matter, as predicted by Equation (24). The magenta line in panel (a) of Figure 6 represents the conformal limit () [138]. More recently, by studying maximally rotating neutron stars, Margaritis et al., 2020, claimed that the sound speed likely exceeds the conformal limit [134,139].
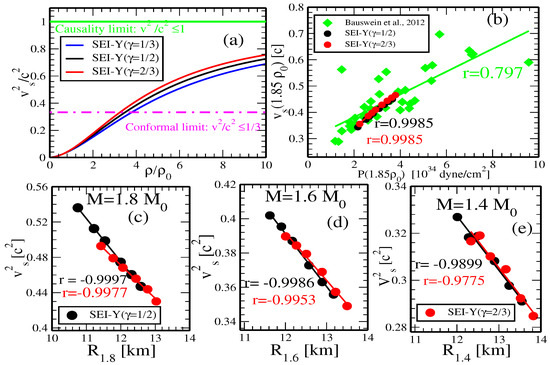
Figure 6.
(a) Speed of sound in NSM as a function density, where for each is the -equilibrium value, obtained for the three EoS corresponding to of SEI-Y. The magenta and green lines are the conformal and casual limit, respectively. (b) Speed of sound as a function of pressure at density (1.85) in NSM for SEI-Y () EoS compared with the results of Bauswein et al., 2012 [123]. The square speed of sound at the central densities of 1.8 , 1.6 and 1.4 NSs as a function of radius , and for the SEI () EoSs corresponding to different values of L in the range 70–110 MeV are shown in panels (c–e), respectively.
In panel (b) of Figure 6, we display the speed of sound in NSM as a function of nucleonic pressure at density 1.85 computed with the SEI-Y () EoSs with different slopes of the symmetry energy L in the range 60–110 MeV, together with the results of the EoSs from Bauswein et al., 2012 [123]. The SEI-Y predictions show a nice linear behavior between the speed of the sound and the pressure, with a correlation coefficient r = 0.998 for both EoSs. This linear behavior is, however, weaker with the set of EoSs selected by Bauswein et al. [123], probably due to the different origin and fitting protocols of these EoSs.
Panels (c), (d) and (e) of Figure 6 show, as a function of the NS radius, the square of the speed of sound, , computed at the central densities, , of the 1.8 , 1.6 and 1.4 NSs obtained by solving the TOV equations using the SEI-Y () EoSs with different values of the slope parameter L in the range 70–110 MeV. For the three considered masses, the square of the speed of the sound shows an inverse linear relationship with the radius of NS, with correlation coefficients close to unity, which show a moderate decreasing trend as the NS mass decreases. The inverse linear relationship in each given mass NS is due to the following. When the slope of the symmetry energy L increases in an EoS of given , the ratio decreases owing to the growth of the radius R, and therefore, the compactness also decreases, which implies a reduction in the incompressibility .
4.4. Gravitational Redshift
The gravitational redshift of a signal from the star’s surface can be written as,
Measurements of the gravitational redshift of spectral lines can provide direct insights into the stellar compactness parameter and, as a result, can constrain the EoS for dense matter. The calculated using the SEI-Y ( and SEI-Y () EoSs as a function of gravitational mass is shown in Figure 7. From this figure, we can see that increases as the mass of the NS rises for both considered EoSs. In the lower mass range, the values for both EoS models are almost the same, but they diverge notably in the higher mass range. EoS having a higher value of incompressibility predicts a lower value of .
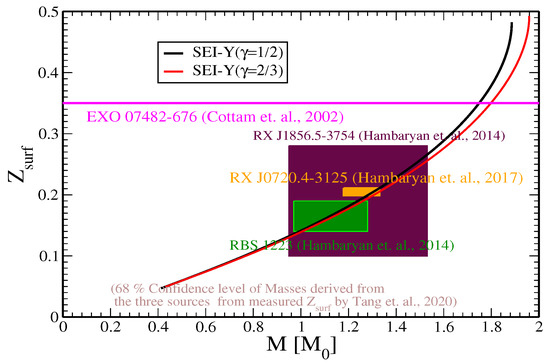
Figure 7.
Gravitational redshift at the neutron star surface as a function of the stellar gravitational mass for the SEI-Y ( and SEI-Y () EoSs. The magenta horizontal line corresponds to the results of Cottam et al., 2002 from the X-ray burst source in the low-mass X-ray binary EXO 07482-676 [140]. The extracted ranges for the three members of the so-called “The Magnificent Seven” NSs are RBS 1223 [Green shaded region], RX J0720.4-3125 [orange shaded region], and RX J1856.5-3754 [maroon shaded region] [141,142,143].
The magenta horizontal line in Figure 7 corresponds to = 0.35. This value was obtained by Cottam et al. from the X-ray burst source in the low-mass X-ray binary EXO 07482-676 [140]. The gravitational redshift of RBS 1223, RX J0720.4-3125, and RX J1856.5-3754, which are members of the so-called “The Magnificent Seven”, are [green shaded region], [orange shaded region], and [maroon shaded region] [141,142] with masses , , and , respectively, at 68% confidence level [143]. These observational data, which are also displayed in Figure 7, are well reproduced by our theoretical calculation using the SEI-Y EoSs, which pass well through the shaded areas representing the uncertainties in the respective observed data.
The gravitational redshift in different masses, NSs, namely (a) 1.8 , (b) 1.6 , and (c) 1.4 , are shown as a function of the auxiliary parameter = in Figure 8 for the SEI-Y () and SEI-Y () EoSs. The auxiliary parameter , which was proposed in Refs. [144,145], is a combination of incompressibility in SNM, , and the slope of the symmetry energy, L. The values of L and extracted from different nuclear experiments and observations constrain the value of in the range MeV from SRIT, RCNP and PREX-II data, as can be seen in Figure 8. From this figure, we can also observe a strong anti-correlation between and predicted by the two considered SEI-Y EoSs for the three NS masses analyzed, namely 1.8 , 1.6 , and 1.4 . The correlation coefficient results for the two EoSs are displayed in the respective panels, which predict a relatively strong correlation coefficient for the stiffer EoS. The values as a function of , predicted by the 44 EoSs of Skyrme, RMF and microscopic interactions used by Alam et al. [112], have been computed for the same masses and shown in the respective panels of Figure 8 as green diamonds. The inverse relation between and is also observed for these EoSs (although it is much weaker) can be assigned due to the different origins of the EoSs considered in [112].
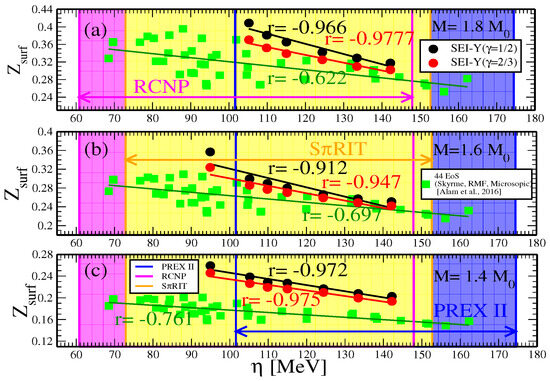
Figure 8.
as a function of for (a) 1.8 , (b) 1.6 , and (c) 1.4 NS for SEI-Y ( and SEI-Y () EoSs. The shaded region is the constrained value of for PREX II [Blue], RCNP [magenta], and SRIT [yellow] [145]. The green diamonds are the data for the 44-EoSs of Ref. [112].
4.5. Neutron Star Mass, Radius and Gravitational Redshift at Different Central Densities
The correlations between the mass M, radius R, and gravitational redshift of NSs with central densities of , , , , and are studied as a function of the slope L in the range 60–110 MeV, using the SEI EoS ( = 2/3). The corresponding results are shown in the three panels of Figure 9, which correspond to masses, radii and gravitational redshift from left to right, respectively.
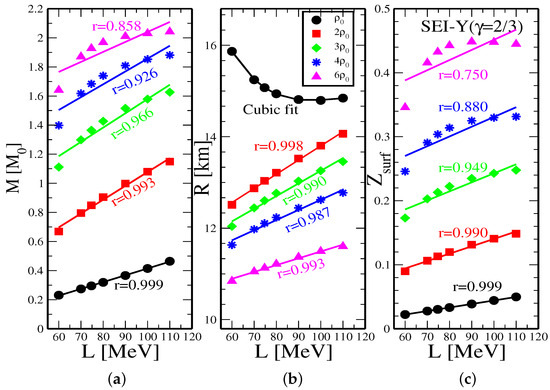
Figure 9.
(a) Neutron star masses, (b) neutron star radius (c) corresponding to central densities of , , , , and as a function of L.
A linear correlation has been observed between L and mass M for the NSs at all central densities , , , , and . The correlation coefficients are r = 0.999, 0.993, 0.966, 0.926, and 0.858, respectively. The correlation becomes weaker as the density increases—a trend similar to the one found in the work of Ref. [146]—which reflects the role of other empirical parameters governing the density dependence of the EoS [146]. For NSs with central densities , , , and , a strong linear correlation between the NSs radii and L is also found. However, for a central density = , the radius decreases as the slope of the symmetry energy L increases. The reason for this behavior is given in Ref. [146]. A higher value of L implies a softer EoS for densities below , which explains the anti-correlation observed in the central panel of Figure 9 for NSs having a central density . In contrast, at higher densities, a larger value of the slope parameter L results in a stiffer EoS above and, consequently, the radius, which is correlated with L in this region, shows an increasing trend. In the right panel of Figure 9, we also found a strong linear correlation between the and L for NSs with central densities , , , , and , which gradually degrades as the central density increases and is a feature similar to the correlation between mass M and L displayed in the left panel of Figure 9.
5. Summary and Outlook
We have used the so-called finite-range simple effective interaction with a Yukawa form-factor to study some non-standard properties of symmetric and asymmetric nuclear matter, such as the Landau parameters associated with this interaction and the high-order derivatives of the energy per particle in symmetric matter and the symmetry energy at saturation density. In addition, we have explored the predictive power of SEI-Y in the high-density neutron-rich domain in describing recent neutron star phenomenology associated with a binary neutron star merger and gravitational redshift.
SEI-Y is a phenomenological effective interaction whose parameters, except the one fitted to finite nuclei data, are systematically fitted under very generic considerations to experimental or empirical data of symmetric nuclear matter and pure neutron matter, which provides a satisfactory account of the nuclear matter properties. An important characteristic of SEI-Y is the fact that the parameters that determine the momentum dependence of the mean-field are decoupled from the ones that fix their density dependence in such a way that each part in the isovector sector can be studied independently of the other without affecting the isoscalar predictions.
We have computed the Landau parameters for the SEI-Y EoSs that give an overall satisfactory account of the nuclear matter saturation properties as well as the sum rules. The nuclear matter properties predicted from the Fermi liquid formulation given in Table 5 are reproduced within a relative difference of approximately ∼ 4 % by the corresponding values computed directly with the parameters of the SEI-Y interaction (see, in this respect, Table 2 for comparisons).
The properties of the higher-order derivatives of the energy per particle and the symmetry energy in nuclear matter at saturation density, namely, , L, and , have remained unconstrained, and their extraction from theoretical calculations, various terrestrial laboratory experiments and astrophysical observations predict values with largely differing uncertainties, as can be seen in Table 7. The results obtained with the different SEI-Y EoSs considered in this work are MeV, MeV, MeV and MeV, at it can be seen in Table 2. These values are found to lie within the range of values extracted from the different studies summarized in Table 7.
However, the main aim of this study is to discuss some recent phenomenology of neutron stars related to the binary neutron star merger and gravitational redshift. The compactness of the maximum mass of a neutron star predicted by the three SEI-Y EoSs lies in the range of , which approximately covers the range of incompressibilities between 220 and 260 MeV, predicting the threshold mass for prompt collapse in the range between 2.61 and 2.94 , which satisfies the minimum threshold mass constraint assessed from the binary masses in the GW170817 event. The of these SEI-Y EoSs lies in the tighter threshold region of ≈ 12 GeV of Perego et al.’s, 2022, analysis using 34 EoSs of different types. The velocity of sound, , computed with the SEI-Y model EoSs, is also found to remain causal in neutron star matter and does not exceed the velocity of light. Using SEI-Y EoSs with given symmetry stiffness (given ) but different slope parameter L in a given neutron star, we find an antilinear relationship between its radius, R, and the square of its sound speed, , computed at its central density. These results are shown in panels (c), (d) and (e) of Figure 6 for neutron stars with masses 1.8 , 1.6 and 1.4 . We have also used the SEI-Y EoSs to study the gravitational redshift at the surface of a neutron star, , which is intrinsically connected to the compactness parameter, as a function of the mass of the neutron star. The SEI-Y predictions of conform to the values constrained from the astrophysical observations on the three neutron stars, namely, RBS 1223, RX J0720.4-3125, and RX J1856.5-3754 in the X-ray binary shown in Figure 7 and whose observed redshifts are , , and , respectively. In a neutron star of a given mass, the redshift parameter shows a decreasing trend if the slope parameter, L, increases when the incompressibility modulus, , is kept fixed. This implies that for a neutron star of a given mass, when the slope parameter L increases, the compactness, C, decreases. This behavior is also verified using the 44 EoSs of Skyrme, RMF and microscopic type given in the work of Alam et al. shown in Figure 8. On the other hand, in a neutron star also grows with increasing central density, which in turn increases the compactness parameter that is a relevant parameter in order to understand the EoS of dense neutron-rich matter. Our immediate objective is to use SEI-Y to study the neutron star phenomenology at finite temperature and finite nuclei properties at non-zero temperature, as well as taking deformation into account.
Author Contributions
Conceptualization, X.V., P.B., Z.N. and T.R.R.; methodology, X.V., P.B., Z.N. and T.R.R.; formal analysis, X.V., P.B., Z.N. and T.R.R.; investigation, X.V., P.B., Z.N. and T.R.R.; data curation, X.V., P.B., Z.N. and T.R.R.; writing—original draft, T.R.R.; writing—review and editing, X.V., P.B., Z.N. and T.R.R.; supervision, X.V., Z.N. and T.R.R. All authors have read and agreed to the published version of the manuscript.
Funding
X.V. availed partial support from Grants No. PID2020-118758GB-I00 and No. CEX2019-000918-M (through the “Unit of Excellence María de Maeztu 2020–2023” award to ICCUB) from the Spanish MCIN/AEI/10.13039/501100011033.
Data Availability Statement
The original contributions presented in the study are included in the article, further inquiries can be directed to the corresponding author.
Acknowledgments
P.B. acknowledges support from the MANF Fellowship of UGC, India. Useful discussions with M. Centelles and J.N. De are also warmly acknowledged. T.R.R. offers sincere thanks to B. Behera for useful discussions.
Conflicts of Interest
The authors declare no conflicts of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.
Appendix A. Relations between the Six Strength Parameters and the Interaction Parameters
The relationships between the six strength parameters in Equation (2) and the interaction parameters in Equation (1) are as follows:
where the superscript indices l and denote the contributions resulting from the nucleon interactions between a like-pair and an unlike-pair. By inverting this set of equations and replacing the strength parameters with their values given in Table 1, one obtains the interaction parameters that are reported in Table A1.

Table A1.
The twelve parameters for the SEI-Y EoSs corresponding to = 1/3, 1/2, and 2/3.
Table A1.
The twelve parameters for the SEI-Y EoSs corresponding to = 1/3, 1/2, and 2/3.
| b [] | [fm] | [] | W [MeV] | ||
|---|---|---|---|---|---|
| 1/3 | 0.4161 | 0.4232 | −0.0630 | 9536.129 | −1380.539 |
| 1/2 | 0.5880 | 0.4242 | −0.112 | 9277.281 | −1321.847 |
| 2/3 | 0.7796 | 0.4250 | −0.153 | 10228.257 | −1214.475 |
| B [MeV] | H [MeV] | M [MeV] | [MeV] | ||
| 128.0918 | −630.968 | −808.871 | 333.5 | 1.151 | 119.3 |
| 100.950 | −575.215 | −832.339 | 566.7 | 0.664 | 118.4 |
| 49.094 | −470.284 | −881.144 | 647.4 | 0.520 | 118.2 |
Appendix B. Landau Parameters
The expression of Landau parameters for SEI-Y EoS are given as follows:
where the normalization constant is the level density at the Fermi surface. The numerical values of the Landau parameters reported in Table 4 are obtained with the help of the interaction parameters given in Table A1 and the effective mass and Fermi momentum at saturation taken from Table 2.
References
- Haar, B.T.; Malfliet, R. Nucleons, mesons and deltas in nuclear matter a relativistic Dirac-Brueckner approach. Phys. Rep. 1987, 149, 207. [Google Scholar] [CrossRef]
- Van Dalen, E.N.E.; Fuchs, C.; Faessler, A. The relativistic Dirac–Brueckner approach to asymmetric nuclear matter. Nucl. Phys. A 2004, 744, 227–248. [Google Scholar] [CrossRef]
- de Jong, F.; Lenske, H. Asymmetric nuclear matter in the relativistic Brueckner-Hartree-Fock approach. Phys. Rev. C 1998, 57, 3099. [Google Scholar] [CrossRef]
- Cugnon, J.; Deneye, P.; Lejeune, A.Z. Neutron matter properties in an extended Brueckner approach. Zeitschrift für Physik A-Atomic Nuclei 1987, 328, 409–415. [Google Scholar] [CrossRef]
- Zuo, W.; Lejeune, A.; Lombardo, U.; Mathiot, J.F. Microscopic three-body force for asymmetric nuclear matter. Eur. Phys. J. A 2002, 14, 469–475. [Google Scholar] [CrossRef]
- Bombaci, I.; Lombardo, U. Asymmetric nuclear matter equation of state. Phys. Rev. C 1991, 44, 1892. [Google Scholar] [CrossRef] [PubMed]
- Day, B.D.; Wiringa, R.B. Brueckner-Bethe and variational calculations of nuclear matter. Phys. Rev. C 1985, 32, 1057. [Google Scholar] [CrossRef] [PubMed]
- Baldo, M.; Burgio, G.F.; Schulze, H.-J. Hyperon stars in the Brueckner-Bethe-Goldstone theory. Phys. Rev. C 2000, 61, 055801. [Google Scholar] [CrossRef]
- Vidaña, I.; Polls, A.; Ramos, A.; Engvik, L.; Hjorth-Jensen, M. Hyperon-hyperon interactions and properties of neutron star matter. Phys. Rev. C 2000, 62, 035801. [Google Scholar] [CrossRef]
- Akmal, A.; Pandharipande, V.R.; Ravenhall, D.G. Equation of state of nucleon matter and neutron star structure. Phys. Rev. C 1998, 58, 1804. [Google Scholar] [CrossRef]
- Mukherjee, A.; Pandharipande, V.R. Variational theory of hot nucleon matter. Phys. Rev. C 2007, 75, 035802. [Google Scholar] [CrossRef]
- Hebeler, K.; Schwenk, A. Chiral three-nucleon forces and neutron matter. Phys. Rev. C 2010, 82, 014314. [Google Scholar] [CrossRef]
- Hebeler, K.; Lattimer, J.M.; Pethick, C.J.; Schwenk, A. Constraints on Neutron Star Radii Based on Chiral Effective Field Theory Interactions. Phys. Rev. Lett. 2010, 105, 161102. [Google Scholar] [CrossRef] [PubMed]
- Haensel, P.; Kutschera, M.; Prószyński, M. Uncertainty in the saturation density of nuclear matter and neutron star models. Astron. Astrophys. 1981, 102, 299–302. Available online: http://adsabs.harvard.edu/abs/1981A%26A...102..299H (accessed on 27 January 2024).
- Skyrme, T.H.R. CVII. The Nuclear Surface. Philos. Mag. 1956, 1, 1043. [Google Scholar] [CrossRef]
- Decharge, J.; Gogny, D. Hartree-Fock-Bogolyubov calculations with the D1 effective interaction on spherical nuclei. Phys. Rev. C 1980, 21, 1568. [Google Scholar] [CrossRef]
- Bertsch, G.; Borysowicz, J.; McManus, H.; Love, W.G. Interactions for inelastic scattering derived from realistic potentials. Nucl. Phys. A 1977, 284, 399–419. [Google Scholar] [CrossRef]
- Behera, B.; Routray, T.R.; Satpathy, R.K. Momentum and density dependence of the mean field in nuclear matter. J. Phys. G Nucl. Part. Phys. 1998, 24, 2073. [Google Scholar] [CrossRef]
- Behera, B.; Routray, T.R.; Pradhan, A.; Patra, S.K.; Sahu, P.K. Momentum and density dependence of the isospin part of nuclear mean field and equation of state of asymmetric nuclear matter. Nucl. Phys. A 2005, 753, 367–386. [Google Scholar] [CrossRef]
- Behera, B.; Viñas, X.; Routray, T.R.; Centelles, M. Study of spin polarized nuclear matter and finite nuclei with finite range simple effective interaction. J. Phys. G Nucl. Part. Phys. 2015, 42, 045103. Available online: http://iopscience.iop.org/0954-3899/42/4/045103 (accessed on 27 January 2024). [CrossRef]
- Behera, B.; Viñas, X.; Bhuyan, M.; Routray, T.R.; Sharma, B.K.; Patra, S.K. Simple effective interaction: Infinite nuclear matter and finite nuclei. J. Phys. G Nucl. Part. Phys. 2013, 40, 095105. Available online: http://iopscience.iop.org/0954-3899/40/9/095105 (accessed on 27 January 2024). [CrossRef]
- Bertsch, G.F.; Das Gupta, S. A guide to microscopic models for intermediate energy heavy ion collisions. Phys. Rep. 1988, 160, 189. [Google Scholar] [CrossRef]
- Gale, C.; Bertsch, G.F.; Das Gupta, S. Heavy-ion collision theory with momentum-dependent interactions. Phys. Rev. C 1987, 35, 1666. [Google Scholar] [CrossRef] [PubMed]
- Gale, C.; Welke, G.M.; Prakash, M.; Lee, S.J.; Das Gupta, S. Transverse momenta, nuclear equation of state, and momentum-dependent interactions in heavy-ion collisions. Phys. Rev. C 1990, 41, 1545. [Google Scholar] [CrossRef]
- Csernai, L.P.; Fai, G.; Gale, C.; Osnes, E. Nuclear equation of state with momentum-dependent interactions. Phys. Rev. C 1992, 46, 736. [Google Scholar] [CrossRef]
- Behera, B.; Routray, T.R.; Satpathy, R.K. Causal violation of the speed of sound and the equation of state of nuclear matter. J. Phys. G 1997, 23, 445. Available online: http://iopscience.iop.org/0954-3899/23/4/005 (accessed on 27 January 2024). [CrossRef]
- Danielewicz, P.; Lacey, R.; Lynch, W.G. Determination of the Equation of State of Dense Matter. Science 2002, 298, 1592. [Google Scholar] [CrossRef]
- Behera, B.; Routray, T.R.; Tripathy, S.K. Neutron–proton effective mass splitting and thermal evolution in neutron-rich matter. J. Phys. G Nucl. Part. Phys. 2011, 38, 115104. Available online: http://iopscience.iop.org/0954-3899/38/11/115104 (accessed on 27 January 2024). [CrossRef]
- Dutra, M.; Lourenço, O.; Martins, J.S.S.; Delfino, A.; Stone, J.R.; Stevenson, P.D. Skyrme interaction and nuclear matter constraints. Phys. Rev. C 2012, 85, 035201. [Google Scholar] [CrossRef]
- Behera, B.; Routray, T.R.; Pradhan, A.; Patra, S.K.; Sahu, P.K. Nuclear mean field and equation of state of asymmetric nuclear matter. Nucl. Phys. A 2007, 794, 132–148. [Google Scholar] [CrossRef]
- Wiringa, R.B. Single-particle potential in dense nuclear matter. Phys. Rev. C 1988, 38, 2967. [Google Scholar] [CrossRef]
- Sammarruca, F. The Microscopic Approach to Nuclear Matter and Neutron Star Matter. Int. J. Mod. Phys. E 2010, 19, 1259–1313. [Google Scholar] [CrossRef]
- Behera, B.; Routray, T.R.; Tripathy, S.K. Temperature dependence of the nuclear symmetry energy and equation of state of charge neutral n + p + e + μ matter in beta equilibrium. J. Phys. G Nucl. Part. Phys. 2009, 36, 125105. [Google Scholar] [CrossRef]
- Sammarruca, F.; Krastev, P.G. Spin polarized neutron matter within the Dirac-Brueckner-Hartree-Fock approach. Phys. Rev. C 2007, 75, 034315. [Google Scholar] [CrossRef]
- Behera, B.; Viñas, X.; Routray, T.R.; Robledo, L.M.; Centelles, M.; Pattnaik, S.P. Deformation properties with a finite-range simple effective interaction. J. Phys. G Nucl. Part. Phys. 2016, 43, 045115. Available online: http://iopscience.iop.org/0954-3899/43/4/045115 (accessed on 27 January 2024). [CrossRef]
- Li, B.A.; Ramos, À.; Verde, G.; Vidaña, I. Topical issue on nuclear symmetry energy. Eur. Phys. J. A 2014, 50, 9. [Google Scholar] [CrossRef]
- Chen, L.W.; Cai, B.J.; Ko, C.M.; Li, B.A.; Shen, C.; Xu, J. Higher-order effects on the incompressibility of isospin asymmetric nuclear matter. Phys. Rev. C 2009, 80, 014322. [Google Scholar] [CrossRef]
- Prakash, M.; Bedell, K.S. Incompressibility of neutron-rich nuclear matter. Phys. Rev. C 1985, 32, 1118(R). [Google Scholar] [CrossRef]
- Shlomo, S.; Kolomietz, V.M.; Colò, G. Deducing the nuclear-matter incompressibility coefficient from data on isoscalar compression modes. Eur. Phys. J. A 2006, 30, 23–30. [Google Scholar] [CrossRef]
- Garg, U.; Colò, G. The compression-mode giant resonances and nuclear incompressibility. Prog. Part. Nucl. Phys. 2018, 101, 55. [Google Scholar] [CrossRef]
- Tagami, S.; Wakasa, T.; Yahiro, M. Slope parameters determined from CREX and PREX2. Res. Phys. 2022, 43, 106037. [Google Scholar] [CrossRef]
- Dutra, M.; Lourenço, O.; Avancini, S.S.; Carlson, B.V.; Delfino, A.; Menezes, D.P.; Providência, C.; Typel, S.; Stone, J.R. Relativistic mean-field hadronic models under nuclear matter constraints. Phys. Rev. C 2014, 90, 055203. [Google Scholar] [CrossRef]
- Stone, J.R.; Stone, N.J.; Moszkowski, S.A. Incompressibility in finite nuclei and nuclear matter. Phys. Rev. C 2014, 89, 044316. [Google Scholar] [CrossRef]
- Avogadro, P.; Bertulani, C.A. Role of pairing in the description of giant monopole resonances. Phys. Rev. C 2013, 88, 044319. [Google Scholar] [CrossRef]
- Khan, E.; Margueron, J.; Vidaña, I. Constraining the Nuclear Equation of State at Subsaturation Densities. Phys. Rev. Lett. 2012, 109, 092501. [Google Scholar] [CrossRef]
- Vretenar, D.; Nikšić, T.; Ring, P. A microscopic estimate of the nuclear matter compressibility and symmetry energy in relativistic mean-field models. Phys. Rev. C 2003, 68, 024310. [Google Scholar] [CrossRef]
- Landau, L.D. The Theory of a Fermi Liquid. J. Exp. Theor. Phys. 1957, 3, 920. Available online: http://jetp.ras.ru/cgi-bin/e/index/e/3/6/p920?a=list (accessed on 27 January 2024).
- Landau, L.D. Oscillations in a Fermi Liquid. J. Exp. Theor. Phys. 1957, 5, 101. Available online: http://jetp.ras.ru/cgi-bin/e/index/e/5/1/p101?a=list (accessed on 27 January 2024).
- Landau, L.D. On the theory of the Fermi liquid. J. Exp. Theor. Phys. 1959, 8, 70. Available online: http://jetp.ras.ru/cgi-bin/e/index/e/8/1/p70?a=list (accessed on 27 January 2024).
- Vautherin, D.; Brink, D.M. Hartree-Fock calculations with Skyrme’s interaction. I. Spherical nuclei. Phys. Rev. C 1972, 5, 626. [Google Scholar] [CrossRef]
- Bäckman, S.O.; Källman, C.G.; Sjöberg, O. Calculation of Landau’s fermi-liquid parameters in pure neutron matter. Phys. Lett. B 1973, 43, 263–266. [Google Scholar] [CrossRef]
- Bäckman, S.O.; Jackson, A.D.; Speth, J. Landau parameters for nuclear matter using the Skyrme interaction. Phys. Lett. B 1975, 56, 209–211. [Google Scholar] [CrossRef]
- Cao, L.-G.; Colò, G.; Sagawa, H. Spin and spin-isospin instabilities and Landau parameters of Skyrme interactions with tensor correlations. Phys. Rev. C 2010, 81, 044302. [Google Scholar] [CrossRef]
- Chabanat, E.; Bonche, P.; Haensel, P.; Meyer, J.; Schaeffer, R. A Skyrme parametrization from subnuclear to neutron star densities Part II. Nuclei far from stabilities. Nucl. Phys. A 1998, 635, 231–256. [Google Scholar] [CrossRef]
- Chabanat, E.; Bonche, P.; Haensel, P.; Meyer, J.; Schaeffer, R. A Skyrme parametrization from subnuclear to neutron star densities. Nucl. Phys. A 1997, 627, 710–746. [Google Scholar] [CrossRef]
- Taqi, A.H.; Khidher, E.G. Nuclear multipole excitations in the framework of self-consistent Hartree–Fock random phase approximation for Skyrme forces. Pramana J. Phys. 2019, 93, 60. [Google Scholar] [CrossRef]
- Goriely, S.; Tondeur, F.; Pearson, J.M. A Hartree-Fock nuclear mass table. At. Data Nucl. Data Tables 2001, 77, 311–381. [Google Scholar] [CrossRef]
- Tselyaev, V.; Lyutorovich, N.; Speth, J.; Reinhard, P.-G.; Smirnov, D. Low-energy M1 excitations in 208Pb and the spin channel of the Skyrme energy-density functional. Phys. Rev. C 2019, 99, 064329. [Google Scholar] [CrossRef]
- Agrawal, B.K.; Shlomo, S.; Kim Au, V. Determination of the parameters of a Skyrme type effective interaction using the simulated annealing approach. Phys. Rev. C 2005, 72, 014310. [Google Scholar] [CrossRef]
- Lahiri, J.; Atta, D.; Basu, D.N. Properties of glitching pulsars in the Skyrme-Hartree-Fock framework. arXiv 2022, arXiv:2207.13384v3. [Google Scholar] [CrossRef]
- Keh-Fei, L.; Hongde, L.; Ma, Z.; Shen, Q.; Moszkowski, S.A. Skyrme-Landau parameterization of effective interactions (I). Hartree-Fock ground states. Nucl. Phys. A 1991, 534, 1–24. [Google Scholar] [CrossRef]
- Vuong, A.K. New Skyrme Nucleon-Nucleon Interaction for the Mean-Field Approximation. Doctoral Dissertation, Texas A & M University, College Station, TX, USA, 2003. Available online: http://hdl.handle.net/1969.1/5996 (accessed on 27 January 2024).
- Dutra, M.; Lourenço, O.; Delfino, A. Consistent Skyrme parametrization and its critical parameter values. J. Phys. Conf. Ser. 2019, 1291, 012040. Available online: https://iopscience.iop.org/article/10.1088/1742-6596/1291/1/012040/meta (accessed on 27 January 2024). [CrossRef]
- Nakada, H. Hartree-Fock approach to nuclear matter and finite nuclei with M3Y-type nucleon-nucleon interactions. Phys. Rev. C 2003, 68, 014316. [Google Scholar] [CrossRef]
- Idini, A.; Bennaceur, K.; Dobaczewski, J. Landau parameters for energy density functionals generated by local finite-range pseudopotentials. J. Phys. G Nucl. Part. Phys. 2017, 44, 064004. [Google Scholar] [CrossRef]
- Margueron, J.; Navarro, J.; Van Giai, N. Instabilities of infinite matter with effective Skyrme-type interactions. Phys. Rev. C 2002, 66, 014303. [Google Scholar] [CrossRef]
- Goriely, S.; Chamel, N.; Pearson, J.M. Further explorations of Skyrme-Hartree-Fock-Bogoliubov mass formulas. XII. Stiffness and stability of neutron-star matter. Phys. Rev. C 2010, 82, 035804. [Google Scholar] [CrossRef]
- Li, B.A.; Han, X. Constraining the neutron–proton effective mass splitting using empirical constraints on the density dependence of nuclear symmetry energy around normal density. Phys. Lett. B 2013, 727, 276–281. [Google Scholar] [CrossRef]
- Oertel, M.; Hempel, M.; Klähn, T.; Typel, S. Equations of state for supernovae and compact stars. Rev. Mod. Phys. 2017, 89, 015007. [Google Scholar] [CrossRef]
- Reed, B.T.; Fattoyev, F.J.; Horowitz, C.J.; Piekarewicz, J. Implications of PREX-2 on the Equation of State of Neutron-Rich Matter. Phys. Rev. Lett. 2021, 126, 172503. [Google Scholar] [CrossRef]
- Estee, J.; Lynch, W.G.; Tsang, C.Y.; Barney, J.; Jhang, G.; Tsang, M.B.; Wang, R.; Kaneko, M.; Lee, J.W.; Isobe, T.; et al. Probing the Symmetry Energy with the Spectral Pion Ratio. Phys. Rev. Lett. 2021, 126, 162701. [Google Scholar] [CrossRef]
- Danielewicz, P.; Singh, P.; Lee, J. Symmetry energy III: Isovector skins. Nucl. Phys. A 2017, 958, 147. [Google Scholar] [CrossRef]
- Xie, W.-J.; Li, B.-A. Bayesian Inference of High-density Nuclear Symmetry Energy from Radii of Canonical Neutron Stars. Astrophys. J. 2019, 883, 174. [Google Scholar] [CrossRef]
- Russotto, P.; Gannon, S.; Kupny, S.; Lasko, P.; Acosta, L.; Adamczyk, M.; Al-Ajlan, A.; Al-Garawi, M.; Al-Homaidhi, S.; Amorini, F.; et al. Results of the ASY-EOS experiment at GSI: The symmetry energy at suprasaturation density. Phys. Rev. C 2016, 94, 034608. [Google Scholar] [CrossRef]
- Senger, P. Probing Dense Nuclear Matter in the Laboratory: Experiments at FAIR and NICA. Universe 2021, 7, 171. [Google Scholar] [CrossRef]
- Zhang, Y.; Liu, M.; Xia, C.J.; Li, Z.; Biswal, S.K. Constraints on the symmetry energy and its associated parameters from nuclei to neutron stars. Phys. Rev. C 2020, 101, 034303. [Google Scholar] [CrossRef]
- Zhang, N.B.; Li, B.A. Extracting nuclear symmetry energies at high densities from observations of neutron stars and gravitational waves. Eur. Phys. J. A 2019, 55, 39. [Google Scholar] [CrossRef]
- Tong, H.; Zhao, P.; Meng, J. Symmetry energy at supra-saturation densities via the gravitational waves from GW170817. Phys. Rev. C 2020, 101, 035802. [Google Scholar] [CrossRef]
- Li, B.-A.; Cai, B.-J.; Xie, W.-J.; Zhang, N.-B. Progress in Constraining Nuclear Symmetry Energy Using Neutron Star Observables Since GW170817. Universe 2021, 7, 182. [Google Scholar] [CrossRef]
- Nakazato, K.; Suzuki, H. Cooling Timescale for Protoneutron Stars and Properties of Nuclear Matter: Effective Mass and Symmetry Energy at High Densities. Astrophys. J. 2019, 878, 25. [Google Scholar] [CrossRef]
- Yue, T.-G.; Chen, L.-W.; Zhang, Z.; Zhou, Y. Constraints on the symmetry energy from PREX-II in the multimessenger era. Phys. Rev. Res. 2022, 4, L022054. [Google Scholar] [CrossRef]
- Xie, W.J.; Li, B.A. Bayesian Inference of the Symmetry Energy of Superdense Neutron-rich Matter from Future Radius Measurements of Massive Neutron Stars. Astrophys. J. 2020, 899, 4. [Google Scholar] [CrossRef]
- Zhou, Y.; Chen, L.-W.; Zhang, Z. Equation of state of dense matter in the multimessenger era. Phys. Rev. D 2019, 99, 121301(R). [Google Scholar] [CrossRef]
- Drischler, C.; Furnstahl, R.J.; Melendez, J.A.; Phillips, D.R. How Well Do We Know the Neutron-Matter Equation of State at the Densities Inside Neutron Stars? A Bayesian Approach with Correlated Uncertainties. Phys. Rev. Lett. 2020, 125, 202702. [Google Scholar] [CrossRef]
- Lonardoni, D.; Tews, I.; Gandolfi, S.; Carlson, J. Nuclear and neutron-star matter from local chiral interactions. Phys. Rev. Res. 2020, 2, 022033(R). [Google Scholar] [CrossRef]
- Chen, L.-W. Symmetry energy systematics and its high density behavior. EPJ Web Conf. 2015, 88, 00017. [Google Scholar] [CrossRef]
- Lynch, W.G.; Tsang, M.B. Decoding the density dependence of the nuclear symmetry energy. Phys. Lett. B 2022, 830, 137098. [Google Scholar] [CrossRef]
- Lattimer, J.M.; Lim, Y. Constraining the symmetry parameters of the nuclear interaction. Astrophys. J. 2013, 771, 51. [Google Scholar] [CrossRef]
- Chen, L.W.; Ko, C.M.; Li, B.A. Nuclear matter symmetry energy and the neutron skin thickness of heavy nuclei. Phys. Rev. C 2005, 72, 064309. [Google Scholar] [CrossRef]
- Bano, P.; Pattnaik, S.P.; Centelles, M.; Viñas, X.; Routray, T.R. Correlations between charge radii differences of mirror nuclei and stellar observables. Phys. Rev. C 2023, 108, 015802. [Google Scholar] [CrossRef]
- Li, B.-A.; Magno, M. Curvature-slope correlation of nuclear symmetry energy and its imprints on the crust-core transition, radius, and tidal deformability of canonical neutron stars. Phy. Rev. C 2020, 102, 045807. [Google Scholar] [CrossRef]
- d’Etivaux, N.B.; Guillot, S.; Margueron, J.; Webb, N.; Catelan, M.; Reisenegger, A. New Constraints on the Nuclear Equation of State from the Thermal Emission of Neutron Stars in Quiescent Low-mass X-ray Binaries. Astrophys. J. 2019, 887, 48. [Google Scholar] [CrossRef]
- Carson, Z.; Steiner, A.W.; Yagi, K. Constraining nuclear matter parameters with GW170817. Phys. Rev. D 2019, 99, 043010. [Google Scholar] [CrossRef]
- Choi, S.; Miyatsu, T.; Cheoun, M.; Saito, K. Constraints on Nuclear Saturation Properties from Terrestrial Experiments and Astrophysical Observations of Neutron Stars. Astrophys. J. 2021, 909, 156. [Google Scholar] [CrossRef]
- Drischler, C.; Hebeler, K.; Schwenk, A. Asymmetric nuclear matter based on chiral two- and three-nucleon interactions. Phys. Rev. C 2016, 93, 054314. [Google Scholar] [CrossRef]
- Newton, W.G.; Crocombe, G. Nuclear symmetry energy from neutron skins and pure neutron matter in a Bayesian framework. Phy. Rev. C 2021, 103, 064323. [Google Scholar] [CrossRef]
- Grams, G.; Somasundaram, R.; Margueron, J.; Khan, E. Nuclear incompressibility and speed of sound in uniform matter and finite nuclei. Phys. Rev. C 2022, 106, 044305. [Google Scholar] [CrossRef]
- Sagawa, H.; Yoshida, S.; Cao, L.G. EoS from terrestrial experiments: Static and dynamic polarizations of nuclear density. AIP Conf. Proc. 2019, 2127, 020002. [Google Scholar] [CrossRef]
- Tews, I.; Lattimer, J.M.; Ohnishi, A.; Kolomeitsev, E.E. Symmetry Parameter Constraints from a Lower Bound on Neutron-matter Energy. Astrophys. J. 2017, 848, 105. [Google Scholar] [CrossRef]
- Zhang, N.B.; Cai, B.J.; Li, B.A.; Newton, W.G.; Xu, J. How tightly is the nuclear symmetry energy constrained by a unitary Fermi gas? Nucl. Sci. Tech. 2017, 28, 181. [Google Scholar] [CrossRef]
- Mondal, C.; Agrawal, B.K.; De, J.N.; Samaddar, S.K.; Centelles, M.; Viñas, X. Interdependence of different symmetry energy elements. Phy. Rev C 2017, 96, 021302(R). [Google Scholar] [CrossRef]
- Sagawa, H.; Yoshida, S.; Zeng, G.M.; Gu, J.Z.; Zhang, X.Z. Isospin dependence of incompressibility in relativistic and nonrelativistic mean field calculations. Phys. Rev. C 2007, 76, 034327. [Google Scholar] [CrossRef]
- Li, T.; Garg, U.; Liu, Y.; Marks, R.; Nayak, B.K.; Rao, P.V.M.; Fujiwara, M.; Hashimoto, H.; Kawase, K.; Nakanishi, K.; et al. Isotopic Dependence of the Giant Monopole Resonance in the Even-A 112–124Sn Isotopes and the Asymmetry Term in Nuclear Incompressibility. Phys. Rev. Lett. 2007, 99, 162503. [Google Scholar] [CrossRef]
- Li, T.; Garg, U.; Liu, Y.; Marks, R.; Nayak, B.K.; Rao, P.V.M.; Fujiwara, M.; Hashimoto, H.; Kawase, K.; Nakanishi, K.; et al. Isoscalar giant resonances in the Sn nuclei and implications for the asymmetry term in the nuclear-matter incompressibility. Phys. Rev. C 2010, 81, 034309. [Google Scholar] [CrossRef]
- Cozma, M.D. Feasibility of constraining the curvature parameter of the symmetry energy using elliptic flow data. Eur. Phys. J. A 2018, 54, 40. [Google Scholar] [CrossRef]
- Centelles, M.; Roca-Maza, X.; Viñas, X.; Warda, M. Nuclear Symmetry Energy Probed by Neutron Skin Thickness of Nuclei. Phys. Rev. Lett. 2009, 102, 122502. [Google Scholar] [CrossRef]
- Cai, B.J.; Chen, L.W. Constraints on the skewness coefficient of symmetric nuclear matter within the nonlinear relativistic mean field model. Nucl. Sci. Tech. 2017, 28, 185. [Google Scholar] [CrossRef]
- Farine, M.; Pearson, J.M.; Tondeur, F. Nuclear-matter incompressibility from fits of generalized Skyrme force to breathing-mode energies. Nucl. Phy. A 1997, 615, 135. [Google Scholar] [CrossRef]
- Xie, W.-J.; Li, B.-A. Bayesian inference of the incompressibility, skewness and kurtosis of nuclear matter from empirical pressures in relativistic heavy-ion collisions. J. Phys. G Nucl. Part. Phys. 2021, 48, 025110. [Google Scholar] [CrossRef]
- Steiner, A.W.; Lattimer, J.M.; Brown, E.F. The Equation of State from Observed Masses and Radii of Neutron Stars. Astrophys. J. 2010, 722, 33–54. [Google Scholar] [CrossRef]
- Alam, N.; Agrawal, B.K.; De, J.N.; Samaddar, S.K.; Colò, G. Equation of state of nuclear matter from empirical constraints. Phys. Rev. C 2014, 90, 054317. [Google Scholar] [CrossRef]
- Alam, N.; Agrawal, B.K.; Fortin, M.; Pais, H.; Providência, C.; Raduta, A.R.; Sulaksono, A. Strong correlations of neutron star radii with the slopes of nuclear matter incompressibility and symmetry energy at saturation. Phys. Rev. C 2016, 94, 052801(R). [Google Scholar] [CrossRef]
- Baym, G.; Bethe, H.A.; Pethick, C.J. Neutron star matter. Nucl. Phys. A 1971, 175, 225–271. [Google Scholar] [CrossRef]
- Baym, G.; Pethick, C.J.; Sutherland, P. The Ground State of Matter at High Densities: Equation of State and Stellar Models. Astrophys. J 1971, 170, 299–317. [Google Scholar] [CrossRef]
- De, J.N.; Samaddar, S.K.; Agrawal, B.K. Reassessing nuclear matter incompressibility and its density dependence. Phys. Rev. C 2015, 92, 014304. [Google Scholar] [CrossRef]
- Capano, C.D.; Tews, I.; Brown, S.M.; Margalit, B.; De, S.; Kumar, S.; Brown, D.A.; Krishnan, B.; Reddy, S. Stringent constraints on neutron-star radii from multimessenger observations and nuclear theory. Nat. Astron. 2020, 4, 625–632. [Google Scholar] [CrossRef]
- Raaijmakers, G.; Greif, S.K.; Hebeler, K.; Hinderer, T.; Nissanke, S.; Schwenk, A.; Riley, T.E.; Watts, A.L.; Lattimer, J.M.; Ho, W.C.J. Constraints on the Dense Matter Equation of State and Neutron Star Properties from NICER’s Mass–Radius Estimate of PSR J0740+6620 and Multimessenger Observations. Astrophys. J. Lett. 2021, 918, L29. [Google Scholar] [CrossRef]
- Miller, M.C.; Lamb, F.K.; Dittmann, A.J.; Bogdanov, S.; Arzoumanian, Z.; Gendreau, K.C.; Guillot, S.; Ho, W.C.G.; Lattimer, J.M.; Loewenstein, M.; et al. The Radius of PSR J0740 + 6620 from NICER and XMM-Newton Data. Astrophys. J. Lett. 2021, 918, L28. [Google Scholar] [CrossRef]
- Pang, P.T.H.; Tews, I.; Coughlin, M.W.; Bulla, M.; Broeck, C.V.D.; Dietrich, T. Nuclear Physics Multimessenger Astrophysics Constraints on the Neutron Star Equation of State: Adding NICER’s PSR J0740 + 6620 Measurement. Astrophys. J. 2021, 922, 14. [Google Scholar] [CrossRef]
- Jiang, J.-L.; Tang, S.-P.; Shao, D.-S.; Han, M.-Z.; Li, Y.-J.; Wang, Y.-Z.; Jin, Z.-P.; Fan, Y.-Z.; Wei, D.-M. The Equation of State and Some Key Parameters of Neutron Stars: Constraints from GW170817, the Nuclear Data, and the Low-mass X-Ray Binary Data. Astrophys. J. 2019, 885, 39. [Google Scholar] [CrossRef]
- Abbott, R.; Abbott, T.D.; Abraham, S.; Acernese, F.; Ackley, K.; Adams, C.; Adhikari, R.X.; Adya, V.B.; Affeldt, C.; Agathos, M.; et al. GW190814: Gravitational Waves from the Coalescence of a 23 Solar Mass Black Hole with a 2.6 Solar Mass Compact Object. (LIGO Scientific Collaboration and Virgo Collaboration). Astrophys. J. 2020, 896, L44. [Google Scholar] [CrossRef]
- Bauswein, A.; Blacker, S.; Lioutas, G.; Soultanis, T.; Vijayan, V.; Stergioulas, N. Systematics of prompt black-hole formation in neutron star mergers. Phys. Rev. D 2021, 103, 123004. [Google Scholar] [CrossRef]
- Bauswein, A.; Janka, H.-T. Hebeler, K.; Schwenk, A. Equation-of-state dependence of the gravitational-wave signal from the ring-down phase of neutron-star mergers. Phys. Rev. D 2012, 86, 063001. [Google Scholar] [CrossRef]
- Annala, E.; Gorda, T.; Kurkela, A.; Vuorinen, A. Gravitational-Wave Constraints on the Neutron-Star-Matter Equation of State. Phys. Rev. Lett. 2018, 120, 172703. [Google Scholar] [CrossRef] [PubMed]
- Fattoyev, F.J.; Piekarewicz, J.; Horowitz, C.J. Neutron Skins and Neutron Stars in the Multimessenger Era. Phys. Rev. Lett. 2018, 120, 172702. [Google Scholar] [CrossRef]
- Bauswein, A.; Just, O.; Janka, H.-T.; Stergioulas, N. Neutron-star Radius Constraints from GW170817 and Future Detections. Astrophys. J. Lett. 2017, 850, L34. [Google Scholar] [CrossRef]
- Bauswein, A.; Baumgarte, T.W.; Janka, H.T. Prompt Merger Collapse and the Maximum Mass of Neutron Stars. Phys. Rev. Lett. 2013, 111, 131101. [Google Scholar] [CrossRef]
- Perego, A.; Logoteta, D.; Radice, D.; Bernuzzi, S.; Kashyap, R.; Das, A.; Padamata, S.; Prakash, A. Probing the Incompressibility of Nuclear Matter at Ultrahigh Density through the Prompt Collapse of Asymmetric Neutron Star Binaries. Phys. Rev. Lett. 2022, 129, 032701. [Google Scholar] [CrossRef] [PubMed]
- Shibata, M.; Taniguchi, K.; Uryū, K. Merger of binary neutron stars with realistic equations of state in full general relativity. Phys. Rev. D 2005, 71, 084021. [Google Scholar] [CrossRef]
- Hotokezaka, K.; Kyutoku, K.; Okawa, H.; Shibata, M.; Kiuchi, K. Binary neutron star mergers: Dependence on the nuclear equation of state. Phys. Rev. D 2011, 83, 124008. [Google Scholar] [CrossRef]
- Köppel, S.; Bovard, L.; Rezzolla, L. A General-relativistic Determination of the Threshold Mass to Prompt Collapse in Binary Neutron Star Mergers. Astrophys. J. Lett. 2019, 872, L16. [Google Scholar] [CrossRef]
- Kashyap, R.; Das, A.; Radice, D.; Padamata, S.; Prakash, A.; Logoteta, D.; Perego, A.; Godzieba, D.A.; Bernuzzi, S.; Bombaci, I.; et al. Numerical relativity simulations of prompt collapse mergers: Threshold mass and phenomenological constraints on neutron star properties after GW170817. Phys. Rev. D 2022, 105, 103022. [Google Scholar] [CrossRef]
- Glendenning, N.K. Compact Stars: Nuclear Physics, Particle Physics, and General Relativity; Springer: Berlin/Heidelberg, Germany, 2000. [Google Scholar] [CrossRef]
- Margaritis, C.; Koliogiannis, P.S.; Moustakidis, C.C. Speed of sound constraints on maximally rotating neutron stars. Phys. Rev. D 2020, 101, 043023. [Google Scholar] [CrossRef]
- Koliogiannis, P.S.; Moustakidis, C.C. Constraints on the equation of state from the stability condition of neutron stars. Astrophys. Space Sci. 2019, 364, 52. [Google Scholar] [CrossRef]
- Blaizot, J.P. Nuclear compressibilities. Phys. Rep. 1980, 64, 171–248. [Google Scholar] [CrossRef]
- Zhang, N.B.; Li, B.A. Impact of symmetry energy on sound speed and spinodal decomposition in dense neutron-rich matter. Eur. Phys. J. A 2023, 59, 86. [Google Scholar] [CrossRef]
- Hartle, J.B. Bounds on the mass and moment of inertia of non-rotating neutron stars. Phys. Rep. 1978, 46, 201–247. [Google Scholar] [CrossRef]
- Reed, B.; Horowitz, C.J. Large sound speed in dense matter and the deformability of neutron stars. Phys. Rev. C 2020, 101, 045803. [Google Scholar] [CrossRef]
- Cottam, J.; Paerels, F.; Mendez, M. Gravitationally redshifted absorption lines in the X-ray burst spectra of a neutron star. Nature 2002, 420, 51–54. [Google Scholar] [CrossRef]
- Hambaryan, V.; Neuhäuser, R.; Suleimanov, V.; Werner, K. Observational constraints of the compactness of isolated neutron stars. J. Phys. Conf. Ser. 2014, 496, 012015. [Google Scholar] [CrossRef]
- Hambaryan, V.; Suleimanov, V.; Haberl, F.; Schwope, A.D.; Neuhäuser, R.; Hohle, M.; Werner, K. The compactness of the isolated neutron star RXJ0720.4-3125. Astron. Astrophys. 2017, 601, A108. [Google Scholar] [CrossRef]
- Tang, S.P.; Jiang, J.L.; Gao, W.-H.; Fan, Y.-Z.; Wei, D.-M. The Masses of Isolated Neutron Stars Inferred from the Gravitational Redshift Measurements. Astrophys. J. 2020, 888, 45. [Google Scholar] [CrossRef]
- Sotani, H.; Iida, K.; Oyamatsu, K.; Ohnishi, A. Mass and radius formulas for low-mass neutron stars. Prog. Theor. Exp. Phys. 2014, 2014, 051E01. [Google Scholar] [CrossRef]
- Sotani, H.; Nishimura, N.; Naito, T. New constraints on the neutron-star mass and radius relation from terrestrial nuclear experiments. Prog. Theor. Exp. Phys. 2022, 2022, 041D01. [Google Scholar] [CrossRef]
- Carlson, B.V.; Dutra, M.; Lourenço, O.; Margueron, J. Low-energy nuclear physics and global neutron star properties. Phys. Rev. C 2023, 107, 035805. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).