Abstract
The World-Class University/Hanyang Project launched in Korea in 2008 led to what is now called the “pseudo-conformal model” that addresses dense compact star matter and is confronted in this short note with the presently available astrophysical observables, with focus on those from gravity waves. The predictions made nearly free of parameters by the model involving “topology change” remain more or less intact “un-torpedoed” by the data.
1. Introduction
In 2008, the Korean Government launched a five-year “World-Class University (WCU)” Project, and the Hanyang University in Seoul was chosen as one of the projects to be under the directorship of Hyun Kyu Lee in the Physics Department. The objective of the WCU/Hanyang was to elevate the university in basic science to the world-class level, in anticipation of the forthcoming establishment of an ambitious research institute called the Institute of Basic Science (IBS). The subject matter picked was “Baryonic Matter under Extreme Conditions in the Universe”, which focused on the superdense matter expected to be found in massive compact stars on the verge of gravitational collapse. This subject matter was already one of the major themes at the Korea Institute of Advanced Studies (KIAS) in late 1990s and early 2000s while I was an invited professor in its School of Physics, working in collaboration with Hyun Kyu Lee, Dong-Pil Min, and Byung-Yoon Park of Korea and Vicente Vento of Spain, all at the KIAS as visiting scholars.
The property of dense baryonic matter in compact stars is in the realm of QCD involving both low and high densities. However, QCD cannot access the density regimes, famously non-perturbative, of nuclear and compact star matter. Therefore, there was no reliable theoretical tool to access the regimes concerned. Neither could it be accessed experimentally, since no accelerators probing dense matter at low temperature involved were available then. What started at the WCU/Hanyang Project was the construction of a single unified theoretical framework to explore these uncharted density regimes starting with what was explored in KIAS. The objective was to formulate an effective field theory approach with a minimal number of unknown parameters, post-dict correctly the known nuclear matter properties at fm, and predict the terrestrial nuclear and compact star properties that were yet to be measured. It was, in our mind, in anticipation of what is to be studied at the costly RIB machine “RAON” approved to be constructed at the IBS.
The status of the model in nuclear physics and astrophysics up to early 2017 before the advent of the recent gravity wave measurements was sketched in [1]. The gravity wave data made feasible the direct confrontation of some of the predictions made then with the oncoming observables.
To the utter surprise—and perhaps more to the incredulity—of the workers in the field, what appears to be an over-simplified “coarse-grained framework” with no parameter fiddling—in stark contrast to the currently favored approaches of hybridizing with “artificially revamped” quark descriptions—has met, so far, with no serious tension in explaining satisfactorily all up-to-date available data. In this paper, I will list the most relevant observables—there are too many to be fair to all—both nuclear and astrophysical, just to show how the predictions that followed from the formulation initiated at the KIAS and pursued at the WCU/Hanyang fare, and how the possible discrepancies, if any, between what is predicted and what is measured can be reconciled within the model. It should be stressed that the spirit of this presentation is basically different from the current activities in the field where various sophisticated statistical analyses in the theoretical inputs and experimental results are focused on. All the results I will give are found essentially in the two papers [2,3], which constituted an important part of the PhD thesis of Won-Gi Paeng and are extensively reviewed in [4,5]. Some trivial numerical errors committed in [3] that remained in [4,5] will be corrected in the predicted results cited in what follows. Only if necessary will I refer to the specific articles for more precision or explanation. Otherwise I will avoid entering into details as much as possible.
2. GEFT
In going from nuclear matter to dense compact star matter, as is commonly believed, there must be present a transition, either a phase change or just a continuous crossover, from the (low-)density regime, say, ∼, of hadrons to the (high-)density regime, say, , of compact stars. This transition is commonly referred to as “hadron-quark continuity (HQC)”, presumed—but not proven—to be encoded in QCD. The strategy that was adopted in the WCU/Hanyang was that this HQC could be effectuated by a change in topology from baryons in the baryonic matter to fractionally charged objects in the compact star matter, an idea anchored on what is referred to as the “Cheshire Cat Principle (CCP)”. This idea followed from the notion that in QCD, a nucleon can be described as a topological object, say, a skyrmion and half-skyrmions at large and at high density when put on a crystal lattice. An early review on this matter can be found in [6].
The key idea of how to implement the skyrmion–half-skyrmion transition—referred to in what follows as “topology change” **(**The topology change involved here could be different in character from what is taking place in condensed matter systems.)—as a mechanism for the HQC was worked out first in early 2000 but appeared in the literature a decade later [7]. The publication of this work was delayed so long due to the referees’ objections to the novel ideas developed in the paper, dismissing them as mere “conjectures” without any counter arguments.
The topology change involved here is best described in terms of skyrmions put on crystal lattice, although it is well known that the skyrmion-half-skyrmion changeover actually makes no sense. This is because whereas the 1/2-skyrmion phase can be justified on crystal lattice at high density (and large limit), low-density matter cannot be in crystal, so the transition, whether bona-fide phase transition or smooth cross-over, cannot be established with skyrmions on crystal lattice [8]. This of course does not mean that the crossover in the skyrmion description in a more general setting does not exist. In fact it is this point that was resolved in [7]; it involves hidden local symmetry (HLS) and hidden scale symmetry (HSS) entering into the baryonic structure. The details given in [4,5] on how the hidden symmetries must figure appear to be somewhat complicated at first sight, but the basic structure is rather simple as I will try to explain. See [9] for more details. I believe this accounts for the lack of attention paid to this development in nuclear and astrophysical communities.
The most crucial ingredient for the topology change is the cusp structure in the symmetry energy (denoted ). It reflects the isospin asymmetry in the energy functional . The cusp is seen when the nucleons are put on a crystal lattice. It appears at the density, denoted , lying above the normal matter density . Identified as the putative HQC density, it is found to be in the range
This cusp is displayed by the dotted red curve in the schematic figure, Figure 1.
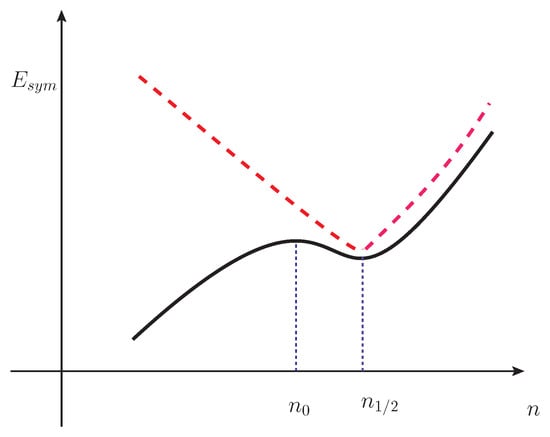
Figure 1.
Schematic illustration of the symmetry energy by the skyrmion crystal (red dashed line)) and by nucleon correlations dominated by the nuclear tensor forces (solid line).
While one can reasonably assume that for makes sense on the crystal lattice, the behavior for , however, cannot be taken seriously, as mentioned above.
First, how does the topology change take place?
It is triggered on the crystal lattice by the bilinear quark condensate , when averaged, going to zero, whereas the pion decay constant remains non-zero. So it does not involve chiral symmetry restoration. It implies that the non-vanishing order parameter may be the quartic quark condensate . There are arguments in the literature that such a symmetry structure is at odds with ’t Hooft anomaly constraints. However, it remains controversial whether such a no-go theorem holds in the present case. In fact there are some cases in condensed matter where this no-go theorem does not seem to hold [10].
To exploit this cusp structure requires knowing how the topology change can be modified in reality. Now how can the topology change be incorporated in a realistic theory?
As shown in [7], it is the hidden symmetries that bring in heavy degrees of freedom to an effective Lagrangian. It is now recognized that Weinberg’s chiral effective field theory (chiEFT) with the nucleons and pions as the only relevant degrees of freedom, which will be called SchiEFT in what follows, with “S” standing for “standard”, works well with a suitable cutoff up to the density and slightly higher. It is bound to break down at higher densities, say, . This success can be considered as a case where Weinberg’s “Folk Theorem” on EFT is “proven”. What was shown in [7] is that the vector mesons and the scalar meson , which is related to what is known as “conformal compensator”, with the former endowed with “vector manifestation fixed point” (VMFP) (at which the mass [11]) and the latter with the “genuine dilaton” with an IR fixed point (at which the dilaton mass tends to ), enable one to go across, in the (more generally the EoS), “smoothly” from below to above . What is in action is the interplay between the VMFP and the nuclear tensor force that leads to at high density () and the “genuine dilaton” with an IR fixed point at at which scale symmetry is restored. The net effect of the interplays at is displayed by the black solid curve in Figure 1. It will be shown later that the cusp, smoothed to an inflection, will play an important role in confronting some of the important gravity wave data, such as the tidal deformability, sound velocity, etc.
The effective theory GnEFT detailed in the reviews [4,5] is formulated with the Lagrangian with the HLS mesons and the genuine dilaton (GD) scalar included as the relevant degrees of freedom in addition to the that figure in SchiEFT. The heavy degrees of freedom (HDFs for short) are to mediate the crossover from hadrons to quark/gluons. In our approach, it is here that the topology change enters as a mechanism for hadron–quark continuity.
Given the Lagrangian , there can be several ways of setting up a GnEFT. What is required is the implementation of the HQC at a density .
It turns out to be feasible to set up a scale-HLS-invariant Lagrangian (with HLS gauge-equivalent to non-linear sigma model, so chiral symmetry is encoded therein [11].) with a power expansion going beyond the chiral expansion employed in the standard chiral EFT by taking into account the hidden symmetries including HLS. The expansion has been worked out to NLO in scale-chiral expansion following [11,12,13]. Unfortunately there are much too many parameters even at NLO that it has remained unexplored.
An alternative approach exploited in the WCU/Hanyang program was to use the “double-decimation” strategy developed in [14], which is to apply (Wilsonian) renormalization group approach to the strongly correlated fermions on the Fermi sphere. The first decimation is made to the Landau(-Migdal) Fermi liquid fixed point (FLFP) with the cutoff on top of the Fermi sea along the line developed in [15] for electrons. Then we carry out the second decimation going beyond the FLFP. It was shown a long time ago that a chiral Lagrangian of the -type, somewhat simplified, can be mapped to Landau(-Migdal) Fermi liquid structure, which worked remarkably well at the FLFP level [16,17]. This structure is incorporated into the GnEFT with the possibility of going beyond the FLFP in the -RG approach, as developed by Tom Kuo with Gerry Brown and collaborators at Stony Brook. Tom Kuo’s role in the initial development resulted in the crucial publication of [2,3]. In the predictions discussed below, it will be primarily at the level of the FLFP approximation. The corrections in the -RG will be quoted to justify the FLFP approximation.
For those who are not familiar with the GnEFT strategy sketched above, let me just mention that this approach can be considered as a “refined” version of covariant density functional approaches anchored on the Hohenberg–Kohn theorem on DFT. The refinement, among others, has to do with the replacement of the high-dimension field operators, injected (arbitrarily) to improve the Walecka-type linear model (e.g., the excessively high nuclear matter compression modulus ), by the parameters of the Lagrangian with the dilaton condensate encoded by the scale-chiral symmetry. The approach is free of arbitrariness and thermodynamically consistent [17].
3. Predictions
Here I will give the predictions obtained in [3] and listed in [4,5]. What is given involves no fiddling in the parameters in the Lagrangian . Only some numerical errors committed in [3] will be corrected.
3.1. Density Regime
First up to , at which the HQC intervenes, what is more or less equivalent to what is given in SchiEFT is reproduced by the mean-field of , the parameters of which are controlled by BR scaling sliding in density in the dilaton condensate (where * stands for the density dependence) known up to . At the equilibrium density , one post-dicts
Just to give an idea what the significance of this result is, let me quote what the present state-of-the-art high-order (NLO) SchiEFT calculation obtains: and . All other nuclear matter properties at the equilibrium density (including the symmetry energy ) do come out essentially the same as what are calculated in SchiEFT at NLO. The only parameter needed is the mass of the “genuine dilaton” identified with . The BR scaling relates the scaling of the dilaton condensate to that of the pion condensate
which is measured in deeply bound atomic nuclei . This is given by chiral symmetry, so is not a parameter. Roughly speaking, the linear HLS with the BR scaling does what covariant density functional models with higher-dimension operators do. The power of this approach over covariant density functional models is that the parameters of higher derivative terms are fixed by hidden local symmetry with thermodynamic consistency [17]. It also captures higher chiral power terms, say, NLO in SchiEFT.
On the other hand, the symmetry energy slope L could be different from what one obtains in SchiEFT. This is because of the onset of the cusp, as shown in Figure 1 at . The cusp as discussed in [7] involves the tensor force structure controlled by the behavior of the HLS gauge coupling running in the RG flow toward the vector manifestation . If were not too far above , then the slope of at would be inevitably affected by the hidden cusp structure. I will not go for higher derivatives of —such as with two derivatives—since they will depend more sensitively on where lies.
The GnEFT predicts for
to be compared with the SchiEFT results
It should be noted that while J is more or less the same as what SchiEFT gives, “soft” in the EoS, L is significantly greater than that of SchiEFT, showing the (smooth) onset of hardness, tending toward what is observed in the PREX/Jefferson experiment [18,19]. What is noteworthy is that the behavior of near in GnEFT manifesting the “pseudo-gap” behavior of the chiral condensate in the topology change predicts naturally the soft-to-hard crossover tendency of the EoS at ∼, which is attributed to the putative HQC in QCD.
3.2. Density Regime
Although the slope L given in (3) can be considered as a prediction, not as a post-diction, of the PCM, one cannot, however, have a great confidence in its precision. The reason is that it is the most difficult density regime in the EoS to theoretically control. At , EFT valid at low density and perturbative QCD valid at high density “meet”. Therefore, the slope L will be sensitive to the location with interplay of different degrees of freedom that can be treated with the least confidence. This aspect will appear significantly in the tidal deformability measured at 1.4 and also in the sound velocity of the star.
While the region is controlled essentially by the scaling factor , accessible both by theory and experiment, the topology change brings in major modifications in the properties of the Lagrangian . This is explained in terms of a series of “Propositions” in [4]. I admit that some of them are superfluous or redundant and could be largely weeded out.
Basically what happens is rather simple.
Phenomenology in nuclear processes suggests the crossover density regime overlaps with the point at which the double decimation is to be made [14]. It has been taken to be [2,3]
The primary mechanism that produces the cusp in the symmetry energy , namely, the skyrmion-1/2-skyrmion transition density, is driven in GnEFT by the nuclear tensor forces sliding with density, going to ∼0 at the range most effective, say, ∼1 fm in nuclear interactions. What was required was that the VM fixed point density be [3], much greater than the ∼ thought to be present in the core of massive stars. This feature required that while the pion decay constant does not go to zero at , it is the gauge coupling that should tend to zero [11]. (I note as a footnote that this feature, which presumably takes place also in temperature, was not taken into account in heavy-ion experiments looking for the dropping mass near the chiral restoration temperature . It led to the erroneous “ruling out of BR scaling” following the NA60 data.) The scenario with differs from [2] in the prediction for the sound speed in compact stars. How the VM density intervenes in the pseudo-conformal behavior of the sound velocity however remains mysterious.
Another important property in is that the dilaton decay constant** (**From here on, I will use the linear conformal compensator field instead of the nonlinear field for the dilaton field, .) gets locked to the pion decay constant in the GD scheme [12,13] and remains more or less constant:
where is a chiral symmetric mass of the quasiparticle in the 1/2-skyrmiom phase. This follows from the emergent parity doubling in the baryon structure. This feature differs from other parity-doubling scenarios where the symmetry is present intrinsically, not emergent, in the effective Lagrangian [20]. It is not clear at the moment how this difference impacts on the properties of compact stars. One of the crucial consequences of this parity doubling is that the symmetry for the and , fairly good in , gets broken by the dynamics involved in the quasiparticle interactions with and exchanges in the 1/2-skyrmion phase
and leads to weakly interacting quasiparticles of two 1/2-skyrmions bound or confined by hidden monopoles [21] with the quasiparticle mass
I will speculate below how the suppression of the monopoles could liberate the half-skyrmions and transform them into fractionized quasiparticles that mimic fractionally charged quarks.
What is given in (6) can also be obtained in what is referred to as “dilaton-limit fixed point” [22] when where in the mean field of GnEFT. In that limit one finds
Since QCD cannot be solved nonperturbatively for the various limiting conditions, the locations of the DLFP, the vector manifestation (VM) fixed point, the IR fixed point, etc., though not too far apart, are not precisely known. For the issue concerned, i.e., the physics of compact stars, whether or not and where they overlap cannot be addressed. They may, however, be irrelevant for the qualitative properties we are interested in near the density regime of HQC.
To be more quantitative, one needs to go beyond the mean-field-level approximation of GnEFT. To do this, the corrections to the Landau Fermi-liquid fixed point approximation—in RG in the double-decimation strategy [14]—could be made as described in [3]. In this reference, a rather involved scaling behavior of the gauge coupling constant in the vicinity of the crossover density was used. Although it has not been checked in detail, it seems most likely that such a complicated scaling behavior is unnecessary because it simply reflects how the gauge coupling moves toward the vector manifestation density that lies way above the density involved in the star. This is indeed supported in the “pseudo-conformal model (PCM)” (defined below) used for making predictions.
In listing the predictions made in GnEFT, there are two additional remarks to make.
First, the predictions have been made for the range of the crossover density
The predictions are roughly the same within that range so I will not favor any specific values in between. The extremes and 4 are somewhat disfavored, although they cannot be dismissed, as we will see. Second, the prediction made in the PCM is checked with the double decimation RG only for . It was concluded that the same should hold for the range (10).
Second, the PCM** ** I must admit that the term “pseudo-conformal” could be a misnomer. It simply indicates that conformal symmetry, both explicitly and spontaneously broken, emerges in dense matter driven by nuclear interactions.) was constructed by replacing the RG for in the energy density of the nucleon by two-parameter analytic form matched at to the for . The matched energy density (PCM) is found to precisely reproduce RG data for the whole range of density. For example, in Figure 2, the symmetry energy in the PCM (solid line) is shown to match exactly the full RG. It also shows that the higher-order terms beyond the mean-field approximation do indeed smoothen the cusp singularity—schematically indicated in Figure 1—as well as correctly treat the density regime .
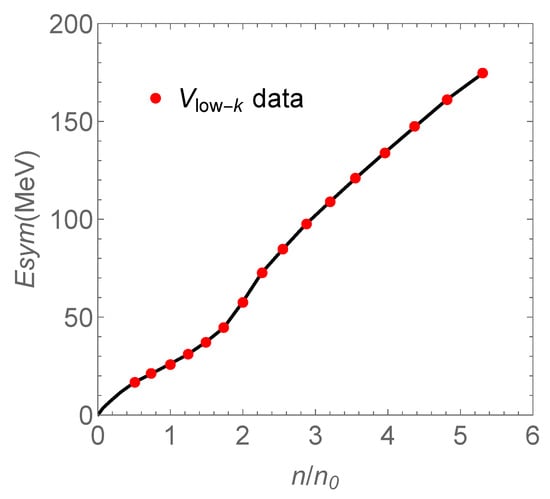
Figure 2.
(solid circle) obtained in the full RG approach for . It is reproduced exactly by the pseudo-conformal model (solid line). Idem for .
This result strongly suggests that the complicated scaling for the HLS gauge coupling used in the RG calculation could well be made much simpler, as mentioned above.
As mentioned, the smooth matching of the skyrmion-1/2-skyrmion property at could be deceptive given the oversimplified joining of hadron–quark degrees of freedom. The PCM may therefore hide complex structure lying just above the crossover density, say, in the density regime ∼. I will point this out in connection with some of the astrophysical observables to be discussed below.
What transpires from the properties (I)–(IV) incorporated into GnEFT for the PCM is that the trace of the energy-momentum-tensor for goes as
This feature, the crucial element in the theory, is reproduced in the RG double-decimation approach, as shown in Figure 2.
3.3. Predictions vs. Observables
Avoiding extensive references, both theory and experiment, I will list only those considered to be well-determined to the extent that it is feasible with the source from [18,19].
- Smoothed cusp of at :The bending-over of influences the slope L and induces the “soft-to-stiff” changeover. It also plays a crucial role in giving rise to the pseudo-conformal sound velocity (to be addressed below). Although as stressed the detailed structure and magnitude cannot be precisely pinned down, its simplicity with intricate topology change in the jungle of theories (as depicted in [9]) is a distinctive prediction of the PCM. It is at odds with the PREX-II/Jefferson data, which give generally stiff EoS, although there are some caveats [18,19]. To date, there are no trustworthy experimental data to quantitatively compare with.
- Maximum mass star: :No empirical data are known to be available at present for the central density . The only information on this quantity inferred—not extracted—from PSR J0740 + 6620 is violently at odds with the PCM prediction. I will address this issue below.
- 1.44 star:The stunning agreements between the PCM predictions and the NICER and XMM-Newton measurements—with the exception of the sound velocity to be addressed below—could not be accidental. Not only does the maximum star mass come out the same, but also the radii agree. Furthermore, the difference , in agreement with the data. We will note later that this support of the PCM by the NICER/XMM-Newton has an even more surprising implication on scale-chiral symmetry in nuclear medium so far unsuspected.
Let me make some further comments here on the PCM results.
What is given falls in the range of . The maximum mass comes out to be ∼ for . However, at this crossover density, although other global properties are not drastically different from the lower values of , the sound speed overshoots the causality bound with a more pronounced bump and the pressure greatly exceeds what is indicated in heavy-ion data. It seems to be ruled out in the PCM of GnEFT.
One observes that the radius comes out to be ∼ km in the wide range of the star mass and central density involved. Thus, the stars of masses ∼ solar mass and ∼ solar mass have almost the same radius. This is in agreement with what is being observed in the gravity wave data.
- Tidal deformabilityThe predicted in the PCM comes out to be ∼550, to be compared with (GW1700817). This may seem to signal a tension. However, there is a basic difficulty in theoretically pinning down . In the PCM, the density at which is measured is ∼. This density sits very close to where the topology change takes place. It is here the SchiEFT is most likely to start breaking down as the cusp in indicates and the pQCD cannot access. This is an “uncharted wilderness” for theory. As can be seen in [4], a small increase in the central density, say, from to (or increase in corresponding star mass), makes drop to 420 while involving no change at all in radius. This means that the location of the HQC will strongly influence the . One can associate this behavior with the increase in attraction in going from toward in the cusp structure as one can see in the schematic plot Figure 1. This clearly suggests that it would be extremely difficult to theoretically pin down in the vicinity of the crossover regime.As noted below, the sound velocity has a complex “bump” structure in the vicinity of the topology change density. This is due to the interplay, encoding the putative HQC, between the hadronic degrees of freedom and the “dual quark-gluon” degrees of freedom. This would complicate significantly the linking of to the structure of the sound velocity below or near . To give an example, let me quote [23] where the bump structure—“the slope, the hill, the drop, the swoosh, etc.”—associated with the possible phase structure of QCD is proposed to pin down by up-coming measurements. The hope here is to determine the possible phase transition near the HQC density. Given the theoretical wilderness inevitably involved, this seems a far-fetched endeavor.In short, contrary to what is claimed by some workers in the field, ruling out an EoS based on the precise value of would be premature.
- Sound speedThe most striking prediction of the PCM, so far not shared by other models, is the sound speed for . It predicts the pseudo-conformal sound speedIt is not to be identified with the conformal sound speed because the energy-momentum tensor is not traceless, i.e., scale symmetry is spontaneously broken.This prediction can be understood as follows.As noted above, the quasiparticle mass goes as the density goes above and the dilaton condensate becomes independent of density, reaching . This has to do with a delicate interplay between the attraction associated with the dilaton exchange and the repulsion, which leads to the parity doubling. Where this interplay starts taking place cannot be pinned down precisely but it must be in the density regime where the symmetry energy is involved, going from to the core of massive stars, say, . In this density regime, the Landau fixed-point approximation with can be taken to be reliable. One can then calculate the trace of the energy-momentum tensor in the mean-field approximation of GnEFT, i.e., LFL fixed-point approximation, which will become density-independent as given by (11). In this density range we will havewhere is the energy density and . It is approximate since there can easily be terms that are compounded with EFT and pQCD at the point where the symmetry energy has the cusp structure. Since there is no Lee-Wick-type state, one must havewhich gives the pseudo-conformal sound speedThe “approximate zero” here stands for the fact that it is pseudo-conformal with scale symmetry broken both explicitly and spontaneously, the dilaton mass and the mass balancing so as to lead to parity doubling in the dense system. The true conformal velocity, within the model, should be reached only at a density much higher than that of the core density of the massive stars. Where precisely the conformality sets in is not relevant to the compact star physics.In Figure 3 is shown the sound speed for (nuclear matter) and 1 (neutron matter) calculated in RG for . They are of the same form for except for the slight shift in the density and the height of . This result serves as an illustration of the arguments to follow.
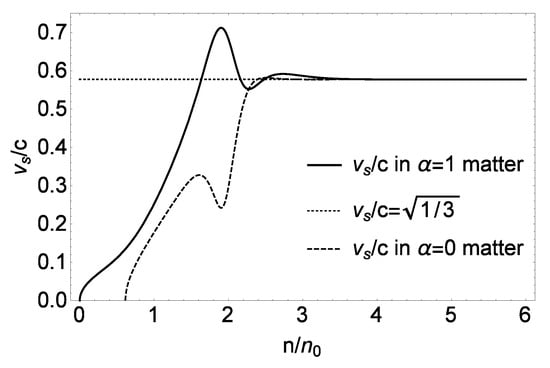 Figure 3. vs. density for (nuclear matter) and (neutron matter) in RG for and .What is noticeable is the large bump in in the vicinity of and the rapid convergence to the speed 1/3. The approximation involved on top of the pseudo-conformality would of course give fluctuations on top of but the point here is it is the pseudo-conformality that “controls” the general structure. The large bump signals a complex interplay between hadronic and non-hadronic degrees of freedom manifested through the pseudo-gap structure of the chiral condensates. I will discuss below how the degrees of freedom in the core of the massive stars could masquerade as “deconfined quarks”.
Figure 3. vs. density for (nuclear matter) and (neutron matter) in RG for and .What is noticeable is the large bump in in the vicinity of and the rapid convergence to the speed 1/3. The approximation involved on top of the pseudo-conformality would of course give fluctuations on top of but the point here is it is the pseudo-conformality that “controls” the general structure. The large bump signals a complex interplay between hadronic and non-hadronic degrees of freedom manifested through the pseudo-gap structure of the chiral condensates. I will discuss below how the degrees of freedom in the core of the massive stars could masquerade as “deconfined quarks”. - Quenched in nucleiThough it is not directly connected with the star properties, a relevant and intriguing observation is what I would call “quasibaryon” in nuclear matter. It follows from the possible existence of the IR fixed point associated with the “genuine dilaton (GD)." The effective in the Gamow–Teller transitions in nuclei, , is observed to be from light nuclei to heavy nuclei and even to the dilaton-limit fixed point at . It has been argued that an approximate scale invariance “emerges” in nuclear interactions [24], in a way most likely related to the way sets in precociously.Returning to , is there any indication in recent astrophysical observations for such a precocious onset of the pseudo-conformal sound velocity?To date, there is no known “smoking-gun” signal for the sound velocity from observations. In the literature, however, there are a gigantic number of articles on the structure of sound velocity deduced from the gravity wave data as well as theoretically. Some argue for phase transitions or continuous ones or simply no crossovers, etc. Some extreme cases are discussed in [9]. I will no go into this wilderness here. Let me just describe one case which illustrates most transparently what can very well be involved.Let us take the case of NICER and XMM-Newton observables (NXN for short) discussed, namely (13) and (14). This case brings out how puzzling the problem can be.In [25], the properties of high-density matter were inferred in most detailed analyses of the NXN data. Ruling out essentially all other scenarios, with or without phase changes, the authors arrive at the sound velocity (“H-bump”) plotted in Figure 4.
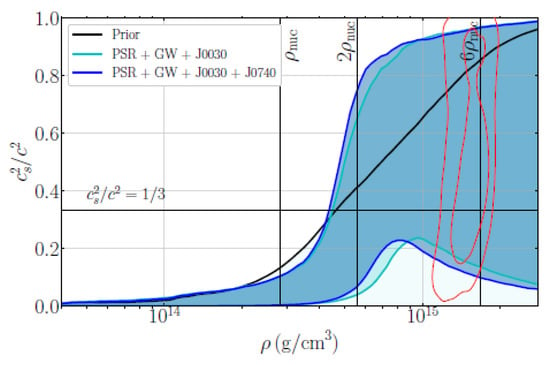 Figure 4. in unit of g/cm (the “H-bump” scenario) taken from [25]. The red contour stands for 50% and 90% inferred sound speed and central density.The central density and the maximum sound velocity inferred wereWhile the star properties they took into account are exactly those reproduced by the PCM, i.e., (13) and (14), the central density and the sound velocity are totally different from the PCM predictions. One can understand the low central density accounting for the sound speed overshooting the conformal bound, characteristic of strongly interacting hadronic phase. In fact there are in the literature numerous scenarios anchored on a variety of density-functional approaches giving rise to the wilderness of one form or other in the sound velocity—including bumps similar to the H-bump—but I am not aware of any that can survive the battery of bona fide constraints coming from the current observations both in theory and experiment as claimed by [25].A puzzle immediately raised is this: How can the PCM with an emergent (pseudo-)conformality and the strong H-bump with no hint of conformal symmetry give the almost identical global star properties (13) and (14)? The only statement one can make at this point is (A) either the sound velocity and the global star properties are totally unrelated or (B) there is something wrong either in the strong H-bump scenario or in the simple PCM structure. Option (A) is hard to accept, so perhaps option (B) is a plausible possibility. My bet is option (B) and the H-bump scenario are at odds with nature.
Figure 4. in unit of g/cm (the “H-bump” scenario) taken from [25]. The red contour stands for 50% and 90% inferred sound speed and central density.The central density and the maximum sound velocity inferred wereWhile the star properties they took into account are exactly those reproduced by the PCM, i.e., (13) and (14), the central density and the sound velocity are totally different from the PCM predictions. One can understand the low central density accounting for the sound speed overshooting the conformal bound, characteristic of strongly interacting hadronic phase. In fact there are in the literature numerous scenarios anchored on a variety of density-functional approaches giving rise to the wilderness of one form or other in the sound velocity—including bumps similar to the H-bump—but I am not aware of any that can survive the battery of bona fide constraints coming from the current observations both in theory and experiment as claimed by [25].A puzzle immediately raised is this: How can the PCM with an emergent (pseudo-)conformality and the strong H-bump with no hint of conformal symmetry give the almost identical global star properties (13) and (14)? The only statement one can make at this point is (A) either the sound velocity and the global star properties are totally unrelated or (B) there is something wrong either in the strong H-bump scenario or in the simple PCM structure. Option (A) is hard to accept, so perhaps option (B) is a plausible possibility. My bet is option (B) and the H-bump scenario are at odds with nature. - Conformailty
In this connection, let me make a remark on the role of conformal symmetry in the sound velocity currently being discussed in the literature. This issue is a focused topic in MDPI’s Special Issue on “Symmetries and Ultra Dense Matter of Compact Stars” being edited with contributions devoted to the issue. Without going into detail, let me just mention that there are a variety of models hybridizing hadronic degree of freedom and “revamped” quark/gluon degrees of freedom at a density . Some of the models such as quarkyonic and holographic QCD do tend to see the conformal symmetry (perhaps involving percolation, etc.) emerge at certain density in going up in density [26,27,28]. Going down the density ladder from asymptotic density where , one seems to observe the approximate conformality which persists down to the crossover regime where the big bump develops as it does in the PCM [29]. This may represent a microscopic rendition of HQC in contrast to the PCM, which presents a coarse-grained picture permeating in dense medium. This point is evidenced in Figure 6 in [30] where the results of quarkyonic models are compared with the PCM prediction Figure 3.
4. Conclusion: The Duck Story
Briefly summarized, I have shown how to go from low density to high density capturing the putative hadron-quark continuity (HQC) by formulating baryonic matter as Landau-Migdal Fermi-liquid matter resulting via renormalization group [15]. It is a sort of generalized density-functional approach (à la the Hohenberg–Kohn theorem), implementing heavy degrees of freedom in terms of hidden symmetries involving a mass scale above that given by standard chiral EFT, which is shown to be valid at nuclear matter density. The resulting effective field theory, GnEFT, exploits the possibility of simulating via duality the HQC in terms of a topology change from skyrmions at low density ∼ to 1/2-skyrmions at high density ∼. The resulting EoS has so far successfully accounted for nuclear matter as well as dense compact star matter. The structure that is arrived at in compact star matter, coined as pseudo-conformality, can be considered as a coarse-grained description of the hadron-to-quarks changeover, e.g., quarkyonic “IdylliQ” [31], captured in terms of “emergent” scale symmetry permeating from low to high density.
The formulation made so far is valid at zero temperature. Upcoming terrestrial laboratory observations complimentary to astrophysical data, e.g, at FAIR of GSI, however, will necessarily involve relatively high temperature. It remains to be formulated in the GnEFT framework to meet the conditions of the terrestrial laboratories. How topology enters in the hot and dense matter is a totally open issue as indicated in recent puzzling manifestations of scale invariance at high temperature [32].
Finally, I touch on fractionalzed “quasibaryon” structure inside the core of the massive star.
When a paper appeared in 2020 [33] with the suggestion that the cores of the most massive neutron stars are characterized by approximate conformal symmetry, with the speed of sound , the polytropic index , and the normalized trace anomaly , indicating that the cores are most likely populated by deconfined fractionally charged objects, identified as quarks, those quantities were quickly calculated in the PCM formulated in 2017 [3]. I considered this as a prediction of the PCM. The predicted results [34] were quite consistent with the conclusion of [33].
Now the question was this: Given that the degrees of freedom in the PCM are quas-ibaryons, albeit fractionalized, how do they carry the characteristics of fractionally charged quarks?
I do not have an immediate answer to this question. However, there are certain ideas that could lead to an understanding of this puzzle [35]. One of them is this: In the skyrmion-half-skyrmion crystal simulation, the half-skyrmions “confined” into a skyrmion by monopoles [21] could be liberated at high density and propagate freely with little interactions as seen in skyrmion crystals [3]. Two half skyrmions can then be rearranged into three 1/3-charged objects as in a schematic model [36]. In fact, in condensed matter physics, with domain walls, there can be stacks of sheets containing deconfined fractionally charged objects behaving like “deconfined quarks” coming from the bulk in which the objects are confined [37].
This reminds one of the “duck test”: “If it looks like a duck, swims like a duck, and quacks like a duck, it probably is a duck.”
Funding
This research received no external funding.
Data Availability Statement
Not applicable.
Conflicts of Interest
Not applicable.
References
- Rho, M. ’Mass without mass’ and nuclear matter. arXiv 2017, arXiv:1703.02277. [Google Scholar]
- Paeng, W.G.; Kuo, T.T.S.; Lee, H.K.; Rho, M. Scale-invariant hidden local symmetry, topology change and dense baryonic matter. Phys. Rev. C 2016, 93, 055203. [Google Scholar] [CrossRef]
- Paeng, W.G.; Kuo, T.T.S.; Lee, H.K.; Ma, Y.L.; Rho, M. Scale-invariant hidden local symmetry, topology change, and dense baryonic matter. II. Phys. Rev. D 2017, 96, 014031. [Google Scholar] [CrossRef]
- Ma, Y.L.; Rho, M. Towards the hadron–quark continuity via a topology change in compact stars. Prog. Part. Nucl. Phys. 2020, 113, 103791. [Google Scholar] [CrossRef]
- Rho, M.; Ma, Y.L. Manifestation of hidden symmetries in baryonic matter: From finite nuclei to neutron stars. Mod. Phys. Lett. A 2021, 36, 2130012. [Google Scholar] [CrossRef]
- Park, B.Y.; Vento, V. Skyrmion approach to finite density and temperature. In The Multifacetted Skyrmion; Brown, G.E., Rho, M., Eds.; World Scientific: Singapore, 2010. [Google Scholar]
- Lee, H.K.; Park, B.Y.; Rho, M. Half-skyrmions, tensor forces and symmetry energy in cold dense matter. Phys. Rev. C 2011, 83, 025206, Erratum in Phys. Rev. C 2011, 84, 059902. [Google Scholar] [CrossRef]
- Adam, C.; García Martín-Caro, A.; Huidobro, M.; Vázquez, R.; Wereszczynski, A. Quantum skyrmion crystals and the symmetry energy of dense matter. Phys. Rev. D 2022, 106, 114031. [Google Scholar] [CrossRef]
- Lee, H.K.; Ma, Y.L.; Paeng, W.G.; Rho, M. Cusp in the symmetry energy, speed of sound in neutron stars and emergent pseudo-conformal symmetry. Mod. Phys. Lett. A 2022, 37, 2230003. [Google Scholar] [CrossRef]
- Garaud, J.; Babaev, E. Effective model and magnetic properties of the resistive electron quadrupling state. Phys. Rev. Lett. 2022, 129, 087602. [Google Scholar] [CrossRef]
- Harada, M.; Yamawaki, K. Hidden local symmetry at loop: A New perspective of composite gauge boson and chiral phase transition. Phys. Rep. 2003, 381, 1. [Google Scholar] [CrossRef]
- Crewther, R.J. Genuine dilatons in gauge theories. Universe 2020, 6, 96. [Google Scholar] [CrossRef]
- Crewther, R.J.; Tunstall, L.C. ΔI = 1/2 rule for kaon decays derived from QCD infrared fixed point. Phys. Rev. D 2015, 91, 034016. [Google Scholar]
- Brown, G.E.; Rho, M. Double decimation and sliding vacua in the nuclear many body system. Phys. Rep. 2004, 396, 1–39. [Google Scholar] [CrossRef]
- Shankar, R. Renormalization group approach to interacting fermions. Rev. Mod. Phys. 1994, 66, 129–192. [Google Scholar] [CrossRef]
- Friman, B.; Rho, M. From chiral Lagrangians to Landau Fermi liquid theory of nuclear matter. Nucl. Phys. A 1996, 606, 303. [Google Scholar] [CrossRef]
- Song, C. Dense nuclear matter: Landau Fermi liquid theory and chiral Lagrangian with scaling. Phys. Rep. 2001, 347, 289–371. [Google Scholar] [CrossRef]
- Piekarewicz, J. The nuclear physics of neutron stars. arXiv 2022, arXiv:2209.14877. [Google Scholar]
- Salinas, M.; Piekarewicz, J. Building an equation of state density ladder. Symmetry 2023, 15, 994. [Google Scholar] [CrossRef]
- He, B.R.; Harada, M. Parity doubling among baryons in a holographic QCD model at finite density. PoS 2013, arXiv:10.22323/1.205.0192, 192. [Google Scholar]
- Zhang, P.; Kimm, K.; Zou, L.; Cho, Y.M. Re-interpretation of Skyrme theory: New topological structures. arXiv 2017, arXiv:1704.05975. [Google Scholar]
- Beane, S.R.; van Kolck, U. The dilated chiral quark model. Phys. Lett. B 1994, 328, 137–142. [Google Scholar] [CrossRef]
- Tan, H.; Dexheimer, V.; Noronha-Hostler, J.; Yunes, N. Finding structure in the speed of sound of supranuclear matter from binary love relations. Phys. Rev. Lett. 2022, 128, 161101. [Google Scholar] [CrossRef]
- Rho, M. Multifarious roles of hidden chiral-scale symmetry: “Quenching” gA in Nuclei. Symmetry 2021, 13, 1388. [Google Scholar] [CrossRef]
- Legred, I.; Chatziioannou, K.; Essick, R.; Han, S.; Landry, P. Impact of the PSR J0740+6620 radius constraint on the properties of high-density matter. Phys. Rev. D 2021, 104, 063003. [Google Scholar] [CrossRef]
- Fujimoto, Y.; Fukushima, K.; McLerran, L.D.; Praszalowicz, M. Trace anomaly as signature of conformality in neutron stars. Phys. Rev. Lett. 2022, 129, 252702. [Google Scholar] [CrossRef] [PubMed]
- Marczenko, M.; McLerran, L.; Redlich, K.; Sasaki, C. Reaching percolation and conformal limits in neutron stars. Phys. Rev. C 2023, 107, 025802. [Google Scholar] [CrossRef]
- Rojas, J.C.; Demircik, T.; Järvinen, M. Popcorn transitions and approach to conformality in homogeneous holographic nuclear matter. Symmetry 2023, 15, 331. [Google Scholar] [CrossRef]
- Annala, E.; Gorda, T.; Hirvonen, J.; Komoltsev, O.; Kurkela, A.; Nättilä, J.; Vuorinen, A. Strongly interacting matter exhibits deconfined behavior in massive neutron stars. arXiv 2023, arXiv:2303.11356. [Google Scholar]
- Ma, Y.L.; Rho, M. The sound speed and core of massive compact stars: A manifestation of hadron-quark duality. arXiv 2021, arXiv:2104.13822. [Google Scholar]
- Fujimoto, Y.; Kojo, T.; McLerran, L.D. Momentum shell in quarkyonic matter from explicit duality: A solvable model nalysis. arXiv 2023, arXiv:2306.04304. [Google Scholar]
- Meng, X.L.; Sun, P.; Alexandru, A.; Horváth, I.; Liu, K.-F.; Wang, G.; Yang, Y.-B. Separation of infrared and bulk in thermal QCD. arXiv 2023, arXiv:2305.09459. [Google Scholar]
- Annala, E.; Gorda, T.; Kurkela, A.; Nättilä, J.; Vuorinen, A. Evidence for quark-matter cores in massive neutron stars. Nat. Phys. 2020, 16, 907–910. [Google Scholar] [CrossRef]
- Ma, Y.L.; Rho, M. What’s in the core of massive neutron stars? arXiv 2020, arXiv:2006.14173. [Google Scholar]
- Rho, M. Fractionalized quasiparticles in dense baryonic matter. arXiv 2020, arXiv:2004.09082. [Google Scholar]
- Sarti, V.M.; Vento, V. The half-skyrmion phase in a chiral-quark model. Phys. Lett. B 2014, 728, 323–327. [Google Scholar] [CrossRef]
- Sulejmanpasic, T.; Shao, H.; Sandvik, A.; Unsal, M. Confinement in the bulk, deconfinement on the wall: Infrared equivalence between compactified QCD and quantum magnets. Phys. Rev. Lett. 2017, 119, 091601. [Google Scholar] [CrossRef] [PubMed]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).