A New Proof of Ramsey’s Theorem

Abstract

Ramsey’s theorem states that for any natural numbers n, m there exists a natural number N such that any red–blue coloring of the graph $K_N$ contains either a red $K_n$ or blue $K_m$ as a subgraph. The smallest such N is called the Ramsey number, denoted as $R(n,m)$. In this paper, we reformulate this theorem and present a proof of Ramsey’s theorem that is novel as far as we are aware.

1. Introduction

Although topics related to Ramsey’s theorem [1] have a well-established history [2], this theorem and its generalizations (see, e.g., [3]) continue to inspire. Ramsey theory now covers a wide range of topics across many areas of mathematics. A common goal of this research is to answer the following question: “How large must a structure be to ensure that a particular property holds?”. Without a doubt, one of the most popular areas of Ramsey theory is graph theory, e.g., [4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22]. Our work also confirms this claim. The paper refers to the origins of Ramsey’s theorem for graphs. We present an original proof of this theorem. Despite the considerable interest in Ramsey theory for graphs, we have not seen too many proofs of Ramsey’s basic theorem. In our opinion, the proof we present is both elegant and beautiful, and it owes much to Lemma 1. Since the considered problems refer to the origins of Ramsey’s theorem, the authors hope that the paper is interesting and inspiring for the readers.

In this paper, we consider simple, finite graphs i.e., non-orientable graphs without multiple edges and loops. Let $G=(V,E)$ be a graph with a set of vertices V and a set of edges E. In the whole text, by r coloring of a graph, we mean r coloring of the edges of a graph. For basic definitions, we refer the reader to any classical textbook on graph theory, e.g., [3,23,24,25].

Our starting point was the following version of Ramsey’s theorem [2].

Theorem 1 (Ramsey).

For integers $n,m\ge 2$, there exists a smallest positive integer $R(n,m)$ such that no matter how the complete graph $K_{R(n,m)}$ is blue–red colored, it contains a blue subgraph $K_n$ or a red subgraph $K_m$.

Remark 1.

Notice that in the above theorem, we can consider any graph G of order $R(n,m)$. Since Ramsey’s theorem holds for every two-coloring, we can, in particular, color all edges of G with one color and all “missing” edges with the other.

${\overline{K}}_n$ denotes the complement of a complete graph on n vertices (denoted by $K_n$), i.e., an empty graph of order n. According to Ramsey’s theorem, if a graph G of an order of at least $R(n,m)$ does not contain ${\overline{K}}_n$ as a subgraph, it must contain $K_m$ as a subgraph. On the other hand, if a graph does not contain ${\overline{K}}_n$, then among any n vertices of this graph, at least two must be adjacent. This allows us to restate Theorem 1 as follows.

Theorem 2.

For any natural numbers $n\ge 2$ and $m\ge 3$, there exists a natural number $N=N(n,m)$ such that every simple graph of an order of at least N that has at least two adjacent vertices in every n-element subset of its set of vertices contains $K_m$ as a subgraph. We the least N is denoted by $N_{opt}(n,m)$.

Remark 2.

Despite the existence of graphs satisfying Ramsey’s theorem that do not satisfy the assumption of Theorem 2 (below, we give some examples for $k=\tau =n=m=3$, $N=6$ – see Figure 1 and Figure 2), it is true that $N_{opt}(n,m)=R(m,n)$. It is obvious that $N_{opt}(n,m)\le R(m,n)$. We show that every graph of an order of at least $N_{opt}(n,m)$ must contain ${\overline{K}}_n$ or $K_m$. Let G be a graph of an order of at least $N_{opt}(n,m)$. If G contains ${\overline{K}}_n$ (or an empty graph of a higher order), then we are done. Now, suppose that G does not contain ${\overline{K}}_n$ as a subgraph. Then, according to Theorem 2, graph G has to contain $K_m$ as a subgraph. Therefore, $R(m,n)\le N_{opt}(n,m)$.

2. A New Proof

In this section we present a proof of Theorem 2 that is, to the best of or knowledge, novel and equivalent to Ramsey’s theorem. The most essential part of the proof is the following lemma.

Lemma 1.

For any $n,M\in \mathbb{N}$, $n,M\ge 3$, if a graph $G=(V,E)$ is simple and the following conditions are satisfied, then graph G has a vertex of a degree of at least M.

(A) 

$\left|V\right|\ge (n-1)\left(1+{\displaystyle \sum _{i=1}^{2(n-1)}}{(M-1)}^{i-1}\right)$;

(B) 

G has at least two adjacent vertices in every n-element subset of V.

Proof. 

We prove it by contradiction. Suppose that for fixed natural numbers $n,M\ge 3$, there exists a simple graph $G=(V,E)$ satisfying conditions (A) and (B) but having no vertex of a degree of at least M, i.e., every vertex of this graph has a degree of, at most, $M-1$.

Graph G contains, at most $n-1$ connected components according to (B). Condition (A) implies that there exists a component $G^{\prime }=\left(V^{\prime },E^{\prime }\right)$ of graph G such that

$$\left|V^{\prime }\right|\ge 1+\sum _{i=1}^{2(n-1)}{(M-1)}^{i-1}.$$

(1)

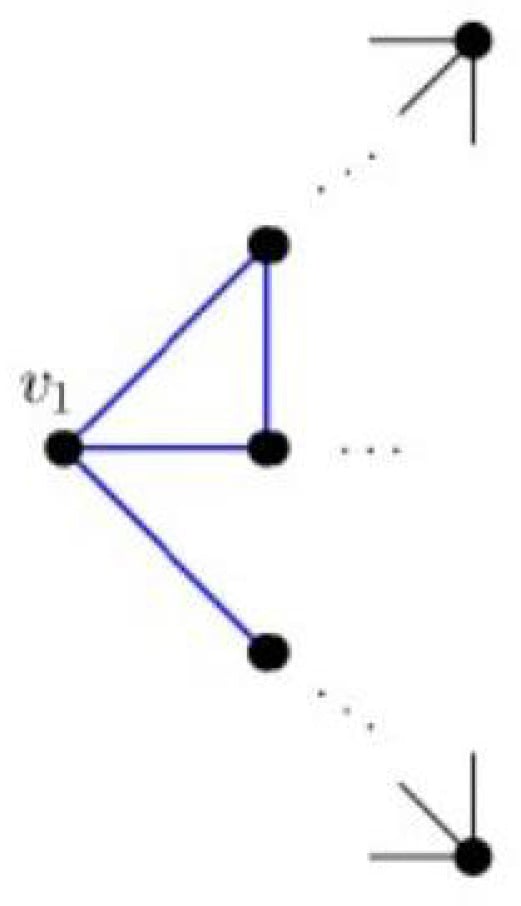
Let us fix any $x\in V^{\prime }$ and consider the following sets (see Figure 3 below):

$$\begin{array}{cc}\hfill A_1& =\left\{x\right\},A_2=\{v\in V^{\prime }:\{x,v\}\in E\},\hfill \\ \hfill A_{k+1}& =\{w\in V^{\prime }\setminus \bigcup _{i=1}^k{A}_i:\exists v\in A_k:\{v,w\}\in E\},k\ge 2.\hfill \end{array}$$

It is easy to see that the vertices in $A_k$ are not adjacent to the vertices in the set:

$$\bigcup _{i\le k-2}{A}_i\cup \bigcup _{j\ge k+2}{A}_j.$$

Since graph $G^{\prime }$ is finite, there exists a number $i_0\in \mathbb{N}$ such that $A_i=\varnothing$ for every $i>i_0$. If $A_{2n-1}\ne \varnothing$, then we can choose one vertex $v_i$ from each set $A_{2i+1},0\le i\le n-1$ and obtain the set ${\left\{v_i\right\}}_{0\le i\le n-1}$ of n non-adjacent vertices, which contradicts condition (B). Therefore, $A_i=\varnothing$ for $i\ge 2n-1$.

By construction of the sets $A_i$ and based on the assumption that every vertex of graph G has a degree of, at most, $M-1$, we have the following estimation:

$$|A_{i+1}|\le (M-1)|A_i|,$$

so $|A_i{|\le (M-1)}^{i-1}$ for $1\le i\le 2(n-1)$. The connectedness of $G^{\prime }$ implies

$$V^{\prime }=\bigcup _{i=1}^{2(n-1)}{A}_i,$$

so we have

$$\left|V\right|\le \sum _{i=1}^{2(n-1)}{(M-1)}^{i-1},$$

which contradicts condition (1). Therefore, a graph G satisfying conditions (A) and (B) contains a vertex of a degree of at least M. □

Now, we prove Theorem 2 by induction, with Lemma 1 playing a key role in our proof.

Proof of Theorem 2.

First, let us consider the case of $n=2$, i.e., when G has at least two adjacent vertices in every n-element subset of its set of vertices. It follows that the considered graph is complete. Thus, we can take $N(2,m)=m$. The next steps of the proof proceed by induction on m.

For $m=3$ and any $n\in \mathbb{N}$, $n\ge 3$ according to Lemma 1 (for $M=n$), and we find that there exists a vertex x of a degree of at least n, i.e., adjacent to at least n other vertices. We assume that among these n vertices, there are at least two adjacent vertices, e.g., u and v. Therefore, vertices x, u, and v induce graph $K_3$. Therefore, it suffices to take

$$N(n,3)=(n-1)\left(1+\sum _{i=1}^{2(n-1)}{(n-1)}^{i-1}\right).$$

Now, let us suppose that Theorem 2 holds for some $m_0\ge 3$ and any $n\ge 3$. According to Lemma 1, for $M=$$N(n,m_0)$, we find that G has a vertex x of a degree of at least $N(n,m_0)$. Let $G^{\prime }$ be the subgraph of G induced by the set of vertices adjacent to x. We assume $G^{\prime }$ contains $K_{m_0}$ as a subgraph, so the set consisting of all vertices of $K_{m_0}$ and vertex x induces the subgraph $K_{m_0+1}$ in G. We can take

$$N(n,m_0+1)=(n-1)\left(1+\sum _{i=1}^{2(n-1)}{\left(N\left(n,m_0\right)-1\right)}^{i-1}\right).$$

□

Remark 3.

The above proof gives an upper bound for Ramsey numbers. However, it increases very rapidly with respect to Ramsey numbers, for example, $R(3,3)=6\le 32$, $R(3,4)\le 61570$.

Remark 4.

Our friend, a specialist in graph theory, informed us that this result can be obtained from Chvátal’s result [26],

$$R(K_{1,M},K_n)=M(n-1)+1,$$

which was prove using an inductive argument.

3. Additional Results

Similarly to Ramsey’s theorem, Theorem 2 and Lemma 1 can also be formulated in terms of set theory. For example, Theorem 2 can be presented as follows (see [27], Chapter 1.2).

Theorem 3.

Let A be a set and ρ be a symmetric, irreflexive relation on A. For any natural numbers $n\ge 2$ and $m\ge 3$, there exists a natural number $N_{\rho }=N_{\rho }(n,m)$ such that every set A of at least $N_{\rho }$ elements that has at least two related elements in any of n-element subsets contains a subset of m elements related to each other.

Corollary 1.

Let A be a given infinite set of some objects (numbers, polynomials, matrices, etc.) and ρ be a given symmetric relation on A. Suppose that there exists a natural number n such that in every n-element subset of A, there are at least two elements related to each other by ρ. Then, there exist subsets of A of any cardinality having this property.

Corollary 2.

Let $(X,\langle ·|·\rangle )$ be an inner product space and $A\subset X$ be an infinite set such that for some $n\in \mathbb{N}$ among any n vectors of A, at least two are orthogonal. Then, for every $M\in \mathbb{N}$, there exist infinitely many M-element orthogonal subsets of A. Moreover A contains an infinite linearly independent subset.

Proof of the above corollary is based on using a countable axiom of choice to fix an orthogonal set $A_n$ of n elements of A without a zero vector for any $n\in \mathbb{N}$. Then, the union of all these sets is infinite and countable, so by setting a sequence $\left\{a_k\right\}$ of all elements of this sum and choosing the following subsequence, we obtain an infinite set of linearly independent vectors.

$$\begin{array}{cc}\hfill b_1& =a_1\hfill \\ \hfill b_2& =a_s,s=min\{n\in \mathbb{N}:n>1,a_1\mathrm{and}{a}_n\mathrm{are}\mathrm{linearly}\mathrm{independent}\}\hfill \end{array}$$

It should be noted that for any finite set $B\subset {\bigcup }_{n\in \mathbb{N}}{A}_n$, there exists a vector with a sufficiently large index that creates a linearly independent set with B (this sum has finite subsets of any cardinality that are linearly independent, namely orthogonal).

The next theorem is a special case of Theorem 2, which provides a better estimation of the order of graph G.

Theorem 4.

Let $G=(V,E)$ be a simple graph. If the following conditions are satisfied, then graph G contains $K_{n+2}$ as a subgraph.

(A) 

$\left|V\right|\ge 3\times 2^n$, $n\in \mathbb{N}$;

(B) 

G has at least two adjacent vertices in every 3-element subset of V.

Proof. 

The theorem is proven by induction on n.

For $n=1$, let us consider a graph $G=(V,E)$ of order 6 such that among any three vertices, there are at least two are adjacent vertices. G can consist of, at most, two connected components (otherwise, (B) is contradicted). Let us consider the following cases.

• If G is not connected, then G consists of two connected components. Assumption (B) implies that these components have to be complete graphs and one of them has to contain at least three vertices. Therefore, G contains $K_3$ as a subgraph.
• G is a connected graph. We show by contradiction that G contains a vertex of a degree of at least 3. Suppose that all vertices in G have a degree of, at most, 2.
• If all vertices of G have a degree of 1, then G is not connected.
• If in G exists a vertex x of degree 2, then according to (B), the vertices of G that are not adjacent to x induce $K_3$ (and, therefore, are of degree 2). At least one of these vertices has to be joined with one of vertices adjacent to x, so there exists a vertex of degree 3, which contradicts our assumption (see Figure 4).

Therefore, within G, there exists a vertex $v_1$ of a degree of at least 3. According to (B), among the vertices adjacent to $v_1$ are two adjacent vertices. These vertices induce a clique $K_3$ with $v_1$ (see Figure 5). Therefore, Theorem 4 is valid for $n=1$.

Now, let us suppose that Theorem 4 holds for some $n\ge 1$. Let $G=(V,E)$ be a simple graph of an order of at least $3\times 2^{n+1}$ such that in any three-element subset of its set of vertices, at least two vertices are adjacent. Let us consider the following cases.

• If G is not connected, then according to (B), it contains, at most, two connected components, both of which are complete graphs. One of those components has an order of at least $3\times 2^n$, so this component contains $K_{n+3}$ (since $3\times 2^n>n+3$) as a subgraph.
• If G is connected, then we show that it contains a vertex of a degree of at least $3\times 2^n$.

Let us suppose that all vertices of G have degree of, at most, $3\times 2^n-1$. Let $x\in V$ and $v_1,v_2,\dots ,v_i\in V$ be the vertices adjacent to x. According to the assumption of $i<3\times 2^n$, the remaining vertices $v_{i+1},v_{i+2},\dots ,v_{3\times 2^{n+1}-1}$ induce a subgraph $K_{3\times 2^{n+1}-i-1}$.

If $i<3\times 2^n-1$, then $3\times 2^{n+1}-i-1>3\times 2^n$, so vertices non-adjacent to x induce at least $K_{3\times 2^n+1}$. All vertices of $K_{3\times 2^n+1}$ have a degree equal to $3\times 2^n$, which contradicts our assumption. Therefore, $i=3\times 2^n-1$. Hence, $K_{3\times 2^{n+1}-i-1}=K_{3\times 2^n}$, and the degree of each vertex of this graph is $3\times 2^n-1$.

Owing to the connectivity of G, at least one vertex of the subgraph $K_{3\times 2^n}$ is adjacent to at least one of vertices $v_1,v_2,\dots v_i$. Therefore, the degree of a certain vertex of the subgraph $K_{3\times 2^n}$ is at least $3\times 2^n$. We obtain a contradiction.

Therefore, G contains a vertex y of a degree of at least $3\times 2^n$. By induction assumption, from the vertices adjacent to y, we can choose $n+2$ vertices inducing graph $K_{n+2}$. Obviously, the set of vertices of $K_{n+2}$ with y induces a subgraph $K_{n+3}$ in G. □

4. Turán’s Theorem

In this section, we compare some obtained facts with Turán’s theorem (see also [28,29]).

Theorem 5

(Turán [30]). Let $G=(V,E)$ be a simple graph where $\left|V\right|=N$ and let $k\ge 2$. If

$$\left|E\right|>\left(1-{\displaystyle \frac{1}{k-1}}\right){\displaystyle \frac{N^2}{2}},$$

then G contains $K_k$ as a subgraph.

In graph theory texts, this is often phrased as a result of k clique-free graphs.

Theorem 6.

If a graph G has no $K_n$ subgraph, $n\ge 2$, then it has, at most,

$$⌊\left(1-{\displaystyle \frac{1}{n-1}}\right){\displaystyle \frac{N^2}{2}}⌋$$

edges, where $N=\left|V\right|$.

Based on the above theorem, we can determine a minimal number of edges in the graphs $G=\left(V,E_n\right)$ satisfying Theorem 2.

Fact 1.

Let $n\ge 2$, $m\ge 3$, $G=\left(V,E_n\right)$ be a simple graph such that among any n vertices, at least two adjacent and $V=N_{opt}(n,m)$, where $N_{opt}(n,m)$ is the number described in Theorem 2. Then, such a graph contains $K_m$ as a subgraph and

$$\left|E_n\right|\ge \left({\displaystyle \genfrac{}{}{0pt}{}{N_{opt}(n,m)}{2}}\right)-⌊\left(1-{\displaystyle \frac{1}{n-1}}\right){\displaystyle \frac{{\left(N_{opt}(n,m)\right)}^2}{2}}⌋$$

Proof. 

Graph G does not contain ${\overline{K}}_n$ as a subgraph, so its complement $\overline{G}$ does not contain $K_n$ as a subgraph. Hence, according to Turán’s theorem, graph $\overline{G}$ has, at most,

$$⌊\left(1-{\displaystyle \frac{1}{n-1}}\right){\displaystyle \frac{{\left(N_{opt}(n,m)\right)}^2}{2}}⌋$$

edges and graph G has at least

$$\left({\displaystyle \genfrac{}{}{0pt}{}{N_{opt}(n,m)}{2}}\right)-⌊\left(1-{\displaystyle \frac{1}{n-1}}\right){\displaystyle \frac{{\left(N_{opt}(n,m)\right)}^2}{2}}⌋$$

edges. □

The number of edges in graphs satisfying Theorem 2 is lower than the number of edges obtained by Turán’s theorem for the same cardinality of the set of vertices. This means that as a result of increasing the order of the graph and assuming that edges appear in G in accordance with the following assumption, a clique $K_m$ appears with fewer edges in G than would follow from random occurrence of edges (as in Turán’s theorem): among any n vertices, G has at least two adjacent vertices (see Figure 6 and Figure 7 below).

Notice that the following also holds.

Fact 2.

With the increase in the number n the difference between the values of $|E_n|$ and $\left|E\right|$ increases. More precisely, for $n\ge 3$, it is bigger than

$$\left({\displaystyle \frac{1}{2}}-{\displaystyle \frac{1}{n-1}}\right){\left(N_{opt}(n,m)\right)}^2+{\displaystyle \frac{N_{opt}(n,m)}{2}}-1\to \infty ,$$

when $N_{opt}(n,m)\to \infty$.

Proof. 

Let $N=N_{opt}(n,m)$; then, we have

$$\begin{array}{cc}\hfill & ⌊\left(1-{\displaystyle \frac{1}{n-1}}\right){\displaystyle \frac{N^2}{2}}⌋+1-\left({\displaystyle \genfrac{}{}{0pt}{}{N}{2}}\right)+⌊\left(1-{\displaystyle \frac{1}{n-1}}\right){\displaystyle \frac{N^2}{2}}⌋\hfill \\ \hfill & \ge \left(1-{\displaystyle \frac{1}{n-1}}\right)N^2-{\displaystyle \frac{1}{2}}N(N-1)-1=\left({\displaystyle \frac{1}{2}}-{\displaystyle \frac{1}{n-1}}\right){\displaystyle \frac{N^2}{2}}+{\displaystyle \frac{N}{2}}-1.\hfill \end{array}$$

□

Table 1. Minimal number of edges.

m	$\mathit{N}(\mathit{n},\mathit{m})$	$\left|{\mathit{E}}_{\mathit{n}}\right|$	$\left|\mathit{E}\right|$
$n=3$
3	6	6	10
4	9	16	21
5	14	42	50
6	18	72	82
$n=4$
4	18	45	109
5	25	92	209

present the minimal number of edges needed for the appearance of $K_m$ in a graph of order $N_{opt}(n,m)$ satisfying Theorem 2 (notation $|E_n|$) and in any graph G of the same order (notation $\left|E\right|$).

5. Open Problem

It is known that Ramsey’s Theorem 1 can be generalized to r colorings for all $r\ge 2$ in the following way (see, e.g., [30]).

Theorem 7 (Ramsey).

For integers $r\ge 2$ and $n_1,\dots ,n_r$, there exists a least positive integer such that any r coloring of a complete graph $K_N$ contains a monochromatic $K_{n_i}$ of color i. The least number N is denoted by $R(n_1,\dots ,n_r)$.

Problem 1.

Can Theorem 2 be generalized in similar way? In other words, is it possible to reformulate Theorem 7?

Let us notice that the following theorem holds.

Theorem 8.

Let $n>m\ge 3$ and r be any natural numbers such that n is sufficiently large. There exists a least natural number $\mathit{N}=\mathit{N}(n,m,r)$ such that any simple graph of order $\mathit{N}$ with every subgraph of order n contains at least r edges for any r coloring satisfying the following condition:

• For any color i among any n vertices, there exist two vertices joined by an edge of color i, containing a monochromatic $K_m$ as a subgraph. The least number $\mathit{N}$ is denoted by ${\mathit{N}}_{opt}(n,m,r)$.

Proof. 

Let n be sufficiently large that a graph of order n is able to have at least r edges, and let $m\ge 3$ and $r\ge 1$ be any natural numbers. Let us notice that for $r=1$, we obtain Theorem 2.

We show that we can take

$$\mathit{N}(n,m,r)=r(n-1)\left(1+\sum _{i=1}^{2(n-1)}{(N(n,m-1)-1)}^{i-1}\right)+n-1,$$

where $N(n,m-1)=\mathit{N}(n,m-1,1)$ is the number described in Theorem 2.

Let us fix any r coloring satisfying the assumptions of Theorem 8, that is, (A) for any color i, among any n vertices, there are two vertices joined by an edge of color i.

Let us take a graph of order $\mathit{N}(n,m,r)$ and consider the partition of the set of its vertices V into the following subsets $V_i$:

$$V_i=\{v\in V:\mathrm{vertex}v\mathrm{is}\mathrm{an}\mathrm{end}\mathrm{of}\mathrm{an}\mathrm{edge}\mathrm{of}\mathrm{colour}i\},i=1,2,\dots ,r.$$

Notice that every vertex may belong to every set $V_i$, that is, at most, r sets. In addition, there may exist vertices that are not endings of any edge (they have a degree of 0), but based on the assumption, there have to be fewer than n such vertices (maximum over r). Therefore, there exists a color $i_0$ such that any subgraph of this color (that is, a subgraph consisting of the edges of color $i_0$ and vertices from set $V_{i_0}$) is of an order of at least

$$(n-1)\left(1+\sum _{k=1}^{2(n-1)}{\left(N(n,m-1)-1\right)}^{k-1}\right)$$

and, based on (A), satisfies the following condition: among any n vertices, there are at least two adjacent vertices. According to Theorem 2, this subgraph contains $K_m$ as a subgraph. □

Let us notice that from Theorem 8 (it is enough to take $m=max\{m_1,\dots m_r\}$), we obtain the following theorem, which is an analog of Theorem 7.

Theorem 9.

Let $m_1,\dots ,m_r\ge 3$, $n>{max}_i\left\{m_i\right\}$ and r be natural numbers such that n is sufficiently large. There exists a natural number $\mathit{N}=\mathit{N}(n,m_1,\dots ,m_r)$ such that every simple graph of order $\mathit{N}$ with any subgraph of order n has at least r edges for any r-coloring satisfying the following condition:

• For any color i, among any n vertices, there exist at least two vertices joined by an edge of color i that contain a monochromatic $K_{m_j}$ as a subgraph for a certain color $j\in \{1,\dots ,r\}$. The least number $\mathit{N}$ is denoted by ${\mathit{N}}_{opt}(n,m_1,\dots ,m_r)$.

Remark 5.

In Ramsey’s Theorem 7, we consider r colorings of a complete graph, whereas in Theorem 9, we do not need graph G to be complete. Therefore, we can assume that in Theorem 9, we have an additional color that corresponds to non-existing edges i.e., all edges of $\overline{G}$ are painted this color. This means that the number ${\mathit{N}}_{opt}(n,m_1,\dots ,m_r)$ has to be compared with $R(n,m_1,\dots ,m_r)$, since in the case of Ramsey’s theorem, we have $r+1$ colorings of a complete graph.

Remark 6.

It is obvious that the following implication is true: Ramsey’s Theorem 7 ⇒ Theorem 9. But similar argumentation, such as that in Remark 2, is not enough in the case of inverse implication. We can only show that $R(n,m_1,m_2,\dots ,m_r)={\mathit{N}}_{opt}(n,m_1,\dots ,m_r,r)$ for any $r+1$ colorings satisfying the following condition: for any color i among any n vertices, there exist two vertices joined by an edge of color i. Let us also notice that according to Ramsey’s Theorem 7, we know that for any complete graph of an order of less than

$$R(n,m_1,m_2,\dots ,m_r)$$

there exists an $r+1$ coloring such that there is neither a $K_n$ of color 0 (which corresponds to ${\overline{K}}_n$) nor a $K_i$ for any $i\in \{1,2,\dots ,r\}$. This leads us to the following problem.

Problem 2.

Can such $r+1$ colorings satisfy the following condition? For any color $i\in \{1,2,\dots ,r\}$ among any n vertices, there exist two vertices joined by an edge of color i. If the answer is no, then

$${\mathit{N}}_{opt}(n,m_1,\dots ,m_r)<R(n,m_1,m_2,\dots ,m_r).$$

Remark 7 (Historical and technical remarks).

The version of Ramsey’s theorem stated in Theorem 1 is the two-color graph version, which also follows from Theorem 2 of Greenwood and Gleason’s paper [31]. It is worth noting that Greenwood and Gleason were not familiar with Ramsey’s theorem at the time. Let us also note that the version of “Ramsey’s theorem” being considered here is the graph version, not the general hypergraph version proven by Ramsey in Theorem B of [1].

Conclusion 1.

In this paper, in the first three sections, the new proof of Ramsey’s theorem is presented. Additional sections compare our findings with Turán’s theorem and present extensions to generalized Ramsey-type results. Some problems were also formulated. Our primary goal was to share with the readers a proof of Ramsey’s theorem with significant educational value. The supplementary chapters align with this didactic approach as well. Naturally, the authors maintained a creative and innovative perspective on the topics discussed throughout the process. Some results, including generalizations, have been omitted from the article due to space limitations. The authors plan to include them in conference materials.