On the Analytic Continuation of Appell’s Hypergeometric Function F2 to Some Symmetric Domains in the Space
Abstract
1. Introduction
- (A)
- The branched continued fractionconverges uniformly on every compact subset of the domainwhereandwhereto the function holomorphic in the domain
- (B)
2. Definitions and Auxiliary Results
- (i)
- if
- (ii)
- if or there exists index such that and
- (*)
- for all
- (**)
- if for there exists a multiindex such that then for and
- (A)
- The branched continued fractionconverges absolutely and uniformly for
- (B)
- The values of the branched continued fraction (14) and of its approximants are in the closed disk
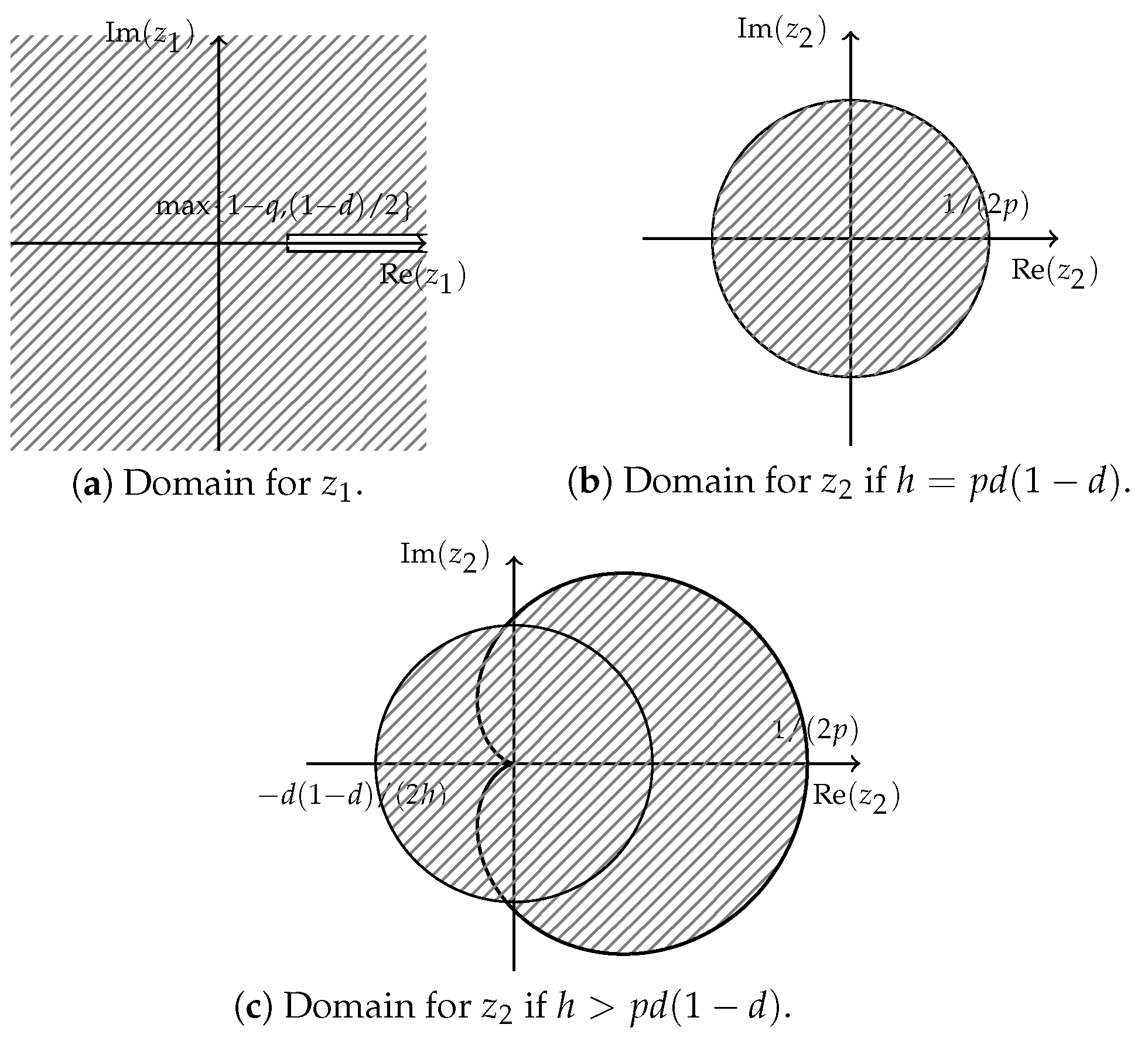
3. Convergence and Analytical Continuation
4. Examples
5. Conclusions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Appell, P. Sur les séries hyper géométriques de deux variables et sur des équations différentielles lineaires aux dérivées partielles. CR Acad. Sci. Paris 1880, 90, 296–298, 731–734. [Google Scholar]
- Appell, P. Sur les fonctions hyper géométriques de deux variables. J. Math. Pures Appl. 1982, 8, 173–216. [Google Scholar]
- Mazars, M. Canonical partition functions of freely jointed chains. J. Phys. A Math. Gen. 1998, 31, 1949–1964. [Google Scholar] [CrossRef]
- Hutchinson, T.P. Compound gamma bivariate distributions. Metrika 1981, 28, 263–271. [Google Scholar] [CrossRef]
- Bentalha, Z.E.A. Representation of the Coulomb matrix elements by means of Appell hypergeometric function F2. Math. Phys. Anal. Geom. 2018, 21, 10. [Google Scholar] [CrossRef]
- Shpot, M.A. A massive Feynman integral and some reduction relations for Appell functions. J. Math. Phys. 2007, 48, 123512. [Google Scholar] [CrossRef]
- Kol, B.; Shir, R. The propagator seagull: General evaluation of a two loop diagram. J. High Energy Phys. 2019, 2019, 83. [Google Scholar] [CrossRef]
- Tarasov, V.F. Multipole matrix elements for DH-systems and their asymptotics. Int. J. Mod. Phys. B 1995, 9, 2699–2718. [Google Scholar] [CrossRef]
- Brychkov, Y.A.; Saad, N. On some formulas for the Appell function F2(a, b, b′; c, c′; w; z). Integral Transforms Spec. Funct. 2013, 25, 111–123. [Google Scholar] [CrossRef]
- Wang, X. Recursion formulas for Appell functions. Integral Transforms Spec. Funct. 2012, 23, 421–433. [Google Scholar] [CrossRef]
- Opps, S.B.; Saad, N.; Srivastava, H.M. Some reduction and transformation formulas for the Appell hypergeometric function F2. J. Math. Anal. Appl. 2005, 302, 180–195. [Google Scholar] [CrossRef]
- Hahne, G.E. Analytic continuation of Appell’s hypergeometric series F2 to the vicinity of the singular point x = 1, y = 1. J. Math. Phys. 1969, 10, 524–531. [Google Scholar] [CrossRef]
- Jaeger, J.C. A continuation formula for Appell’s function F2. J. Lond. Math. Soc. 1938, 13, 254. [Google Scholar] [CrossRef]
- Sud, K.; Wright, L.E. A new analytic continuation of Appell’s hypergeometric series F2. J. Math. Phys. 1976, 17, 1719–1721. [Google Scholar] [CrossRef]
- Mimachi, K. Integral representations of Appell’s F2, F3, Horn’s H2 and Olsson’s Fp functions. Kyushu J. Math. 2020, 74, 1–13. [Google Scholar] [CrossRef]
- Slater, L.J. The integration of hypergeometric functions. Math. Proc. Camb. Philos. Soc. 1955, 51, 288–296. [Google Scholar] [CrossRef]
- Chelo, F.; López, J.L. The Appell’s function F2 for large values of its variables. Q. Appl. Math. 2010, 68, 701–712. [Google Scholar] [CrossRef]
- Hang, P.-C.; Luo, M.-J. Asymptotics of Saran’s hypergeometric function FK. J. Math. Anal. Appl. 2025, 541, 128707. [Google Scholar] [CrossRef]
- Minton, B.M. A note on the asymptotic expansion of the second Appell function. Math. Proc. Camb. Philos. Soc. 1968, 64, 1055. [Google Scholar] [CrossRef]
- Luo, M.-J.; Raina, R.K. On certain results related to the hypergeometric function FK. J. Math. Anal. Appl. 2021, 504, 125439. [Google Scholar] [CrossRef]
- Ananthanarayan, B.; Bera, S.; Friot, S.; Marichev, O.; Pathak, T. On the evaluation of the Appell F2 double hypergeometric function. Comput. Phys. Commun. 2023, 284, 108589. [Google Scholar] [CrossRef]
- Bodnar, D.I. Expansion of a ratio of hypergeometric functions of two variables in branching continued fractions. J. Math. Sci. 1993, 64, 1155–1158. [Google Scholar] [CrossRef]
- Antonova, T.; Cesarano, C.; Dmytryshyn, R.; Sharyn, S. An approximation to Appell’s hypergeometric function F2 by branched continued fraction. Dolomites Res. Notes Approx. 2024, 17, 22–31. [Google Scholar] [CrossRef]
- Dmytryshyn, R.I. Convergence of multidimensional A- and J-fractions with independent variables. Comput. Methods Funct. Theory 2022, 22, 229–242. [Google Scholar] [CrossRef]
- Bodnar, D.I. Branched Continued Fractions; Naukova Dumka: Kyiv, Ukraine, 1986. (In Russian) [Google Scholar]
- Antonova, T. On structure of branched continued fractions. Carpathian Math. Publ. 2024, 16, 391–400. [Google Scholar] [CrossRef]
- Wall, H.S. Analytic Theory of Continued Fractions; D. Van Nostrand Co.: New York, NY, USA, 1948. [Google Scholar]
- Antonova, T.M. On convergence of branched continued fraction expansions of Horn’s hypergeometric function H3 ratios. Carpathian Math. Publ. 2021, 13, 642–650. [Google Scholar] [CrossRef]
- Antonova, T.; Dmytryshyn, R.; Goran, V. On the analytic continuation of Lauricella-Saran hypergeometric function FK(a1, a2, b1, b2; a1, b2, c3; z). Mathematics 2023, 11, 4487. [Google Scholar] [CrossRef]
- Cuyt, A.A.M.; Petersen, V.; Verdonk, B.; Waadeland, H.; Jones, W.B. Handbook of Continued Fractions for Special Functions; Springer: Dordrecht, The Netherlands, 2008. [Google Scholar]
- Shabat, B.V. Introduce to Complex Analysis. Part II. Functions of Several Variables; American Mathematical Society: Providence, RI, USA, 1992. [Google Scholar]
- Vladimirov, V.S. Methods of the Theory of Functions of Many Complex Variables; The MIT Press: Cambridge, MA, USA, 1966. [Google Scholar]
- Dmytryshyn, R.; Lutsiv, I.-A.; Dmytryshyn, M. On the analytic extension of the Horn’s hypergeometric function H4. Carpathian Math. Publ. 2024, 16, 32–39. [Google Scholar] [CrossRef]
- Antonova, T.; Dmytryshyn, R.; Sharyn, S. Branched continued fraction representations of ratios of Horn’s confluent function H6. Constr. Math. Anal. 2023, 6, 22–37. [Google Scholar] [CrossRef]
- Hladun, V.; Rusyn, R.; Dmytryshyn, M. On the analytic extension of three ratios of Horn’s confluent hypergeometric function H7. Res. Math. 2024, 32, 60–70. [Google Scholar] [CrossRef]
- Antonova, T.; Dmytryshyn, R.; Sharyn, S. Generalized hypergeometric function 3F2 ratios and branched continued fraction expansions. Axioms 2021, 10, 310. [Google Scholar] [CrossRef]
- Bodnar, D.I.; Manzii, O.S. Expansion of the ratio of Appel hypergeometric functions F3 into a branching continued fraction and its limit behavior. J. Math. Sci. 2001, 107, 3550–3554. [Google Scholar] [CrossRef]
- Bodnar, D.I. Multidimensional C-fractions. J. Math. Sci. 1998, 90, 2352–2359. [Google Scholar] [CrossRef]
- Hladun, V.R.; Hoyenko, N.P.; Manzij, O.S.; Ventyk, L. On convergence of function F4(1, 2; 2, 2; z1, z2) expansion into a branched continued fraction. Math. Model. Comput. 2022, 9, 767–778. [Google Scholar] [CrossRef]
- Manzii, O.S. On the approximation of an Appell hypergeometric function by a branched continued fraction. J. Math. Sci. 1998, 90, 2376–2380. [Google Scholar] [CrossRef]
- Dmytryshyn, R.; Antonova, T.; Dmytryshyn, M. On the analytic extension of the Horn’s confluent function H6 on domain in the space C2. Constr. Math. Anal. 2024; accept. [Google Scholar]
- Bodnar, D.I.; Bilanyk, I.B. Parabolic convergence regions of branched continued fractions of the special form. Carpathian Math. Publ. 2021, 13, 619–630. [Google Scholar] [CrossRef]
- Bodnar, D.I.; Bilanyk, I.B. Two-dimensional generalization of the Thron-Jones theorem on the parabolic domains of convergence of continued fractions. Ukr. Math. J. 2023, 74, 1317–1333. [Google Scholar] [CrossRef]
- Bodnar, D.I.; Bilanyk, I.B. Estimation of the rates of pointwise and uniform convergence of branched continued fractions with inequivalent variables. J. Math. Sci. 2022, 265, 423–437. [Google Scholar] [CrossRef]
- Bodnar, D.I.; Bilanyk, I.B. On the convergence of branched continued fractions of a special form in angular domains. J. Math. Sci. 2020, 246, 188–200. [Google Scholar] [CrossRef]
- Antonova, T.M.; Dmytryshyn, M.V.; Vozna, S.M. Some properties of approximants for branched continued fractions of the special form with positive and alternating-sign partial numerators. Carpathian Math. Publ. 2018, 10, 3–13. [Google Scholar] [CrossRef]
- Antonova, T.M.; Sus’, O.M. Sufficient conditions for the equivalent convergence of sequences of different approximants for two-dimensional continued fractions. J. Math. Sci. 2018, 228, 1–10. [Google Scholar] [CrossRef]
- Antonova, T.M.; Sus’, O.M.; Vozna, S.M. Convergence and estimation of the truncation error for the corresponding two-dimensional continued fractions. Ukr. Math. J. 2022, 74, 501–518. [Google Scholar] [CrossRef]
- Bodnar, D.I.; Bodnar, O.S.; Bilanyk, I.B. A truncation error bound for branched continued fractions of the special form on subsets of angular domains. Carpathian Math. Publ. 2023, 15, 437–448. [Google Scholar] [CrossRef]
- Bodnar, O.S.; Dmytryshyn, R.I.; Sharyn, S.V. On the convergence of multidimensional S-fractions with independent variables. Carpathian Math. Publ. 2020, 12, 353–359. [Google Scholar] [CrossRef]
- Dmytryshyn, R.; Cesarano, C.; Lutsiv, I.-A.; Dmytryshyn, M. Numerical stability of the branched continued fraction expansion of Horn’s hypergeometric function H4. Mat. Stud. 2024, 61, 51–60. [Google Scholar] [CrossRef]
- Hladun, V.R.; Bodnar, D.I.; Rusyn, R.S. Convergence sets and relative stability to perturbations of a branched continued fraction with positive elements. Carpathian Math. Publ. 2024, 16, 16–31. [Google Scholar] [CrossRef]
- Hladun, V.R. Some sets of relative stability under perturbations of branched continued fractions with complex elements and a variable number of branches. J. Math. Sci. 2016, 215, 11–25. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dmytryshyn, R.
On the Analytic Continuation of Appell’s Hypergeometric Function F2 to Some Symmetric Domains in the Space
Dmytryshyn R.
On the Analytic Continuation of Appell’s Hypergeometric Function F2 to Some Symmetric Domains in the Space
Dmytryshyn, Roman.
2024. "On the Analytic Continuation of Appell’s Hypergeometric Function F2 to Some Symmetric Domains in the Space
Dmytryshyn, R.
(2024). On the Analytic Continuation of Appell’s Hypergeometric Function F2 to Some Symmetric Domains in the Space





