Out-of-Plane Equilibrium Points in the Photogravitational Hill Three-Body Problem
Abstract
1. Introduction
2. Photogravitational Hill’s Equations of Motion
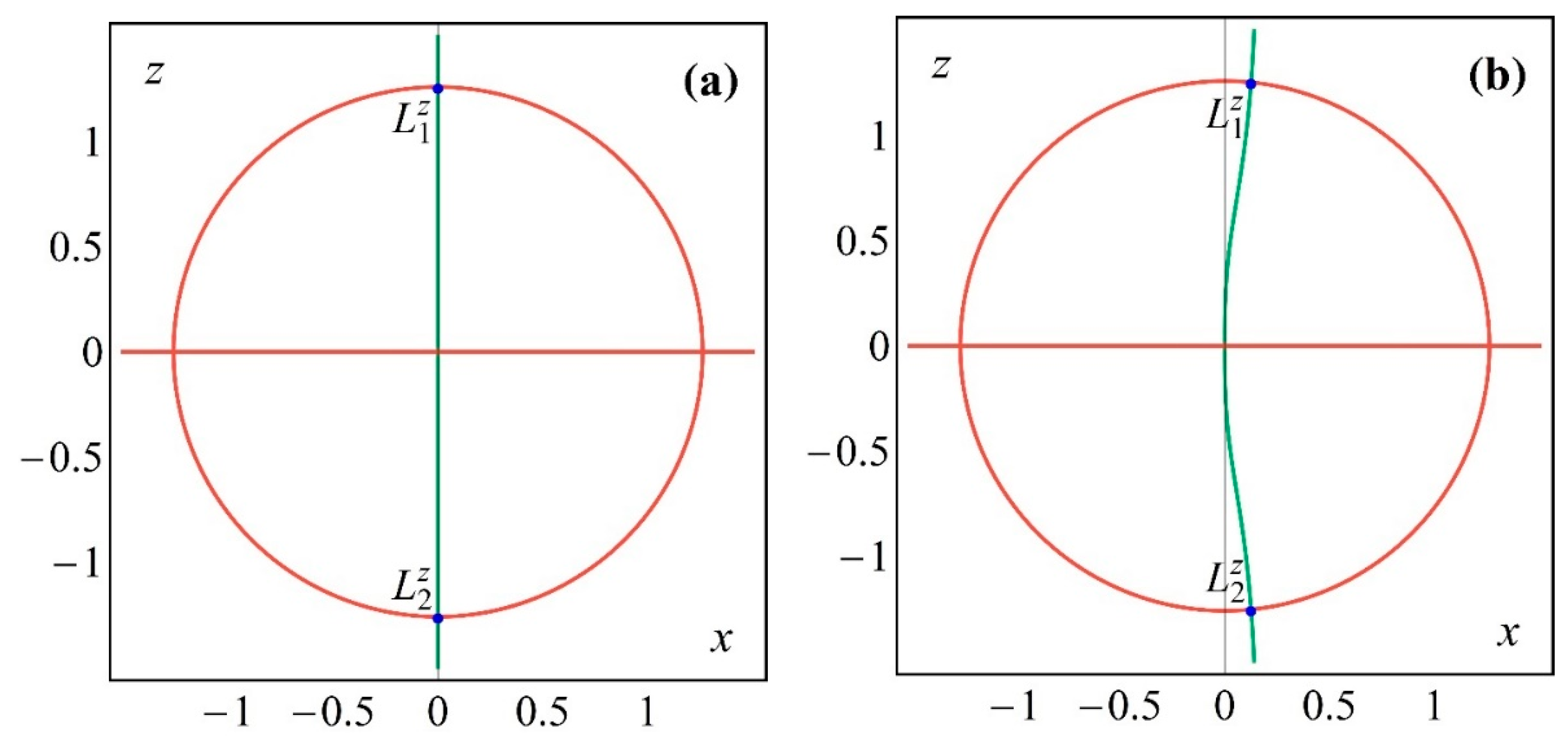
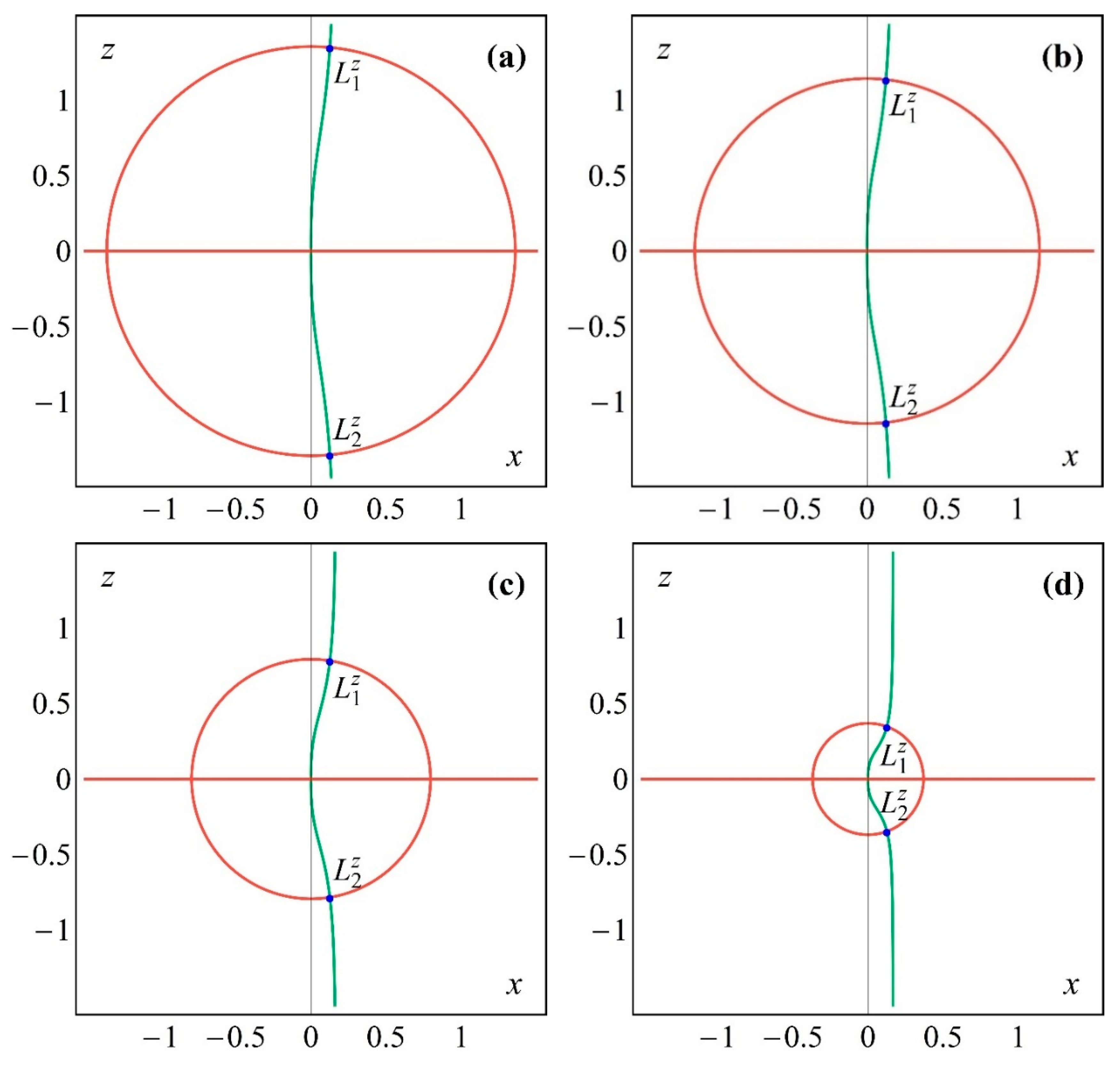
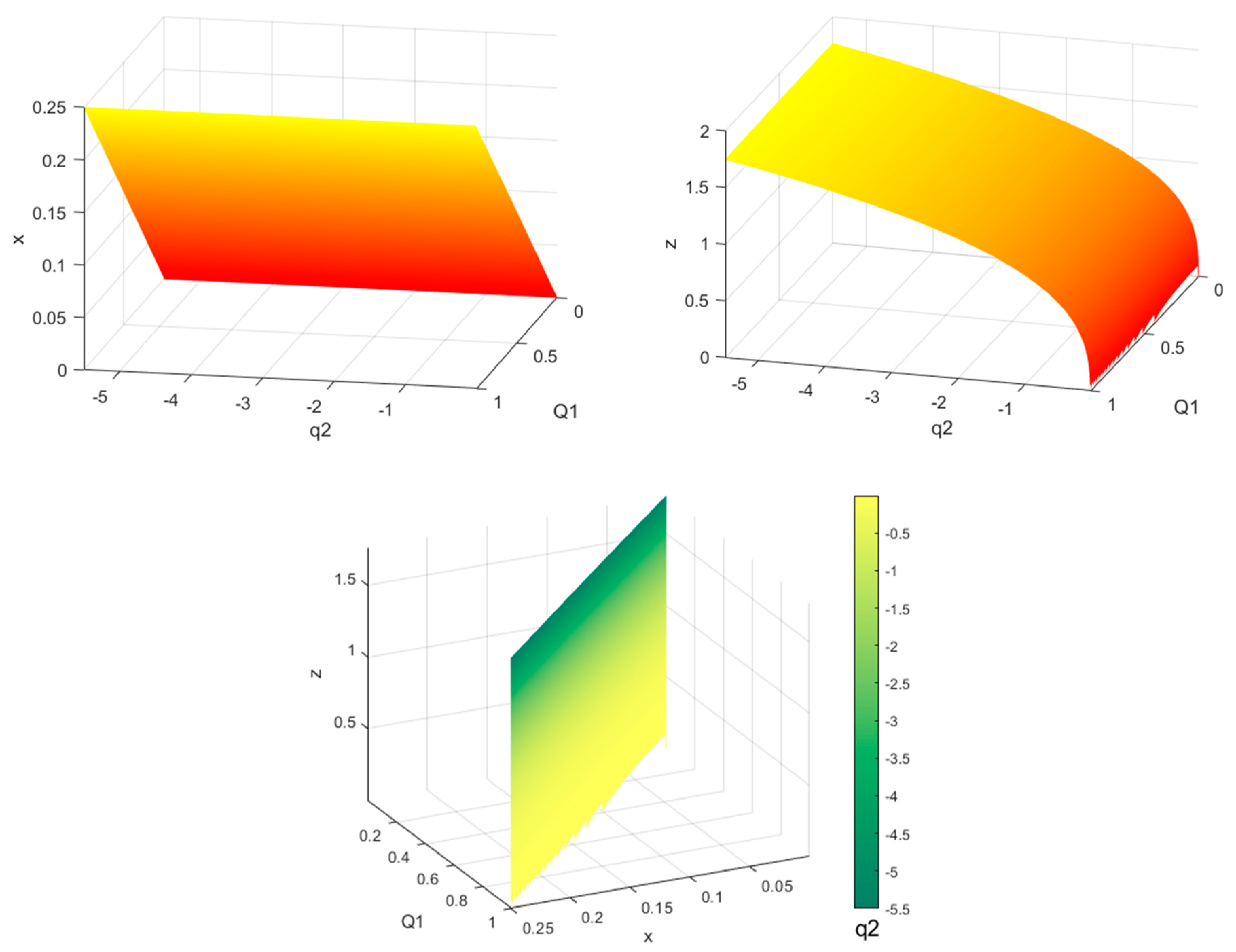
3. Existence and Location of the Equilibrium Points of the System
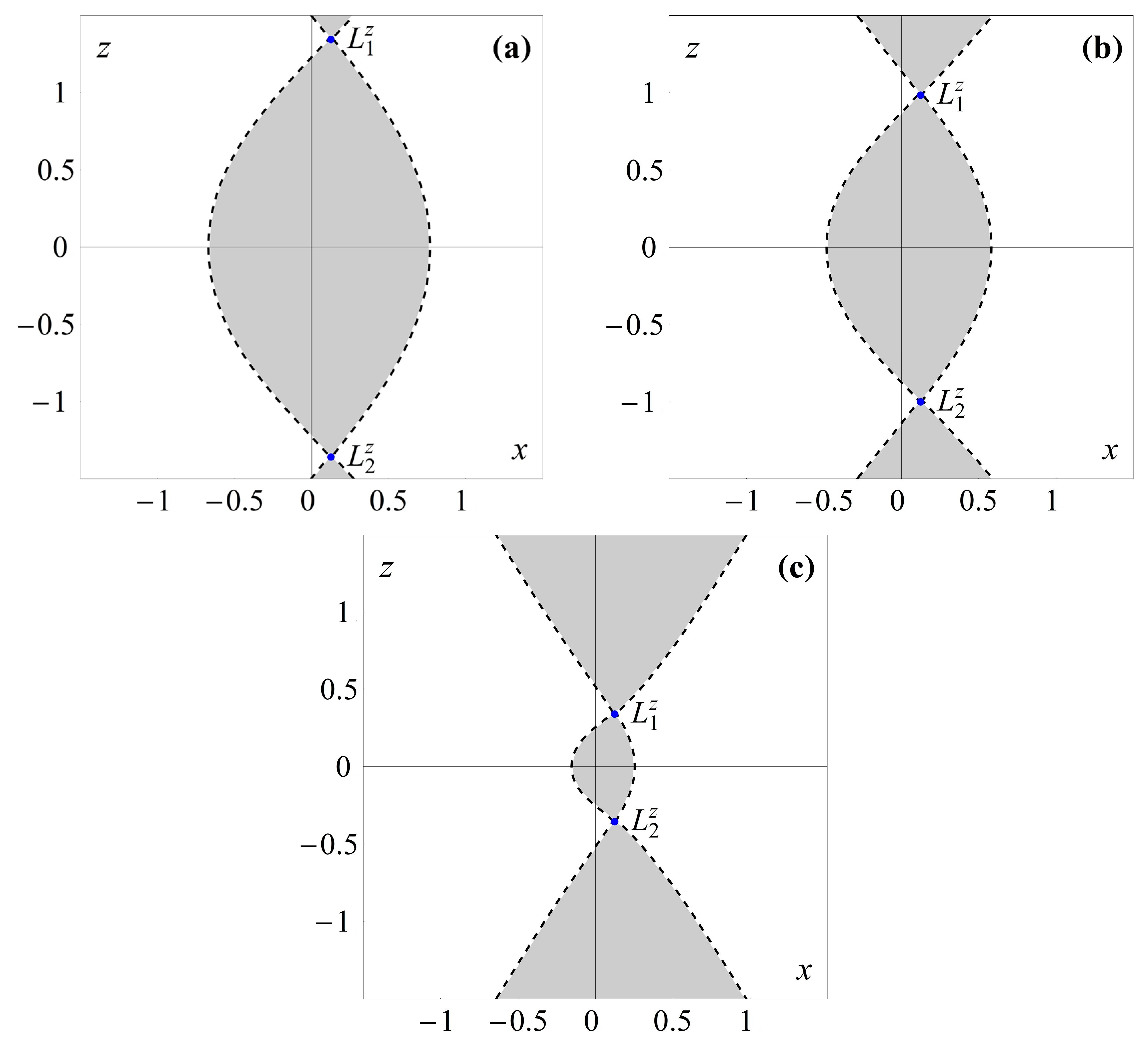
4. Zero-Velocity Curves in the () Plane
5. Stability of the Out-of-Plane Equilibrium Points
6. Discussion and Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Hill, G.W. Researches in the lunar theory. Am. J. Math. 1878, 1, 5–26. [Google Scholar] [CrossRef]
- Tsirogiannis, G.A.; Perdios, E.A.; Markellos, V.V. Improved grid search method: An efficient tool for global computation of periodic orbits: Application to Hill’s problem. Celest. Mech. Dyn. Astron. 2009, 103, 49–78. [Google Scholar]
- Liu, K.Y.-Y.; Villac, B. Periodic orbits families in the Hill’s three-body problem with solar radiation pressure. Adv. Astronaut. Sci. 2010, 136, 285–300. [Google Scholar]
- de Bustos, M.T.; Lopez, M.A.; Martinez, R.; Vera, J.A. On the periodic solutions emerging from the equilibria of the Hill Lunar problem with oblateness. Qual. Theory Dyn. Syst. 2018, 17, 331–344. [Google Scholar]
- Aydin, C. The Conley–Zehnder indices of the spatial Hill three-body problem. Celest. Mech. Dyn. Astron. 2023, 135, 32. [Google Scholar]
- Frauenfelder, U.; Moreno, A. On GIT quotients of the symplectic group, stability and bifurcations of periodic orbits (with a view towards practical applications). J. Symplect. Geom. 2023, 21, 723–773. [Google Scholar] [CrossRef]
- Xu, X. Determination of the doubly symmetric periodic orbits in the restricted three-body problem and Hill’s lunar problem. Celest. Mech. Dyn. Astron. 2023, 135, 8. [Google Scholar]
- Hénon, M. Numerical exploration of the restricted problem V. Hill’s case: Periodic orbits and their stability. Astron. Astrophys. 1969, 1, 223–238. [Google Scholar]
- Zagouras, C.; Markellos, V.V. Three-dimensional periodic solutions around equilibrium points in Hill’s problem. Celes. Mech. 1985, 35, 257–267. [Google Scholar]
- Villac, B.F.; Scheeres, D.J. Escaping trajectories in the Hill three–body problem and applications. J. Guid. Control Dyn. 2003, 26, 224–232. [Google Scholar]
- Zotos, E.E. Comparing the fractal basins of attraction in the Hill problem with oblateness and radiation. Astrophys. Space Sci. 2017, 362, 190. [Google Scholar] [CrossRef]
- Kalantonis, V.S. Numerical Investigation for Periodic Orbits in the Hill Three-Body Problem. Universe 2020, 6, 72. [Google Scholar] [CrossRef]
- Asano, Y.; Satoh, S.; Yamada, K. Analysis of period-multiplying bifurcations of distant retrograde orbits in the Hill three-body problem. Adv. Space Res. 2022, 70, 3016–3033. [Google Scholar] [CrossRef]
- Moneer, E.M.; Alanazi, M.; Elaissi, S.; Allawi, Y.; Dubeibe, F.L.; Zotos, E.Z. Orbital dynamics in the Hill problem with oblateness. Results Phys. 2023, 53, 106936. [Google Scholar] [CrossRef]
- Ibrahim, M.K.; Rabeh, T.; Abouelmagd, E.I. Dynamical Properties of Perturbed Hill’s System. Math. Comput. Appl. 2024, 29, 66. [Google Scholar] [CrossRef]
- Radzievskii, V. The space photogravitational restricted three-body problem. Astron. Zh 1953, 30, 265–269. [Google Scholar]
- Schuerman, D. The restricted three-body problem including radiation pressure. Astrophys. J. 1980, 238, 337–342. [Google Scholar] [CrossRef]
- Simmons, J.; McDonald, A.; Brown, J. The restricted 3-body problem with radiation pressure. Celest. Mech. 1985, 35, 145–187. [Google Scholar] [CrossRef]
- Suraj, M.S.; Aggrawal, R.; Shalini, K.; Asique, M.C. Out-of-plane equilibrium points and regions of motion in photogravitational R3BP when the primaries are heterogeneous spheroids with three layers. New Astron. 2018, 63, 15–26. [Google Scholar] [CrossRef]
- Suraj, M.S.; Aggrawal, R.; Asique, M.C.; Mittal, A. The effect of radiation pressure on the basins of convergence in the restricted four-body problem. Chaos Soliton Fract. 2020, 141, 110347. [Google Scholar] [CrossRef]
- Wang, R.; Wang, Y.; Gao, F. Bifurcation analysis and approximate analytical periodic solution of ER3BP with radiation and albedo effects. Astrophys. Space Sci. 2021, 366, 29. [Google Scholar] [CrossRef]
- Moneer, E.M.; Allawi, Y.M.; Alanazi, M.; Zotos, E.Z. Revealing the properties of the out-of-plane points of equilibrium of the restricted 3-body problem with non-spherical radiating bodies. New Astron. 2023, 103, 102061. [Google Scholar] [CrossRef]
- Sheth, D.; Pathak, N.M.; Thomas, V.O.; Abouelmagd, E.I. Periodic orbits analysis of elliptical Sun-Saturn system. Astron. Rep. 2023, 67, 520–535. [Google Scholar] [CrossRef]
- Gahlot, P.; Kishor, R. Invariant manifolds of Lyapunov periodic orbits in the RCD solar sail problem with dipole secondary. Nonlinear Dyn. 2024, 112, 14143–14157. [Google Scholar] [CrossRef]
- Ragos, O.; Zagouras, C.G. Periodic solutions about the “out of plane” equilibrium points in the photogravitational restricted three-body problem. Celest. Mech. 1988, 44, 135–154. [Google Scholar] [CrossRef]
- Ragos, O.; Zagouras, C.G. On the existence of the “out of plane” equilibrium points in the photogravitational restricted three-body problem. Astrophys. Space Sci. 1988, 209, 267–271. [Google Scholar] [CrossRef]
- Gao, F.; Wang, R. Bifurcation analysis and periodic solutions of the HD 191408 system with triaxial and radiative perturbations. Universe 2020, 6, 35. [Google Scholar] [CrossRef]
- Kalantonis, V.S.; Vincent, E.A.; Gyegwe, J.M.; Perdios, E.A. Periodic solutions around the out-of-plane equilibrium points in the restricted three-body problem with radiation and angular velocity variation. In Nonlinear Analysis and Global Optimization; Rassias, T.M., Pardalos, P.M., Eds.; Springer: Cham, Switzerland, 2021; Volume 167, pp. 251–275. [Google Scholar]
- Vincent, E.A.; Singh, J. Out-of-plane equilibria in the perturbed Photogravitational restricted three-body problem with Poynting-Robertson (P-R) drag. Heliyon 2022, 8, e09603. [Google Scholar] [CrossRef]
- Suraj, M.S.; Aggarwal, R.; Aggarwal, V.K.; Asique, M.C. Combined effect of small perturbations in the Coriolis and centrifugal forces and three-body interaction on the existence of stationary points in the R3BP. New Astron. 2021, 89, 101630. [Google Scholar] [CrossRef]
- Suraj, M.S.; Aggarwal, R.; Asique, M.C.; Mittal, A. On the modified circular restricted three-body problem with variable mass. New Astron. 2021, 84, 101510. [Google Scholar] [CrossRef]
- Suraj, M.S.; Aggarwal, R.; Asique, M.C.; Mittal, A. On the Basins of Convergence in the Magnetic-Binary Problem with Angular Velocity. Comp. Math. Methods 2021, 3, 1161. [Google Scholar] [CrossRef]
- Suraj, M.S.; Aggarwal, R.; Asique, M.C.; Mittal, A. The influence of third order terms on basins of convergence in the Hénon-Heiles type system. New Astron. 2022, 94, 101761. [Google Scholar] [CrossRef]
- Markellos, V.V.; Roy, A.E.; Velgakis, M.J.; Kanavos, S.S. A photogravitational Hill problem and radiation effects on Hill stability of orbits. Astrophys. Space Sci. 2000, 271, 293–301. [Google Scholar] [CrossRef]
- Kanavos, S.S.; Markellos, V.V.; Perdios, E.A.; Douskos, C.N. The photogravitational Hill problem: Numerical exploration. Earth Moon Planets 2002, 91, 223–241. [Google Scholar] [CrossRef]
- Papadakis, K.E. The planar photogravitational Hill problem. Int. J. Bifurc. Chaos 2006, 16, 1809–1821. [Google Scholar] [CrossRef]
- Markakis, M.P.; Perdiou, A.E.; Douskos, C.N. The photogravitational Hill problem with oblateness: Equilibrium points and Lyapunov families. Astrophys. Space Sci. 2008, 315, 297–306. [Google Scholar] [CrossRef]
- Douskos, C. Collinear equilibrium points of Hill’s problem with radiation and oblateness and their fractal basins of attraction. Astrophys. Space Sci. 2010, 326, 263–271. [Google Scholar] [CrossRef]
- Perdiou, A.E.; Perdios, E.A.; Kalantonis, V.S. Periodic orbits of the Hill problem with radiation and oblateness. Astrophys. Space Sci. 2012, 342, 19–30. [Google Scholar] [CrossRef]
- Kalantonis, V.S.; Perdiou, A.E.; Douskos, C.N. Asymptotic orbits in Hill’s problem when the larger primary is a source of radiation. In Applications of Nonlinear Analysis; Rassias, T.M., Ed.; Springer: Cham, Switzerland, 2018; Volume 134, pp. 523–535. [Google Scholar]
- Bairwa, L.K.; Pal, A.K.; Kumari, R.; Alhowaity, S.; Abouelmagd, E.I. Study of Lagrange points in the earth–moon system with continuation fractional potential. Fractal Fract. 2022, 6, 321. [Google Scholar] [CrossRef]
- Abouelmagd, E.I. New model for Hill’s problem in the framework of continuation fractional potential. Math. Comput. Appl. 2024, 29, 34. [Google Scholar] [CrossRef]
- Vincent, E.A.; Abouelmagd, E.I.; Perdios, A.E.; Kalantonis, V.S. Numerical exploration of the quantized Hill problem dynamics. Chaos Solitons Fractals 2024, 181, 114688. [Google Scholar] [CrossRef]
- Yárnoz, D.G.; Scheeres, D.J.; McInnes, C.R. On the a and and g families of orbits in the Hill problem with solar radiation pressure and their application to asteroid orbiters. Celest. Mech. Dyn. Astron. 2015, 121, 365–384. [Google Scholar] [CrossRef][Green Version]
- Szebehely, V. Theory of Orbits; Academic Press: New York, NY, USA, 1967. [Google Scholar]
- Xuetang, Z.; Lizhong, Y. Photogravitational restricted three-body problem and coplanar libration points. Chin. Phys. Lett. 1993, 10, 61–64. [Google Scholar]


| −0.05 | (0, ±0.36840315) | (0.08750000, ±0.35786119) | (0.12500000, ±0.34654853) |
| −0.04 | (0, ±0.34199519) | (0.08750000, ±0.33061225) | (0.12500000, ±0.31833270) |
| −0.03 | (0, ±0.31072325) | (0.08750000, ±0.29814877) | (0.12500000, ±0.28447133) |
| −0.02 | (0, ±0.27144176) | (0.08750000, ±0.25695210) | (0.12500000, ±0.24094736) |
| −0.01 | (0, ±0.21544347) | (0.08750000, ±0.19687468) | (0.12500000, ±0.17547333) |
| () | |||
|---|---|---|---|
| −5.5 | (0, ±1.765174168) | ±1.732050807 | ±(1.118033988 ± 0.8660254037) |
| −4.0 | (0, ±1.587401052) | 1.732050808 | ±(1.118033989 ± 0.8660254038) |
| −2.0 | (0, ±1.259921050) | ±1.732050807 | ±(1.118033989 ± 0.8660254038) |
| −1.0 | (0, ±1.000000000) | ±1.732050808 | ±(1.118033989 ± 0.8660254038) |
| −0.01 | (0, ±0.215443469) | ±1.732050808 | ±(1.118033989 ± 0.8660254038) |
| −0.005 | (0, ±0.170997595) | ±1.732050807 | ±(1.118033988 ± 0.8660254037) |
| () | |||
|---|---|---|---|
| −5.5 | (0.12500000, ±1.760742696) | ±1.730962960 | ±(1.116769707 ± 0.8654814802) |
| −4.0 | (0.12500000, ±1.582471832) | ±1.730705035 | ±(1.116469855 ±0.8653525173) |
| −2.0 | (0.12500000, ±1.253704930) | ±1.729911465 | ±(1.115547067 ± 0.8649557326) |
| −1.0 | (0.12500000, ±0.992156742) | 1.728647057 | ±(1.114076068 ± 0.8643235285) |
| −0.01 | (0.12500000, ±0.175473327) | ±1.647106082 | ±(1.017211303 ± 0.8235530413) |
| −0.005 | (0.12500000, ±0.116684092) | ±1.579922392 | ±(0.933871550 ± 0.7899611956) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vincent, A.E.; Tsirogiannis, G.A.; Perdiou, A.E.; Kalantonis, V.S. Out-of-Plane Equilibrium Points in the Photogravitational Hill Three-Body Problem. Symmetry 2024, 16, 1374. https://doi.org/10.3390/sym16101374
Vincent AE, Tsirogiannis GA, Perdiou AE, Kalantonis VS. Out-of-Plane Equilibrium Points in the Photogravitational Hill Three-Body Problem. Symmetry. 2024; 16(10):1374. https://doi.org/10.3390/sym16101374
Chicago/Turabian StyleVincent, Aguda E., George A. Tsirogiannis, Angela E. Perdiou, and Vassilis S. Kalantonis. 2024. "Out-of-Plane Equilibrium Points in the Photogravitational Hill Three-Body Problem" Symmetry 16, no. 10: 1374. https://doi.org/10.3390/sym16101374
APA StyleVincent, A. E., Tsirogiannis, G. A., Perdiou, A. E., & Kalantonis, V. S. (2024). Out-of-Plane Equilibrium Points in the Photogravitational Hill Three-Body Problem. Symmetry, 16(10), 1374. https://doi.org/10.3390/sym16101374





