Improved Generalized-Pinball-Loss-Based Laplacian Twin Support Vector Machine for Data Classification

Abstract

Nowadays, unlabeled data are abundant, while supervised learning struggles with this challenge as it relies solely on labeled data, which are costly and time-consuming to acquire. Additionally, real-world data often suffer from label noise, which degrades the performance of supervised models. Semi-supervised learning addresses these issues by using both labeled and unlabeled data. This study extends the twin support vector machine with the generalized pinball loss function (GPin-TSVM) into a semi-supervised framework by incorporating graph-based methods. The assumption is that connected data points should share similar labels, with mechanisms to handle noisy labels. Laplacian regularization ensures uniform information spread across the graph, promoting a balanced label assignment. By leveraging the Laplacian term, two quadratic programming problems are formulated, resulting in LapGPin-TSVM. Our proposed model reduces the impact of noise and improves classification accuracy. Experimental results on UCI benchmarks and image classification demonstrate its effectiveness. Furthermore, in addition to accuracy, performance is also measured using the Matthews Correlation Coefficient (MCC) score, and the experiments are analyzed through statistical methods.

1. Introduction

Support vector machine (SVM) [1] is an efficient machine learning model that remains widely utilized today. This is due to its simplicity and ability to explain its mathematical principles easily. It can find a global classification solution, dividing data by creating a single optimal hyperplane. Although the support vector machine is highly popular, it has to solve large matrices when attempting to find solutions using quadratic programming problems (QPPs).

To improve computational efficiency, Jayadeva et al. [2] developed the twin support vector machine (TSVM), which finds two nonparallel hyperplanes, each closer to one class. This reduces problem-solving time by splitting it into two smaller QPPs. Due to its lower computational cost and better generalization than an SVM, many adaptations of the TSVM have emerged. Kumar et al. [3] introduced a least-squares TSVM (LS-TSVM) to simplify computations by replacing QPPs with linear equations. Mei et al. [4] extended TSVMs to multi-task learning with a multi-task LS-TSVM algorithm. Rastogi et al. [5] proposed a robust parametric TSVM (RP-TWSVM), which adjusts the margin to handle heteroscedastic noise. Further extensions of TSVMs are discussed in [6,7,8,9].

A TSVM assigns equal importance to all data, making it sensitive to noise, outliers, and class imbalances [10], which can lead to reduced predictive capability or overfitting. To address these issues, Rezvani et al. [11] introduced Intuitionistic Fuzzy Twin SVMs (IFTSVMs) using intuitionistic fuzzy sets. Xu et al. [12] proposed PinTSVMs for noise insensitivity, and Tanveer et al. [13] introduced the general TSVM with pinball loss (Pin-GTSVM), which reduced sensitivity to outliers. However, TSVMs and Pin-GTSVMs lose model sparsity, motivating Tanveer et al. [14] to propose a Sparse Pinball TSVM (SP-TSVM) using the $ϵ$-insensitive-zone pinball loss. Rastogi et al. [15] developed the generalized pinball loss, which extends the pinball and hinge loss functions. Panup et al. [16] applied this generalized pinball loss to a TSVM, resulting in the GPin-TSVM. The GPin-TSVM improves accuracy in pattern classification, handles noise and outliers effectively, and retains model sparsity, enhancing scalability. Its structure, based on solving two smaller QPPs, reduces computational complexity and increases efficiency.

The model discussed above is classified as supervised learning, which relies on labeled data for training. However, a key challenge with this approach is the requirement for labeled data, which can be difficult and costly to obtain. Additionally, real-world data often suffer from label noise, where incorrect labels degrade the performance of supervised models. To overcome this limitation, unsupervised learning [17] has been developed, allowing models to be built using unlabeled data. To combine the advantages of both labeled and unlabeled data, a method called semi-supervised learning has emerged, enabling models to utilize both types of data effectively. This area has seen significant growth.

Semi-supervised learning (SSL) [18] integrates both labeled and unlabeled data to enhance the effectiveness of supervised learning. The goal is to build a more robust classifier by leveraging large volumes of unlabeled data alongside a relatively small set of labeled data. Recent advancements in deep learning, such as GACNet, CVANet, and CATNet, apply semi-supervised techniques and attention mechanisms to address data scarcity and improve feature extraction. GACNet [19] uses a semi-supervised GAN to augment hyperspectral datasets, while CVANet [20] and CATNet [21] enhance image resolution and classification with attention modules. These methods collectively demonstrate the power of combining semi-supervised learning and attention for robust image processing across various domains. In addressing noisy labels, the ECMB framework [22] introduced real-time correction with a Mixup entropy and a balance term to prevent overfitting. Then, C2MT [23] advanced this with a co-teaching strategy and the Median Balance Strategy (MBS) to maintain class balance. In 2024, BPT-PLR [24] improved accuracy and robustness by addressing class imbalance and optimization conflicts through a Gaussian mixture model and a pseudo-label relaxed contrastive loss.

While these advancements strengthened noisy label learning, a graph-based approach offers a more structured solution for combining labeled and unlabeled data. The Laplacian Twin Support Vector Machine (Lap-TSVM) [25] enhances the TSVM by incorporating Laplacian regularization to exploit the underlying data structure. This technique smooths the decision function across the data manifold, making the Lap-TSVM especially effective for data with local structures. Widely used in machine learning, spectral clustering, and semi-supervised learning, it captures the structural properties of graphs to improve model performance [26]. One notable feature of the graph Laplacian is its symmetry; when the graph is undirected, the Laplacian matrix is symmetric. This symmetry is critical in many spectral graph algorithms, simplifying computations and ensuring the stability of solutions derived from the matrix. The Laplacian matrix’s symmetry and regularization make it effective for graph-based representations in machine learning, particularly in semi-supervised learning. To further reduce computational time, Chen et al. [27] developed a least-squares version of Lap-TSVM that solved linear equations. Additionally, the Lap-PTSVM [28] was introduced, integrating pinball loss with Lap-TSVM and yielding promising results in classification tasks.

In earlier discussions, the GPin-TSVM extended SVM to nonparallel hyperplanes, offering a resilient model that tackled challenges like noise and sparsity, making it highly reliable for practical applications. To further improve classification performance, particularly when labeled data are limited, the GPin-TSVM is extended by integrating a Laplacian graph-based technique, resulting in the LapGPin-TSVM, a semi-supervised model. The LapGPin-TSVM leverages both labeled and unlabeled data, making it more robust in real-world scenarios where large-scale labeling is impractical.

Our approach involves formulating two quadratic programming problems (QPP) to solve for hyperplanes. We evaluate the model across 13 UCI benchmark datasets using 5-fold cross-validation and varying the ratio of unlabeled data (20%, 40%, 60%, 80%) and noise (0%, 5%, 10%). Additionally, we investigate its performance in image classification using CIFAR-10. The results are analyzed using the Wilcoxon signed-rank test to determine statistical significance. The overall concept of this study is stated in Figure 1. Our proposed approach is outlined and characterized by the following:

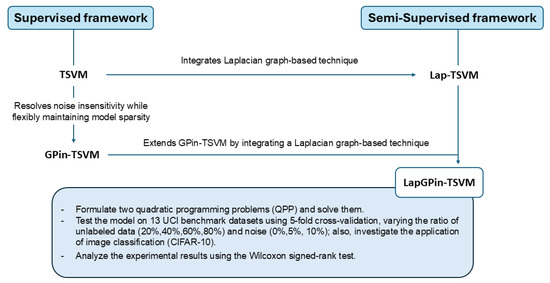
Figure 1. A conceptual diagram illustrating the development of LapGPin-TSVM by integrating a Laplacian graph-based technique into the GPin-TSVM framework, evolving from both supervised and semi-supervised methods.

• We combine the twin support vector machine based on the generalized pinball loss (GPin-TSVM) with the Laplacian technique, introducing a novel semi-supervised framework named LapGPin-TSVM. Additionally, we demonstrate noise insensitivity along with a corresponding analysis.
• We evaluate the efficacy of our model through experiments on the UCI dataset, using various ratios of unlabeled data and noise, and compare the results with three state-of-the-art models. Moreover, we also investigate the application of our approach to image classification.
• To analyze the performance of LapGPin-TSVM, we employ the win/tie/loss method, average rank, and use the Wilcoxon signed-rank test to better describe the effectiveness of our proposed method.

The rest of the paper is organized as follows: The preliminary section covers the notation used in the study. We then describe key models, including the TSVM, GPin-TSVM, and semi-supervised Lap-TSVM. Section 3 discusses the primary and dual problems, along with the property of the model. Section 4 provides a model comparison, and Section 5 presents the experimental results. Section 6 offers the discussion, followed by the conclusion in Section 7.

2. Preliminaries

To understand the fundamental concepts, we define the notation and symbols used in this work as follows. For a matrix denoted as M and a vector represented by x, their transposes are denoted as $M^{\top }$ and $x^{\top }$, respectively. The inverse matrix of M is expressed as $M^{-1}$. Here, we are dealing with a binary semi-supervised classification problem in a d-dimensional real space $R^d$. The complete dataset is denoted as $M=(x_1,y_1),\dots ,(x_l,y_l),\left(x_{l+1}\right),\dots ,\left(x_{l+u}\right)$, where $y_i\in \{-1,+1\}$, and $x_i$ for $i=1,\dots ,l$ represents labeled data, while $x_i$ for $i=l+1,\dots ,l+u$ represents unlabeled data. Assume that we have $l_1$ and $l_2$ samples belonging to the labeled data corresponding to classes +1 and −1, respectively. The positively labeled samples are represented in the matrix $A\in R^{l_1\times d}$, and the negatively labeled samples are denoted by the matrix $B\in R^{l_2\times d}$.

2.1. Twin Support Vector Machine (TSVM)

This method is based on the idea of identifying two nonparallel hyperplanes that classify the data points into their respective classes. It involves a pair of nonparallel planes given by:

$$\begin{array}{c}\hfill x^{\top }{w}_1+b_1=0\mathrm{and}{x}^{\top }{w}_2+b_2=0,\end{array}$$

(1)

where $w_1,w_2\in R^n$ and $b_1,b_2\in R$. This approach requires solving two small-sized quadratic programming problems (QPPs), formulated as follows:

$$\begin{array}{cc}\hfill & \underset{w_1,b_1,\xi }{min}{\displaystyle \frac{1}{2}}{\parallel A{w}_1+e_1{b}_1\parallel }^2+c_1{e}_2^{\top }\xi \hfill \\ \hfill & \text{s.t.}-(B{w}_1+e_2{b}_1)+\xi \ge e_2,\hfill \\ \hfill & \xi \ge 0,\hfill \end{array}$$

(2)

and

$$\begin{array}{cc}\hfill & \underset{w_2,b_2,\xi }{min}{\displaystyle \frac{1}{2}}{\parallel B{w}_2+e_2{b}_2\parallel }^2+c_2{e}_1^{\top }\xi \hfill \\ \hfill & \text{s.t.}(A{w}_2+e_1{b}_2)+\xi \ge e_1,\hfill \\ \hfill & \xi \ge 0,\hfill \end{array}$$

(3)

where $\xi$ is a slack variable, and $c_1,c_2$ are positive penalty parameters. $e_1$ and $e_2$ are unit vectors of the appropriate size. As the twin support vector machine demonstrates commendable performance, researchers are working to enhance it further. They are currently exploring the integration of a new type of loss called the generalized pinball loss, with a specific focus on improving its handling of classification tasks.

2.2. Twin Support Vector Machine with Generalized Pinball Loss (GPin-TSVM)

Panup et al. [16] recently introduced a variant of the TSVM called the generalized pinball loss TSVM, denoted as GPin-TSVM. The definition of the generalized pinball loss function is given as follows

$$\begin{array}{c}\hfill {\ell }_{{\tau }_1,{\tau }_2}^{{ϵ}_1,{ϵ}_2}\left(u\right)=\left\{\begin{array}{cc}{\tau }_1\left(u-{\displaystyle \frac{{ϵ}_1}{{\tau }_1}}\right),\hfill & u>{\displaystyle \frac{{ϵ}_1}{{\tau }_1}},\hfill \\ 0,\hfill & -{\displaystyle \frac{{ϵ}_2}{{\tau }_2}}\le u\le {\displaystyle \frac{{ϵ}_1}{{\tau }_1}},\hfill \\ -{\tau }_2\left(u+{\displaystyle \frac{{ϵ}_2}{{\tau }_2}}\right),\hfill & u<-{\displaystyle \frac{{ϵ}_2}{{\tau }_2}},\hfill \end{array}\right.\end{array}$$

(4)

where $u=1-y(w^{\top }x+b)$ and ${\tau }_1,{\tau }_2,{ϵ}_1,{ϵ}_2\ge 0$. This improvement from the $ϵ$-insensitive zone [29] results in enhanced model sparsity while retaining all the inherent properties of the original. The optimization problems are outlined as follows:

$$\begin{array}{cc}\hfill \underset{w_1,b_1,\xi }{min}& {\displaystyle \frac{1}{2}}{\parallel A{w}_1+e_1{b}_1\parallel }^2+c_1{e}_2^{\top }\xi \hfill \\ \hfill \text{s.t.}& -(B{w}_1+e_2{b}_1)\ge e_2-{\displaystyle \frac{1}{{\tau }_1}}(\xi +e_2{ϵ}_1),\hfill \\ \hfill & -(B{w}_1+e_2{b}_1)\le e_2+{\displaystyle \frac{1}{{\tau }_2}}(\xi +e_2{ϵ}_2),\hfill \\ \hfill & \xi \ge 0,\hfill \end{array}$$

(5)

and

$$\begin{array}{cc}\hfill \underset{w_2,b_2,\xi }{min}& {\displaystyle \frac{1}{2}}{\parallel B{w}_2+e_2{b}_2\parallel }^2+c_2{e}_1^{\top }\xi \hfill \\ \hfill \text{s.t.}& (A{w}_2+e_1{b}_2)\ge e_1-{\displaystyle \frac{1}{{\tau }_3}}(\xi +e_1{ϵ}_3),\hfill \\ \hfill & (A{w}_2+e_1{b}_2)\le e_1+{\displaystyle \frac{1}{{\tau }_4}}(\xi +e_1{ϵ}_4),\hfill \\ \hfill & \xi \ge 0,\hfill \end{array}$$

(6)

where ${\tau }_1,{\tau }_2,{\tau }_3,{\tau }_4,{ϵ}_1,{ϵ}_2,{ϵ}_3,$ and ${ϵ}_4$ are non-negative parameters. Define $P=\left[\begin{array}{cc}A& e_1\end{array}\right]$, $Q=\left[\begin{array}{cc}B& e_2\end{array}\right]$. Their dual problems are as follows:

$$\begin{array}{cc}\hfill \underset{\alpha ,\lambda }{min}& {\displaystyle \frac{1}{2}}{\lambda }^{\top }Q{\left(P^{\top }P\right)}^{-1}{Q}^{\top }\lambda -{\lambda }^{\top }{e}_2(1+{\displaystyle \frac{{ϵ}_2}{{\tau }_2}})+{\alpha }^{\top }{e}_2({\displaystyle \frac{{ϵ}_1}{{\tau }_1}}+{\displaystyle \frac{{ϵ}_2}{{\tau }_2}})\hfill \\ \hfill \text{s.t.}& 0\le ({\displaystyle \frac{1}{{\tau }_1}}+{\displaystyle \frac{1}{{\tau }_2}})\alpha -{\displaystyle \frac{\lambda }{{\tau }_2}}\le c_1{e}_2,\hfill \\ \hfill & \alpha \ge 0,\alpha -\lambda \ge 0,\hfill \end{array}$$

(7)

and

$$\begin{array}{cc}\hfill \underset{\omega ,\mu }{min}& {\displaystyle \frac{1}{2}}{\mu }^{\top }P{\left(Q^{\top }Q\right)}^{-1}{P}^{\top }\mu -{\mu }^{\top }{e}_1(1+{\displaystyle \frac{{ϵ}_4}{{\tau }_4}})+{\omega }^{\top }{e}_1({\displaystyle \frac{{ϵ}_3}{{\tau }_3}}+{\displaystyle \frac{{ϵ}_4}{{\tau }_4}})\hfill \\ \hfill \text{s.t.}& 0\le ({\displaystyle \frac{1}{{\tau }_3}}+{\displaystyle \frac{1}{{\tau }_4}})\omega -{\displaystyle \frac{\mu }{{\tau }_4}}\le c_2{e}_1,\hfill \\ \hfill & \omega \ge 0,\omega -\mu \ge 0,\hfill \end{array}$$

(8)

where $\alpha ,\lambda ,\omega$, and $\mu \ge 0$ are Lagrange multipliers. After solving the QPPs, the separating hyperplanes are obtained from

$$\begin{array}{c}\hfill \left[\begin{array}{c}{w}_1\\ b_1\end{array}\right]=-{\left(P^{\top }P\right)}^{-1}{Q}^{\top }\lambda ,\end{array}$$

(9)

and

$$\begin{array}{c}\hfill \left[\begin{array}{c}{w}_2\\ b_2\end{array}\right]={\left(Q^{\top }Q\right)}^{-1}{P}^{\top }\mu .\end{array}$$

(10)

The GPin-TSVM improves the SVM model by allowing nonparallel hyperplanes, helping it handle various challenges while maintaining strong performance compared to the TSVM. It uses a special loss function called the generalized pinball loss, which is better at handling noise and outliers than the original TSVM. This means that noisy data have less effect on the decision boundaries, making it a reliable choice for real-world applications. Additionally, its increased sparsity makes it easier to compute, improving its scalability.

However, as a purely supervised method, the TSVM relies on labeled data, which can be limited in practice. While effective on well-annotated datasets, the TSVM struggles in scenarios where labeling large volumes of data is costly or impractical. To address this limitation, a method called semi-supervised learning (SSL) has emerged. SSL enables the use of abundant unlabeled data to improve classifier robustness and accuracy while requiring fewer labeled examples. Next, we discuss a semi-supervised learning model based on the TSVM.

2.3. Laplacian Twin Support Vector Machine

The Lap-TSVM model [25] is formulated by integrating a semi-supervised learning framework derived from the TSVM. As mentioned above, the semi-supervised technique uses the Laplacian matrix, which finds applications in various domains, particularly in spectral graph theory and graph-based machine learning. It has properties and eigenvalues that are related to the structure and connectivity of the underlying graph. The Lap-TSVM finds a pair of nonparallel-planes as follows:

$$\begin{array}{c}\hfill x^{\top }{w}_1+b_1=0\mathrm{and}{x}^{\top }{w}_2+b_2=0,\end{array}$$

(11)

where $w_1,w_2\in R^n$ and $b_1,b_2\in R$. The primal problems of this work can be expressed as

$$\begin{array}{cc}\hfill \underset{w_1,b_1,\xi }{min}& {\displaystyle \frac{1}{2}}{\parallel A{w}_1+e_1{b}_1\parallel }^2+c_1{e}_2^{\top }\xi +c_2(\parallel w_1{\parallel }^2+b_1^2)+c_3(w_1^{\top }{M}^{\top }+e^{\top }{b}_1)L(M{w}_1+e{b}_1)\hfill \\ \hfill \text{s.t.}& -(B{w}_1+e_2{b}_1)+\xi \ge e_2,\hfill \\ \hfill & \xi \ge 0,\hfill \end{array}$$

(12)

and

$$\begin{array}{cc}\hfill \underset{w_2,b_2,\xi }{min}& {\displaystyle \frac{1}{2}}{\parallel B{w}_2+e_2{b}_2\parallel }^2+c_1{e}_1^{\top }\xi +c_2(\parallel w_2{\parallel }^2+b_2^2)+c_3(w_2^{\top }{M}^{\top }+e^{\top }{b}_2)L(M{w}_2+e{b}_2)\hfill \\ \hfill \text{s.t.}& A{w}_2+e_1{b}_2+\xi \ge e_1,\hfill \\ \hfill & \xi \ge 0.\hfill \end{array}$$

(13)

The first three terms are concepts from the TSVM. The fourth term is the Laplacian term that considers the entire dataset. Here, M is the matrix that represents both labeled and unlabeled data. L denotes the graph Laplacian, defined as $L=D-A$, where D is the diagonal matrix of vertex degrees, and A is the adjacency matrix of the graph derived from the weight matrix defined by k-nearest neighbors, expressed as follows:

$$\begin{array}{c}\hfill W_{ij}=\left\{\begin{array}{cc}\exp (-\parallel x_i-x_j{\parallel }_2^2/2{\sigma }^2),\hfill & \mathrm{if}{x}_i,x_j\mathrm{are}\mathrm{neighbors};\hfill \\ 0,\hfill & \mathrm{otherwise},\hfill \end{array}\right.\end{array}$$

(14)

where $\sigma$ is a parameter that controls the width of the Gaussian kernel, influencing the similarity measure between neighboring points. The decision function of this problem is derived from:

$$\begin{array}{c}\hfill \mathrm{class}\left(i\right)=\arg \underset{i=1,2}{min}{\displaystyle \frac{|x^{\top }{w}_i+b_i|}{\parallel w_i\parallel }},\end{array}$$

(15)

where $|.|$ is the perpendicular distance of point x to the two hyperplanes $x^{\top }{w}_1+b_1$ and $x^{\top }{w}_2+b_2$.

In summary, integrating semi-supervised learning into the TSVM framework offers the benefit of utilizing information from both labeled and unlabeled data. This can enhance model performance, particularly in situations where labeled data are limited.

3. Proposed Work

Inspired by the concepts of GPin-TSVMs and Lap-TSVMs, we developed the LapGPin-TSVM model. This extension shifts from supervised to semi-supervised learning by integrating the Laplacian regularization term.

The motivation behind our interest in semi-supervised learning is rooted in the challenges posed by relying solely on labeled data. When dealing with problems that involve the entire dataset, labeled data alone may not be sufficient to establish the most accurate nonparallel hyperplane. This limitation is clearly demonstrated in Figure 2. As stated in Figure 2a, which illustrates the distribution of the entire dataset, the solid circles represent labeled data with two colors: red for the positive class and green for the negative class. The plus symbols, both red and green, represent unlabeled data. The original GPin-TSVM, a supervised learning model, can only be trained using labeled data, as illustrated in Figure 2b. However, in the new approach, LapGPin-TSVM, where the Laplacian term is incorporated into a GPin-TSVM, the model learns from labeled and unlabeled data, as demonstrated in Figure 2c. This approach results in a more reasonable nonparallel hyperplane that better corresponds to the data distribution.

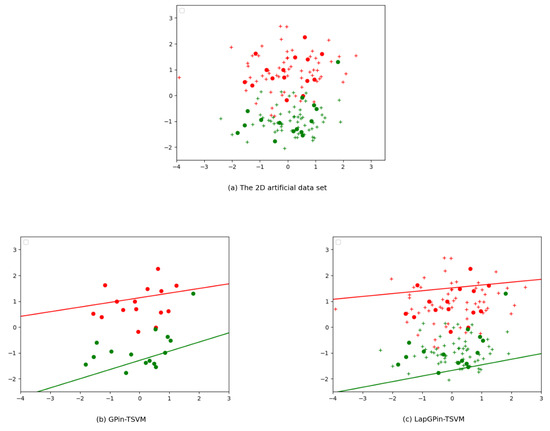
Figure 2. Visual representations of classification results on a 2D artificial dataset using the GPin-TSVM (supervised framework) and our proposed LapGPin-TSVM (semi-supervised framework), highlighting the impact of unlabeled data on the classifier. The solid circles represent labeled data, with red indicating the positive class and green indicating the negative class. The plus symbols, both red and green, represent unlabeled data.

3.1. Primal Problem

The classification task aims to define two nonparallel hyperplanes, similar to (11). We derive this by applying the frameworks of GPin-TSVM ((5) and (6)) and Lap-TSVM ((12) and (13)) to find the positive and negative hyperplanes. This leads to the following optimization problem:

$$\begin{array}{cc}\hfill \underset{w_1,b_1,\xi }{min}& {\displaystyle \frac{1}{2}}{\parallel A{w}_1+e_1{b}_1\parallel }^2+c_1{e}_2^{\top }\xi +{\displaystyle \frac{c_2}{2}}({\parallel w_1\parallel }^2+b_1^2)+{\displaystyle \frac{c_3}{2}}{(M{w}_1+e{b}_1)}^{\top }L(M{w}_1+e{b}_1)\hfill \\ \hfill \text{s.t.}& -(B{w}_1+e_2{b}_1)\ge e_2-{\displaystyle \frac{1}{{\tau }_1}}(\xi +e_2{ϵ}_1),\hfill \\ \hfill & -(B{w}_1+e_2{b}_1)\le e_2+{\displaystyle \frac{1}{{\tau }_2}}(\xi +e_2{ϵ}_2),\hfill \\ \hfill & \xi \ge 0,\hfill \end{array}$$

(16)

and

$$\begin{array}{cc}\hfill \underset{w_2,b_2,\xi }{min}& {\displaystyle \frac{1}{2}}{\parallel B{w}_2+e_2{b}_2\parallel }^2+c_1{e}_1^{\top }{\xi }_1+{\displaystyle \frac{c_2}{2}}({\parallel w_2\parallel }^2+b_2^2)+{\displaystyle \frac{c_3}{2}}{(M{w}_2+e{b}_2)}^{\top }L(M{w}_2+e{b}_2)\hfill \\ \hfill \text{s.t.}& (A{w}_2+e_1{b}_2)\ge e_1-{\displaystyle \frac{1}{{\tau }_3}}(\xi +e_1{ϵ}_3),\hfill \\ \hfill & (A{w}_2+e_1{b}_2)\le e_1+{\displaystyle \frac{1}{{\tau }_4}}(\xi +e_1{ϵ}_4),\hfill \\ \hfill & \xi \ge 0,\hfill \end{array}$$

(17)

where $c_1,c_2,c_3$ are non-negative parameters, and ${\tau }_1,{\tau }_2,{\tau }_3,{\tau }_4,{ϵ}_1,{ϵ}_2,{ϵ}_3,{ϵ}_4\ge 0$. $e_1$ and $e_2$ are unit vectors of the appropriate size. If we set $c_2$ and $c_3$ to 0 in (16) and (17), the problems reduce to a GPin-TSVM, demonstrating that our proposed model is a generalization of the previous one.

In problem (16), the first term aims to minimize the sum of the squared distances of labeled samples to the hyperplane, while the second term represents the slack variable controlling the loss of samples by employing the concept of generalized pinball loss. The term ${\parallel w_1\parallel }^2+b_1^2$ serves as regularization to prevent ill-conditioning. The fourth term is the Laplacian regularization term, introducing a penalty for deviations from smoothness in the decision function across the data manifold. It encourages the model to respect the underlying geometric structure of the data, promoting a more coherent decision boundary.

The given minimization problems can be converted into an unconstrained optimization format by interpreting the constraint as the significance of the generalized pinball loss. This leads to the formulation of the new problem as follows:

$$\begin{array}{cc}\hfill \underset{w_1,b_1}{min}& {\displaystyle \frac{1}{2}}{\parallel A{w}_1+e_1{b}_1\parallel }^2+c_1{e}_2^{\top }{\mathcal{L}}_{{\tau }_1,{\tau }_2}^{{ϵ}_1,{ϵ}_2}\left(e_2+(B{w}_1+e_2{b}_1)\right)+c_2(\parallel w_1{\parallel }^2+b_1^2)\hfill \\ \hfill & +c_3(w_1^{\top }{M}^{\top }+e^{\top }{b}_1)L(M{w}_1+e{b}_1),\hfill \end{array}$$

(18)

and

$$\begin{array}{cc}\hfill \underset{w_2,b_2}{min}& {\displaystyle \frac{1}{2}}{\parallel B{w}_2+e_2{b}_2\parallel }^2+c_1{e}_1^{\top }{\mathcal{L}}_{{\tau }_1,{\tau }_2}^{{ϵ}_1,{ϵ}_2}\left(e_1-(A{w}_2+e_1{b}_2)\right)+c_2(\parallel w_2{\parallel }^2+b_2^2)\hfill \\ \hfill & +c_3(w_2^{\top }{M}^{\top }+e^{\top }{b}_2)L(M{w}_2+e{b}_2).\hfill \end{array}$$

(19)

These problems may yield different representations of the constrained optimization (16) and (17), but they have equivalent solutions to the original problems.

In seeking the solution to the optimization problems (16) and (17), we reformulate it into dual forms and utilize quadratic programming problems (QPPs) for resolution. This is further discussed in the next section.

3.2. Dual Problem

For considering the dual form and solving the problem, we focus on problem (16), as the computation method for problem (17) is the same. Here, we introduce Lagrange multiplier $\alpha ,\gamma ,\beta \ge 0$ and then obtain the following form:

$$\begin{array}{cc}\hfill \mathcal{L}(w_1,b_1,\xi ,\alpha ,\gamma ,\beta )=& {\displaystyle \frac{1}{2}}{\parallel A{w}_1+e_1{b}_1\parallel }^2+c_1{e}_2^{\top }\xi +{\displaystyle \frac{c_2}{2}}({\parallel w\parallel }^2+b^2)\hfill \\ \hfill & +{\displaystyle \frac{c_3}{2}}{(M{w}_1+e{b}_1)}^{\top }L(M{w}_1+e{b}_1)\hfill \\ \hfill & -{\alpha }^{\top }(-(B{w}_1+e_2{b}_1)-e_2+{\displaystyle \frac{1}{{\tau }_1}}(\xi +e_2{ϵ}_1))\hfill \\ \hfill & -{\gamma }^{\top }(e_2+{\displaystyle \frac{1}{{\tau }_2}}(\xi +e_2{ϵ}_2)+(B{w}_1+e_2{b}_1))-{\beta }^{\top }\xi .\hfill \end{array}$$

(20)

Next, we apply the KKT optimality conditions to obtain the following results:

$$\begin{array}{cc}\hfill {\displaystyle \frac{\partial \mathcal{L}}{\partial w_1}}=& A^{\top }(A{w}_1+e_1{b}_1)+c_2{w}_1+c_3{M}^{\top }L(M{w}_1+e{b}_1)+{\alpha }^{\top }B-{\gamma }^{\top }B=0,\hfill \end{array}$$

(21)

$$\begin{array}{cc}\hfill {\displaystyle \frac{\partial \mathcal{L}}{\partial b_1}}=& e_1^{\top }(A{w}_1+e_1{b}_1)+c_2{b}_1+c_3{e}^{\top }L(M{w}_1+e{b}_1)+{\alpha }^{\top }{e}_2-{\gamma }^{\top }{e}_2=0,\hfill \end{array}$$

(22)

$$\begin{array}{cc}\hfill {\displaystyle \frac{\partial \mathcal{L}}{\partial \xi }}=& c_1{e}_2-{\displaystyle \frac{\alpha }{{\tau }_1}}-{\displaystyle \frac{\gamma }{{\tau }_2}}-\beta =0,\hfill \end{array}$$

(23)

$$\begin{array}{cc}\hfill & -{\alpha }^{\top }(-(B{w}_1+e_2{b}_1)-e_2+{\displaystyle \frac{1}{{\tau }_1}}(\xi +e_2{ϵ}_1))=0,\hfill \end{array}$$

(24)

$$\begin{array}{cc}\hfill & -{\gamma }^{\top }(e_2+{\displaystyle \frac{1}{{\tau }_2}}(\xi +e_2{ϵ}_2)+(B{w}_1+e_2{b}_1))=0,\hfill \end{array}$$

(25)

$$\begin{array}{cc}\hfill & -{\beta }^{\top }\xi =0.\hfill \end{array}$$

(26)

Since $\beta \ge 0$, we have

$$\begin{array}{c}\hfill c_1{e}_2-{\displaystyle \frac{\alpha }{{\tau }_1}}-{\displaystyle \frac{\gamma }{{\tau }_2}}=\beta \ge 0,\end{array}$$

(27)

which implies that

$$\begin{array}{c}\hfill c_1{e}_2\ge {\displaystyle \frac{\alpha }{{\tau }_1}}+{\displaystyle \frac{\gamma }{{\tau }_2}}.\end{array}$$

(28)

Now, we define $F=\left[\begin{array}{cc}B& e_2\end{array}\right]$, $H=\left[\begin{array}{cc}A& e_1\end{array}\right]$, $J=\left[\begin{array}{cc}M& e\end{array}\right]$, $z_1={\left[\begin{array}{cc}{w}_1& b_1\end{array}\right]}^{\top }$ and $z_2={\left[\begin{array}{cc}{w}_2& b_2\end{array}\right]}^{\top }$. By combining (21) and (22) and using (27), the dual form of the problem (16) is obtained as follows:

$$\begin{array}{cc}\hfill \underset{\alpha ,\gamma }{min}& {\displaystyle \frac{1}{2}}{(\alpha -\gamma )}^{\top }F{(H^{\top }H+c_{2}I+c_3{J}^{\top }LJ)}^{-1}{F}^{\top }(\alpha -\gamma )+{(\alpha -\gamma )}^{\top }{e}_2(1+{\displaystyle \frac{{ϵ}_2}{{\tau }_2}})-{\alpha }^{\top }{e}_2({\displaystyle \frac{{ϵ}_1}{{\tau }_1}}+{\displaystyle \frac{{ϵ}_2}{{\tau }_2}})\hfill \\ \hfill \text{s.t.}& {\displaystyle \frac{\alpha }{{\tau }_1}}+{\displaystyle \frac{\gamma }{{\tau }_2}}\le c_1{e}_2,\hfill \\ \hfill & \alpha ,\gamma \ge 0.\hfill \end{array}$$

(29)

Since the above dual form is considered a quadratic programming problem, we solve it to find the solution. Once solved, we obtain the values of $\alpha$ and $\gamma$, and then we obtain:

$$\begin{array}{c}\hfill z_1=-{(H^{\top }H+c_{1}I+c_3{J}^{\top }LJ)}^{-1}{F}^{\top }(\alpha -\gamma ).\end{array}$$

(30)

Similar to the negative hyperplane (17), we obtain

$$\begin{array}{cc}\hfill \underset{\mu ,\eta }{min}& {\displaystyle \frac{1}{2}}{(\mu -\eta )}^{\top }H{(F^{\top }F+c_{5}I+c_6{J}^{\top }LJ)}^{-1}{H}^{\top }(\mu -\eta )+{(\mu -\eta )}^{\top }{e}_1(1+{\displaystyle \frac{{ϵ}_4}{{\tau }_4}})-{\mu }^{\top }{e}_1({\displaystyle \frac{{ϵ}_3}{{\tau }_3}}+{\displaystyle \frac{{ϵ}_4}{{\tau }_4}})\hfill \\ \hfill \text{s.t.}& {\displaystyle \frac{\mu }{{\tau }_3}}+{\displaystyle \frac{\eta }{{\tau }_4}}\le c_4{e}_1,\hfill \\ \hfill & \mu ,\eta \ge 0,\hfill \end{array}$$

(31)

where $\mu ,\eta \ge 0$ are Lagrange multipliers. The solution of this problem is

$$\begin{array}{c}\hfill z_2={(F^{\top }F+c_{5}I+c_6{J}^{\top }LJ)}^{-1}{H}^{\top }(\mu -\eta ).\end{array}$$

(32)

After acquiring the two hyperplanes, we categorize the new data sample $x_i$ using the following expression:

$$\begin{array}{c}\hfill \mathrm{class}\left(i\right)=\arg \underset{i=1,2}{min}{\displaystyle \frac{|x^{\top }{w}_i+b_i|}{\parallel w_i\parallel }}.\end{array}$$

(33)

In this context, $|.|$ represents the perpendicular distance of the data from the hyperplane. The data are assigned to the class of the hyperplane to which they have the minimum distance. The Algorithm of our proposed is shown in Algorithm 1.

Algorithm 1 LapGPin-TSVM

1: Input: Labeled data: $(x_1,y_1),\dots ,(x_l,y_l)$ where $y_i\in \{-1,+1\}$ Unlabeled data: $\left(x_{l+1}\right),\dots ,\left(x_{l+u}\right)$ Parameters: $c_1,c_2,c_3,{\tau }_1,{\tau }_2,{\tau }_3,{\tau }_4,{ϵ}_1,{ϵ}_2,{ϵ}_3,{ϵ}_4$ 2: Preprocess Data: Combine labeled and unlabeled data into matrix M Build Laplacian matrix L using a graph-based approach Split labeled data into positive class $\left(A\right)$ and negative class $\left(B\right)$ 3: Define two nonparallel hyperplanes: $$\begin{array}{c}\hfill x^{\top }{w}_1+b_1=0\mathrm{and}{x}^{\top }{w}_2+b_2=0.\end{array}$$ 4: Formulate the primal optimization problems as (16) and (17), and convert the primal problem to the dual form using Lagrange multipliers as stated in (29) and (31), respectively. 5: Solve the quadratic programming problems (29) and (31) for $\alpha ,\gamma ,\mu$, and $\eta$. 6: Compute the final separating hyperplanes by using (30) and (32): $$\begin{array}{c}\hfill z_1=-{(H^{\top }H+c_{1}I+c_3{J}^{\top }LJ)}^{-1}{F}^{\top }(\alpha -\gamma )\end{array}$$ and $$\begin{array}{c}\hfill z_2={(F^{\top }F+c_{5}I+c_6{J}^{\top }LJ)}^{-1}{H}^{\top }(\mu -\eta ).\end{array}$$ 7: Classify new data point $x_i$: Calculate the distance from $x_i$ to both hyperplanes and assign class based on the minimal distance: $$\mathrm{class}\left(i\right)=arg\underset{i=1,2}{min}{\displaystyle \frac{|x^T{w}_i+b_i|}{\parallel w_i\parallel }}$$ 8: Output: The two separating hyperplanes.

3.3. Property of the Lap-GPTSVM

Noise Insensitivity

We explore how the LapGPin-PTSVM tackles the problem of sensitivity to noise. To be concise, we concentrate on the linear case and resolve the issue presented in (18). However, it is worth noting that the same analysis is applicable to the nonlinear case. Define the generalized sign function ${\mathrm{sgn}}_{{\tau }_1,{\tau }_2}^{{ϵ}_1,{ϵ}_2}\left(u\right)$ as

$${\mathrm{sgn}}_{{\tau }_1,{\tau }_2}^{{ϵ}_1,{ϵ}_2}\left(u\right)=\left\{\begin{array}{cc}{\tau }_1\hfill & \mathrm{if}u>{\displaystyle \frac{{ϵ}_1}{{\tau }_1}},\hfill \\ [0,{\tau }_1]\hfill & \mathrm{if}u={\displaystyle \frac{{ϵ}_1}{{\tau }_1}},\hfill \\ 0\hfill & \mathrm{if}-{\displaystyle \frac{{ϵ}_2}{{\tau }_2}}<u<{\displaystyle \frac{{ϵ}_1}{{\tau }_1}},\hfill \\ [{\tau }_2,0]\hfill & \mathrm{if}u=-{\displaystyle \frac{{ϵ}_2}{{\tau }_2}},\hfill \\ -{\tau }_2\hfill & \mathrm{if}u<-{\displaystyle \frac{{ϵ}_2}{{\tau }_2}},\hfill \end{array}\right.$$

(34)

where $u=1-y(w^{\top }x+b)$, and ${\mathrm{sgn}}_{{\tau }_1,{\tau }_2}^{{ϵ}_1,{ϵ}_2}\left(u\right)$ represents the subgradient of the generalized pinball loss function. By employing the Karush–Kuhn–Tucker (KKT) optimality condition for Equation (18), we can formulate it as follows:

$$\begin{array}{c}\hfill \mathbf{0}\in c_1\sum _{i=1}^{m_2}{\mathrm{sgn}}_{{\tau }_1,{\tau }_2}^{{ϵ}_1,{ϵ}_2}(1+(w_1{x}_i^{-}+b_1))x_i^{-}+c_2{w}_1+c_3{M}^{\top }L(M{w}_1+e{b}_1)+A^{\top }(A{w}_1+e_1{b}_1).\end{array}$$

(35)

Here, $\mathbf{0}$ represents the zero vector, $x_i^{-}\in B$, and $m_2$ is the number of negative samples. Given $w_1$ and $b_1$, we can partition the index set of B into five distinct sets:

$$\begin{array}{cc}\hfill V_1^{+}& =\{i:1+(w_1^{\top }{x}_i^{-}+b_1)>{\displaystyle \frac{{ϵ}_1}{{\tau }_1}}\},\hfill \\ \hfill V_2^{+}& =\{i:1+(w_1^{\top }{x}_i^{-}+b_1)={\displaystyle \frac{{ϵ}_1}{{\tau }_1}}\},\hfill \\ \hfill V_3^{+}& =\{i:-{\displaystyle \frac{{ϵ}_2}{{\tau }_2}}<1+(w_1^{\top }{x}_i^{-}+b_1)<{\displaystyle \frac{{ϵ}_1}{{\tau }_1}}\},\hfill \\ \hfill V_4^{+}& =\{i:1+(w_1^{\top }{x}_i^{-}+b_1)=-{\displaystyle \frac{{ϵ}_2}{{\tau }_2}}\},\hfill \\ \hfill V_5^{+}& =\{i:1+(w_1^{\top }{x}_i^{-}+b_1)<-{\displaystyle \frac{{ϵ}_2}{{\tau }_2}}\},\hfill \end{array}$$

where $i\in \{1,2,3,\dots ,m_2\}$. By introducing the notation $V_1^{+},V_2^{+},V_3^{+},V_4^{+}$, and $V_5^{+}$, Equation (35) can be reformulated to assert the existence of ${\varphi }_i\in [0,{\tau }_1]$ and ${\theta }_i\in [-{\tau }_2,0]$ for which:

$$\begin{array}{cc}\hfill & {\tau }_1\sum _{i\in V_1^{+}}{x}_i^{-}+\sum _{i\in V_2^{+}}{\varphi }_i{x}_i^{-}+\sum _{i\in V_4^{+}}{\theta }_i{x}_i^{-}-{\tau }_2\sum _{i\in V_5^{+}}{x}_i^{-}+\hfill \\ \hfill & {\displaystyle \frac{1}{c_1}}{A}^{\top }(A{w}_1+e_1{b}_1)+{\displaystyle \frac{c_2}{c_1}}{w}_1+{\displaystyle \frac{c_3}{c_1}}{M}^{\top }L(M{w}_1+e{b}_1)=\mathbf{0}.\hfill \end{array}$$

(36)

As indicated in Equation (34), the samples in $V_3^{+}$ may not contribute to the improvement of $w_1$ due to the fact that the generalized sign function is zero. However, $V_3^{+}$ directly influences the sparsity of the model. It is important to note that the quantities ${ϵ}_1$ and ${ϵ}_2$ regulate the number of samples in $V_3^{+}$. As ${ϵ}_1$ and ${ϵ}_2$ approach zero, sparsity diminishes. Conversely, when ${ϵ}_1\to \infty$ and ${ϵ}_2\to \infty$, we enhance sparsity by including a greater number of samples in $V_3^{+}$.

Proposition 1.

If there exists a solution to the optimization problem (16) or (29), the following inequalities must be satisfied:

$$\begin{array}{c}\hfill -{\displaystyle \frac{1}{c_1{\tau }_1{m}_2}}[e_1^{\top }(A{w}_1+e_1{b}_1)+c_2{b}_1+c_3{e}^{\top }L(M{w}_1+e{b}_1)]\le 1,\end{array}$$

(37)

and

$$\begin{array}{c}\hfill {\displaystyle \frac{p_1}{m_2}}\le 1-{\displaystyle \frac{{\tau }_1+\frac{e_1^{\top }(A{w}_1 + e_1{b}_1) + c_2{b}_1 + c_3{e}^{\top }L(M{w}_1 + e{b}_1)}{c_1{m}_2}}{{\tau }_1+{\tau }_2}},\end{array}$$

(38)

where $p_1$ denotes the number samples in $V_1^{+}$.

Proof. 

Consider an arbitrary negative point, denoted as $x_{i_0}^{-}$, belonging to the set $V_1^{+}$. Utilizing the KKT conditions represented by equations (25) and (26), we derive that ${\beta }_{i_0}={\gamma }_{i_0}=0$. Further analysis of the KKT condition (23) leads to the conclusion that ${\alpha }_{i_0}=c_1{\tau }_1$, resulting in ${\alpha }_{i_0}-{\gamma }_{i_0}=c_1{\tau }_1$.

Define $\lambda =\alpha -\gamma$, and consequently, ${\lambda }_{i_0}=c_1{\tau }_1$. Additionally, the expression $-\left(e_1^{\top }(A{w}_1+e_1{b}_1)+c_2{b}_1+c_3{e}^{\top }L(M{w}_1+e{b}_1)\right)=p_1{c}_1{\tau }_1+{\sum }_{i\notin E_1^{+}}{\lambda }_i$ is obtained from (22).

Considering the constraints ${\alpha }_i\ge 0$ and ${\gamma }_i\ge 0$, it follows that $-c_1{\tau }_2\le {\lambda }_i\le c_1{\tau }_1$. Thus, the sum of ${\lambda }_i$ over points not in $V_1^{+}$ is given by

$$\begin{array}{c}\hfill \sum _{i\notin V_1^{+}}{\lambda }_i=-[e_1^{\top }(A{w}_1+e_1{b}_1)+c_2{b}_1+c_3{e}^{\top }L(M{w}_1+e{b}_1)]-p_1{c}_1{\tau }_1.\end{array}$$

(39)

Consequently, we establish that $-c_1{\tau }_2\le {\displaystyle \frac{{\sum }_{i\notin V_1^{+}}{\lambda }_i}{m_2-p_1}}\le c_1{\tau }_1$. This leads to the inequality:

$$\begin{array}{c}\hfill -[e_1^{\top }(A{w}_1+e_1{b}_1)+c_2{b}_1+c_3{e}^{\top }L(M{w}_1+e{b}_1)]-(m_2-p_1)c_1{\tau }_1\le p_1{c}_1{\tau }_1,\end{array}$$

(40)

and

$$\begin{array}{c}\hfill p_1{c}_1{\tau }_1\le -[e_1^{\top }(A{w}_1+e_1{b}_1)+c_2{b}_1+c_3{e}^{\top }L(M{w}_1+e{b}_1)]+(m_2-p_1)c_1{\tau }_1.\end{array}$$

(41)

This completes the proof of our argument. □

When analyzing the aforementioned proposition, we find that the values of ${\tau }_1,{\tau }_2$ affect the number of samples in the set $V_1^{+}$. Decreasing the ${\tau }_1,{\tau }_2$ values results in fewer members in $V_1^{+}$, causing the decision boundary to be more sensitive to noise. Conversely, increasing the ${\tau }_1,{\tau }_2$ values make the decision boundary less sensitive to noise. Additionally, there is a term related to the graph-based approach, namely, the Laplacian term. This introduces the consideration that the analysis of both labeled and unlabeled data influences the creation of the classification boundary.

In considering the negative hyperplane, we define a set in a similar manner but with respect to positive samples instead. These sets are as follows:

$$\begin{array}{cc}\hfill V_1^{-}& =\{i:1-(w_2^{\top }{x}_i^{+}+b_2)>{\displaystyle \frac{{ϵ}_3}{{\tau }_3}}\},\hfill \\ \hfill V_2^{-}& =\{i:1-(w_2^{\top }{x}_i^{+}+b_2)={\displaystyle \frac{{ϵ}_3}{{\tau }_3}}\},\hfill \\ \hfill V_3^{-}& =\{i:-{\displaystyle \frac{{ϵ}_4}{{\tau }_4}}<1-(w_2^{\top }{x}_i^{+}+b_2)<{\displaystyle \frac{{ϵ}_3}{{\tau }_3}}\},\hfill \\ \hfill V_4^{-}& =\{i:1-(w_2^{\top }{x}_i^{+}+b_2)=-{\displaystyle \frac{{ϵ}_4}{{\tau }_4}}\},\hfill \\ \hfill V_5^{-}& =\{i:1-(w_2^{\top }{x}_i^{+}+b_2)<-{\displaystyle \frac{{ϵ}_4}{{\tau }_4}}\},\hfill \end{array}$$

where $i\in \{1,2,3,\dots ,m_1\}$. For the analysis, we use the same approach. Consequently, we obtain the following proposition.

Proposition 2.

If there exists a solution to the optimization problem (17) or (31), the following inequalities must be satisfied:

$$\begin{array}{c}\hfill {\displaystyle \frac{1}{c_1{\tau }_3{m}_1}}[e_2^{\top }(B{w}_2+e_2{b}_2)+c_2{b}_2+c_3{e}^{\top }L(M{w}_2+e{b}_2)]\le 1,\end{array}$$

(42)

and

$$\begin{array}{c}\hfill {\displaystyle \frac{p_2}{m_1}}\le 1-{\displaystyle \frac{{\tau }_3+\frac{e_2^{\top }(B{w}_2 + e_2{b}_2) + c_2{b}_2 + c_3{e}^{\top }L(M{w}_2 + e{b}_2)}{c_1{m}_1}}{{\tau }_3+{\tau }_4}},\end{array}$$

(43)

where $p_2$ denote the number samples in $V_1^{-}$.

The inclusion of Laplacian regularization in LapGPin-TSVM contributes to enhanced generalization and robustness, particularly in scenarios where the data exhibit intrinsic geometric properties.

4. Comparison of the Models

We compare our model with three other models: GPin-TSVM [16], Lap-TSVM [25], and Lap-PTSVM [28].

4.1. LapGPin-TSVM vs. GPin-TSVM

Both the original GPin-TSVM and the new LapGPin-TSVM find solutions using the dual problem and obtain nonparallel hyperplanes. They utilize the same generalized pinball loss function to enhance model performance. Additionally, both approaches are designed to tackle issues of sparsity and noise sensitivity. However, the GPin-TSVM operates using only labeled data, while the LapGPin-TSVM can leverage both labeled and unlabeled data. Moreover, in the LapGPin-TSVM framework, setting the third term’s coefficient $c_3$ to zero reduces the problem to a GPin-TSVM, making the LapGPin-TSVM a more generalized approach.

4.2. LapGPin-TSVM vs. Lap-TSVM

The LapGPin-TSVM and Lap-TSVM generate two nonparallel hyperplanes and solve the dual problem. They operate within a semi-supervised framework that incorporates the Laplacian term. However, there are key differences between them. The Lap-TSVM is based on the study of TSVMs and hinge loss, which does not tackle the noise sensitivity problem since this loss penalizes only misclassified data. In contrast, the LapGPin-TSVM is improved based on the GPin-TSVM, which utilizes the generalized pinball loss function, penalizing all data, even if correctly classified. This makes the LapGPin-TSVM stable for resampling and imparts noise insensitivity to the model.

4.3. LapGPin-TSVM vs. Lap-PTSVM

The LapGPin-TSVM and Lap-PTSVM generate two nonparallel hyperplanes and address the dual problem within a semi-supervised framework. They differ notably in their loss functions. The Lap-PTSVM uses a pinball loss, which penalizes deviations from a specific threshold, focusing on particular quantile issues but not necessarily handling all data points uniformly. On the other hand, the LapGPin-TSVM utilizes a generalized pinball loss, which offers a more flexible and thorough approach to penalization. This type of loss considers the entire range of errors, including those from correctly classified instances, thus boosting the model’s robustness. Consequently, the LapGPin-TSVM enhances model sparsity and offers improved generalization, making it more adaptable to various datasets and resistant to noise.

5. Numerical Experiments

In this section, the GPin-TSVM [16], Lap-TSVM [25], and Lap-PTSVM [28] are compared with the LapGPin-TSVM. We selected 13 benchmark datasets to evaluate the performance of our proposed model. A comprehensive overview of these datasets is presented in Table 1. A Grid Search was employed to explore a range of hyperparameters. We fine-tuned the parameters $c_1$, $c_2$, and $c_3$ from the set $\{{10}^i,i=-5,-4,-3,-2,-1,0,1,2,3,4,5\}$, while ${\tau }_1$, ${\tau }_2$, ${\tau }_3$, ${\tau }_4$, ${ϵ}_1$, ${ϵ}_2$, ${ϵ}_3$, and ${ϵ}_4$ were selected from the range $(0,1)$. In the context of nonlinear cases, the kernel parameter $\sigma$ was tuned from the set $\{{10}^i,i=-3,-2,-1,0,1,2,3\}$.

Table 1. The detailed description of the 13 benchmark datasets.

Datasets	No. of Samples	No. of Features
Ionosphere	351	33
Bupa	345	6
Fertility	100	10
Pima	768	8
Banknote	1372	4
Monk-2	432	7
Sonar	208	60
Diabetes	769	9
Spambase	4601	57
WDBC	569	30
Australian	690	14
Heart	303	13
Specf heart	267	22

All experiments were executed in Python 3.9.5 on a Windows 10 system, utilizing an Intel(R) Core(TM) i7-4500U CPU @ 1.80 GHz 2.40 GHz. The experimental results were obtained from a 5-fold cross-validation. Our investigation focused on the model performance, emphasizing the effects of varying ratios of unlabeled data and noise. The bold type indicates the best result.

5.1. Evaluation Metrics

In addition to standard measures such as accuracy (ACC), we employed the Matthews Correlation Coefficient (MCC) as a pivotal metric for evaluating the overall classification performance of the models. It takes into account true positives ($TP$), true negatives ($TN$), false positives ($FP$), and false negatives ($FN$). The formula for MCC is as follows:

$$\begin{array}{c}\hfill \mathrm{MCC}={\displaystyle \frac{TP\times TN-FP\times FN}{\sqrt{(TP+FP)(TP+FN)(TN+FP)(TN+FN)}}}.\end{array}$$

(44)

It ranges from $-1$ to $+1$, where 1 indicates perfect prediction, 0 indicates random prediction, and −1 indicates total disagreement between predictions and actual outcomes.

5.2. Variation in Ratio of Unlabeled Data

The LapGPin-TSVM extends the GPin-TSVM by considering the incorporation of Laplacian techniques and transforming the model into a semi-supervised model. To test the performance of our model, we systematically changed the proportion of unlabeled data in the dataset. We considered ratios ranging from $20\%$ to $80\%$ of the total data. The accuracy results for both the linear and nonlinear cases (using the RBF kernel) are shown in Table 2, Table 3, Table 4 and Table 5, respectively. Each table corresponds to a different percentage of unlabeled data: Table 2 presents the results for $20\%$ of unlabeled data, Table 3 for $40\%$, Table 4 for $60\%$, and Table 5 for $80\%$.

Table 2. The average values of accuracy, MCC score, and time for experimenting with data containing 20% of unlabeled data on the UCI dataset.

		GPin-TSVM	Lap-TSVM	Lap-PTSVM	LapGPin-TSVM
Datasets		Acc (%)	Acc (%)	Acc (%)	Acc (%)
		MCC	MCC	MCC	MCC
		Time (s)	Time (s)	Time (s)	Time (s)
Fertility	Linear	88.00 ± 5.10	88.00 ± 5.10	88.00 ± 5.10	88.00 ± 5.10
		0.0500	0.000	0.000	0.000
		0.0352	0.0361	0.0397	0.0404
	RBF	88.00 ± 4.00	88.00 ± 4.00	88.00 ± 4.00	88.00 ± 4.00
		0.0000	0.000	0.000	0.000
		0.0469	0.0421	0.0521	0.0570
Banknote	Linear	93.88 ± 1.97	98.98 ± 0.63	97.52 ± 1.43	98.03 ± 0.94
		0.8804	0.9793	0.9516	0.9607
		2.1492	0.6919	0.9516	0.9607
	RBF	100.00 ± 0.00	99.78 ± 0.18	99.85 ± 0.29	100.00 ± 0.00
		1.000	0.9956	0.9971	1.000
		2.2177	0.6225	2.6625	2.1435
Bupa	Linear	60.00 ± 3.85	68.41 ± 4.80	67.53 ± 3.50	67.25 ± 3.73
		0.8804	0.9793	0.9516	0.9607
		2.1492	0.6919	0.9516	0.9607
	RBF	68.69 ± 7.25	66.67 ± 4.80	67.53 ± 3.50	67.25 ± 3.73
		0.8804	0.9793	0.9516	0.9607
		2.1492	0.6919	0.9516	0.9607
Ionosphere	Linear	81.48 ± 3.75	88.03 ± 2.51	87.74 ± 2.35	90.88 ± 2.66
		0.6207	0.7419	0.7365	0.8040
		0.3662	0.1751	0.1499	0.1080
	RBF	89.19 ± 3.94	92.89 ± 4.21	91.18 ± 3.11	91.18 ± 2.74
		0.7709	0.8443	0.8065	0.8068
		0.1506	0.0732	0.1158	0.1205
Monk-2	Linear	79.17 ± 3.74	83.81 ± 1.98	86.35 ± 2.04	80.55 ± 2.25
		0.5914	0.6769	0.7278	0.6264
		0.1253	0.0956	0.1670	0.1221
	RBF	96.29 ± 3.71	97.22 ± 3.33	97.22 ± 3.33	97.22 ± 3.33
		0.9272	0.9464	0.9464	0.9464
		0.1726	0.0986	0.1809	0.1586
Pima	Linear	68.36 ± 2.76	75.39 ± 1.41	75.39 ± 1.41	76.95 ± 1.06
		0.2343	0.4251	0.4251	0.4687
		0.5448	0.1411	0.6538	0.4987
	RBF	72.67 ± 4.82	75.79 ± 3.06	79.97 ± 4.15	76.05 ± 4.01
		0.3663	0.4424	0.4716	0.4499
		0.5341	0.1874	0.4813	0.5510
Sonar	Linear	75.45 ± 9.58	77.86 ± 6.07	78.36 ± 6.25	77.86 ± 6.54
		0.5380	0.5585	0.5723	0.5605
		0.0632	0.0688	0.0710	0.0704
	RBF	75.45 ± 3.08	77.92 ± 6.17	79.83 ± 2.28	77.91 ± 4.79
		0.5185	0.5605	0.5955	0.5642
		0.0552	0.0546	0.0779	0.0661
Diabetes	Linear	75.39 ± 1.62	74.48 ± 2.19	77.73 ± 1.95	76.82 ± 2.11
		0.4350	0.4093	0.4928	0.4722
		0.4728	0.1441	0.6376	0.5980
	RBF	75.77 ± 2.03	76.43 ± 1.47	76.82 ± 1.63	76.95 ± 1.13
		0.4433	0.4611	0.4715	0.4744
		0.5273	0.2047	0.6880	0.5473
Spambase	Linear	84.08 ± 1.01	90.45 ± 0.91	91.32 ± 1.11	91.12 ± 0.95
		0.7106	0.8000	0.8177	0.8135
		50.0703	16.4100	61.5567	42.6016
	RBF	88.41 ± 0.97	90.30 ± 1.09	91.28 ± 0.57	91.41 ± 0.51
		0.7569	0.7971	0.8186	0.8194
		41.5564	17.3560	79.4900	70.7805
WDBC	linear	88.93 ± 1.17	92.96 ± 1.86	94.90 ± 1.52	95.78 ± 1.41
		0.7729	0.8594	0.8927	0.9106
		0.2742	0.1037	0.3075	0.2995
	RBF	93.15 ± 1.02	95.26 ± 2.57	95.26 ± 2.63	95.43 ± 2.79
		0.8597	0.8992	0.8991	0.9051
		0.2595	0.1216	0.3249	0.3304
Australian	linear	64.35 ± 3.79	85.65 ± 4.21	85.94 ± 4.36	86.09 ± 3.95
		0.3319	0.7192	0.7272	0.7265
		0.3362	0.1195	0.3587	0.3109
	RBF	67.68 ± 2.08	76.81 ± 3.67	84.20 ± 4.00	76.23 ± 1.96
		0.3676	0.5298	0.6865	0.5216
		0.3553	0.1410	0.4298	0.5042
Heart	linear	75.56 ± 5.90	81.85 ± 4.59	84.07 ± 3.01	84.81 ± 2.16
		0.5169	0.6301	0.6756	0.6905
		0.0691	0.0630	0.0919	0.0879
	RBF	79.62 ± 1.17	83.70 ± 2.46	81.48 ± 3.70	81.48 ± 4.05
		0.5923	0.6664	0.6317	0.6279
		0.1039	0.0735	0.1030	0.0836
Spect heart	linear	77.16 ± 3.16	77.53 ± 3.90	79.03 ± 3.78	79.41 ± 3.91
		0.1456	0.0212	0.0107	0.000
		0.0691	0.0630	0.0919	0.0879
	RBF	76.42 ± 4.45	77.19 ± 5.04	81.62 ± 3.92	82.01 ± 4.84
		0.0981	0.0547	0.2136	0.2701
		0.0817	0.0651	0.1078	0.1036
Win/tile/loss		22/3/1	15/4/7	13/4/9

Table 3. The average values of accuracy, MCC score, and time for experimenting with data containing 40% of unlabeled data on the UCI dataset.

		GPin-TSVM	Lap-TSVM	Lap-PTSVM	LapGPin-TSVM
Datasets		Acc (%)	Acc (%)	Acc (%)	Acc (%)
		MCC	MCC	MCC	MCC
		Time (s)	Time (s)	Time (s)	Time (s)
Fertility	Linear	79.00 ± 11.58	85.00 ± 7.75	88.00 ± 5.10	88.00 ± 5.10
		0.0111	−0.0439	0.000	0.000
		0.0339	0.0303	0.0365	0.0441
	RBF	88.00 ± 4.00	88.00 ± 4.00	88.00 ± 4.00	88.00 ± 4.00
		0.0000	0.000	0.000	0.000
		0.0376	0.0521	0.0472	0.0427
Banknote	Linear	94.31 ± 1.74	98.76 ± 0.68	97.45 ± 1.36	98.17 ± 0.73
		0.8880	0.9749	0.9502	0.9635
		1.1178	0.3627	1.1045	1.1202
	RBF	99.78 ± 0.43	99.78 ± 0.29	99.56 ± 0.42	99.85 ± 0.42
		0.9956	0.9956	0.9912	0.9971
		1.0669	0.4062	1.4074	1.1707
Bupa	Linear	62.60 ± 5.53	65.21 ± 5.50	65.22 ± 6.28	64.93 ± 6.18
		0.2042	0.2718	0.2701	0.2636
		0.0587	0.0572	0.0712	0.0680
	RBF	64.93 ± 6.82	65.70 ± 6.12	67.25 ± 5.91	66.96 ± 6.69
		0.2809	0.2990	0.3407	0.3362
		0.0694	0.0520	0.0876	0.0795
Ionosphere	Linear	82.04 ± 2.82	86.60 ± 3.36	88.03 ± 2.17	89.17 ± 4.30
		0.6305	0.7067	0.7467	0.7660
		0.1310	0.0682	0.1060	0.0849
	RBF	88.05 ± 4.60	90.04 ± 3.47	90.62 ± 3.37	88.89 ± 3.97
		0.7402	0.7798	0.7904	0.7554
		0.0838	0.0567	0.0895	0.0954
Monk-2	Linear	80.57 ± 3.85	84.73 ± 1.31	84.27 ± 2.74	84.24 ± 4.66
		0.6198	0.6928	0.6880	0.6954
		0.0999	0.0587	0.1280	0.1051
	RBF	96.75 ± 2.88	97.21 ± 3.34	97.22 ± 3.34	97.22 ± 3.34
		0.9331	0.9461	0.9464	0.9464
		0.0935	0.0848	0.1213	0.1084
Pima	Linear	68.23 ± 2.72	75.65 ± 1.16	75.91 ± 1.09	76.95 ± 1.24
		0.2272	0.4303	0.4375	0.4695
		0.2582	0.1118	0.3220	0.2599
	RBF	72.41 ± 4.14	75.66 ± 3.24	75.66 ± 4.13	75.92 ± 3.77
		0.3505	0.4328	0.4344	0.4429
		0.2719	0.1302	0.2659	0.2874
Sonar	Linear	72.62 ± 8.57	76.96 ± 10.079	79.35 ± 7.86	77.91 ± 8.48
		0.4729	0.5431	0.6057	0.5743
		0.0542	0.0434	0.0577	0.0595
	RBF	73.53 ± 7.69	75.53 ± 4.40	73.10 ± 5.53	75.47 ± 4.67
		0.4680	0.5192	0.4635	0.5154
		0.0497	0.0543	0.0677	0.0586
Diabetes	Linear	73.57 ± 1.92	73.83 ± 2.41	76.69 ± 1.37	77.08 ± 1.76
		0.3883	0.3966	0.4736	0.4801
		0.2361	0.1030	0.3358	0.3023
	RBF	74.99 ± 2.24	75.78 ± 1.98	76.30 ± 1.69	77.60 ± 2.21
		0.4218	0.4445	0.4599	0.4877
		0.2482	0.1479	0.3597	0.2975
Spambase	Linear	84.10 ± 1.36	88.82 ± 0.36	90.86 ± 1.17	90.78 ± 1.05
		0.7113	0.7656	0.8081	0.8062
		23.1552	7.7955	26.8444	20.8474
	RBF	88.21 ± 0.84	89.97 ± 0.95	91.12 ± 0.77	91.15 ± 0.69
		0.7534	0.7901	0.8135	0.8138
		20.1447	8.5742	38.3108	38.6832
WDBC	Linear	88.40 ± 2.02	93.84 ± 2.69	94.72 ± 1.48	95.78 ± 1.03
		0.7616	0.8734	0.8890	0.9099
		0.1466	0.0845	0.1730	0.1735
	RBF	93.32 ± 0.88	94.38 ± 3.53	94.38 ± 2.63	95.08 ± 2.25
		0.8627	0.8796	0.8794	0.8966
		0.1378	0.1044	0.1781	0.0065
Australian	linear	64.49 ± 3.58	85.36 ± 4.45	85.80 ± 3.57	86.09 ± 3.38
		0.3435	0.7098	0.7211	0.7217
		0.1923	0.0912	0.1931	0.2084
	RBF	69.57 ± 4.69	74.92 ± 3.26	81.88 ± 4.74	75.51 ± 1.41
		0.3791	0.4920	0.6426	0.5080
		0.1821	0.1089	0.2568	0.2597
Heart	linear	74.81 ± 8.65	80.74 ± 5.93	83.33 ± 5.10	83.33 ± 4.96
		0.5050	0.6071	0.6597	0.6610
		0.0520	0.0493	0.0818	0.0719
	RBF	77.41 ± 3.59	78.89 ± 3.43	80.37 ± 3.43	81.85 ± 2.16
		0.5667	0.5689	0.6072	0.6312
		0.0777	0.0687	0.0886	0.0817
Spect heart	linear	78.27 ± 2.26	80.16 ± 2.38	79.02 ± 4.49	79.03 ± 3.22
		0.2266	0.1670	0.0390	0.0231
		0.0604	0.0521	0.0756	0.0707
	RBF	76.43 ± 6.79	75.66 ± 4.87	80.51 ± 4.27	80.89 ± 5.62
		0.1111	−0.0399	0.2659	0.2863
		0.0638	0.0537	0.0734	0.0787
Win/tile/loss		25/1/0	19/1/6	15/3/8

Table 4. The average values of accuracy, MCC score, and time for experimenting with data containing 60% of unlabeled data on the UCI dataset.

		GPin-TSVM	Lap-TSVM	Lap-PTSVM	LapGPin-TSVM
Datasets		Acc (%)	Acc (%)	Acc (%)	Acc (%)
		MCC	MCC	MCC	MCC
		Time (s)	Time (s)	Time (s)	Time (s)
Fertility	Linear	75.00 ± 10.95	85.00 ± 8.94	86.00 ± 4.90	88.00 ± 5.10
		0.0709	0.0882	−0.0306	0.000
		0.0228	0.0355	0.0372	0.0347
	RBF	88.00 ± 4.00	88.00 ± 4.00	89.00 ± 3.74	88.00 ± 4.00
		0.0000	0.000	0.1092	0.000
		0.0277	0.0382	0.0399	0.0467
Banknote	Linear	94.31 ± 2.45	98.47 ± 0.78	97.45 ± 1.51	97.96 ± 0.94
		0.888	0.9690	0.9502	0.9591
		0.3644	0.2067	0.4249	0.4271
	RBF	99.19 ± 0.74	99.13 ± 0.91	99.71 ± 0.27	99.85 ± 0.18
		0.9838	0.9823	0.9941	0.9971
		0.3521	0.2644	0.5851	0.4778
Bupa	Linear	60.28 ± 5.53	65.21 ± 5.50	65.22 ± 6.28	64.93 ± 6.18
		0.2042	0.2718	0.2701	0.2636
		0.0587	0.0572	0.0712	0.0680
	RBF	64.64 ± 3.85	66.96 ± 2.95	67.83 ± 7.52	68.12 ± 6.54
		0.2566	0.3162	0.3405	0.3512
		0.0657	0.0506	0.0608	0.0658
Ionosphere	Linear	79.77 ± 3.57	86.61 ± 1.47	87.45 ± 3.57	87.75 ± 5.00
		0.5971	0.7098	0.7323	0.7385
		0.2376	0.0538	0.0722	0.0612
	RBF	86.05 ± 5.25	86.35 ± 6.12	86.62 ± 2.27	87.20 ± 5.83
		0.7010	0.6965	0.7054	0.7202
		0.0653	0.0560	0.0627	0.0599
Monk-2	Linear	78.71 ± 3.02	78.25 ± 3.10	78.95 ± 2.12	84.04 ± 3.13
		0.5904	0.5601	0.5752	0.6840
		0.0548	0.0504	0.0784	0.0755
	RBF	95.60 ± 2.69	97.22 ± 3.33	96.75 ± 3.24	97.22 ± 3.33
		0.9102	0.9464	0.9373	0.9464
		0.0617	0.0657	0.0878	0.0799
Pima	Linear	69.27 ± 2.35	74.99 ± 1.73	75.00 ± 1.73	77.08 ± 1.03
		0.2693	0.4188	0.4188	0.4703
		0.1095	0.0741	0.1552	0.1421
	RBF	73.32 ± 5.46	75.14 ± 3.78	75.66 ± 3.54	75.92 ± 4.19
		0.3803	0.4232	0.4336	0.4423
		0.1224	0.1209	0.1507	0.1578
Sonar	Linear	66.91 ± 12.22	74.56 ± 5.99	71.72 ± 8.78	72.68 ± 9.93
		0.3398	0.5016	0.4567	0.4740
		0.0399	0.0543	0.0481	0.0452
	RBF	66.36 ± 3.54	71.65 ± 2.61	68.75 ± 4.78	69.24 ± 8.48
		0.3353	0.4334	0.3879	0.3932
		0.0350	0.0402	0.0469	0.0461
Diabetes	Linear	73.96 ± 2.18	73.83 ± 2.18	76.17 ± 1.89	76.56 ± 2.28
		0.3983	0.3938	0.4572	0.4685
		0.1118	0.0800	0.1773	0.1562
	RBF	76.30 ± 1.99	76.69 ± 1.25	76.95 ± 2.50	77.08 ± 1.79
		0.4556	0.4695	0.4770	0.4823
		0.1293	0.1041	0.1670	0.1552
Spambase	Linear	84.60 ± 1.15	88.77 ± 1.47	90.82 ± 1.13	90.88 ± 1.01
		0.7177	0.7645	0.8069	0.8084
		7.8185	3.3341	9.7254	7.8930
	RBF	87.32 ± 0.90	89.45 ± 1.28	91.28 ± 0.71	91.02 ± 0.93
		0.7347	0.7792	0.8168	0.8113
		7.2114	3.4492	12.8823	11.6014
WDBC	Linear	85.94 ± 2.02	94.19 ± 0.89	94.73 ± 2.15	95.43 ± 1.69
		0.7110	0.8783	0.8892	0.9023
		0.1014	0.0632	0.1276	0.1188
	RBF	93.49 ± 1.05	94.38 ± 2.51	94.20 ± 2.45	94.03 ± 2.30
		0.8666	0.8806	0.8761	0.8750
		0.0735	0.0836	0.1322	0.1245
Australian	linear	65.07 ± 4.48	84.05 ± 4.85	85.22 ± 4.24	85.94 ± 4.04
		0.3513	0.6841	0.7110	0.7216
		0.1013	0.0742	0.1169	0.1065
	RBF	69.27 ± 4.68	74.78 ± 2.56	78.12 ± 4.62	73.48 ± 2.85
		0.3754	0.4888	0.5657	0.4656
		0.1071	0.0860	0.1388	0.1552
Heart	linear	72.96 ± 5.32	81.11 ± 5.90	82.96 ± 4.28	82.22 ± 5.19
		0.4608	0.6166	0.6534	0.6396
		0.0572	0.0556	0.0638	0.0525
	RBF	76.67 ± 2.51	80.00 ± 1.39	80.00 ± 0.74	80.00 ± 3.59
		0.5680	0.5952	0.6002	0.6034
		0.0587	0.0540	0.0685	0.0645
Spect heart	linear	74.89 ± 3.92	77.54 ± 2.23	78.65 ± 4.02	78.65 ± 3.47
		0.2415	0.1317	0.0952	0.0139
		0.0394	0.0378	0.0685	0.0584
	RBF	75.65 ± 3.52	77.51 ± 4.68	79.43 ± 3.94	77.18 ± 4.46
		0.0578	0.1535	0.2400	0.2137
		0.0648	0.0439	0.0552	0.0544
Win/tile/loss		25/1/0	17/2/7	18/0/8

Table 5. The average values of accuracy, MCC score, and time for experimenting with data containing 80% of unlabeled data on the UCI dataset.

		GPin-TSVM	Lap-TSVM	Lap-PTSVM	LapGPin-TSVM
Datasets		Acc (%)	Acc (%)	Acc (%)	Acc (%)
		MCC	MCC	MCC	MCC
		Time (s)	Time (s)	Time (s)	Time (s)
Fertility	Linear	50.00 ± 15.17	78.00 ± 12.08	85.00 ± 8.37	89.00 ± 4.90
		0.0140	0.0926	0.0453	0.1092
		0.0256	0.0926	0.0366	0.0274
	RBF	88.00 ± 4.00	87.00 ± 4.00	86.00 ± 5.83	88.00 ± 4.00
		0.0000	−0.0153	0.0677	0.000
		0.0268	0.0346	0.0364	0.0320
Banknote	Linear	93.88 ± 2.36	97.45 ± 0.8	97.38 ± 1.16	98.54 ± 0.73
		0.8803	0.9485	0.9487	0.9704
		0.2019	0.1419	0.1605	0.1552
	RBF	97.38 ± 1.95	98.32 ± 1.18	98.69 ± 1.56	98.84 ± 1.47
		0.9473	0.9661	0.9739	0.9768
		0.1054	0.1865	0.2345	0.2183
Bupa	Linear	63.77 ± 3.89	63.76 ± 6.01	68.12 ± 4.10	67.25 ± 2.98
		0.2306	0.2474	0.3315	0.3129
		0.0274	0.0403	0.0463	0.0411
	RBF	62.61 ± 4.79	62.90 ± 4.16	65.80 ± 4.20	66.09 ± 4.81
		0.2228	0.2718	0.3221	0.3300
		0.0270	0.0517	0.0495	0.0514
Ionosphere	Linear	78.89 ± 4.25	83.18 ± 1.95	82.89 ± 4.38	84.32 ± 5.12
		0.5896	0.6360	0.6283	0.6576
		0.0334	0.0506	0.0500	0.0377
	RBF	84.60 ± 2.95	86.34 ± 3.58	84.62 ± 2.91	88.05 ± 3.61
		0.6584	0.7010	0.6611	0.7438
		0.0378	0.0490	0.0512	0.0492
Monk-2	Linear	73.40 ± 3.79	69.93 ± 6.92	77.57 ± 5.45	79.17 ± 1.53
		0.4962	0.3903	0.5516	0.5878
		0.0377	0.0385	0.0560	0.0480
	RBF	92.60 ± 2.14	94.90 ± 3.34	94.90 ± 3.34	97.21 ± 3.86
		0.8542	0.8986	0.8993	0.9470
		0.0362	0.0502	0.0541	0.0591
Pima	Linear	68.36 ± 2.00	74.74 ± 3.09	75.13 ± 3.19	76.43 ± 1.27
		0.2287	0.4141	0.4251	0.4556
		0.0534	0.0570	0.0791	0.0822
	RBF	73.45 ± 4.57	75.27 ± 3.04	75.14 ± 3.08	76.18 ± 3.03
		0.3814	0.4227	0.4237	0.4487
		0.0553	0.0840	0.0970	0.0982
Sonar	Linear	65.38 ± 6.91	68.79 ± 4.80	67.31 ± 5.41	67.31 ± 5.58
		0.3085	0.3804	0.3613	0.3613
		0.0313	0.0463	0.0401	0.0396
	RBF	61.56 ± 4.83	66.89 ± 6.01	61.61 ± 7.61	68.39 ± 10.48
		0.2221	0.3369	0.2459	0.3813
		0.0301	0.0522	0.0418	0.0399
Diabetes	Linear	73.18 ± 3.03	74.74 ± 1.88	77.47 ± 2.63	77.21 ± 2.76
		0.3766	0.4123	0.4829	0.4801
		0.0540	0.0817	0.0895	0.0881
	RBF	74.22 ± 1.74	75.40 ± 3.41	74.48 ± 2.61	75.66 ± 3.61
		0.4023	0.4462	0.4327	0.4449
		0.0606	0.0843	0.1097	0.0968
Spambase	Linear	85.25 ± 1.74	88.54 ± 1.58	91.16 ± 1.35	91.28 ± 1.21
		0.7233	0.7598	0.8142	0.8165
		1.1479	1.2968	2.3394	2.1206
	RBF	86.12 ± 1.70	88.17 ± 1.46	90.38 ± 1.23	90.58 ± 1.07
		0.7104	0.7510	0.7980	0.8020
		1.3286	1.3474	2.7166	2.6171
WDBC	Linear	81.55 ± 3.44	83.13 ± 7.10	93.32 ± 1.07	94.02 ± 1.71
		0.6239	0.6379	0.8574	0.8727
		0.0446	0.0541	0.0696	0.0700
	RBF	91.73 ± 3.27	92.80 ± 2.67	91.57 ± 2.10	92.97 ± 2.47
		0.8373	0.8495	0.8221	0.8501
		0.0595	0.0636	0.0850	0.0752
Australian	linear	63.91 ± 1.41	84.20 ± 3.34	85.22 ± 4.04	85.80 ± 3.54
		0.3266	0.6861	0.7056	0.7132
		0.0516	0.0556	0.0841	0.0782
	RBF	64.05 ± 3.02	71.45 ± 2.65	68.41 ± 3.85	70.00 ± 3.32
		0.2872	0.4249	0.3608	0.3944
		0.0514	0.0701	0.0926	0.0932
Heart	linear	62.22 ± 10.70	75.19 ± 7.64	73.33 ± 8.96	76.30 ± 6.13
		0.2552	0.5033	0.4636	0.5198
		0.0341	0.0432	0.0458	0.0492
	RBF	70.37 ± 5.61	78.15 ± 1.38	80.00 ± 2.15	80.74 ± 2.77
		0.4747	0.5570	0.5981	0.6141
		0.0458	0.0553	0.0569	0.0553
Spect heart	linear	62.94 ± 7.16	65.51 ± 5.16	77.15 ± 4.36	79.04 ± 4.45
		0.1669	0.1130	0.0525	0.0792
		0.0373	0.0412	0.0503	0.0518
	RBF	64.88 ± 10.93	58.43 ± 6.85	70.04 ± 2.59	69.66 ± 3.21
		0.1066	0.1136	0.2132	0.2100
		0.0290	0.0411	0.0455	0.0384
Win/tile/loss		25/1/0	24/0/2	23/0/3

We present the win/tie/loss count for accuracy in the last column of each table. To provide a clearer view, Figure 3 illustrates the results for each percentage of unlabeled data. Each graph represents 26 cases, showing that our proposed model achieved more wins than the others. In some cases, with 60% and 80% unlabeled data, there were no ties or losses. The average rank of accuracy and MCC score of all cases was computed and is shown in Table 6. Here, ranks were assigned by ordering the values in ascending order, then the smallest values as rank 1. Thus, a higher average rank generally indicated better performance.

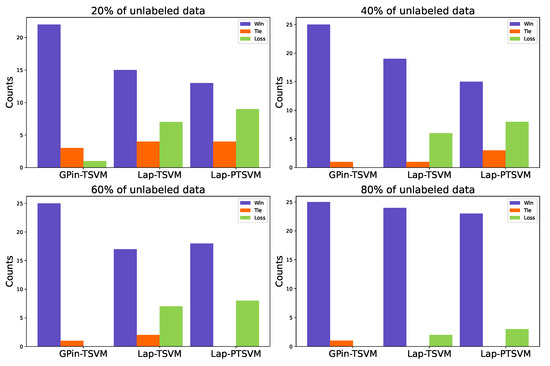
Figure 3. The count of wins, ties, and losses for accuracy at each percentage of unlabeled data is shown. If there is no color, it means the value is 0.

Table 6. Average rank of all methods when considering different ratios of unlabeled data.

Model	Mean Rank of Accuracy		Mean Rank of MCC
	Linear	Nonlinear	Linear	Nonlinear
GPin-TSVM	1.44	1.37	1.31	1.30
Lap-TSVM	2.38	2.43	2.44	2.42
Lap-PTSVM	3.05	2.85	2.84	2.89
LapGPin-TSVM	3.45	3.38	3.28	3.38

It can be observed that in almost every case where the percentage of unlabeled data increased, the GPin-TSVM method exhibited lower accuracy compared to other methods as stated in Figure 4. The MCC score for this method consistently yielded results in the same direction showing in Figure 5. This is because this method is a supervised learning approach that builds a classifier using only labeled data.

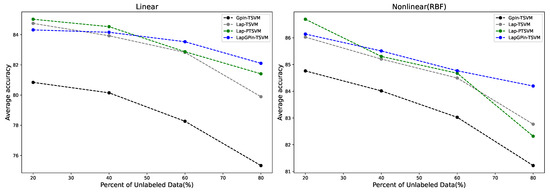
Figure 4. Comparison of average accuracy in linear and nonlinear (RBF) cases across different percentages of unlabeled data.

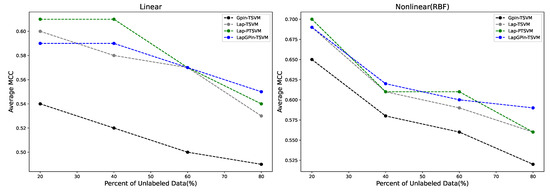
Figure 5. Comparison of average MCC in linear and nonlinear (RBF) cases across different percentages of unlabeled data.

From Figure 4, in the linear case, the GPin-TSVM, Lap-TSVM, Lap-PTSVM, and LapGPin-TSVM were evaluated as the percentage of unlabeled data increased from 20% to 80%. Initially, the Lap-PTSVM performed better with lower percentages of unlabeled data (20%) but dropped in accuracy as the percentage increases. The LapGPin-TSVM, on the other hand, started strong and maintained relatively stable performance, particularly as the percentage increased, indicating its robustness in handling larger proportions of unlabeled data. The Lap-TSVM also showed consistent performance, though with a slight downward trend as the quantity of unlabeled data increased.

In the nonlinear case using an RBF kernel, all methods generally performed better than in the linear case. The LapGPin-TSVM maintained the highest accuracy levels, even as the percentage of unlabeled data reached 80%, demonstrating its adaptability and superior performance in nonlinear cases.

As shown in Table 2, it is evident that our method outperformed others in both linear and nonlinear cases on WDBC, Heart, and Specf heart data. However, for Sonar, Bupa and Monk-2 data, our method exhibited lower accuracy compared to the Lap-TSVM and Lap-PTSVM. When considering the scenario where the proportion of unlabeled data was 40% of the total data in Table 3, it was observed that our method achieved the highest accuracy in Pima, Diabetes, and WDBC data. Similar to Table 4, our method continued to demonstrate the highest accuracy in both cases when considering Pima, Diabetes, Ionosphere and Monk-2 data. However, for Bupa and Specf heart data, the Lap-PTSVM achieved the highest accuracy. Additionally, in the case of Sonar data, the Lap-TSVM outperformed our approach in both cases. For Table 5, the LapGPin-TSVM outperformed most other methods, except on the Bupa, Sonar, Diabetes, Australian, and Specf heart data.

In addition to the evaluation based on accuracy, we now turn our attention to the results concerning the MCC score. In Table 2, the maximum MCC score for the nonlinear scenario in Monk-2 data was consistent across the Lap-TSVM, Lap-PTSVM, and our method, standing at 0.9464 and closely approaching 1. Furthermore, in Table 3, within the same datasets, our LapGPin-TSVM consistently outperformed in both cases, but the highest accuracy in the linear case belonged to Lap-TSVM. Notably, as indicated in Table 4, the Lap-TSVM outperformed other methods on the Sonar data. Nevertheless, our proposed method surpassed the others on the Ionosphere and Monk-2 data. These outcomes demonstrated a similar pattern to those observed in Table 5.

In conclusion, within the linear scenario, the LapGPin-TSVM showed superior performance in both accuracy and MCC, as evidenced by the values in Table 6, where it held an average rank of 3.45 for accuracy and 3.38 for MCC, while the Lap-PTSVM achieved 3.05 and 2.85, respectively. A higher average rank generally indicates better performance. Similarly, in the nonlinear case, our proposed exhibited the best performance, as highlighted by the average rank values for accuracy and MCC of 3.28 and 3.38, respectively, as presented in Table 6. This investigation put the emphasis on the ability of the LapGPin-TSVM to utilize unlabeled instances, thereby leading to enhanced generalization and adaptability of decision boundaries.

Computational Efficiency of Model

Figure 6 shows that the Lap-PTSVM had the highest average computation time across all percentages of unlabeled data, making it the most computationally demanding. This is due to its use of the pinball loss function, which reduces model sparsity and increases processing time. The LapGPin-TSVM, the second most time-consuming method, uses the generalized pinball loss function to restore sparsity. Both models also require Laplacian matrix calculations, which further increase their processing time compared to GPin-TSVM.

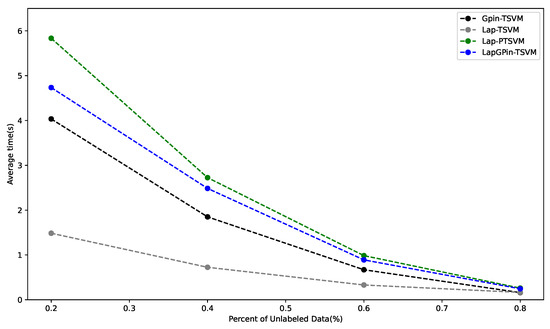
Figure 6. The graph shows the average computational time for the GPin-TSVM, Lap-TSVM, Lap-PTSVM, and LapGPin-TSVM across different unlabeled data percentages.

In contrast, the GPin-TSVM and Lap-TSVM had the lowest average times. The GPin-TSVM avoids Laplacian matrix computations and benefits from the generalized pinball loss function, which restores sparsity. Despite needing Laplacian matrix calculations, the Lap-TSVM remains efficient due to its sparsity properties. As the percentage of unlabeled data increased, all models showed reduced computational time, suggesting that larger volumes of unlabeled data are less computationally demanding to process.

5.3. Ablation Study

An ablation study, often applied in the context of neural networks [30], involves systematically altering specific components to assess their impact on a model’s performance. In our investigation, we focused on the effects of ablation on the proposed model by modifying its Laplacian regularization term. This allowed us to evaluate the influence of the modification. After analyzing all test cases with unlabeled data, we identified the optimal configuration of our proposed LapGPin-TSVM model that achieved the highest accuracy.

To assess the impact of the Laplacian regularization term on model performance, we carried out ablation experiments on the Ionosphere dataset. The goal was to examine how the inclusion of the Laplacian regularization term affected the model’s overall accuracy. In this experiment, we tested the problems (16) and (17) of the LapGPin-TSVM without the Laplacian regularization by setting the parameter $c_3=0$. The results in Table 7 reveal that the model’s performance declined when the Laplacian term was excluded. This decrease in accuracy likely resulted from information loss, as the model struggled to make effective use of the unlabeled data. However, when the Laplacian regularization was included, the performance improved notably, boosting accuracy from 80.91% to 82.91% on the Ionosphere dataset.

Table 7. Effects of the Laplacian term.

Model	Percentage of Unlabeled Data
	30%	50%	70%
LapGPin-TSVM	89.74 ± 2.11	88.04 ± 2.91	82.91 ± 1.94
LapGPin-TSVM without Laplacian term	89.74 ± 2.12	86.62 ± 4.25	80.91 ± 2.93

5.4. Variation in Ratio of Noise

Due to the fact that the LapGPin-TSVM utilizes error measurement through the computation of the generalized pinball loss, a characteristic that follows this type of loss is its ability to handle noise issues in the data. Therefore, to test the model performance regarding this feature, we conducted experiments on datasets with noise, having a zero mean and different variances of 0, 0.05, and 0.1. Here, we denote the percentage of noise in the data as r. The results are presented in Table 8 for the linear case. For the nonlinear case, the results are displayed in Table 9. Similarly, we computed and presented the average rank for all cases in Table 10.

Table 8. The mean and standard deviation of test accuracy with various amounts of noise on the UCI dataset calculated using a linear kernel.

		GPin-TSVM	Lap-TSVM	Lap-PTSVM	LapGPin-TSVM
Datasets	r	Acc (%)	Acc (%)	Acc (%)	Acc (%)
		MCC	MCC	MCC	MCC
		Time (s)	Time (s)	Time (s)	Time (s)
Fertility	0	88.00 ± 2.45	87.00 ± 2.45	88.00 ± 2.45	88.00 ± 2.45
		0.0000	−0.0153	0.0939	0.000
		0.0242	0.0297	0.0361	0.0292
	0.05	88.00 ± 2.45	88.00 ± 2.45	88.00 ± 2.45	88.00 ± 2.45
		0.0000	0.0000	0.000	0.000
		0.0233	0.0325	0.0220	0.0352
	0.1	88.00 ± 2.45	88.00 ± 2.45	88.00 ± 2.45	88.00 ± 2.45
		0.0000	0.0000	0.0658	0.000
		0.0206	0.0280	0.0311	0.0303
Banknote	0	94.39 ± 1.97	98.24 ± 1.09	98.25 ± 0.70	98.40 ± 1.04
		0.8916	0.9654	0.9650	0.9675
		0.1121	0.1076	0.1505	0.1667
	0.05	94.32 ± 1.95	98.24 ± 1.90	98.47 ± 0.70	98.54 ± 1.03
		0.8903	0.9654	0.9694	0.9706
		0.1027	0.1073	0.1612	0.1706
	0.1	94.46 ± 2.24	98.25 ± 1.09	98.32 ± 0.67	98.54 ± 0.46
		0.8933	0.9654	0.9664	0.9705
		0.111	0.1230	0.1597	0.1648
Bupa	0	63.48 ± 3.23	66.09 ± 4.36	67.25 ± 4.82	67.54 ± 4.45
		0.2176	0.2774	0.3014	0.3193
		0.0346	0.0365	0.0509	0.0433
	0.05	64.35 ± 2.68	66.09 ± 3.50	67.54 ± 4.73	68.41 ± 4.88
		0.2387	0.2796	0.3080	0.3409
		0.0260	0.0372	0.0505	0.0439
	0.1	64.05 ± 2.65	66.09 ± 3.95	66.67 ± 4.93	68.12 ± 4.39
		0.2322	0.2779	0.2896	0.3341
		0.0531	0.0406	0.0516	0.0424
Ionosphere	0	84.03 ± 8.07	86.03 ± 2.34	85.74 ± 5.29	83.75 ± 2.82
		0.6499	0.7039	0.6901	0.6510
		0.0352	0.0402	0.0546	0.0515
	0.05	81.18 ± 4.77	84.33 ± 0.91	84.33 ± 1.60	85.76 ± 1.23
		0.5865	0.6603	0.6608	0.6962
		0.0381	0.0494	0.0510	0.0540
	0.1	79.49 ± 4.99	84.33 ± 1.80	84.33 ± 1.60	85.75 ± 1.59
		0.5515	0.6542	0.6612	0.6909
		0.0383	0.0404	0.0520	0.0437
Monk-2	0	79.19 ± 6.15	78.95 ± 4.38	78.50 ± 6.45	80.11 ± 5.23
		0.5845	0.5771	0.5712	0.5987
		0.0413	0.0507	0.0828	0.0962
	0.05	78.96 ± 5.39	79.18 ± 4.71	79.43 ± 6.36	80.34 ± 4.93
		0.5788	0.5798	0.5894	0.6044
		0.0443	0.0473	0.0880	0.0663
	0.1	78.26 ± 6.22	78.72 ± 4.55	78.96 ± 6.41	79.41 ± 5.01
		0.5613	0.5702	0.5812	0.5860
		0.0347	0.0503	0.0566	0.0705
Pima	0	75.78 ± 1.29	77.60 ± 1.48	77.73 ± 0.77	77.60 ± 1.58
		0.4385	0.4821	0.4867	0.4843
		0.0699	0.0796	0.0970	0.0863
	0.05	76.30 ± 1.48	77.99 ± 1.78	78.38 ± 1.27	77.60 ± 1.96
		0.4535	0.4923	0.5026	0.4831
		0.0624	0.0671	0.0908	0.0920
	0.1	76.18 ± 1.92	76.82 ± 1.46	77.73 ± 1.28	78.00 ± 1.11
		0.4501	0.4644	0.4844	0.4929
		0.0609	0.0679	0.1022	0.0910
Sonar	0	66.40 ± 5.56	70.66 ± 2.92	74.02 ± 7.29	73.05 ± 4.79
		0.3387	0.4221	0.4811	0.4678
		0.0340	0.0461	0.0429	0.0419
	0.05	64.38 ± 7.85	71.14 ± 4.61	71.13 ± 5.66	69.71 ± 3.27
		0.3085	0.4247	0.4258	0.4043
		0.0267	0.0424	0.0385	0.0404
	0.1	62.49 ± 6.59	68.75 ± 3.03	68.77 ± 2.36	70.21 ± 4.79
		0.2653	0.3741	0.3811	0.4041
		0.0278	0.0421	0.0430	0.0332
Diabetes	0	75.27 ± 4.29	76.30 ± 4.66	77.22 ± 2.34	77.48 ± 2.96
		0.4240	0.4520	0.4770	0.4849
		0.0902	0.0693	0.0971	0.0985
	0.05	76.05 ± 4.03	76.56 ± 4.60	77.48 ± 3.07	78.13 ± 2.87
		0.4444	0.4584	0.4817	0.4980
		0.0681	0.0570	0.1013	0.1179
	0.1	76.31 ± 4.53	76.43 ± 4.06	76.83 ± 3.46	77.48 ± 2.88
		0.4534	0.4528	0.4679	0.4832
		0.111	0.1230	0.1597	0.1648
Spambase	0	90.36 ± 1.55	91.58 ± 1.07	90.67 ± 1.08	91.39 ± 1.32
		0.8019	0.8231	0.8039	0.8188
		2.2855	1.4991	2.6345	3.1632
	0.05	89.19 ± 1.93	91.34 ± 0.95	90.82 ± 1.10	90.47 ± 1.15
		0.7794	0.8181	0.8073	0.7999
		2.3051	1.4790	2.632	2.9123
	0.1	88.97 ± 1.51	90.30 ± 0.70	90.47 ± 0.52	89.75 ± 0.86
		0.7729	0.7961	0.8000	0.7848
		2.2058	1.4714	2.7201	2.8718
WDBC	0	85.77 ± 3.43	95.78 ± 1.29	95.95 ± 1.21	94.37 ± 1.82
		0.7086	0.9092	0.9135	0.8799
		0.0586	0.0684	0.0789	0.0738
	0.05	83.13 ± 1.48	93.15 ± 1.87	94.02 ± 2.58	94.03 ± 1.15
		0.6475	0.8525	0.8716	0.8729
		0.0539	0.0698	0.0818	0.0731
	0.1	84.01 ± 3.86	93.50 ± 2.04	94.37 ± 2.13	94.38 ± 2.12
		0.6686	0.8615	0.8804	0.8787
		0.0609	0.0679	0.0984	0.1074
win/tile/loss		26/3/1	21/2/7	19/3/8

Table 9. The mean and standard deviation of test accuracy with various amounts of noise on the UCI dataset calculated using an RBF kernel.

		GPin-TSVM	Lap-TSVM	Lap-PTSVM	LapGPin-TSVM
Datasets	r	Acc (%)	Acc (%)	Acc (%)	Acc (%)
		MCC	MCC	MCC	MCC
		Time (s)	Time (s)	Time (s)	Time (s)
Fertility	0	88.00 ± 2.45	87.00 ± 2.45	87.00 ± 2.45	88.00 ± 2.45
		0.0000	−0.0153	0.1593	0.000
		0.0243	0.0331	0.0327	0.0334
	0.05	88.00 ± 2.45	88.00 ± 2.45	88.00 ± 2.45	88.00 ± 2.45
		0.0000	0.0000	−0.0306	0.1542
		0.0239	0.0323	0.0324	0.0421
	0.1	88.00 ± 2.45	88.00 ± 2.45	87.00 ± 2.45	88.00 ± 2.45
		0.0000	0.0000	0.0501	0.000
		0.0232	0.0332	0.0332	0.0340
Banknote	0	98.90 ± 0.89	99.48 ± 0.72	99.34 ± 0.58	100.00 ± 0.00
		0.9780	0.9898	0.9868	1.000
		0.1315	0.1907	0.2853	0.2806
	0.05	98.90 ± 0.89	99.34 ± 0.99	99.42 ± 0.55	100.00 ± 0.00
		0.9780	0.9870	0.9882	1.000
		0.1447	0.2174	0.2851	0.2734
	0.1	98.76 ± 1.14	99.34 ± 0.81	99.49 ± 0.50	100.00 ± 0.00
		0.9752	0.9869	0.9897	1.000
		0.1388	0.2004	0.2735	0.2652
Bupa	0	68.11 ± 3.77	70.72 ± 3.59	70.14 ± 5.31	70.72 ± 6.37
		0.3249	0.3917	0.3823	0.3749
		0.0357	0.0387	0.0589	0.0580
	0.05	68.41 ± 4.14	70.14 ± 4.05	70.43 ± 4.98	71.01 ± 5.86
		0.3313	0.3787	0.3861	0.3848
		0.0404	0.0416	0.0571	0.0612
	0.1	68.41 ± 4.61	70.43 ± 3.12	70.72 ± 5.05	70.43 ± 4.72
		0.3312	0.3857	0.3929	0.3773
		0.0358	0.0464	0.0560	0.0624
Ionosphere	0	85.18 ± 4.93	87.47 ± 2.07	86.03 ± 3.58	87.46 ± 2.63
		0.6781	0.7332	0.6990	0.7245
		0.0412	0.0573	0.0525	0.0457
	0.05	84.03 ± 6.50	86.32 ± 1.96	87.75 ± 1.13	88.88 ± 3.45
		0.6505	0.7077	0.7413	0.7613
		0.0419	0.0502	0.0535	0.0481
	0.1	82.32 ± 3.93	85.46 ± 4.49	87.45 ± 4.84	87.46 ± 1.69
		0.6174	0.6856	0.7305	0.7266
		0.0382	0.0521	0.0478	0.0494
Monk-2	0	94.20 ± 4.53	96.05 ± 3.93	96.29 ± 3.41	96.99 ± 3.34
		0.8919	0.9216	0.9281	0.9420
		0.0404	0.0579	0.0748	0.0747
	0.05	93.52 ± 4.42	95.59 ± 3.48	96.51 ± 3.60	96.52 ± 3.21
		0.8799	0.9138	0.9323	0.9327
		0.0550	0.0584	0.0700	0.0726
	0.1	91.44 ± 3.34	95.36 ± 2.45	95.36 ± 2.66	94.21 ± 3.75
		0.8409	0.9073	0.9072	0.8912
		0.0385	0.0676	0.0715	0.0718
Pima	0	76.04 ± 2.99	76.17 ± 2.65	77.21 ± 1.71	76.56 ± 2.60
		0.4520	0.4545	0.4772	0.4624
		0.0714	0.1229	0.1462	0.1324
	0.05	76.04 ± 2.89	76.69 ± 2.33	77.21 ± 1.71	76.56 ± 2.83
		0.4526	0.4665	0.4776	0.4632
		0.0779	0.1187	0.1450	0.1418
	0.1	76.04 ± 2.71	76.30 ± 2.71	76.43 ± 1.52	76.69 ± 2.83
		0.4498	0.4756	0.4572	0.4662
		0.0639	0.1137	0.1370	0.1359
Sonar	0	68.32 ± 11.04	69.23 ± 9.27	71.21 ± 9.81	73.12 ± 6.82
		0.3671	0.3852	0.4232	0.4663
		0.0296	0.0388	0.0427	0.0405
	0.05	69.71 ± 3.23	72.13 ± 2.32	73.03 ± 7.23	71.64 ± 2.77
		0.3972	0.4496	0.4600	0.4400
		0.0285	0.0425	0.0370	0.0431
	0.1	64.91 ± 1.69	65.92 ± 7.41	67.80 ± 8.41	69.72 ± 7.30
		0.2931	0.3145	0.3564	0.3876
		0.0295	0.0427	0.0418	0.0395
Diabetes	0	76.04 ± 4.75	76.82 ± 3.53	78.12 ± 3.64	78.39 ± 4.18
		0.4445	0.4688	0.4939	0.5017
		0.0645	0.1021	0.1357	0.1281
	0.05	76.56 ± 4.45	76.69 ± 3.33	77.87 ± 4.10	78.39 ± 4.18
		0.4577	0.4632	0.4888	0.5015
		0.0669	0.0927	0.1293	0.1216
	0.1	76.69 ± 4.56	76.82 ± 3.28	78.13 ± 3.77	78.65 ± 4.70
		0.4593	0.4663	0.4958	0.5073
		0.0703	0.0914	0.1279	0.1239
Spambase	0	89.01 ± 1.38	90.04 ± 1.66	90.75 ± 1.29	90.91 ± 1.15
		0.7688	0.7905	0.8057	0.8089
		2.8210	3.9467	4.2431	3.9955
	0.05	89.06 ± 1.08	89.88 ± 1.48	90.49 ± 1.01	90.56 ± 0.62
		0.7699	0.7873	0.8003	0.8018
		2.7608	4.0191	3.9964	3.7862
	0.1	88.16 ± 0.93	89.42 ± 1.30	89.58 ± 0.99	89.43 ± 0.82
		0.7513	0.7780	0.7808	0.7776
		2.6906	3.9297	3.9392	3.6749
WDBC	0	92.99 ± 0.96	93.32 ± 1.22	93.84 ± 2.31	94.72 ± 1.78
		0.8499	0.8574	0.8680	0.8869
		0.0588	0.0681	0.0893	0.0878
	0.05	92.97 ± 0.96	93.49 ± 1.34	94.02 ± 2.34	94.99 ± 1.72
		0.8497	0.8614	0.8719	0.8907
		0.0544	0.0736	0.0817	0.0930
	0.1	93.33 ± 1.62	93.66 ± 1.32	94.02 ± 2.27	94.72 ± 1.26
		0.8572	0.8655	0.8722	0.8871
		0.0605	0.0698	0.0941	0.0885
win/tile/loss		27/3/0	23/3/4	23/1/6

Table 10. Average rank of all methods when considering different ratios of noise.

Model	Mean Rank of Accuracy		Mean Rank of MCC
	Linear	Nonlinear	Linear	Nonlinear
GPin-TSVM	1.27	1.20	1.23	1.13
Lap-TSVM	2.40	2.28	2.32	2.45
Lap-PTSVM	3.00	2.97	3.15	3.10
LapGPin-TSVM	3.33	3.55	3.30	3.32

The results are categorized into linear and nonlinear cases. For the linear case presented in Table 8, our method achieved the best performance at 70% (21 out of 30 instances). On the Fertility data, the experimental results for each model were comparable. On the Pima, Sonar, and Spambase data, our proposed loss outperformed other models. Considering the case where $r=0.05$ on the Sonar data, although the Lap-TSVM had the highest accuracy, the highest MCC score was achieved by the Lap-PTSVM. The results are shown in Figure 7.

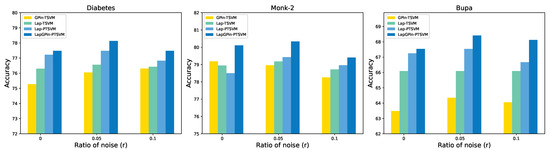
Figure 7. The accuracy on the Diabetes, Monk-2, and Bupa datasets varies with different noise ratios in the linear cases.

In Table 9, which display the results of the nonlinear case, our model achieved the highest accuracy in 23 out of 30 instances, equating to 76.67%. Similarly to the previous findings on the Fertility data, all models produced closely aligned results. In the Bupa data, considering $r=0$ and $0.05$, our model achieved the highest accuracy, but the highest MCC values belonged to the Lap-TSVM and Lap-PTSVM, respectively. Similar trends emerged on the Ionosphere and Monk-2 data when considering $r=0.1$. Some results are shown in Figure 8.

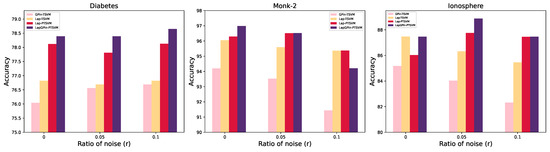
Figure 8. The accuracy on the Diabetes, Monk-2, and Ionosphere datasets varies with different noise ratios in the nonlinear cases.

Analyzing the average rank values for accuracy and MCC in Table 10, it is evident that our method attained the highest average rank. This denotes superior performance compared to other models, with the second-ranking model being the Lap-PTSVM. This outcome is attributed to the fact that the generalized pinball loss is derived from the pinball loss, which possesses the capability to handle noise. Therefore, in addition to our model being a generalized version of the Lap-PTSVM, it also exhibits better sensitivity to noise.

This comprehensively assesses robustness and performance under different levels of noise. The Laplacian regularization term in the LapGPin-TSVM improves model generalization by considering the local data structure, particularly beneficial for datasets with complex intrinsic geometry.

Furthermore, we also conducted a statistical analysis to assess the differences between the model we proposed and other models [31]. Due to the non-normal distribution of our data, we chose to employ the Wilcoxon signed-rank test [32]. This test is a non-parametric statistical test employed to compare two related samples and determine whether there is a significant difference between the paired observations in a sample, employing a significance level of 0.05 for our analysis.

In this analysis, we employed accuracy as the metric, and the results are presented in Table 11 and Table 12. Table 11 compares our model with others, incorporating data from Table 2, Table 3, Table 4 and Table 5, which present results based on the ratio of unlabeled samples. Table 12, on the other hand, extracts data from Table 8 and Table 9. As observed in both tables, the LapGPin-TSVM exhibited significant differences compared to the GPin-TSVM, Lap-TSVM, and Lap-PTSVM.

Table 11. The results of the Wilcoxon signed-rank test analysis of the models when examining changes in the ratio of unlabeled data.

Compare with LapGPin-TSVM	Negative Ranks			Positive Ranks			Test Statistics
	n	Mean Rank	Sum of Ranks	n	Mean Rank	Sum of Ranks	Ties	p-Value
Linear case
GPin-TSVM	0	NaN	0.00	51	26.00	1326.00	1	≤0.001 *
Lap-TSVM	11	13.73	151.00	39	28.82	1124.00	2	≤0.001 *
Lap-PTSVM	15	18.53	278.00	35	28.49	997.00	2	≤0.001 *
Nonlinear case
GPin-TSVM	1	11.50	11.50	46	24.27	1116.50	5	≤0.001 *
Lap-TSVM	11	22.50	247.50	36	24.46	880.50	5	≤0.001 *
Lap-PTSVM	13	30.35	394.50	34	21.57	733.50	5	0.073

* Indicates a statistically significant change.

Table 12. The results of the Wilcoxon signed-rank test analysis of the models when examining changes in the ratio of noise.

Compare with LapGPin-TSVM	Negative Ranks			Positive Ranks			Test Statistics
	n	Mean Rank	Sum of Ranks	n	Mean Rank	Sum of Ranks	Ties	p-Value
Linear case
GPin-TSVM	1	1.00	1.00	26	14.50	377.00	3	≤0.001 *
Lap-TSVM	7	12.86	90.00	21	15.05	361.00	2	0.010 *
Lap-PTSVM	8	17.06	136.50	19	12.71	241.50	3	0.207
Nonlinear case
GPin-TSVM	0	NaN	0.00	27	14.00	378.00	3	≤0.001 *
Lap-TSVM	4	7.88	31.50	23	15.07	346.50	3	≤0.001 *
Lap-PTSVM	6	15.67	94.00	23	14.83	341.00	1	0.008 *

* Indicates a statistically significant change.

5.5. Experiment on an Image Dataset

We evaluated the proposed model on a binary classification task using the CIFAR-10 dataset [33], which is a widely used dataset for image retrieval and classification, comprising 60,000 samples from ten classes: airplane, automobile, bird, cat, deer, dog, frog, horse, ship, and truck, as shown in Figure 9. Each class contains 6000 samples. For the binary classification experiments, specific class pairs were chosen: airplane vs. automobile, ship vs. truck, deer vs. shore, and dog vs. cat. In each instance, feature extraction utilized the ResNet18 architecture to enhance image representation for classification, and the percentage of unlabeled data was set at 70%.

Figure 9. An illustration of the CIFAR-10 dataset.

As shown in Table 13, it is evident that the LapGPin-TSVM outperformed most other models across various datasets, including the Lap-PTSVM and Lap-TSVM. For instance, in the “deer vs. shore” classification, the LapGPin-TSVM achieved the highest accuracy of 92.85%, surpassing the Lap-PTSVM (92.46%), Lap-TSVM (91.76%), and the supervised GPin-TSVM (91.15%). Similarly, for the “ship vs. truck” dataset, the LapGPin-TSVM led with an accuracy of 98.03%, exceeding both Lap-PTSVM and Lap-TSVM.

Table 13. Test accuracy of four models using a 5-fold cross-validation. The table includes accuracy for each fold and the average accuracy for each model.

Dataset	Model	Fold 1	Fold 2	Fold 3	Fold 4	Fold 5	Average Accuracy
Airplane vs.	GPin-TSVM	96.79	97.29	97.58	96.71	96.83	97.04 ± 0.34
Automobile	Lap-TSVM	97.96	98.46	98.25	98.33	98.54	98.31 ± 0.20
	Lap-PTSVM	98.00	98.17	98.17	97.79	97.79	97.98 ± 0.17
	LapGPin-TSVM	97.92	97.96	98.29	97.75	97.96	97.98 ± 0.18
Ship vs.	GPin-TSVM	90.50	91.29	90.46	89.08	89.38	90.14 ± 0.81
Truck	Lap-TSVM	97.21	98.42	97.33	97.67	97.33	97.59 ± 0.44
	Lap-PTSVM	97.92	98.38	97.38	97.79	97.75	97.84 ± 0.32
	LapGPin-TSVM	98.08	98.71	97.54	97.96	97.83	98.03 ± 0.39
Deer vs.	GPin-TSVM	89.92	91.67	91.54	91.75	90.88	91.15 ± 0.69
Shore	Lap-TSVM	91.30	91.88	91.75	92.83	91.04	91.76 ± 0.62
	Lap-PTSVM	92.71	92.58	92.46	92.46	92.08	92.46 ± 0.21
	LapGPin-TSVM	92.54	92.96	93.29	92.96	92.50	92.85 ± 0.29
Dog vs.	GPin-TSVM	79.30	78.75	79.17	79.96	80.88	79.61 ± 0.74
Cat	Lap-TSVM	83.05	81.71	83.00	83.04	84.25	83.01 ± 0.80
	Lap-PTSVM	85.46	83.79	85.96	85.42	85.75	85.28 ± 0.77
	LapGPin-TSVM	85.26	84.96	85.83	86.04	87.67	85.95 ± 0.94

6. Discussion

In our proposed method, the addition of the Laplacian term offers significant benefits but also introduces potential challenges. One of the primary concerns is the increase in computational complexity, as calculating the Laplacian matrix requires constructing a data graph based on similarity measures. Another challenge is related to data noise. While the Laplacian regularization helps enforce smoothness in the decision boundary, it may cause the model to overfit when dealing with noisy data, thus reducing generalization performance.

However, our method addresses these concerns by leveraging the robust properties of the generalized pinball loss function, which inherently handles noise more effectively. This ensures that despite the inclusion of the Laplacian term, the model can manage noisy data and still maintain high performance.

7. Conclusions

This study investigated the LapGPin-TSVM, a novel adaptation of the twin support vector machine (TSVM) enriched with the Laplacian graph-based technique, making it well suited for semi-supervised learning tasks. The LapGPin-TSVM improved model performance by integrating unlabeled data, leading to enhanced generalization, particularly in situations with limited labeled datasets. Our proposed model established a smooth decision boundary, enhancing robustness in the presence of noise, as guaranteed by theoretical foundations. The solution involved solving the quadratic programming problems to determine the classification’s hyperplanes. Additionally, this work considered an extended scenario, encompassing previous studies. A potential direction for future research is to develop techniques for semi-supervised learning that align with advancements in Laplacian matrix methodologies.