A Topological Approach to the Bézout’ Theorem and Its Forms
Abstract
:1. Introduction
1.1. Preliminaries
1.2. Motivations
1.3. Contributions
2. Topology and Algebraic Curves
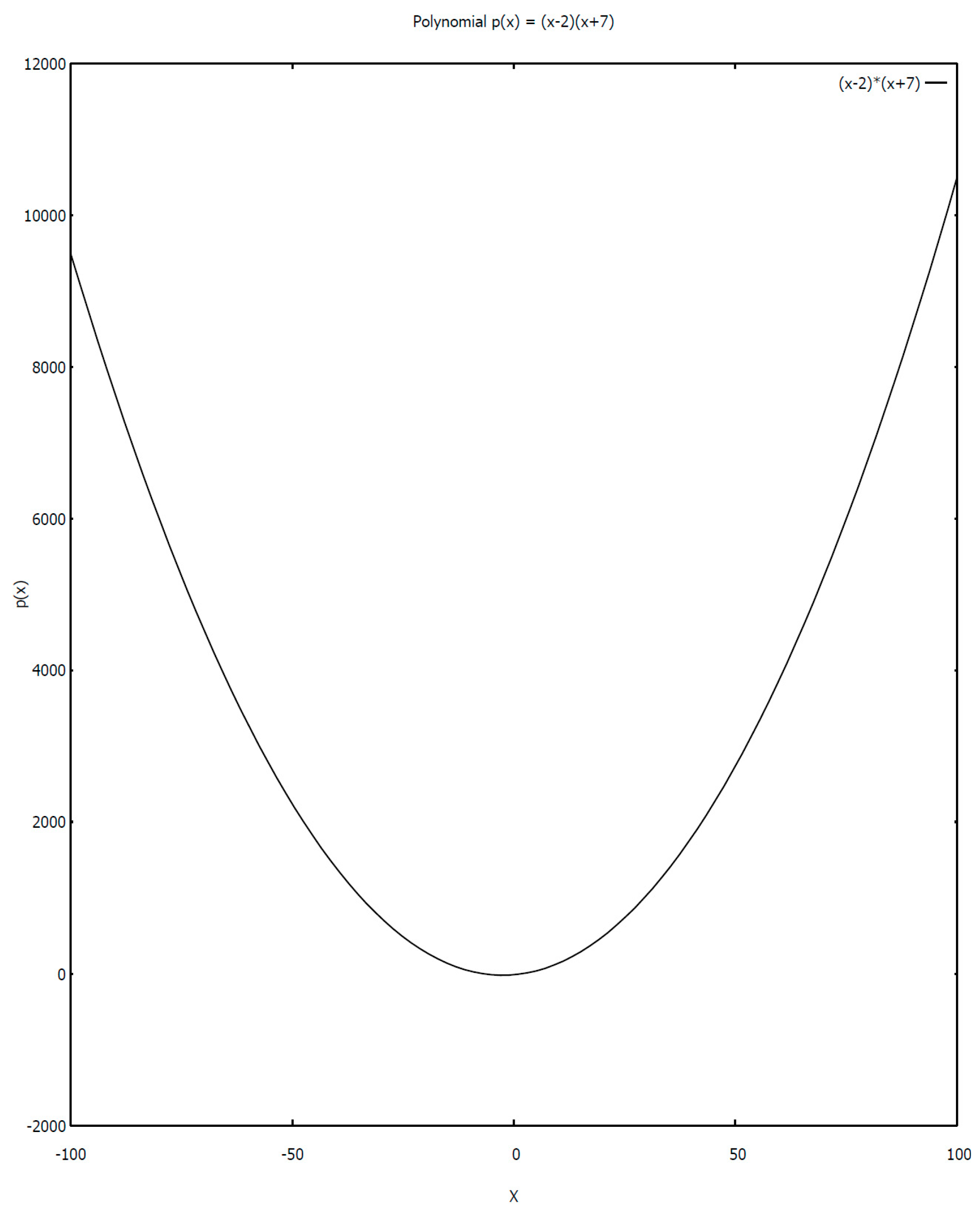
3. Topological Proof of Bézout’s Theorem
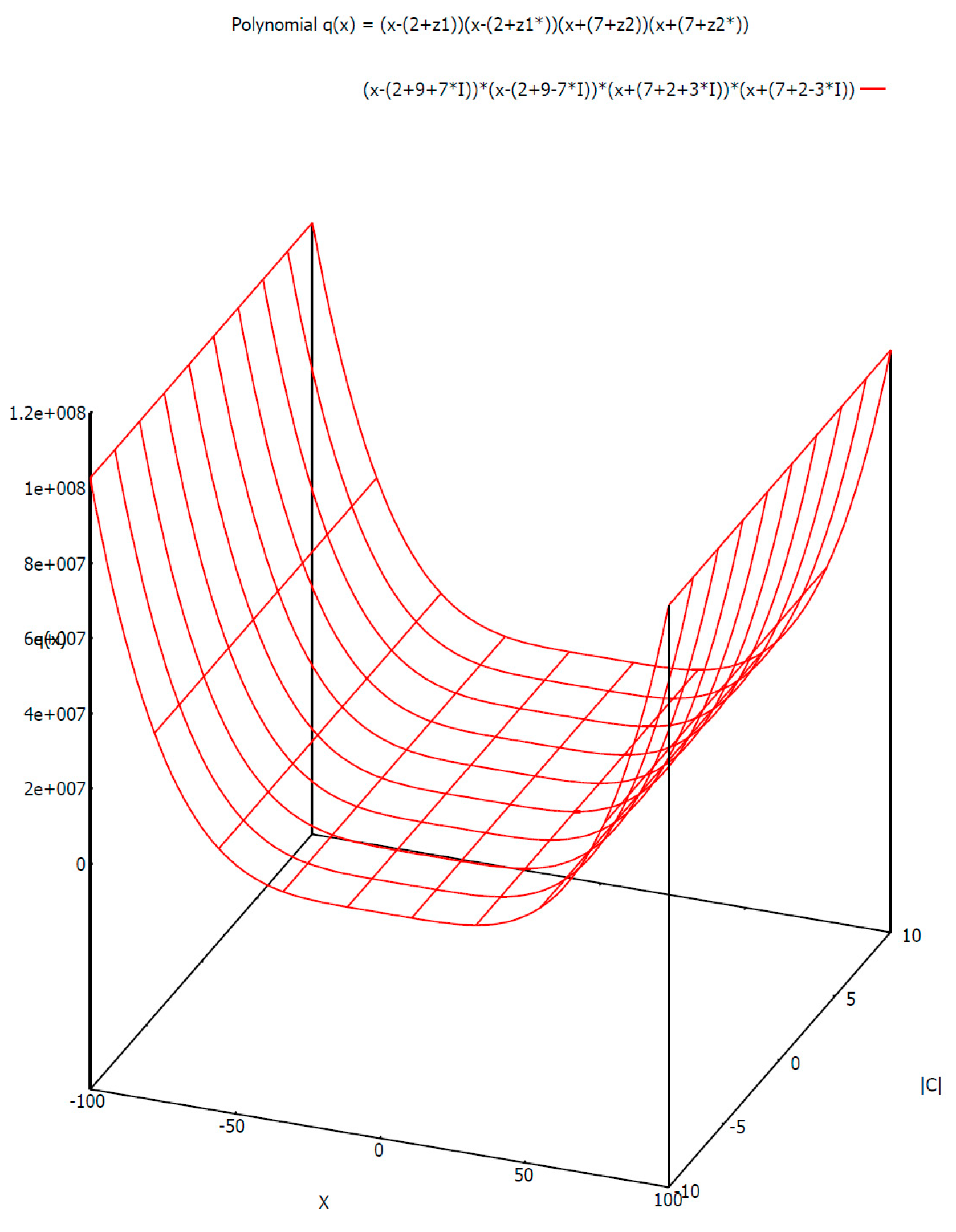
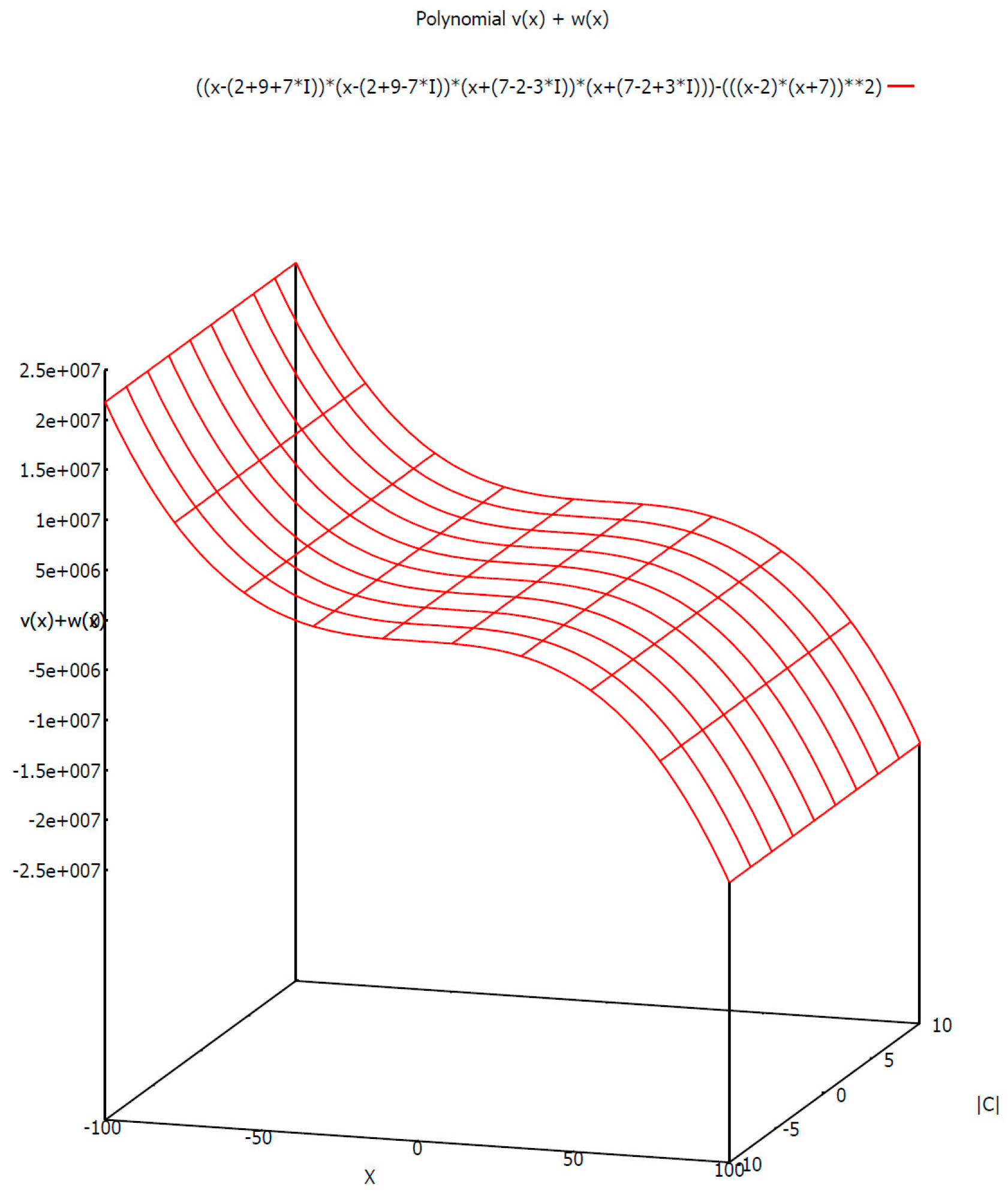
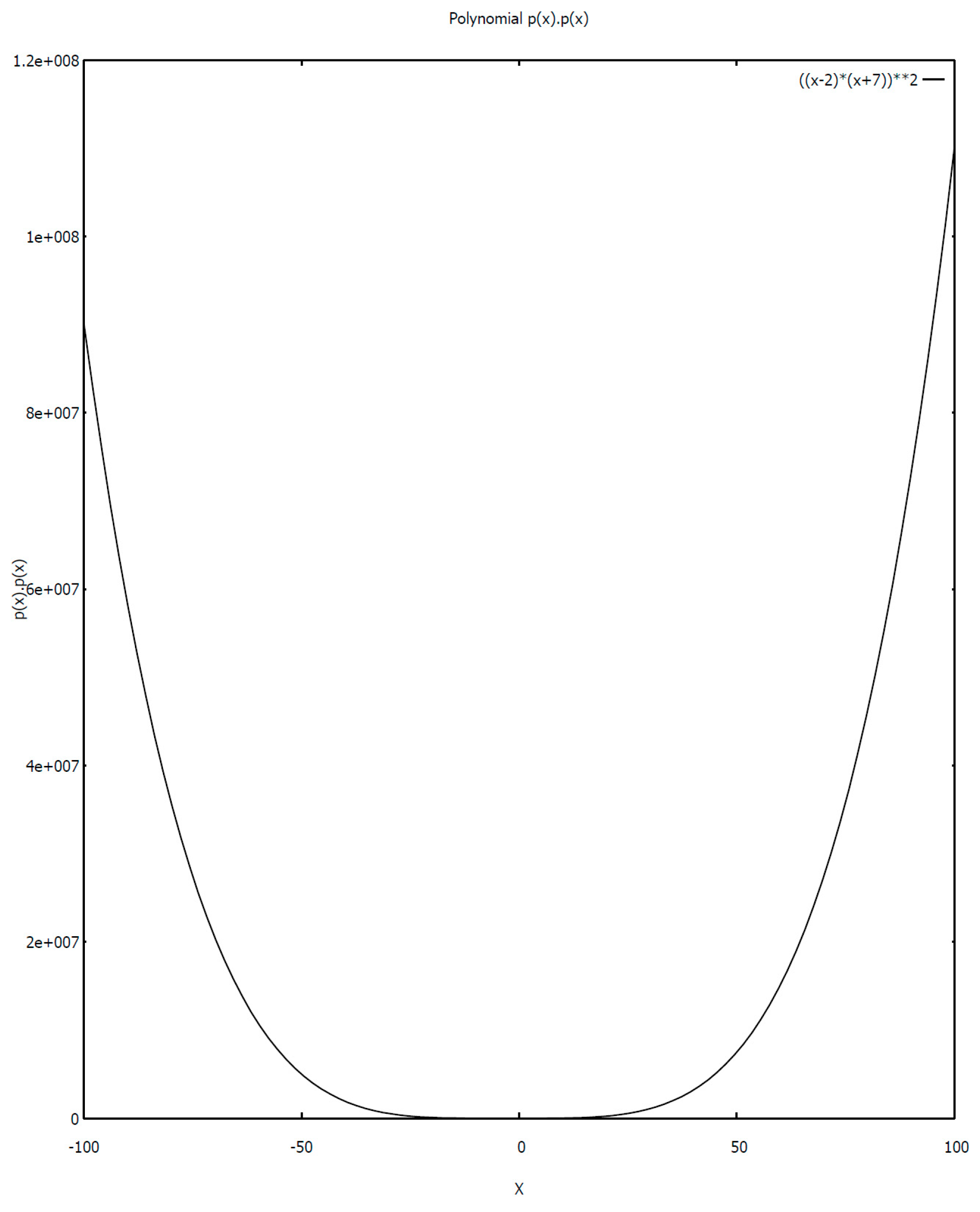
4. Complex Translations and Topological Properties
5. Applicational Aspects and Topological Comparisons
6. Conclusions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Shub, M.; Smale, S. Complexity of Bezout’s theorem. I: Geometric aspects. J. Am. Math. Soc. 1993, 6, 459–501. [Google Scholar]
- Brownawell, D. Bounds for the degrees in the Nullstellensatz. Ann. Math. 1987, 126, 577–591. [Google Scholar] [CrossRef]
- Canny, J. Generalized characteristic polynomials. J. Symb. Comput. 1990, 9, 241–250. [Google Scholar] [CrossRef]
- Wright, A. Finding all solutions to a system of polynomial equations. Math. Comp. 1985, 44, 125–133. [Google Scholar] [CrossRef]
- Zulehner, W. A simple homotopy method for determining all isolated solutions to polynomial systems. Math. Comp. 1988, 50, 167–177. [Google Scholar]
- Kunz, E. Introduction to Plane Algebraic Curves; Belshoff, R.G., Ed.; Birkhäuser: Boston, MA, USA, 2005. [Google Scholar]
- Weil, A. Foundation of Algebraic Geometry, 2nd ed.; American Mathematical Society Colloquium Publications; American Mathematical Society: New York, NY, USA, 1962; Volume 29. [Google Scholar]
- Boda, E.; Vogel, W. On system of parameters, local intersection multiplicity and Bezout’s theorem. Proc. Am. Math. Soc. 1980, 78, 1–7. [Google Scholar] [CrossRef]
- Alonso, M.E.; Lombardi, H. Local Bézout Theorem. J. Symp. Comp. 2010, 45, 975–985. [Google Scholar] [CrossRef]
- Dobbs, D. Locally Hanselian going-down domains. J. Commut. Algebra 1996, 24, 1621–1635. [Google Scholar] [CrossRef]
- Nagata, M. On the theory of Hanselian rings. Nagoya Math. J. 1953, 5, 45–57. [Google Scholar] [CrossRef]
- Campo-Montalvo, E.; Sevilla, M.F.; Benedicto, J.R.M.; Perez-Diaz, S. Some new symbolic algorithms for the computation of generalized asymptotes. Symmetry 2023, 15, 69. [Google Scholar] [CrossRef]
- Fan, X.; Luo, Z.; Zhang, J.; Zhou, X.; Jia, Q.; Luo, D. Characteristic number: Theory and its application to shape analysis. Axioms 2014, 3, 202–221. [Google Scholar] [CrossRef]
- Arnold, V.; Varchenko, A.; Goussein-Zadé, S. Singularities of Differentiable Maps (The Classification of Critical Points, Caustics and Wave Fronts); Monographs in Mathematics; Birkhauser: Boston, MA, USA, 1985; Volume I. [Google Scholar]
- Gunning, R.; Rossi, H. Analytic Functions of Several Complex Variables; Prentice-Hall Inc.: Englewood Cliffs, NJ, USA, 1965. [Google Scholar]
- Bagchi, S. Topological Properties of Braid-Paths Connected 2-Simplices in Covering Spaces under Cyclic Orientations. Symmetry 2021, 13, 2382. [Google Scholar] [CrossRef]
- Kass, J.L.; Wickelgren, K. The class of Eisenbud–Khimshiashvili–Levine is the local A1-Brouwer degree. Duke Math. J. 2019, 168, 429–469. [Google Scholar] [CrossRef]
- McKean, S. An arithmetic enrichment of Bézout’s theorem. Math. Ann. 2021, 379, 633–660. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bagchi, S. A Topological Approach to the Bézout’ Theorem and Its Forms. Symmetry 2023, 15, 1784. https://doi.org/10.3390/sym15091784
Bagchi S. A Topological Approach to the Bézout’ Theorem and Its Forms. Symmetry. 2023; 15(9):1784. https://doi.org/10.3390/sym15091784
Chicago/Turabian StyleBagchi, Susmit. 2023. "A Topological Approach to the Bézout’ Theorem and Its Forms" Symmetry 15, no. 9: 1784. https://doi.org/10.3390/sym15091784
APA StyleBagchi, S. (2023). A Topological Approach to the Bézout’ Theorem and Its Forms. Symmetry, 15(9), 1784. https://doi.org/10.3390/sym15091784




